Constancy and Variability in the Output of a Central Pattern Generator

Abstract

Experimental and corresponding modeling studies have demonstrated a twofold to fivefold variation of intrinsic and synaptic parameters across animals, whereas functional output is maintained. These studies have led to the hypothesis that correlated, compensatory changes in particular parameters can at least partially explain the biological variability in parameters. Using the leech heartbeat central pattern generator (CPG), we selected three different segmental motor neurons that fire in a functional phase progression but receive input from the same four premotor interneurons. Previous work suggested that the phase progression arises because the pattern of relative strength of the four inputs varies systematically across the segmental motor neurons. Nevertheless, there was considerable animal-to-animal variation in the absolute strengths of these connections. We tested the hypothesis that functional output is maintained in the face of variation in the absolute strength of connections because relative strengths onto particular motor neurons are maintained. We found that relative strength is not strictly maintained across animals even as functional output is maintained, and animal-to-animal variations in relative strength of particular inputs do not correlate strongly with output phase. In parallel with this variation in synaptic strength, the firing phase of the premotor inputs to these motor neurons varies considerably across individuals. We conclude that the number (four) of inputs to each motor neuron, which each vary in strength, and the phase diversity of the temporal pattern of input from the CPG diminish the influence of individual inputs. We hypothesize that each animal arrives at a unique solution for how the network produces functional output.

Introduction

To make complex movements, motor neurons must produce precise patterns of activity. For rhythmic behaviors such as locomotion and breathing, autonomously active neuronal networks called central pattern generators (CPGs) participate with sensory feedback in timing and coordinating motor neuron activity (Marder and Calabrese, 1996). Invertebrate CPGs have been intensely studied because they are composed of small numbers of identifiable neurons and are thus simpler to analyze in detail (Kristan et al., 2005; Marder et al., 2005).

Driven by systematic studies of parameter variation in conductance-based neuronal models, there is now an appreciation that a very large group of different parameter sets, each corresponding to different maximal conductances for intrinsic membrane and synaptic current, can yield very similar CPG activity that is functional (Prinz et al., 2004; Prinz, 2007; Günay et al., 2008). These modeling studies, particularly those in the crustacean stomatogastric CPGs, have galvanized experimental studies to determine the range of animal-to-animal variation in such parameters commensurate with functional output. In the stomatogastric CPGs, there is a twofold to fivefold variation of intrinsic and synaptic parameters across animals, yet functional output is maintained (Marder and Goaillard, 2006; Marder et al., 2007). Experimental and theoretical analyses have led to the hypothesis that correlated compensatory changes in particular parameters can at least partially explain the biological variability in parameters (Schulz et al., 2006, 2007; Olypher and Calabrese, 2007, 2009; Tobin et al., 2009; Grashow et al., 2010).

In this study, we took advantage of our knowledge of the leech heartbeat CPG and our ability to easily assess the strength of inhibitory connections from the CPG onto motor neurons to ask how different inputs to the same motor neuron covary across animals, whereas functional network output is maintained (Norris et al., 2006, 2007a,b). We studied three different segmental motor neurons that fire in a functional phase progression but receive input from the same four premotor interneurons (see Fig. 1). Previous work suggested that the phase progression arises because the relative strength of the four inputs varies systematically across the segmental motor neurons. Nevertheless, there is a large animal-to-animal variation in the absolute strengths of these connections (Norris et al., 2007a). Here we tested the hypothesis that functional output is maintained despite variation in the absolute strength of connections because relative strengths onto particular motor neurons are maintained across animals. What we found was both more interesting and more daunting. Relative strength is not strictly maintained across animals even as functional output is maintained, and animal-to-animal variations in relative strength of particular inputs do not correlate strongly with output phase. In parallel with this variation in synaptic strength, the firing phase of the premotor inputs to these motor neurons varies considerably across individuals. We conclude that the number (four) of inputs to each motor neuron, which each vary in strength, and the phase diversity of the temporal pattern of input from the CPG diminish the influence of the strength of individual inputs.

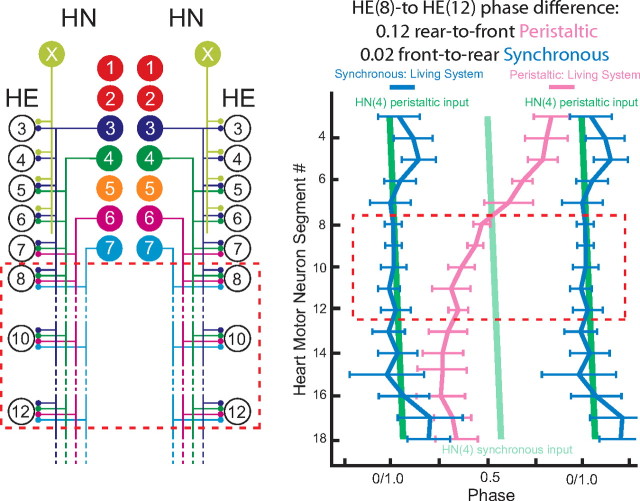
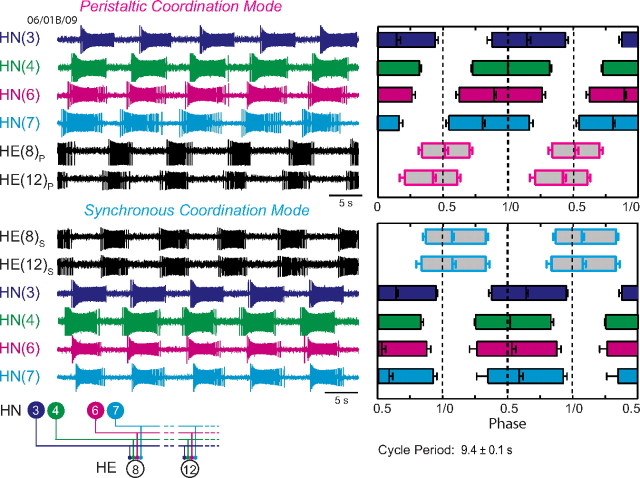
Figure 1.

Connections from the heart interneurons of the leech heartbeat CPG onto motor neurons in the first 12 midbody segmental ganglia and the bilateral output pattern of heart motor neurons. Left, Bilateral circuit diagram including all the HN interneurons of the CPG [identified HN(3), HN(4), HN(6), HN(7) and unidentified HN(X)] and their pattern of synaptic connections to HE motor neurons in HE(3)–HE(12). Large colored circles are cell bodies and associated input processes. Lines indicate cell processes, and small colored/black circles indicate inhibitory chemical synapses. Standard colors for the identified interneurons are used (for color code, see Materials and Method), e.g., lime green is used for the X interneuron. Right, Simplified composite phase diagram showing the average ± SD phase of heart motor neuron output in the living system for both peristaltic and synchronous coordination. Data are replotted from Norris et al. (2007b) and represent averages from n = 61 different preparations. The bilateral absolute phase of each segmental motor neuron with the peristaltic HN(4) interneuron as the phase reference is shown. Two synchronous (blue) and one peristaltic (pink) phase curves are shown. The phase of the peristaltic HN(4) interneuron is indicated with a slanted green straight line, and the phase the corresponding synchronous HN(4) interneuron is indicated with a slanted light green straight line. The slopes of these lines reflect the conduction delays from segment to segment. In this study, we focused on the HE(8)–HE(12) motor neurons, and their representations are bordered by a red dashed line in each panel.

Materials and Methods

Animals and solutions.

Leeches (Hirudo sp.) were obtained from commercial suppliers (Leeches USA and Biopharm) and maintained in artificial pond water at 15°C. After the animals were anesthetized in ice, they were dissected in cold saline to prepare chains of ganglia consisting of the head brain to at least midbody ganglion 15 for recording the heart interneuron activity rhythm and the IPSC strength pattern in heart motor neurons. The preparations were pinned (ventral surface up) in 60 mm Petri dishes lined with Sylgard (Dow Corning). Ganglia in which heart interneurons or heart motor neurons were to be recorded were desheathed using fine scissors or microscalpels. The preparation was superfused continuously with normal leech saline containing the following (in mm): 115 NaCl, 4 KCl, 1.8 CaCl₂, 10 glucose, and 10 HEPES buffer, adjusted to pH 7.4 with NaOH (at 1–2 ml/min; bath volume of 6–8 ml). Heart motor neurons and interneurons were identified based on soma size, soma location in the ganglion, and ultimately identified by their characteristic bursting activity (see Fig. 3).

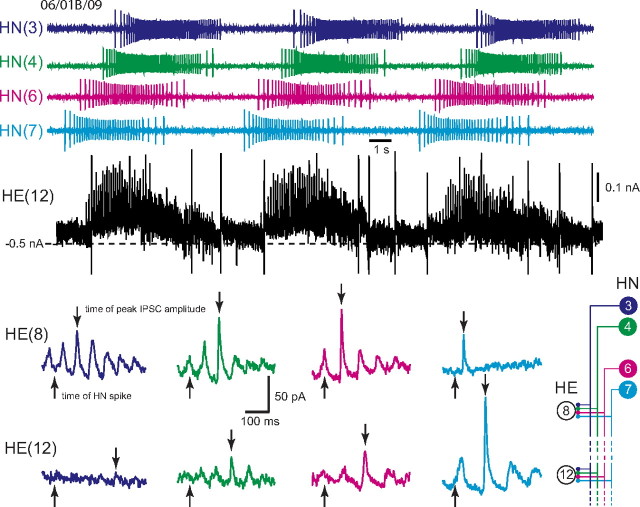
Figure 3.

Determining the absolute and relative synaptic strength of each input to a heart motor neuron. In the top, an HE(12) motor neuron was recorded in voltage clamp (holding potential, −45 mV) simultaneously with extracellular recording from four ipsilateral premotor heart interneurons, HN(3), HN(4), HN(6), and HN(7). HN spikes from 11 bursts (including the ones illustrated) from each interneuron were used to generate the spike-triggered averages of IPSCs in the HE(12) motor neuron, and subsequently similar recordings were used to generate the spike-triggered averages of IPSCs for the HE(8) motor neuron in the same preparation. Upward arrows indicate the time of the triggering HN spike, and the downward arrows indicate the peak of the averaged IPSC used to measure amplitude: standard colors identify each heart interneuron and associated spike-triggered average IPSC. Iconic unilateral circuit diagram (bottom right) identifies the recorded neurons. Preparations are specified by the day on which they were recorded: letters accompany the day designation if more than one preparation was recorded on that day.

Extracellular and intracellular recording techniques.

For intracellular voltage and voltage-clamp recordings from heart motor neurons, we used sharp intracellular electrodes (∼20–30 MΩ filled with 2 m KAc, 20 mm KCl) following the methods described by Norris et al. (2007a,b). Briefly, intracellular recordings were performed using an Axoclamp-2B amplifier (Molecular Devices) operating in discontinuous current-clamp or discontinuous single-electrode voltage-clamp mode with a sample rate of 2.5–2.8 kHz. The electrode potential was monitored to ensure that it settled during each sample cycle. Output bandwidth was 0.3 kHz. Voltage-clamp gain was 0.8–2.0 nA/mV. The voltage-clamp holding potential for recording spontaneous IPSCs in motor neurons was −45 mV in all experiments. At the end of each experiment, the electrode was withdrawn from the motor neuron, and, except in one case, the electrode potential was within ±5 mV of ground. Thus, holding potentials were normally accurate within ±5 mV.

For extracellular recordings from heart interneurons and heart motor neurons, we used suction electrodes filled with normal leech saline. Electrodes were pulled on a Flaming/Brown micropipette puller (P-97; Sutter Instruments) from borosilicate glass (1 mm outer diameter, 0.75 mm inner diameter; A-M Systems) and placed in a suction electrode holder (E series; Warner Instruments). To ensure a tight fit between the cell and electrode, the electrode tips had a final inner diameter of ∼20 μm for interneurons and of ∼30 μm for motor neurons, approximately the diameter of heart interneuron/motor neuron somata, respectively. The electrode tip was brought in contact with the cell body, and light suction was applied using a syringe until the entire cell body was inside the electrode. Extracellular signals were monitored with a differential alternating current amplifier (model 1700; A-M Systems) at a gain of 1000 with the low- and high-frequency cutoff set at 100 and 1000 Hz, respectively. Noise was reduced with a 60 Hz notch filter and a second amplifier (model 410; Brownlee Precision) amplified the signal appropriately for digitization.

Data acquisition and analysis.

Data were digitized (>5 kHz sampling rate) using a digitizing board (Digi-Data 1200 Series Interface; Molecular Devices) and acquired using pClamp software (Molecular Devices) on a personal computer.

Determining the premotor heart interneuron to heart motor neuron synaptic strength and conduction delay.

To determine the strength of each heart interneuron to heart motor neuron inhibitory synaptic connection, we recorded extracellularly from all four ipsilateral premotor interneurons that connect to the ipsilateral motor neurons (HE) in HE(8)–HE(12). We then voltage clamped an ipsilateral segmental series of HE(8)–HE(12) heart motor neurons (−45 mV holding potential) one after another, recording spontaneous IPSCs. The heart motor neurons can be coordinated in two regularly alternating coordination modes, described in detail in Results, and our recordings always included multiple burst cycles usually spanning both coordination modes. Sixty-five preparations were used in these experiments: of these, (1) 22 preparations were subjected to complete analysis of the interneuron activity pattern simultaneously with the HE(10) motor neuron activity pattern by extracellular recording in both coordination modes, followed by measurement of the synaptic strength in the motor neuron in question, and (2) 12 preparations were subject to complete analysis of the interneuron activity pattern and the pattern of synaptic strengths in both the HE(8) and the HE(12) motor neurons. We used off-line spike-triggered averaging of IPSCs to determine strength. Because no significant differences were noted between coordination modes in synaptic strength in an extensive previous study (Norris et al., 2007a), we performed the analysis in the first suitable 11 bursts, in either peristaltic or synchronous coordination mode. Spike and IPSC detection/averaging were performed offline using custom-made Matlab software (MathWorks) as described previously (Norris et al., 2007a). The strength of a synaptic connection was defined as the amplitude (measured from the preceding baseline current) of the primary peak of the spike-triggered averaged IPSC derived from the spikes of a particular presynaptic heart interneuron. For each presynaptic interneuron, we used 21 spikes per burst (±10 spikes of the middle spike) of 11 bursts (except for one experiment in which we used 10 bursts). Heart interneurons 6 and 7 sometimes had fewer than 25 spikes per burst, in which case we used fewer spikes (middle spike ±5–8). In some cases, no detectable synaptic current above noise level was detectable in the spike-triggered average and the average strength for that connection in that preparation was assigned 0. All IPSCs were converted to conductances using a reversal potential of −62 mV (Angstadt and Calabrese, 1991). We also calculated the relative strength of each connection for each motor neuron. Relative strength of a connection from HN(i) was defined as the strength of the HN(i) connection divided by the sum of the strengths of the HN(3), HN(4), HN(6), and HN(7) connections in the same motor neuron. The conduction delay for each synaptic connection was determined as the time between the triggering spike and the peak of the averaged IPSC.

Determining the heart interneuron/motor neuron activity pattern and phase relations.

For analysis of extracellularly recorded spike trains to determine the heart interneuron/motor neuron activity pattern and phase relations, 34 total preparations were used, 22 in which the HE(10) motor neuron was recorded and 12 in which the HE(8) and the HE(12) motor neurons were recorded. In every case, all four premotor heart (HN) interneurons that connect to the HE(8)–HE(12) motor neurons were recorded, i.e., the ipsilateral HN(3), HN(4), HN(6), and HN(7) heart interneurons. Spike detection and phase analysis were performed offline using custom-made Matlab software (MathWorks) as described previously (Norris et al., 2007a). Briefly, spikes were detected with a discrimination window. When voltage crossed a lower threshold value but did not exceed an upper threshold, a spike event was detected and was indicated by a raster point above the spike. The upper threshold eliminated transient artifacts in the recording. To prevent multiple detection of the same spike, a refractory period (20 ms), during which spikes could not be recognized, was applied after each detected event. To ensure that all spikes were detected, the refractory period was considerably shorter than the shortest interspike interval (∼50 ms). In our recordings, heart interneuron/motor neuron spikes were easily discernable by eye because the only units present in the recording and spike amplitude remained constant over periods of 20 min to 1 h or more.

For analysis of burst characteristics, period, duty cycle, and intraburst spike frequency, spikes were grouped into bursts as follows. After an interburst interval (≥1 s) elapsed without any spikes detected, the next spike event was identified as the first spike of a burst. Subsequent spikes with interspike intervals less than the interburst interval were grouped into that burst. To eliminate the effects of occasional stray spikes in heart motor neurons and interneurons, groups of less than five spikes were not considered as bursts. In this paper, specific symbols and specific colors (when color was used) are used in some traces, graphs, and diagrams to represent heart interneurons from specific midbody ganglia: diamond/red, HN(1)/HN(2) interneurons; circle/dark blue, HN(3) interneurons; asterisk/dark green, HN(4) interneurons; open circle/orange, HN(5) interneurons; triangle/magenta, HN(6) interneurons; square/cyan, HN(7) interneurons; cross/lime green, HN(X) interneurons.

We then calculated burst period (T), phase (ϕ), and duty cycle (D) for each recorded cell. To make file size manageable in Matlab, data were reduced from the original acquisition rate to 1 kHz preserving the minima and maxima of the signals. Every effort was made to maximize the number of representative bursts analyzed within a coordination mode. Bursts were not included if the neuron showed signs of injury, had one to two cycles of disrupted patterning, or if one of the heart interneurons was no longer following 1:1 with the other heart interneurons. For this analysis, an average ± SD of 13.2 ± 2.7 cycles was used per preparation for each coordination mode with a minimum number of eight cycles used. To represent the burst period of the entire central pattern generator, the burst period of a HN(4) interneuron was determined.

Burst period was defined as the interval in seconds from middle spike to middle spike of consecutive bursts and the mean burst period (T_I) was determined for each cell (I) (interneuron or motor neuron). The unilateral phase of a given heart motor neuron (or interneuron) was defined on a cycle-by-cycle basis as the time (t) difference between the middle spike of its burst (t_I) and the middle spike of the burst of the preceding ipsilateral HN(4) heart interneuron (t₄; ipsilateral phase reference cell). The time difference was then normalized to the burst period of the ipsilateral phase reference cell and expressed as a decimal number (between 0 and 1): ϕ_I = $\left(\frac{\Delta t_{I-4}}{T_4}\right)$ . A phase of 1.0/0.0 indicated a cell with no phase difference relative to the phase reference, the ipsilateral HN(4) heart interneuron, whereas a 0.50 phase difference indicated an anti-phasic relationship. To unify phase calculations in the two different modes or in bilateral recordings, the unilateral phase calculated in the synchronous coordination mode were offset by 0.511, corresponding to the empirically measured phase difference (0.5106 ± 0.0216; n = 10) in bilateral recording between the peristaltic HN(4) interneuron (defined as 0.0 phase) and the synchronous HN(4) interneuron [i.e., the peristaltic HN(4) interneuron became the absolute phase reference] (Norris et al., 2006). All phases were expressed modulo 1 (the computing operation “a modulo n” computes the non-integer remainder left when a is divided by n). This adjustment allowed a complete assessment of motor neuron phase with respect to the HN(4) interneurons in each coordination mode in one composite phase diagram (absolute phase). To calculate the duty cycle and for the purpose of phase whisker-box diagrams, we also calculated the mean absolute phase of the first and the last spikes of the bursts, as above for the middle spike. Mean duty cycle (D) was then determined by subtracting the mean first spike phase from the mean last spike phase, adding 1, and expressing the value modulo 1. Duty cycle was thus calculated without SD and represents the fraction of the burst period occupied by the burst. The mean duty cycle for each interneuron/motor neuron was then displayed as whisker-box diagrams (normalized burst duration) in the composite phase diagrams described below.

Composite phase diagrams of motor neuron firing with respect to the HN(4) interneuron were used to illustrate phase relations between heart interneurons and heart motor neurons. A vertical line that bisects each phase box near its midpoint indicates the mean phase for each heart interneuron [the average middle spike time in a series of bursts relative to the middle spike time of the absolute phase reference cell, which is assigned 1.0/0.0 phase on the diagram, the HN(4) interneuron in the peristaltic mode]. The beginning and end of each box indicate the average time of the first and last spike, respectively, in a series of bursts relative to the middle spike time of the absolute phase reference cell. Error bars indicate the SD around the mean first, middle, and last spike in a burst.

Standard heart motor neuron ensemble model.

We compared data from our physiological experiments to a previously developed heart motor neuron ensemble model (García et al., 2008). Briefly, the motor neurons in this model were single-compartment conductance-based models and contained a minimal set of intrinsic properties (i.e., no currents responsible for postinhibitory rebound, etc.), as well as electrical coupling. Inhibitory synaptic input to model motor neurons was derived from the living system (see below) and included the synaptic dynamics (facilitation and depression) observed in the living system. The model motor neurons were hand tuned to fire tonically in the absence of synaptic inputs, as observed in the living system. In these modeling studies, we restricted our analysis to the HE(8) and HE(12) model motor neurons.

The premotor inhibitory synaptic inputs to the model motor neurons consisted of both a temporal and spatial pattern. The firing pattern of the premotor interneurons (referred to here as the temporal pattern) consisted of spike times in a time series. It was taken from 100 s of simultaneous extracellular recordings from a single preparation of the ipsilateral premotor HN(3), HN(4), HN(6), and HN(7) interneurons recorded serially in the peristaltic and synchronous coordination modes with 11 bursts of the heart interneurons for each mode (preparation 5/27B/09) (see Fig. 8). The peristaltic and synchronous input patterns were aligned to each other to create a bilateral pattern left synchronous/right peristaltic by assigning a phase of 0.0 to the middle spike of the peristaltic HN(4) burst (i.e., the absolute phase reference) and a phase of 0.51 to the middle spike of the synchronous HN(4) burst (these values represent the average side-to-side phases measured in the living system). The period of the input pattern was 7.8 s (in our 12 samples of the living system, the average period was 8.6 ± 1.2 s, with a range of 6.7–10.8 s). The temporal pattern (peristaltic and synchronous) was the same in each segment, offset by a spike-conduction delay of 20 ms per segment or 80 ms between HE(8) and HE(12) model motor neurons. Because timing information used in our temporal pattern came from data from an experimental preparation, the temporal pattern is not precisely regular and therefore the average motor neuron phases calculated in our model display a variance.

Figure 8.

Complete analysis of input and output temporal patterns and synaptic strength patterns (spatial pattern) for three different preparations from our sample of 12 (summarized in Fig. 7). Temporal patterns were determined as in Figure 6, but the two ipsilateral phase diagrams were fused into a composite for ease of presentation. The strength pattern of the inputs, determined as in Figure 3, is shown to the right of each composite phase diagram. Standard colors and symbols are used throughout. Preparations are specified by the day on which they were recorded: letters accompany the day designation if more than one preparation was recorded on that day.

The distribution of synaptic weights, expressed as maximal conductances across all segmental heart motor neurons (referred to here as the spatial pattern of synaptic strength), also came from the experiments in 12 different leech nerve cord preparations described here. For each preparation, we generated spike-triggered averages of the IPSCs for each presynaptic heart interneuron to each heart motor neuron and expressed the synaptic strength as the average peak synaptic conductance as described above. The conductance values from the preparation 5/27B/09 (see Fig. 8) were used as our standard or canonical values in the model. In the course of our analysis, we then varied the absolute strength of one input at a time to each motor neuron using all 12 values for that input in our sample while keeping the absolute strength of all other inputs constant. We then recalculated the relative strength of varied input with each variation.

The heart motor neuron ensemble model is implemented in GENESIS (for General Neural Simulator System), with each model motor neuron receiving the appropriate combination of spike times and synaptic strengths. We ran the model for 100 s of model time, with a time step of 0.0001 s. The 11 bursts of inhibitory synaptic input sculpted 12 bursts of the motor neurons, with the middle 10 bursts used to assess the phase of the model fictive motor pattern (see below). For details, including all model equations, see García et al. (2008).

Correlational analysis and statistics.

For correlational analysis, the phase difference or relative phase rather than the absolute phase described above was sometimes calculated. Phase difference or relative phase is the absolute value of the difference in absolute phase between the activity of two neurons. In some cases, the average phase of all four premotor interneurons [HN(3), HN(4), HN(6), and HN(7)] or of just the HN(6) and HN(7) interneurons was calculated. For the average phase of all four premotor interneurons, we subtracted 1 from phase of all neurons with absolute phase of >0.5.

Correlations were performed in Excel (Microsoft), and they were considered significant and R² is reported when p < 0.05. In some cases in which the sign of the correlation is important, r is also reported. Data combined across different preparations are usually displayed as box-and-whisker plots showing the median, the first and third quartiles, the range, and outliers, beyond 1.5 times the interquartile range. Means are presented ± SD.

To test for differences in the distributions of Figure 4, we performed one-way ANOVA both between segments and within a segment: p < 0.05 was used as a measure of significance.

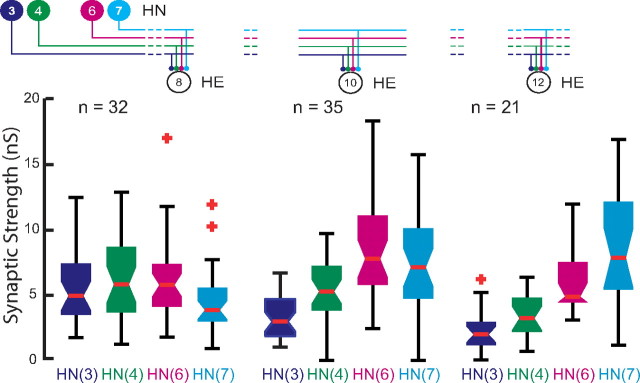
Figure 4.

Whisker-box diagram of absolute synaptic strength of inputs to the HE(8), HE(10), and HE(12) motor neurons determined as illustrated in Figure 3. Iconic unilateral circuit diagram (above) identifies the recorded neurons for each diagram, and standard colors are used to indicate the strength of each HN input in each diagram. Each box shows the median value at its waist and the third and first quartile at its top and base, respectfully. The whisker ends indicate the lowest datum still within 1.5 * IQR (interquartile range) of the lower quartile, and the highest datum still within 1.5 * IQR of the upper quartile with outliers indicated by red crosses. The strength profile across the four inputs, HN(3), HN(4), HN(6), and HN(7) interneurons, is distinctive for each motor neuron but with considerable variability in the strength of each input in each motor neurons across animals (n).

Results

Background

The two longitudinal heart tubes of medicinal leeches are innervated in each midbody segment (3–18) by the ipsilateral member of a single bilateral pair of heart [HE(3)–HE(18)] motor neurons (Maranto and Calabrese, 1984). The heart motor neurons are rhythmically inhibited ipsilaterally by a set of four bilateral pairs of identified and one unidentified pair of premotor heart [HN(3), HN(4), HN(6), HN(7), and HN(X) corresponding to segments 3, 4, 6, 7, and unknown] interneurons that are members of the heartbeat CPG (Fig. 1A). The fictive motor pattern for heartbeat is bilaterally asymmetric: motor neurons on one side fire in a rear-to-front progression (peristaltic), whereas those on the other fire in near synchrony (synchronous) and there is side-to-side coordination of the two patterns (Wenning et al., 2004b; Norris et al., 2007b) (Fig. 1B). The asymmetry is not permanent, but rather the motor neurons of the two sides change roles (patterns) every 20–40 heartbeat cycles. The temporal pattern of the activity of the premotor interneurons has been described quantitatively and, like that of the motor neurons, is bilaterally asymmetric with strict side-to-side coordination and regular side-to-side switches of peristaltic and synchronous patterns (Norris et al., 2006, 2007b). The pattern of strength of the inhibitory connections from the premotor interneurons to the motor neurons (spatial pattern) has been quantitatively described and is bilaterally symmetric. There are distinct segmental trends in this strength pattern. Nevertheless, there is a large animal-to-animal variation in the strength of individual inputs (Norris et al., 2007a). We have also constructed a model of the entire heart motor neuron ensemble and all their inputs, which is useful in assessing how the temporal pattern of the premotor neuron inputs and their spatial pattern of connection strengths onto motor neurons interact to produced coordinated output by the motor neurons (functional activity) (García et al., 2008).

Accounting for the synaptic input to the HE(8), HE(10), and HE(12) motor neurons

Our original aim in this study was to test the hypothesis that functional output of the heartbeat CPG was maintained in the face of animal-to-animal variation in the absolute strength of connections onto heart motor neurons, because relative strengths onto particular motor neurons were maintained across animals. Therefore, we characterized as quantitatively as possible variability in the actual and relative strength of the inhibitory synapses from premotor heart interneurons onto the segmental heart motor neurons HE(8), HE(10), and HE(12).

Our first step was to prove that the four premotor heart interneurons previously known to connect to these motor neurons would account for all their synaptic input (Fig. 1A). We recorded action potentials extracellularly from premotor interneurons HN(3), HN(4), HN(6), and HN(7) while sequentially voltage-clamping heart motor neurons HE(8), HE(10), and HE(12) (Fig. 2). We selected 13 experiments with low noise and a low level of escape spiking in which we had attempted to record sequentially all three ipsilateral motor neurons HE(8), HE(10), and HE(12). From each of these experiments, we chose two barrages of IPSCs in each recorded motor neuron, and, for every spike recorded in a premotor interneuron, we dropped a line to the voltage-clamp current trace recorded from the motor neuron and found the corresponding IPSC. The drop line was placed at an interval from the premotor interneuron spike corresponding to the conduction delay computed from the spike-triggered average IPSC (see Materials and Methods). Figure 2 shows this process for the central section of an IPSC barrage in an HE(10) motor neuron associated with one premotor interneuron burst sequence. Two such successive barrages were analyzed, and all IPSCs recorded could be accounted for by the premotor interneuron spike trains recorded. Note also that the size of the individual IPSCs recorded in the middle of the barrage compare favorably with spike-triggered averaged IPSCs derived from the same presynaptic burst sequences. Similar results were observed in several preparations for all three motor neurons considered, with only a very few of the IPSCs unaccounted for by the premotor interneuron spikes recorded (Table 1). Using this approach, all IPSCs were accounted for in 9 of 12 successful recordings from the HE(8) motor neuron, in 5 of 7 successful recordings from the HE(10) motor neuron, and in 2 of 7 successful recordings from the HE(12) motor neuron. When they occurred, unaccounted-for IPSCs were typically identified at the beginning of each IPSC barrage, approximately one to three per barrage. In one HE(12) motor neuron, we found 11 unaccounted-for IPSCs in two barrages associated with 381 premotor interneuron spikes. Thus, even in this (worst) case, we accounted for 97% of the IPSCs.

Figure 2.

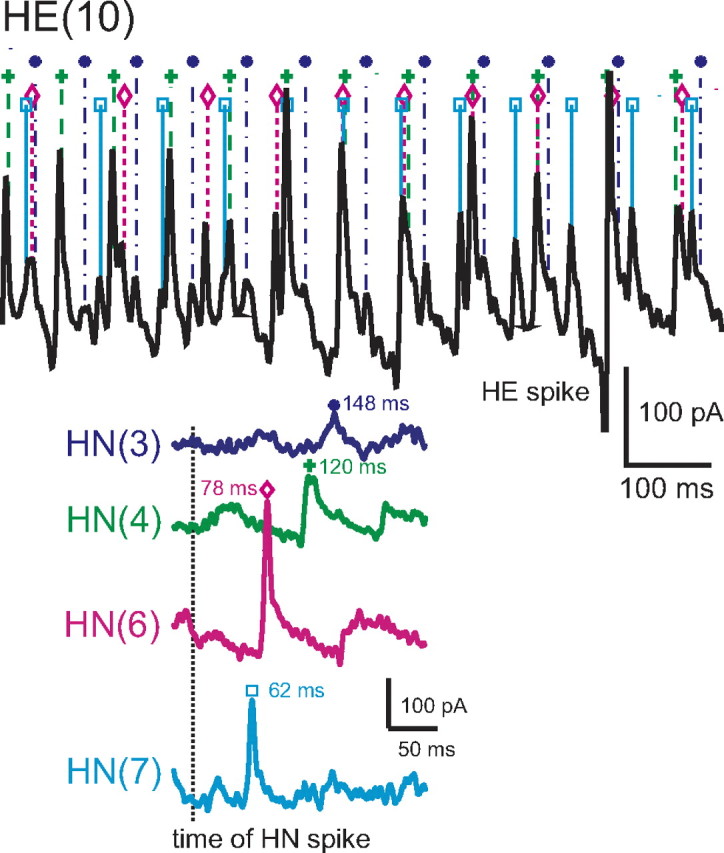
Accounting for all the inhibitory synaptic inputs to a HE(10) motor neuron. An HE(10) motor neuron was recorded in voltage clamp (holding potential −45 mV) simultaneously with extracellular recording from four ipsilateral premotor heart interneurons, HN(3), HN(4), HN(6), and HN(7). Here and throughout interneurons and motor neurons are indexed by segmental ganglion number, thus HN(7) is the heart interneuron of segmental ganglion 7, and all recordings are ipsilateral. One to three bursts of HN firing were analyzed in each preparation: in this preparation three were used. In the portion of one burst illustrated (preparation was in synchronous mode here), standard symbols and colors are used to plot each HN spike, and dropped dashed lines from each HN spike symbol indicate the associated IPSC in the HE current trace. For clarity only a short portion of the trace associated with the HN burst is illustrated. 100% of the recorded IPSCs over 3 bursts were matched by a spike recorded from one of the HN interneurons with the correct latency in this HE(10) motor neuron. HN spikes from 11 bursts (including the one illustrated) from each interneuron were also used to generate the spike-triggered averages of IPSCs in the motor neuron shown on the lower right. The vertical dashed line indicates the time of the triggering interneuronal spike, standard colors identify each spike-triggered average, and standard symbols indicate the latency of the peak average IPSC from this triggering event. Note that the amplitude of the individual IPSCs from each identified HN spike match the amplitude expected from the spike-triggered average.

Table 1.

Accounting for all the inhibitory synaptic inputs to the HE(8), HE(10), and HE(12) heart motor neurons

HE(8)		HE(10)		HE(12)		Preparation
Unaccounted IPSCs	Total # of HN spikes	Unaccounted IPSCs	Total # of HN spikes	Unaccounted IPSCs	Total # of HN spikes
0	304	Not recorded		5	336	7/23
0	528	Not recorded		Not recorded		8/1B
3	307	Not recorded		Not recorded		8/4A
0	322	4	382	Not recorded		8/13
0	459	Not recorded		8	393	8/15
2	459	1	454	2	461	8/22B
0	384	0	376	4	374	9/3
Not recorded		0	399	Not recorded		9/4A
0	373	Not recorded		Not recorded		9/8B
0	328	0	242	0	349	9/15
0	366	0	410	0	374	9/18A
0	421	0	369	11	381	9/22A
2	445	Not recorded		Not recorded		9/22B

In 26 heart motor neurons [HE(8), HE(10), and HE(12)] from 13 preparations, IPSCs were assigned to each spike in two bursts of the four premotor heart interneurons based on the conduction delay time (see Results). The total number of spikes in the two bursts in the four premotor heart interneurons is given. The number of unaccounted IPSCs is given with a “0,” indicating that no unaccounted IPSCs were found. In the worst case, the HE(12) motor neuron from prep 9/22A, 11 unaccounted IPSCs were found, which is 2.8% of the total number of spikes (381) recorded from the interneurons.

We conclude that the HN(3), HN(4), HN(6), and HN(7) premotor interneurons are the only inputs to these three motor neurons, HE(8), HE(10), and HE(12), and that our spike-triggered averages are good estimates of the strength of individual IPSCs evoked by spikes in the middle of a premotor burst. In all subsequent figures and tables, the data are derived only from experiments in which all four of these premotor interneurons were recorded simultaneously.

Synaptic strength patterns of the inputs to the HE(8), HE(10), and HE(12) motor neurons

Using spike-triggered averages, we compared the absolute and relative synaptic strength of the four premotor inputs to our chosen motor neurons. Figure 3 shows an experiment in which the HE(8) and the HE(12) motor neurons were serially held in voltage clamp to measure IPSC amplitude while activity in all four premotor interneuron inputs was recorded. The two motor neurons show distinctive profiles of synaptic strength: in the HE(8) motor neuron, input from the HN(4) and HN(6) interneurons predominates whereas the HN(3) and HN(7) inputs are at ∼75% their strength, but in the HE(12) motor neuron, input from the HN(7) interneuron greatly predominates whereas the HN(4) and HN(6) inputs are at ∼25% their strength and the HN(3) input is insignificant. Across all such experiments, across all animals, this strength pattern was reflected in the composite data and the HE(10) input showed an intermediate strength pattern (Fig. 4).

To determine whether strengths of the premotor HN synaptic inputs were different within a segment and across segments, we performed one-way ANOVA on the data of Figure 4. We found significant differences both between segments for each premotor interneuron [HN(3), F = 18.11, df = 2, p < 0.01; HN(4), F = 7.5, df = 2, p < 0.01; HN(6), F = 5.07, df = 2, p = 0.01; HN(7), F = 12.19, df = 2, p < 0.01] and within a segment for the four premotor interneurons [HE(8), F = 3.06, df = 3, p < 0.03; HE(10), F = 20.71, df = 3, p < 0.01; HE(12), F = 22.93, df = 3, p < 0.01]. These results indicate that the synaptic strengths of the premotor interneurons are different both across segments and within a given segment, i.e., the segmental input patterns to the HE(8), HE(10), and HE(12) motor neurons are different across animals.

Are the synaptic strength patterns of the inputs to the HE(8), HE(10), and HE(12) motor neurons observed across animals preserved in all individuals?

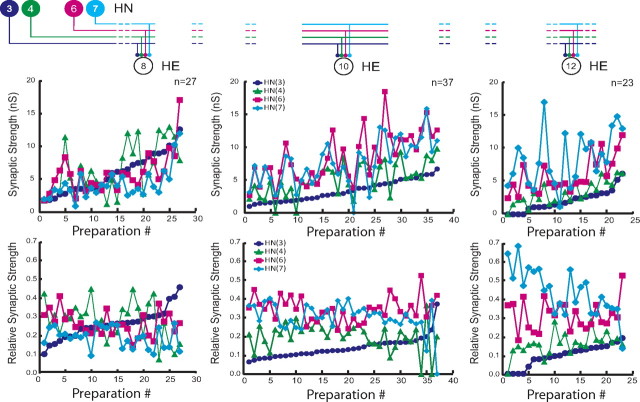
When the composite data of Figure 4 are plotted individually, it is clear that, although most individuals conform to the strength patterns observed in composite, several individuals show very different patterns (Fig. 5). This lack of consistency is apparent whether one considers absolute (top panels; presented as conductance) or relative (bottom panels) synaptic strength. For example, in the HE(12) motor neuron, input from HN(7) is usually the strongest, with HN(6) sometimes having equal strength. However, in one preparation (preparation 11), the HN(7) input was the weakest (Fig. 5, top right graph). We conclude that, although relative strengths of inputs to the different motor neurons show clear trends, there is no hard mechanism either developmental or homeostatic enforcing relative strength. Moreover, it is apparent by going left to right on the absolute strength graphs of Figure 5 that the total amount of inhibition that a motor neuron receives is not regulated, because the sum of all the individual absolute strengths onto a given motor neuron varies tremendously across animals. Nevertheless, it is possible that there is some compensatory mechanism at work such that variation in the strength of one input is compensated by an opposite variation in another input. To examine this possibility, we performed a correlational analysis of the strength of each input against each other input for all three motor neurons (Table 2). All correlations of input pairs to each motor neuron were significant, relatively strong, and positive. A lack of negative correlations indicates that opposing variation does not occur in this system at least for pairs of inputs.

Figure 5.

Viewing the animal-to-animal variation in absolute synaptic strength illustrated in Figure 3. Iconic unilateral circuit diagram (above) identifies the recorded neurons for each graph, and standard colors and symbols are used to indicate the strength of each HN input in each graph. Absolute strength (in nanosiemens; top graphs) or relative strength (bottom graphs) is plotted versus preparation ordered by the absolute or relative strength of the HN(3) input, respectively.

Table 2.

Correlation (r) of the absolute strength (conductance in nanosiemens) of each heart interneuron input versus each other heart interneuron input for HE(8), HE(10), and HE(12) motor neurons

	HN(4)	HN(6)	HN(7)
HE(8) (n = 26)
HN(3)	0.56**	0.72***	0.70***
HN(4)		0.45*	0.43*
HN(6)			0.81***
HE(10) (n = 37)
HN(3)	0.65***	0.72***	0.66***
HN(4)		0.64***	0.69***
HN(6)			0.77***
HE(12) (n = 22)
HN(3)	0.80***	0.74***	0.48*
HN(4)		0.80***	0.63***
HN(6)			0.60**

*p ≤ 0.05;

**p ≤ 0.01;

***p ≤ 0.001.

Individual animals show wide variation in temporal and strengths patterns of inputs as well as temporal pattern of outputs

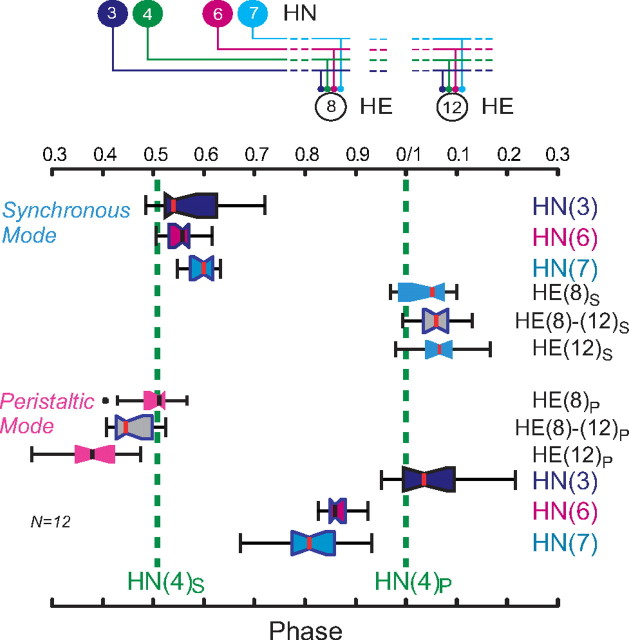
The above observations led us to speculate that perhaps variations in relative strength of inputs are compensated by adjustments in the firing pattern of the premotor interneurons (temporal pattern of inputs) or reflected in the firing pattern of the motor neurons (firing phase or intersegmental phase difference, also known as temporal pattern). We therefore undertook experiments to measure all the relevant parameters (temporal pattern of the premotor interneurons, strength patterns of their inputs to the motor neurons, and phase of the motor neurons all in both peristaltic and synchronous coordination modes) in a small series of individuals.

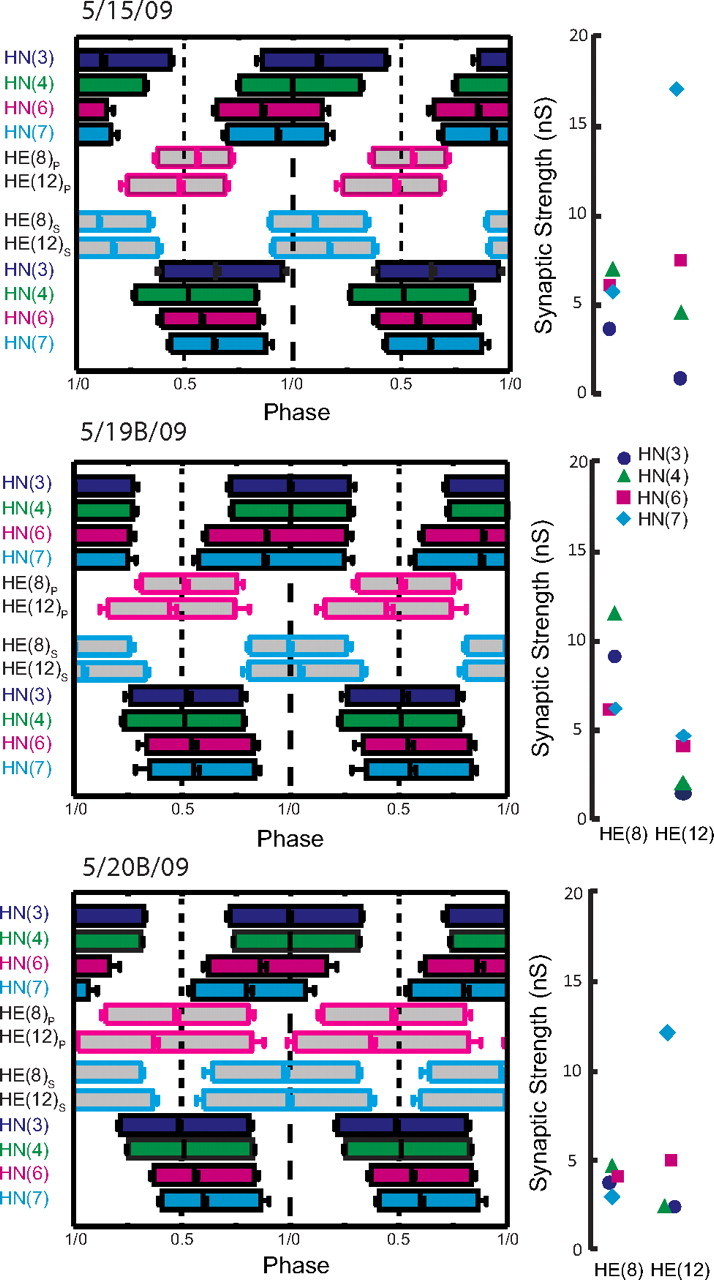
We concentrated on the HE(8) and HE(12) motor neurons, recording simultaneously and extracellularly from all four premotor heart interneurons and from the HE(8) and HE(12) motor neurons in 12 preparations to determine the temporal patterns of their inputs and their output as shown in Figure 6 for a single preparation. We then sequentially voltage clamped the HE(8) and HE(12) motor neurons to measure the pattern of the synaptic strength of their inputs. Figure 3 illustrates this procedure for the same individual as in Figure 6. The strength data were combined and displayed as whisker-box diagrams (Fig. 7). Figures 8 and 9 show complete composite phase diagrams (input and output temporal patterns) and complete strength data for 6 of the 12 preparations in our sample. The variability in the input and output temporal patterns from these 12 preparations is summarized in the whisker-box diagram of Figure 10. The mean period across the 12 preparations was 8.62 ± 1.16 s (range, 6.7–10.8 s), and no aspect of input phase or output phase was correlated with period (data not shown). We observed a wide variation in individual animals in the temporal and strengths patterns of inputs as well as the temporal pattern of outputs (Figs. 8, 9). Particularly variable was the firing phase of the HN(3) and HN(7) interneurons in the peristaltic mode (noted previously by Norris et al., 2006) and the firing phase of the HE(12) motor neuron in the peristaltic mode (Fig. 10). Note that intersegmental phase differences in the motor neuron firing are also variable. There is corresponding variability in the pattern of input strengths (Fig. 10).

Figure 6.

Determining the input and output temporal pattern of the HE(8) and HE (12) motor neurons. Left, Simultaneous extracellular recordings were made of ipsilateral HN(3), HN(4), HN(6), and HN(7) premotor interneurons (inputs) (standard color code) and HE(8) and HE (12) motor neurons (outputs) (black) in both peristaltic (P) and synchronous (S) coordination modes. Right, Summary phase diagram of the premotor interneurons (standard color code) and the HE(8) and HE(12) motor neurons in both the peristaltic (pink-outlined boxes) and synchronous (light blue-outlined boxes) coordination modes. For both motor neurons and interneurons, the average duty cycle is indicated by the length of the bar: the left edge of each bar indicates the average phase of the first spike of the burst, and the right edge indicates the average phase of the last spike of the burst. Average phase is indicated by a vertical line within the bar. Error bars indicate SDs. A phase diagram of the interneurons was first constructed from measurements of activity phase relative to the middle spike of the ipsilateral HN(4) interneuron for both synchronous and peristaltic coordination modes. To align these ipsilateral phase diagrams, the synchronous HN(4) interneuron was assigned a phase of 0.511, as measured with respect to the peristaltic HN(4) interneuron in bilateral recordings (Norris et al., 2006). All other synchronous interneurons were then offset by the same amount as the phase of the synchronous HN(4) interneuron.

Figure 7.

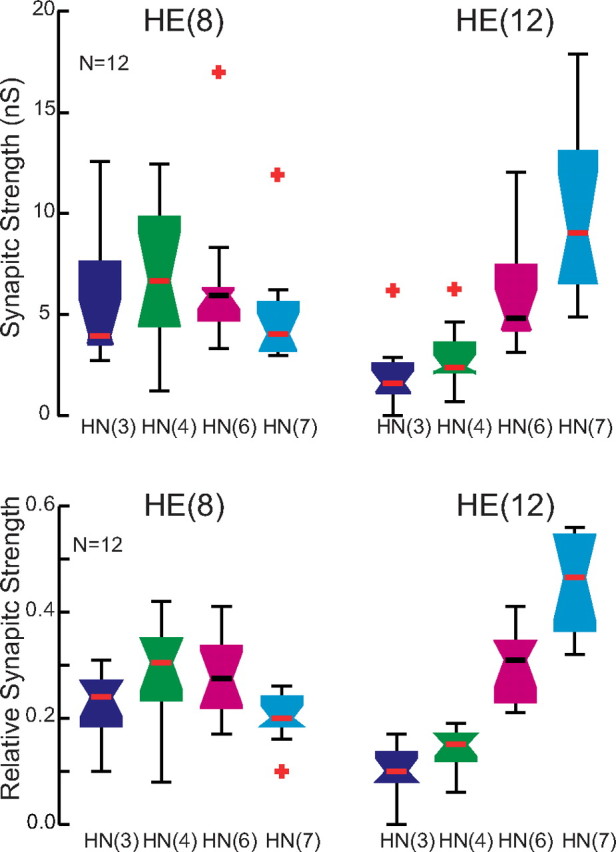
Whisker-box diagrams of absolute and relative synaptic strength of inputs to the HE(8) and HE(12) motor neurons. Data were drawn from a series of 12 preparations in which the input and output temporal pattern of the HE(8) and HE(12) motor neurons was completely specified as illustrated in Figure 6 and in which the strength pattern of the inputs to both motor neurons was also measured, as illustrated in Figure 3. The strength profile across the four inputs, HN(3), HN(4), HN(6), and HN(7) interneurons (standard color code used), is similar to that for the larger population illustrated in Figure 4, indicating that our sample is representative.

Figure 9.

Complete analysis of input and output temporal patterns and synaptic strength patterns (spatial pattern) for three different preparations from our sample of 12 (summarized in Fig. 7). Temporal patterns were determined as in Figure 6, but the two ipsilateral phase diagrams were fused into a composite for ease of presentation. The strength pattern of the inputs, determined as in Figure 3, is shown to the right of each composite phase diagram. Standard colors and symbols are used throughout. Preparations are specified by the day on which they were recorded: letters accompany the day designation if more than one preparation was recorded on that day.

Figure 10.

Whisker-box diagrams of the (middle spike) phase of the HE(8) and HE(12) motor neurons (boxes light blue in synchronous coordination mode and pink in the synchronous coordination mode) and their inputs (standard color code used) for the series of 12 preparations in which the input and output temporal patterns and strength patterns were completely specified as illustrated in Figures 8 and 9. Iconic unilateral circuit diagram (above) identifies the recorded neurons. The gray whisker boxes show the intersegmental phase differences between the HE(8) and the HE(12) motor neurons for the two coordination modes. The median at the waist of these gray whisker boxes is placed exactly halfway between the median HE(8) phase and the median HE(12) phase for each coordination mode.

The individualized phase diagrams with associated strength diagrams shown in Figures 8 and 9 are maps of input temporal pattern and output temporal pattern linked by the strength pattern that show variability at all levels. The coordination modes in each are easily recognizable, but it is difficult to say how the output pattern of heart motor neurons, including duty cycle, phase, and intersegmental phase difference, depends on the temporal pattern of the premotor interneuron inputs or on their strengths. In every case, a functional peristaltic or synchronous intersegmental pattern of motor neuron discharge is achieved: in the peristaltic mode, the HE(12) motor neuron leads the HE(8) motor neuron by a minimum of 0.07 phase units (maximum of 0.18 phase units), whereas in the synchronous mode, the HE(12) motor neuron lags the HE(8) motor neuron by a maximum of 0.09 phase units or leads by a maximum of 0.04 phase units. The phase relations for all 12 preparations (corresponding to the strengths patterns of Fig. 7) are summarized in the whisker-box diagrams of Figure 10. [We also performed similar experiments recording only the HE(10) motor neuron (n = 22) with very comparable results (data not shown).]

Correlational analysis failed to illuminate how each animal achieved this functionality (Table 3). We attempted to correlate the phase of motor neuron discharge with synaptic strength of each input and with various strength ratios and linear combinations. The relative phase of HE(8) discharge in both the peristaltic (R² = 0.729, p < 0.0004) and synchronous (R² = 0.618, p < 0.0024) coordination modes was strongly correlated with the relative strength of the input of the HE(8) motor neuron from the HN(3) interneuron, whereas there were relatively weak correlations between HE(12) phase in the peristaltic mode and HN(3) (R² = 0.413, p < 0.00242) and HN(4) (R² = 0.47, p < 0.0138) input strengths. No other correlations between motor neuron phase and input strength were observed. Most important is that the phase difference between the HE(8) and the HE(12) motor neuron is not correlated with any of our measures of strength, in either coordination mode.

Table 3.

Correlation (R²) of the relative phase [φHE(i)_HN(i)] versus relative strength of each heart interneuron [HN(i)] input for HE(8) and HE(12) motor neurons in peristaltic and synchronous coordination modes in 12 sample preparations from the living system for which the temporal pattern of the inputs and outputs and the strengths patterns of the inputs were all determined (top row) and in the heart motor neuron ensemble model using the temporal pattern of preparation 5/27B/09 (Fig. 9) (bottom row)

	Relative strength
	HN(3)	HN(4)	HN(6)	HN(7)
Peristaltic
HE(8) (n = 12)
φHE(8)HN(i) living	0.73***
φHE(8)HN(i) model	0.98***	0.92***	0.88***	0.87***
HE(12) (n = 12)
φHE(12)HN(i) living	0.41**	0.47*
φHE(12)HN(i) model	0.77***	0.99***	0.89***	0.89***
Synchronous
HE(8) (n = 12)
φHE(8)HN(i) living	0.62**
φHE(8)HN(i) model	0.95***	0.94**	0.93***	0.98***
HE(12) (n = 12)
φHE(12)HN(i) living
φHE(12)HN(i) model	0.82***	0.99***	0.97***	0.95***

*p ≤ 0.05;

**p ≤ 0.01;

***p ≤ 0.001.

We also attempted to correlate the relative phase (see Materials and Methods) of motor neuron discharge with phase of each input (Table 4). The analysis is inherently flawed because phase requires a reference, and the HN(4) interneuron being the reference must be at 0.0 phase peristaltic and 0.51 synchronous. The relative phase of HE(8) discharge in both the peristaltic (R² = 0.68, p < 0.0010) and synchronous (R² = 0.50, p < 0.0103) coordination modes, and the relative phase of HE(12) discharge in both the peristaltic (R² = 0.55, p < 0.0059) and synchronous (R² = 0.52, p < 0.0082) coordination modes were each moderately correlated with the phase of the HN(3) interneuron. The relative phase of the HE(8) motor neuron was weakly correlated (R² = 0.52, p < 0.0084) with the phase of the HN(7) interneuron in the peristaltic coordination mode but not in the synchronous coordination mode.

Table 4.

Correlation (R²) of the relative phase (φ [HN(i)]) versus phase (φ) of each heart interneuron input for HE(8) and HE(12) motor neurons in peristaltic and synchronous coordination modes in 12 sample preparations from the living system for which the temporal pattern of the inputs and outputs and the strengths patterns of the inputs were all determined

	φ HN(3)	φ HN(6)	φ HN(7)
Peristaltic
HE(8) (n = 12)
Relative φ [HN(3)]	0.68***
Relative φ [HN(4)]		0.38*
Relative φ [HN(6)]
Relative φ [HN(7)]			0.52**
HE(12) (n = 12)
Relative φ [HN(3)]	0.55**
Relative φ [HN(4)]		0.39*	0.73***
Relative φ [HN(6)]
Relative φ [HN(7)]
Synchronous
HE(8) (n = 12)
Relativeφ [HN(3)]	0.50**
Relativeφ [HN(4)]
Relativeφ [HN(6)]
Relativeφ [HN(7)]
HE(12) (n = 12)
Relativeφ [HN(3)]	0.52**
Relativeφ [HN(4)]
Relativeφ [HN(6)]
Relativeφ [HN(7)]

*p ≤ 0.05;

**p ≤ 0.01;

***p ≤ 0.001.

We then attempted to correlate the absolute phase of motor neuron discharge with two linear combinations of the phase of the inputs: (1) the average phase of the HN(6) and HN(7) interneurons (these are the interneurons that change phase between coordination modes) and (2) the average phase of all four premotor interneurons; only this last measure considers the firing time of the HN(4) interneuron (phase reference) on an equal basis with the other interneurons. In the peristaltic coordination mode, the absolute phase of the HE(12) motor neuron was strongly correlated (R² = 0.76, p < 0.0002) with the average phase of the HN(6) and HN(7) interneurons and moderately correlated with the average phase of all four premotor interneurons (R² = 0.52, p < 0.0080) but not in the synchronous coordination mode. In the peristaltic coordination mode, the absolute phase of the HE(8) motor neuron was weakly correlated (R² = 0.37, p < 0.0351) with the average phase of the HN(6) and HN(7) interneurons but not with the average phase of all four premotor interneurons and not in the synchronous coordination mode. In the peristaltic coordination mode, the absolute phase of the HE(8) (R² = 0.38, p < 0.0320) and the absolute phase of the HE(12) (R² = 0.73, p < 0.0001) motor neurons were each just as strongly correlated with the phase of the HN(7) interneuron as with the average phase of the HN(6) and HN(7) interneurons.

Under the reasoning that the onset firing phase of the heart motor neurons might be determined by the offset firing phase of their inhibitory heart interneuron inputs, we correlated relative onset (first spike) phase of the HE(8) and HE(12) motor neurons with the offset (last spike) phase of each of the four premotor heart interneurons. No significant correlations were observed (data not shown). Our past experience with the heartbeat system and the analysis here indicates in any case that middle spike phase is a better indicator of circuit timing and interaction than either the first or last spike phase.

We further attempted to correlate the phase difference between the HE(8) and HE(12) motor neurons with the maximum phase difference in their input [“maximum phase difference” is the greater of either the HN(3) to HN(7) or HN(4) to HN(7) phase difference] for the peristaltic and for synchronous coordination modes. The only correlation to emerge was a weak one between the HE(8) to HE(12) phase difference and the maximum HN phase difference in the synchronous mode (R² = 0.34, p < 0.0460). No other correlations between motor neuron phase measures and interneuron phase measures were observed. The weakness and diversity of the observed correlations suggests that motor neuron firing is dependent on many characteristics of the temporal pattern of the interneurons and not governed primarily by just one or two.

Is motor neuron phase determined by the strength of each input?

When one considers that motor neuron phase is dependent on eight measured parameters (four heart interneuron firing phases and four heart interneuron synaptic strengths) and probably on many unmeasured parameters, such as motor neuron intrinsic properties, it is not surprising that our correlational analysis did not turn up many strong relationships. Implicit in this argument is the hypothesis that the phase of heart motor neuron firing can indeed be influenced by the strength of each input, but animal-to-animal variation in the other important parameters obscures these relationships. Thus, to elucidate the consequence of biological variation in any given parameter, it is helpful to eliminate “random” variation in the other parameters. We used a simple model of the heart motor neuron ensemble (García et al., 2008) to perform this feat.

As inputs to the model HE(8) and HE(12) motor neurons, we chose a set of spike trains of the sort illustrated in Figure 6 recorded from one of our sample of 12 preparations and started with the corresponding preparation-specific HE(8) and HE(12) strength patterns. We chose preparation 5/27B/09 (Fig. 8) because the measured temporal and spatial patterns of input and temporal pattern of output were near the average, as was the period (7.8 s; mean across the 12 preparations, 8.62 ± 1.16 s; range, 6.7–10.8 s). Intrinsic properties of the model motor neurons were in all cases identical and were explicitly simplified (for details, see Materials and Methods).

We varied the absolute strength of one input at a time to each motor neuron using all 12 values for that input in our sample preparations (Fig. 7) while keeping the absolute strength of all other inputs constant. We then performed a similar correlation analysis as described above for the experimental preparations (Table 3): first we attempted to correlate the relative phase of motor neuron discharge with the relative synaptic strength of each input. Except for the correlation of HE(12) relative phase with HN(3) relative strength (peristaltic, R² = 0.77; synchronous, R² = 0.82), these correlations are universally very strong, with R² values exceeding 0.85 (usually >0.9) and all are highly significant (Table 4). The relative weakness of the correlations between HN(3) strength and HE(12) phase arises because the HN(3) absolute strength is universally low and has a restricted range in the HE(12) motor neuron. In each case, as the relative strength of the varied input increased, the relative phase approached closer to 0.5 as might be expected. In the living system, this effect is probably obscured because the phase and strength of the other inputs also vary across preparations. We next correlated heart motor neuron absolute phase and heart interneuron relative strength and found as expected that they are identical to the corresponding ones for relative heart motor neuron phase, explicitly because the phases of the heart interneuron inputs were constant across all variations in the model (i.e., the input temporal pattern was always the same). This correspondence is not seen in the living system, in which no significant absolute phase correlations were observed, whereas there were significant relative phase correlations (Table 3). Apparently, variation in heart interneuron phasing and strengths across preparations obscures heart motor neuron phase versus heart interneuron strength correlations. Nevertheless, our modeling results indicate that motor neuron phase is indeed determined by the relative strength of each input when all other parameters are kept constant.

Individual animals appear to arrive at individual solutions to produce functional motor outflow from the heartbeat CPG

Given that biological variability probably obscures the contribution of individual parameters to output, how then may we express the complex relation between input and output for leech heart motor neurons? The solutions arrived at by individual animals seem currently best expressed by presenting phase diagrams with associated strength diagrams for each animals as shown in Figures 8 and 9.

Discussion

Our goal in this study was to determine how motor neurons receiving inhibitory input from a rhythmically active central pattern generator can produce a functional pattern of output across animals despite wide animal-to-animal variation in the strength of their synaptic inputs. We performed our experiments in leeches in which a well-defined heartbeat CPG uses inhibitory synapses to coordinate motor neurons located in different segmental ganglia to fire in different phase relations so that one side produces a rear-to-front progression in motor neuron bursting (peristaltic), whereas the other produced near synchrony (synchronous) across segments (Fig. 1). We concentrated on two motor neuron pairs far enough apart (midbody segments 8 and 12) to have a relatively large phase difference on the peristaltic side yet no phase difference on the synchronous side (but included one motor neuron in between in segment 10). Most importantly, all these motor neurons received the same complement of synaptic inputs from the same four pairs of premotor interneurons of the CPG. Our previous work, in which we examined averaged data across a large number of animals, suggested that the peristaltic phase difference arises because of an average phase lead of the HN(7) and HN(6) interneurons over the HN(4) and HN (3) interneurons and a corresponding greater average strength of HN(7) and HN(6) input onto the more rear motor neurons and a greater average strength of HN(4) and HN(3) input to the more front motor neurons (Norris et al., 2007a,b). This average pattern, temporal and spatial (i.e., segmental distribution of synaptic strengths), is well exemplified by the typical preparation of Figure 3 and the averaged data of Figure 7. On the synchronous side, the near synchrony (on average) in firing of the premotor interneurons neutralizes the spatial pattern of synaptic strengths and so the motor neurons fire nearly synchronously. Paired comparisons of synaptic strengths before and after a switch in coordination mode showed that the strength of an input does not change with a change in coordination mode. Thus, the change in coordination phase of a motor neuron after a switch in coordination mode must arise from the change in the pattern of premotor interneuron firing.

Still, there was a disturbing aspect of the previous work (Norris et al., 2007a): across preparations, there was threefold to fivefold variation in synaptic strength. We thus entertained the hypothesis that, although absolute strength varied in a particular motor neuron from animal to animal over a vast range, the relative strength of the inputs to the motor neuron was maintained. By concentrating on the HE(8), HE(10), and HE(12) motor neurons (Fig. 1), by showing definitively that they did indeed each receive input from all and only the four pairs of premotor HN(3), HN(4), HN(6), and HN(7) interneurons (Fig. 2), and by assessing the strength of inputs from these four interneurons simultaneously (Fig. 3), we were able to test this hypothesis rigorously. Our results show that, although relative strength shows clear trends seen in averaged data (Norris et al., 2007a), it is by no means preserved faithfully (Fig. 4). How then does this small central pattern generator achieve functional output across animals?

Numerous theoretical and experimental studies suggest that network output can be similar despite differences in neuronal intrinsic properties and even synaptic strengths. We explored this view here by pushing our analyses one level deeper. We measured both the spatial and temporal pattern of input to the HE(8) and HE(12) motor neurons as well as the firing phases of these two motor neurons in both peristaltic and synchronous coordination modes in 12 individual preparations (Figs. 8, 9). These 12 preparations conform to previously described average data for both the pattern of synaptic strength (Norris et al., 2007a) (Fig. 7) and the temporal pattern of interneuronal input and motor neuron output (Fig. 10) (Norris et al., 2007b), yet within this sample there is wide variation in every measured parameter including input temporal pattern, spatial pattern of synaptic strength, and temporal pattern of motor neuron output. Despite this variation, the peristaltic and synchronous coordination modes are not only perceptible in every preparation at both the interneuronal and motor neuronal levels but apparently functionally appropriate (when compared with the animal-to-animal variation in the blood flow patterns of intact leeches) (Wenning et al., 2004a).

A corresponding study in the crustacean stomatogastric nervous system focusing on the core network of the pyloric CPG showed that the output phase of the lateral pyloric (LP) motor neuron is correlated with the strengths of its two different inhibitory synaptic inputs from a pacemaker core in the network, as well as with its intrinsic membrane currents and the response of a specific membrane current to a modulator (Goaillard et al., 2009). In contrast, here we did not observe strong or consistent correlations between the strengths of particular inputs and the firing phase of the HE(8) and the HE(12) heart motor neurons motor neurons. As in the pyloric CPG study, we defined the strength of inputs to a motor neuron and correlated motor neuron firing phase with the strength of a synaptic input. However, in a simple model of the heart motor neuron ensemble, using observed variation in synaptic strengths for particular inputs while all other inputs were kept constant in strength and the temporal pattern of input was also kept constant, clear, strong, and consistent correlations were observed. This observation suggests that motor neuron firing phase is influenced by the strength of each of it inputs, but this influence is not detectable on the background of temporal and strength variation of the four inputs.

There are differences in the organization of the leech heartbeat CPG and the crustacean pyloric CPG that may account for the differences in results. In the heartbeat system, the four premotor inputs are flexibly coordinated and show significant phase diversity across animals, and motor neurons do not feed back onto the premotor inputs. In the pyloric CPG, the two premotor inputs are tightly electrically coupled and act in concert as a pacemaker core. This coupling eliminates phase diversity among the inputs to the LP neuron. Moreover, because phase is measured with respect to the pacemaker core, the pacemaker core by definition always has the same phase, and, because the LP motor neuron feeds back inhibition to the pacemaker core, input phase is partially determined by output phase (Goaillard et al., 2009). This network organization coupled with only two inputs may allow correlations to emerge. Apparently in the heartbeat system, the larger number (four) of inputs to each motor neuron, which each vary in strength, and the phase diversity of the temporal pattern diminish the impact of individual inputs and confound the relationship between input strength and firing phase. Conversely, this organization allows tremendous flexibility in arriving at functional output so that myriad individual solutions seem possible. One may then expect that, in more complex systems, such as mammalian spinal CPGs, even greater flexibility and diversity in network solutions will be observed.

We were not able to measure the intrinsic properties of the heart motor neurons as was done for the LP neuron of the pyloric CPG (Goaillard et al., 2009), and certainly such properties must contribute to motor neuron firing phase. The strongest, most consistent, and universal correlations were observed when we correlated the absolute strengths of the various inputs to the motor neurons. These correlations were all positive. This observation suggests that motor neurons vary in excitability and that all inputs must be adjusted up or down to accommodate the level of excitability. Conversely, in a hybrid system, analysis of gastric motor neurons in the stomatogastric nervous system configured as half-center oscillators with reciprocal synapses and h-current, no correlations across animals of synapse strength with any of a diversity of individual excitability measures were observed (Grashow et al., 2010).

How then are we to understand how phase differences are created between heart motor neurons?

To understand how leech heart motor neurons are coordinated by their input into their appropriate segmental phase, both peristaltic and synchronous, we must consider the firing phase of each input, strength of each input, and the intrinsic properties of the motor neuron. Moreover, our analyses of the 12 different preparations suggest that the target values for each motor neuron output phase is itself variable across preparations but somehow constrained so that a functional peristaltic or synchronous pattern is attained. No one or several factors emerge from our analyses as being of primary importance in determining motor neuron output phase. Our approach will now be to use data from individual animals as both input (temporal and spatial) and output target in conductance based models of heart motor neurons. Such models can help us to explore what role, if any, motor neuron intrinsic properties play in the coordination of heart motor neuron by their inputs and may suggest novel hypotheses that can be tested experimentally.