Abstract
Singlet oxygen (1O2) is the major cytotoxic agent responsible for cell killing for type-II photodynamic therapy (PDT). An empirical four-parameter macroscopic model is proposed to calculate the “apparent reacted 1O2 concentration”, [1O2]rx, as a clinical PDT dosimetry quantity. This model incorporates light diffusion equation and a set of PDT kinetics equations, which can be applied in any clinical treatment geometry. We demonstrate that by introducing a fitting quantity “apparent singlet oxygen threshold concentration” [1O2]rx,sd, it is feasible to determine the model parameters by fitting the computed [1O2]rx to the Photofrin-mediated PDT-induced necrotic distance using interstitially-measured Photofrin concentration and optical properties within each mouse. After determining the model parameters and the [1O2]rx,sd, we expect to use this model as an explicit dosimetry to assess PDT treatment outcome for a specific photosensitizer in an in vivo environment. The results also provide evidence that the [1O2]rx, because it takes into account the oxygen consumption (or light fluence rate) effect, can be a better predictor of PDT outcome than the PDT dose defined as the energy absorbed by the photosensitizer, which is proportional to the product of photosensitizer concentration and light fluence.
Keywords: photodynamic therapy, explicit dosimetry, singlet oxygen, mathematical modeling
1. INTRODUCTION
Photodynamic therapy (PDT) is an attractive treatment modality for cancer and other localized disease [1–4]. For type-II photochemical reactions, the PDT processes involve photosensitizer excitation by light and its subsequent reaction with ground state oxygen 3O2, which leads to the creation of major cytotoxic agent singlet oxygen (1O2). PDT has several advantages over surgery and conventional radiation therapy. Due to limited light penetration in tissue, the light source geometry can be chosen to localize the cell-killing PDT dose within the tumor volume, thereby reducing damage to the surrounding healthy tissue. PDT can also be used repeatedly without inducing secondary diseases because it employs non-ionizing radiation as opposed to the ionizing wavelengths used in conventional radiation therapy. The cosmetic outcome of the PDT treatment is often superior to that resulting from surgical procedures. However, there are still obstacles preventing the widespread use of PDT in clinic. Prominent among these limitations is the lack of a PDT dosimetry quantity that correlates with PDT efficacy.
In explicit PDT dosimetry, the most well defined biophysical dosimetry quantity is PDT dose, i.e., the light dose absorbed by photosensitizer. This quantity is proportional to the time integral of the product of local photosensitizer concentration and light fluence rate. Under well-oxygenated conditions, PDT dose can be a good predictor of treatment outcome. However, in tumors, which are frequently poorly oxygenated to begin with [5], high fluence-rate PDT modality can create even more severe hypoxia during illumination and result in less-effective treatment. This has been described theoretically [6] and observed in animal models [7]. Therefore, to completely characterize the PDT treatment outcome, it is necessary to account for the oxygen consumption.
Correlating the concentration of 1O2 with tumor death has been a long term goal in PDT dosimetry. Direct measurement of 1O2 luminescence at 1270 nm has been suggested as a potential dosimetry tool to track the cumulative 1O2 production during treatment [8–10]. Yamamoto et al. [10] observed higher cumulative 1O2 concentration when a low fluence rate was used, which correlated with better treatment outcome in an in vivo animal model. These measurements were made using a NIR photomultiplier tube and nanosecond-pulsed laser system. However, the weak luminescence and the corresponding low signal-to-noise ratio are major obstacles to its clinical application, especially in interstitial applications.
Besides experimental methods, microscopic models have been proposed to calculate singlet oxygen concentration [6, 11–15]. These models use a coupled rate equation to describe the production of 1O2, which involves complex reactions among photosensitizer, oxygen molecules, and the treatment light. Foster et al. [6] first applied a Krogh cylinder model to a Type II mechanism of PDT. This one-dimensional steady state model explored the treatment consequence derived from low and high fluence rates, and capillary density in a microscopic scale. This model was significantly extended into a time-dependent scheme by incorporating photobleaching, oxygen unloading from hemoglobin, non-uniform photosensitizer distribution and blood flow [11]. Utilizing the experimentally-measured photophysical parameters and non-uniform photosensitizer distribution for meso-tetra-hydroxyphenyl-chlorin (mTHPC, Foscan®), Wang et al. [15] is able to evaluate the validity of 1O2 dosimetry with respect to long-term tumor response for mTHPC-PDT.
Although such microscopic models provide a deeper understanding of basic photochemical mechanisms during PDT, directly applying these models in a clinical setting is still difficult or practically impossible. This is because modelling the heterogeneity of tumor microvascular networks coupling with PDT processes is at present impractical due to vast amount of computational requirement. In addition, the necessary model parameters, such as the photophysical parameters describing the PDT processes and the physiological parameter addressing oxygen supply rate, are usually adopted from literature on data collected from either an in vitro setting or an in vivo setting different from the actual clinical setting, resulting in inconsistencies and errors in model predictions.
In this work, we propose an empirical macroscopic 1O2 model, which utilizes the complete set of PDT kinetic equations, light diffusion equation, and oxygen supply mechanism. First, we propose to use the model to calculate a dosimetry quantity “apparent reacted 1O2 concentration”, [1O2]rx, as the accumulated concentration of 1O2 reacting with cellular targets. We can approximately express the [1O2]rx to be proportional to the time integration of the product of oxygen-dependent 1O2 quantum yield and the PDT dose rate. By considering the PDT-induced oxygen variation, the [1O2]rx is expected to be better correlated with treatment outcome than the PDT dose. Second, we have developed a non-linear fitting algorithm which is able to fit calculated [1O2]rx to the measured PDT-induced necrotic distance for a specific photosensitizer under in vivo environment. Our numerical results simulating in vivo Photofrin-PDT show the level of [1O2]rx hardly reaching the published threshold dose [16], and the similar result was also reported for other theoretical study for in vivo mTHPC-PDT [15]. A new quantity “apparent singlet oxygen threshold concentration” [1O2]rx,sd is introduced to enable the computed [1O2]rx fit the necrotic distance. The photophysical and physiological model parameters involved in the PDT kinetics equations are determined from the fitting. If these model parameters and [1O2]rx,sd can be rigorously determined, we expect to use this macroscopic model to assess the PDT treatment outcome for a specific photosensitizer under in vivo environment. Third, we demonstrate that this macroscopic model can be potentially applied to the clinical case as a dosimetry quantity for different type of sensitizers and light source geometries.
In this paper, we calculate the spatially and temporally-resolved [1O2]rx, photosensitizer, and oxygen concentration during PDT with interstitial linear sources suitable for illumination of prostate [17, 18]. The sensitivity of the model parameters to calculated [1O2]rx profiles is explored for interstitial condition. Preliminary results are presented on fitting the necrotic radius induced by interstitial Photofrin-mediated PDT to obtain model parameters and [1O2]rx,sd. The advantage of [1O2]rx over PDT dose as a dosimetry quantity is discussed. A comparison of computed [1O2]rx distributions is made among different light source geometries (point, linear, or planar) and photosensitizers (Photofrin, mTHPC, or ALA-PpIX), which potentially can be correlated to differences in PDT efficacy.
2. METHODS AND MATERIALS
2.1 The Macroscopic 1O2 model
Based on the Type-II PDT processes with 1O2-mediated bleaching mechanism, we can devise a complete set of coupled differential equations describing the photochemical reactions for each species [14, 19, 20],
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where [S0], [S1] and [T] are the ground, first excited singlet and triplet sensitizer concentration, respectively, and [3O2] and [1O2] are the ground triplet and excited singlet state oxygen concentration, respectively, and P and [A] are the oxygen supply term and the concentration of 1O2 acceptor excluding sensitizer molecule. δ is a low photosensitizer concentration correction term [11, 21, 22]. In most clinical environments, the sensitizer concentration is low enough that the 1O2 molecule is more likely to react with its parent sensitizer than would be predicted based solely on the species’ relative concentrations. Therefore, the introduction of the δ term improves the theoretical description of the bleaching mechanism in a low photosensitizer concentration environment. The definitions of the other photochemical parameters k1 to k7 are listed in Table 1. The accumulated [1O2]rx killing cell targets can be expressed as,
| (7) |
where f is the fraction of the reaction between 1O2 and [A], which effectively leads tumor cell death (in this work, we set f as one). Using the convention list in Table 1, we can simplify the Eqs. (1–7) and write down the governing equations of our macroscopic model with the addition of the light diffusion equation;
| (8) |
| (9) |
| (10) |
| (11) |
Table 1.
Parameter list for Photofrin at 630 nm, mTHPC at 650 nm, and ALA-PpIX at 633 nm
| Symbol | Definition [20] | |||
|---|---|---|---|---|
| k0 | Photon absorption rate of photosensitizer per photosensitizer concentration | |||
| k1 | Bimolecular rate for 1O2 reaction with ground-state photosensitizer | |||
| k2 | Bimolecular rate of triplet photosensitizer quenching by 3O2 | |||
| k3 | Decay rate of first excited singlet state photosensitizer to ground state photosensitizer | |||
| k4 | Rate of monomolecular decay of the photosensitizer triplet state | |||
| k5 | Decay Rate of first excited state photosensitizer to triplet state photosensitizer | |||
| k6 | 1O2 to 3O2 decay rate | |||
| k7 | Bimolecular rate of reaction of 1O2 with biological substrate [A] | |||
| Symbol | Definition | Value | References | |
| SΔ | Fraction of triplet-state photosensitizer-3O2 reactions to produce 1O2 | 0.5 | [20] | |
| δ (µM) | Low concentration correction | 33 | [21] | |
| ξ (cm2 mW−1 s−1) |
|
Photofrin: 3.7 × 10−3 | [16, 38]* | |
| Photofrin: (2.1±0.3) × 10−3 | fitted value | |||
| mTHPC: 0.03 | [30] | |||
| ALA-PpIX: 3.7 × 10−3 ** | ** | |||
| σ (µM−1) | k1/k7[A] | Photofrin: 7.6 × 10−5 | [16] | |
| mTHPC: 2.97 × 10−5 | [30] | |||
| ALA-PpIX: 9 × 10−5 | [39] | |||
| β (µM) | k4/k2 | Photofrin: 11.9 | [16] | |
| mTHPC: 8.7 | [30] | |||
| ALA-PpIX: 11.9** | ||||
The calculation of the parameter ξ are based on the study of Georgakoudi et al. [16] and Mitra et al. [30] from tumor spheroid studies. Using the convention from reference [30] and [16], ξ is equal to βPDT/[S0]. βPDT is a proportional constant between photochemical oxygen consumption rate and the fluence rate. The ξ can be calculated according to the βPDT value and photosensitizer concentration provided in the references [16, 30, 38].
The photochemical parameters, ξ and β, for ALA-PpIX are currently not available in the literatures. We adopted the values of Photofrin.
The derivation details for Eqs. (8–11) are given in the Appendix section. Equation (7) can be rewritten and linked to PDT dose, DPDT;
| (12) |
Here, ϕ is light fluence rate, S is the source term, and μa and μs’ are the absorption and reduced scattering coefficient of the (tumor) tissue, respectively. The optical properties used in the calculations of the paper are listed in Table 2, with the exception of the calculations for Figs. 3c, 4 and 6, for which measured optical properties for individual mouse were used. The photochemical parameters (k1–k7) are simplified into 3 independent photophysical parameters, ξ, σ, and β. ξ represents the photochemical oxygen consumption rate per light fluence rate and photosensitizer concentration under the condition of infinite 3O2 supply and prior to photobleaching. For a given photosensitizer concentration, σ is the probability ratio of a 1O2 molecule reacting with ground-state photosensitizer compared to the 1O2 molecule reacting with a cellular target [A]. β represents the ratio of the monomolecular decay rate of the triplet state photosensitizer to the bimolecular rate of the triplet photosensitizer quenching by 3O2 (Table 1). Equation (12) implies that the [1O2]rx is proportional to the time integration of the product of oxygen-dependent 1O2 quantum yield and the PDT dose rate. For Photofrin at 630 nm, the photosensitizer extinction coefficient ε is 0.0035 (cm−1 uM−1) (Table 1) and the initial in vivo Photofrin concentration is around 7 µM at 24 hr after 5 mg/kg i.v. injection [20]. Therefore, the absorption coefficient for Photofrin is 0.025 cm−1, which is significantly lower than the absorption coefficient of tumor tissue measured interstitially (1.03 cm−1, see Table 2). In this work, we ignore the light absorption by Photofrin in Eq. (8). Equation (8) is a steady state equation so it can be solved independently from the other three time-dependent Eqs. (9–11). The oxygen supply term P in Eq. (4) is not necessarily a constant. In the current macroscopic model, the oxygen supply term is expressed as [19, 20]
| (13) |
in Eq. (10), where [3O2](t = 0) is the initial oxygen concentration before PDT treatment, and g is the maximum oxygen supply rate when there is no oxygen gradient. Equation (13) limits the oxygen level to not exceed the initial value. The exact form of Eq. (13) can be further modified to agree better with the results of oxygen distribution obtained using microscopic models with vascular oxygen transport [11]. g can be a function of time to account for blood flow change during PDT [23, 24]. The effect of blood flow and/or tissue oxygenation can be dynamical which will result in the optical properties to change over time during PDT. However, our recent preclinical experience demonstrated that the PDT-induced oxygen variation has almost no effect on the tissue optical properties since the light fluence rate does not change during PDT [25]. Equations (8–11) constitute a set of universal PDT kinetic equations incorporating light transport which can be used for any treatment geometry.
Table 2.
Boundary and initial conditions and optical properties used for the macroscopic model
| Boundary conditions& | ∇ϕ = 0, ∇[3O2] = 0, ∇[1O2] = 0, ∇[S0] = 0 |
|
|---|---|---|
| Initial conditions | [S0] | 7 µM [19] |
| [3O2] | 83 µM [20] | |
| [1O2] | 0 | |
| Optical properties | μa | 1.03+/−0.46 (cm−1)* |
| μs’ | 13.46+/−2.43 (cm−1)* | |
| Maximum oxygen supply rate | g | 0.7 (µM/s)** |
| 0.69±0.4 (µM/s), fitted value | ||
The optical properties used in this study were extracted from in vivo interstitial measurement performed in C3H tumor models. The values provided in Table 2 are the average values from 12 mice.
It is well-known that tumor oxygenation is much lower than normal tissue [5]. If we choose high oxygen supply rate, g, the fluence rate induced treatment difference will be diminished. Therefore, we pick an appropriate value 0.7 for g for demonstration purpose.
For planar source calculation involving tissue-air boundary, we use ϕ + 2ADn̂ · ∇ϕ = 0 for the boundary [40]. D is diffusion coefficient. We use D = 1/(3µs’) as the definition. n̂ is the normal direction vector of the interface. A is a constant that can be calculated based on the index of the refractions of the tissue and air at the boundary. A is 2.9 for the tissue-air boundary.
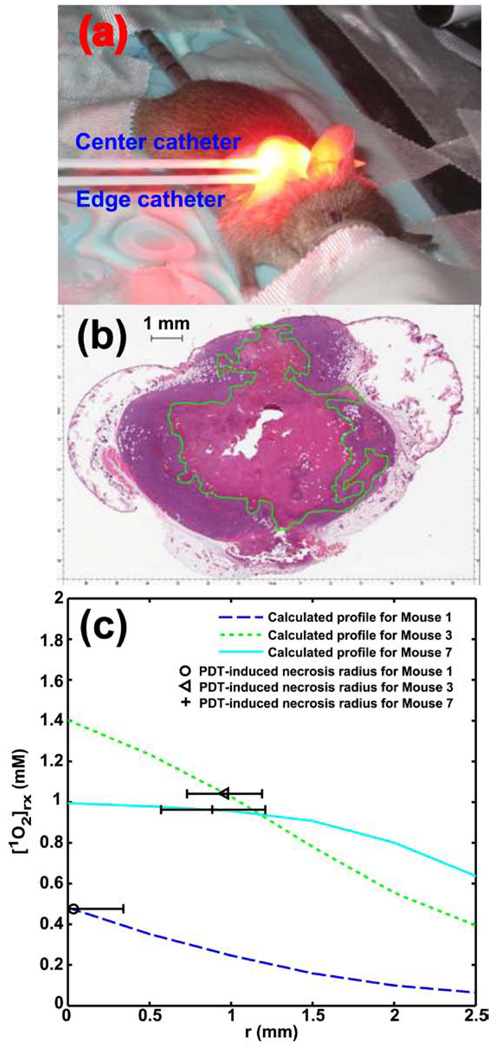
Figure 3.
(a) A standard setup of interstitial PDT treatment in a mouse tumor. The center catheter encloses the 1 cm linear source used for treatment light delivery. Before and after PDT, the fluorescence probe is placed in the center catheter for fluorescence measurement. For optical properties measurement before PDT, a point or linear light source and an isotropic point detector is placed in the center catheter and edge catheter, respectively. (b) H&E staining of a section from a tumor treated with Photofrin-PDT at 146 mW/cm, 24 J/cm. The necrotic region is circled by green line. (c) Fitting result of necrotic radius using computed [1O2]rx profiles. The horizontal error bars represent the standard deviation of experimentally-measured necrotic radius for individual animal.
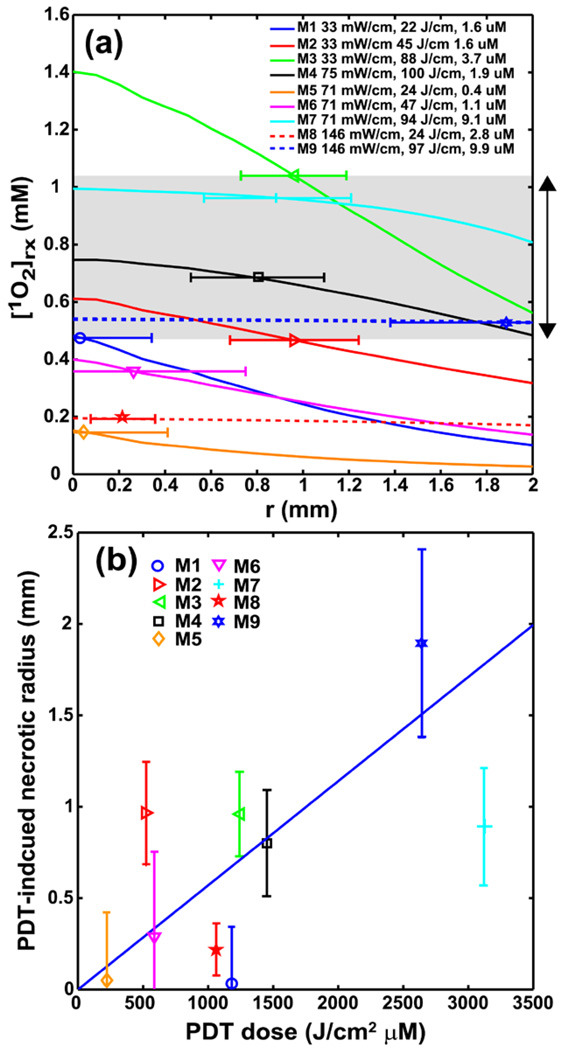
Figure 4.
(a) Individual [1O2]rx profiles for 9 mice using the same model parameters (ξ, σ, β, g) from Fig. 3c. The legend shows the corresponding source strength, total energy released per unit length, and initial photosensitizer concentration for each mouse. The symbol with error bar indicates the PDT-induced necrotic radius with standard deviation for each mouse. The gray area indicates the range of the [1O2]rx, sd. (b) PDT-induced necrotic radius vs. PDT dose (J/cm2 µM) for mice shown in figure (a). The necrotic radius for mouse 2 and 7 deviate from the linear relationship between necrotic radius and PDT dose.
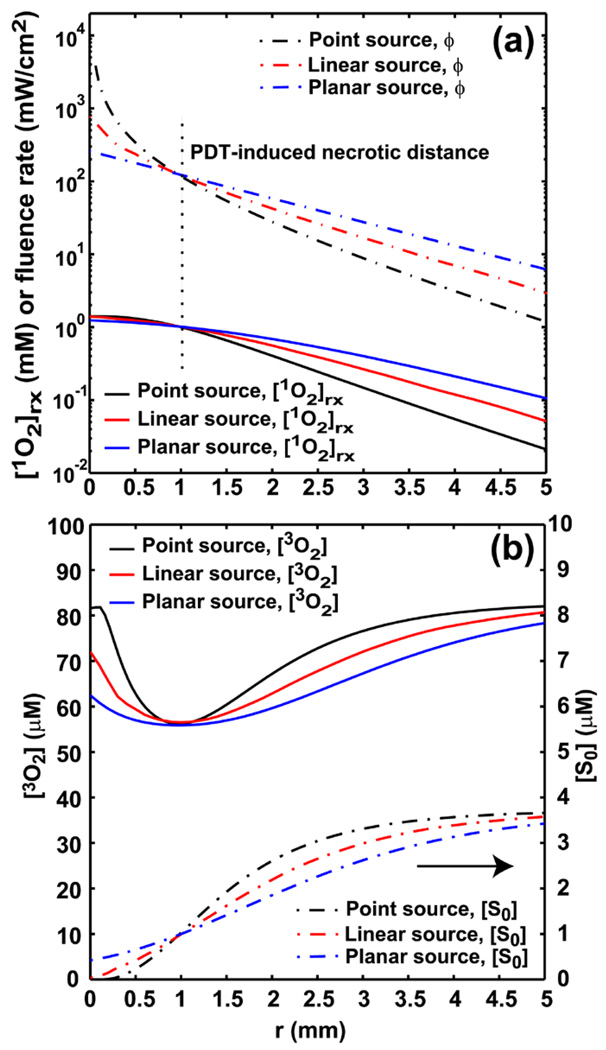
Figure 6.
(a) The spatial distributions of [1O2]rx and fluence rate for point, linear, and planar source. For point and linear source, r is the radial distance relative to the source. For planar source, r is the depth relative to tissue surface. The light fluence rate at r = 0.96 mm is fixed for the 3 sources setting, and the delivered fluence at 0.96 mm is 332 J/cm2. The vertical dash line shown in Fig. 6a indicates the location of r = 0.96 mm, PDT-induced necrotic distance, away from source locations. Fig. 6b shows the corresponding [3O2] and [S0] distributions for the 3 source setting.
Equations (8–11) can be solved numerically using the finite element method (FEM). Commercial FEM software (COMSOL 3.5 (COMSOL Inc., Burlington, MA, United States) and MATLAB 7.5 (The MathWorks, Inc., Natick, MA, United States)) was chosen for this purpose. For a given value of light fluence rate ϕ, Eqs. (9–11) can be solved independently from Eq. (8). In the other words, the spatially-resolved light fluence rate profile can be firstly constructed by solving Eq. (8). The profile will be passed to the next step, the calculation of PDT kinetics equation (Eqs. (9 – 11)). In this study, three cases of light illumination with point, linear, and planar sources are considered. Due to the symmetrical feature of point source, a one-dimensional light fluence rate profile along the radial axis obtained from Eq. (8) is used in the simulation. For the case of planar source, we consider collimated light shooting into a semi-infinite plane. The light fluence rate within the plane is assumed to be only depth dependent. For the linear source simulation, we consider a 4 cm finite length linear source. A one-dimensional fluence rate distribution along radial axis with respect to the linear source center is used in this work. After passing the fluence rate profiles to Eqs. (9–11), we can obtain the corresponding one-dimensional spatial distributions of [3O2], [S0], and [1O2]rx for a given treatment time point. In the case of in vivo experimental setup described in the following section, a 1 cm linear source was used as the treatment source. From our simulation result, we notice that with the measured optical properties (Table 2), the light fluence rate distribution within 4 mm radial distance with respect to the center of the linear source does not show distinguishable difference for the case of 4 and 1 cm linear sources (Data not shown). The 4 mm radial distance is larger than the actual simulation distance used in the following fitting procedure. Therefore, the 4 cm linear source geometry is used for the simulations throughout this work. Our program developed in the COMSOL-MATLAB environment is able to solve Eqs. (9–11) in approximately 1 sec for a given linear source strength in a tissue slab with homogeneous optical properties and photosensitizer concentration, using a desktop computer with Intel Dual Core 2.4 GHz processor and 2 GB of RAM. The initial and boundary conditions are also listed in Table 2. Except for the calculations used to generate the data shown in Figs. 3c, 4, and 6, all the model parameters are listed in Table 1 and 2.
2.2 in vivo experiment for Photofrin-PDT
A series of preclinical mouse experiments was performed to quantify the parameters for the macroscopic model of Photofrin-mediated PDT. Explicit dosimetry was performed to determine the optical properties of tumor tissue, photosensitizer concentration, and PDT-induced necrosis for each mouse. For the purpose of these studies, radiation-induced fibrosarcoma (RIF) tumors were propagated on the shoulders of female C3H mice (9–11 weeks old; NCI-Frederick, Frederick, MD) by the intradermal injection of a suspension of 3 × 105 in vitro-maintained cells. Animals were entered in the study when their tumors reached ~8 mm in diameter (about 10–14 days after cell injection). The mice received Photofrin 5 mg/kg i.v. at 24 hrs before light delivery. At the time of light delivery two parallel catheters were inserted into the tumor (Fig. 3a); one was positioned through the center of the tumor while the other was outside the tumor but close to the bottom of the tumor edge. A side-cut fiber, which served as both an excitation source and a detector, was inserted into the center catheter to measure the Photofrin emission spectrum along the catheter axis, using a 405 nm diode laser as an excitation light source. The in vivo Photofrin fluorescence was separated from the measured spectrum using a singular value decomposition (SVD) method [26], and corrected by the measured optical properties to account for the reduction of fluorescence intensity resulting from the strong optical absorption in the tumor tissue [27]. The in vivo photosensitizer concentration was obtained by comparing the in vivo Photofrin fluorescence with that measured in phantoms of known Photofrin concentration. For optical property measurement, point or linear source fibers coupled to a 630 nm diode laser (Biolitec, Inc., East Longmeadow, MA, USA) were inserted into the central catheter. An isotropic point detector was placed in the peripheral catheter where it was used to measure the fluence rate profile before treatment, and the spatially-resolved optical properties were then extracted by fitting this fluence rate profile [28]. After these measurements, the tumors were treated interstitially using a 1 cm linear source coupled to 630 nm light delivered by the same diode laser. In this study, source strength ranged from 33 to 146 mW/cm, and total energy released per unit linear source length ranged from 22 to 100 J/cm.
To assess the necrotic radius around the linear source, treated tumors were excised from euthanized animals at 24 h after PDT and fixed in formalin. Sectioning and hematoxylin and eosin (H&E) staining was performed at the Pathology Core Labs of Children’s Hospital of Philadelphia (CHOP). A total of five to eleven sections, each ~400 µm apart, were cut perpendicular to the catheter insertion axis. Slides were read and the area of necrosis, At, around the treatment fiber was quantified using ScanScope (Model type: CS, Aperio Technologies, Inc, Vista, CA, USA) (Fig. 3b) with the assistance of a pathologist. The radius of necrosis rt was calculated using the equation, . An average radius of necrosis was calculated for each tumor among the multiple sections collected from that tumor. Because the tumor shrank during processing a correction factor was also introduced in the calculation of the necrotic radius. To quantify the reduction in tumor size due to tissue processing, we compared the in vivo measured tumor cross section area perpendicular to the catheter insertion axis with this area in the tumor sections. The reduction in necrotic radius is estimated at approximately 30 % from 3 available data sets, and the amount of the reduction was corrected in the calculation of necrosis radius. Furthermore, spontaneous necrosis, and the necrosis induced by catheter insertion and/or photosensitizer toxicity was subtracted from the final necrosis result, based on data obtained from control mice with Photofrin injection and catheter insertion but no PDT treatment. Controls were included among each batch of animals studied, with the average necrotic radius among these controls (r0), being 2.3 mm calculating by . The PDT-induced necrotic radius is given by: rn = 1.3(rt − r0).
2.3 Fitting necrotic radius using [1O2]rx to extract model parameters
The main task in this work is to use calculated [1O2]rx to fit the necrotic radius and extract the model parameters (g, ξ, σ, β). In order to fit the measured necrotic radius using the [1O2]rx profiles, we introduce a fitting quantity, “apparent singlet oxygen threshold concentration”, [1O2]rx,sd. During the process, our fitting routine varies the model parameters globally so that the [1O2]rx at the necrotic radius for each animal is close to the [1O2]rx,sd. The [1O2]rx spatial distribution is optimized for each mouse by using the measured initial photosensitizer concentration and optical properties. An efficient direct-search algorithm for nonlinear problems, the differential evolution algorithm [29], was chosen as the inverse solver and implemented in COMSOL-MATLAB environment. Based on previous work with mTHPC [15] and our own simulation results (Fig. 1), we estimate that the value of [1O2]rx,sd can be largely lower than the measured threshold dose in a microsphereoid model [16] by a factor of 10. In the current fitting routine, an initial guess of [1O2]rx,sd is assigned randomly within the range of 0.4 to 1.1 mM and the value is fixed throughout the subsequent fitting procedure. The differential evolution algorithm adjusts g and ξ to vary the [1O2]rx at the necrotic radius to match the assigned [1O2]rx,sd. Constant values of σ and β obtained from literature (Table 1) are used throughout the fitting process, since the current algorithm will encounter convergence issues when given too many free floating parameters and the calculated [1O2]rx is less sensitive to these quantities than the other model parameters. The objective function of the fitting algorithm is the maximum relative difference between measurements and calculation of the threshold singlet oxygen concentration, , where [1O2]rx,i(rn) is the computed reacted singlet oxygen at a necrotic radius for ith mouse. The fitting is terminated when the maximum deviation is less than 10% variation of [1O2]rx,sd, based on the uncertainty of threshold dose measurement [30]. Typically 800 iterations and 30 minutes are sufficient to the extract the two fitting parameters g and ξ, if a reasonable [1O2]rx,sd is chosen. The result of this fitting is a single set of the parameters g, ξ, and a narrow range of [1O2]rx,sd applicable to the entire set of animal measurements. While each animal’s specific optical properties and sensitizer concentration are used in the calculation, these fundamental parameters kept the same across animals.
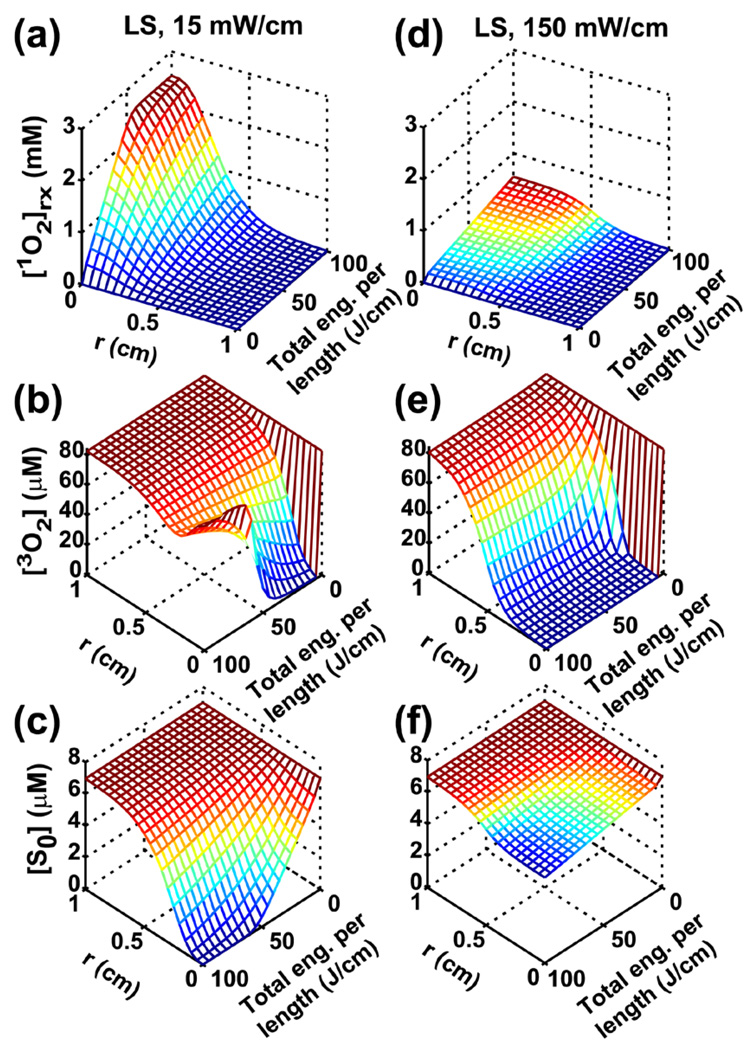
Figure 1.
Spatially- and temporally-resolved distributions for [1O2]rx (a and d), [3O2] (b and e) and [S0] (c and f) for 15 and 150 mW/cm, respectively. r is the radial distance relative to the center of the linear source (LS). For a given total energy released per unit length, 15 mW/cm treatment deposits higher [1O2]rx compared to 150 mW/cm (a vs. d). Oxygen recovery, due to 1O2-mediated photobleaching effect, is clearly shown in (b) (15 mW/cm), which is consistent with the significant photosensitizer degradation shown in (c).
3. RESULTS
The computed spatial and temporal distributions of [1O2]rx, [3O2], and [S0] are shown in Fig. 1 for linear source strengths of 15 (a–c) and 150 (d–f) mW/cm. r is the perpendicular radial distance from the center of linear source. The total energy released per unit source length shown as the third axis is equal to time, t multiplied by the linear source strength. Figure 1 (a) and (d) show that 15 mW/cm deposits higher [1O2]rx than 150 mW/cm for a given total energy released per length, especially in the region close to the linear source. In the 15 mW/cm case, the photosensitizer is almost completely depleted in the region close to light source (Fig. 1c). Photosensitizer concentration decreases due to photobleaching. Figure 1b shows that oxygen replenishes to its pre-treatment level after 100 J/cm light delivery in the 15 mW/cm case.
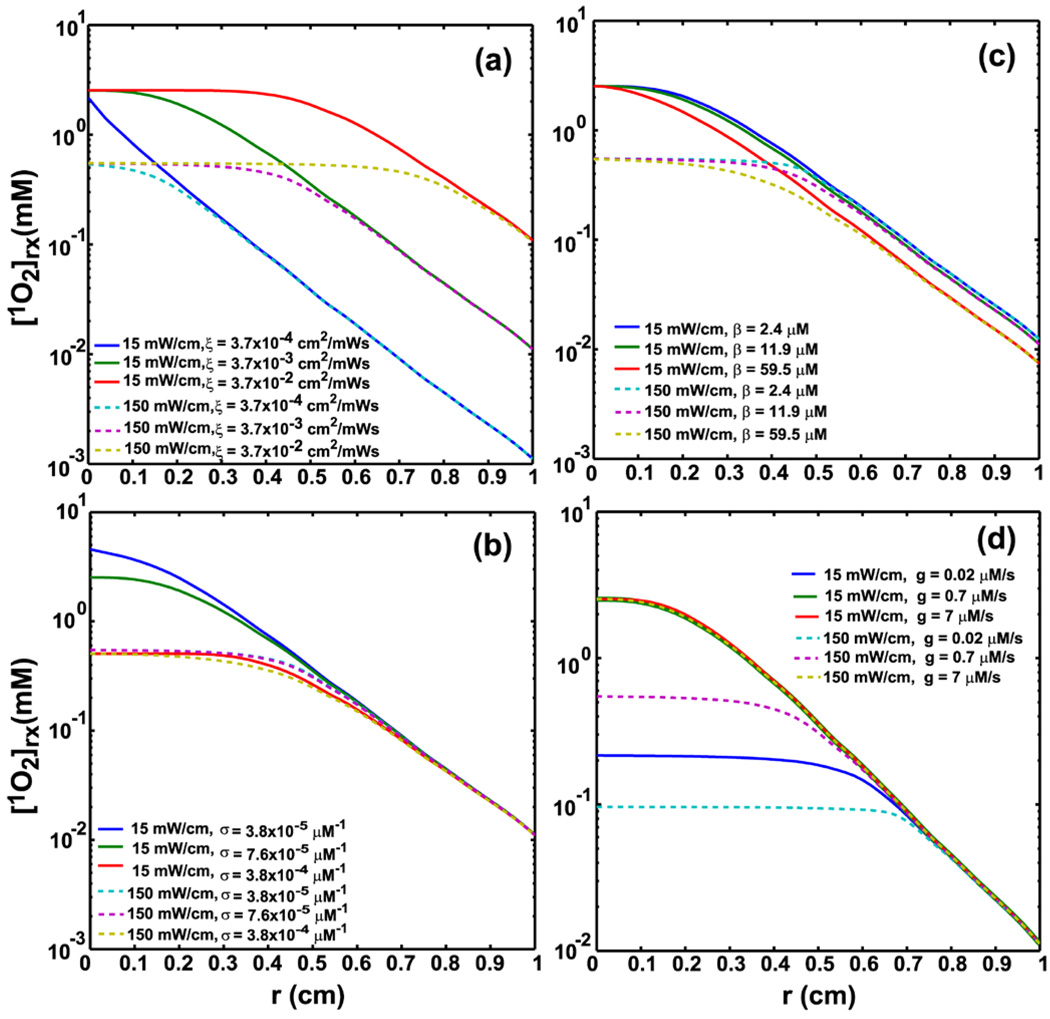
The sensitivity of model parameters ξ, σ, β, and g correlated with [1O2]rx spatial distributions is illustrated in Fig. 2. In each panel, the [1O2]rx is calculated as a function of radial distance from the diffuser while varying one of these parameters. This illustrates the effect of changes in each parameter on the predicted [1O2]rx distribution. Results for two linear source strengths of 15 and 150 mW/cm, respectively, are shown for a delivered energy of 100 J/cm.
Figure 2.
[1O2]rx spatial profiles for 15 and 150 mW/cm for 100 J/cm, in response to the variations of ξ (cm2mW−1s−1) (a), σ (µM−1) (b), β (µM) (c), and g (µM/s) (d). (a) shows the extension of [1O2]rx plateau increases with the increase of ξ. (b) shows that the variations of σ affect mostly on [1O2]rx distributions for the 15 mW/cm case. (c) demonstrates that for small values of β, [1O2]rx profiles is less sensitive to the variations of β. (d) shows that large g values reduce the difference of [1O2]rx spatial distributions for 15 and 150 mW/cm cases.
The result of fitting the PDT-induced necrotic radius with the calculated [1O2]rx is shown in Fig. 3c. The symbols represent the necrotic radius, 0.03, 0.96, and 0.89 mm, for mouse 1, 3, and 7. The way to name these animals is simply to be consistent with the naming used in Fig. 4. The horizontal error bars represent the standard deviation in the experimentally-measured necrotic radius, which is the variation between histology slices for individual mouse. Treatment light is delivered through a cylindrical diffusing fiber (CDF), 1 cm in length, which was inserted into the center catheter as shown in Fig. 3a. The necrotic area is determined on H&E-stained sections made from the treated tumor (as shown in Fig. 3b). Notice the necrotic region (green highlighted area) around the fiber insertion location (the empty space central in the section). The linear source strength and total energy released per length for mouse 1, 3, and 7 are (33 mW/cm and 22 J/cm), (33 mW/cm and 88 J/cm), and (71 mW/cm and 94 J/cm), respectively. The initial photosensitizer concentrations for mouse 1, 3, and 7 were 1.6, 3.7, and 9.1 µM, respectively. The optical properties, (μa and μs’), for mouse 1, 3, and 7 were (1.12 and 19.31), (1.51 and 12.29), and (1.98 and 13) (cm−1). The lines in Fig. 3c are the best fits to the necrotic radius using the measured initial photosensitizer concentrations and optical properties, and the resulting [1O2]rx,sd for mouse 3 and 7 is 1.04 and 0.96 mM, respectively. The [1O2]rx of mouse 1 is below the [1O2]rx,sd and thus the tumor in this mouse should not exhibit PDT-induced necrosis. The observed necrotic radius of mouse 1 can be attributed to experimental uncertainty in the measurement of the necrotic radius. The model parameters obtained from fitting the set of 3 mice are g = 0.69 ± 0.04 (µM/s), and ξ = 0.0021 ± 0.0003 (cm2 mW−1 s−1). The uncertainty of g and ξ is estimated by calculating the [1O2]rx at the location of the necrotic radius within 10 % of the assigned [1O2]rx, sd.
We increase the fitted objects from 3 mice to 9 mice, and the results are shown in Fig. 4a. Figure 4a shows the PDT-induced necrotic radius as symbols with error bars, and the corresponding [1O2]rx for nine mice. Mouse 1, 3, 7 in Fig. 4a are the same animal described in Fig. 3c. The source strength (mW/cm), total energy released per unit length (J/cm), and the initial photosensitizer concentration (µM) for each individual mouse is shown in the legend. To fit this larger group of PDT-induced necrotic radius, we can use the consistent set of model parameters (g, ξ, σ, β) as described in Fig. 3c, but different values of [1O2]rx,sd within narrow range need to be chosen. For this set of mice, the fitted [1O2]rx,sd is determined as 1.04, 0.96, 0.68, 0.53, and 0.47 mM for mouse 3, 7, 4, 9 and 2, respectively. The necrotic radii for mice 1, 5, 6, and 8 were negligible since the values were less than 0.3 mm and can be attributed to measurement uncertainties. Figure 4b plots the PDT-induced necrotic radius vs. PDT dose (J/cm2 µM) for the same nine mice as in Fig. 4a. The PDT dose for each mouse is calculated using the product of delivered light fluence at the edge of PDT-induced necrotic radius and the interstitially measured Photofrin concentration. The solid line is the best linear fit to the data. The linear correlation coefficient between the PDT dose and the necrotic radius is 0.646 corresponding to p-value 0.065.
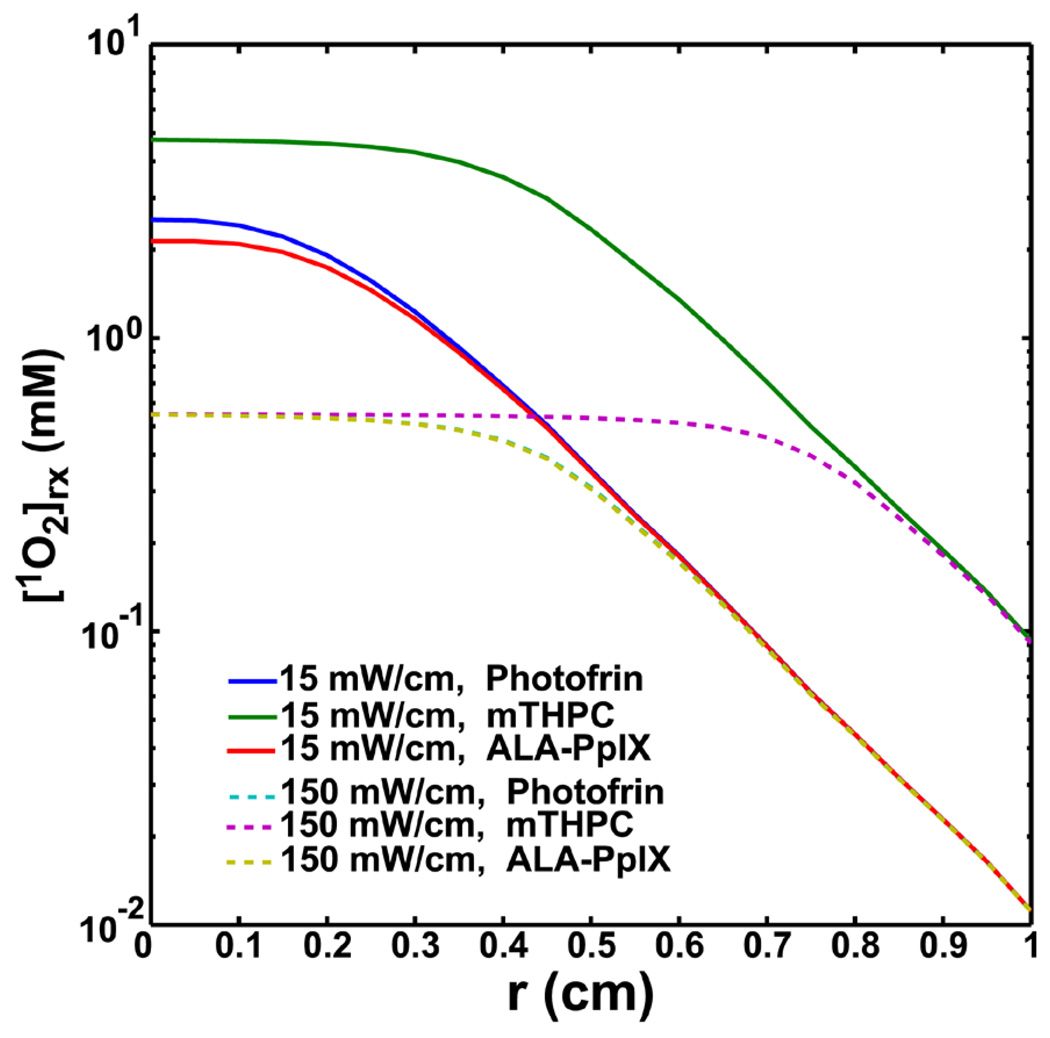
Figure 5 compares the [1O2]rx distributions for Photofrin, mTHPC, and ALA-PpIX for 15 and 150 mW/cm at 100 J/cm at the same concentration as shown in Table 2 (7 µM). Photofrin and ALA-PpIX show very similar behavior due to similar parameters (Table 1). A comparison of the computed [1O2]rx distributions and the corresponding light fluence rate distributions vs. distance r for different light source geometry, point, linear, and, planar source is shown in Fig. 6 (a). For point and linear source, r is the radial distance relative to the source. For planar source, r is the depth relative to tissue surface. We simulate the [1O2]rx and fluence rate distributions with the measured optical properties and sensitizer concentration for mouse 3 described in Fig. 3c and use the results as an example for the comparison for different light source geometry (Fig. 6a). From our in vivo interstitial-PDT using linear source, 0.96 mm, PDT-induced necrotic radius, for mouse 3 is obtained (Fig. 3c). The light fluence rate at 0.96 mm away from the linear source is 126 mW/cm2 by calculating light diffusion equation (Eq. (8)) with the measured optical properties. By fixing the light fluence rate at r = 0.96 mm for the 3 sources setting, we are able to explore the different light geometry setting which give the same PDT-induced necrotic distance. The total treatment time for mouse 3 is 2632 sec which is equal to 332 J/cm2 delivered at the location of 0.96 mm. The vertical dash line shown in Fig. 6a indicates the location of r = 0.96 mm, PDT-induced necrotic distance, away from source locations. Fig. 6b shows the corresponding [3O2] and [S0] distributions for the 3 source setting.
Figure 5.
Spatially-resolved [1O2]rx distributions for Photofrin, mTHPC, and ALA-PpIX for 15 and 150 mW/cm at 100 J/cm. mTHPC-PDT is expected to produce higher [1O2]rx than the other two photosensitizers for both source strength cases. The initial photosensitizer concentration used in the simulation was kept the same for all 3 photosensitizers. The model parameters for this figure are shown in Tables 1 and 2.
4. DISCUSSION
In the time since the first large series of clinical trials for PDT was initiated in 1978 [31] the modality has been approved for the treatment of certain cancers and localized diseases [1–4]. The application of PDT in the clinical setting would be greatly facilitated by a dosimetry metric that can integrate the interactions among light fluence rate, tissue oxygenation, and photosensitizer distribution to predict the treatment efficacy. Currently, the most commonly used PDT dosimetry quantity is the PDT dose, defined as the product of light fluence and photosensitizer concentration. However, the influence of tissue oxygen concentration is not completely taken into account using PDT dose. [1O2]rx proposed in this work is a more advanced quantity than PDT dose because it accounts for the effect of tissue oxygenation. From Eq. (12), in an ample oxygen environment ([3O2] ≫ β), [1O2]rx is directly proportional to PDT dose. In other words, [1O2]rx is equivalent to PDT dose when no hypoxia is induced, but for high fluence rate treatments or treatment in hypoxic tissue, [1O2]rx is a more accurate dosimetric quantity. A general oxygen supply term (Eq. (13)) has also been incorporated in the model to account for the microscopic oxygen diffusion and convection mechanism [11]. To further improve the model’s predicative power, PDT-induced blood flow changes [23, 24] can be included by modifying g as a function of treatment time, PDT dose, or reacted singlet oxygen concentration.
The 15 and 150 mW/cm treatment scenario shown in Fig. 1 represent the interstitial PDT at low and high fluence rate, respectively. From Fig. 1b, our results show that oxygen recovers to its pre-treatment level after 100 J/cm light delivery in the low fluence rate case. However, oxygen concentrations fail to recover in the high fluence rate case (Fig. 1e), and, as a result, less [1O2]rx is produced (Fig. 1 d and e vs. a and b). Therefore, better treatment outcome is expected for the 15 mW/cm (or low fluence rate) case. The fluence rate effect on the treatment efficacy cannot be evaluated using the “PDT dose” alone.
Production of [1O2]rx is determined by several factors. The initial photosensitizer concentration and tissue optical properties can be determined by interstitial fluorescence measurement [27] and a light dosimetry system [28], as described in Method section. Even though the initial oxygen concentration is fixed as a constant in the current simulation (Table 2), more realistic tissue oxygenation can, in principle, be derived from hemoglobin oxygen saturation using absorption spectroscopy in future practice [32, 33]. Besides explicit dosimetry necessary for light fluence, photosensitizer concentration, and oxygen concentration, determining the four model parameters (g, ξ, σ, β) is also essential to calculate the [1O2]rx. Figure 2a shows the maximum value of the [1O2]rx for a given source strength increases with increasing ξ. The physiological parameter g characterizes the oxygen perfusion rate. Figure 2d suggests that a large value of g, e.g., g = 7 µM/s, is inappropriate because under these circumstances the [1O2]rx profiles are indistinguishable for 15 and 150 mW/cm cases, thus producing a result that is contradictory to the preclinical finding [7, 34] that high and low fluence rate treatment produce different treatment outcome. The g value is extremely sensitive to change in the shape of the [1O2]rx profile, especially for the 150 mW/cm condition. This result suggests the accuracy of the g value is especially important for the treatment involving high fluence rate treatment. Increasing σ will increase photosensitizer photobleaching but will reduce [1O2]rx, which is obvious for 15 mW/cm case (Fig. 2b). Fig. 2b also indicates that σ is sensitive to [1O2]rx only at low linear source strength (15 mW/cm) but not at high source strength (150 mW/cm). This observation renders that σ is not sensitive to [1O2]rx when high fluence rate treatment is performed. Compared to the other parameters, β has less influence on the shape of the [1O2]rx concentration (Fig. 2 c vs. a, b, and d). From the study of Georgakoudi et al. [16] and Mitra et al. [30] (Table 1), the β value is almost a constant for different photosensitizers. One can simply use Eq. (12) to calculate the in vivo [1O2]rx with a fixed β value, if the [3O2] concentration is known. Our current model is capable of varying all four parameters (g, ξ, σ, β) simultaneously, with a random assigned [1O2]rx,sd to fit the PDT-induced necrotic radius. However, due to random selection of the fitting model parameters in the differential evolution method, some combination of the model parameters will produce divergence solution for the PDT kinetics equations. Therefore, to stabilize the current fitting routine, we choose to vary the most important parameters, g and ξ and fix the other two parameters. As indicated in Fig. 2 and from published literature [16] [30], we conclude that the value of β is insensitive to the [1O2]rx. Since we have relatively high linear source strength (> 33 mW/cm) used in this study, we choose to fix σ using published data. Future works include improving the fitting methodology, such as constructing a [1O2]rx library as a function of model parameters, fluence rate, and, sensitizer concentration. Fitting algorithm can thus search valid [1O2]rx solutions, specified in the library, to fit the necrotic radius, and avoid the divergence.
Comparing Figs. 1a and c, we notice that the highest [1O2]rx concentration after depleting all the photosensitizer is only 2.5 mM, about 4.8 times lower than the published threshold dose of 11.9 mM for Photofrin [16]. This is consistent with published literature, e.g., none of the calculated 1O2 concentrations for in vivo mTHPC-PDT [15] are close to the mTHPC threshold dose 7.9 mM [30]. To reasonably fit the necrotic radius, the resulting quantity, [1O2]rx,sd, should be in the 0.1 – 1 mM range.
Using the current algorithm and necrosis data, we are able to extract the model parameters (g and ξ) and [1O2]rx,sd for in vivo Photofrin-mediated PDT (Fig. 3c) using a non-linear optimization algorithm. The fitted ξ is 0.0021 (cm2 mW−1 s−1), which is 43 % lower than the published value 0.0037 (cm2 mW−1 s−1) extracted from the spheroid model [16]. The values of σ and β are taken from the literature and held constant during the fitting (see Table 1). The threshold value of the apparent reacted singlet oxygen concentration, [1O2]rx,sd = 1 ± 0.04 mM, was determined from the fitting to data for the 2 mice (3 and 7) used in Fig. 3c. Fig. 3c demonstrates that the full set of model parameters (ξ, σ, β, g) and [1O2]rx,sd can be potentially obtained by fitting the computed [1O2]rx to the PDT-induced necrotic radius. Thus, after those parameters determined rigorously, the computed [1O2]rx can be used to assess the treatment outcome of Photofrin-mediated PDT under clinical environment.
We want to emphasize that the macroscopic model calculated value is named “apparent” reacted singlet oxygen [1O2]rx because it is not necessarily numerically the same as the actual 1O2 distribution on the microscopic scale [6, 11–13]. The intention is to use the empirical model to improve the PDT dosimetry as a predictor of tumor necrosis.
The fitting result is further examined using a larger group of mice data by adding another 6 mice to the previously described 3 mice (Fig. 3c), as shown in Fig. 4a. From this preliminary result, we are able to fit the computed [1O2]rx to the necrotic radii of mouse 3, 7, 4, 9, and 2 with the consistent set of model parameters (ξ, σ, β, g) described in Fig. 3c. However, a single value of [1O2]rx,sd cannot explain this larger group of data; instead different values of [1O2]rx,sd, within a narrow range are found. Our result suggests three values of [1O2]rx,sd, i.e., 1 mM for mouse 3 and 7, 0.68 mM for mouse 4, and 0.5 mM for mouse 2 and 9. This result suggests an average value for [1O2]rx,sd of 0.74 mM with a standard deviation of 0.25 mM. We attribute this 34 % deviation to be due to the uncertainty of interstitial photosensitizer concentration, optical properties, and necrosis measurements in the mice. Future works are needed to reduce the range of [1O2]rx,sd by minimizing the experimental uncertainties. Even though the necrotic radius is generally proportional to the PDT dose as shown in Fig. 4b, the statistical analysis (p = 0.065) does not demonstrate that the PDT dose and the PDT-induced necrotic radius are significantly correlated. PDT dose alone cannot predict light fluence rate effect, e.g., the result for mouse 7 deviates from a linear relationship between necrotic radius and PDT dose. Using the [1O2]rx with a set of model parameters and a single [1O2]rx, sd (Fig. 4a), we are able to predict the necrotic radius for mouse 3 and 7. This provides evidence that the calculated [1O2]rx by the macroscopic model is better than PDT dose alone for clinical use.
Figures 5 and 6 demonstrate the potential dependence of the computational [1O2]rx on choice of photosensitizer and light source geometry, respectively. The differences of [1O2]rx distributions shown in Fig. 5 probably reflect the photosensitizer dependency of the model parameters (Table 1). Due to larger ξ and smaller σ values, mTHPC-PDT produced higher amount of [1O2]rx and induced larger extension of the flat region, consistent with the finding of Fig. 2a and b. The numerical study of Wang et al. [15] demonstrated that the 1O2 dosimetry is not able to predict long-term tumor response at several drug-light interval for in vivo mTHPC-PDT. In our current study, we show the “apparent reacted singlet oxygen” [1O2]rx can be a practical clinical dosimetry quantity if we empirically optimize the model parameters and [1O2]rx, sd for the specific photosensitizer under in vivo environment (Fig. 3c). Therefore, the methodology proposed in this work can be potentially applied to in vivo mTHPC-PDT. Fig. 6a shows that the difference among [1O2]rx profiles is reduced in regions close to the source because the high 1O2 production almost completely degrades the sensitizer amount in this region even abundant oxygen is available (Fig. 6b). We notice that after r = 0.96 mm, the level of the [1O2]rx is highest for the planar source among the three light source geometries due to the highest fluence rate emitted from the planar source (Fig. 6a). This result suggest that under the condition of the optical properties, sensitizer concentration, and tissue oxygenation used in this simulation, the planar source geometry may have better treatment outcome than the others.
It is well known that PDT can not only induce cell death through necrosis but also apoptosis [35]. Lilge et al. quantified the incidence of apoptosis in normal brain and intracranial VX2 tumor 24 hours following PDT with 5 different photosensitizers (Photofrin, ALA/PpIX, chloroaluminium phthalocyanine (AlClPc), Tin Ethyl Etiopurpurin (SnET2), and mTHPC) [36]. Except for AlClPc, PDT with other photosensitizers produced apoptotic cells near the region of coagulative necrosis. The occurrence of apoptosis beyond the boundary of necrosis indicates that the model parameters and [1O2]rx, sd estimated by the macroscopic model incorporating the necrotic radius can be possibly different if larger cell death boundary is considered. Future work on quantifying the spatial distributions of in vivo PDT-induced apoptosis, such as incorporating TUNEL assay combined with molecular image modality [36, 37], is expected to improve the current methodology.
The computational speed of this macroscopic model is generally fast and can be applied to clinical use for any heterogeneous distributions of light sources and photosensitizer distributions, with a calculation time of better than 300 seconds for forward calculation of [1O2]rx. In the future we will focus on improving the ability of fitting the model parameters for Photofrin and other photosensitizers by matching necrotic radius with [1O2]rx. We will also reduce the measurement uncertainties to minimize the variation of [1O2]rx,sd. The “apparent singlet oxygen concentration”, [1O2]rx, coupled with explicit dosimetry of in vivo photosensitizer concentration, tissue optical properties, and tissue oxygenation, can be potentially used as a clinically practical dosimetry quantity.
5. CONCLUSION
A four parameter (ξ, σ, β, g) empirical macroscopic model is proposed in this work. The apparent singlet oxygen concentration, [1O2]rx can be used as an improved dosimetry quantity (vs. PDT dose) because it accounts for the fluence rate dependence due to oxygen consumption. From our preliminary results for Photofrin, we are able to fit the measured necrotic radius using the computed [1O2]rx to obtain essential model parameters g and ξ, and the fitted [1O2]rx,sd. More comprehensive studies are needed to refine the optimization procedures to improve the robustness and convergence of the fitting algorithm and reduce measurement uncertainties. Once the model parameters and [1O2]rx,sd are determined for a particular photosensitizer, we expect this macroscopic model to be used directly in clinical trials to potentially better predict the treatment outcome.
ACKNOWLEDGEMENTS
The authors would like to thank pathologist Dr. Michael D. Feldman for his help in reading the H&E-stained slides and for providing ScanScope and the image software. We would also like to thank Elizabeth Rickter and Amanda Mass for invaluable help in setting up the mice experiments. This work is supported by grants from National Institute of Health (NIH) RO1 CA109456 and PO1 CA87971.
Biographies

Dr. Ken Kang-Hsin Wang received his Ph.D in 2008 in Physics from the University of Rochester, and came to the Radiation Oncology department in the University of Pennsylvania as a postdoctoral researcher. Explicitly characterizing reacted singlet oxygen [1O2]rx and optical properties of tumor tissue are important subjects in photodynamic therapy (PDT). His current research subjects are developing a macroscopic modeling which can be used as an explicit dosimetry for clinical PDT, and reconstructing images of tissue optical properties using interstitial light measurement.

Jarod C. Finlay received his Ph.D. in Physics in 2004 from the University of Rochester, where he specialized in optical spectroscopy and its use in photodynamic therapy. He is currently an Assistant Professor of Radiation Oncology at the University of Pennsylvania. Dr. Finlay’s research focuses on clinical and pre-clinical studies of photodynamic therapy, with an emphasis on quantitative dosimetry and optical spectroscopy.

Theresa M. Busch received her Ph.D. in Biophysics from the Roswell Park Cancer Institute Graduate Division of the University of Buffalo, State University of NY. She is currently an assistant professor in the Department of Radiation Oncology, School of Medicine, University of Pennsylvania. She is interested in the effects of photodynamic therapy on tumor microenvironment, and her research includes the study of factors such as fluence rate, photosensitizer concentration, blood flow, and tumor oxygenation as modulators of therapeutic response to PDT.

Stephen M. Hahn, MD is the Chair and Henry K. Pancoast Professor of Radiation Oncology at the University of Pennsylvania School of Medicine. Dr. Hahn is an active clinician, with particular expertise in treating lung and genitourinary cancers and in the use of photodynamic therapy. Board certified in Internal Medicine, Radiation Oncology, and Hematology/Oncology, Hahn received his medical degree from Temple University School of Medicine and his undergraduate degrees from Rice University. In 1987, he completed his residency and served as Chief Resident of Internal Medicine at the University of California, San Francisco. Hahn also completed a Medical Oncology Fellowship at the NCI in 1991, and a Radiation Oncology Residency at the NCI in 1994. Hahn has served as Director of Penn’s Photodynamic Therapy program, which treats cancer patients through a minimally invasive process that uses a photosensitizer and concurrent laser light to selectively destroy tumors. He also directs the Farnesyltransferase Inhibitor Program for Treatment of cancer of the lung, head and neck and pancreas. In addition, Hahn is the Co-Program Leader of the Radiation Biology and Imaging Research Program in the Abramson Cancer Center of the University of Pennsylvania.

Timothy C. Zhu received his Ph.D in 1992 in Physics from Brown University. He is currently an associate professor at the Radiation Oncology department of the University of Pennsylvania. His current research interests include explicit PDT dosimetry, integrated system for interstitial PDT, diffuse optical tomography, in-vivo dosimetry, and external beam radiation transport.
APPENDIX
Derivation of the governing equations for the macroscopic model
We start from the Type II PDT kinetics equations with 1O2-mediated bleaching mechanism to derive the governing equations for the macroscopic model.
| (A1) |
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
All the definitions for the parameter and variables are either defined in the Method section or Table 1 and 2. Since the lifetime of the excited species [S1], [T], and [1O2] are much shorter than their ground state species [S0] and [3O2] (ns to µs vs. s to hrs). We can treat [S1], [T], and [1O2] as reaching instantaneous steady state relative to the ground state sensitizer and oxygen population. We are only interested in the variation in the time scale from second to hours. This assumption allows us to simplify Eqs. (A2), (A3), and (A5) by setting d[S1]/dt, d[T]/dt, and d[1O2]/dt to equal to zero. The approximated kinetic equations can be written as follows,
| (A8) |
| (A9) |
| (A10) |
| (A11) |
| (A12) |
Notice that the term (k1[S0]+δ) + k7[A] in the denominators of Eqs. (A8), (A9), and (A12) was replaced by k7[A] since k1[S0]+δ ≪ k7[A]. The accumulated [1O2]rx killing cell targets can be estimated by calculating time integral of Eq. (A6),
| (A13) |
We can rewrite Eq. (A13) using Eq. (A12) as,
| (A14) |
Applying the definition of the variables defined in Table 1 to Eqs. (A8), (A9), and (A14), then taking time derivative of Eq. (A14), and incorporating the light diffusion equation, we can write down the governing equations of our macroscopic model;
| (A15) |
| (A16) |
| (A17) |
| (A18) |
Footnotes
PACS: 87.54.Fj
REFERENCES
- 1.Brown SB, Brown EA, Walker I. Lancet Oncol. 2004;5(8):497–508. doi: 10.1016/S1470-2045(04)01529-3. [DOI] [PubMed] [Google Scholar]
- 2.Moore CM, Pendse D, Emberton M. Nat. Clin. Pract. Urol. 2009;6(1):18–30. doi: 10.1038/ncpuro1274. [DOI] [PubMed] [Google Scholar]
- 3.Nyst HJ, Tan IB, Stewart FA, Balm AJ. Photodiagnosis Photodyn. Ther. 2009;6(1):3–11. doi: 10.1016/j.pdpdt.2009.03.002. [DOI] [PubMed] [Google Scholar]
- 4.Zhu TC, Finlay JC. Med Phys. 2008;35(7):3127–3136. doi: 10.1118/1.2937440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gulledge CJ, Dewhirst MW. Anticancer Res. 1996;16(2):741–749. [PubMed] [Google Scholar]
- 6.Foster TH, Murant RS, Bryant RG, Knox RS, Gibson SL, Hilf R. Radiat Res. 1991;126(3):296–303. doi: 10.2307/3577919. [DOI] [PubMed] [Google Scholar]
- 7.Sitnik TM, Hampton JA, Henderson BW. Br J Cancer. 1998;77(9):1386–1394. doi: 10.1038/bjc.1998.231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lee S, Vu DH, Hinds MF, Davis SJ, Liang A, Hasan T. J Biomed Opt. 2008;13(6) doi: 10.1117/1.3042265. 064035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jarvi MT, Niedre MJ, Patterson MS, Wilson BC. Photochem Photobiol. 2006;82(5):1198–1210. doi: 10.1562/2006-05-03-IR-891. [DOI] [PubMed] [Google Scholar]
- 10.Yamamoto J, Yamamoto S, Hirano T, Li S, Koide M, Kohno E, Okada M, Inenaga C, Tokuyama T, Yokota N, Terakawa S, Namba H. Clin Cancer Res. 2006;12(23):7132–7139. doi: 10.1158/1078-0432.CCR-06-0786. [DOI] [PubMed] [Google Scholar]
- 11.Wang KK, Mitra S, Foster TH. Med Phys. 2007;34(1):282–293. doi: 10.1118/1.2401041. [DOI] [PubMed] [Google Scholar]
- 12.Henning JP, Fournier RL, Hampton JA. Radiat Res. 1995;142(2):221–226. [PubMed] [Google Scholar]
- 13.Pogue BW, Hasan T. Radiat Res. 1997;147(5):551–559. doi: 10.2307/3579621. [DOI] [PubMed] [Google Scholar]
- 14.Hu XH, Feng Y, Lu JQ, Allison RR, Cuenca RE, Downie GH, Sibata CH. Photochem Photobiol. 2005;81(6):1460–1468. doi: 10.1562/2005-05-04-RA-513. [DOI] [PubMed] [Google Scholar]
- 15.Wang KK, Mitra S, Foster TH. Med Phys. 2008;35(8):3518–3526. doi: 10.1118/1.2952360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Georgakoudi I, Nichols MG, Foster TH. Photochem. Photobiol. 1997;65(1):135–144. doi: 10.1111/j.1751-1097.1997.tb01889.x. [DOI] [PubMed] [Google Scholar]
- 17.Patel H, Mick R, Finlay J, Zhu TC, Rickter E, Cengel KA, Malkowicz SB, Hahn SM, Busch TM. Clin Cancer Res. 2008;14(15):4869–4876. doi: 10.1158/1078-0432.CCR-08-0317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nathan TR, Whitelaw DE, Chang SC, Lees WR, Ripley PM, Payne H, Jones L, Parkinson MC, Emberton M, Gillams AR, Mundy AR, Bown SG. J Urol. 2002;168(4 Pt 1):1427–1432. doi: 10.1016/S0022-5347(05)64466-7. [DOI] [PubMed] [Google Scholar]
- 19.Wang KK-H, Busch TM, Finlay JC, Zhu TC. Proc. of SPIE. 2009;7164 doi: 10.1117/12.809024. 71640O. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhu TC, Finlay JC, Zhou X, Li J. Proc. SPIE. 2007;6427:1–12. doi: 10.1117/12.701387. 642708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dysart JS, Singh G, Patterson MS. Photochem Photobiol. 2005;81(1):196–205. doi: 10.1562/2004-07-23-RA-244. [DOI] [PubMed] [Google Scholar]
- 22.Finlay JC. Ph.D. Thesis. Rochester: University of Rochester; 2003. Reflectance and fluorescence spectroscopies in photodynamic therapy. [Google Scholar]
- 23.Yu G, Durduran T, Zhou C, Wang HW, Putt ME, Saunders HM, Sehgal CM, Glatstein E, Yodh AG, Busch TM. Clin Cancer Res. 2005;11(9):3543–3552. doi: 10.1158/1078-0432.CCR-04-2582. [DOI] [PubMed] [Google Scholar]
- 24.Wang KK, Cottrell WJ, Mitra S, Oseroff AR, Foster TH. Lasers Surg Med. 2009;41(9):686–696. doi: 10.1002/lsm.20847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Busch TM, Xing X, Yu G, Yodh A, Wileyto EP, Wang HW, Durduran T, Zhu TC, Wang KK. Photochem Photobiol Sci. 2009;8(12):1683–1693. doi: 10.1039/b9pp00004f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Finlay JC, Conover DL, Hull EL, Foster TH. Photochem Photobiol. 2001;73(1):54–63. doi: 10.1562/0031-8655(2001)073<0054:pbapis>2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 27.Finlay JC, Zhu TC, Dimofte A, Stripp D, Malkowicz SB, Busch TM, Hahn SM. Photochem Photobiol. 2006;82(5):1270–1278. doi: 10.1562/2005-10-04-RA-711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dimofte A, Finlay JC, Zhu TC. Phys. Med. Biol. 2005;50(10):2291–2311. doi: 10.1088/0031-9155/50/10/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Storn R, Price K. J. Global Optimization. 1996;11:341–359. [Google Scholar]
- 30.Mitra S, Foster TH. Photochem. Photobiol. 2005;81(4):849–859. doi: 10.1562/2005-02-22-RA-447. [DOI] [PubMed] [Google Scholar]
- 31.Dougherty TJ, Kaufman JE, Goldfarb A, Weishaupt KR, Boyle D, Mittleman A. Cancer Res. 1978;38(8):2628–2635. [PubMed] [Google Scholar]
- 32.Finlay JC, Wang KK-H, Hu Y, Zhu TC. Proc. of SPIE. 2009;7380 doi: 10.1117/12.822964. 738044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang HW, Zhu TC, Putt ME, Solonenko M, Metz J, Dimofte A, Miles J, Fraker DL, Glatstein E, Hahn SM, Yodh AG. J Biomed Opt. 2005;10(1):14004. doi: 10.1117/1.1854679. [DOI] [PubMed] [Google Scholar]
- 34.Sitnik TM, Henderson BW. Photochem Photobiol. 1998;67(4):462–466. [PubMed] [Google Scholar]
- 35.Oleinick NL, Morris RL, Belichenko I. Photochem Photobiol Sci. 2002;1(1):1–21. doi: 10.1039/b108586g. [DOI] [PubMed] [Google Scholar]
- 36.Lilge L, Portnoy M, Wilson BC. Br J Cancer. 2000;83(8):1110–1117. doi: 10.1054/bjoc.2000.1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bogaards A, Varma A, Zhang K, Zach D, Bisland SK, Moriyama EH, Lilge L, Muller PJ, Wilson BC. Photochem Photobiol Sci. 2005;4(5):438–442. doi: 10.1039/b414829k. [DOI] [PubMed] [Google Scholar]
- 38.Nichols MG, Foster TH. Phys Med Biol. 1994;39(12):2161–2181. doi: 10.1088/0031-9155/39/12/003. [DOI] [PubMed] [Google Scholar]
- 39.Georgakoudi I, Foster TH. Photochem Photobiol. 1998;67(6):612–625. [PubMed] [Google Scholar]
- 40.Li J, Zhu TC, Finlay JC. Proc. SPIE. 2006;6139 doi: 10.1117/12.646251. 61390M. [DOI] [PMC free article] [PubMed] [Google Scholar]