Quantification of the optical properties of two-layered turbid media by simultaneously analyzing the spectral and spatial information of steady-state diffuse reflectance spectroscopy

Abstract

We applied hyperspectral imaging to measure spatially-resolved diffuse reflectance spectra in the visible range and an iterative inversion method based on forward Monte Carlo modeling to quantify optical properties of two-layered tissue models. We validated the inversion method using spectra experimentally measured from liquid tissue mimicking phantoms with known optical properties. Results of fitting simulated data showed that simultaneously considering the spatial and spectral information in the inversion process improves the accuracies of estimating the optical properties and the top layer thickness in comparison to methods fitting reflectance spectra measured with a single source-detector separation or fitting spatially-resolved reflectance at a single wavelength. Further development of the method could improve noninvasive assessment of physiological status and pathological conditions of stratified squamous epithelium and superficial stroma.

1. Introduction

Diffuse reflectance spectroscopy (DRS) has been widely used to interrogate the scattering and absorption properties of turbid media such as soft tissue. Quantification of tissue optical properties, namely, the absorption coefficient (μ_a) and the reduced scattering coefficient (µ_s'), enables noninvasive probing of blood content, oxygenation status and microstructure of the tissue. One application with a significant impact on health care is to noninvasively detect changes in tissue optical properties associated with intraepithelial neoplasia, a precursor of carcinoma or cancer [1–5]. Early detection of cancer and its precursor leads to more effective treatments and therefore lower mortality and higher quality of life. During the progression of intraepithelial neoplasia, scattering of light in the epithelium increases due to increased nuclear-to-cytoplasmic ratio and denser chromatin clumps of epithelial cells. In the stroma which consists mainly of connective tissue and blood vessels, hemoglobin absorption increases due to angiogenesis accompanying the development of precancers. Moreover, there have been experimental evidences indicating that scattering in the stroma decreases due possibly to the breakdown of collagen network [1,2,6,7].

Extraction of tissue optical properties from diffuse reflectance measurements is typically achieved by establishing a forward model to predict the diffuse reflectance given average optical properties of the bulk tissue and then fitting the predicted reflectance to the measured data or comparing the measured data to a pre-calculated database. Various forward models have been developed to describe photon propagation in turbid media and used to quantify tissue optical properties from simulated data or experimental data from tissue mimicking phantoms. Examples of forward models include analytical models using the diffusion approximation to solve the radiative transport equation [8–14], numerical models based on Monte Carlo (MC) simulations [15–20] and empirical models [5,21]. Instruments used to measure diffuse reflectance for the quantification of tissue optical properties can be categorized into time-resolved [22], frequency-domain [23] and steady-state methods [5,8–21]. Time-resolved and frequency-domain approaches are limited to near-infrared wavelengths with relatively large penetration depths (>2 mm) and are not be suitable for detecting optical properties of epithelium and superficial stroma where epithelial precancer and early cancer reside. Steady-state detection of diffuse reflectance can be achieved with UV-visible light which has shallower penetration depths in tissue of less than 1 mm [24]. Therefore, we focus on steady-state DRS techniques in this paper. By measuring and analyzing diffuse reflectance at multiple source-detector separations (SDS) which is known as spatially-resolved diffuse reflectance, reasonably high accuracies of quantifying the optical properties of homogeneous tissue mimicking phantoms have been demonstrated [9,13–15,18–21]. Spatially-resolved steady-state DRS systems can be equipped with a broadband light source and a spectral detection device to achieve fast acquisition of full spectra and more robust identification and quantification of multiple chromophores present in the tissue [13,14,18,19].

On the other hand, there have been studies showing that a diffuse reflectance spectrum measured from only one location at the sample surface, either with a single optical fiber or by combining photons collected with multiple fibers, is sufficient to quantify tissue optical properties when proper constraints are applied to the spectral dependences of the optical coefficients [5,8,10–12,16,17]. In principle, tissue optical properties can be determined as long as the number of measured wavelengths is at least equal to the number of unknown parameters to be determined. In practice, spectra are usually measured with many more wavelengths to reduce the effect of inevitable noise. Detecting reflectance from a single area of tissue has the advantage of making compact probes which are highly desired for in vivo applications [5,10–12,17]. However, accurate descriptions of the wavelength-dependent absorption and scattering properties of tissues, which might be difficult to obtain in vivo, are necessary to get accurate results by using this approach.

Applying DRS for noninvasive detection of precancer in stratified squamous epithelium such as that in the uterine cervix, oral cavity and skin faces a challenge that changes in the reduced scattering coefficients associated with neoplasia are in opposite directions for the epithelium and the stroma. Using a homogeneous tissue model to fit DRS data of two-layered tissues in which the layers have different optical properties may result in large errors in extracted optical properties [25]. Despite the fact that various forward models have been established to describe photon propagation in layered scattering media, extracting optical properties of two-layered media [25–28] are less successful than extracting optical properties of homogeneous tissues. The development of a DRS-based method capable of accurately quantifying the reduced scattering coefficients of the epithelium and the stroma separately could improve the sensitivity of detecting precancerous changes in stratified squamous epithelium and may have great impact on early diagnosis of cancer.

We propose the applications of hyperspectral imaging to obtain diffuse reflectance spectra from each pixel in a two-dimensional image and iterative inversion based on forward MC modeling to extract optical properties of a two-layered tissue model. Hyperspectral imaging-based systems have been used to measure spatially-resolved diffuse reflectance spectra for the determination of absorption and scattering properties of turbid media [19,27]. Our approach differs in two aspects. First, we use an imaging fiber-optic bundle in contact with the sample to collect reflected photons as opposed to the previously reported noncontact configuration. Second, we impose spectral constraints on the optical properties and include both the spectral and the spatial characteristics of the measured diffuse reflectance data as the input to the inversion process. After validating the forward MC method and the inversion procedure by comparing with independent MC simulations and experimentally measuring homogeneous tissue mimicking phantoms, respectively, we demonstrate that simultaneously analyzing diffuse reflectance spectra collected at multiple source-detector separations (SDSs) improves the accuracy of estimating the optical properties and top layer thickness of two-layered tissue models.

2. Materials and methods

2.1. Experimental setup for spatially-resolved DRS

We incorporated an industrial grade plastic imaging fiber bundle (Tonder Lock Industrial Corp.) into a hyperspectral imaging system based on imaging Fourier transform spectrometry to measure spatially-resolved reflectance spectra from turbid media. A schematic diagram of the experimental setup is shown in Fig. 1 . Detailed descriptions of the optical setup and characteristics of the hyperspectral imaging system have been published [29]. Briefly, a hyperspectral imaging data cube was obtained by capturing a series of images at regularly spaced optical path-length differences between two beams in an interferometer, recording the interference intensity as a function of the optical path-length difference for each pixel (interferogram), and Fourier transforming the interferograms pixel by pixel. We acquired a hyperspectral imaging data cube in 5 seconds with an exposure time of 50 ms per image. The fiber bundle consisted of 7400 fibers with a nominal numerical aperture (NA) of 0.5 and core diameters of about 20 μm. A single fiber with a core diameter of 200 μm was tightly attached to the distal end of the fiber bundle to couple white light from a Xenon arc lamp to the turbid media. The end surface of the source fiber was level with that of the fiber bundle. The proximal end of the fiber bundle was imaged by a 4 × microscope objective.

Fig. 1.

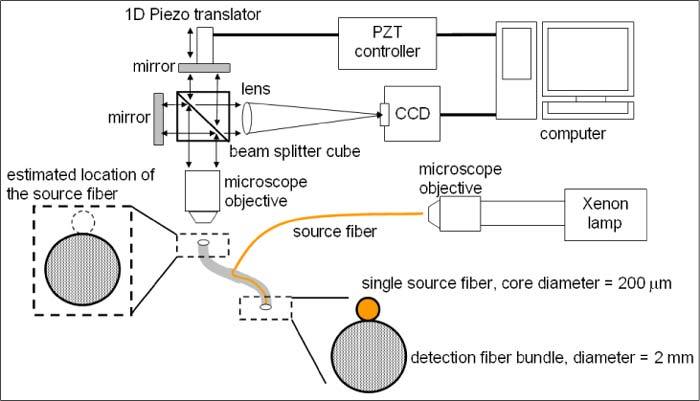
Schematic diagram of the experimental setup. One source fiber and an imaging fiber bundle formed a simple fiber package whose distal end was in contact with the sample. The proximal end of the fiber bundle was positioned at the focal plane of the objective for the acquisition of hyperspectral images of the sample via the fiber bundle.

2.2. Forward MC model

The numerical MC method was used to model photon transport in this study mainly because of its flexibility to work for arbitrary probe geometry. The main shortcoming of MC modeling is computational complexity which impedes its application as an inverse model to extract optical properties from diffuse reflectance spectra. We adopted the strategy proposed by Liu et al., using fast scaling MC as the forward model to obtain a diffuse reflectance spectrum of layered media with a single MC run [30]. First, a conventional two-layered variable weight MC code similar to the MCML method was developed in C/C++ [31]. Photons were launched in a single ray to create a photon trajectory database or an impulse response of a baseline medium with µ_a = 0 cm⁻¹ and µ_s' = 100 cm⁻¹. The Henyey-Greenstein phase function was used to model the probability distribution of single scattering angle. The coordinates of all the photon scattering events were recorded and used to scale photon propagation steps according to the optical coefficients of the target medium relative to those of the baseline medium [32]. Total number of scattering events for each photon exiting the sample was also recorded to calculate the photon weight. All photons leaving the sample from the top surface were considered to be collected by the detection fibers to increase computational efficiency. The effect of ignoring the finite NA of the detection fibers was assumed to be equivalent to multiplying the reflectance by a proportional constant, which could be corrected by proper calibration. Because fibers with finite areas were used to illuminate the sample and collect reflected photons, convolution of the impulse response was performed after scaling to estimate the detected reflectance given the SDS and the diameters of the source and detection fibers [15].

To establish a two-layered tissue model for MC simulations, the absorption coefficients (µ_a), scattering coefficients (µ_s) and anisotropy factors (g) of the two layers and the thickness of the top layer needed to be predetermined. We assumed that hemoglobin is the dominant absorber in non-skin soft tissues under visible light illumination and expressed the wavelength-dependent absorption coefficient of the tissue model by the equation [8,15]

$${\mu }_a(\lambda )=f_{Hb}[St{O}_2{\mu }_a{}^{oxy}(\lambda )+(1-StO{}_2){\mu }_a{}^{deoxy}(\lambda )]$$ (1)

where μ_a^oxy(λ) and μ_a^deoxy(λ) are wavelength-dependent absorption coefficients of oxygenated hemoglobin and deoxygenated hemoglobin, respectively [33]. f_Hb is total hemoglobin concentration and StO₂ is oxygen saturation of the tissue. This equation could be modified to include melanin absorption for modeling epidermis/skin or water absorption for wavelengths longer than about 800 nm. The reduced scattering coefficient, μ_s' = μ_s(1−g), combines µ_s with g into one parameter to describe approximately isotropic diffusion of photon energy in turbid media. In soft tissues, the wavelength-dependent reduced scattering coefficient has been modeled as a power-law equation [5,13]

$${\mu }_s\text{'}(\lambda )=A{\lambda }^{-k}$$ (2)

where A and k are constants. Given f_Hb, StO₂, A and k of the top and the bottom layers, µ_a and µ_s' of each wavelength were computed by using Eqs. (1) and (2) and were used to calculate SDS-dependent reflectance at the corresponding wavelength. For all MC simulations a constant g of 0.9 was used and the refractive indices of the medium and the fibers were 1.338 and 1.462, respectively. The thickness of the top layer, if used, was 0.3 mm to represent the epithelium. The bottom layer was semi-infinite with a thickness of 50 mm to represent the stroma.

2.3. Inversion procedure to quantify optical properties

An iterative nonlinear curve fitting method, the Levenberg-Marquardt algorithm, was used to minimize the difference between input data and reflectance spectra calculated by using the forward scaling MC code [17]. Because the intensity of diffuse reflectance decreases monotonically with SDS, the accuracy of the inversion procedure is mostly determined by detection regions near the source. In order to address this issue, we multiplied both the calculated and the input spectra by the same constant for each SDS to equalize the influences of different SDSs on fitting accuracy. The constant for an SDS was set to be inversely proportional to the corresponding average reflectance in the wavelength range of 590–620 nm of the input spectra. The same constants were used both in the calculated and in the input spectra to preserve the information of relative intensities between SDSs.

In order to determine the initial values of the parameters to be fitted, we performed a quick search for the best fits between the input data and reflectance spectra calculated by using 100 sets of randomly assigned values of the input parameters. Initial values of the free parameters were set as averages of the input parameters from the best five results in the quick search. To improve the efficiency of the quick search, we used 10⁴ photons per set to calculate reflectance spectra by the scaling MC code and discarded photons undergoing over 1500 scattering events without exiting the tissue. After picking the initial values of the free parameters, a complete curve fitting was performed using 10⁵ photons in the scaling MC code during each iteration of the Levenberg-Marquardt algorithm to search for the global minimum. The inversion procedure was implemented in MATLAB (The MathWorks, Inc.) with a graphical user interface to facilitate interactive file management and setting of parameters. Computational time for simulations depended on the speed of CPU used. For example, on a computer with a CPU of Intel Core i5-760 2.8GHz and 8MB memory, a single MC run of a non-absorbing homogeneous medium with 10⁶ photons took about 1 hour and the fitting process took about 8–12 hours depending on the number of free parameters to be fitted.

2.4. Phantom experiments

In order to validate the inversion procedure described in Section 2.3, we fit spatially-resolved diffuse reflectance spectra experimentally measured from tissue mimicking phantoms and compared the extracted optical properties with the known values. Three homogenous liquid phantoms were prepared by using 1.04 μm diameter polystyrene beads (Bangs Lab Inc.) as scatterers and red ink as the absorber. All phantoms had the same concentration of polystyrene beads in water, 6.07x10⁹ particles per milliliter. Phantom 1 consisted of only the scatterers without any absorber and served as the calibration phantom. The liquid phantoms were contained in transparent plastic containers with a diameter of 10 mm and a height of 20 mm. During data acquisition the distal end of the fiber package was dipped into the liquid phantom about 3–5 mm below the surface and the liquid phantom was continuously stirred using a magnetic stirrer to prevent sedimentation of the beads.

Wavelength-dependent conversion factors between the experimentally measured spectra and the absolute reflectance calculated by MC simulations were determined by using the calibration phantom. We calculated spatially-resolved reflectance spectra of the calibration phantom by using the reduced scattering coefficients predicted with Mie theory in the scaling MC code. The conversion factors were then obtained by dividing the calculated spectra by the measured spectra of the calibration phantom wavelength by wavelength. Spatially-resolved reflectance spectra of phantoms 2 and 3 were calibrated with the conversion factors for each detection region separately, which corrected the effects of wavelength-dependent system response and eliminated the influence of ignoring the NA of the detection fibers in the scaling MC code. In order to account for any remaining variability of reflectance intensities measured from the phantoms due to instabilities in light source intensity or in coupling efficiencies of white light into the source fiber as well as reflected light into the detection fiber bundle, calibrated spectra of each phantom were normalized to the corresponding reflectance intensity measured at 600 nm wavelength with an SDS of 1.8 mm. The reflectance spectra calculated by the scaling MC code during inversion were also normalized to the simulated reflectance intensity of the same SDS and wavelength. The normalized spectra were taken as the input data to the inversion procedure as described in Section 2.3.

For extracting the optical properties of the phantoms, the forward MC model described in Section 2.2 was modified so that µ_s'(λ) of the beads were calculated according to Mie theory and µ_a(λ) of hemoglobin was replaced with that of the red ink measured by a UV/visible spectrophotometer (Biochrom WPA Biowave II). Due to the limitation of the scaling MC method in which g must be constant, we calculated µ_s(λ) using this equation μ_s = μ_s'/(1−g) instead of using the µ_s(λ) obtained directly from Mie theory to prevent deviations in µ_s'(λ) from Mie. Free parameters to be fitted were the size and concentration of the beads and the concentration of the red ink.

2.5. Simulated DRS data of two-layered tissue models

To evaluate the ability of the proposed method to extract optical properties of two-layered tissue models, we used simulated DRS data of two-layered tissue models to investigate whether simultaneously analyzing diffuse reflectance spectra measured from multiple SDSs are advantageous over methods which fit the reflectance spectrum measured with a single SDS or fit the spatially-resolved reflectance measured at a single wavelength. In general, including more wavelengths in the inversion procedure improved the accuracies of quantifying μ_a(λ) and µ_s'(λ) (data not shown). A moderate number of 100 wavelengths were selected in the range of 400–800 nm for the following analyses based on considerations of the accuracy and efficiency of inversion and experimentally feasible spectral resolution. Spatially-resolved diffuse reflectance spectra of a two-layered tissue model were generated by using the scaling MC code with 5 × 10⁶ photons. The diameters of both the source fiber and the detection fibers were set to be 0.2 mm. Random noise with a normal distribution and 5% standard deviation was added to the simulated reflectance values to take into account the uncertainties in real measurements. The simulated reflectance spectra with noise were used as the input data for inversion as described in Section 2.3.

We designed two fitting scenarios for performance evaluation. In the first scenario, we compared the performance of simultaneously analyzing spectra obtained from multiple SDSs to that of analyzing the reflectance spectrum collected at a single SDS. We used the inversion procedure to extract optical properties of only the bottom layer while the top layer optical properties were fixed at the true values. The single-SDS cases analyzed were 0.2 mm, 1.0 mm and 2.0 mm. The multi-SDS condition used 9 SDSs between 0.4 mm and 2.0 mm with an increment of 0.2 mm. The input parameters, f_Hb, StO₂, A and k, of the top layer were 0.4 [g/l], 0.9, 5000, 1, and those of the bottom layer were 1 [g/l], 0.9, 5000 and 0.865, respectively. The ranges of µ_a(λ) and µ_s'(λ) of the top layer were 0.01–7.22 cm⁻¹ and 6.25–12.50 cm⁻¹ and those of the bottom layer were 0.03–18.06 cm⁻¹ and 15.41–28.06 cm⁻¹, respectively, for λ = 400–800 nm. These values were selected according to previously reported optical properties of the epithelium and the stroma in the oral cavity [34]. The same absorber (hemoglobin) was used in both layers in order to compare our method with a previous study using a similar inversion method and a single SDS of 1.5 mm [30], not to suggest that hemoglobin exists in the top layer representing the epithelium. Fittings with the top layer thickness d as known or unknown were both performed. The ranges for possible values of f_Hb, StO₂, A, k and d were 0.5–1.5, 0.5–1, 4800–5300, 0.8–1.2, and 0.1–0.6 mm, respectively.

In the second scenario, we assumed all parameters of the two layers were unknown to assess the capability of the proposed method to quantify all optical properties of two-layered tissue models. Instead of using Eq. (1), the wavelength-dependent absorption coefficient of the top layer was calculated by using the equation

$${\mu }_{a1}(\lambda )=C{\mu }_{epi}(\lambda )$$ (3)

where μ_epi(λ) is the wavelength-dependent absorption coefficient of epithelial tissue reported in the literature [34] and C is a proportional constant. For calculating simulated DRS data using the scaling MC code, C was set to 1 and all the other input parameters of the two-layered model were the same as in the first scenario. The range of µ_a1(λ) was 0.51–3.33 cm⁻¹ in the wavelength range of 400–800 nm. The range of C to be searched in the inversion process was 0.5–1.5. Fittings with the top layer thickness d as known or unknown were both performed.

3. Simulation and phantom results

3.1. Validation of the scaling MC code

To confirm the accuracy of the scaling MC code, we first compared total reflectance of two-layered media calculated by using our conventional MC simulation code with that obtained by using the MCML code. Ten random combinations of optical properties were used as input parameters and 10⁵ photons were launched for each combination. If the total reflectance calculated with MCML was taken as the true value, the mean percent error (MPE) of total reflectance calculated with the conventional MC code was 1.3%. MPE was defined as

$$MPE(\%)=\frac{{\displaystyle \sum _{i=1}^n\left(\frac{X_{fi}-X_{ti}}{X_{ti}}\right)}}{n}\times 100\%$$ (4)

where n, X_ti and X_fi were the total number of samples, the true values and the estimated values, respectively. After validating the conventional MC code, we compared total reflectance calculated using the conventional MC code and the scaling MC code with a wide range of optical properties. The ranges of μ_a and μ_s' of the top layer were 1–4 cm⁻¹ and 9.5–14 cm⁻¹, and those of the bottom layer were 1.5–10 cm⁻¹ and 19.7–28 cm⁻¹, respectively. A total of 9500 random combinations of optical properties were tested with 10⁵ photons launched per combination. The scaling MC code showed an MPE of only 1.67% in total reflectance while the computation time was reduced by at least two orders of magnitude.

3.2. Quantifying optical properties of homogeneous liquid phantoms

Spatially-resolved reflectance spectra of each of the 3 phantoms were averaged from 5 measurements taken with the hyperspectral imaging system. To prevent high levels of uncertainty in the calibrated spectra due to low sensitivity of the CCD at wavelengths shorter than 450 nm, we selected the spectral range between 450 nm and 800 nm for the following analyses. The coefficient of variation in the measured reflectance intensity averaged over the selected wavelength range was 4%. The spectral resolution was 8067 cm⁻¹, corresponding to about 16.4 nm at a wavelength of 450 nm. Figure 2 shows a grayscale image of the proximal end of the detection fiber bundle collected by the microscope objective. Because the source fiber was not attached to the fiber bundle at the proximal end, the location of the source fiber relative to the fiber bundle was estimated assuming that the pixel with the highest intensity was the contact point between the source fiber and the fiber bundle. The center of the fiber bundle and the pixel with the highest reflectance intensity were automatically detected using a program developed with LabVIEW (National Instrument Inc.). We defined 8 circular detection regions along a line connecting the center of the fiber bundle and the pixel with the highest intensity. The SDSs were between 0.4 mm and 1.8 mm with an increment of 0.2 mm which was the diameter of each detection region. Reflectance spectra of all pixels within each detection region were summed together to obtain the reflectance spectrum for the corresponding SDS. During the analysis of spatially-resolved diffuse reflectance spectra of the phantoms, both the regions with the shortest SDS of 0.2 mm and the longest SDS of 2.0 mm were not used due to insufficient dynamic range of the CCD to acquire spatially-resolved reflectance spectra with adequate signal-to-noise ratios across the whole fiber bundle.

Fig. 2.

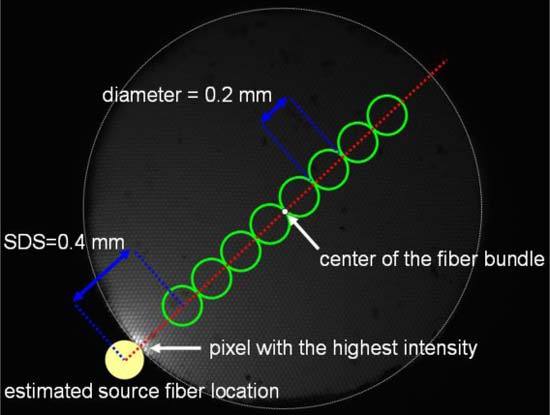
Image of the proximal end of the fiber bundle captured with the microscope objective. The center of the fiber bundle and the pixel with the highest intensity determine the line passing through the center of the source fiber. The 8 green circles indicate the regions for measuring diffuse reflectance spectra.

Figure 3 shows that the curve fitting results of phantom 3 matched well with the reflectance spectra measured at the 8 SDSs. The accuracies of extracting µ_a(λ) and µ_s'(λ) from the measurements were expressed as the root-mean-square percent error (RMSE%) which was calculated as

Fig. 3.

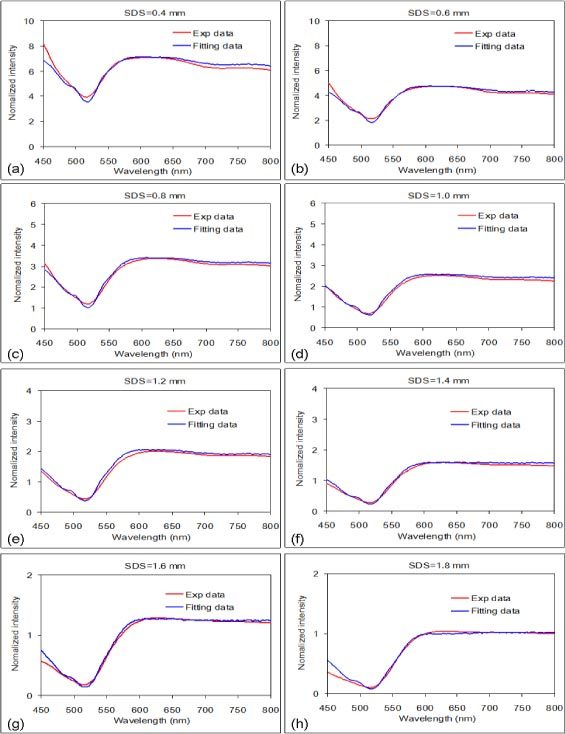
Spatially-resolved reflectance spectra of phantom 3 with SDSs from 0.4 mm to 1.8 mm and their corresponding fits.

$$RMSE\%=\sqrt{\frac{{\displaystyle \sum _{i=1}^m{\left[\left(\frac{X_{fi}-X_{ti}}{X{}_{ti}}\right)\times 100\right]}^2}}{m}}\%$$ (5)

where m was the total number of wavelengths analyzed. X_ti was the expected value based on phantom compositions and X_fi was the fitted value at the same wavelength. The RMSE% averaged from the results of phantoms 2 and 3 were 4.33% and 2.25% for μ_a(λ) and μ_s'(λ), respectively.

Figures 4(a) and 4(b) compare the expected µ_a(λ) and µ_s'(λ) with their corresponding fits for phantoms 2 and 3, respectively. The red lines represent µ_a(λ) and the blue lines represent µ_s'(λ). The MPE of the free parameters, the size and concentration of the beads and the concentration of the red ink, were 0.72%, −1.6% and 3.5%, respectively.

Fig. 4.

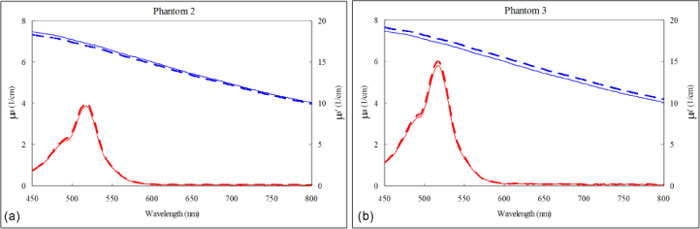
Extracted µ_a(λ) (red lines) and µ_s'(λ) (blue lines) of the phantom experiments. The solid lines represent the expected values based on phantom compositions and the dashed lines represent the spectra extracted from DRS data.

3.3. Quantifying optical properties of two-layered tissue models from simulated DRS data

Figure 5 shows an example of multi-SDS curve fitting results with d as a known parameter in the first fitting scenario. The MPE of hemoglobin parameters and RMSE% of µ_a(λ) and µ_s'(λ) of the bottom layer were summarized in Table 1 . The mean and standard deviations of MPE and RMSE% were the statistical results of 10 independent fittings with different random noise added to the simulated DRS data. Smaller mean and standard deviation of errors indicated higher accuracy and precision, respectively. We note that analyzing the spectrum of a single SDS = 1.0 mm resulted in errors slightly higher or comparable to those obtained by analyzing multi-SDS spectra. However, the errors for the other single-SDS cases were significantly higher (data not shown for the unknown d case). The best single SDS for the extraction of optical properties is highly dependent on the optical properties of the medium which are unknown in advance. Using hyperspectral imaging to collect DRS enables flexible selection of SDSs which can be optimized for minimizing differences between the input data and fitted spectra.

Fig. 5.

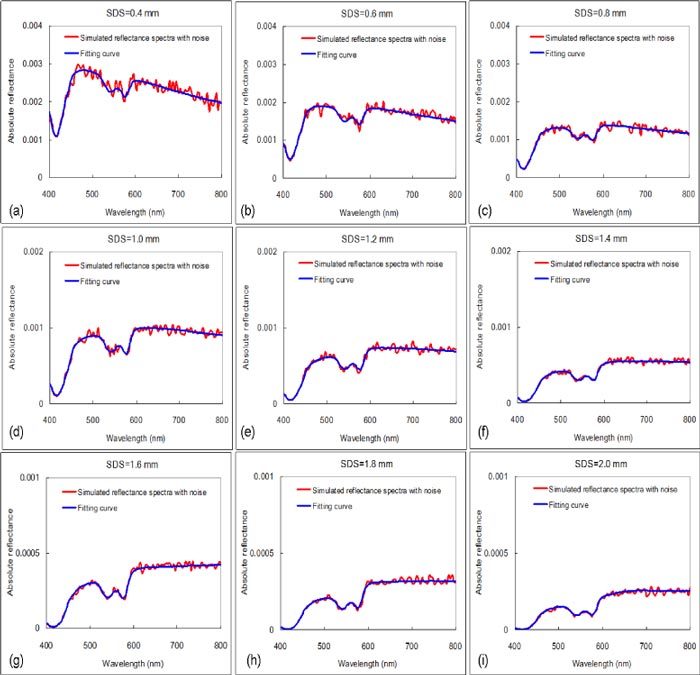
Example of simulated diffuse reflectance spectra with noise and curve fitting results at multiple SDSs.

Table 1. MPE of estimating hemoglobin parameters and RMSE% of quantifying µ_a(λ) and µ_s'(λ) of the bottom layer with known optical properties of the top layer. The numbers are expressed as mean ± standard deviation among 10 independent runs.

	MPE (%)			RMSE%
	fHb	StO2	d	µa	µs'
(a) d was known
SDS = 0.2 mm	−3 ± 13	−10 ± 10	NA	14.1 ± 7.4	2.0 ± 1.1
SDS = 1.0 mm	−8 ± 3	−5 ± 5	NA	8.3 ± 3.0	1.8 ± 0.7
SDS = 2.0 mm	−2 ± 15	−10 ± 6	NA	14.5 ± 9.1	18.0 ± 10.4
Multiple SDSs = 0.4-2.0 mm	−2 ± 7	−6 ± 5	NA	6.6 ± 4.4	0.9 ± 0.5
(b) d was unknown
SDS = 1.0 mm	0 ± 8	−4 ± 4	6 ± 11	7.9 ± 4.3	1.7 ± 0.9
Multiple SDSs = 0.4-2.0 mm	5 ± 4	−1 ± 3	4 ± 3	6.2 ± 4.2	1.8 ± 1.0

The results of the second fitting scenario in which all optical properties of a two-layered tissue model were quantified were summarized in the Table 2 . µ_a1(λ) and µ_s1'(λ) represent the absorption and the reduced scattering coefficients of the top layer and µ_a2(λ) and µ_s2'(λ) represent those of the bottom layer, respectively. The accuracies in quantifying µ_a1(λ) and µ_s1'(λ) were higher when d was known than unknown. The errors in quantifying µ_a2(λ) and µ_s2'(λ) were less than 10% regardless of whether d was known. The generally larger errors in extracted absorption and reduced scattering coefficients of the top layer than those of the bottom layer are attributed to lower sensitivity of diffuse reflectance to the top layer with a thin thickness of 0.3 mm. The sensitivity to the top layer optical properties might be enhanced by using smaller SDSs and shorter wavelengths in the inversion procedure.

Table 2. MPE of estimating input parameters and RMSE% of quantifying µ_a1(λ), µ_s1'(λ), µ_a2(λ), and µ_s2'(λ) of a two-layered tissue model with or without knowing the thickness of the top layer, d. The values are expressed as mean ± standard deviation among 10 independent runs.

	MPE (%)				RMSE%
	C	fHb	StO2	d	µa1	µs1'	µa2	µs2'
d was known	5 ± 6	1 ± 5	3 ± 3	NA	6.0 ± 5.0	4.3 ± 2.8	4.7 ± 3.7	1.4 ± 1.2
d was unknown	12 ± 8	6 ± 6	3 ± 5	2 ± 3	12.0 ± 7.2	6.2 ± 5.1	7.2 ± 4.1	1.2 ± 1.0

4. Discussion and summary

The major novelty of the proposed method is the use of a hyperspectral imaging system and an imaging fiber-optic bundle in contact with the tissue to obtain spatially-resolved diffuse reflectance spectra, enabling simultaneous analysis of the spatial and the spectral information of collected photons. The fiber package design consisted of a source fiber and a dense fiber bundle provides not only the flexibility in choosing regions of interest to be analyzed but also high spatial-resolution imaging capability which has the potential to detect heterogeneities in optical properties of the tissue. For example, using a source fiber in the center of a detection fiber bundle and analyzing radially-resolved reflectance spectra could estimate tissue optical properties along various directions. Compared with the previously reported noncontact imaging configuration, the proposed method does not need to consider the point spread function of the imaging system because of the high spatial resolution provided by the microscope objective [19]. In addition, the effect of uneven tissue surface on measured reflectance intensities needs to be taken into account for the noncontact imaging approach [35]. To investigate this potential issue, we performed an experiment on solid tissue phantoms consisted of polystyrene beads in Agar by raising the distal end of the fiber package above the phantom surface and keeping the gap between the fiber surface and the phantom filled with water. The difference between the reflectance measured with the fiber at a height of 0.7 mm and the average reflectance measured with the fiber at the phantom surface was less than one standard deviation of 5 repeated measurements at the phantom surface. This suggests that correction for slightly uneven tissue surfaces is not necessary in future clinical applications of the proposed method.

Based on the results of fitting the simulated data, we demonstrated accurate extraction of optical properties of two-layered media. The performance of analyzing simulated diffuse reflectance spectra of multiple SDSs versus single SDS is shown in Table 1 and benchmarked against a previous study by Liu and Ramanujam who used a scaling MC-based inversion to quantify the bottom layer optical properties and the top layer thickness from simulated diffuse reflectance spectra of a single SDS = 1.5 mm [30]. RMSE% of our study in µ_a(λ) and µ_s'(λ) of the bottom layer and thickness of the top layer in the wavelength range of 360–660 nm were 8.1%, 1.8% and 4%, respectively. The values are all smaller than those reported in the previous study, which were 9.5%, 5.9% and 9.6%, respectively. We note that the accuracies of extracting input parameters are affected by a number of factors that may differ in different studies but are not directly related to the performance of the inverse model itself. The range and shape of wavelength-dependent µ_a(λ) and µ_s'(λ) and number of unknown parameters are prominent examples. For MC-based methods, the number of useful photons to represent the detected signal is crucial to the model’s accuracy due to stochasticity of the MC method. Since none of the factors is in favor of our study, we conclude that fitting diffuse reflectance spectra measured with multiple SDSs is advantageous over fitting the diffuse reflectance spectrum measured with a single SDS. Although in this study we used fixed size and pattern for the detection regions, different combinations of SDSs and wavelength range could be used in the inversion process to further optimize fitting results [36].

Spatially-resolved reflectance of a turbid medium contains information of photons going through different depths in the medium. Thus it has the potential to be used for detecting optical properties of different layers. Table 3 compares the proposed method with studies reported by other groups on the accuracies of quantifying all optical properties (µ_a1, µ_s1', µ_a2 and µ_s2') in two-layered tissue models with known thickness of the top layer [25,27,28]. For practical applications of DRS techniques, the thickness of the top layer could possibly be measured by other techniques such as optical coherence tomography. The performance of the proposed method is evidently better than other studies with the exception of µ_s1' compared with Ref [25]. We note that Ref [25] used a top layer thickness of 4 mm and a wavelength of 650 nm; the much thicker top layer might contribute to the insensitivity of the reflectance to changes in µ_s2' and large errors in extracted µ_a2. In addition, with the top layer thickness restricted to be within 25% of the true value, quantifying all 5 parameters including top layer thickness of a two-layered model resulted in errors of 23.5%, 1.2% and 83.6% for µ_a1, µ_s1' and µ_a2, respectively [25]. Results of the proposed method, as listed in Table 2, showed that 8 parameters (C, A, k of the top layer, f_Hb, StO₂, A, k of the bottom layer and d) of a two-layered model were accurately determined. Higher accuracies achieved by the proposed method could be mainly attributed to the consideration of both spectral and spatial information of the input data in the inversion process as opposed to the other studies analyzing spatially-resolved reflectance at a single wavelength. Photons with different wavelengths have different optical properties and penetrate to different depths. By measuring a wealth of depth-sensitive information through hyperspectral imaging, the possibility that different tissue optical properties result in similar reflectance spectra is slim. We want to emphasize two key features which made the inversion procedure successful. First, applying spectral constraints based on a priori knowledge of the spectral dependencies of tissue optical properties reduces the number of free parameters and improves the stability of curve fitting results. Second, the scaling method enables efficient analysis of large data sets (100 wavelengths at each of the 8 or 9 SDSs) using accurate and flexible MC-based models.

Table 3. Comparison of methods used and errors (%) in quantified optical properties of two-layered tissue models with the thickness of the top layer known.

Source of data	Inverse model	Reflectance source	Noise level (%)	µa1	µs1'	µa2	µs2'
This study	Iterative based on scaling MC	Spatially-resolved reflectance	5	6.0	4.3	4.7	1.4
Ref [28]	Two-layered diffusion equation	Spatially-resolved reflectance	1	<10	<5	<30	12–20
Ref [27]	Two-layered diffusion equation	Spatially-resolved reflectance	2	14.5	8.1	29.3	9.1
Ref [25]	Planar photon density wave model	Spatially-modulated reflectance imaging	Phantom data	17.2	1.2	99.5	21.2a

^aµ_s2' stays within 5% of initial guess.

There are several assumptions and limitations in this proof of concept study, many of which can be readily addressed. First, in phantom experiments both µ_s and g are functions of wavelength while in the scaling MC code g is a constant. We set values of µ_s'(λ) in accordance with Mie theory, which may cause large errors in reflectance at short SDSs where diffusion approximation fails. In addition, the phase function of polystyrene beads is different from the Henyey-Greenstein phase function used in the MC code. For future applications on quantitative in vivo measurements for diagnostic purposes, other phase functions or additional absorbers could be used to better model light transport in specific tissues of interest. Second, the performance of the proposed method on accurately extracting optical properties of two-layered tissue models were only demonstrated with simulated data. Evaluation of the proposed method using solid two-layered phantoms is ongoing. Third, in the current implementation of the inversion method scaling of photons is done in line with the main MC code and the fitting process needs to run a new MC simulation each time it iterates. In the future all the photon trajectory information of the baseline MC run will be saved in the memory and available to subsequent scaling calculations. We expect to improve the efficiency of the inversion process by at least one order of magnitude. Forth, the NA of the detection fibers is ignored in the current scaling MC code to improve computational efficiency. The effects of NA could be easily taken into account by modifying the MC code and the variance of MC simulations could be kept low by increasing the number of photons. Fifth, the refractive indices of the two layers in the tissue model must match in order for the layered scaling algorithm to work.

In conclusion, quantification of optical properties of two-layered turbid media by analyzing steady-state spatially-resolved diffuse reflectance spectra with an iterative inversion procedure based on fast scaling MC simulation was successfully demonstrated on simulated data. The forward scaling MC code was validated with a conventional MC code which in turn was validated with the MCML method. The inversion procedure was validated with experimental data measured from homogeneous liquid phantoms by using a custom-built hyperspectral imaging system. Results of analyzing simulated diffuse reflectance spectra using the proposed method showed great potential for quantifying optical parameters of two-layered soft tissues, which could be applied to gather diagnostically useful information about epithelial microstructures and stromal microstructures, vasculature and oxygenation status. We believe that further development of this method could facilitate applications of steady-state diffuse reflectance spectroscopy on noninvasive interrogation of superficial stratified tissues for various clinical applications in the future.