Abstract
Near Infra-Red Spectroscopy (NIRS) is a non-invasive technique which can be used to investigate cerebral haemodynamics and oxygenation with high temporal resolution. When combined with measures of Cerebral Blood Flow (CBF), it has the potential to provide information about oxygen delivery, utilization and metabolism. However, the interpretation of experimental results is complex. Measured NIRS signals reflect both scalp and cerebral haemodynamics and are influenced by many factors. The relationship between Arterial Blood Pressure (ABP) and CBF has been widely investigated and it central to cerebral autoregulation. Changes in arterial blood gas levels have a significant effect on ABP and CBF and these relationships have been quantified previously. The relationship between ABP and NIRS signals, however, has not been fully characterized. In this paper, we thus investigate the influence of changes in arterial blood gas levels both experimentally and theoretically, using an extended mathematical model of cerebral blood flow and metabolism, in terms of the phase angle at 0.1 Hz. The autoregulation response is found to be strongly dependent upon the carbon dioxide (CO2) partial pressure but much less so upon changes in arterial oxygen saturation (SaO2). The results for phase angle sensitivity to CO2 show good agreement between experimental and theory, but a poorer agreement is found for the sensitivity to SaO2.
OCIS codes: (170.3880) Medical and biological imaging, (170.5380) Physiology
1. Introduction
Near Infra-Red Spectroscopy (NIRS) has been used to study cerebral haemodynamics and oxygenation, through measurement of changes in oxyhaemoglobin (O2Hb) and deoxyhaemoglobin (HHb) concentration, see for example [1]. It is particularly valuable when used in conjunction with measurements of cerebral blood flow velocity (CBFV), as measured using transcranial Doppler, and has the twin advantages of high temporal resolution and simplicity of use. However, there are two primary difficulties in interpreting such measurements: firstly, the NIRS signals are influenced by changes in both cerebral blood flow (CBF) and Cerebral Blood Volume (CBV), and secondly, the signals reflect several compartments, having components from both scalp and brain tissue and from both arterial and venous oxygenation [2].
Mathematical models can play a valuable part in the analysis of NIRS signals, particularly for estimating the effects of confounding factors. The relationship between ABP and CBFV, for example, is well known to be strongly affected by changes in arterial carbon dioxide (CO2) partial pressure [3,4]. Using the results from these studies, it is now possible to compensate for these changes, see for example [5], where the phase angle between ABP and CBFV is corrected for fluctuations in arterial CO2 partial pressure. The three-way relationship between ABP, CO2 and CBFV is thus well understood and characterized. However, the multivariate relationships between ABP, CO2 and O2Hb/HHb concentrations are less well characterized.
In [6] a model was proposed for haemoglobin flow dynamics, based on earlier models [7] and analysis [8], which predicted the transfer functions governing O2Hb and HHb concentrations in response to both ABP and CO2. This showed that the ratio of arterial to venous blood volume has a strong influence on the phase dynamics, which are also strongly influenced by changes in respiration. They concluded that it was difficult to infer any conclusions about changes in the status of dynamic cerebral autoregulation, as quantified by the phase angles between ABP and CBFV and ABP and O2Hb, under conditions of stroke, given the large variability caused by CO2 effects and the different respiration protocols used in the published studies.
In addition to the confounding effects of CO2 on the phase angles between ABP and O2Hb/HHb, it is likely that changes in baseline arterial oxygen saturation (SaO2) will also affect the flow dynamics of haemoglobin in the brain, through changes in the Oxygen Extraction Fraction (OEF) that allow cerebral metabolism to be maintained at baseline levels. Understanding the relationships between ABP, arterial blood gas levels and O2Hb/HHb concentrations is vital if such measurements are to be interpreted correctly and to be exploited clinically.
In this paper, we present the results of both experimental and mathematical studies into the effects of arterial blood gas levels on the phase angles between ABP and CBFV, O2Hb and Hbdiff (O2Hb-HHb). Through the use of novel signal processing techniques, combined with a mathematical model of the cerebral vasculature, we illustrate how such analysis can be used to interpret multiple experimental data acquired from healthy subjects and hence to interrogate the control of blood flow in the brain.
2. Theory
The model proposed by [7] and extended by [6] is used as the basis for the model proposed detailed here. The flow component of the model is based on the well-established electrical equivalent circuit model, shown in Fig. 1 , where the vasculature is divided into three compartments (arterial, capillary and venous). The first and last compartments are sub-divided into ‘small’ and ‘large’ vessels and have variable volume and resistance, whereas the capillary compartment has fixed (small) volume and resistance (and is subsumed into the small vein compartment for simplicity). The small arterial vessels exhibit autoregulation of flow, through changes in arterial compliance, based on a simple first order feedback process with fixed gain and time constant, based on CBF (taken to be the capillary flow). This feedback is also affected by changes in arterial CO2 blood gas levels; the model having been validated against a range of experimental data for both static and dynamic changes in ABP and CO2 levels. This part of the model is used unchanged here. Note that the autoregulation and CO2 responses are assumed linear and additive, i.e. independent.
Fig. 1.
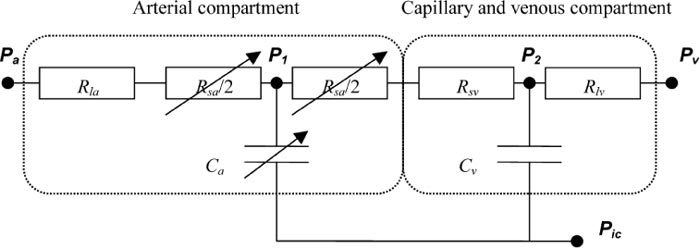
Schematic of model. Pa, systemic arterial pressure; Rla, resistance of non-regulating arterial compartment; P1, Rsa, and Ca, pressure, resistance, and compliance of regulating arterial compartment; Rsv, resistance of capillary compartment and small veins; Cv, venous compliance; P2, venous pressure; Pv and Rlv, venous pressure and resistance of large veins, respectively; Pic, intracranial pressure.
The model extension for haemoglobin flow dynamics, presented by [6] is now adapted for variable arterial saturation, since this will directly influence the transport of oxyhaemoglobin and deoxyhaemoglobin. In all of the equations below, o is used to denote the amount of oxyhaemoglobin in a given compartment and h the amount of deoxyhaemoglobin, both as a fraction of their baseline values, the subscripts a and v being used for arterial and venous compartments respectively. In the arterial compartment, conservation of mass gives:
| (1) |
| (2) |
where the arterial time constant, Ta, is defined as the ratio of baseline arterial blood volume to flow rate. v denotes volume and and are the arterial inlet and outlet flows respectively.
The corresponding equations for the venous compartment are:
| (3) |
| (4) |
where E denotes OEF and Eo baseline OEF, which is set both by baseline CBF and oxygen saturation. The venous time constant is defined in the same way as the arterial time constant.
It is assumed throughout that the metabolic rate of oxygen (CMRO2) remains invariant, which results in the following relationship between changes (denoted by Δ) in OEF and fractional CBF, q:
| (5) |
The validity of this assumption will be discussed below after the results have been presented. Since the capillary compartment is assumed to have fixed volume, CBF is equal to both arterial outflow and venous inflow. In the steady state, changes in arterial saturation will also induce changes in OEF relative to its baseline value. From conservation of mass, assuming that baseline flow remains unaltered:
| (6) |
where OEF is equal to baseline OEF when arterial saturation, Sa, is equal to baseline arterial saturation, , taken here to be 100%.
The same small signal analysis as in [8] and [6], is adopted here, linearizing Eqs. (1)- (4) about their baseline conditions and expressing the resulting transfer functions in terms of the Laplace transform variable, s:
| (7) |
| (8) |
| (9) |
| (10) |
using the same non-dimensional groups as in [6], the baseline values for and definitions of which are given in Table 1 . Since , the volume/flow time constant is not quoted as it is not an independent parameter. Note that these values are calculated directly from the model parameter values quoted in [7], since these values were found to provide a good fit to experimental data for both flow and CO2 changes. The values are somewhat different from those used in [6], but this is not found to affect the analysis substantially.
Table 1. Baseline values, definitions and descriptions of non-dimensional groups and time constants, taken from [7] and [6].
| Definition (where applicable) | Physical meaning | Baseline value | |
|---|---|---|---|
| α1 | Arterial transit time/Arterial outflow time constant | 0.98 | |
| α2 | Non-dimensional feedback gain for CBF | 8.18 | |
| τ | CBF feedback time constant | 20 s | |
| τα | Arterial inflow time constant | 0.60 s | |
| β1 | Fractional resistance | 0.40 | |
| αv | Venous transit time/Venous outflow time constant | 5.23 | |
| τv | Venous outflow time constant | 0.55 s | |
| β | Arteriole resistance/Total resistance | 0.69 | |
| Eo | Baseline Oxygen Extraction Fraction | 0.4 |
The volume-flow relationship in Eqs. (7). and (8) is given by [6]
| (11) |
Total oxyhaemoglobin is a volume weighted average of the arterial and venous oxyhaemoglobin concentrations, which in fractional form becomes:
| (12) |
where, in the steady state:
| (13) |
Equation (10) then becomes:
| (14) |
This is exactly as in [6], but with OEF calculated by Eq. (6) as a function of arterial saturation, rather than being equal to its baseline value.
Total deoxyhaemoglobin is, likewise, a volume weighted average of the arterial and venous deoxyhaemoglobin concentrations:
| (15) |
where, in the steady state, by definition:
| (16) |
and, through conservation of haematocrit:
| (17) |
Eq. (15) then becomes:
| (18) |
This is substantially different from the result in [6], since there are now two components, representing the arterial and venous compartments. In the limit as arterial saturation tends towards one, however, this tends towards the previous result, as expected. The transfer function relating changes in CBF to fluctuations in ABP is not directly affected by changes in arterial saturation and so is not repeated here for reasons of space.
3. Experimental data
Data analyzed here are provided by two separate studies approved by the Joint Research Ethics Committee of the National Hospital for Neurology and Neurosurgery and the Institute of Neurology and involved a hypoxia protocol followed by a CO2 (hypocapnia and hypercapnia phases) protocol. The details of the experimental protocols, measurement methodologies and signal analysis are provided in previous publications [9–12].
3.1. Measurements
In brief, a modified anaesthetic machine delivered gas to the subject via a mouthpiece. Inspired oxygen concentration (FiO2) was measured using an inline gas analyzer (Hewlett Packard, UK) and a beat-to-beat pulse oximeter probe (Novametrix Medical Systems Inc., USA) measured SaO2. End tidal CO2 (EtCO2), a surrogate of PaCO2 and respiratory rate were measured continuously (CO2SMO Novametrix Medical Systems Inc.) synchronously with heart rate (HR) and mean blood pressure (MBP) using a Portapres finger cuff (Biomedical Instrumentation, TNO Institute of Applied Physics, Belgium).
CBFV in the basal right middle cerebral artery was collected at 50 Hz using a 2 MHz transcranial Doppler (TCD) ultrasonography probe (Pioneer TC2020, Nicolet, UK) fixed in place over the right temporal region. Mean velocity of the middle cerebral artery (Vmca) was calculated from the velocity envelope using a trapezoidal integration function (MatLab, Mathworks Inc.).
A NIRO 300 monitor (Hamamatsu Photonics KK) was used to collect NIRS data. The source detector optode pair was fixed in a black rubber holder with a source-detector separation of 5 cm over the right side of the forehead in the midpupillary line, avoiding the sinuses. The optode holder was secured to the head using an elasticated crepe bandage to prevent optode movement and covered with a light absorbing cloth to eliminate stray light. NIRS data were collected at 6 Hz. Absolute Δ[O2Hb] and Δ[HHb] were calculated and the change in haemoglobin difference concentration Δ[Hbdiff] defined as Δ[O2Hb]- Δ[HHb] derived. Although the difference concentration has been used as a measure of CBF, see for example [13] and [14], this is only under tight restrictions, which are invalid here. We use this signal as simply an additional means of interrogating the underlying physiology: its interpretation is not trivial under the conditions considered here and this further underlines the need for a mathematical model to help to interpret experimental data.
3.2. Hypoxia Protocol
A hypoxia study was performed on 9 healthy volunteers (median age 31 years, range 30-36). The hypoxia protocol commenced with five minutes monitoring at normoxia. Nitrogen was then added to the inspired gases to induce a gradual fall in SaO2 to 80% and, immediately after this was achieved, the FiO2 was returned to normoxia for five minutes. This cycle was repeated three times. Throughout the study EtCO2 and breathing rate were measured continuously and were fed back to subjects in order to adjust their minute ventilation to maintain normocapnia.
3.3. CO2 Protocol
A hypocapnia/hypercapnia study was performed on 14 healthy subjects (median age 32 years, range 30-39). The CO2 protocol commenced with five minutes monitoring at normoxia and normocapnia. The subjects then hyperventilated to reduce EtCO2 by 1.5 kPa below baseline. This was maintained for 5 minutes and then a normal breathing rate was resumed, allowing EtCO2 to return to baseline over approximately 5 minutes. Following this approximately 6% CO2 was added to the inspired gas and titrated to induce an increase in EtCO2 of 1.5 kPa. This was maintained for 5 minutes and the inspired CO2 fraction was then returned to zero for another 5 minutes.
3.4. Analysis
All signals were interpolated onto a common time base sampled at 1 Hz. To calculate phase angle, the continuous complex Morlet wavelet transform was used to convert each time series into a complex time series as a function of wavelet scale and time. The complex argument of the time series gives a representation of the instantaneous phase at each point in time. The analysis was performed exactly as in [5], for consistency. Throughout this paper a scale of 10 was used, which corresponds, for a sampling frequency of 1 Hz, to a frequency of 0.1 Hz.
The behavior of oscillations at this frequency has been widely investigated [15,16], particularly in the context of vasomotion, whereby spontaneous oscillations in vascular tone are observed [17]. Payne et al. [6], also showed that this is frequency at which the magnitude of the ABP-O2Hb transfer function is greatest, thus most likely providing the largest signal and highest robustness to noise, and it is the frequency component investigated in the study by [18], which provides, to the best of our knowledge, the only other previous measure of the phase angles between ABP and O2Hb/HHb in the literature.
The instantaneous phase difference between two time series is straightforwardly calculated as the difference in instantaneous phase. This time-varying phase is then used to calculate two parameters, circular mean phase:
| (19) |
and the synchronization index, an inverse circular statistical analogue of variance:
| (20) |
where N is the number of time points in the time series. The value of synchronization index is in the range : a value of 1 represents an instantaneous phase angle that is invariant with time, indicating a perfect level of coupling between the two variables; conversely a value of 0 indicates no or perfectly random coupling. A threshold value of 0.5 is typically used, see for example [5], for a value of circular mean phase to be taken as valid.
4. Results
4.1. Changes in arterial blood gas O2 levels
The phase angle calculated for MBP/CBFV at 0.1 Hz was found to be 54° ± 8° over the 9 subjects, when averaged over the time series for values of SaO2 greater than 95% only, all synchronization index values being found to be > 0.5. The corresponding phase angle for MBP/[O2Hb] was 7° ± 4° and for MBP/[ΔHbdiff] 3° ± 6°. We used these two measures of haemoglobin for analysis as these were found to have the greatest signal to noise ratio, the MBP/[ΔHHb] signal containing relatively large amounts of noise. However, these two measures are still a linearly independent combination of the two underlying variables.
The values quoted by [18], which is the only other study to publish these haemoglobin-based phase angles, are 65° ± 26° (MBP/CBFV), −24° ± 24° (MBP/[ΔO2Hb]) and −26° ± 22° (MBP/[ΔHbdiff]). The flow phase angle is in very good agreement and the haemoglobin-based phase angles are only slightly different. It is difficult to make a direct comparison, however, due to the fact that the values measured by Reinhard et al. were obtained under conditions of paced breathing at 0.1 Hz, which [6] showed to have a significant effect on the estimate of phase angle. In addition, the subjects analyzed here are young, compared to those of [18], who had an average age greater than 60 years.
To calculate the sensitivity of these phase angles to changes in arterial saturation, for each subject the instantaneous phase angle values were binned in intervals of 5% width in arterial saturation from 80 to 100%. The circular mean phase and average saturation was then calculated for each bin and the value retained for further analysis only if the synchronization index value was greater than 0.5. This was performed for all three phase angles above (MBP/CBFV, MBP/[ΔO2Hb] and MBP/[ΔHbdiff]). The results, Fig. 2 , show that there is a significant increase in the MBP/CBFV phase of 0.75°/%, with a correlation coefficient of 0.42 (p = 0.014), but that the corresponding change in MBP/[ΔO2Hb] phase angle is only 0.05°/% and for MBP/[ΔHbdiff] 0.09°/% (p>0.1 for both).
Fig. 2.
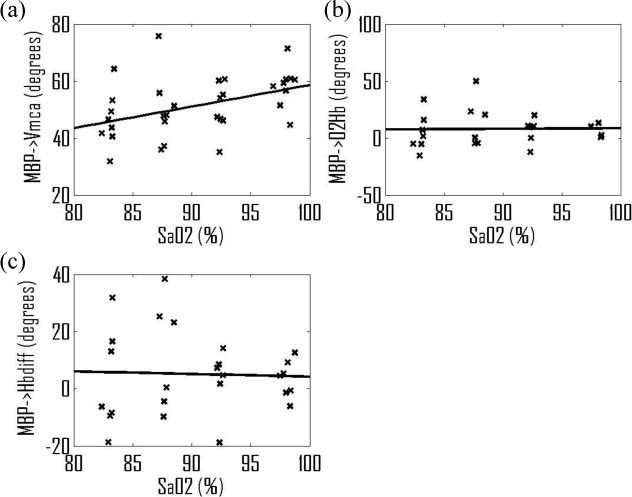
Changes in phase angle with arterial saturation: (a) MBP/CBFV; (b) MBP/[ΔO2Hb]; (c) MBP/ [ΔHbdiff]; each data point representing the value for an individual subject within a 5% wide bin of SaO2.
4.2. Changes in arterial blood gas CO2 levels
The instantaneous phase angle values calculated for MBP/CBFV, MBP/[ΔO2Hb] and MBP/[ΔHbdiff] were binned in the ranges of EtCO2 of 25-35 mmHg (defined as hypocapnia), 35-45 mmHg (normocapnia) and 45-60 mmHg (hypercapnia). The results across all subjects in these three conditions are given in Table 2 in terms of their means and standard deviations. Note that these results are presented differently from those for changes in SaO2 since the experimental protocol is different, involving continuous changes in SaO2 but discrete changes in CO2. Significant changes in phase angle are found between hypocapnia and normocapnia for both MBP/CBFV and MBP/[ΔHbdiff] (p<0.0001 and p<0.01 respectively, calculated using a paired t-test), but not for the MBP/[ΔO2Hb] phase angle. No significant changes in any of the phase angles are found between normocapnia and hypercapnia (p>0.1).
Table 2. Variation in phase angles with CO2 levels.
| Hypocapnia (25-35 mmHg) | Normocapnia (35-45 mmHg) | Hypercapnia (45-60 mmHg) | |
|---|---|---|---|
| MBP/CBFV | 81° ± 13° | 59° ± 13° | 49° ± 13° |
| MBP/[ΔO2Hb] | 12° ± 20° | 1° ± 19° | −4° ± 19° |
| MBP/[ΔHbdiff] | 16° ± 9° | 3° ± 7° | 3° ± 10° |
We again compare the baseline values of phase angle with those given by [18] and the values quoted above. The agreement between the two studies presented here is very reassuring, there being no statistically significant different between any of the baseline phase angles. Likewise the level of agreement with Reinhard et al. is also reassuring, given the difficulties of comparing these studies mentioned above.
Finally, in Table 3 is given the resulting sensitivities to both SaO2 and CO2 of the phase angles for MBP/CBFV, MBP/[ΔO2Hb] and MBP/[ΔHbdiff], to provide a summary of the experimental results for ease of comparison with the model predictions that will now be presented.
Table 3. Sensitivity of phase angle to SaO2 and CO2.
| Sensitivity to SaO2 | Sensitivity to PaCO2 (hypocapnia only) | |
|---|---|---|
| MBP/CBFV | 0.75°/% | −2.15°/mmHg |
| MBP/[ΔO2Hb] | 0.05°/% | −1.08°/mmHg |
| MBP/[ΔHbdiff] | 0.09°/% | −1.32°/mmHg |
4.3. Model predictions
It has been shown experimentally that hypocapnia and hypercapnia induce substantial alterations in flow [19] through large changes in arterial resistance, compliance and volume. All of these affect the phase angle through changes in many of the non-dimensional parameters that are used to calculate the phase angle. The feedback model proposed by [7], which has been validated against changes in static arterial CO2 blood gas levels, is now used to predict the effect of changes in baseline CO2 on the phase angles measured above to aid in interpretation of the results.
For a wide range of CO2 partial pressure (approximately 25-75 mmHg), the model equations given in [7] are solved in the steady state and the values of the non-dimensional parameters and time constants calculated, as shown in Fig. 3 . The resulting values of the phase angles, Fig. 4 , are shown for MBP/CBFV, MBP/[ΔO2Hb] and MBP/[ΔHbdiff].
Fig. 3.
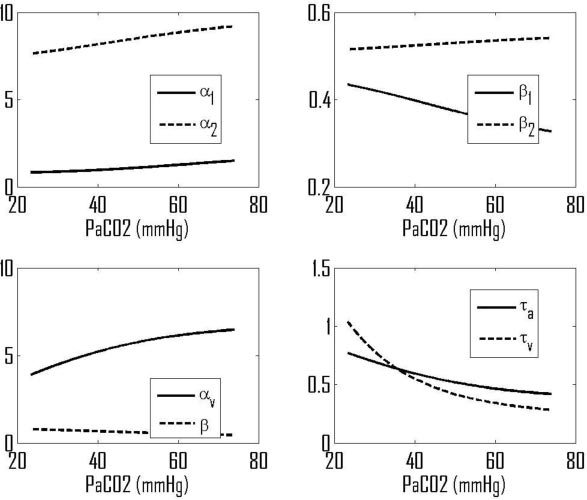
Predicted variations in model non-dimensional groups and time constants with PaCO2.
Fig. 4.
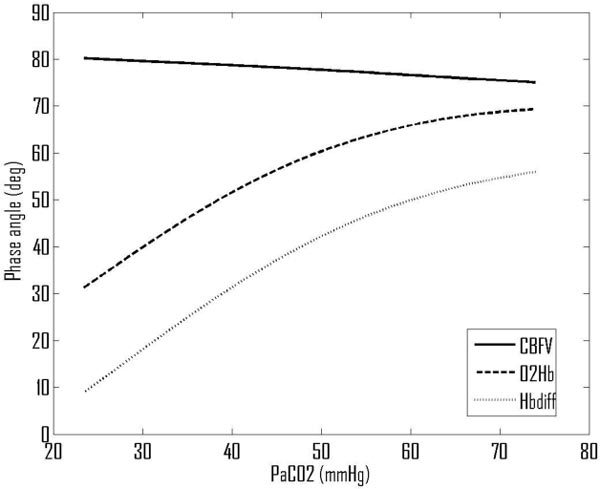
Predicted variations in phase angles with PaCO2.
The predicted baseline values for phase angles are 79° for CBFV, 51° for O2Hb and 31° for MBP/[ΔHbdiff]. The predicted value for MBP/CBFV is just slightly higher than would be expected from the experimental literature, but the values for MBP/[ΔO2Hb] and MBP/[ΔHbdiff] are predicted to be a little higher than measured experimentally (both by us and by Reinhard et al.). The effect of changes in arterial CO2 blood gas levels on the MBP/CBFV phase angle is very small, varying by only 5° over this wide range of CO2 pressures. However, there are much larger changes in the haemoglobin-based phase angles, dropping by approximately 1°/mmHg decrease in PaCO2 and rising with increased PaCO2 but saturating above approximately 60 mmHg PaCO2.
The corresponding variations over a range of SaO2, Fig. 5 , show that SaO2 is predicted to have no impact on the MBP/CBFV phase angle, as it is assumed only to affect the haemoglobin flow dynamics. However, the MBP/[ΔO2Hb] phase angle increases by approximately 0.3°/% and the MBP/[ΔHbdiff] phase angle by approximately 1°/%. We now examine these results in the context of autoregulation.
Fig. 5.
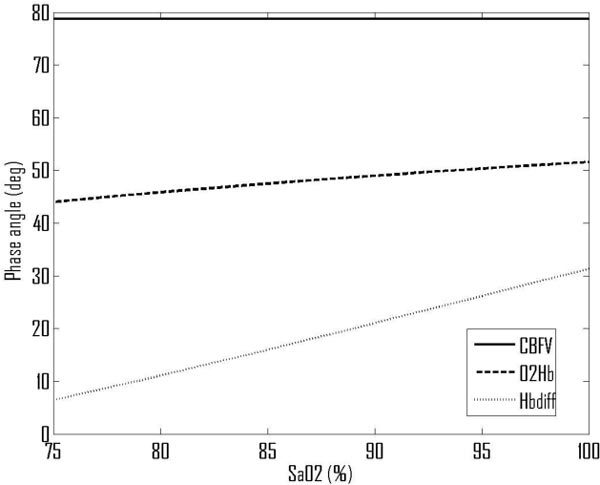
Predicted variations in phase angles with SaO2.
5. Discussion
5.1. Changes in arterial blood gas O2 levels
The model used here predicts that SaO2 has no impact on the MBP/CBFV phase angle, since the autoregulation feedback mechanisms are assumed only to act on flow, rather than oxygenation levels. It predicts a small change in haemoglobin-based phase angles. The experimental data, however, show that there is a small change in the MBP/CBFV phase angle of approximately 0.75°/%, which suggests that the autoregulation mechanisms are not independent of blood O2 levels. This is not surprising, since many physiological processes are likely to be sensitive to oxygenation levels.
To aid in quantifying the effects of changes in SaO2, the effects of changes in both feedback gain and feedback time constant (the two parameters in the model governing autoregulation strength and speed respectively) on all of the phase angles were predicted. Using small changes in these parameters, we calculated that the MBP/CBFV phase angle depends upon the feedback gain with a slope of approximately 0.41°/% around baseline conditions. The relevant haemoglobin phase angles sensitivities to % changes in feedback gain are predicted to be approximately 0.63°/% (MBP/[ΔO2Hb]) and 0.55°/% (MBP/[ΔHbdiff]). The corresponding sensitivities to % changes in feedback time constant are −0.36°/% (MBP/CBFV), −0.58°/% (MBP/[ΔO2Hb]) and −0.50°/% (MBP/[ΔHbdiff]).
The experimentally derived sensitivity of MBP/CBFV phase angle to SaO2 (0.75°/%) could thus be ascribed to either a sensitivity of approximately 1.8% change in feedback gain per % change in SaO2, a −2.1% change in feedback time constant per % change in SaO2 or a weighted combination of these two. This last is the most probable since it seems unlikely that only one parameter changes, given that the feedback gain and time constant are lumped parameters mimicking multiple complicated pathways in a simple first order feedback mechanism.
Such changes in the autoregulation feedback mechanisms would directly explain the MBP/CBFV phase angle. Estimating the changes in the haemoglobin-based phase angles is more complicated since such changes are induced by two factors: direct changes due to SaO2 affecting the haemoglobin flow dynamics; and indirect changes due to SaO2 affecting the feedback mechanism parameters. This can be expressed mathematically as:
| , | (21) |
where φ is the phase angle, x denotes blood gas level (SaO2 here) and F is the feedback parameter (gain or time constant).
Taking the scaling factor of 1.8% change in feedback gain per % change in SaO2 estimated from the MBP/CBFV response predicts a net sensitivity to SaO2 of 1.4°/% (MBP/[ΔO2Hb]) and 2.0°/% (MBP/[ΔHbdiff]) calculated using Eq. (21). This is not shown by the experimental data (Fig. 2), which show no significant change in phase angle. However, it should be noted that the data are much sparser for the haemoglobin-based phase angles than for the flow-based phase angle, due to the greater levels of noise. It is possible that the experimental data do exhibit sensitivity to SaO2, but that this is hidden by the noise on the data.
In a recent paper [20] it was found that there is a small (non-significant) decrease in MBP/CBFV phase angle with decreasing SaO2 (with a significant reduction in Autoregulation Index in hypoxia), which is in good agreement with our results. Further investigation will be required, however, to quantify the effects of hypoxia on haemoglobin flow dynamics, in particular by obtaining more detailed and less noisy experimental data.
5.2. Changes in arterial blood gas CO2 levels
As CO2 levels are reduced to hypocapnic conditions, we find experimentally that the MBP/CBFV phase angle increases by approximately 2°/mmHg drop in CO2 partial pressure, with the MBP/[ΔHbdiff] phase angle increasing by approximately 1.3°/mmHg drop in CO2 partial pressure, Table 2. This is only true for reductions in CO2 levels, increases in CO2 having no significant effect on the phase angles, in good agreement with the model predictions, Fig. 4.
The predicted sensitivities of the phase angles to changes in CO2 around the baseline conditions are approximately −0.1°/mmHg (MBP/CBFV), 1.0°/mmHg (MBP/[ΔO2Hb]) and 1.2°/mmHg (MBP/[ΔHbdiff]). There is a large difference between the experimental and predicted values for the MBP/CBFV phase angle sensitivity. This is likely to be due to changes in the feedback parameters with CO2 levels, previous work by Aaslid et al. having already shown that the rate of recovery (a measure of the speed of response of CBFV to a change in MBP) was inversely related to CO2 levels.
We can calculate the expected sensitivity of the feedback parameters to CO2 levels in the same manner as for the SaO2 response. The resultant values are −4.6% change in feedback gain per mmHg CO2 partial pressure, or 5.3% change in feedback time constant per mmHg CO2 partial pressure. As expected, there is a greater sensitivity to CO2 than to O2 levels.
We can then calculate the predicted changes in the haemoglobin-based phase angles with CO2 levels, based on the combined effects of direct changes due to CO2 changes and indirect due to CO2-induced changes in autoregulation, using Eq. (21). The resulting values are −1.9°/mmHg (MBP/[ΔO2Hb]) and −1.3°/mmHg (MBP/[ΔHbdiff]). Note particularly that the combined sensitivity is significantly different from the direct sensitivity, underlining the importance of including both components of the sensitivity.
The overall sensitivity of MBP/[ΔO2Hb] is very similar to that of MBP/CBFV, which is not shown by the data; however, the result for MBP/[ΔHbdiff] is very similar to the experimental value (both being approximately −1.3°/mmHg). The results for the former, however, contain significantly more noise, the [ΔHbdiff] signal having the highest signal to noise ratio. The good agreement shown by the prediction for MBP/[ΔHbdiff] is thus very encouraging, comprising as it does two effects in different proportions.
Similar calculations based on changes in feedback time constant yield an overall sensitivity of −1.45°/mmHg for MBP/[ΔHbdiff], which is also very similar to the experimental value. It is thus not possible to determine which feedback parameter (or combination of which) is affected by the CO2 levels, only that the overall sensitivity to CO2 levels is not significantly different for either assumption. This may not, however, be of significant concern when processing clinical data, if the overall effect of the changes is very similar.
Our results are in good general agreement with the recent study by [21], although since these authors used Autoregulation Index and looked at the dynamic changes, direct comparisons are difficult to make. This other study does, however, illustrate the importance of further work in interpreting the dynamic response to changes in CO2 levels, which we have not investigated here.
We note that CO2 is usually assumed to be metabolically neutral; however there are still open questions over this assumption, which has been made throughout here [22]. In one recent study of brain metabolism, it was found that mild hypercapnia resulted in a suppression of CMRO2 by 13.4% [23]; however, analysis of the NIRS measured signal cytochrome c oxidase showed an increase in oxidative metabolism in healthy volunteers during hypercapnia that cannot be exclusively attributed to the increase in oxygen delivery [9]. This remains an open question, but we note that the model proposed here could easily be extended in future to investigate the effects of changes in CMRO2 on phase angle and hence to provide an additional technique to investigate this question.
Finally, it should be noted that the experimental data contain a significant proportion of scalp flow as well as brain flow, whereas the model is based on only brain flow with well-mixed compartments. A further extension to the model could easily be made in future to quantify the effect of largely unregulated scalp flow on the phase angles and hence to interpret the experimental data more rigorously. This will be the subject of a future paper. This will also be required to aid in the investigation of the differences in baseline values of the haemoglobin-based phase angles between different experimental studies and different pathological conditions such as stroke and brain trauma. This will be vital for these results to translate into clinical practice, where real time bedside monitoring of cerebral blood and metabolism could have a valuable role in quantifying recovery from stroke or brain injury and in adding to existing vital signs monitoring systems.
6. Conclusions
The results outlined above show that autoregulation status is strongly affected under conditions of hypocapnia, less so for hypercapnia. If it is assumed that only feedback gain is affected, then we estimate that there is a −4.6% change in this parameter per % change in CO2 partial pressure, a result that is backed up by measurements of both flow and haemoglobin dynamics. The sensitivity of phase angle at 0.1 Hz is affected both directly by changes induced directly by CO2 and by indirect alterations caused by changes in autoregulation status. The effects of SaO2 on autoregulation status are less clear, the MBP/CBFV phase angle indicating that there is a change of 1.8% in feedback gain per % change in SaO2, but the haemoglobin phase angles not being in agreement with this.
Acknowledgments
The authors would like to thank the Wellcome Trust (088429/Z/09/Z). Parts of this work was undertaken at University College London Hospitals and partially funded by the UK Department of Health's National Institute for Health Research Centres funding scheme. We would also like to thank the two reviewers for their help in making the manuscript clearer and more focused.
References and links
- 1.Wolf M., Ferrari M., Quaresima V., “Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications,” J. Biomed. Opt. 12(6), 062104 (2007). 10.1117/1.2804899 [DOI] [PubMed] [Google Scholar]
- 2.Al-Rawi P. G., Smielewski P., Kirkpatrick P. J., “Evaluation of a near-infrared spectrometer (NIRO 300) for the detection of intracranial oxygenation changes in the adult head,” Stroke 32(11), 2492–2500 (2001). 10.1161/hs1101.098356 [DOI] [PubMed] [Google Scholar]
- 3.Panerai R. B., Simpson D. M., Deverson S. T., Mahony P., Hayes P., Evans D. H., “Multivariate dynamic analysis of cerebral blood flow regulation in humans,” IEEE Trans. Biomed. Eng. 47(3), 419–423 (2000). 10.1109/10.827312 [DOI] [PubMed] [Google Scholar]
- 4.Peng T., Rowley A. B., Ainslie P. N., Poulin M. J., Payne S. J., “Multivariate system identification for cerebral autoregulation,” Ann. Biomed. Eng. 36(2), 308–320 (2008). 10.1007/s10439-007-9412-9 [DOI] [PubMed] [Google Scholar]
- 5.Peng T., Rowley A. B., Ainslie P. N., Poulin M. J., Payne S. J., “Wavelet phase synchronization analysis of cerebral blood flow autoregulation,” IEEE Trans. Biomed. Eng. 57(4), 960–968 (2010). 10.1109/TBME.2009.2024265 [DOI] [PubMed] [Google Scholar]
- 6.Payne S. J., Selb J., Boas D. A., “Effects of autoregulation and CO2 reactivity on cerebral oxygen transport,” Ann. Biomed. Eng. 37(11), 2288–2298 (2009). 10.1007/s10439-009-9763-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Payne S. J., “A model of the interaction between autoregulation and neural activation in the brain,” Math. Biosci. 204(2), 260–281 (2006). 10.1016/j.mbs.2006.08.006 [DOI] [PubMed] [Google Scholar]
- 8.Payne S. J., Tarassenko L., “Combined transfer function analysis and modelling of cerebral autoregulation,” Ann. Biomed. Eng. 34(5), 847–858 (2006). 10.1007/s10439-006-9114-8 [DOI] [PubMed] [Google Scholar]
- 9.Tachtsidis I., Tisdall M. M., Leung T. S., Pritchard C., Cooper C. E., Smith M., Elwell C. E., “Relationship between brain tissue haemodynamics, oxygenation and metabolism in the healthy human adult brain during hyperoxia and hypercapnea,” Adv. Exp. Med. Biol. 645, 315–320 (2009). 10.1007/978-0-387-85998-9_47 [DOI] [PubMed] [Google Scholar]
- 10.Tisdall M. M., Tachtsidis I., Leung T. S., Elwell C. E., Smith M., “Near-infrared spectroscopic quantification of changes in the concentration of oxidized cytochrome c oxidase in the healthy human brain during hypoxemia,” J. Biomed. Opt. 12(2), 024002 (2007). 10.1117/1.2718541 [DOI] [PubMed] [Google Scholar]
- 11.Tisdall M. M., Tachtsidis I., Leung T. S., Elwell C. E., Smith M., “Changes in the attenuation of near infrared spectra by the healthy adult brain during hypoxaemia cannot be accounted for solely by changes in the concentrations of oxy- and deoxy-haemoglobin,” Adv. Exp. Med. Biol. 614, 217–225 (2008). 10.1007/978-0-387-74911-2_25 [DOI] [PubMed] [Google Scholar]
- 12.Tisdall M. M., Taylor C., Tachtsidis I., Leung T. S., Elwell C. E., Smith M., “The effect on cerebral tissue oxygenation index of changes in the concentrations of inspired oxygen and end-tidal carbon dioxide in healthy adult volunteers,” Anesth. Analg. 109(3), 906–913 (2009). 10.1213/ane.0b013e3181aedcdc [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wong F. Y., Leung T. S., Austin T., Wilkinson M., Meek J. H., Wyatt J. S., Walker A. M., “Impaired autoregulation in preterm infants identified by using spatially resolved spectroscopy,” Pediatrics 121(3), 604–611 (2008). 10.1542/peds.2007-1487 [DOI] [PubMed] [Google Scholar]
- 14.Soul J. S., Taylor G. A., Wypij D., Duplessis A. J., Volpe J. J., “Noninvasive detection of changes in cerebral blood flow by near-infrared spectroscopy in a piglet model of hydrocephalus,” Pediatr. Res. 48(4), 445–449 (2000). 10.1203/00006450-200010000-00005 [DOI] [PubMed] [Google Scholar]
- 15.Rowley A. B., Payne S. J., Tachtsidis I., Ebden M. J., Whiteley J. P., Gavaghan D. J., Tarassenko L., Smith M., Elwell C. E., Delpy D. T., “Synchronization between arterial blood pressure and cerebral oxyhaemoglobin concentration investigated by wavelet cross-correlation,” Physiol. Meas. 28(2), 161–173 (2007). 10.1088/0967-3334/28/2/005 [DOI] [PubMed] [Google Scholar]
- 16.Tachtsidis I., Elwell C. E., Leung T. S., Lee C. W., Smith M., Delpy D. T., “Investigation of cerebral haemodynamics by near-infrared spectroscopy in young healthy volunteers reveals posture-dependent spontaneous oscillations,” Physiol. Meas. 25(2), 437–445 (2004). 10.1088/0967-3334/25/2/003 [DOI] [PubMed] [Google Scholar]
- 17.Nilsson H., Aalkjaer C., “Vasomotion: mechanisms and physiological importance,” Mol. Interv. 3(2), 79–89, 51 (2003). 10.1124/mi.3.2.79 [DOI] [PubMed] [Google Scholar]
- 18.Reinhard M., Wehrle-Wieland E., Grabiak D., Roth M., Guschlbauer B., Timmer J., Weiller C., Hetzel A., “Oscillatory cerebral hemodynamics--the macro- vs. microvascular level,” J. Neurol. Sci. 250(1-2), 103–109 (2006). 10.1016/j.jns.2006.07.011 [DOI] [PubMed] [Google Scholar]
- 19.Reivich M., “Arterial PCO2 and cerebral hemodynamics,” Am. J. Physiol. 206, 25–35 (1964). [DOI] [PubMed] [Google Scholar]
- 20.Subudhi A. W., Panerai R. B., Roach R. C., “Acute hypoxia impairs dynamic cerebral autoregulation: results from two independent techniques,” J. Appl. Physiol. 107(4), 1165–1171 (2009). 10.1152/japplphysiol.00498.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dineen N. E., Brodie F. G., Robinson T. G., Panerai R. B., “Continuous estimates of dynamic cerebral autoregulation during transient hypocapnia and hypercapnia,” J. Appl. Physiol. 108(3), 604–613 (2010). 10.1152/japplphysiol.01157.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Siesjö B. K., “Cerebral metabolic rate in hypercarbia--a controversy,” Anesthesiology 52(6), 461–465 (1980). 10.1097/00000542-198006000-00001 [DOI] [PubMed] [Google Scholar]
- 23.Xu F., Uh J., Brier M. R., Hart J., Jr, Yezhuvath U. S., Gu H., Yang Y., Lu H., “The influence of carbon dioxide on brain activity and metabolism in conscious humans,” J. Cereb. Blood Flow Metab. 31(1), 58–67 (2011). 10.1038/jcbfm.2010.153 [DOI] [PMC free article] [PubMed] [Google Scholar]


