Defining an informativeness metric for clustering gene expression data

Abstract

Motivation: Unsupervised ‘cluster’ analysis is an invaluable tool for exploratory microarray data analysis, as it organizes the data into groups of genes or samples in which the elements share common patterns. Once the data are clustered, finding the optimal number of informative subgroups within a dataset is a problem that, while important for understanding the underlying phenotypes, is one for which there is no robust, widely accepted solution.

Results: To address this problem we developed an ‘informativeness metric’ based on a simple analysis of variance statistic that identifies the number of clusters which best separate phenotypic groups. The performance of the informativeness metric has been tested on both experimental and simulated datasets, and we contrast these results with those obtained using alternative methods such as the gap statistic.

Availability: The method has been implemented in the Bioconductor R package attract; it is also freely available from http://compbio.dfci.harvard.edu/pubs/attract_1.0.1.zip.

Contact: jess@jimmy.harvard.edu; johnq@jimmy.harvard.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Clustering methods were among the first methods to be applied to DNA microarray data (Eisen et al., 1998; Michaels et al., 1998) and they remain one of the most commonly used techniques in the analysis of high-dimensional genomic data. The assumption is that samples sharing similar patterns of expression across large numbers of genes are members of a particular molecular class or that genes grouped in clusters are co-regulated across samples because they belong to a common functional group or pathway. While these assumptions have proven useful, determining where a cluster begins and ends, or equivalently, how many gene or sample clusters are present in a dataset is often arbitrary or treated as a post-clustering analysis problem. In either case, the lack of a robust and reliable method can lead to potentially incorrect conclusions. Underestimating the number of clusters can artificially group unrelated elements while overestimating can split related groups into subgroups that confound further analysis.

Here we focus on the problem of identifying informative gene expression clusters in experimental datasets resulting from comparison of multiple biological classes (such as treatment and control, or different cell types). The question we are trying to address is very specific: given a number of distinct phenotypic groups, what is the optimal cluster number (and membership) such that the clusters are maximally informative in their ability to distinguish the sample classes?

Given the history of using clustering approaches in gene expression analysis and for other applications, it is surprising that this problem has not been more effectively addressed. Statistical methods that evaluate the optimal number of clusters within a dataset exist but are rarely used in a systematic manner and may reflect the fact that there are an array of experimental applications in which clustering is used as a discovery tool.

Model-based cluster analysis methods assume that the collection of gene expression profiles can be decomposed into subgroups in which the genes display coordinated patterns of expression. Model-based approaches use statistical methods to search for the number of subgroups for which the consensus profiles best fit the available data (McLachlan et al., 2002). For model-based methods, metrics such as the Akaike Information Criterion (Akaike, 1974) and the Bayesian Information Criterion (Schwarz, 1978) are both based on likelihood values and can be used to evaluate how well one model fits the data relative to another model. While these have been applied in other domains, in the analysis of microarray data, model selection can become difficult since there is often no a priori way of knowing what the structure of the underlying ‘true’ model might be. These approaches also may require the estimation of a large number of parameters, and in some cases, the number of samples may not be sufficient to accurately complete this task. Finally, most model-based clustering algorithms assume a Gaussian distribution for variation that may not generally be appropriate for genomic profiling data.

For the analysis of microarray data, a number of methods have been developed for estimating optimal cluster number based on an assessment of two properties of ‘good’ gene clusters: compactness and stability. A compact cluster is defined such that the intra-cluster variability is small relative to the average inter-cluster variability. Metrics assessing compactness that have been applied to array data include the gap statistic (Tibshirani et al., 2001), the Silhouette width (Rousseeuw, 1987), the Dunn index (Dunn, 1974) and the connectivity score (Handl et al., 2005). A stable cluster on the other hand, is one that is robust to the removal of a small number of samples from the dataset. Stable cluster metrics include the average proportion of non-overlap (APN), the average distance (AD), the average distance between means (ADM) (Datta and Datta, 2003) and the figure of merit (FOM) (Yeung et al., 2001). These too fundamentally look at the relationship between intra- and inter-cluster variability. The aim of these metrics is to identify a set of clusters that individually displays tightly grouped representative profiles, while finding clusters that are each distinct from the others.

Despite the propagation of methods, none of these has become established as a de facto solution to the problem of estimating cluster number. However, this problem is not unique and predates arrays; in a comparative study of thirty statistical metrics on a variety of simulated datasets, which concluded that while some metrics performed adequately some of the time, the best metric to use may be arbitrarily data dependent (Milligan and Cooper, 1985).

In the analysis of most genomic datasets, the question is generally less abstract. What we often want to know is whether there are subsets of genes (in other words, clusters) that are informative relative to the known classes of samples in our analysis. This is a question that spans the boundary between unsupervised clustering and statistical analysis on a gene-by-gene basis since we are searching for gene groups that share similar profiles, and which are distinct from the profiles in other groups, and which have profiles that distinguish the various phenotypic classes being analyzed (such as treated versus control).

To best use phenotypic class information to our advantage, we define our informativeness metric based on simple ANOVA statistics that come from comparing gene expression profiles between phenotypic groups and which is, therefore, focused on differences between groups rather than differences within groups. The informativeness metric satisfies properties of both a compactness metric and a stability metric, since it leverages the ANOVA framework to detect the number of clusters that minimizes within-cluster variance but equally requires these profiles to be consistent across the samples collected. Implicit in defining this metric is the assumption that there are replicate measures for members within each experimental group and that group membership is known ahead of time.

Ultimately, the test of any statistical measure is how well it performs relative to other measures in its ability to produce a biologically meaningful and relevant result. As a measure of the ability of our proposed metric to identify functionally relevant clusters, we compared its performance to eight other metrics using both simulated and experimental datasets and using complete linkage agglomerative hierarchical clustering with a Pearson correlation coefficient-based distance metric as our primary clustering method.

2 METHODS

Consider a dataset consisting of g genes and n samples, where the samples are drawn from m classes or experimental groups, and which is partitioned into a set of p non-overlapping clusters of genes using complete-linkage clustering (or any other clustering method). We assume that each group has n_k replicate samples for groups k = 1,…, m and the total number of samples in the dataset is given by n = ∑_k=1^m n_k. The number of genes in a single cluster c is denoted by g_c and we assume that every gene appears in one of the p clusters, g = ∑_c=1^p g_c.

Let Y_ijk,c represent the expression value of the i-th gene of replicate sample jfor group k where i = 1,…, g_c genes; j = 1,…, n_k replicates; k = 1,…, m groups and c = 1,…, p clusters.

The mean expression profile for cluster c is given by the n-dimensional vector,

(1)

where

(2)

represents the mean expression value for a replicate sample j from group k that has been averaged over the g_c genes in cluster c. Here the dot notation indicates the index over which the summation takes place. For example, 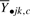represents the value averaged over all genes (as indexed by i) from i = 1 up to the number of genes g_c for a particular cluster c.

For each of the p clusters, we then fit an analysis of variance (ANOVA) model to the mean expression profile of that cluster which estimates the degree of dependency between the mean expression profile 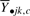and a covariate that denotes group membership; in other words, we are able to quantify how much of the variability in 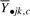can be explained by group membership alone. We call a cluster ‘informative’ if its mean expression distinguishes the different biological classes or groups as defined by a statistically significant model fit.

Formally, we fit a one-way fixed-effects ANOVA model to the mean expression profile 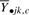[as defined in (2)] of each cluster c using a single factor that denotes each sample's group effect through the model parameter μ_k,c for k = 1,…, m groups; a standard representation of the linear model underlying the ANOVA is represented by the following model equation:

(3)

where μ_c represents the overall mean, μ_k,c measures the effect of group k and ε_jk,c represents the random normal residual error term.

The null hypothesis, H_0(c):μ_1,c = μ_2,c = … = μ _m,c, states all group means are equivalent while the alternative hypothesis, H₁ assumes that not all μ_k's are equal or, equivalently, that at least two groups have different mean expression values.

The mean expression for group k in cluster c is given by

(4)

which is simply the expression averaged over the genes in cluster c, then averaged over the n_k replicates. Note this is reflected by the double dot notation which indicates the two indices over which the summations occur, one over the gene index i [from 1 to g_c as shown in (2)] and the second over the replicate index j (from 1 to n_k for the k-th group).

The overall mean value represents the average of all m group means in cluster c,

(5)

where the triple dots indicate summations over the gene index i (from 1 to g_c genes for cluster c), the replicate index j (from 1 to n_k replicates for the k-th group) and the group index k (from 1 to m groups).

From the fitted model (30 for cluster c, we obtain the MSS_c statistic (also known as the mean treatments sum of squares) which captures the amount of variation attributed to group-specific effects:

(6)

and the RSS_c statistic (the residual sum of squares, also known as the mean error sum of squares) which represents the residual variation remaining after group-specific effects have been accounted for (Fig. 1),

(7)

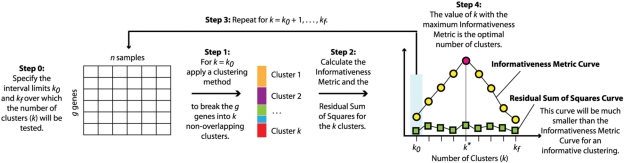
Fig. 1.

Overall workflow of the informativeness metric-based approach.

An informative cluster c will yield a large MSS_c statistic relative to the RSS_c statistic. This is because when genuine group structure exists in the data, this is manifested by observing group means that adopt distinctly different values. In this situation, the sum of squares calculation in the MSS_c statistic is large whereas the sum of squares calculation in the RSS_c statistic shrinks to zero (Fig. 2).

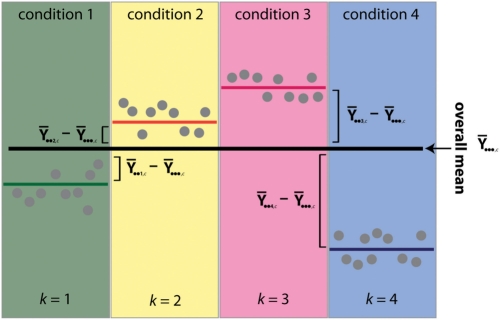
Fig. 2.

Schematic diagram of the assumptions underlying calculation of the informativeness metric. Individual dots represent data points that represent an expression profile; by definition, an informative profile will be one whose points sit far away from the overall mean in each condition.

In calculating the RSS_c statistic, we are always comparing elements of the mean expression profile back to their respective group means and so the statistic is not influenced by the presence of group structure in the data. The MSS_c statistic on the other hand compares the group means to the overall mean directly (which ignores any group structure) and therefore the more distinct the group means become, the sum of the deviations from the overall mean will increase giving rise to a larger MSS_c statistic.

We define two final measures that collectively represent how informative the overall cluster analysis is. These measures are obtained by averaging the cluster-specific MSS_c and RSS_c statistics for the p clusters found in the dataset:

(8)

and

(9)

Given that a single informative cluster c will be associated with a large MSS_c and a small RSS_c value then by extension, the overall MSS^(p) and RSS^(p) values will be large and small respectively, for an informative set of p clusters. The MSS^(p) statistic best captures the size of the group-specific effect directly for each of the p clusters and therefore we define the informativeness metric to be the MSS^(p) statistic defined in (8).

In standard ANOVA analysis, it is more common to focus on the ratio of the MSS and RSS statistics or equivalently, the F statistic:

to assess the significance of a fitted model.

For the p clusters generated by the cluster analysis, we can extend the F_c cluster-based statistic and similarly define F^(p) in the following way:

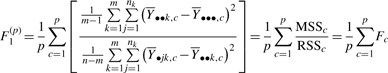(10)

Our results presented for the modified F statistic are calculated from the F₁^(p) definition. Note that there is an alternative way to define F^(p):

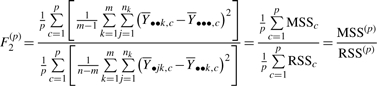(11)

In theory, the F-based statistic appears to be potentially useful as a means to measure informativeness since a large MSS_c and small RSS_c will give rise to a large F value. However, based on tests using simulated datasets, the F-based statistic as defined in (10) was inconsistently incorrect in estimating the correct number of clusters (see Supplementary Material). For the experimental dataset, the F-based statistic estimated a set of clusters which were sub-optimal describing the diversity of expression profiles for the biological classes in this dataset. This can be demonstrated by comparing the profiles in panel A versus B in Figure 3 where the emergence of Cluster 1 in panel B reveals a cluster that would otherwise have been masked when fewer numbers of clusters are specified, as shown in panel A (and Supplementary Material). Therefore, our tests of the F-based statistics on both simulated and experimental datasets indicate that these statistics do not perform reliably as measures of cluster information content.

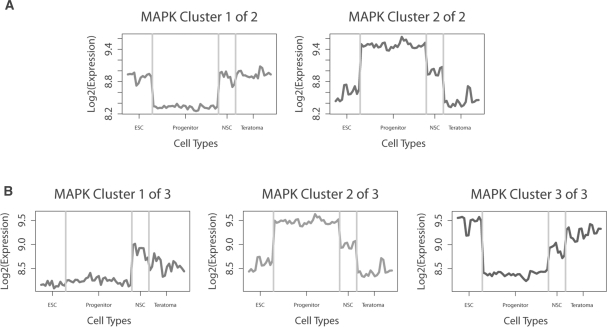
Fig. 3.

Average expression profiles for the MAPK pathway with different numbers of cluster applied. These clusters were generated from complete linkage agglomerative hierarchical clustering, using Pearson's correlation metric. (A) Two clusters. (B) Average cluster expression profiles for the MAPK pathway with the number of clusters prescribed by the informativeness metric. Note the appearance of the first cluster which has an expression profile distinct from those identified using other methods.

By clustering the expression dataset, the goal is to reveal underlying sub-structures that reflect the gene sets driving the group-specific differences observed. Changing the number of clusters will effectively alter the resolution at which those substructures can be observed, and the optimal number of clusters will give rise to a set of clusters that highlight these group-specific differences at maximum resolution. Therefore, as the number of clusters (p) approaches this optimal value, the clusters become more informative, as reflected by an increase in the MSS^(p) statistic and a much smaller RSS^(p) statistic. The F^(p)-based statistic failed to provide reliable discriminatory power and a careful analysis of all three collective measures on both simulated and real data indicate that MSS^(p) has the greatest discriminatory power and consequently, we chose MSS^(p) as a measure of cluster information content—the informativeness metric, coupled with the simple expectation that an informative set of clusters will be associated with a much smaller RSS^(p) statistic.

To determine the optimal number of clusters using the informativeness metric, we vary the number of clusters in a cluster analysis over a finite range and calculate the informativeness metric for each value within this space (Fig. 1). The value which maximizes the informativeness metric is taken to be the optimal number of clusters with the accompanying condition that the RSS^(p) statistic computed for the p clusters should be much smaller than the informativeness metric. Instances where the informativeness metric and the RSS^(p) statistic produce similar values over the interval in which the number of clusters is altered suggest there is an absence of group structure (see Supplementary Material). The range over which the number of clusters (p) is tested can be chosen arbitrarily. In practice, the approach we have adopted is to set the lower limit of this range to one and the upper limit is determined by the maximum value of p that gives rise to clusters that have a minimum number of genes (for example, a minimum of five genes).

3 RESULTS

3.1 Evaluation of the informativeness metric

To evaluate the performance of the informativeness metric relative to other eight other widely used measures (Datta and Datta, 2003; Dunn, 1974; Rousseeuw, 1987; Tibshirani et al., 2001; Yeung et al., 2001), we chose to use both simulated and an experimental dataset. The advantage of a simulated dataset is that it allows us to assess performance where the number of clusters are known and can be used as an objective measure of performance while an experimental dataset provides the opportunity to evaluate whether the results lead to biologically relevant conclusions.

As noted previously, the clustering algorithm adopted throughout our analyses was agglomerative hierarchical clustering where clusters were joined based on complete linkage and the distance metric used was based on (1−R) where R is the Pearson correlation coefficient. Complete linkage was used instead of the more commonly used average linkage because the former produced a much more stable clustering. Complete linkage has been shown to perform better than average linkage for non-ratio based expression values (Gibbons and Roth, 2002). Since the informativeness metric simply measures the optimal number of clusters given a particular clustering algorithm, we chose not to explore the effect of the clustering method and instead focused only on the ability of cluster metrics to identify the optimal number of clusters within a given clustering result.

3.2 Comparison of performance on simulated dataset

We evaluated cluster-number metric performance of three simulated datasets which had four, six and eight clusters, respectively. To construct these, we simulated a small gene expression dataset under a Normal distribution for 300 genes and 100 samples. For each dataset, the samples were grouped into four sets of 25 representing distinct phenotypic classes on which we had repeated measures. Supplementary Figures 1, 2 and 3 shows the distinct expression profiles for data representing six, four and eight clusters, respectively. For each cluster we assume that expression is normally distributed with a standard deviation held constant at 1.5.

Of the nine metrics analyzed, only the informativeness metric was successful in correctly estimating the number of clusters for all three simulated datasets (Table 1). For both the six-cluster and the eight-cluster datasets, the gap statistic and the informativeness metric identified the correct number of clusters. For these two datasets, all of the other compactness-based methods underestimated the optimal number of clusters (Table 1). None of the stability-based methods (APN, AD, ADM and FOM) were able to correctly pick the number of clusters (half of the methods underestimated this number, the other half overestimated). Given that the gap statistic is the most widely used method for determining the optimal number of clusters in applied statistics, it is interesting that it overestimated the optimal number of clusters for the four-cluster simulated dataset.

Table 1.

Optimal number of clusters inferred for the simulated datasets

Number of simulated clusters	Compactness Metrics				Stability Metrics				F-statistic	Informativeness metric
	Gap statistic	Connectivity	Dunn index	Silhouette width	APN	AD	ADM	FOM
4	5	2	3	3	2	6	2	6	1	4
6	6	2	5	4	2	13	2	11	2	6
8	8	2	7	6	2	9	2	8	2	8

All metrics require the user to specify a finite range over which the number of clusters is optimized. For the eight existing metrics presented in our article, the lower limit of this range permitted was two, and the upper limit was determined by choosing the maximum number of clusters that produced clusters with at least five genes. The lower limit allowed by our informativeness metric was one, and we applied the same criterion to determine the upper limit.

We also extended our simulation study to evaluate the performance of the informativeness metric against the other nine metrics in the context of (i) a larger number of genes than samples (2000 genes, 100 samples); (ii) 100 simulated datasets where the number of clusters is known to be four, six and eight clusters; (iii) clusters produced by both hierarchical clustering and k-means clustering; (iv) no clustering structure; (v) a simulated dataset with unequal sample sizes for each phenotypic group (300 genes, 110 samples with 20, 20, 30, 40 replicates per group); (vi) a simulated dataset with a larger number of genes and small number of samples (1800 genes, 40 samples); (vii) unequal variance between clusters where each cluster in the dataset is simulated under a different variance parameter; and (viii) unequal variance within clusters where different genes within each cluster were simulated under different variance parameters (see Supplementary Material). In almost all of these simulations, the informativeness metric accurately estimated the correct number of clusters simulated, with the only other metric, the gap statistic demonstrating similar consistent performance, while the remaining metrics performed on average, quite poorly. In instances where the informativeness metric failed to estimate the correct number of clusters exactly, it usually gave the estimate closest to the true parameter, compared to the other metrics.

3.3 Comparison of performance on experimental datasets

We then extended our evaluation to an experimental dataset which studied cell type-specific gene expression differences in distinct human stem cell populations (Muller et al., 2008) (NCBI GEO accession number GSE11508). This dataset surveyed 20 different cell lines, but to simplify our analyses we limited ourselves to evaluating the ability of clustering metrics to predict the optimal number of gene expression clusters between four cell types: embryonic stem cells, neural progenitor cells, neural stem cells and a teratoma-differentiated cell line. We further restricted the samples to those that had been used on the same Illumina BeadChip platform (WG-6), giving a total of n = 68 samples, where the number of samples for each group was n₁ = 12, n₂ = 31, n₃ = 8, n₄ = 17, respectively. We applied a quality filter which retained a probe only if it passed a 0.99 detection score in 75% of samples for at least one of the four cell types. These filtering processes resulted in a total of 11 044 probes.

While it is possible to apply a cluster analysis to all genes in this dataset, we instead preferred to interpret gene clusters within the context of literature-supported biological pathways. Therefore, we used gene sets defined by biological pathways from the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa and Goto, 2000) and for the purposes of this article, chose to demonstrate the performance of the informativeness metric on three pathways which were selected to reflect relevant aspects of the biology associated with the four cell types we have selected from the Müller dataset. We then applied a cluster analysis method separately to each of the top three most significant and largest KEGG pathways: the mitogen-activated protein kinase (MAPK) signaling pathway (g = 154 genes), the focal adhesion pathway (g = 136 genes) and the regulation of actin cytoskeleton pathway (g = 138 genes). In this way, for each KEGG pathway, we obtain a final set of clusters using the informativeness metric that describe the distinct repertoire of expression patterns between cell types supported by the genes that participate in that pathway. Note that we also tested these metrics on clusters derived from a more conventional analysis that began by filtering out genes from the entire dataset and clustering about 2000 genes (Supplementary Material).

Unlike the simulated dataset, here we have no prior knowledge of what the ‘real’ number of clusters is. If, however, we compare the gene expression profiles across phenotypic groups as a function of the number of clusters, we can gauge how informative the results are and whether the optimal number of clusters has been identified. The majority of methods estimated the optimal number of clusters to be two (Table 2) for all three pathways, except the Dunn index, which estimated the optimal number to be two (MAPK), four (focal adhesion) and 10 (actin cytoskeleton).

Table 2.

Optimal number of clusters inferred for the Müller dataset

Experimental datasets	Compactness metrics				Stability metrics				F-statistic	Informativeness metric
	Gap statistic	Connectivity	Dunn index	Silhouette width	APN	AD	ADM	FOM
MAPK (KEGG ID 04010)	2	2	2	2	4	6	4	6	2	3
Focal adhesion (KEGG ID 04510)	2	2	4	2	2	7	2	5	2	4
Regulation of actin cytoskeleton (KEGG ID 04810)	2	2	10	2	2	11	2	5	3	5

In contrast, the informativeness metric identified three, four and five optimal clusters for the MAPK pathway, focal adhesion pathway and regulation of actin cytoskeleton pathway, respectively.

The risk with underestimating the optimal number of clusters is that important features of the data might be hidden. Figure 3A shows the two clusters, produced by the hierarchical clustering of the MAPK pathway, that were identified by all four compactness-based metrics tested. The predominant patterns observed were genes that are up-regulated and down-regulated in the neural progenitor samples relative to the other cell types. When we examine the three clusters predicted by the informativeness metric, we see that in addition to the patterns observed in the original two cluster, a third cluster (cluster 1, Fig. 3B) appears that uniquely highlights similarities in the expression patterns between the embryonic stem cells and neural stem cells versus increased expression in the neural progenitors and the teratoma-differentiated cells. While the original two clusters highlight the uniqueness of the neural stem cell niche, the additional cluster revealed by the informativeness metric identifies an important biological pattern—a shared phenotype of embryonic stem cells and neural progenitors—that would otherwise have been masked.

For the focal adhesion pathway, we find similar results (Supplementary Material). When the genes are split into two clusters, the dominant themes represented are genes up-regulated or down-regulated in the neural progenitor cells relative to the other cell types. However, the four gene clusters identified using the informativeness metric also identifies patterns of teratoma-differentiated specific expression changes (Supplementary Material, Supplementary Fig. S4B, cluster 3) and embryonic stem cell-specific expression changes (Supplementary Material, Supplementary Fig. S4B, cluster 4). Note that the Dunn index was also able to identify the same four clusters as the informativeness metric.

For the regulation of actin cytoskeleton pathway (Supplementary Material, Supplementary Fig. S5), the two primary clusters found by most metrics distinguish the progenitor cells from the three other phenotypic groups. For the additional clusters found using the informativeness metric and Dunn index, we see two separate embryonic stem cells and progenitor cells from the neural stem cells and teratoma-differentiated cells, with genes either up-regulated (Supplementary Fig. S5B, cluster 2) or down-regulated (Supplementary Material, Supplementary Fig. S5B, cluster 5) in the ESC/progenitor cell group. We also see a cluster with a less easily interpreted expression pattern (Supplementary Material, Supplementary Fig. S5B, cluster 4). Although this cluster does not have a clear interpretation in terms of its differential expression pattern, it may nonetheless capture some of the underlying biology of the actin cytoskeletal system, which is important to the structural integrity of the cell types profiled by Müller et al. (2008), all of which have similar cell shapes. Regardless, the identification of two additional and clearly relevant clusters through the use of the informativeness metric underscores its overall utility.

While we found additional biologically relevant structure by adding new clusters, there is clearly an upper limit. For the actin pathway, the Dunn index suggested 10 clusters (compared to 5 as suggested by the informativeness metric). However, having 10 clusters does not provide a set of clusters that are overall informative (Supplementary Material, Supplementary Fig. S6), where, for example, clusters 6, 9, 10 are essentially the same profile, containing genes that are invariant across the phenotypic group.

Unlike the situation in using simulated data, it is difficult to objectively determine whether the number of gene clusters identified by any method captures the underlying biology being explored in the experiment. The informativeness metric generally identified a larger number of clusters than other approaches and in each occasion these provided additional, relevant discriminating patterns between the cell types. In the one instance in which additional clusters were identified by another method, the Dunn index, these provided no additional insight into patterns discriminating between cell types. The evidence here suggests that our informativeness metric strikes the right balance, and succeeds in teasing out more informative clusters from the expression data.

4 DISCUSSION

The motivation underlying all clustering methods is to determine whether the data can be partitioned into useful groups that provide insight into the relationship between group members, or the discriminating elements between groups. While identifying clusters that reflect finer substructures may be desirable, there are also instances where a dataset may have no such underlying structure and can therefore be described adequately by a single cluster. The eight metrics that we assessed neglect this possibility and make the assumption that further substructure is present in the data. While this may be a valid assumption for situations where the entire dataset is being clustered, this is rarely the primary focus of cluster analysis in bioinformatics. Indeed, there are often many other applications of cluster analysis that involve smaller, more targeted gene lists. In order to avoid making assumptions that may not be appropriate, at a minimum the user should be able to test for the presence of any clustering structure versus none (i.e. whether the optimal number of clusters is one or more than one) and the eight metrics assessed lack this ability. In contrast, the informativeness metric can easily test for the existence of any clustering structure, including a single group (see Supplementary Material).

Tests on the simulation datasets revealed that only the informativeness metric was able to correctly uncover the true clustering structure of the data in every situation. The gap statistic made only one incorrect estimate, however all four of the compactness metrics consistently underestimated the correct number of clusters, and estimates given by the four stability metrics were scattered above and below the true number of clusters in the data. Tests on the experimental datasets demonstrated that the informativeness metric was more accurate in uncovering the number of clusters that would summarize the data into its most distinct set of cluster patterns relevant to the cell types being studied. We saw examples where the other metrics underestimated the number of optimal clusters, only to find that the larger number, as prescribed by the informativeness metric, sub-divided the data into a greater number of distinct cluster patterns that highlighted unique properties of certain cell types. Similarly, we also gave one example of where the Dunn index estimated a larger number of clusters than the informativeness metric, and where the cluster profiles produced from the former were not really distinct from each other. Taken together, both sets of results on experimental and simulated datasets suggest that the informativeness metric is successful in isolating the distinct set of cluster profiles for replicated data collected for different experimental groups.

5 CONCLUSION

We provide an alternative way to validate the results of a cluster analysis that explicitly takes into account the experimental design which produced the dataset. This validation method is independent of the method used to generate the clusters. Given the additional insights into data structure provided by our approach, we hope that the simplicity of our method will make the integration of cluster validation approaches a more mainstream part of the cluster analysis procedure.

6 IMPLEMENTATION

The routines implementing this metric and associated tools for visualization are freely available as an R package attract and has been submitted to Bioconductor. We have also uploaded a script which details the calculations performed as well the data analyzed in this article, available from http://compbio.dfci.harvard.edu/pubs/informativeness.zip. The Bioconductor R package clValid (Datta and Datta, 2006) contains functions that calculate the six other metrics: the connectivity score, the Dunn Index, the silhouette width, APN, AD, ADM and FOM. To our knowledge, the Bioconductor package SAGx contains the only implementation of the Gap statistic in R.