How much detail and accuracy is required in plant growth sub-models to address questions about optimal management strategies in agricultural systems?

The amount of detail and accuracy required in plant growth sub-models within agricultural systems management models depends strongly on the question being addressed. Taking an ‘as-simple-as-possible’ approach has advantages such as keeping models transparent and easy to analyse while remaining appropriate to the question of interest.

Abstract

Background and aims

Simulations that integrate sub-models of important biological processes can be used to ask questions about optimal management strategies in agricultural and ecological systems. Building sub-models with more detail and aiming for greater accuracy and realism may seem attractive, but is likely to be more expensive and time-consuming and result in more complicated models that lack transparency. This paper illustrates a general integrated approach for constructing models of agricultural and ecological systems that is based on the principle of starting simple and then directly testing for the need to add additional detail and complexity.

Methodology

The approach is demonstrated using LUSO (Land Use Sequence Optimizer), an agricultural system analysis framework based on simulation and optimization. A simple sensitivity analysis and functional perturbation analysis is used to test to what extent LUSO's crop–weed competition sub-model affects the answers to a number of questions at the scale of the whole farming system regarding optimal land-use sequencing strategies and resulting profitability.

Principal results

The need for accuracy in the crop–weed competition sub-model within LUSO depended to a small extent on the parameter being varied, but more importantly and interestingly on the type of question being addressed with the model. Only a small part of the crop–weed competition model actually affects the answers to these questions.

Conclusions

This study illustrates an example application of the proposed integrated approach for constructing models of agricultural and ecological systems based on testing whether complexity needs to be added to address particular questions of interest. We conclude that this example clearly demonstrates the potential value of the general approach. Advantages of this approach include minimizing costs and resources required for model construction, keeping models transparent and easy to analyse, and ensuring the model is well suited to address the question of interest.

Introduction

The issues of scale, detail and accuracy are important questions when modelling plants in agricultural and ecological systems, just as they are when modelling any system (Soetaert and Herman 2008). The builder of a process-based model of an agricultural or ecological system is likely to be interested in using the model to address particular management questions at the field or farm scale. For example: What is the best amount of nitrogen fertilizer to apply to this field, given that a legume crop was grown last season and we have had a certain pattern of rainfall so far this season? What is the best way to allocate the land use across the farm over the next few years and what profit is this likely to result in? If I have grown a cereal crop 4 years in a row, should I sow a cereal again next year? These questions are likely to be of different types, requiring answers that may be quantitative or qualitative, simple or more complex. But in constructing the model they hope will help answer these higher-level questions, the modeller will have to decide whether to represent underlying processes at a greater or lesser level of detail. Aiming for greater detail and accuracy may seem attractive in terms of realism, but will almost always require more investment of money, time and other resources. Is this greater detail and accuracy necessary to address the particular question of interest?

Process-based models represent the system of interest in terms of interactions between underlying lower-level objects or systems. For example, a crop growth modeller might want to represent interactions between leaves, roots and soil. The creator of a model always needs to decide at what scale and level of detail to represent these underlying processes. For example: Should plants be represented as homogeneous layers of photosynthetic material across the field with another series of layers of roots within the soil, or rather as plants, individual leaves or even individual cells? If layers are chosen to represent plants in the field, then should the roots and soil be represented in layers that are a metre in depth, a centimetre in depth or a millimetre in depth? Should time be modelled at the scale of minutes, days or years?

Choosing to address underlying lower-level objects and systems within a model at a greater level of detail can help add to the credibility of the model, because people tend to equate more detailed and finer-scaled representation of biological processes with greater ‘realism’, especially in situations where the processes are well understood. For example, since detailed models of soil-water physics have been built and tested (e.g. Ritchie 1972; Connolly et al. 2002; Suleiman and Ritchie 2003; Stewart et al. 2006), basing a crop growth model on a simpler soil-water model (e.g. Probert et al. 1998; Oliver et al. 2009) instead of the more complex model may reduce its credibility. Similarly, people may have more confidence in a crop model that uses a detailed model of photosynthesis (e.g. Johnson and Thornley 1984) than in one that uses a simple radiation-use efficiency approach (e.g. McCown et al. 1996; Keating et al. 2003). People may also tend to believe that greater detail leads to greater accuracy. On the other hand, choosing to address underlying lower-level objects and systems at a lesser level of detail has the great advantage of increasing the simplicity and transparency (in the sense of easily seeing how each parameter influences model output) of the model, thus potentially making it easier to construct, analyse, adapt to new questions and communicate to others. A modelling approach that focuses on the ‘top level’ of the modelled system and does not represent underlying lower-level objects, systems and processes may be called a ‘top-down’ approach, while an approach that focuses on representing the underlying lower-level objects, systems and processes may be called a ‘bottom-up’ approach (Haefner 2005).

This paper first discusses the possibility of ‘middle-up’ approaches intermediate between the full ‘top-down’ and ‘bottom-up’ approaches, and of ‘meta-modelling’ approaches that can bridge these various approaches. It then describes an integrated ‘as-simple-as-possible’ approach that can combine some of the advantages of these different approaches. We explore and illustrate this integrated approach using the example of a deterministic agro-ecosystem-scale model called LUSO (Land Use Sequence Optimizer) (Lawes and Renton 2010), built to simulate the short- and long-term effects of farm management decisions on ecological processes affecting farm profit. For example, it simulates the effects of land-use allocation decisions on weed population dynamics over many subsequent years. LUSO thus enables different management options to be evaluated while taking into account both their short- and long-term implications. We summarize the LUSO model and analysis framework, and show how it is currently based on an intermediate ‘middle-up’ approach. Next we focus on the field-scale crop–weed competition sub-model used in LUSO and explain how we tested the sensitivity of the overall LUSO model to variations in this sub-model, by addressing some particular management questions at the level of the farming system. We present the results of this analysis, concluding that in this case, only for certain types of questions, would it be worth devoting resources to try to improve model precision. Finally, we discuss the wider implications for this kind of integrated ‘as-simple-as-possible’ approach.

Materials and methods

Different approaches to model development

Top-down, bottom-up and middle-up approaches

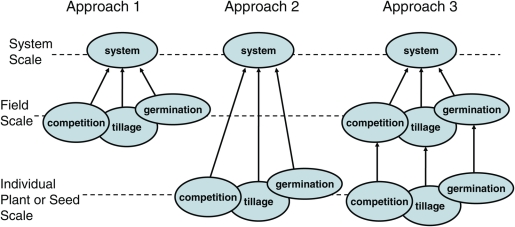
Take an example situation where we are interested in building a farming-system-scale model that can predict the effect of different farm management options regarding agricultural land-use rotations on the long-term profitability of an area of land, such as a field. We want to take into account both short- and long-term effects of management options. We may know that weeds are one of the main factors that influence profitability and are affected by land-use rotation, and so we want to represent in the model processes such as weed germination, weed population dynamics, effects of weed management such as tillage, and competition between weeds and crop. We could opt for greater realism and represent these underlying processes in our model at a more detailed, lower organizational level, such as the scale of individual plants and seeds, in what might be called a bottom-up approach (Fig. 1, Approach 2). Or we could opt for simplicity and abstraction and attempt to construct empirical functions predicting the profitability of different land-use rotations with no representation of underlying processes, in what might be called a top-down approach. (Note that the pure top-down approach is not illustrated in Fig. 1; if it was included, it would consist of a single oval on the ‘systems-scale’ line.) Or we could opt for an intermediate approach and represent these underlying processes at a less detailed, intermediate organizational level, such as the scale of the population within a field, in what might be called a middle-up approach (Fig. 1, Approach 1). Plant competition can also be modelled in many different ways (Park et al. 2003); in Approach 1 we might represent crop–weed competition using a single empirical density-based competition function (Firbank and Watkinson 1985) or a simple mechanistic model with relatively few parameters, such as the Conductance model (Aikman and Scaife 1993; Benjamin and Park 2007), while in Approach 2 we might represent crop–weed competition using an individual-based model (Grimm and Railsback 2004; Berger et al. 2008). In the search for detailed realism, we could go even further in the ‘bottom-up’ direction and use a linked collection of functional–structural plant models where each individual plant is itself represented as a collection of components such as leaves, internodes and flowers, together with the interactions between these components and their environment, such as photosynthesis, water uptake, transport and allocation of resources, respiration and growth (Godin and Sinoquet 2005; Vos et al. 2007; Fourcaud et al. 2008; Hanan and Prusinkiewicz 2008). Similarly, in Approach 1 we might represent germination using a single constant germination proportion (e.g. Pannell et al. 2004; Renton 2009; Lawes and Renton 2010), while in Approach 2 we might calculate germination proportion using a hydro-thermal model that depends on weather (Bradford 1997; Alvarado and Bradford 2002; Allen 2003), or go even further and represent every seed individually, with its own unique position in the soil and individual history of after-ripening and imbibition (Renton et al. 2008) or its own genetics (Renton 2009). The advantages of Approach 2 are greater biological realism, which allows a greater depth of biological understanding and may make the model more credible to a biological audience, while the advantages of Approach 1 are simplicity and greater transparency, in the sense that there will be fewer parameters and it will be easier to see how each parameter influences model output.

Fig. 1.

Three process-based approaches to modelling weed dynamics in an agricultural system. In Approach 1, the processes influencing the system are represented at the field scale, and so the model is more transparent, but less realistic; in Approach 2, the processes influencing the system are represented directly at the individual-plant or individual-seed scale, and so the model is less transparent, but more realistic; in Approach 3, the processes influencing the system are represented at the field scale, but these field-scale sub-models are built using models that represent processes at the individual-plant or individual-seed scale or lower, and so the model of the agricultural system is more transparent, and more realistic.

Meta-model approach

A third approach that may appear to combine the best of Approach 1 and Approach 2 (more realism without sacrificing transparency) is linking several models that work at different scales through simpler descriptive ‘summary’ models or meta-models (Figure. 1, Approach 3) (Haefner 2005). In this approach we might start by using a linked collection of detailed functional–structural plant models to represent plant competition. By running a large number of simulations of these models, enough output data could be obtained to parameterize simple empirical field-scale models of competition, such as those used in Approach 1, and then these could be used as the sub-models in the system-scale model. These could be known as ‘meta-models’ because they ‘model’ or provide a simplified representation of the more detailed model. In this way, we have depth of realism, because the biological detail and complexity of the individual-plant scale are included, and effects at this scale can be explored, via the summary model. The biological detail and complexity may make the model more credible to a biological audience; some people may be more confident in our field-scale model, because it has been constructed using lower-level models that may be easier to test directly against experimental data. And we also have transparency, because the relationships between the agro-ecosystem-scale model and the field-scale model, and between the field-scale model and the individual-plant-scale model, are simpler to analyse because there is less ‘distance’ between levels (fewer parameters to synthesize) than in Approach 2. However, despite its benefits, Approach 3 is likely to be more time-consuming than Approach 2, and much more time-consuming than Approach 1, since it effectively requires building all the higher-system-level, medium-field-level and lower-individual-plant-level models involved in the other two approaches.

‘As-simple-as-possible’ approach

This paper illustrates an integrated ‘as-simple-as-possible’ approach that combines the simplicity and transparency of Approach 1 and the realism of Approach 2, yet potentially avoids the investment of time and resources required for a complete version of Approach 3 (Fig. 1). The approach is based on the idea of starting simple and adding complexity and detail only if required to address the specific intended purpose of the model. The modeller starts by clarifying the question(s) they want to address with the model at the scale of the agro-ecosystem, and then follows Approach 1 and constructs an agro-ecosystem-scale model based on relatively simple sub-models of the important underlying processes. The modeller then tests the sensitivity of the agro-ecosystem-scale model to variations in the simple sub-models to see how much difference it makes to the agro-ecosystem-scale model's output. If the modeller finds that the answers they are interested in at the agro-ecosystem level rely on the accuracy of a sub-model to a large degree, then the modeller can either move on to building that lower-level model in order to then use it to construct a more accurate summary model, or alternatively, if possible, to collecting more experimental data to refine the accuracy of the sub-model. If the modeller finds that the answers do not rely on the accuracy of the sub-model to the extent that would justify building the lower-level model or collecting the additional data, then they can stay with the current model of the underlying process. The result of this integrated approach is thus to only build the lower-level models for the field-level summary models that ‘really matter’, so if we were to illustrate it in Fig. 1, it would therefore look like a mix of Approach 1 and Approach 3.

LUSO overview

LUSO can be thought of as a framework based on simulation and optimization for analysing different management decisions and options with long-term implications within agricultural systems. It represents an agricultural land-use unit, such as a field, and simulates the processes of weed dynamics, plant disease dynamics and soil nitrogen status changing from season to season with different land uses, and affecting crop yield in the current and future seasons. These processes are each represented in a relatively simple mechanistic way, but in combination result in a fairly complex model involving multiple interactions. A summary of the model is provided here; further details have been provided elsewhere (Lawes and Renton 2010). LUSO aims to improve on previous models of optimal land-use sequencing involving weed management (e.g. Pandey and Medd 1991; Swinton and King 1994; Sells 1995; Wu 2001; Pannell et al. 2004; Haneveld and Stegeman 2005; Detlefsen and Jensen 2007; Doole and Pannell 2008; Benjamin et al. 2009; Parsons et al. 2009) by accounting for weed germination and long-term dormancy, density-dependent weed seed production, and disease and nitrogen effects, by allowing completely flexible land-use sequences and by including automated routines for optimization of economic outcomes and for sensitivity analyses on these results.

The simulation component of LUSO works on an annual time step and takes as input a sequence of annual land uses of any length. For example, this input might be wheat–lupins–wheat–canola–wheat–pasture (WLWCWP), which means that wheat is grown in the first, third and fifth year, lupins in the second, canola in the fourth and a sown pasture in the sixth. Other required input includes a parameter file specifying possible land uses (Table 1), and another parameter file specifying general parameters and the initial condition of the system (Table 2). LUSO was initially parameterized for a Western Australian agricultural system where wheat is the dominant crop, and thus the disease and weed sub-models focus on weeds and diseases of wheat (Lawes and Renton 2010). However, the system has been designed so that land uses and general parameters can be easily added, changed and removed, and so it can be easily adapted to represent any seasonal agricultural system. For the purpose of this paper, a simple version of LUSO with four possible land uses was used, as specified in Tables 1 and 2. More complex versions are discussed elsewhere (Renton and Lawes 2009; Lawes and Renton 2010).

Table 1.

Land uses and their default parameter values used for this study. Potential yield y_p (t ha⁻¹), price received p ($ t⁻¹), variable cost Cv ($ ha⁻¹), nitrogen requirement Nr (kg ha⁻¹), nitrogen boost per tonne of crop yield or pasture biomass grown Nb (kg t⁻¹), disease multiplier dm (−1 means return to minimum level), disease effect on crop s (proportion), weed seed survival p_s (proportion), competition index k_c, sowing density d_c (plants m⁻²), crop–weed antagonism index a_wc and weed seed return wsr (proportion).

Name	yp	p	Cv	Nr	Nb	dm	s	ps	kc	dc	awc	wsr
Wheat	3	350	250	160	0	3	1	0.05	0.091	150	1	1
Lupins	1.5	250	200	0	50	−1	0	0.03	0.08	40	1	1
Pasture	3	0	80	0	25	−1	0	0.03	0.08	50	1	0.1
Canola	1.3	550	250	120	0	−1	0	0.03	0.08	100	1	1

Table 2.

General parameters and their default values used for this study.

Parameter	Symbol	Value
Length of sequence (years)	y	10
Seedbank population at year 0	sb0	50
Weed germination (%)	pg	0.8
Weed competition index	kw	1/33
Weed maximum seed set	SSmax	30 000
Nitrogen cost ($ kg−1)	Ncst	2
Soil nitrogen	Ns0	0
Soil disease population at year 0	D0	0.03
Fixed costs accrued per ha every year	Cf	150
Discount rate	dis	0.05
Cost per weed seed	WScst	0.1

The system (the land-use unit) is simulated for the number of seasons (land uses) specified in the input sequence, and calculates a yield and thus a profit for each of these seasons. Different land uses leave different amounts of soil nitrogen for the following crop, thus affecting the amount of fertilizer required by that crop, and thus profit. Different land uses also have different effects on the population dynamics of weeds and disease; for example, pasture allows better weed control and reduces the population of wheat pathogens. In turn, the weed and disease load each year affects the crop yield in that year, thus also affecting profit. The overall profitability of a land-use sequence is then calculated as the net present value: the sum of annual profits with future profits discounted by a specified discount rate.

The LUSO analysis framework allows for easy sensitivity analysis on a given land-use sequence, showing how the profitability of the land-use sequence changes with changes in one or two model parameter values. This allows the user, for example, to look at how the simulated profitability of different land-use sequences changes with nitrogen price, or level of weed control, or any other value of interest. The framework also enables optimization, finding the most profitable land-use sequence (or sequences) for any set of parameter values. Moreover, the framework allows for a simple and intuitive sensitivity analysis on this optimal sequence, showing how the optimal profitability and the optimal land-use sequence strategy both change with variation in one or two parameters of interest. The kind of sensitivity analysis and the graphical way in which it is presented are aimed at non-technical model users, such as agricultural researchers, agronomists and farmers. More sophisticated, technical and complete sensitivity analyses, such as global analyses or analyses on the interaction of more than two variables, can also be used (Saltelli et al. 2004, 2008; Saltelli 2008), and the results of these are presented more precisely and accurately in tables. These more sophisticated, technical and complete sensitivity analyses have been very usefully applied to plant growth models aimed at providing precise accurate numerical predictions (e.g. Kirschbaum 1999; Choudhury 2000; Dunbabin 2007; Pathak et al. 2007; Confalonieri 2010; Varella et al. 2010). However, our experience agreed with previous reports (Pannell 1997) arguing that simpler, less technical and more graphical approaches may be appropriate for interactive use with users who are less familiar with mathematics and modelling, particularly when a model is designed to provide qualitative management recommendations and analyses of agronomic changes, and general quantification of likely resulting profit, rather than precise accurate numerical predictions. One of the points of this paper is that these relatively simple approaches were also adequate to achieve the aim of this study: to investigate and clearly demonstrate how much detail and accuracy is required in plant growth sub-models to address particular questions about optimal management strategies in agricultural systems.

Full details of the soil nitrogen, weed seedbank and germination, and disease dynamics sub-models, and how they are used to calculate yield and profit have been provided elsewhere (Lawes and Renton 2010). Since this paper focuses on crop–weed competition, more detail on this sub-model is now provided here.

Crop–weed competition sub-model

LUSO's crop–weed competition sub-model is based on the well-established hyperbolic function model (Firbank and Watkinson 1986, as modified by Maxwell et al. 1990; Diggle et al. 2003). For a single crop species and a single weed species, this equation can be written as

(1)

where seed set is the actual number of weed seeds produced (m⁻²), SS_max is a model parameter representing the theoretical maximum weed seed set possible (seeds m⁻², default value 30000), k_w is a model parameter representing the size or competitiveness of the weed (default value 1/33), k_c is a model parameter representing the size or competitiveness of the crop species, which depends on the land use, d_w is the weed density (plants m⁻²), which varies from year to year, d_c is the crop density (plants m⁻²), which depends on the land use, and a_wc is an inter-specific ‘antagonism’ factor that allows for asymmetric competition between the crop and the weed, which is set to one (symmetric competition) by default in the standard LUSO model. The default parameter values for the weed are taken from the Ryegrass Integrated Management (RIM) model (Pannell et al. 2004), and thus represent ryegrass, although they can easily be varied to represent other weeds. The default parameter values for the different crops are also taken from the RIM model. This model can be adapted to multiple species (Monjardino et al. 2003), but this is not considered in the present analysis.

The hyperbolic function described above is also modified to give the multiplication factor for the effect of weed competition on crop yield (wcf):

(2)

The value of wcf will thus always be between zero and one, and it will be closer to one when weed density is high and closer to zero when weed density is low.

Varying the competition sub-model

In order to test the sensitivity of the integrated LUSO to errors or changes in its crop–weed competition sub-model, we considered four aspects of the competition model: maximum weed seed production, competitiveness of weed, competitiveness of crop, antagonism, and local perturbation to functional form, and looked at how changes to these aspects affected the answers we got to our three farming-systems-scale questions (Fig. 2). For the sake of simplicity, and ease of communicating results, we chose to use a ‘one-at-a-time’ sensitivity analysis, rather than considering the interactive effect of varying multiple parameters together (Saltelli 2008; Lawes and Renton 2010). Although a more complete sensitivity analysis as discussed above would have benefits such as showing how non-independent parameters interact to affect model results, the results presented here show that this simpler and potentially more intuitive approach was appropriate to achieve the aims of this paper.

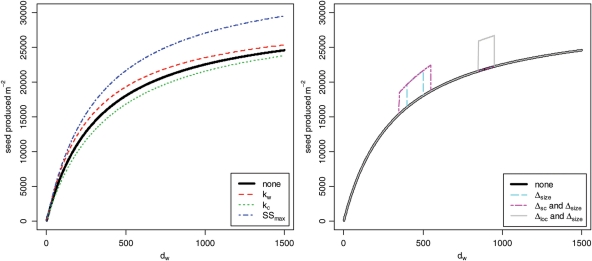
Fig. 2.

Plots showing how increasing three parameters of the crop– weed competition sub-model (left) and parameters of the perturbation function (right) affects the shape of the function describing weed seed produced m⁻² versus weed density m⁻². Parameters were increased by 20 %, except for Δ_loc and Δ_sc, which were increased by 100 %.

By varying the parameter SS_max, which is a measure of the maximum weed seed production m⁻², not a measure of fecundity per individual plant, as in some variants of the hyperbolic competition model (e.g. Damgaard 2004), we were, in effect, asking the question, ‘To what extent does it matter if we get the maximum weed seed production per area somewhat wrong in our model?' By varying the parameters k_w, k_c and a_wc, we were, in effect, asking the question, ‘To what extent does it matter if we get the competitiveness of the weed or competitiveness of the crop or the inter-species antagonism wrong in our model?' Rather than considering all the possible crops, we only considered the competitiveness and antagonism of the main crop, wheat, and assumed that the competitiveness and antagonism of the other crops did not change. Other crops could have been considered independently using the same approach if this was of interest, or the competitiveness of all crops could have been varied in synchronization if this was of more biological relevance.

Finally, we considered a general localized functional perturbation (Hearne et al. 2007) to the hyperbolic competition function. We decided to use a simple continuous perturbation function

where pf (d_w) is the perturbation factor at weed density d_w, Δ_size is a parameter that represents the size of the perturbation (the maximum proportional change to the function), Δ_loc is a parameter that represents the location of the perturbation (the weed density value at which the perturbation is greatest) and Δ_sc is a parameter that represents the scale of the perturbation (the spread or range of weed densities over which it has an effect). The weed seed production function was multiplied by this perturbation factor pf (d_w) to investigate the effect of a perturbation to this production function. Examples of the effect on the weed seed production function resulting from such perturbations are illustrated in Fig. 2. The parameter Δ_size has a default value of one, which means that at this default value pf= 1 for all values of d_w, and so there is no perturbation to the weed seed production function. For our analysis the value of the parameter Δ_size was switched to 1.1 to cause a 10 % perturbation to the production function. Initially we gave the parameter Δ_sc a value of 50 and varied Δ_loc around a value of 450 to find the most sensitive perturbation location. Since we found Δ_loc= 5 to be the most sensitive location for perturbation (as shown in Results), we set Δ_loc to be constant at a value of 5 and then varied Δ_sc around a value of 50 to determine the extent of functional perturbation sensitivity.

Other non-linear variations to the basic linear hyperbolic competition function with more biological meaning have been suggested and studied (e.g. Damgaard 2004; Weigelt et al. 2007), but we decided to use this functional perturbation approach because it is simple, is independent of other parameters, allows for perturbations with local or wider extent, and preserves the pattern of seed production tending towards SS_max and crop yield tending towards zero as weed density tends towards infinity. This means that local perturbation of functional form can be considered completely separately from biological parameters.

Note that changing k_w and k_c directly affects both the weed seed production function and the crop yield function, while a_wc, SS_max, Δ_loc, Δ_size and Δ_sc directly affect only the weed seed production function. However, all parameters have an indirect effect on the whole model dynamics and crop yield over all years through ‘flow-on effects’, because weed seed production in one given year affects weed density in the subsequent year. This affects both crop yield and weed seed production in the subsequent year, which affects weed density, crop yield and weed seed production in the year after that, and so on. Also note that the effect on the weed seed production function of increasing the antagonism parameter a_wc by a certain proportion is the same as increasing the crop competitiveness parameter k_c, which is why this parameter is not illustrated separately in Fig. 2. However, the effect of these two parameters on the overall model dynamics and long-term profitability is different, because k_c directly affects crop yield but a_wc does not.

LUSO used to address three types of questions

For this study, we used LUSO to address three questions addressing long-term farming-system management issues. Two are relatively simple. First, what is the optimal land-use sequence for a farmer to employ over 10 years? Second, what is the total profit for this 10-year sequence? To answer these questions, LUSO was simply used to find the optimal land-use sequence S_opt and the corresponding optimal profit P(V, S_opt) for the original unchanged competition functions. We also used LUSO to address a third, more qualitative and subtle, long-term farming-system-scale question: how do the optimal profit and the optimal land-use sequence change as the amount of weed seed returned to the seedbank is reduced? This represents an analysis of the value and effect of possible weed management measures, such as separating the chaff fraction that contains much of the weed seed in the harvester and removing it from the field, which is interesting and particularly relevant to the purpose for which LUSO was constructed because it provides an estimate of the overall value of introducing new weed management technologies or practices. To address this question, we examined how the optimal land-use sequence and the optimal profit varied as the parameter representing weed seed return in wheat was varied.

These three questions all concern long-term farming-system management, but represent three different types of questions with three different types of answers. The first provides a management recommendation: what land-use sequence should the farmer or land manager plan for his land assuming current technologies and prices remain constant? The second provides a quantitative prediction: what profit will the farmer or land manager achieve if he implements the recommended management sequence. The third question concerning the overall value of introducing new weed management technologies or practices is more general and the answer to this question is better represented graphically as a relationship between improvement in technology and change in profit, rather than a precise profit value or land-use sequence like the answers to the other two questions.

Once we had obtained the answers to the three questions with the original unchanged model, we then investigated whether, and to what extent, the more precise answers to the first two questions depended on changes or errors in the crop–weed competition sub-model. To do this, we varied the competition curve parameters discussed above and recorded how the optimal profitability changed, and if and when the optimal sequence changed. As well as calculating how the optimal profitability changed with the altered competition curves, we also calculated how the profitability of the original optimal sequence changed with the altered competition curves. To explain this more precisely, we define S_opt to be the optimal sequence under the original unchanged competition parameter values V and P(V, S_opt) to be the corresponding profit of this sequence at those parameter values. We then define S_opt^* to be the optimal sequence under the new changed parameter values V*, P(V*, S_opt^*) to be the profit given by the new optimal sequence under the new changed parameter values V*, and P(V*, S_opt) to be the profit given by the originally optimal sequence under the new changed parameter values V*. Thus, we considered how both P(V*, S_opt^*) and P(V*, S_opt) varied with different values of V*. We could also determine the difference in profitability between the original optimal sequence under the original parameter values and the new optimal sequence under the new changed parameter values: P_diff = P(V*, S_opt^*) − P(V, S_opt), which represents the error in predicted profit due to not improving the model. More interestingly, we could also determine the difference in profitability between the original optimal sequence and the new optimal sequence under the new changed parameter values: P_cost = P(V*, S_opt^*) − P(V*, S_opt). If V represents an original model version and V* represents a potential improved version obtained by more detailed modelling (or better experimental data), then P_cost corresponds to the value to the farm manager of using the improved version of the model to make decisions instead of the original version. Equivalently P_cost represents the cost to the farmer of not improving the model.

Finally, we repeated this analysis, showing how P(V*, S_opt^*) and P(V*, S_opt) varied with varying values of different weed competition parameters, for several values of the weed seed return parameter. This allowed us to consider how the answer to the third more general question, regarding the overall value of introducing new weed management technologies or practices, would depend on changes or errors or improvements in the crop–weed competition sub-model. This in turn informs the modeller's or research funder's decision about whether it is expedient to do the work to make these possible improvements or correct these possible errors in order to satisfactorily address this question about the value of new weed management technologies or practices.

Results

Initial answers to three farm management questions

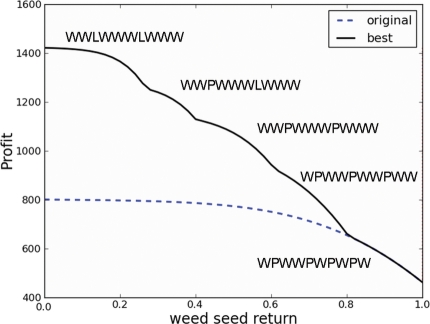
The optimal sequence was WPWWPWPWPW (where W is wheat and P is pasture) and its net present value (total profitability over 10 years, accounting for discounting of future profit) was $462.04 ha⁻¹. Figure 3 (top) shows how the yield penalty due to weeds and disease changes over the seasons depending on the land-use sequence in this optimal sequence, with regular pasture rotations necessary to allow control of weeds, despite providing little short-term profit. Figure 4 shows how the changes in the weed seed return parameter affected the profitability of both the original optimal sequence and the actual optimal sequence for the changed weed seed return parameter value. Note how lower values of weed seed return, corresponding to improved techniques or technologies for capturing or destroying weed seeds, allow more crops (wheat and lupins) to enter the land-use sequence, with correspondingly higher profit overall. Figure 3 (bottom) shows how the yield penalty due to weeds and disease changes over the seasons depending on the land-use sequence in the sequence that was found to be optimal when the weed seed return parameter was set to 0.1, representing new techniques or improved technology for weed seed catching and removal or destruction. Note that the weed seedbank is much lower relative to disease burden in this case than in Fig. 3 (top), indicating that disease rather than weed burden is driving the need for rotation in the land-use sequence in this case.

Fig. 3.

Weed seedbank density (seeds m⁻²) and disease load (relative value out of 1000 maximum) changing over time under the optimal land-use rotation for default parameter values and with the weed seed return parameter set to 1.0 (top) and to 0.1 (bottom).

Fig. 4.

The effect of changes in the weed seed return parameter on the profitability of both the original optimal land-use sequence and the actual optimal land-use sequence for the changed value of the weed seed return parameter wsr. The actual optimal land-use sequences for various weed seed return parameter value ranges are also shown.

Effect of changes to SS_max and k_w on the first two answers

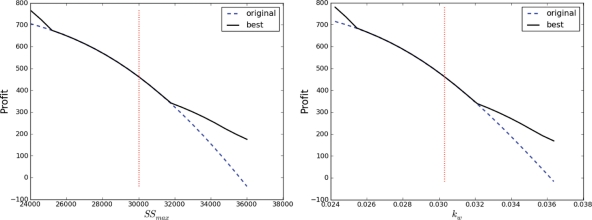
Changes in the maximum weed seed set parameter SS_max affected the profitability of the original optimal sequence and the actual optimal sequence as shown in Fig. 5 (left). Note that P_cost, the cost to the farmer of not improving the model, corresponds to the difference between the two lines in the figure. The values of SS_max where the two lines overlay correspond to the region where the original optimal sequence is still the actual optimal sequence for the changed competition curve, and thus there would be no cost at all to the farmer for using the inferior model. While the profitability of LUSO's best sequence is changing with changes in SS_max in this interval, the actual recommended land-use sequence is not. The values of SS_max where the lines diverge are regions where a different sequence is now optimal. When the lines are close together, the difference P_cost between LUSO's original recommendation and its new recommendation based on the improved competition curve is small, but as the lines spread further apart, the difference between LUSO's original recommendation and its new improved recommendation becomes more important. Changes in the weed competitiveness parameter k_w affected the profitability of the original optimal sequence and the actual optimal sequence as shown in Fig. 5 (right). Note that increasing potential weed seed set and weed competitiveness both reduce the maximum profitability of the farming system, as would be expected.

Fig. 5.

Profitability of the original optimal sequence and the actual optimal sequence changing for different values of the crop–weed competition parameters SS_max (left) and k_w (right). Note that these figures are very similar but not identical. In each case, the region where the two lines overlay corresponds to the region where the original optimal sequence is still the actual optimal sequence for the changed competition parameter value.

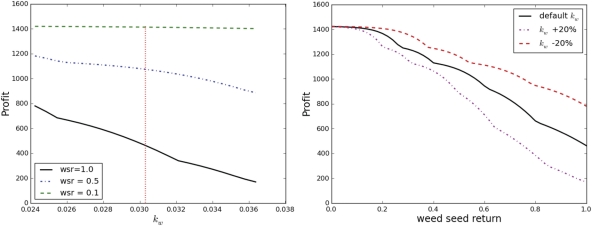
Effect of changes to SS_max and k_w on the third answer

Figure 6 shows how the profitability of the optimal land-use sequence changes with variation in the weed competitiveness parameter k_w and the weed seed return parameter wsr in interaction. Note that the two subplots show orthogonal sections of the same three-dimensional surface. The left plot shows clearly that the effect of errors or variation in k_w makes a much greater difference when the value of wsr is larger. As this was true for all weed competition parameters, we only show results for the greatest value of wsr= 1 as a ‘worst-case scenario’ in subsequent plots. The right subplot shows that the general pattern of the relationship between wsr and optimal profitability is not greatly affected by variation in k_w of up to 20 %; for all three examples there is a clear pattern of improved profit with lower weed seed return.

Fig. 6.

Profitability of the optimal land-use sequence changing with variation in the weed competitiveness parameter k_w for three separate values of the weed seed return parameter wsr (left), and profitability of the optimal land-use sequence changing with variation in the weed seed return parameter wsr for three separate values of the weed competitiveness parameter k_w (right).

Effect of changes to k_c and a_wc on the three answers

Changes in the wheat crop competitiveness parameter k_c affected the profitability of the original optimal sequence and the actual optimal sequence as shown in Fig. 7 (left). Changes in the wheat crop vs. weed antagonism parameter a_wc affected the profitability of the original optimal sequence and the actual optimal sequence as shown in Fig. 7 (right). Note that increasing wheat crop competitiveness and wheat crop vs. weed antagonism both increase the maximum profitability of the farming system, as would be expected.

Fig. 7.

Profitability of the original optimal sequence and the actual optimal sequence changing for different values of the crop–weed competition parameters k_c (left) and a_wc (right). In each case, the region where the two lines overlay corresponds to the region where the original optimal sequence is still the actual optimal sequence for the changed competition parameter value.

Effect of changes to Δ_loc and Δ_sc on the three answers

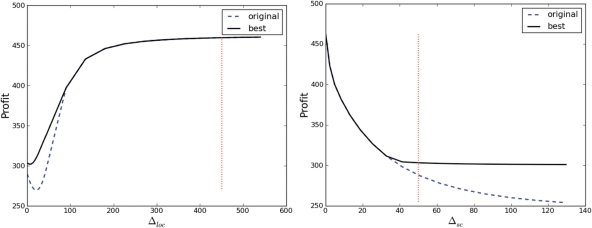
Varying the crop–weed competition function perturbation parameters Δ_loc and Δ_sc as described above in Materials and methods affected the profitability of the original optimal sequence and the actual optimal sequence as shown in Fig. 8. Note that importantly there are regions where varying these parameters made no difference at all, as discussed below.

Fig. 8.

Profitability of the original optimal sequence and the actual optimal sequence changing for different values of the crop–weed competition function perturbation parameters Δ_loc (left) and Δ_sc (right). On the right, Δ_loc is set constant to its most sensitive value 5, rather than its default value while Δ_sc is varied. In each case, the region where the two lines overlay corresponds to the region where the original optimal sequence is still the actual optimal sequence for the changed competition parameter value.

Discussion

The results show that the amount of accuracy required when representing crop–weed competition within the LUSO framework strongly depends on the kind of management question being addressed. Errors in the crop–weed competition sub-model had a much smaller effect on recommendations for management decisions (what is the most profitable land-use sequence to employ?) than on quantitative predictions (how much profit will result from this recommended management decision?).

Addressing the first question about the recommended land-use sequence did not require great accuracy. Figures 5 and 7 show that small differences in the competition parameters make no difference to which land-use sequence is optimal. Larger differences (up to 20 %) in any of the four parameters can change which land-use sequence is optimal, but P_cost, the difference in profitability between the new optimal land-use sequence and the original optimal land-use sequence under the new parameter values, is still relatively small. Importantly, this means that the cost to the farmer of the model recommending the ‘wrong’ (original) land-use sequence rather than the ‘correct’ (new) optimal land-use sequence would be small. The main effects on model recommendations are when maximum potential weed seed set or weed competitiveness is increased, or when wheat crop competitiveness or wheat-weed antagonism is decreased. In fact, increasing wheat crop competitiveness or wheat-weed antagonism by up to 20 % made no difference to which land-use sequence was optimal.

Addressing the third question regarding the value of reducing weed seed return rate did not require great accuracy either. Taking k_w as an example, Fig. 6 shows that an error in k_w makes no difference to the left-hand end of the ‘best’ line in Fig. 4. On the other hand, a 20 % error in k_w results in the right-hand end of the ‘best’ line being shifted up to about $800 or down to about $200. However, it is clear that this would have a relatively small effect on the general shape of the ‘best’ line, or the conclusions that have been drawn from this figure above. It is always true that reducing weed seed return significantly improves profitability. The effect of errors in other crop–weed competition parameters in Fig. 4 is similar to that of errors in k_w (data not shown), but is smaller, since the optimal profitability is less sensitive to the other crop–weed competition parameters. It thus appears that errors or changes in the crop–weed competition sub-model will have a relatively small effect on the results of general qualitative analyses of agronomic factors such as this analysis of the value of reducing weed seed return rate.

The story is quite different for the second question about the optimal predicted profit value, which is quite strongly affected by variation in the crop–weed competition parameters. For example, a 20 % increase in weed competitiveness more than halves profitability from $462 to about $200 and a 20 % increase in this parameter almost doubles profitability from $462 to about $800 (Fig. 5, right). The biggest effects on absolute predicted profit are also when maximum potential weed seed set or weed competitiveness is increased, or when wheat crop competitiveness or wheat–weed antagonism is decreased, but even in the other direction (decreasing maximum potential weed seed set or weed competitiveness, or increasing wheat crop competitiveness or wheat–weed antagonism) there is a big change in predicted profit.

The results also show that only a small section of the crop–weed competition curve is important in the analysis we considered here. Figure 8 (left) shows that perturbing the function at a location larger than 100 has no effect, while perturbing at a location close to zero has a larger effect. Figure 8 (right) shows that when perturbing the function at its most sensitive location, the extent or range of the perturbation is only important up to a certain point; after this point, a larger extent of perturbation makes no difference to the optimal profitability. These results thus show clearly that for the weed competition curve shown in Fig. 2, only that particular section where d_w is <200 is important in addressing the particular questions we have considered. Errors or changes or variability in the function at other sections of the curve, at values of d_w >200 (such as those shown in Fig. 2), would have little or no effect on the answers to these questions. As the LUSO model was constructed to address exactly these kinds of management questions, this indicates that it would be a waste of time, money and other resources to conduct more detailed modelling (or experimental work) aimed at improving or even testing the accuracy of the curve for values of d_w >200.

This analysis has significant implications regarding the need for devoting costly resources to more detailed modelling or experimentation aimed at making the crop–weed competition sub-model more accurate. Great accuracy is not required for providing the recommendation of greatest practical importance to a farmer regarding what farm management decision should actually be made. A researcher, interested in the relative benefits of new methods of reducing the return of weed seed to the seedbank at harvest in wheat, can also conclude that the simple model is adequate. If we are interested in exact profitability but are very confident in the section of the crop–weed competition curve close to zero, we can again conclude that our simple crop–weed competition model is adequate. Even if we are interested in exact profitability and are not confident in the section of the crop–weed competition curve close to zero, this analysis has still provided important information. If we decide that exact profitability results are important enough to justify the cost of further experiments or the building of more complex lower-level sub-models to refine the accuracy of the crop–weed competition curve, we would know to focus this modelling or experimental work on relatively low weed densities, since that is the part of the curve that matters (as explained in detail above). In this example, all parameters tested were found to be important, but in another case it may be discovered that the answers to the various kinds of questions regarding management options that we are using the model to address are much more sensitive to errors in certain parameters, in which case further modelling or experimentation can be focused on specifying these particular parameters more accurately. Furthermore, whatever is found regarding the need for further modelling or experimentation, this kind of analysis also helps us gain some estimate of confidence in the answers currently provided by the model.

What should be done if we did actually need LUSO to provide an accurate prediction of profit, or in any case where an analysis like this shows that the existing sub-models are not adequate to address a particular agro-ecosystem-level question? Modelling and experimentation are both options that could be used to try to improve the accuracy of crop–weed competition sub-models, but both have limitations. Experimental or agricultural field-trial results are always limited to a particular soil type, a particular set of environmental conditions, and particular genotypes of weed and crop; carrying out enough experiments to accurately represent the range of conditions that a general bio-economic management analysis tool like LUSO is trying to cover is likely to be impossible, or at least extremely expensive. More detailed mechanistic lower-level modelling may thus be an attractive option, with various levels of detail possible. A simple approach might involve canonical modelling, where qualitative aspects of plant function are explicitly included in the model, but quantitative aspects are fitted empirically, resulting in an ‘intermediate-level’ model that combines the ability of process-based models to represent dynamic processes and thus new situations with the relative simplicity of empirical models (Renton et al. 2005b; Jankowski and Gozdowski 2010). More mechanistic and thus more complex approaches could involve using detailed biophysical crop growth models (Bouman et al. 1996; McCown et al. 1996; Deen et al. 2003; Jones et al. 2003; Keating et al. 2003; Stöckle et al. 2003) that might represent details of the soil and canopy as layers across a field, and then linking these with the weed seedbank models in some way (e.g. Smith et al. 2005; Thornby and Walker 2009); individual-based models that represent plants as individual entities interacting in space (Grimm and Railsback 2004; Berger et al. 2008); or even as collections of functional–structural plant models where plant components are represented individually (Godin and Sinoquet 2005; Vos et al. 2007; Fourcaud et al. 2008; Hanan and Prusinkiewicz 2008) and growth patterns are determined either through empirical functions (Renton et al. 2005a; Costes et al. 2008) or through more deeply mechanistic modelling involving nutrient transport and signalling (e.g. Allen et al. 2005) and environmental competition between plants for resources such as light and water (Bastiaans et al. 1997; Chelle and Andrieu 1999; Cici et al. 2008). The problem is that any more detailed mechanistic lower-level modelling will require additional data for model construction and validation, as well as the resources involved in model construction itself. The range of validity of the overall model will be limited to the smallest range of validity of any of its sub-models, so the more sub-models, the more extensive the amount of validation required. Typically, choosing to model at deeper levels of detail and mechanism will require more data, a wider range of types of data, data that are more specific to a particular situation, and more time and money for both data collection and model construction. The exception will be where an appropriate model already exists and has been tested, and the related danger is that an inappropriate model is used just because it already exists and has been tested. Even if resources are available for experimentation or construction of more detailed models, there is no guarantee that this will result in more accurate crop-competition sub-models. For example, after evaluating the ability of four relatively complex simulation models to predict experimental crop–weed competition results, Deen et al. (2003) concluded that ‘Increasing model complexity did not appear to dramatically improve model accuracy’. More detailed models will inevitably contain more component sub-models, with more parameters overall, which increases the possibility of accumulation of error from multiple sources.

More optimistically, an analysis like that presented in this paper can indicate that a simple sub-model can be even further simplified, with resulting advantages. For example, the crop–weed competition curve used in LUSO is clearly non-linear, as evidenced in Fig. 2, but the fact that only a small section of this curve was important for the presented analysis suggests that the curve could be approximated well by a piecewise linear model with little loss of accuracy. This could allow much more efficient optimization analysis through using mathematical programming techniques such as linear programming or integer programming (Wolsey 1998), rather than the computationally intensive exhaustive or heuristic methods currently employed in the LUSO framework.

Conclusions and forward look

This paper has illustrated an integrated ‘as-simple-as-possible’ approach to modelling an agricultural system for the purpose of simulation and optimization analysis. This approach is relevant to the modelling of any system, but is particularly suited to modelling biological and ecological systems because of their complexity and thus the possibility of constructing overly complex and thus expensive models. The value of this approach has been demonstrated with this LUSO example by showing that a high degree of detail and accuracy in LUSO's crop–weed competition sub-model is more important for addressing some kinds of questions than for others. An advantage of this ‘as-simple-as-possible’ approach is that it starts simple and adds complexity only as required, thus minimizing costs, time and resources required. Another advantage is that model construction and the need for additional complexity are driven by particular questions or modelling aims, ensuring that the resulting model is ‘fit for purpose’. Moreover, the model is kept as simple as possible, without extra components that have little effect on the question of interest, thus improving model transparency and ease of analysis. A fourth advantage is minimizing the accumulation of error from multiple sub-models and a greater number of parameters, and a final advantage is that less validity testing of model components is required. So we can conclude perhaps that the answer to the initial question ‘How much detail and accuracy is required when representing crop–weed competition within simulations of agricultural systems?' is ‘…exactly as much detail and accuracy as is required to achieve the modelling aim, and no more', thus agreeing with Einstein's well-known quote ‘Make everything as simple as possible, but not simpler’. This paper provides a demonstration of a practical approach for testing just how simple ‘as simple as possible' should be for biological sub-models within agro-ecological simulations, and we suggest that a similar approach should be undertaken with future biological, ecological and agricultural modelling studies, particularly when they are aimed at identifying management recommendations.

Sources of funding

The work was funded by the School of Plant Biology at the University of Western Australia and CSIRO Ecosystem Sciences.

Conflict of interest statement

None declared.