Abstract
The success of prostate brachytherapy critically depends on delivering adequate dose to the prostate gland. Intraoperative localization of the implanted seeds provides potential for dose evaluation and optimization during therapy. A reduced-dimensionality matching algorithm for prostate brachytherapy seed reconstruction (REDMAPS) that uses multiple X-ray fluoroscopy images obtained from different poses is proposed. The seed reconstruction problem is formulated as a combinatorial optimization problem, and REDMAPS finds a solution in a clinically acceptable amount of time using dimensionality reduction to create a smaller space of possible solutions. Dimensionality reduction is possible since the optimal solution has approximately zero cost when the poses of the acquired images are known to be within a small error. REDMAPS is also formulated to address the “hidden seed problem” in which seeds overlap on one or more observed images. REDMAPS uses a pruning algorithm to avoid unnecessary computation of cost metrics and the reduced problem is solved using linear programming. REDMAPS was first evaluated and its parameters tuned using simulations. It was then validated using five phantom and 21 patient datasets. REDMAPS was successful in reconstructing the seeds with an overall seed matching rate above 99% and a reconstruction error below 1 mm in less than 5 s.
Index Terms: Brachytherapy, combinatorial optimization, integer programming, linear programming, optimal matching, prostate cancer
I. Introduction
Carcinoma of the prostate is one of the most prevalent and fatal cancers in men in North America. Prostate cancer alone accounts for 25% of cancer cases and 9% of cancer deaths in men with 192 280 estimated new cases and 27 360 estimated deaths in 2009 in the United States alone [1]. During the past decade, ultrasound-guided low dose rate (LDR) transperineal brachytherapy has become one of the popular choices of therapy for patients with early prostate cancer [2]–[4], It involves the implantation of radioactive seeds (either 125I or 103Pd) into the prostate, and its success critically depends on adequately dosing the target gland by implanting a sufficient number and distribution of radioactive seeds while avoiding excessive radiation toxicity to adjacent organs, most notably urethra, bladder, and rectum.
In the contemporary prostate brachytherapy procedure, an implant plan is made either preoperatively [5] or intraoperatively [6] based on transrectal ultrasound (TRUS) imaging. The physician first contours the prostate and the planning target volume from TRUS images, and then a treatment planning system is used to create a seed implant plan to deliver the prescribed dose to the target. During the implant procedure, the patient lies on his back with his legs in a high lithotomy position. The physician places the seeds into the planned locations in the prostate via needles inserted transperineally through a template guide using TRUS guidance as depicted in Fig. 1.
Fig. 1.
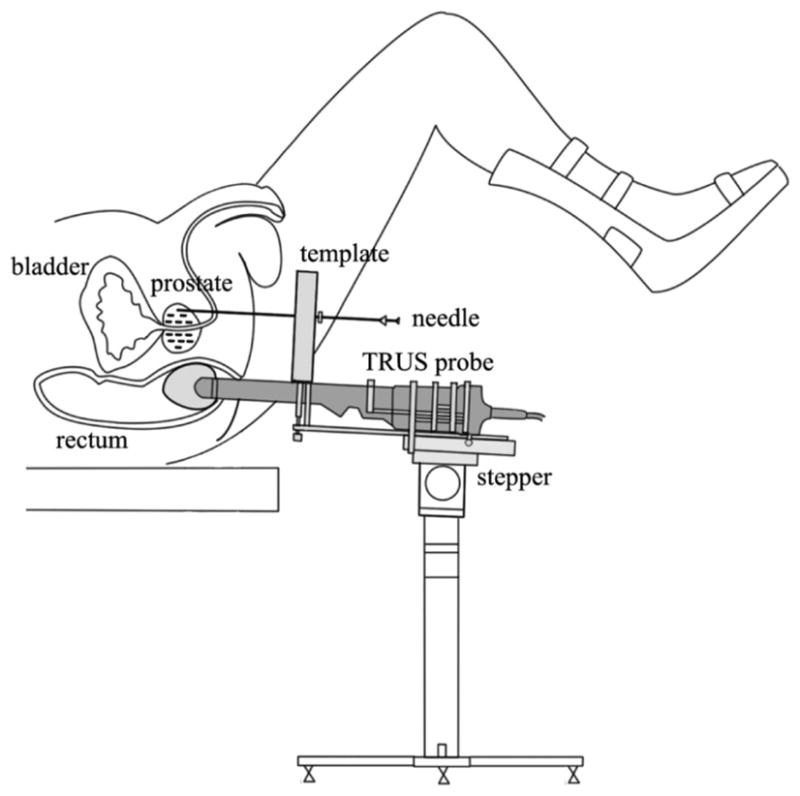
Schematic describing prostate brachytherapy procedure.
One of the greatest challenges of the current TRUS-guided implant method is that it is difficult to visualize the implanted seeds on TRUS. Seed positions may be estimated intraoperatively at the time of deposition based on visualization of the needle tip on TRUS images, but this method is subject to inaccuracies due to procedural variations such as patient motion, needle deviation, seed migration, and prostatic edema [7]–[9]. As a consequence, seed positioning variations cannot be identified intraoperatively during the procedure. An additional seed implant session (which can be technically challenging) or supplemental external beam radiation is sometimes necessary to cover underdosed regions [10], [11]. The future direction of prostate brachytherapy involves the development of a system that intraoperatively assists the brachytherapist to achieve optimal dosimetric quality with a favorable dose profile to the target and surrounding normal tissues [4], [9].
In order to achieve concurrent visualization of the anatomy and implanted seeds, systems that use ultrasound imaging and X-ray fluoroscopy have been proposed to permit both monitoring of the implant process and reconstruction of the implanted seeds for intraoperative treatment optimization [12]–[17]. In particular, X-ray projection images can be acquired using conventional mobile C-arms and the 3-D seed positions can be reconstructed from these data. The reconstructed seeds can then be registered to the prostate volume that is visualized using the TRUS images. Overall, this process provides sufficient information for the computation of an intraoperative dose distribution at intermediate implant stages in relation to the target from which a modification to the original seed placement plan can be computed and carried out during the same therapeutic procedure.
There has been extensive previous work on the reconstruction of brachytherapy seeds from multiple X-ray images [18]–[31]. The most common approaches consist of the following tasks: 1) acquire several X-ray images from different orientations; 2) segment the seeds and find their 2-D coordinates in every image; 3) determine which segmented seeds in each image correspond to the same physical seed (“seed matching”); and 4) compute the positions of each physical seed from the corresponding seeds (“triangulation”). In order to minimize the chances of having multiple, equally-valid solutions to this problem, at least three images are required. Regardless of the number of acquired images, the resulting optimization problem required for seed matching is closely related to NP-hard problems such as the k-partite matching problem [29]–[31], which implies that most reconstruction algorithms must be approximate since carrying out an exhaustive search is too time-consuming for routine clinical practice. Most of the current approaches assume that every seed can be individually identified in every image; but, in reality, each image will generally contain some seeds whose projections overlap [32]. Both the computational demands and the so-called “hidden seed problem” represent significant impediments to the routine application of currently known seed reconstruction methods in clinical practice.
In recent years, several methods have been proposed for solving the hidden seed problem. Su et al. [32] developed a statistical classifier to determine the number of seeds in a self-connected region in the segmented seed images and extended fast-CARS [27] to reconstruct seed locations from images where the number of identified seeds in each image differs. However, it may reconstruct a greater number of seeds than were actually implanted, depending on the accuracy of seed image location and the accuracy of calibration of the imaging device and relative pose of the X-ray images. Narayanan et al. [33] proposed a seed reconstruction method based on epipolar geometry using a pseudo-seed-matching strategy. Since epipolar geometry is defined only over two projections, it requires a co-planar imaging constraint in order to use three images. It also requires at least one of the three projections to be complete—i.e., all the seeds are identified—in order to reliably solve the hidden seed problem. Furthermore, the algorithm cannot reconstruct undetected seeds if they are in the same search restriction band in all three images. Kon et al. [34] extended MARSHAL [29] to deal with the hidden seed problem. They solve a series of bipartite matching problems projected from the original multipartite matchings to guarantee a polynomial time solution. However, the resulting solution is only locally optimal and may not be close to the globally optimal solution in the presence of errors in seed segmentation or errors in the estimation of pose of the C-arm (referred to shortly herein as pose error).
Su et al. [35] proposed reconstruction methods based on two versions of adaptive-grouping techniques where seed images are divided into groups for efficient seed reconstruction. It showed improved performance compared to the epipolar geometry-based reconstruction [33] in terms of accuracy and computation time. However, it may fail to detect overlapping seeds when the projection with the largest number of seed images among the divided groups is incomplete. Also, overdividing due to incorrect division of triplets may produce false positive seeds. Hong et al. [36] developed a localization method that is able to separate overlapping seeds based on the distance between seeds in each film using three-film technique, but the overall seed detection rate in phantom data was only 94% or lower. Tutar et al. [37] designed a tomosynthesis-based selective backprojection and Lam et al. [38] utilized a Hough trajectory that is unique for each 3-D seed coordinate. However, these methods require a large number of images and wide image acquisition angles to guarantee stable reconstruction. Murphy and Todor [39] have reported a preliminary work using a forward iterative method that simultaneously estimates the seed positions and camera parameters. This optimization method is prone to yield only locally optimal solutions and was tested only on clean simulated images. In earlier work, we proposed a tomosynthesis seed reconstruction approach with Gaussian blurring followed by a false positive removal process using optimal coverage cost [40]. It is able to reliably reconstruct the implanted seeds even when the image acquisition angle is very small, e.g., 5°, but it still needs 5–6 images to reliably reconstruct the seeds and requires at least three images whose image poses are known with high accuracy.
There have been attempts to formulate the seed reconstruction problem as an integer program and to solve it using a linear programming approach. Siebert et al. [30] proposed a fast linear programming approach combined with randomized rounding. In order to reduce the number of useful seed triples, they trim away instances that have larger cost values than a certain threshold determined from their histogram analysis of patient data. However, since their algorithm utilizes both ends of the uniquely identified seeds and defines the seeds as straight lines, not as points, it requires more complicated seed segmentation than other seed-matching algorithms that identify the 2-D seed images as points. For certain manufacturers’ seed types that do not leave line-like traces in the 2-D image, this method would not be applicable. Also, when there are hidden seeds (i.e., number of identified seeds in each image differs), it can only reconstruct the smallest number of identified seeds. The remaining seeds are recovered by manual interaction through a visualization software, which makes the entire seed reconstruction process significantly slower and impractical for clinical adoption. Singh et al. [31] also formulated seed reconstruction as a minimization integer program with geometric approaches to exploit the special structure of the problem and solved it using linear programming techniques. Through investigation of the upper bound on the maximal error, they could reduce the original problem by using a ball-sweep process. However, it is designed for the case where all seeds in every image are identified with their 2-D image coordinates, and conversion of their formulation for handling the hidden seed problem is not trivial. Even when all seeds are identified and the images are acquired along very wide acquisition angles (AP, lateral, and two oblique views), their matching accuracy remains only about 95%.
In summary, existing seed reconstruction methods have at least one of the following fundamental limitations: 1) they are sensitive to pose errors of the imaging device, 2) they cannot resolve the hidden seed problem, 3) they require a large number of images, large image acquisition angles, and a long time to compute a converging solution, and 4) they require constrained motion of the imaging device, e.g., isocentric circular trajectory. Among these limitations, one may resolve the issues 1) and 4) by using accurate tracking device and isocentric imaging system, but they are generally very expensive and may not be available in many hospitals. Even with a good tracking device, a reconstruction algorithm that is robust to tracking errors is crucial because the reconstruction is very sensitive to tracking errors due to the small size of the implanted seeds. Therefore, the approach described in this paper addresses all of these problems and was designed to be robust to these limitations and to work on any type of X-ray imaging system. This is critical because all four limitations must be solved in order for the method to be suitable for standard clinical use. We present a seed-matching algorithm that is able to find the 3-D seed locations from multiple X-ray images in the presence of hidden seeds and pose errors of the imaging device in polynomial time. We named our algorithm REDMAPS for REduced-Dimensionality Matching Algorithm for Prostate brachytherapy Seed reconstruction. REDMAPS adopts a dimensionality reduction approach to efficiently solve the NP-hard combinatorial optimization problem. The key insight to dimensionality reduction is the practical observation that the optimal solution of our problem has near-zero cost if the pose of the imaging device is known to within a small error. We also apply a pruning algorithm for efficient cost computation that allows us to significantly reduce the total computation time. The reduced problem is efficiently solved using linear programming in polynomial time.
REDMAPS was designed to work on conventional mobile C-arms, which are often available to most brachytherapy practitioners, unlike other approaches that require expensive isocentric X-ray equipment [27], [33], [37] or even CT scanners [41]. Importantly, REDMAPS is able to provide implant reconstruction at the end of the procedure for the purpose of exit dosimetry quality assurance when there is the largest number of seeds and correspondingly higher rates of overlaps. Finally, although REDMAPS assumes that the image acquisition poses are known, it was designed to be robust to the level of realistic pose errors that is commonly observed in mobile C-arm applications. REDMAPS has been tested extensively in simulations, with phantoms, and actual clinical brachytherapy images recorded in an IRB-approved clinical trial, and the results are reported here.
II. Methods
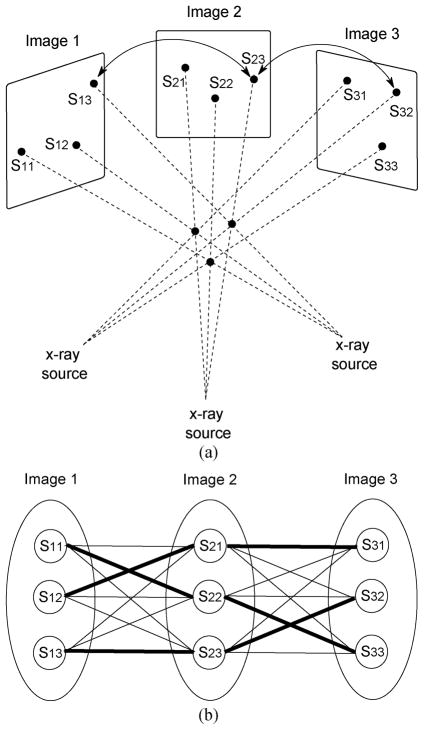
It is well known that three or four non-coplanar images are practically sufficient to reconstruct prostate brachytherapy implants [25], [29]. Fig. 2 shows an example of the reconstruction process for three implanted seeds observed in three projections. As shown in Fig. 2(b), the most common way to solve the seed reconstruction problem is to consider it as a multipartite seed-matching problem (i.e., resolving correspondence between point tuples). In this approach, segmented seeds are considered as nodes (S11, S12, … S33) and every two nodes that belong to different images are connected by weighted edges that represent the matching costs. The goal of the multipartite seed-matching proble m is to find a set of edges [e.g., thick edges in Fig. 2(b)] that gives the smallest total weight (matching cost) while covering each node from each image exactly once. Once the correspondences between nodes are resolved, computing the 3-D locations of the physical seeds is straightforward.
Fig. 2.
(a) Schematic describing a simple geometry in brachytherapy seed matching from three projections. Arrows indicate an example of a correct seed correspondence between the projected seeds 〈S13,S23,S32〉. (b) Diagram showing all possible combinations and the true combination of seeds in every image. Each seed in every image can be considered as a node and two nodes in two different images are connected by a weighted edge. Thick edges indicate the correct matches in the simple case shown in (a).
For a general case when at least three (I ≥ 3) images are used and all the N seeds are segmented with their 2-D image coordinates in every image, the seed reconstruction problem can be formulated as a 3-D assignment problem (3DAP) [29], [30] in the following way:
| (1) |
| (2) |
where xi1i2i3 … iI is equal to one when the match 〈i1, i2, i3, … iI〉 is chosen and is zero otherwise, and ci1i2i3…iI are the costs associated with the matches. This integer programming problem requires the matching of each and every seed in any one image with unique seeds in each of the other images in such a way that the additive cost associated with all matched seeds is minimized. The cost associated with any I paired seeds can be defined in several ways, and should be large if the paired seeds are not actually associated with a single seed in 3-D.
When I ≥ 3, 3DAP given by (1) and (2) is NP-hard [29]–[31], [42] and is generally impractical to solve exactly except when there is a very small number of seeds. Thus, approximate solutions are predominant in the literature. Also, the problem statement does not account for the presence of hidden seeds, which becomes inevitable as the number of seeds rises to a therapeutically relevant level. Although solutions to the hidden seed problem exist, they are either computationally intensive or ultimately require manual intervention. In the following sections, we extend the problem statement to include hidden seeds and then find the solution by using dimensionality reduction. The algorithm turns out to be computationally feasible in clinically relevant scenarios.
A. Extended Assignment Problem for Hidden Seeds
3DAP requires exactly N implanted seeds to be identified and matched in each image. In realistic scenarios, however, several seeds are often overlapping in each projection such that only Ni seed locations are identified in image i, where Ni ≤ N. We can still construct an appropriate assignment problem by thinking about matching the locations of N seeds rather than the seeds themselves. Accordingly, we define the following extended assignment problem (EAP) that is able to handle the hidden seed problem. For I(≥ 3) X-ray images
| (3) |
| (4) |
The differences between 3DAP and EAP are minimal but important. First, (3) sums only over the identified seed locations in each image. It is therefore not necessary in this framework to try to “disambiguate” seed locations in order to arrive at N seeds in each image. Second, inequalities in (4) replace the equalities in (2) in order to handle the occurrence of hidden seeds. Unlike the equalities of (2), these inequalities permit more than one assignment to each identified seed location in each image. (If that happens during optimization, then the “hidden seeds” have been automatically identified.) Third, the new equality constraint that appears in (4) and not in (2) guarantees that exactly N seeds are matched. This constraint was not necessary in 3DAP because the N equality constraints implied this constraint.
EAP can be stated in a very concise way. Let N′ = N1N2 … NI, and let x ∈ {0,1}N′ and c ∈ℝN′ be vector forms of xi1i2i3 … iI and ci1i2i3 … iI in (3), respectively. Let M be a matrix form of the inequality constraints in (4). Then, EAP (3), (4) can be formulated as the following binary integer program (BIP):
| (5) |
| (6) |
where 1I = [1,1,…, 1]T ∈ ℤI and a ≥ b means that, for every ith element, ai ≥ bi. Since each element of x is either 0 or 1 and there must be N 1’s, (5) is equivalent to choosing N cost coefficients that minimize the overall cost while satisfying (6).
B. Cost-Metric and Seed Reconstruction
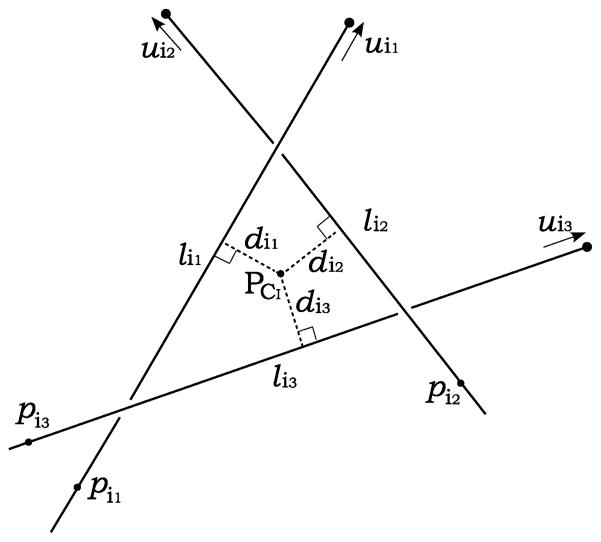
In order to fully specify EAP in (3), (4) or (5), (6), the cost coefficients c must be specified. Among the various costs that have been proposed in the literature [24], [25], [43], the reconstruction accuracy (RA) is appealing due to its simple geometric interpretation, its speed of computation, and its utility in cost pruning (described below). The basic idea of RA is as follows. Consider a proposed match comprising I seed locations from I different images. If the locations truly correspond to the same 3-D seed, then the I lines connecting their positions on the detectors with their corresponding X-ray source positions should intersect at the true 3-D seed position, and RA = 0. The more likely situation, as illustrated in Fig. 3 for the case of I = 3, is that the lines will “narrowly” miss each other due to calibration and pose errors. In this case, the RA will be greater than zero but still small if calibration and pose errors are not too large. At the same time, if one or more lines does not correspond to the same 3-D seed as the other lines, then the estimated intersection will not, in general, be close to any line, and the RA will be large, which reflects a poor match.
Fig. 3.
An example of symbolic intersection computation for I = 3. lij (j ∈ {1,2,3}) is a line connecting a seed position chosen from image j with the X-ray source position corresponding to that image. A symbolic intersection PCI is calculated by finding the point with minimum mean square distances from the lines.
To arrive at a mathematical definition of RA, for I images, assume that there are Nj identified seeds in image j with seed index ij = 1, 2,…, Nj. Let line lij be defined by the point Pij e.g., the seed ij identified in the image j, and the unit direction uij = (aij., bij, cij), as illustrated in Fig. 3. Let CI be a multi-index representing the combination (i1,i2, …, iI). For each combination CI, we define the estimated intersection point PCI of I lines as the point that minimizes the sum of the square distances from PCI to the I lines. Then RA for the combination CI is defined as the root mean square distance from PCI to each line, as follows:
| (7) |
where d(PCI, lij) is the Euclidean distance from PCI to line lij. The best matches comprise lines passing close to a single estimated intersection point and are therefore those that minimize the RA (CI). It should be noted that we have specifically chosen the 2-norm rather than the 1-norm or ∞-norm because it permits fast computations, as we shall see.
It is convenient to minimize the square of RA (CI), which we can write and expand as follows:
| (8) |
where Uij is a skew-symmetric matrix formed from the elements of uij. as follows:
| (9) |
Since, by definition, PCI achieves the minimum of the square of RA (CI), it can be analytically computed by solving ∇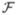 = 0 as
= 0 as
| (10) |
where . Note that PCI can be computed very efficiently by using just a few summations followed by a 3 × 3 matrix inversion.
Once EAP is solved, the 3-D locations of the N implanted seeds are declared to be the estimated intersection points PCI’s of all N matches.
C. Dimensionality Reduction in EAP
Given I images each having N seeds (i.e., no hidden seeds), there are N1 cost coefficients and (N!)I−1 feasible solutions. Since the number of implanted seeds in prostate brachytherapy can be easily over 100 and at least three images are required for unique reconstruction, it is practically impossible to compute all the cost coefficients and consider every feasible solution. However, both 3DAP and EAP have a salient geometrical feature that we can exploit: the optimal solution has a near-zero cost when the pose error is small. We use this observation to reduce the number of variables in our problem, thus permitting us to get the optimal solution at reasonable computational complexity.
Lemma II. 1
Let cℓ be the ℓth element of c, and assume that cℓ > 0. Let x0 be a feasible solution. The integer linear problem 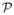 defined by (5), (6) is equivalent to the following integer linear problem (i.e., they share the same optimal solutions):
defined by (5), (6) is equivalent to the following integer linear problem (i.e., they share the same optimal solutions):
| (11) |
| (12) |
where
| (13) |
and mP(x) = cTx is the cost of problem 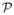 at the feasible solution x.
at the feasible solution x.
Proof
Let x* be an optimal solution to problem 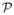 . We have for all x0 that satisfy (6)
. We have for all x0 that satisfy (6)
| (14) |
Let us consider cℓ > mp(x0). From (14) we have Cℓ > mP(x*). Since cℓ are positive and are binary, we have necessarily .
Given a feasible solution, Lemma II.1 states that all cost coefficients that are greater than the cost associated with this solution cannot be selected in the optimal solution. Since those coefficients can never be selected, the dimension of the problem can be reduced by removing those coefficients from further consideration. The dimensionality reduction can be illustrated as follows:
| (15) |
This means that the original problem 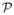 is equivalent to the following problem of reduced dimensionality:
is equivalent to the following problem of reduced dimensionality:
| (16) |
| (17) |
where c̃ ∈ ℝK (K ≤ N′) and M̃ = MR with a dimensionality reduction matrix R such that [xi1 … 0 … xii … 0 … xiK]T= R[x̃1x̃2 … x̃K]T.
Once the reduced problem 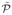 is solved with a solution x̃*, the optimal solution to the original problem
is solved with a solution x̃*, the optimal solution to the original problem 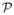 is simply given by x* = Rx̃*. If the dimensionality reduction is sufficiently large, then the new problem can be solved exactly in reasonable time even though the original problem is far too costly to solve. Therefore, the practical interest clearly depends on the dimensionality reduction ratio (K/N′).
is simply given by x* = Rx̃*. If the dimensionality reduction is sufficiently large, then the new problem can be solved exactly in reasonable time even though the original problem is far too costly to solve. Therefore, the practical interest clearly depends on the dimensionality reduction ratio (K/N′).
D. Pruning Algorithm for Efficient Cost Computation and Dimensionality Reduction
The dimensionality reduction approach in Section II-C requires the computation of only K cost coefficients that are lower than the threshold mP(x0) in (13). But how can one efficiently determine whether a cost coefficient is higher than the threshold without actually computing it? The following lemma provides the key.
Lemma II.2
When I images are used, every RA(CI) cost coefficient for every combination CI obeys the following lower bound:
| (18) |
where d(lij, lik) is the Euclidean distance between lines lij and lik that originate from seeds ij and ik in images j and k with unit direction vectors uij and uik, respectively.
Proof
The symbolic intersection PCI for the combination CI = 〈i1, i2, …,iI〉 from I images is computed as (10) from . Let
then
Using the fact that
we get
Therefore,
Finally, this together with (8) give us (18).
Lemma II.2 provides the key for limiting our cost computations. We start by computing d(lij, lik)2 for all line pairs in all images. Now consider the partial sums for the combination Cm = 〈i1,i2 … im〉 from the first m images defined by
| (19) |
which includes all line-pair distances among the Crn. This partial sum can be recursively computed for the first m images as follows:
| (20) |
We see that b(Cm) is an increasing function and it is related to our RA bound [see (18)] in the following way: RA(CI)2 ≥ b(CI)/(2I(I − 1)). This means that once b(Cm) has achieved a certain threshold, say η, the RA of any possible matches that include the currently selected m lines must be larger than . Accordingly, the computation of b(CI)is not necessary because the current collection of lines (from only images 1, …, m) cannot possibly be part of the solution.
This property can be used in a recursive algorithm in which one image is added at each iteration and all coefficients that remain lower than η are updated. Once all I images have been considered, the actual RA cost coefficients can be computed from the matches that remain below η, the dimensionality reduction threshold. This pruning approach is capable of culling a huge number of possible solutions and removing their cost computation from the overall computational workload.
The underlying idea of the pruning algorithm is similar to the ball-sweep process in [31] and the trimming based on histogram analysis in [30] in the sense that the size of the problem can be reduced by removing combinations with larger cost values than a certain threshold. However, the ball-sweep process removes only a pair of vertices not belonging to any single ball, therefore a combination may survive if each pair in that combination belongs to different balls, e.g., a combination 〈i, j, k〉 may survive if 〈i, j〉 belongs to ball 1 and 〈j, k〉 belongs to ball 2 even though the cost of the combination 〈i, j, k〉 is large. The trimming process can eliminate more seed combinations because it considers the cost values for all triples. However, it first requires to compute cost values for all possible triples before trimming, which is not the case in our pruning. The pruning algorithm described above also considers the cost values for all combinations, but without computing all cost values, thus achieving more reduction of infeasible combinations than [31] in a more efficient manner than [30].
E. Linear Programming
The resulting integer program (IP) in 3DAP and EAP can be directly solved with standard techniques such as branch and bound [44]. However, IP problems are generally NP-hard and may take an exponential amount of computation time. Our problem is a binary integer program (BIP) where variables have to be 0 or 1 and is also NP-hard [30], [31]. Similar to [30] and [31], we convert the reduced-BIP into a corresponding linear program (LP) and solve a relaxed LP with a fractional constraint x ∈ [0,1]K instead of the binary constraint x ∈ {0,1}K. The relaxed LP is solved by the interior-point method [45] followed by a test to see if the solution is binary (up to numerical errors) using MATLAB command linprog.
It is well known that linear programs can be solved optimally in polynomial time using the interior point method [31], [46], [47]. If the solution of the LP with fractional constraints turns out to be binary, it is optimal for the BIP because its optimality is proven by the LP solver. However, for some cases, the solution of the LP is fractional (i.e., some elements of the solution x are not binary), and we must perform rounding of this fractional solution to get a binary solution. In such cases, we perform rounding under the assumption that the elements with higher fractional values in the solution are more likely to be 1 [30], [31]. Therefore, we first sort the fractional solution in a descending order and the first N elements of the solution are rounded to 1.
In case that multiple elements in the fractional solution have the same value, the algorithm compares their corresponding cost coefficients and selects the elements with lower cost coefficients until N (total number of implanted seeds) is reached. (Notice that if the number of 1’s in the solution after rounding all of these multiple elements is still less or equal to N, no selection is necessary and all of them will be rounded to 1). If these same-valued multiple elements show the same corresponding costs, the algorithm randomly selects elements until the number of 1’s in the rounded solution reaches N. Our extensive experiments show that over 85% of the LP solutions are already binary, therefore the rounding affects the optimality of the solution in only 15% of the cases.
The following describes the overall REDMAPS workflow. It takes 2-D seed coordinates and the image poses as inputs, and outputs the 3-D locations of the reconstructed seeds along with the resolved seed correspondences.
| REDMAPS workflow: |
|---|
|
III. Results
REDMAPS was implemented using MATLAB 7.1 and tested on a 2.5 GHz PC. Image acquisition angles were limited in both simulations and phantom studies to a range that is practically achievable in the clinical operating room (OR) setting.
A. Image Acquisition and Preprocessing
In our phantom experiments and clinical study, fluoroscopy images were acquired using mobile C-arms with an X-ray image intensifier (XRII). Prior to the implant procedure, we precomputed the intrinsic camera parameters of the C-arm and the geometric distortion of the image using a custom-made calibration fixture [40], [48]. The pose of the C-arm was estimated by using a fluoroscope tracking fiducial (FTRAC) [49] that provides a tracking accuracy of 0.33° in rotation and 0.56 mm in translation. Once an image was acquired, it was first preprocessed for geometric distortion correction using precomputed distortion parameters in the calibration step. The FTRAC fiducial and the seeds were segmented from distortion-corrected images using algorithms developed by Kuo et al. [50]. The estimated C-arm camera parameters and the segmented seeds (with their 2-D image coordinates) are the input to REDMAPS.
B. Simulations: Robustness and Sensitivity
Assuming a set of clinically realistic C-arm imaging parameters and seed configuration, we created synthetic projection images. We considered a nominal 50 cc prostate with seven different seed densities varying from 1.0 to 2.5 seeds/cc with 0.25 seeds/cc steps, resulting in N = {54,60,72,84,96,112,128} implanted seeds. Each seed was modeled as a cylinder with a dimension of 1.45 mm in length and 0.8 mm in diameter, which is similar to the size of the radio-opaque marker in a 103Pd seed. We assumed that the focal length of the C-arm is 1000 mm and its image pixel size is 0.44 × 0.44 mm2. For each seed density, 10 different datasets were generated with four projection images in each dataset. The images were created within limited cone angles varying from 5° to 25° around the AP-axis. In each image, 5.5% on average and up to 10.2% seeds were hidden. In order to evaluate the robustness of REDMAPS to various errors, we added random errors that are uniformly distributed on [−h, h] (we report this as an h error) to the known parameters. All reconstructions were computed first by REDMAPS, and then by the extended-MARSHAL (X-MARSHAL) algorithm [34] which is a fast and reliable seed-matching algorithm for performance comparison.
Seed Density
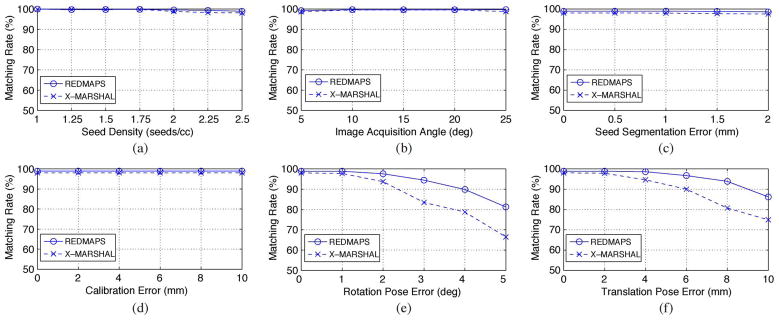
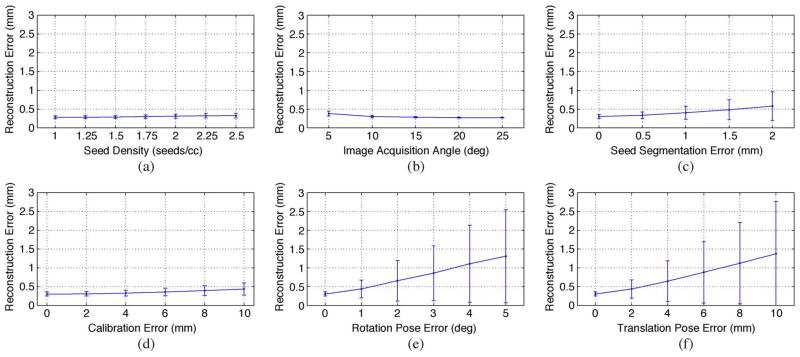
It is obvious that the matching problem becomes more complicated as the seed density increases. In prostate brachytherapy, seed density typically varies from 1.5 to 2 seeds/cc [51]. In order to evaluate the sensitivity of REDMAPS to seed density, we computed total 1400 reconstructions (7 seed densities × 10 datasets × 4C3 combinations × 5 image acquisition angles) using three images with known poses. Fig. 4(a) shows the seed matching rate as a function of seed density. Both REDMAPS and X-MARSHAL almost perfectly resolved the correspondence, but REDMAPS performs slightly better as the seed density increases. Reconstruction errors of the matched seeds are displayed in Fig. 5(a). Overall, REDMAPS achieved a matching rate of >99% and reconstruction error of less than 0.5 mm, regardless of seed density, assuming that the C-arm is calibrated and the pose is known with no errors.
Fig. 4.
Averaged seed matching rate as a function of (a) seed density, (b) image acquisition angle, (c) seed segmentation error, (d) calibration error, (e) rotation pose error, and (f) translation pose error. Both REDMAPS and extended-MARSHAL (X-MARSHAL) are used for performance comparison.
Fig. 5.
Reconstruction error mean ± STD of the matched seeds as a function of (a) seed density, (b) image acquisition angle, (c) seed segmentation error, (d) calibration error, (e) rotation pose error, and (f) translation pose error.
Image Acquisition Angle
In clinical settings where the patient lies on his back with his legs in high lithotomy position, the C-arm usually has only a limited rotational mobility of less than 25° around the AP-axis due to various obstacles such as the surgical table, the stepper stand or stabilizing arm attachment, and the patient’s legs. As a consequence, the angular separation between consecutive C-arm images is very small. Therefore, an algorithm that is robust to a small image acquisition angle is desirable. We have evaluated REDMAPS on various image acquisition angles. The angles varied from 5° to 25° with a step size of 5°. A total of 1400 reconstructions (7 seed densities × 10 datasets × 4C3 combinations × 5 image acquisition angles) were computed using three images and the results as functions of image acquisition angle are shown in Fig. 4(b) and Fig. 5(b). We can see that the matching rate is slightly lower and the reconstruction error is larger when the image acquisition angle is narrower. However, the seed matching is almost perfect (>99%) and the reconstruction errors are very small, i.e., less than 0.5 mm even when the images are acquired within 5° cone. Both algorithms performed near-perfectly, but REDMAPS was slightly better.
Seed Segmentation Error
The 2-D image coordinates of the seeds are input to REDMAPS and errors in the 2-D coordinates of the segmented seeds will propagate through the matching and reconstruction process to yield higher reconstruction errors. To simulate this effect, random seed segmentation error varying from 0 mm to 2.0 mm with a step size of 0.5 mm was added to each 2-D seed coordinate. A total of 7000 reconstructions (7 seed densities × 10 datasets × 4C3 combinations × 5 image acquisition angles × 5 error levels) were computed using three images and the results are shown in Fig. 4(c) and Fig. 5(c). Naturally, the reconstruction error increases as the seed segmentation error increases, but it still remains under 1 mm even at the maximum segmentation error of 2 mm. Also note that REDMAPS achieved near perfect matching rate (>99%) and showed better performance than X-MARSHAL.
Calibration Error
The intrinsic camera parameters (focal length and image origin) of the C-arm vary as the pose of the C-arm changes. Therefore, in theory, we must calibrate the C-arm for each pose at which we acquire an image. However, this is a time-consuming process. The authors of [52] investigated this problem and stated that the calibration errors do not critically affect the reconstruction results when the images are acquired within a small acquisition angle. In our clinical workflow, we calibrate the C-arm only once prior to the surgery to save time in the OR, and apply the pre-calibrated camera parameters to all acquired images during the procedure. Therefore, this approximate calibration introduces errors, and it is desirable to have a robust algorithm to these calibration errors even though C-arm calibration is not critical to the reconstruction. Image distortion also changes with pose which manifests in segmentation errors that we have simulated and shown to have negligible effect. To evaluate the robustness of REDMAPS to C-arm calibration errors, we added random errors varying from 0 to 10 mm with 2 mm steps to the intrinsic camera parameters of the C-arm. When we added errors, we considered the fact that the focal length error is always greater than the image origin error. A total of 8400 reconstructions (7 seed densities × 10 datasets × 4C3 combinations × 5 image acquisition angles × 6 error levels) were computed and the results are shown in Fig. 4(d) and Fig. 5(d). Similar to the previous simulations, REDMAPS achieved near perfect matching rate (>99%) and performed better than X-MARSHAL.
Rotation and Translation Pose Error
For rotation, random errors varying from 0° to 5° with 1° steps were added to the known rotation at each pose around random rotation axes. Translation errors varied from 0 mm to 10 mm with 2 mm steps. When we generated translation errors, we incorporated the fact that translation errors in depth are always significantly greater than those parallel to the plane [29]. A total of 8400 reconstructions (7 seed densities × 10 datasets × 4C3 combinations × 5 image acquisition angles × 6 error levels) were computed for each error type. Shown in Fig. 4(e) and (f), the results demonstrate that REDMAPS reliably finds the correct match and reconstructs the seeds with >97.5% accuracy with up to 2° rotation error and 5 mm translation error. The reconstruction error increases as the pose error increases as shown in Fig. 5(e) and (f) because the pose errors shift the reconstructed seed positions. In comparison to X-MARSHAL, REDMAPS performs much better when the pose errors are large. Also, note that REDMAPS performs almost perfectly in the pose error range that contemporary tracking systems such as FTRAC can easily achieve [49].
C. Realistic Simulations
For realistic simulation, we used the same data sets in the Section III-B, but added truncated additive white Gaussian noise (AWGN) to the known C-arm camera parameters. For the pose, we used the FTRAC pose recovery errors reported in [49, Sec. 7-B]; AWGN with mean 0.33° and STD 0.21° for rotation and AWGN with mean 0.56 mm and STD 0.33 mm for translation. For calibration and seed segmentation, we added zero mean AWGN with STD’s 5 mm and 0.22 mm (= 1/2 pixel) to the known C-arm calibration parameters and each segmented seed coordinates, respectively. The resulting errors were truncated at 3 × STD from the mean. In order to understand how much additional images can improve the overall performance in terms of seed matching rate and reconstruction error, we computed total 1400 reconstructions (7 seed densities × 10 datasets × 4C3 combinations × 5 image acquisition angles) and 350 reconstructions (7 seed densities × 10 datasets × 4C4 combinations × 5 image acquisition angles) using 3 and 4 images, respectively.
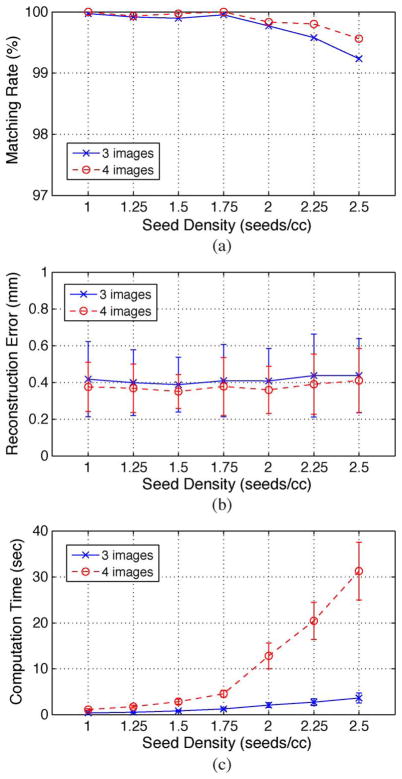
As shown in Fig. 6(a) and (b), REDMAPS reconstructed the seeds with a seed matching rate over 99% and reconstruction error less than 0.5 mm regardless of the seed density. The results imply that we can improve the seed matching rate and the reconstruction error by adding an extra image, but the improvement is minor. Considering the increase of computation time caused by adding an additional image, three images seems to be sufficient for the clinical purpose (note that the performance with only three images under realistic errors is already sufficient).
Fig. 6.
Reconstruction results when using three and four images. (a) Seed matching rate. (b) Reconstruction error. (c) Computation time.
As described in Section II-C, achieving sufficiently large dimensionality reduction is the key to success of REDMAPS. Therefore, we are particularly concerned about the dimensionality reduction ratio and computation time. We computed the dimensionality reduction ratio (K/N′) and the computation time for all possible combinations. In a total of 1750 reconstructions with three and four images, we could eliminate over 99% of the original variables and solved the optimization problem with less than 1% of all variables. Also, the computation time of REDMAPS was less than 5 s for up to 128 seeds when using three images [see Fig. 6(c)].
D. Phantom Experiments
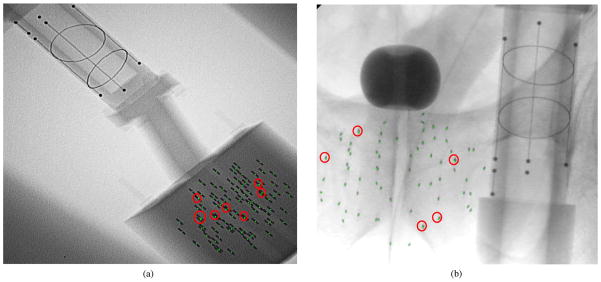
REDMAPS was tested on five phantom datasets with N = {40,55,70,85,100} nonradioactive seeds. Each seed was made of stainless steel and had a dimension of 4.9 mm in length and 0.8 mm in diameter, which is similar in size to 1251 seeds. The phantom was precisely fabricated with twelve 5-mm-thick acetol slabs and each slab has 11 × 11 holes with 5 mm interval where we inserted seeds keeping seed density at about 1.56 seeds/cc. The FTRAC was attached to the phantom at a known position for both assuring ground-truth seed locations and tracking the C-arm. For each dataset, we acquired six images within a 20° cone around the AP-axis using a Philips Integris V3000 mobile C-arm. On average, 5.5% and up to 22.5% of the seeds were hidden in each image. The C-arm was calibrated prior to the image acquisition and the acquired fluoroscopy images were preprocessed for geometric distortion correction. We computed a total of 100 reconstructions (6C3 combinations × 5 datasets) using three images and compared the results with ground-truth. Table I summarizes the results and Fig. 7(a) shows an example of phantom image onto which the detected seeds were reprojected. REDMAPS successfully localized the seeds with overall mean match rate of 98.9% and the mean reconstruction error of 0.9 mm within 5 s.
TABLE I.
Phantom Experiment Results
| Number of seeds | Mean match rate (%) | Recon. error Mean ± STD (mm) |
|---|---|---|
| 40 | 97.9 | 0.9 ± 0.7 |
| 55 | 100.0 | 0.6 ± 0.3 |
| 70 | 99.3 | 0.8 ± 0.3 |
| 85 | 97.6 | 1.1 ± 0.6 |
| 100 | 99.9 | 1.2 ± 0.5 |
Fig. 7.
Fluoroscopy images with the reprojection of the estimated seed centroids (green dots). Red circles indicate hidden seeds. Cylinder with beads, lines, and ellipses shown in both images is the FTRAC. (a) Phantom image with 100 seeds. (b) Patient image with 70 seeds.
E. Clinical Study
A total of twenty one patient datasets were collected from eight patients under IRB-approved protocols. For all patients, 103Pd seeds (Theragenics, Buford, GA) were implanted. The C-arm was calibrated prior to the surgery and the FTRAC was attached to the needle insertion template at a known position for computing the C-arm pose. Images were taken using an OEC 9800 mobile C-arm and the image acquisition angle was limited to within about 20° around the AP-axis. There were 0.9% on average and up to 7.8% hidden seeds in each image. A total of 21 reconstructions were computed using three images and the results are shown in Table II. Since we did not know the exact locations of the seeds, we visually assessed the correspondence between the reprojection of the estimated seeds and the actual seeds shown in each image, and computed projection errors (PE). REDMAPS almost perfectly localized the seeds in all cases with mean PE less than 1 mm. Among all the implanted seeds, we classified only two seeds as mismatched because the projection of them looked matched in some images but looked ambiguous in others. Thus, the true detection rate was between 98.1% and 100%—in either case, it is a clinically excellent performance. The computation time was less than 5 s for all cases. Fig. 7(b) shows an example of fluoroscopy image onto which the detected seeds were reprojected.
TABLE II.
Clinical Study Results
| Patient ID | Num. seeds | Match rate (%) | PE (mm) Mean ± STD |
|---|---|---|---|
| 1 | 22 | 100 | 0.5 ± 0.3 |
| 44 | 100 | 0.7 ± 0.4 | |
| 65 | 100 | 0.3 ± 0.2 | |
| 66 | 100 | 0.4 ± 0.2 | |
| 2 | 39 | 100 | 0.3 ± 0.2 |
| 82 | 100 | 0.3 ± 0.3 | |
| 84 | 100 | 0.9 ± 0.5 | |
| 3 | 33 | 100 | 0.2 ± 0.1 |
| 67 | 100 | 0.6 ± 0.5 | |
| 70 | 100 | 0.6 ± 0.6 | |
| 4 | 35 | 100 | 0.9 ± 0.5 |
| 68 | 100 | 0.2 ± 0.1 | |
| 77 | 98.7 | 0.5 ± 0.3 | |
| 5 | 24 | 100 | 0.6 ± 0.6 |
| 48 | 100 | 0.7 ± 0.6 | |
| 53 | 98.1 | 0.6 ± 0.5 | |
| 6 | 33 | 100 | 0.3 ± 0.4 |
| 61 | 100 | 0.1 ± 0.1 | |
| 66 | 100 | 0.1 ± 0.1 | |
| 7 | 81 | 100 | 0.3 ± 0.2 |
| 8 | 33 | 100 | 0.3 ± 0.2 |
IV. Discussion
A. Optimality
REDMAPS solves the reduced BIP by using linear programming with relaxed fractional constraints. In an ideal case when there is no calibration or tracking error of the imaging system, the globally optimal solution of this reduced BIP can be achieved as binary even though the constraints are fractional because all cost values that correspond to the correct seed matches are zero and the objective function c̃Tx̃ in (16) is bounded below (i.e., ≥0). In reality, however, the optimal solution can be fractional due to nonzero costs caused by image pose errors, and this requires rounding to obtain a binary solution. We have investigated our solutions (for realistic simulations, phantom and clinical experiments) and observed that about 85% (with three images) and 90% (with four images) of the LP solutions were binary, which means that no rounding is necessary for most of the cases and the resulting binary solution is already globally optimal. Since rounding usually happens when some of the image pose errors are relatively large, the optimality can be improved by using a more accurately calibrated and tracked imaging system (note that we used non-encoded, non-isocentric, and XRII-based mobile C-arm).
B. Dimensionality Reduction
It may be asked whether dimensionality reduction is always possible. In the prostate brachytherapy application, it is always possible because the seeds are implanted with reasonable spacing (~5 mm) between adjacent seeds, and therefore wrong correspondences will result in relatively large matching costs compared to the correct correspondences that have near zero costs. Considering the fact that there are about 100 implanted seeds and at least three images are used, there are more than (100!)2 possible combinations out of which we have to find only 100 combinations. Among ((100!)2−100) incorrect combinations, a significant number will show very large matching cost. The dimensionality reduction rate may vary depending on the configuration of the implanted seeds, e.g., it may be smaller when the seeds are implanted within a very small region, but in our experiments, we observed that over 99% of the original variables could be eliminated and the optimization problem could be solved with less than 1% of all variables.
C. Processing Time
The seed reconstruction process encompasses image acquisition, tracking, and seed localization. For successful clinical use, the entire process time should be minimized in order to achieve minimal effect on the clinical workflow. On a typical implant configuration, the running time of REDMAPS with three images is less than 5 s, and the image acquisition with mobile C-arm takes less than a minute. In our current system, seeds and FTRAC segmentation is completely automatic [50] within the image acquisition pipeline so that both seeds and FTRAC are segmented in seconds as soon as an image is acquired while a technician is rotating the C-arm to the next pose. Therefore, the entire seed reconstruction process will add only a couple of minutes at most to the current procedure.
Performance comparison with previously published seed reconstruction methods is difficult because most of them are not designed for handling hidden seed problem and are not publically available. Also, many of them are based on circular image acquisition geometry with a radiation therapy simulator, and therefore cannot be directly used with non-isocentric mobile C-arm systems. We have compared the performance of REDMAPS with X-MARSHAL that is designed for general X-ray imaging system use including non-isocentric mobile C-arm with the capability of resolving the hidden seed problem and is very fast and reliable [30], [34]. In the comparison study, REDMAPS is equivalently fast, but more robust to the pose tracking errors, thus allowing for more generous image acquisition conditions.
D. Registration Between Fluoroscopy and Ultrasound
REDMAPS reconstructs the 3-D positions of brachytherapy seeds expressed in C-arm fluoroscopy coordinates. In the clinical context, the reconstructed seeds must be transformed to TRUS coordinates, i.e., fluoroscopy space must be registered to TRUS space. In our current clinical implementation [17], FTRAC is mounted to the needle insertion template in a pre-calibrated position, so its relative position to the template is known. Because the template is registered to TRUS through a calibration process of the commercial brachytherapy treatment planning system, the transformation between the X-ray frame and the TRUS frame is known. Following registration, a commercial treatment planning system (Interplant, originally developed by Burdette Medical Systems, Inc., Champaign, IL) calculates the resulting dose distribution relative to the anatomy outlined in TRUS and re-optimizes the remainder of the implant plan.
E. Missing and Spurious Seeds
In rare cases, additional “apparent” seeds can be introduced from the anatomical background during the segmentation (spurious seeds), and more often, implanted seeds can be migrated from their implant site by entering into blood vessel or urinary tract, resulting in missing seeds. Since REDMAPS currently utilizes the knowledge of the number of implanted seeds to perform correct seed reconstruction including hidden seeds, false assignment may happen when this information is incorrect. However, our current implementation provides visual validation so that clinician can validate the reconstruction quality in the images with reprojected seed centroids or in three different orthogonal views of the reconstructed volume. Since false assignment usually creates a relatively large corresponding cost and the resulting seed may be positioned far from the reconstructed seed cloud, it can be detected at this stage.
Even though spurious and missing seeds do not occur very frequently and can be detected by visual inspection, the clinical workflow could benefit from automatic detection of false assignments caused by spurious and missing seeds during the reconstruction. By exploiting the fact that false assignments can be detected by its relatively large matching cost and may even be rejected by the pruning process, these problems can be effectively addressed within the framework of REDMAPS, and this is a subject of current research.
V. Conclusion
This paper presents REDMAPS, a computationally efficient and clinically practical seed matching algorithm for prostate brachytherapy seed reconstruction using multiple X-ray images. REDMAPS solves the seed matching problem in reduced dimension and finds a solution in polynomial time. A pruning algorithm allows for an efficient computation of cost coefficients and in turn significant dimensionality reduction. It can automatically solve the hidden seed problem by permitting a different number of identified seeds in each image, i.e., it does not require any manual intervention to identify overlapping seeds that are not automatically separated.
In simulations, REDMAPS matched over 99% of the seeds with a reconstruction error less than 0.5 mm on average using three images when there are realistic calibration and pose errors. Further simulations showed that REDMAPS is robust to significantly large errors introduced to seed segmentation, calibration, and pose estimation. REDMAPS was validated on five phantom and 21 clinical datasets, and it localized the seeds with the overall seed matching rate over 99% and reconstruction (or projection) error less than 1 mm using only three images. Since, in general, over 95% seed detection rate with less than 2 mm reconstruction error is considered to be clinically acceptable, the performance of REDMAPS (above 99% seed matching rate and below 1 mm reconstruction error) is considered as clinically excellent. If seed locations are accurate to about ± 1 mm, there is no clinical difference in dosimetry (except perhaps at the posterior border immediately adjacent to the rectum). Although REDMAPS is formulated for any number of images, it achieves this excellent seed reconstruction accuracy by using only three images. In comparison with X-MARSHAL [34], a fast and reliable seed matching algorithm that is able to recover hidden seeds, REDMAPS was equivalently fast (in the order of seconds) while being more robust to pose errors.
In summary, REDMAPS was found to be sufficiently accurate, robust, and computationally efficient to enable intraoperative dynamic, optimized brachytherapy. By compensating for pose errors and resolving hidden seeds, REDMAPS aspires to promote dynamic dosimetry in brachytherapy with conventional low-end C-arms without altering the clinical workflow, thereby allowing for wide-scale clinical deployment in the community care setting. REDMAPS is currently slated for prospective clinical trial in the Johns Hopkins Hospital.
Acknowledgments
This work was supported in part by the National Institutes of Health/National Cancer Institute (NIH/NCI) under Grant 2R44CA099374 and Grant 1R01CA151395, and in part by the Department of Defense (DoD) under Grant W81XWH-05-1-0407.
The authors thank X. X. Ma for the illustration of prostate brachytherapy procedure.
Contributor Information
Junghoon Lee, Email: junghoon@jhu.edu, Department of Electrical and Computer Engineering, Johns Hopkins University, Baltimore, MD 21218 USA.
Christian Labat, Department of Computer Science, Johns Hopkins University, Baltimore, MD 21218 USA.
Ameet K. Jain, Philips Research North America, Briarclif, NY 10510 USA
Danny Y. Song, Department of Radiation Oncology, Johns Hopkins University School of Medicine, Baltimore, MD 21205 USA
Everette Clif Burdette, Acoustic MedSystems Inc., Champaign, IL 61820 USA.
Gabor Fichtinger, School of Computing, Queen’s University, Kingston, ON K7L 3N6, Canada and also with the Department of Computer Science, Johns Hopkins University, Baltimore, MD 21218 USA.
Jerry L. Prince, Department of Electrical and Computer Engineering, Johns Hopkins University, Baltimore, MD 21218 USA.
References
- 1.Jemal A, Siegel R, Ward E, Hao Y, Xu J, Thun MJ. Cancer statistics. CA Cancer J Clin. 2009;59(4):225–249. doi: 10.3322/caac.20006. [DOI] [PubMed] [Google Scholar]
- 2.Nag S. Brachytherapy for prostate cancer: Summary of american brachytherapy society recommendations. Seminars Urologic Oncol. 2000;18(2):133–136. [PubMed] [Google Scholar]
- 3.Potters L. Permanent prostate brachytherapy: Lessons learned, lessons to learn. Oncology. 2000;14(7):981–999. [PubMed] [Google Scholar]
- 4.Potters L. Permanent prostate brachytherapy in men with clinically localised prostate cancer. Clin Oncol. 2003;15:301–315. doi: 10.1016/s0936-6555(03)00152-3. [DOI] [PubMed] [Google Scholar]
- 5.Cavanagh W, Blasko JC, Grimm PD. Transient elevation of serum prostate-specific antigen following (125)i/(103)pd brachytherapy for localized prostate cancer. Semin Urol Oncol. 2000;18:160–165. [PubMed] [Google Scholar]
- 6.Zelefsky MJ, Yamada Y, Cohen G, Venkatraman ES, Albert YCF, Furhang E, Silvern D, Zaider M. Postimplantation dosimetric analysis of permanent transperineal prostate implantation: Improved dose distributions with an intraoperative computer optimized conformal planning technique. Int J Radiat Oncol Biol Phys. 2000;48:601–608. doi: 10.1016/s0360-3016(00)00655-6. [DOI] [PubMed] [Google Scholar]
- 7.Prestidge BR, Prete JJ, Buchholz TA, Friedland JL, Stock RG, Grimm PD, Bice WS. A survey of current clinical practice of permanent prostate brachytherapy in the united states. Int J Radiat Oncol Biol Phys. 1998;40:461–465. doi: 10.1016/s0360-3016(97)00715-3. [DOI] [PubMed] [Google Scholar]
- 8.Beyer DC, Shapiro RH, Puente F. Real-time optimized intraoperative dosimetry for prostate brachytherapy: A pilot study. Int J Radiat Oncol Biol Phys. 2000;48:1583–1589. doi: 10.1016/s0360-3016(00)01363-8. [DOI] [PubMed] [Google Scholar]
- 9.Nag S, Ciezki J, Cormack R, Doggett S, DeWyngaert K, Edmundson G, Stock R, Stone N, Yu Y, Zelefsky M. Intraoperative planning and evaluation of permanent prostate brachytherapy. Int J Radiat Oncol Biol Phys. 2001;51:1422–1430. doi: 10.1016/s0360-3016(01)01616-9. [DOI] [PubMed] [Google Scholar]
- 10.Davis BJ, Herman MG, LaJoie WN, King BF, Kofler JM, Hadaway MA, Wilson TM, Pisansky TM. Supplemental implantation for suboptimal permanent prostate brachytherapy: A prostate phantom study. Radiother Oncol. 2000;55S:91–92. [Google Scholar]
- 11.Keyes M, Pickles T, Agranovich A, KW, Morris WJ. 125i reimplantation in patients with poor initial dosimetry after prostate brachytherapy. Int J Radiat Oncol Biol Phys. 2004;60:40–50. doi: 10.1016/j.ijrobp.2004.02.011. [DOI] [PubMed] [Google Scholar]
- 12.Gong L, Cho P, Han B, Wallner K, Sutlief S, Pathak S, Haynor D, Kim Y. Ultrasonography and fluoroscopic fusion for prostate brachytherapy dosimetry. Int J Radiat Oncol Biol Phys. 2002;1:1322–1330. doi: 10.1016/s0360-3016(02)03754-9. [DOI] [PubMed] [Google Scholar]
- 13.Todor D, Zaider M, Cohen G, Worman M, Zelefsky M. Intraoperative dynamic dosimetry for prostate implants. Phys Med Biol. 2003;48:1153–1171. doi: 10.1088/0031-9155/48/9/306. [DOI] [PubMed] [Google Scholar]
- 14.Reed DR, Wallner KE, Narayanan S, Sutlief SG, Ford EC, Cho PS. Intraoperative fluoroscopic dose assessment in prostate brachytherapy patients. Int J Radiat Oncol Biol Phys. 2005;63(1):301–307. doi: 10.1016/j.ijrobp.2005.05.039. [DOI] [PubMed] [Google Scholar]
- 15.Orio PF, III, Tutar IB, Narayanan S, Arthurs S, Cho PS, Kim Y, Merrick G, Wallner KE. Intraoperative ultrasound-fluoroscopy fusion can enhance prostate brachytherapy quality. Int J Radiat Oncol Biol Phys. 2007;69(1):302–307. doi: 10.1016/j.ijrobp.2007.04.072. [DOI] [PubMed] [Google Scholar]
- 16.Westendorp H, Hoekstra CJ, Minken RAAW, Immerzeel JJ. Intraoperative adaptive brachytherapy of iodine-125 prostate implants guided by c-arm cone-beam computed tomography-based dosimetry. Brachytherapy. 2007;6:231–237. doi: 10.1016/j.brachy.2007.08.005. [DOI] [PubMed] [Google Scholar]
- 17.Jain AK, Deguet A, Chintalapani G, Blevins J, Le Y, Armour E, Burdette C, Song D, Fichtinger G. Intraoperative 3D guidance in prostate brachytherapy using a non-isocentric C-arm. LNCS. 2007;4792:9–17. doi: 10.1007/978-3-540-75759-7_2. [DOI] [PubMed] [Google Scholar]
- 18.Amols HI, Rosen II. A three-film technique for reconstruction of radioactive seed implants. Med Phys. 1981;8:210–214. doi: 10.1118/1.594935. [DOI] [PubMed] [Google Scholar]
- 19.Biggs PJ, Kelley DM. Geometric reconstruction of seed implants using a three-film technique. Med Phys. 1983;10:701–704. doi: 10.1118/1.595408. [DOI] [PubMed] [Google Scholar]
- 20.Rosenthal MS, Nath R. An automatic seed identification technique for interstitial implants using three isocentric radiographs. Med Phys. 1983;10:475–479. doi: 10.1118/1.595394. [DOI] [PubMed] [Google Scholar]
- 21.Altschuler MD, Findlay PA, Epperson P. Rapid, accurate three-dimensional location of multiple seeds in implant radiotherapy treatment planning. Phys Med Biol. 1983;28:1305–1318. doi: 10.1088/0031-9155/28/11/010. [DOI] [PubMed] [Google Scholar]
- 22.Jackson DD. An automatic method for localizing radioactive seeds in implant dosimetry. Med Phys. 1983;10:370–372. doi: 10.1118/1.595275. [DOI] [PubMed] [Google Scholar]
- 23.Kumar P, Good R, Epstein B, Hussain M, Bartone F. Fluoroscopy guided transperineal percutaneous permanent 125iodine implantation of prostate cancer. Int J Radiat Oncol Biol Phys. 1985;3:161–167. [PubMed] [Google Scholar]
- 24.Siddon RL, Chin LM. Two-film brachytherapy reconstruction algorithm. Med Phys. 1985;12:77–83. doi: 10.1118/1.595738. [DOI] [PubMed] [Google Scholar]
- 25.Altschuler MD, Kassaee A. Automated matching of corresponding seed images of three simulator radiographs to allow 3D triangulation of implanted seeds. Phys Med Biol. 1997;42:293–302. doi: 10.1088/0031-9155/42/2/003. [DOI] [PubMed] [Google Scholar]
- 26.Tubic D, Zaccarin A, Beaulieu L, Pouliot J. Automated seed detection and three-dimensional reconstruction, ii. Reconstruction of permanent prostate implants using simulated annealing. Med Phys. 2001;28:2272–2279. doi: 10.1118/1.1414309. [DOI] [PubMed] [Google Scholar]
- 27.Narayanan S, Cho P, Marks R. Fast cross-projection algorithm for reconstruction of seeds in prostate brachytherapy. Med Phys. 2002;29:1572–1579. doi: 10.1118/1.1489044. [DOI] [PubMed] [Google Scholar]
- 28.Todor DA, Cohen GN, Amols HI, Zaider M. Operator-free, film-based 3D seed reconstruction in brachytherapy. Phys Med Biol. 2002;47(12):2031–2048. doi: 10.1088/0031-9155/47/12/303. [DOI] [PubMed] [Google Scholar]
- 29.Jain AK, Zhou Y, Mustafa T, Burdette EC, Chirikjian GS, Fichtinger G. Matching and reconstructoin of brachytherapy seeds using the hungarian algorithm (MARSHAL) Med Phys. 2005;32:3475–3492. doi: 10.1118/1.2104087. [DOI] [PubMed] [Google Scholar]
- 30.Siebert FA, Srivastav A, Kliemann L, Fohlin H, Kovacs G. Three-dimensional reconstruction of seed implants by randomized rounding and visual evaluation. Med Phys. 2007;34(3):967–975. doi: 10.1118/1.2436975. [DOI] [PubMed] [Google Scholar]
- 31.Singh V, Mukherjee L, Xu J, Hoffmann KR, Dinu PM, Podgorsak M. Brachytherapy seed localization using geometric and linear programming technique. IEEE Trans Med Imag. 2007 Sep;26(9):1291–1304. doi: 10.1109/TMI.2007.900740. [DOI] [PubMed] [Google Scholar]
- 32.Su Y, Davis BJ, Herman MG, Robb RA. Prostate brachytherapy seed localization by analysis of multiple projections: Identifying and addressing the seed overlap problem. Med Phys. 2004;31:1277–1287. doi: 10.1118/1.1707740. [DOI] [PubMed] [Google Scholar]
- 33.Narayanan S, Cho PS, Marks RJ., II Three-dimensional seed reconstruction from an incomplete data set for prostate brachytherapy. Phys Med Biol. 2004;49:2394–3483. doi: 10.1088/0031-9155/49/15/012. [DOI] [PubMed] [Google Scholar]
- 34.Kon R, Jain A, Fichtinger G. Hidden seed reconstruction from C-arm images in brachytherapy. IEEE Int Symp Biomed Imag. 2006 Apr;:526–529. [Google Scholar]
- 35.Su Y, Davis BJ, Furutani KM, Herman MG, Robb RA. Prostate brachytherapy seed reconstruction using adaptive grouping technique. Med Phys. 2007;34(7):2975–2984. doi: 10.1118/1.2745936. [DOI] [PubMed] [Google Scholar]
- 36.Hong JY, Rah JE, Suh TS, Jang HS, Kim S. Overlapped seed localization in seed implant brachytherapy. Med Eng Phys. 2009;31:261–267. doi: 10.1016/j.medengphy.2008.07.008. [DOI] [PubMed] [Google Scholar]
- 37.Tutar IB, Managuli R, Shamdasani V, Cho PS, Pathak SD, Kim Y. Tomosynthesis-based localization of radioactive seeds in prostate brachytherapy. Med Phys. 2003;30:101–109. doi: 10.1118/1.1624755. [DOI] [PubMed] [Google Scholar]
- 38.Lam ST, Cho PS, Marks RJ, II, Narayanan S. Three-dimensional seed reconstruction for prostate brachytherapy using hough trajectories. Phys Med Biol. 2004;49(4):557–569. doi: 10.1088/0031-9155/49/4/007. [DOI] [PubMed] [Google Scholar]
- 39.Murphy MJ, Todor DA. Demonstration of a forward iterative method to reconstruct brachytherapy seed configurations from X-ray projections. Phys Med Biol. 2005;50:2715–2737. doi: 10.1088/0031-9155/50/11/019. [DOI] [PubMed] [Google Scholar]
- 40.Lee J, Liu X, Jain AK, Song DY, Burdette EC, Prince JL, Fichtinger G. Prostate brachytherapy seed reconstruction with Gaussian blurring and optimal coverage cost. IEEE Trans Med Imag. 2009 Dec;28(12):1955–1968. doi: 10.1109/TMI.2009.2026412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kaplan ID, Meskell P, Oldenburg NE, Saltzman B, Kearney GP, Holupka EJ. Real-time computed tomography dosimetry during ultrasound-guided brachytherapy for prostate cancer. Brachytherapy. 2006;5(3):147–151. doi: 10.1016/j.brachy.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 42.Cormen TH, Leiserson CE, Rivest R. Introduction to Algorithms. 2. Cambridge: MIT Press; 1990. [Google Scholar]
- 43.Renner WD, Cantwell JP, O’Connor TP, Bermudez NM. A review of photogrammetry with applications to implant film calibration and seed matching. Med Dosim. 1989;14:103–108. doi: 10.1016/0958-3947(89)90179-9. [DOI] [PubMed] [Google Scholar]
- 44.Nemhauser GL, Wolsey LA. Discrete Mathematics and Optimization. II.4 New York: Wiley; 1988. Integer and Combinatorial Optimization, ser. [Google Scholar]
- 45.Zhang Y. Tech Rep TR96–01. Univ. Maryland; Baltimore, MD: 1995. Solving large-scale linear programs by interior-point methods under the Matlab environment. [Google Scholar]
- 46.Karmarkar N. A new polynomial-time algorithm for linear programming. ACM Symp Theory Copmut. 1984:302–311. [Google Scholar]
- 47.Yu Y. Discrete Mathematics and Optimization. I New York: Wiley; 1997. Interior Point Algorithms: Theory and Analysis, ser. [Google Scholar]
- 48.Jain AK. PhD dissertation. Johns Hopkins Univ; Baltimore, MD: 2007. Computation of 3D Implant Coordinates for Prostate Brachytherapy. [Google Scholar]
- 49.Jain AK, Mustafa T, Zhou Y, Burdette C, Chirikjian GS, Fichtinger G. FTRAC—A robust fluoroscope tracking fiducial. Med Phys. 2005;32:3185–3198. doi: 10.1118/1.2047782. [DOI] [PubMed] [Google Scholar]
- 50.Kuo N, Lee J, Deguet A, Song DY, Burdette EC, Prince JL. Automatic segmentation of seeds and fluoroscope tracking (FTRAC) fiducial in prostate brachytherapy X-ray images. Proc SPIE Med Imag. 2010;7625:76 252T1–76 252T9. doi: 10.1117/12.844520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wallner K, Blasko J, Dattoli M. Prostate Bachytherapy Made Complicated. 2. Seattle, WA: Smart Medicine; 2001. [Google Scholar]
- 52.Jain AK, Kon R, Zhou Y, Fichtinger G. C-arm calibration—Is it really necessary. Proc MICCAI: LNCS. 2005;3749:639–646. doi: 10.1007/11566465_79. [DOI] [PubMed] [Google Scholar]