USING LINEAR PREDICTORS TO IMPUTE ALLELE FREQUENCIES FROM SUMMARY OR POOLED GENOTYPE DATA

Abstract

Recently-developed genotype imputation methods are a powerful tool for detecting untyped genetic variants that affect disease susceptibility in genetic association studies. However, existing imputation methods require individual-level genotype data, whereas in practice it is often the case that only summary data are available. For example this may occur because, for reasons of privacy or politics, only summary data are made available to the research community at large; or because only summary data are collected, as in DNA pooling experiments. In this article, we introduce a new statistical method that can accurately infer the frequencies of untyped genetic variants in these settings, and indeed substantially improve frequency estimates at typed variants in pooling experiments where observations are noisy. Our approach, which predicts each allele frequency using a linear combination of observed frequencies, is statistically straight-forward, and related to a long history of the use of linear methods for estimating missing values (e.g. Kriging). The main statistical novelty is our approach to regularizing the covariance matrix estimates, and the resulting linear predictors, which is based on methods from population genetics. We find that, besides being both fast and flexible – allowing new problems to be tackled that cannot be handled by existing imputation approaches purpose-built for the genetic context – these linear methods are also very accurate. Indeed, imputation accuracy using this approach is similar to that obtained by state-of-the art imputation methods that use individual-level data, but at a fraction of the computational cost.

1. Introduction

Genotype imputation [Servin and Stephens (2008), Guan and Stephens (2008), Marchini et al. (2007), Howie et al. (2009), Browning and Browning (2007), Huang et al. (2009)] has recently emerged as a useful tool in the analysis of genetic association studies as a way of performing tests of association at genetic variants (specifically Single Nucleotide Polymorphisms, or SNPs) that were not actually measured in the association study. In brief, the idea is to exploit the fact that untyped SNPs are often correlated, in a known way, with one or more typed SNPs. Imputation-based approaches exploit these correlations, using observed genotypes at typed SNPs to estimate, or impute, genotypes at untyped SNPs, and then test for association between the imputed genotypes and phenotype, taking account of uncertainty in the imputed genotypes. (Although in general statistics applications the term “imputation” may imply replacing unobserved data with a single point estimate, in the genetic context it is often used more broadly to include methods that consider the full conditional distribution of the unobserved genotypes, and this is the way we use it here.) These approaches have been shown to increase overall power to detect associations by expanding the number of genetic variants that can be tested for association [Servin and Stephens (2008), Marchini et al. (2007)], but perhaps their most important use has been in performing meta-analysis of multiple studies that have typed different, but correlated, sets of SNPs (e.g. Zeggini et al. (2008)).

Existing approaches to imputation in this context have been developed to work with individual-level data: given genotype data at typed SNPs in each individual they attempt to impute the genotypes of each individual at untyped SNPs. From a general statistical viewpoint, one has a large number of correlated discrete-valued random variables (genotypes), whose means and covariances can be estimated, and the aim is to predict values of a subset of these variables, given observed values of all the other variables. Although one could imagine applying off-the-shelf statistical methods to this problem (e.g. Yu and Schaid (2007) consider approaches based on linear regression), in practice the most successful methods in this context have used purpose-built methods based on discrete Hidden Markov Models (HMMs) that capture ideas from population genetics (e.g. Li and Stephens (2003), Scheet and Stephens (2005)).

In this paper we consider a related, but different, problem: given the frequency of each allele at all typed SNPs, we attempt to impute the frequency of each allele at each untyped SNP. We have two main motivations for considering this problem. The first is that, although most large-scale association studies collect individual-level data, it is often the case that, for reasons of privacy [Homer et al. (2008b), Sankararaman et al. (2009)] or politics, only the allele frequency data (e.g. in cases vs controls) are made available to the research community at large. The second motivation is an experimental design known as DNA pooling [Homer et al. (2008a), Meaburn et al. (2006)], in which individual DNA samples are grouped into “pools” and high-throughput genotypings are performed on each pool. This experimental design can be considerably cheaper than separately genotyping each individual, but comes at the cost of providing only (noisy) estimates of the allele frequencies in each pool. In this setting the methods described here can provide not only estimates of the allele frequencies at untyped SNPs, but also more accurate estimates of the allele frequencies at typed SNPs.

From a general statistical viewpoint this problem of imputing frequencies is not so different from imputing individual genotypes: essentially it simply involves moving from discrete-valued variables to continuous ones. However, this change to continuous variables precludes direct use of the discrete HMM-based methods that have been applied so successfully to impute individual genotypes. The methods we describe here come from our attempts to extend and modify these HMM-based approaches to deal with continuous data. In doing so we end up with a considerably simplified method that might be considered an off-the-shelf statistical approach: in essence, we model the allele frequencies using a multivariate normal distribution, which results in unobserved frequencies being imputed using linear combinations of the observed frequencies (as in Kriging, for example). Some connection with the HMM based approaches remains though, in how we estimate the mean and variance-covariance matrix of the allele frequencies. In particular, consideration of the HMM-based approaches lead to a natural way to regularize the estimated variance-covariance matrix, making it sparse and banded: something that is important here for both computational and statistical reasons. The resulting methods are highly computationally efficient, and can easily handle very large panels (phased or unphased). They are also surprisingly accurate, giving estimated allele frequencies that are similar in accuracy to those obtained from state-of-the-art HMM-based methods applied to individual genotype data. That is, one can estimate allele frequencies at untyped SNPs almost as accurately using only the frequency data at typed SNPs as using the individual data at typed SNPs. Furthermore, when individual-level data are available one can also apply our method to imputation of individual genotypes (effectively by treating each individual as a pool of 1), and this results in imputation accuracy very similar to that of state-of-the-art HMM-based methods, at a fraction of the computational cost. Finally, in the context of noisy data from pooling experiments, we show via simulation that the method can produce substantially more accurate estimated allele frequencies at genotyped markers.

2. Methods and models

We begin by introducing some terminology and notation.

A SNP (Single Nucleotide Polymorphism) is a genetic marker that usually exhibits two different types (alleles) in a population. We will use 0 and 1 to denote the two alleles at each SNP with the labeling being essentially arbitrary.

A haplotype is a combination of alleles at multiple SNPs residing on a single copy of a genome. Each haplotype can be represented by a string of binary (0/1) values. Each individual has two haplotypes, one inherited from each parent. Routine technologies read the two haplotypes simultaneously to produce a measurement of the individual’s genotype at each SNP, which can be coded as 0,1 or 2 copies of the 1 allele. Thus the haplotypes themselves are not usually directly observed, although they can be inferred using statistical methods [Stephens et al. (2001)]. Genotype data where the haplotypes are treated as unknown are referred to as “unphased”, whereas if the haplotypes are measured or estimated they are referred to as “phased”.

In this paper we consider the following form of imputation problem. We assume that data are available on p SNPs in a reference panel of data on m individuals samples from a population, and that a subset of these SNPs are typed on a further study sample of individuals taken from a similar population. The goal is to estimate data at untyped SNPs in the study sample, using the information on the correlations among typed and untyped SNPs that is contained in the reference panel data.

We let M denote the panel data, and h₁,…,h_2n denote the 2n haplotypes in the study sample. In the simplest case, the panel data will be a 2m × p binary matrix, and the haplotypes h₁,…,h_2n can be thought of as additional rows of this matrix with some missing entries whose values need “imputing”. Several papers have focused on this problem of “individual-level” imputation [Servin and Stephens (2008), Scheet and Stephens (2005), Marchini et al. (2007), Browning and Browning (2007), Li et al. (2006)].

In this paper, we consider the problem of performing imputation when only summary-level data are available for h₁,…,h_2n. Specifically, let

$$\mathit{y}=(y_1\dots y_p)\prime =\frac{1}{2n}{\displaystyle \sum _{i=1}^{2n}{\mathit{h}}_i},$$ (2.1)

denote the vector of allele frequencies in the study sample. We assume that these allele frequencies are measured at a subset of typed SNPs, and consider the problem of using these measurements, together with information in M, to estimate the allele frequencies at the remaining untyped SNPs. More formally, if (y_t, y_u) denotes the partition of y into typed and untyped SNPs, our aim is to estimate the conditional distribution y_u|y_t, M.

Our approach is based on the assumption that h₁,…,h_2n are independent and identically distributed (i.i.d.) draws from some conditional distribution Pr(h|M). Specifically, in common with many existing approaches to individual-level imputation [Stephens and Scheet (2005), Marchini et al. (2007), Li et al. (2006)], we use the HMM-based conditional distribution from Li and Stephens (2003), although other choices could be considered. It then follows by the central limit theorem, provided that the sample size 2n is large, the distribution of y|M can be approximated by a multivariate normal distribution:

$$\mathit{y}|\mathit{M}~{\mathrm{N}}_p(\mathit{\mu },\mathrm{\Sigma }),$$ (2.2)

where μ = E(h|M) and $\mathrm{\Sigma }=\frac{1}{2n}\text{Var}(\mathit{h}|\mathit{M})$.

From this joint distribution, the required conditional distribution is easily obtained. Specifically, by partitioning μ and Σ in the same way as y, according to SNPs’ typed/untyped status, (2.2) can be written,

$$\left(\begin{array}{c}{\mathit{y}}_u\\ {\mathit{y}}_t\end{array}|\mathit{M}\right)~{\mathrm{N}}_p\left(\left(\begin{array}{c}{\mathit{\mu }}_u\\ {\mathit{\mu }}_t\end{array}\right),\left(\begin{array}{cc}{\mathrm{\Sigma }}_{\mathit{\text{uu}}}& {\mathrm{\Sigma }}_{\mathit{\text{ut}}}\\ {\mathrm{\Sigma }}_{\mathit{\text{tu}}}& {\mathrm{\Sigma }}_{\mathit{\text{tt}}}\end{array}\right)\right),$$ (2.3)

and

$${\mathit{y}}_u|{\mathit{y}}_t,\mathit{M}~{\mathrm{N}}_q({\mathit{\mu }}_u+{\mathrm{\Sigma }}_{\mathit{\text{ut}}}{\mathrm{\Sigma }}_{\mathit{\text{tt}}}^{-1}({\mathit{y}}_t-{\mathit{\mu }}_t),{\mathrm{\Sigma }}_{\mathit{\text{uu}}}-{\mathrm{\Sigma }}_{\mathit{\text{ut}}}{\mathrm{\Sigma }}_{\mathit{\text{tt}}}^{-1}{\mathrm{\Sigma }}_{\mathit{\text{tu}}}).$$ (2.4)

The mean of this last distribution can be used as a point estimate for the unobserved frequencies y_u, while the variance gives an indication of the uncertainty in these estimates. (In principle the mean can lie outside the range [0, 1), in which case we use 0 or 1, as appropriate, as the point estimate; however this happens very rarely in practice).

The parameters μ and Σ must be estimated from the panel data. It may seem natural to estimate these using the empirical mean f^panel and the empirical covariance matrix Σ^panel from the panel. However, Σ^panel is highly rank deficient because the sample size m in the panel is far less than the number of SNPs p, and so this empirical matrix cannot be used directly. Use of the conditional distribution from Li and Stephens solves this problem. Indeed, under this conditional distribution E(h|M) = μ̂ and Var(h|M) = Σ̂ can be derived analytically (appendix A) as:

$$\widehat{\mathit{\mu }}=(1-\theta ){\mathit{f}}^{\text{panel}}+\frac{\theta }{2}\mathbf{1},$$ (2.5)

$$\widehat{\mathrm{\Sigma }}={(1-\theta )}^{2}S+\frac{\theta }{2}(1-\frac{\theta }{2})I,$$ (2.6)

where θ is a parameter relating to mutation, and S is obtained from Σ^panel by shrinking off-diagonal entries towards 0. Specifically,

$$S_{\mathit{\text{ij}}}=\{\begin{array}{cc}{\mathrm{\Sigma }}_{\mathit{\text{ij}}}^{\text{panel}}\hfill & i=j\hfill \\ \text{exp}(-\frac{{\rho }_{\mathit{\text{ij}}}}{2m}){\mathrm{\Sigma }}_{\mathit{\text{ij}}}^{\text{panel}}\hfill & i\ne j\hfill \end{array}$$ (2.7)

where ρ_ij is an estimate of the population-scaled recombination rate between SNPs i and j (e.g. Hudson (2001), Li and Stephens (2003), McVean et al. (2002)). We use the value of θ suggested by Li and Stephens (2003),

$$\theta =\frac{{({\mathrm{\Sigma }}_{i=1}^{2m-1}\frac{1}{i})}^{-1}}{2m+{({\mathrm{\Sigma }}_{i=1}^{2m-1}\frac{1}{i})}^{-1}},$$ (2.8)

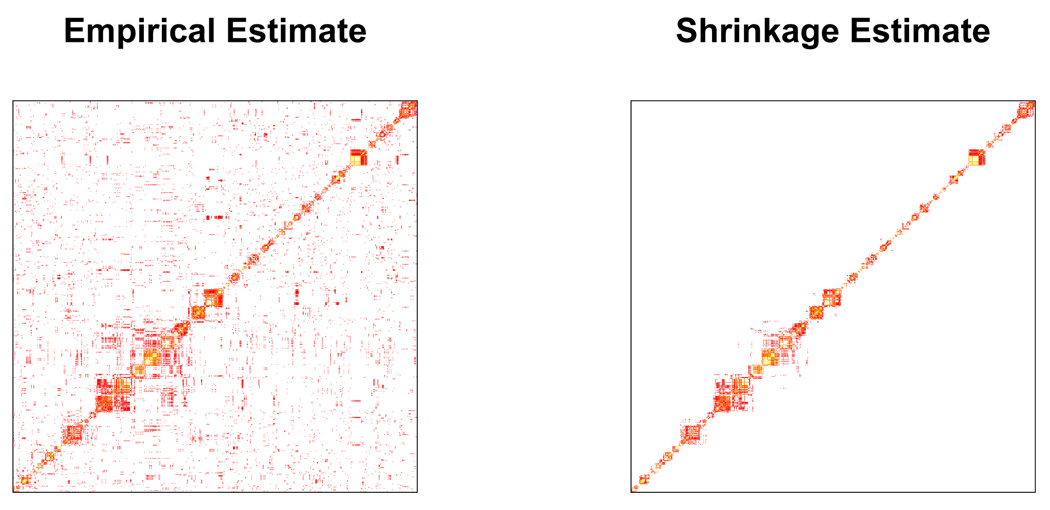
and values of ρ_ij obtained by applying the software PHASE [Stephens and Scheet (2005)] to the HapMap CEU data, which are conveniently distributed with the IMPUTE software package. For SNPs i and j that are distant, $\text{exp}(-\frac{{\rho }_{\mathit{\text{ij}}}}{2m})\approx 0$. To exploit the benefits of sparsity we set any value that was less than 10⁻⁸ to be 0, which makes Σ̂ sparse and banded: see Figure 1 for illustration. This makes matrix inversion in (2.4) computationally feasible and fast, using standard Gaussian elimination.

FIG 1.

Comparison of empirical and shrinkage estimates (based on Li and Stephens Model) of squared correlation matrix from the panel. Both of them are estimated using Hapmap CEU panel with 120 haplotypes. The region plotted is on chromosome 22 and contains 1000 Affymetrix SNPs which cover a 15Mb genomic region. Squared correlation values in [0.05, 1.00] are displayed using R’s heat.colors scheme, with gold color representing stronger correlation and red color representing weaker correlation.

2.1. Incorporating measurement error and over-dispersion

Our treatment above assumes that the allele frequencies of typed SNPs, y_t, are observed without error. In some settings, for example in DNA pooling experiments, this is not the case. We incorporate measurement error by introducing a single parameter ε², and assume

$${\mathit{y}}_t^{\text{obs}}|{\mathit{y}}_t^{\text{true}}~{\mathrm{N}}_{p-q}({\mathit{y}}_t^{\text{true}},{\epsilon }^{2}I),$$ (2.9)

where random vectors ${\mathit{y}}_t^{\text{obs}}\text{ and }{\mathit{y}}_t^{\text{true}}$ represent the observed and true sample allele frequencies for typed SNPs respectively, and subscript p − q denotes the number of typed SNPs. We assume that, given ${\mathit{y}}_t^{\text{true}}$, the observations ${\mathit{y}}_t^{\text{obs}}$ are conditionally independent of the panel data (M) and the allele frequencies at untyped SNPs $({\mathit{y}}_u^{\text{true}})$.

Our treatment in the previous section also makes several other implicit assumptions: for example, that the panel and study individuals are sampled from the same population, and that the parameters ρ and θ are estimated without error. Deviations from these assumptions will cause over-dispersion: the true allele frequencies will lie further from their expected values than the model predicts. To allow for this, we modify (2.2) by introducing an over-dispersion parameter σ²:

$${\mathit{y}}^{\text{true}}|\mathit{M}~{\mathrm{N}}_p(\widehat{\mathit{\mu }},{\sigma }^2\widehat{\mathrm{\Sigma }}).$$ (2.10)

Over-dispersion models like this are widely used for modeling binomial data [McCullagh and Nelder (1989)].

In our applications below, for settings involving measurement error (i.e. DNA pooling experiments), we estimate σ², ε² by maximizing the multivariate normal likelihood:

$${\mathit{y}}_t^{\text{obs}}|\mathit{M}~{\mathrm{N}}_{p-q}({\widehat{\mathit{\mu }}}_t,{\sigma }^2{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}+{\epsilon }^{2}I).$$ (2.11)

For settings without measurement error, we set ε² = 0 and estimate σ² by maximum likelihood.

From the hierarchical model defined by (2.9) and (2.10), the conditional distributions of allele frequencies at untyped and typed SNPs are given by:

$${\mathit{y}}_u^{\text{true}}|{\mathit{y}}_t^{\text{obs}},\mathit{M}~{\mathrm{N}}_q\left({\widehat{\mathit{\mu }}}_u+{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{ut}}}{({\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}+\frac{{\epsilon }^2}{{\sigma }^2}I)}^{-1}({\mathit{y}}_t^{\text{obs}}-{\widehat{\mathit{\mu }}}_t),{\sigma }^2({\widehat{\mathrm{\Sigma }}}_{\mathit{\text{uu}}}-{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{ut}}}{({\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}+\frac{{\epsilon }^2}{{\sigma }^2}I)}^{-1}{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tu}}})\right),$$ (2.12)

and

$${\mathit{y}}_t^{\text{true}}|{\mathit{y}}_t^{\text{obs}},\mathit{M}~{\mathrm{N}}_{p-q}\left({(\frac{1}{{\sigma }^2}{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}^{-1}+\frac{1}{{\epsilon }^2}I)}^{-1}(\frac{1}{{\sigma }^2}{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}^{-1}{\widehat{\mathit{\mu }}}_t+\frac{1}{{\epsilon }^2}{\mathit{y}}_t^{\text{obs}}),{(\frac{1}{{\sigma }^2}{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}^{-1}+\frac{1}{{\epsilon }^2}I)}^{-1}\right).$$ (2.13)

We use (2.12) to impute allele frequencies at untyped SNPs. In particular, we use the conditional mean

$${\widehat{\mathit{y}}}_u^{\text{true}}={\widehat{\mathit{\mu }}}_u+{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{ut}}}{({\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}+\frac{{\epsilon }^2}{{\sigma }^2}I)}^{-1}({\mathit{y}}_t^{\text{obs}}-{\widehat{\mathit{\mu }}}_t),$$ (2.14)

as a natural point estimate for these allele frequencies. In settings involving measurement error, we use (2.13) to estimate allele frequencies at typed SNPs, again using the mean

$${\widehat{\mathit{y}}}_t^{\text{true}}={(\frac{1}{{\sigma }^2}{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}^{-1}+\frac{1}{{\epsilon }^2}I)}^{-1}(\frac{1}{{\sigma }^2}{\widehat{\mathrm{\Sigma }}}_{\mathit{\text{tt}}}^{-1}{\widehat{\mathit{\mu }}}_t+\frac{1}{{\epsilon }^2}{\mathit{y}}_t^{\text{obs}}),$$ (2.15)

as a point estimate. Note that this mean has an intuitive interpretation as a weighted average of the observed allele frequency at that SNP and information from other nearby, correlated, SNPs. For example, if two SNPs are perfectly correlated, then in the presence of measurement error, the average of the measured frequencies will be a better estimator of the true frequency than either of the single measurements (assuming measurement errors are uncorrelated). The lower the measurement error, ε², the greater the weight given to the observed frequencies; and when ε² = 0 the estimated frequencies are just the observed frequencies.

Remark. For both untyped and typed SNPs, our point estimates for allele frequencies, (2.14) and (2.15)) are linear functions of the observed allele frequencies. Although these linear predictors were developed based on an appeal to the Central Limit Theorem, and resultant normality assumption, there are alternative justifications for use of these particular linear functions that do not rely on normality. Specifically, assuming that the two haplotypes making up each individual are i.i.d draws from a conditional distribution Pr(h|M) with mean μ̂ and variance covariance matrix σ²Σ̂, then the linear predictors (2.14) and (2.15)) minimize the integrated risk (assuming squared error loss) among all linear predictors [West and Harrison (1997)]. In this sense they are the best linear predictors, and so we refer to this method of imputation as Best Linear IMPutation or BLIMP.

2.2. Extension to imputing genotype frequencies

The development above considers imputing unobserved allele frequencies. In some settings one might also want to impute genotype frequencies. A simple way to do this is to use an assumption of Hardy–Weinberg equilibrium: that is, to assume that if y is the allele frequency at the untyped SNP, then the three genotypes have frequencies (1 − y)², 2y(1 − y) and y². Under our normal model, the expected values of these three quantities can be computed:

$$\begin{array}{c}\mathrm{E}({(1-y)}^2|{\mathit{y}}_t^{\text{obs}},\mathit{M})={(1-\mathrm{E}(y|{\mathit{y}}_t^{\text{obs}},\mathit{M}))}^2+\text{Var}(y|{\mathit{y}}_t^{\text{obs}},\mathit{M})\\ \mathrm{E}(y^2|{\mathit{y}}_t^{\text{obs}},\mathit{M})={(\mathrm{E}(y|{\mathit{y}}_t^{\text{obs}},\mathit{M}))}^2+\text{Var}(y|{\mathit{y}}_t^{\text{obs}},\mathit{M})\\ \mathrm{E}(2y(1-y)|{\mathit{y}}_t^{\text{obs}},\mathit{M})=1-\mathrm{E}({(1-y)}^2|{\mathit{y}}_t^{\text{obs}},\mathit{M})-\mathrm{E}(y^2|{\mathit{y}}_t^{\text{obs}},\mathit{M}),\end{array}$$ (2.16)

where $\mathrm{E}(y|{\mathit{y}}_t^{\text{obs}},\mathit{M})\text{and Var}(y|{\mathit{y}}_t^{\text{obs}},\mathit{M})$ are given in (2.12). These expectations can be used as estimates of the unobserved genotype frequencies.

The method above uses only allele frequency data at typed SNPs. If data are also available on genotype frequencies, as might be the case if the data are summary data from a regular genome scan in which all individuals were individually genotypes, then an alternative approach that does not assume HWE is possible. In brief, we write the unobserved genotype frequencies as means of the genotype indicators, 𝟙_[g=0] and 𝟙_[g=2] (analogous to expression (2.1)), and then derive expressions for the means and covariances of these indicators both within SNPs and across SNPs. Imputation can then be performed by computing the appropriate conditional distributions using the joint normal assumption, as in (2.4). See appendix B for more details.

In practice, we have found these two methods give similar average accuracy (results not shown), although this could be because our data conform well to Hardy–Weinberg equilibrium.

2.3. Individual-level genotype imputation

Although we developed the above model to tackle the imputation problem when individual genotypes are not available, it can also be applied to the problem of individual-level genotype imputation when individual-level data are available, by treating each individual as a pool of two haplotypes (application of these methods to small pool sizes is justified by the Remark above). For example, doubling (2.14) provides a natural estimate of the posterior mean genotype for an untyped SNP. For many applications this posterior mean genotype may suffice; see Guan and Stephens (2008) for the use of such posterior means in downstream association analyses. If an estimate that takes a value in {0,1,2} is desired, then a simple ad hoc procedure that we have found works well in practice is to round the posterior mean to the nearest integer. Alternatively, a full posterior distribution on the three possible genotypes can be computed by using the genotypic version of our approach (appendix B).

2.4. Using unphased genotype panel data

Our method can be readily adapted to settings where the panel data are unphased. To do this, we note that the estimates (2.5, 2.6) for μ and Σ depend on the panel data only through the empirical mean and variance covariance matrix of the panel haplotypes. When the panel data are unphased, we simply replace these with 0.5 times the empirical mean and variance covariance matrix of the panel genotypes (since, assuming random mating, genotypes are expected to have twice the mean and twice the (co)variance of haplotypes); see Weir (1979) for related discussion.

2.5. Imputation without a panel

In some settings, it may be desired to impute missing genotypes in a sample where no individuals are typed at all SNPs (i.e. there is no panel M), and each individual is typed at a different subset of SNPs. For example, this may arise if many individuals are sequenced at low coverage, as in the currently-ongoing 1000 genomes project (http://www.1000genomes.org). In the absence of a panel we cannot directly obtain the mean and variance-covariance estimates μ̂ and Σ̂ as in (2.5) and (2.6). An alternative way to obtain these estimates is to treat each individual genotype vector as a random sample from multivariate normal distribution N_p(μ̂, Σ̂), and apply the ECM algorithm [Meng and Rubin (1993)] to perform maximum likelihood estimation. However, this approach does not incorporate shrinkage. We therefore modify the algorithm in an ad-hoc way to incorporate shrinkage in the conditional maximization step. See Appendix C for details.

3. Data application and results

We evaluate methods described above by applying them to data from a subset of the WTCCC Birth Cohort, consisting of 1376 unrelated British individuals genotyped on the Affymetrix 500K platform [Wellcome Trust Case Control Consortium (2007)]. For demonstration purpose, we use only the 4329 SNPs from chromosome 22. We impute data at these SNPs using the 60 unrelated HapMap CEU parents [The International HapMap Consortium (2005)] as the panel. For the recombination parameters required in (2.7) we use the estimates distributed in the software package IMPUTE v1 [Marchini et al. (2007)], which were estimated from the same panel using the software package PHASE [Stephens and Scheet (2005)].

In our evaluations, we consider three types of application: frequency imputation using summary-level data, individual-level genotype imputation, and noise reduction in DNA pooling experiments. We examine both the accuracy of point estimates, and calibration of the credible intervals.

3.1. Frequency imputation using summary-level data

In this section, we evaluate the performance of (2.14) for imputing frequencies at untyped SNPs. The observed data consist of the marginal allele frequencies at each SNP, which we compute from the WTCCC individual-level genotype data. To assess imputation accuracy, we perform the following cross-validation procedure: we mask the observed data at every 25th SNP, then treat the remaining SNPs as typed and use them to impute the frequencies of masked SNPs and compare the imputation results with the actual observed frequencies. We repeat this procedure 25 times by shifting the position of the first masked SNP. Because in this case, the observed frequencies are obtained through high quality individual-level genotype data, we assume the experimental error parameter ε² = 0.

To provide a basis for comparison, we also perform the same experiment using the software package IMPUTE v1 [Marchini et al. (2007)], which is among the most accurate of existing methods for this problem. IMPUTE requires individual-level genotype data, and outputs posterior genotype probabilities for each unmeasured genotype. We therefore input the individual-level genotype data to IMPUTE and estimate the allele frequency at each untyped SNP using the posterior expected frequency computed from the posterior genotype probabilities. Like our method, IMPUTE performs imputation using the conditional distribution from Li and Stephens [Li and Stephens (2003)]; however, it uses the full conditional distribution whereas our method uses an approximation based on the first two moments. Furthermore, IMPUTE uses individual-level genotype data. For both these reasons, we would expect IMPUTE to be more accurate than our method, and our aim is to assess how much we lose in accuracy by our approximation and by using summary-level data.

To assess accuracy of estimated allele frequencies, we use the Root Mean Squared Error (RMSE),

$$\text{RMSE}=\sqrt{\frac{1}{J}{\displaystyle \sum _{j=1}^J{(y_j-{\widehat{y}}_j)}^2,}}$$ (3.1)

where J is the number of SNPs tested (4329) and y_j, ŷ_j are observed and imputed allele frequencies for SNP j respectively.

The RMSE from our method was 0.0157 compared with 0.0154 from IMPUTE (Table 1). Thus, for these data, using only summary-level data sacrifices virtually nothing in accuracy of frequency imputation. Furthermore, we found that using an unphased panel (replacing the phased HapMap CEU haplotypes with the corresponding unphased genotypes) resulted in only a very small decrease in imputation accuracy: RMSE = 0.0159. In all cases the methods are substantially more accurate than a “naive method” that simply estimates the sample frequency using the panel frequency (Table 1).

TABLE 1.

Comparison of accuracy of BLIMP and IMPUTE for frequency and individual-level genotype imputations. The RMSE and Error rate, defined in the text, provide different metrics for assessing accuracy; in all cases BLIMP was very slightly less accurate than IMPUTE. The “naive method” refers to the strategy of estimating the sample frequency of each untyped SNP by its observed frequency in the panel; this ignores information in the observed sample data, and provides a baseline level of accuracy against which the other methods can be compared.

Frequency imputation
	RMSE	Error Rate
naive method	0.0397	NA
BLIMP (phased panel)	0.0157	NA
BLIMP (unphased panel)	0.0159	NA
IMPUTE	0.0154	NA
Individual genotype imputation
	RMSE	Error Rate
BLIMP (phased panel)	0.2339	6.46%
BLIMP (unphased panel)	0.2407	6.77%
IMPUTE	0.2303	6.30%

We also investigated the calibration of the estimated variances of the imputed frequencies from (2.12). To do this, we constructed a Z-static for each test SNP j,

$$Z_j=\frac{y_j-\mathrm{E}(y_j|{\mathit{y}}^t,\mathit{M})}{\sqrt{\text{Var}(y_j|{\mathit{y}}^t,\mathit{M})}},$$ (3.2)

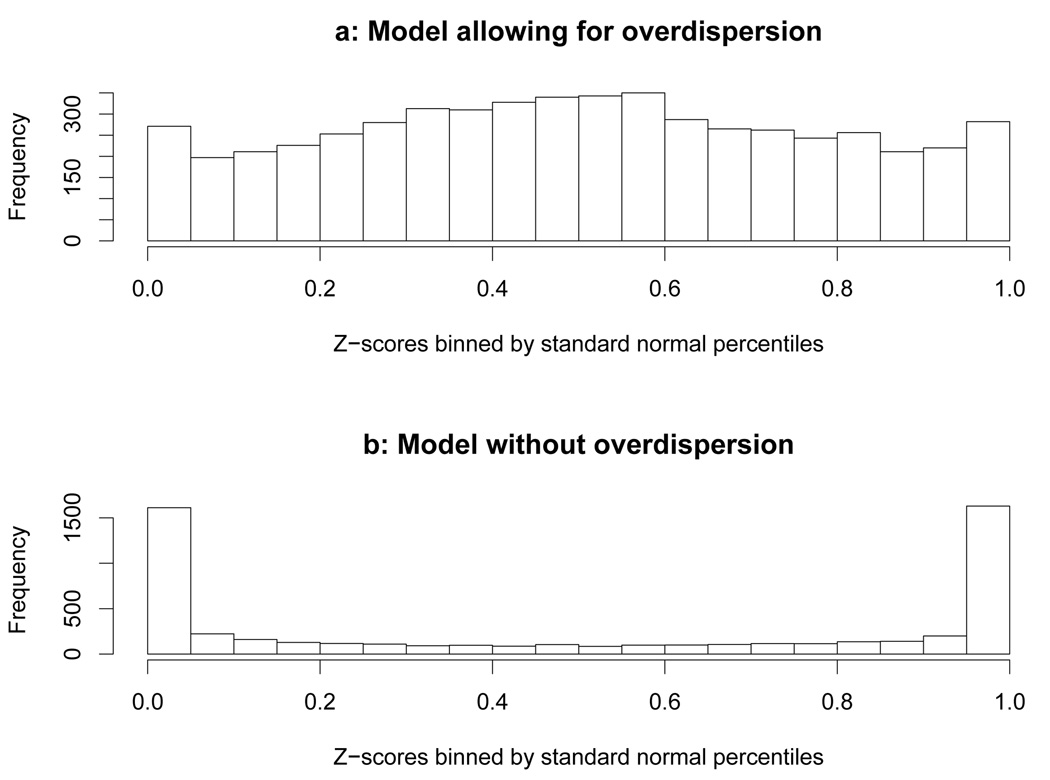
where y_j is true observed frequency, and the conditional mean and variance are as in (2.12). If the variances are well calibrated, the Z-scores should follow a standard normal distribution (with slight dependence among Z-scores of neighboring SNPs due to LD). Figure 2a shows that, indeed, the empirical distribution of Z-scores is close to standard normal (results are shown for phased panel; results for unphased panel are similar). Note that the over-dispersion parameter plays a crucial role in achieving this calibration. In particular, the Z-scores produced by the model without over-dispersion (2.2) do not follow a standard normal distribution, with many more observations in the tails (Figure 2b) indicating that the variance is under-estimated.

FIG 2.

Comparison of variance estimation in models with and without over-dispersions. The Z-scores are binned according to the standard normal percentiles, e.g. the first bin (0 to 0.05) contains Z-score values from −∞ to −1.645. If the Z-scores are i.i.d. and strictly follows standard normal distribution, we expect all the bins having approximately equal height.

3.1.1. Comparison with un-regularized linear frequency estimator

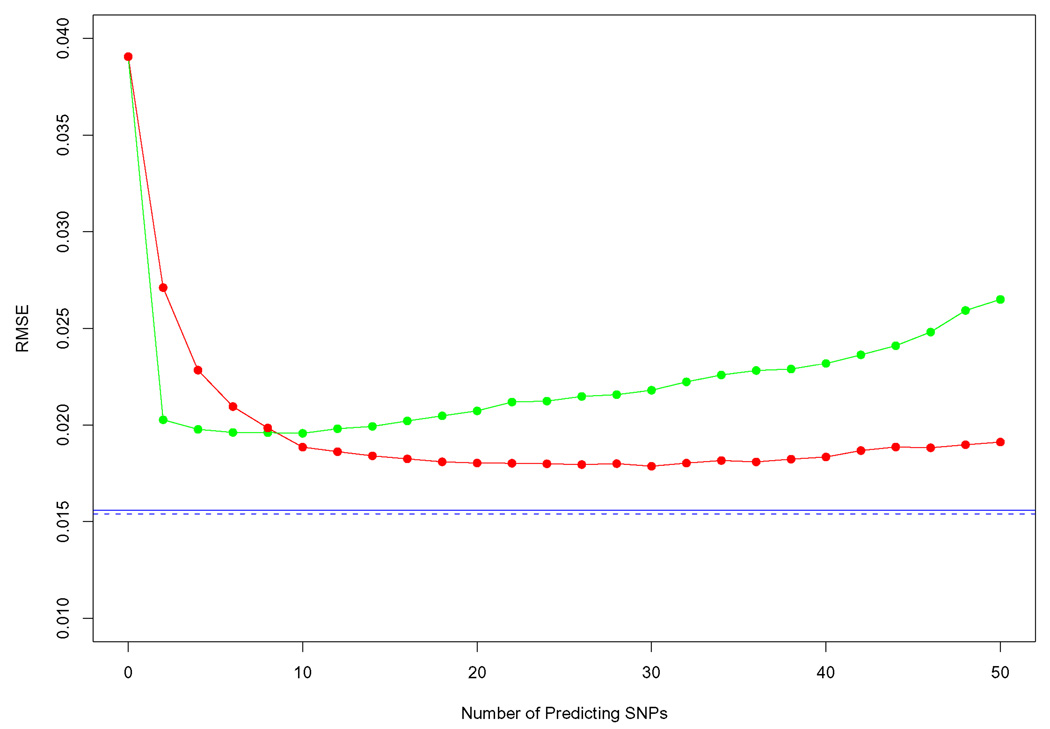
To assess the role of regularization, we compared the accuracy of BLIMP with simple un-regularized linear frequency estimators based on a small number of near-by “predicting” SNPs. (In fact, selecting a small number of SNPs can be viewed as a kind of regularization, but we refer to it as un-regularized for convenience.) The un-regularized linear estimator has the same form as in (2.4), but uses the un-regularized estimates f^panel and Σ^panel for μ and Σ. We consider two schemes to select predictors: the first scheme selects k flanking SNPs on either side of the target SNP (so 2k predictors in total); the second scheme selects the 2k SNPs with the highest marginal correlation with the target SNP. Figure 3 shows RMSE as predicting SNPs increases from 0 to 50. We find that the best performance of the un-regularized methods is achieved by the first scheme, with a relatively large number of predicting SNPs (20–40); however its RMSE is larger than that of IMPUTE and BLIMP.

FIG 3.

Comparison between BLIMP estimator and un-regularized linear estimators. The lines show the RMSE of each allele frequency estimator vs. number of predicting SNPs. Results are shown for two schemes for selecting predicting SNPs: flanking SNPs (red line) and correlated SNPs (green line). Neither scheme is as accurate as BLIMP (blue solid line) or IMPUTE (blue dashed line).

3.2. Individual-level genotype imputation

Although very satisfactory methods already exist for individual-level genotype imputation, BLIMP has the potential advantage of being extremely fast and low on memory-usage (see computational comparisons, below). We therefore also assessed its performance for individual-level genotype imputation. We used the same cross-validation procedure as in frequency imputation, but using individual-level data as input. As above, we compared results from our approach with those obtained using IMPUTE v1.

We again use RMSE to measure accuracy of imputed (posterior mean) genotypes:

$$\text{RMSE}=\sqrt{\frac{1}{\mathit{\text{mp}}}{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{i=1}^m{(g_j^i-{\widehat{g}}_j^i)}^2}}}$$ (3.3)

where m is the number of the individuals (1376), p is the total number of tested SNPs (4329) and $g_j^i,{\widehat{g}}_j^i$ are observed and estimated (posterior mean) genotypes for individual i at SNP j respectively.

For comparison purpose, we also use a different measure of accuracy that is commonly used in this setting: the genotype error rate, which is the number of wrongly imputed genotypes divide by the total number of imputed genotypes. To minimize the expected value of this metric, one should use the posterior mode genotype as the estimated genotype. Thus, for IMPUTE v1 we used the posterior mode genotype for this assessments with this metric. However, for simplicity, for our approach we used the posterior mean genotype rounded to the nearest integer. (Obtaining posterior distributions on genotypes using our approach, as outlined in appendix B, is considerably more complicated, and in fact produced slightly less accurate results, not shown).

We found that, under either metric BLIMP provides only very slightly less accurate genotype imputations than IMPUTE (Table 1). Further, as before, replacing the phased panel with an unphased panel produces only a small decrease in accuracy (Table 1).

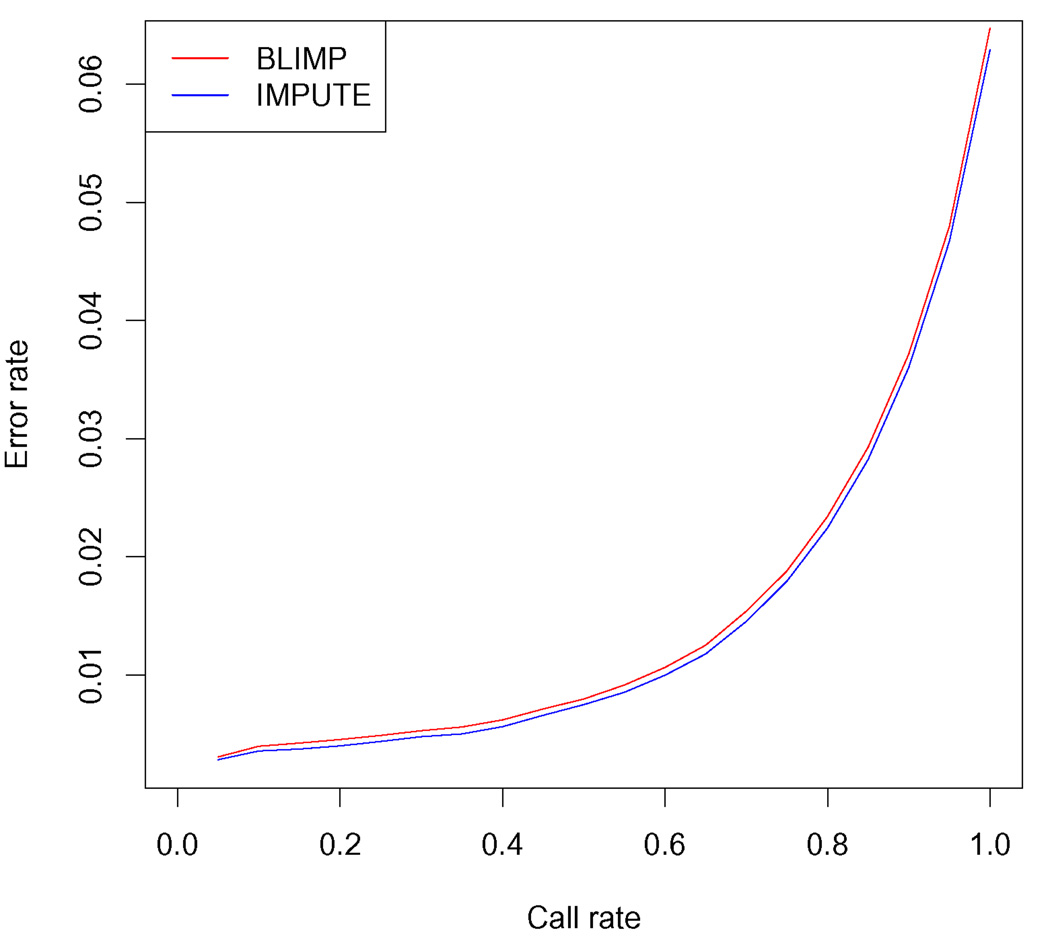
These results show average accuracy when all untyped SNPs are imputed. However, it has been observed previously (e.g. Marchini et al. (2007), Guan and Stephens (2008)) that accuracy of calls at the most confident SNPs tends to be considerably higher than the average. We checked that this is also true for BLIMP. To obtain estimates of the confidence of imputations at each SNP we first estimated σ by maximum likelihood using the summary data across all individuals, and then compute the variance for each SNP using (2.12); note that this variance does not depend on the individual, only on the SNP. We then considered performing imputation only at SNPs whose variance was less than some threshold, plotting the proportion of SNPs imputed (“call rate”) against their average genotype error rate as this threshold varies. The resulting curve for BLIMP is almost identical to the corresponding curve for IMPUTE (Figure 4).

FIG 4.

Controlling individual-level genotype imputation error rate on a per-SNP basis. For BLIMP, the error rate is controlled by thresholding on the estimated variance for imputed SNP frequencies; for IMPUTE the call threshold is determined by average maximum posterior probability. These two different measures of per-SNP imputation quality are strongly correlated (correlation coefficient = −0.983).

3.3. Individual-level genotype imputation without a panel

We use the same WTCCC Birth Cohort data to assess our modified ECM algorithm for performing individual-level genotype imputation without using a panel. To create a data set with data missing at random we mask each genotype, independently, with probability m. We create multiple data sets by varying m from 5% to 50%. For each data set we run our ECM algorithm for 20 iterations. (Results using different starting points for the ECM algorithm were generally very consistent, and so results here are shown for a single starting point.)

We compare the imputation accuracy with the software package BIMBAM [Guan and Stephens (2008)] which implements the algorithms from Scheet and Stephens (2005).

BIMBAM requires the user to specify a number of “clusters”, and other parameters related to the EM algorithm it uses: after experimenting with different settings we applied BIMBAM on each data set assuming 20 clusters, with 10 different EM starting points, performing 20 iterations for each EM run. (These settings produced more accurate results than shorter runs.)

Overall, imputation accuracy of the two methods was similar (Table 2), with BLIMP being slightly more accurate with larger amounts of missing data and BIMBAM being slightly more accurate for smaller amounts of missing data.

TABLE 2.

Comparison of imputation error rates from BLIMP and BIMBAM for individual genotype imputation without a panel.

	Missing Rate
	5%	10%	20%	50%
BIMBAM	5.79%	6.35%	7.15%	9.95%
BLIMP ECM	6.07%	6.49%	7.31%	9.91%

We note that in this setting, some of the key computational advantages of our method are lost. In particular, when each individual is missing genotypes at different SNPs, one must effectively invert a different covariance matrix for each individual. Furthermore, this inversion has to be performed multiple times, due to the iterative scheme. For small amounts of missing data the results from BLIMP we present here took less time than the results for BIMBAM, but for larger amounts the run times are similar.

3.4. Noise reduction in pooled experiment

We used simulations to assess the potential for our approach to improve allele frequency estimates from noisy data in DNA pooling experiments (equation (2.13)). To generate noisy observed data we took allele frequencies of 4329 genotyped SNP from the WTCCC Birth Cohort chromosome 22 data as true values, and added independent and identically distributed N(0, ε²) noise terms to each true allele frequency. Real pooling data will have additional features not captured by these simple simulations (e.g. biases towards one of the alleles), but our aim here is simply to illustrate the potential for methods like ours to reduce noise in this type of setting. We varied ε from 0.01 – 0.18 to to examine different noise levels. Actual noise levels in pooling experiments will depend on technology and experimental protocol; to give a concrete example, Meaburn et al. (2006) found differences between allele frequency estimates from pooled genotyping and individual genotyping of the same individuals, at 26 SNPs, in the range 0.008 to 0.077 (mean 0.036).

We applied our method to the simulated data by first estimating σ and ε using (2.12), and then, conditional on these estimated parameters, estimating the allele frequency at each observed SNP using the posterior mean given in equation (2.13). We assessed the accuracy (RMSE) of these allele frequency estimates by comparing them with the known true values.

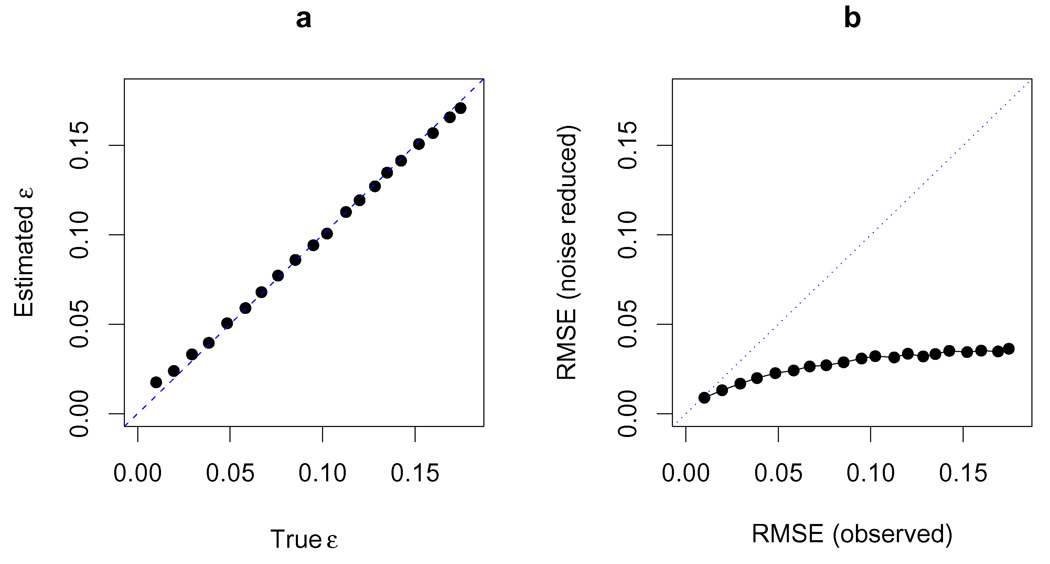
We found that our method was able to reliably estimate the amount of noise present in the data: the estimated values for the error parameter ε show good correspondence with the standard deviation used to simulate the data (Figure 5a), although for high noise levels we underestimate the noise because some of the errors are absorbed by the parameter σ.

FIG 5.

a. Detection of experimental noise in simulated data. The simulated data sets are generated by adding Gaussian noise N(0, ε²) to the actual observed WTCCC frequencies. The estimated ε values are plotted against the true ε values used for simulation. We estimate ε using maximum likelihood by (2.11). b. An illustration on the effect of noise reduction in varies noise levels. RMSE from noise reduced estimates are plotted against RMSE from direct noisy observations. The noise reduced frequency estimates are posterior means obtained from model (2.13).

More importantly, we found our estimated allele frequency estimates were consistently more accurate than the direct (noisy) observations, with the improvement being greatest for higher noise levels (Figure 5b). For example, with ε = 0.05 our method reduced the RMSE by more than half, to 0.024.

3.5. Computational efficiency

Imputation using our implementation of BLIMP is highly computationally efficient. The computational efficiency is especially notable when dealing with large panels: the panel is used only to estimate μ̂ and Σ̂, which is both quick and done just once, after which imputation computations do not depend on panel size. Our implementations also take advantage of the sparsity of Σ̂ to increase running speed and reduce memory usage. To give a concrete indication of running speed, we applied BLIMP to the WTCCC Birth Cohort data on chromosome 22, containing 4,329 genotyped and 29,697 untyped Hapmap SNPs on 1376 individuals, using a Linux system with eight-core Intel Xeon 2.66GHz processors (although only one processor is used by our implementation). The running time is measured by ’real’ time reported by the Unix “time” command. For frequency imputation, BLIMP took 9 minutes and 34 seconds, with peak memory usage of 162 megabytes; for individual-level genotype imputation BLIMP took 25 minutes, using under 300 megabytes of memory. As a comparison, IMPUTE v1 took 195 minutes for individual-level genotype imputation, with memory usage exceeding 5.1 gigabytes.

Since these comparisons were done we note that a new version of IMPUTE (v2) has been released [Howie et al. (2009)]. This new version gives similar imputation accuracy in the settings we described above; it runs more slowly than v1 but requires less memory.

4. Conclusion and discussion

Imputation has recently emerged as an important and powerful tool in genetic association studies. In this paper, we propose a set of statistical tools that help solve the following problems:

1. Imputation of allele frequencies at untyped SNPs when only summary-level data are available at typed SNPs.

2. Noise reduction for estimating allele frequencies from DNA pooling-based experiments.

3. Fast and accurate individual-level genotype imputation.

The proposed methods are simple, yet statistically elegant, and computationally extremely efficient. For individual-level genotype imputation the imputed genotypes from this approach are only very slightly less accurate than state-of-the-art methods. When only summary-level data are available we found that imputed allele frequencies were almost as accurate as when using full individual genotype data.

The linear predictor approach to imputation requires only an estimate of the mean and the covariance matrix among SNPs. Our approach to obtaining these estimates is based on the conditional distribution from Li and Stephens (2003); however, it would certainly be possible to consider other estimates, and specifically to use other approaches to shrink the off-diagonal terms in the covariance matrix. An alternative, closely-related, approach is to obtain a linear predictor directly by training a linear regression to predict each SNP, using the panel as a training set, and employing some kind of regularization scheme to solve potential problems with over-fitting caused by large p small n. This approach has been used in the context of individual-level genotype imputation by A. Clark (personal communication), and Yu and Schaid (2007). However, the choice of appropriate regularization is not necessarily straightforward, and different regularization schemes can provide different results [Yu and Schaid (2007)]. Our approach of regularizing the covariance matrix using the conditional distribution from Li and Stephens (2003) has the appeal that this conditional distribution has already been shown to be very effective for individual genotype imputation, and for modeling patterns of correlation among SNPs more generally [Li and Stephens (2003), Stephens and Scheet (2005), Servin and Stephens (2008), Marchini et al. (2007)]. Furthermore, the fact that, empirically, BLIMP’s accuracy is almost as good as the best available purpose-built methods for this problem suggests that alternative approaches to regularization are unlikely to yield considerable improvements in accuracy.

The accuracy with which linear combinations of typed SNPs can predict untyped SNPs is perhaps somewhat surprising. That said, theoretical arguments for the use of linear combinations have been given in previous work. For example, Clayton et al. (2004) showed by example that, when SNP data are consistent with no recombination (as might be the case for markers very close together on the genome), each SNP can be written as a linear regression on the other SNPs. Conversely, it is easy to construct hypothetical examples where linear predictors would fail badly. For example, consider the following example from Nicolae (2006a): 3 SNPs form 4 haplotypes, 111, 001, 100 and 010, each at frequency 0.25 in a population. Here the correlation between every pair of SNPs is 0, but knowing any 2 SNPs is sufficient to predict the third SNP precisely. Linear predictors cannot capture this ”higher order” interaction information, so produce sub-optimal imputations in this situation. In contrast, other methods (including IMPUTE) could use the higher-order information to produce perfect imputations. The fact that, empirically, the linear predictor works well suggests that this kind of situation is rare in real human population genotype data. Indeed, this is not so surprising when one considers that, from population genetics theory, SNPs tend to be uncorrelated only when there is sufficiently high recombination rate between them, and recombination will tend to break down any higher-order correlations as well as pairwise correlations.

Besides HMM-based methods, another type of approach to genotype imputation that has been proposed is to use “multi-marker” tagging [de Bakker et al. (2005), Purcell et al. (2007), Nicolae (2006b)]. A common feature of these methods is to pre-select a (relatively small) subset of “tagging” SNPs or haplotypes from all typed SNPs based on some LD measure threshold, and then use a possibly non-linear approach to predicting untyped SNPs from this subset. Thus, compared with our approach, these methods generally use a more complex prediction method based on a smaller number of SNPs. Although we have not compared directly with these methods here, published comparisons [Howie et al. (2009)] suggest that they are generally noticeably less accurate than HMM-based methods like IMPUTE, and thus by implication less accurate than BLIMP. That is, it seems from these results that, in terms of average accuracy, it is more important to make effective use of low-order correlations from all available SNPs that are correlated with the target untyped SNP, than to take account of unusual higher-order correlations that may occasionally exist.

Our focus here has been on the accuracy with which untyped SNP allele frequencies can be imputed. In practice an important application of these imputation methods is to test untyped alleles for association with an outcome variable (e.g. case-control status). Because our allele frequency predictors are linear combinations of typed SNP frequencies, each test of an untyped SNP is essentially a test for differences between a given linear combination of typed SNPs in case and control groups. Several approaches to this are possible; for example the approach in Nicolae (2006b) could be readily applied in this setting. The resulting test would be similar to the test suggested in Homer et al. (2008a) which also uses a linear combination of allele frequencies at typed SNPs to test untyped SNPs for association with case-control status in a pooling context. The main difference is that their proposed linear combinations are ad hoc, rather than being chosen to be the best linear imputations; as such we expect that appropriate use of our linear imputations should result in more powerful tests, although a demonstration of this lies outside the scope of this paper.

APPENDIX A: LEARNING FROM PANEL USING LI AND STEPHENS MODEL

In this section, we show the calculation of μ̂ and Σ̂ using phased population panel data. Following the Li and Stephens model, we assume that there are K template haplotypes in the panel. For a new haplotype h sampled from the same population, it can be modeled as an imperfect mosaic of existing template haplotypes in the panel. Let e_j denote the jth unit vector in K dimensions (1 in the jth coordinate, 0’s elsewhere), we define random vector Z_t to be e_j if haplotype h at locus t copies from jth template haplotype. The model also assumes Z₁,…,Z_n form a Markov chain in state space {e₁,…,e_K} with transition probabilities

$$\text{Pr}({\mathit{Z}}_t={\mathit{e}}_m|{\mathit{Z}}_{t-1}={\mathit{e}}_n,\mathit{M})=(1-r_t){\mathrm{𝟙}}_{[{\mathit{e}}_m={\mathit{e}}_n]}+r_t{\mathbf{e}\prime }_m\mathit{\alpha },$$ (A.1)

where $\mathit{\alpha }=\frac{1}{K}·\mathbf{1}$ and r_t = 1 − exp(−ρ_t/K) is a parameter that controls the probability that h switches copying template at locus t. The initial-state probabilities of the Markov chain is given by

$$\pi ({\mathit{Z}}_1={\mathit{e}}_k|\mathit{M})=\frac{1}{K}\text{ for }k=1,\cdots ,K.$$ (A.2)

It is easy to check that the initial distribution π is also the stationary distribution of the described Markov chain. Because the chain is initiated at the stationary state, it follows that conditional on M

$${\mathit{Z}}_1{=}^d{\mathit{Z}}_2{=}^d\cdots {=}^d{\mathit{Z}}_p{=}^d\pi .$$ (A.3)

Therefore marginally, the means and variances of Z_ts have following simple forms:

$$\mathrm{E}({\mathit{Z}}_1|\mathit{M})=\cdots =\mathrm{E}({\mathit{Z}}_p|\mathit{M})=\mathit{\alpha },$$ (A.4)

$$\text{Var}({\mathit{Z}}_1|\mathit{M})=\cdots =\text{Var}({\mathit{Z}}_n|\mathit{M})=\text{diag}(\mathit{\alpha })-\mathit{\alpha }\mathit{\alpha }\prime .$$ (A.5)

Let K-dimensional vector ${\mathit{q}}_t^{\text{panel}}$ denote the binary allelic state of panel haplotypes at locus t and scalar parameter θ represents mutation. The emission distribution in Li and Stephens model is given by

$$\text{Pr}(h_t=1|{\mathit{Z}}_t={\mathit{e}}_k,\mathit{M})=(1-\theta ){\mathit{e}}_k^{\prime }{\mathit{q}}_t^{\text{panel}}+\frac{1}{2}\theta ,$$ (A.6)

that is, with probability 1 − θ, h perfectly copies from k-th template in the panel at locus t, while with probability θ, a mutation occurs and h_t “mutates” to allele 0 or 1 equally likely. If we define ${\mathit{p}}_t=(1-\theta ){\mathit{q}}_t^{\text{panel}}+\frac{\theta }{2}\mathbf{1}$, then the emission distribution can be written as

$$\text{Pr}(h_t=1|{\mathit{Z}}_t,\mathit{M})=\mathrm{E}(h_t|{\mathit{Z}}_t,\mathit{M})={\mathit{p}}_t^{\prime }{\mathit{Z}}_t.$$ (A.7)

The goal here is to find the closed-form representations of first two moments of joint distribution (h₁, h₂,…,h_p) given the observed template panel M. For marginal mean and variance of h_t, it follows that

$$\begin{array}{cc}\mathrm{E}(h_t|\mathit{M})\hfill & =\mathrm{E}(\mathrm{E}(h_t|{\mathit{Z}}_t,\mathit{M})|\mathit{M})\hfill \\ \hfill & ={\mathit{p}}_t^{\prime }\mathrm{E}({\mathit{Z}}_t|\mathit{M})\hfill \\ \hfill & =(1-\theta )·f_t^{\text{panel}}+\frac{\theta }{2},\hfill \end{array}$$ (A.8)

$$\text{Var}(h_t|\mathit{M})={(1-\theta )}^2{f}_t^{\text{panel}}(1-f_t^{\text{panel}})+\frac{\theta }{2}(1-\frac{\theta }{2}),$$ (A.9)

where $f_t^{\text{panel}}={\mathit{q}}_t^{\prime }·\mathit{\alpha }$ is the observed allele frequency at locus t from panel M. Finally, to compute Cov(h_s, h_t) for some loci s < t, we notice that conditional on Z_s and M, h_s and h_t are independent and

$$\begin{array}{cc}\mathrm{E}(h_s·h_t|\mathit{M})\hfill & =\mathrm{E}(\mathrm{E}(h_s·h_t|{\mathit{Z}}_s,\mathit{M})|\mathit{M})\hfill \\ \hfill & =\mathrm{E}(\mathrm{E}(h_s|{\mathit{Z}}_s,\mathit{M})·\mathrm{E}(h_t|{\mathit{Z}}_s,\mathit{M})|\mathit{M}).\hfill \end{array}$$ (A.10)

Let r_st denote the switching probability between s and t, and E(h_t|Z_s, M) can be calculated from

$$\begin{array}{cc}\mathrm{E}(h_t|{\mathit{Z}}_s,\mathit{M})\hfill & =\mathrm{E}(\mathrm{E}(h_t|{\mathit{Z}}_t,{\mathit{Z}}_s,\mathit{M})|{\mathit{Z}}_s,\mathit{M})\hfill \\ \hfill & =\mathrm{E}({\mathit{Z}}_t^{\prime }{\mathit{p}}_t|{\mathit{Z}}_s,\mathit{M})\hfill \\ \hfill & =((1-r_{\mathit{\text{st}}}){\mathit{Z}}_s^{\prime }+r_{\mathit{\text{st}}}\mathit{\alpha }\prime ){\mathit{p}}_t.\hfill \end{array}$$ (A.11)

Therefore,

$$\begin{array}{cc}\mathrm{E}(h_s·h_t|\mathit{M})\hfill & ={\mathit{p}}_s^{\prime }\mathrm{E}({\mathit{Z}}_s((1-r_{\mathit{\text{st}}}){\mathit{Z}}_s^{\prime }+r_{\mathit{\text{st}}}\mathit{\alpha }\prime )|\mathit{M}){\mathit{p}}_t\hfill \\ \hfill & =(1-r_{\mathit{\text{st}}}){\mathit{p}}_s^{\prime }\text{Var}({\mathit{Z}}_s){\mathit{p}}_t+{\mathit{p}}_s^{\prime }\mathit{\alpha }\mathit{\alpha }\prime {\mathit{p}}_t\hfill \\ \hfill & =(1-r_{\mathit{\text{st}}})·{\mathit{p}}_s^{\prime }(\text{diag}(\mathit{\alpha })-\mathit{\alpha }\mathit{\alpha }\prime ){\mathit{p}}_t+\mathrm{E}(h_s|\mathit{M})\mathrm{E}(h_t|\mathit{M}),\hfill \end{array}$$ (A.12)

It follows that

$$\text{Cov}(h_s,h_t|\mathit{M})={(1-\theta )}^2(1-r_{\mathit{\text{st}}})(f_{\mathit{\text{st}}}^{\text{panel}}-f_s^{\text{panel}}{f}_t^{\text{panel}}),$$ (A.13)

where $f_{\mathit{\text{st}}}^{\text{panel}}$ is the panel frequency of the haplotype “1 − 1” consisting of loci s and t.

In conclusion, under the Li and Stephens model, the distribution h | M has expectation

$$\widehat{\mathit{\mu }}=\mathrm{E}(\mathit{h}|\mathit{M})=(1-\theta ){\mathit{f}}^{\text{panel}}+\frac{\theta }{2}\mathbf{1},$$ (A.14)

where f^panel is the p-vector of observed frequencies of all p SNPs in the panel, and variance

$$\widehat{\mathrm{\Sigma }}=\text{Var}(\mathit{h}|\mathit{M})={(1-\theta )}^{2}S+\frac{\theta }{2}(1-\frac{\theta }{2})I,$$ (A.15)

where matrix S has the structure

$$S_{\mathit{\text{ij}}}=\{\begin{array}{cc}{f}_i^{\text{panel}}(1-f_i^{\text{panel}})\hfill & i=j\hfill \\ (1-r_{\mathit{\text{ij}}})(f_{\mathit{\text{ij}}}^{\text{panel}}-f_i^{\text{panel}}{f}_j^{\text{panel}})\hfill & i\ne j\hfill \end{array}$$ (A.16)

APPENDIX B: DERIVATION OF JOINT GENOTYPE FREQUENCY DISTRIBUTION

In this section, we derive the joint genotype frequency distribution based on the Li and Stephens model.

Let g_it denote the genotype of individual i at locus t. The sample frequency of genotype 0 at locus t is given by

$$\text{Pr}(g_t=0)=p_0^{g_t}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathrm{𝟙}}_{[g_{\mathit{\text{it}}}=0].}}$$ (B.1)

Similarly, genotype frequencies $p_1^{g_t}=\text{Pr}(g_t=1)\text{ and }{p}_2^{g_t}=\text{Pr}(g_t=2)$ can be obtained by averaging indicators 𝟙_[git=1] and 𝟙_[git=2] over the samples respectively. Because of the restriction

$${\mathrm{𝟙}}_{[g_{\mathit{\text{it}}}=0]}+{\mathrm{𝟙}}_{[g_{\mathit{\text{it}}}=1]}+{\mathrm{𝟙}}_{[g_{\mathit{\text{it}}}=2]}=1,$$ (B.2)

given any two of the three indicators, the third one is uniquely determined. Let g_i denote 2p-vector (𝟙_[gi1=0], 𝟙_[gi1=2],…,𝟙_[gip=0], 𝟙_[gip=2]) and

$${\mathit{y}}_{\mathit{g}}=(p_0^{g_1}{p}_2^{g_1}\dots p_0^{g_p}{p}_2^{g_p})\prime =\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathit{g}}_i.}$$ (B.3)

Assuming that g₁,…,g_n are i.i.d draws from conditional distribution Pr(g|M), by central limit theorem as sample size n is large, it follows

$${\mathit{y}}_{\mathit{g}}|\mathit{M}~{\mathrm{N}}_{2p}({\mathit{\mu }}_{\mathit{g}},{\mathrm{\Sigma }}_g),$$ (B.4)

where μ_g = E(g|M) and Σ_g = Var(g|M).

For the remaining part of this section, we derive the closed-form expressions for μ_g and Σ_g based on the Li and Stephens model.

Let h^a and h^b denote the two composing haplotypes for some genotype sampled from population. Note that

$$\begin{array}{c}{\mathrm{𝟙}}_{[g_t=0]}=(1-h_t^a)(1-h_t^b),\hfill \\ {\mathrm{𝟙}}_{[g_t=2]}=h_t^a{h}_t^b.\hfill \end{array}$$ (B.5)

Given panel M, the two composing haplotypes are also assumed to be independent and identically distributed. Following the results from Appendix A, we obtain that

$$\begin{array}{cc}\hfill \mathrm{E}({\mathrm{𝟙}}_{[g_t=0]}|\mathit{M})& ={(1-\mathrm{E}(h_t|\mathit{M}))}^2,\hfill \\ \hfill \mathrm{E}({\mathrm{𝟙}}_{[g_t=2]}|\mathit{M})& =\mathrm{E}{(h_t|\mathit{M})}^2,\hfill \\ \hfill \text{Var}({\mathrm{𝟙}}_{[g_t=0]}|\mathit{M})& ={(1-\mathrm{E}(h_t|\mathit{M}))}^2·(1-{(1-\mathrm{E}(h_t|\mathit{M}))}^2),\hfill \\ \hfill \text{Var}({\mathrm{𝟙}}_{[g_t=2]}|\mathit{M})& =\mathrm{E}{(h_t|\mathit{M})}^2·(1-\mathrm{E}{(h_t|\mathit{M})}^2)\hfill \\ \hfill \text{Cov}({\mathrm{𝟙}}_{[g_t=0]},{\mathrm{𝟙}}_{[g_t=2]}|\mathit{M})& =-{(1-\mathrm{E}(h_t|\mathit{M}))}^2·\mathrm{E}{(h_t|\mathit{M})}^2\hfill \end{array}$$ (B.6)

where E(h_t|M) is given by (A.8).

To compute covariance across different loci s and t, we note that

$$\begin{array}{c}{\mathrm{𝟙}}_{[g_s=0]}{\mathrm{𝟙}}_{[g_t=0]}=(1-h_s^a)(1-h_s^b)(1-h_t^a)(1-h_t^b),\hfill \\ {\mathrm{𝟙}}_{[g_s=2]}{\mathrm{𝟙}}_{[g_t=2]}=h_s^a{h}_s^b{h}_t^a{h}_t^b,\hfill \\ {\mathrm{𝟙}}_{[g_s=0]}{\mathrm{𝟙}}_{[g_t=2]}=(1-h_s^a)(1-h_s^b)h_t^a{h}_t^b,\hfill \\ {\mathrm{𝟙}}_{[g_s=2]}{\mathrm{𝟙}}_{[g_t=0]}=h_s^a{h}_s^b(1-h_t^a)(1-h_t^b)\hfill \end{array}$$ (B.7)

Then all the covariance terms across different loci can be represented using E(h_sh_t|M), which is given by (A.12). For example,

$$\text{Cov}({\mathrm{𝟙}}_{[g_s=2],}{\mathrm{𝟙}}_{[g_t=2]}|\mathit{M})=\text{Cov}{(h_s,h_t|\mathit{M})}^2+2\mathrm{E}(h_s|\mathit{M})·\mathrm{E}(h_t|\mathit{M})·\text{Cov}(h_s,h_t|\mathit{M}).$$ (B.8)

APPENDIX C: MODIFIED ECM ALGORITHM FOR IMPUTING GENOTYPES WITHOUT A PANEL

In this section, we show our modified ECM algorithm for genotype imputation without a panel.

By our assumption, each individual genotype p-vector gⁱ is a random sample from the multivariate normal distribution N_p(μ̂, Σ̂), and different individual vectors may have different missing entries. Suppose we have n individual samples, let G_obs denote the set of all typed genotypes across all individuals and ${\mathit{g}}_{\text{obs}}^i$ denote the typed genotypes for individual i.

In the E step of ECM algorithm, we compute the expected values of the sufficient statistics ${\displaystyle {\sum }_{i=1}^n{g}_j^i\text{ for }j=1,\dots ,p\text{ and }}{\displaystyle {\sum }_{i=1}^n{g}_j^i{g}_k^i\text{ for }j,k=1,\dots ,p}$ conditional on G_obs and current estimate for (μ̂, Σ̂). Specifically, in t-th iteration,

$$\mathrm{E}({\displaystyle \sum _{i=1}^n{g}_j^i|{\mathit{G}}_{\text{obs}},{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})={\displaystyle \sum _{i=1}^n{g}_j^{i,(t)},}}$$ (C.1)

$$\mathrm{E}({\displaystyle \sum _{i=1}^n{g}_j^i{g}_k^i|{\mathit{G}}_{\text{obs}},{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})={\displaystyle \sum _{i=1}^n(g_j^{i,(t)}}{g}_k^{i,(t)}+c_{\mathit{\text{jk}}}^{i,(t)}),}$$ (C.2)

where

$$g_j^{i,(t)}=\{\begin{array}{cc}{g}_j^i\hfill & \text{if}{g}_j^i\text{is typed}\hfill \\ \mathrm{E}(g_j^i|{\mathit{g}}_{\text{obs}}^i,{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})\hfill & \text{if}{g}_j^i\text{is untyped},\hfill \end{array}$$ (C.3)

and

$$C_{\mathit{\text{jk}}}^{i,(t)}=\{\begin{array}{cc}0\hfill & \text{if}{g}_j^i\text{ or }{g}_k^i\text{is typed}\hfill \\ \text{Cov}(g_j^i,g_k^i|{\mathit{g}}_{\text{obs}}^i,{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})\hfill & \text{if}{g}_j^i\text{ and }{g}_k^i\text{are both untyped}.\hfill \end{array}$$ (C.4)

The calculation of $\mathrm{E}(g_j^i|{\mathit{g}}_{\text{obs}}^i,{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})\text{and Cov}(g_j^i,g_k^i|{\mathit{g}}_{\text{obs}}^i,{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})$ follows directly from (2.4).

In the conditional maximization step, we first update the estimates for f^panel and Σ^panel sequentially, i.e.

$$f_j^{\text{panel},(t+1)}=\frac{1}{n}\mathrm{E}({\displaystyle \sum _{i=1}^n{g}_j^i|{\mathit{G}}_{\text{obs}},}{\widehat{\mathit{\mu }}}^{(t)}),\text{for}j=1,\dots ,p,$$ (C.5)

and

$${\mathrm{\Sigma }}_{\mathit{\text{jk}}}^{\text{panel},(t+1)}=\frac{1}{n}\mathrm{E}({\displaystyle \sum _{i=1}^n{g}_j^i{g}_k^i|{\mathit{G}}_{\text{obs}},{\widehat{\mathit{\mu }}}^{(t)},{\widehat{\mathrm{\Sigma }}}^{(t)})-f_j^{\text{panel},(t+1)}{f}_k^{\text{panel},(t+1)},\text{for}j,k}=1,\dots ,p.$$ (C.6)

Finally, we update the shrinkage estimates μ̂ and Σ̂ using

$${\widehat{\mathit{\mu }}}^{(t+1)}=(1-\theta ){\mathit{f}}^{\text{panel},(t+1)}+\frac{\theta }{2}\mathbf{1},$$ (C.7)

$${\widehat{\mathrm{\Sigma }}}^{(t+1)}={(1-\theta )}^2{S}^{(t+1)}+\frac{\theta }{2}(1-\frac{\theta }{2})I,$$ (C.8)

where

$$S_{\mathit{\text{jk}}}^{(t+1)}=\{\begin{array}{cc}{\mathrm{\Sigma }}_{\mathit{\text{jk}}}^{\text{panel},(t+1)}\hfill & j=k\hfill \\ \text{exp}(-\frac{{\rho }_{\mathit{\text{jk}}}}{2n}){\mathrm{\Sigma }}_{\mathit{\text{jk}}}^{\text{panel},(t+1)}\hfill & j\ne k.\hfill \end{array}$$ (C.9)

We initiated ECM algorithm by setting f^panel,(0) to the marginal means from all observed data and Σ^panel,(0) to a diagonal matrix with diagonal entries being empirical variance computed from typed SNPs.