Extensional flow of blood analog solutions in microfluidic devices

Abstract

In this study, we show the importance of extensional rheology, in addition to the shear rheology, in the choice of blood analog solutions intended to be used in vitro for mimicking the microcirculatory system. For this purpose, we compare the flow of a Newtonian fluid and two well-established viscoelastic blood analog polymer solutions through microfluidic channels containing both hyperbolic and abrupt contractions∕expansions. The hyperbolic shape was selected in order to impose a nearly constant strain rate at the centerline of the microchannels and achieve a quasihomogeneous and strong extensional flow often found in features of the human microcirculatory system such as stenoses. The two blood analog fluids used are aqueous solutions of a polyacrylamide (125 ppm w∕w) and of a xanthan gum (500 ppm w∕w), which were characterized rheologically in steady-shear flow using a rotational rheometer and in extension using a capillary breakup extensional rheometer (CaBER). Both blood analogs exhibit a shear-thinning behavior similar to that of whole human blood, but their relaxation times, obtained from CaBER experiments, are substantially different (by one order of magnitude). Visualizations of the flow patterns using streak photography, measurements of the velocity field using microparticle image velocimetry, and pressure-drop measurements were carried out experimentally for a wide range of flow rates. The experimental results were also compared with the numerical simulations of the flow of a Newtonian fluid and a generalized Newtonian fluid with shear-thinning behavior. Our results show that the flow patterns of the two blood analog solutions are considerably different, despite their similar shear rheology. Furthermore, we demonstrate that the elastic properties of the fluid have a major impact on the flow characteristics, with the polyacrylamide solution exhibiting a much stronger elastic character. As such, these properties must be taken into account in the choice or development of analog fluids that are adequate to replicate blood behavior at the microscale.

INTRODUCTION

The human blood is a multiphase complex fluid that carries vital substances to cell tissues and organs of the body. It consists of a suspension of cellular elements in an aqueous matrix, the plasma, of which 98% are erythrocytes [red blood cells (RBCs)], and the remainder are leukocytes (white blood cells), platelets, proteins, and other solutes.¹ Blood viscosity depends on blood composition (e.g., hematocrit),² temperature, shear rate, vessel diameter (e.g., Fåhraeus–Lindqvist effect),³ cell aggregation level, shape, deformation, and orientation, in addition to plasma viscosity,⁴ and is an important parameter since it provides valuable information about human health. Even though plasma can be considered as a Newtonian fluid, with a shear viscosity of about 1.1 mPa s at 37 °C,⁵ whole blood is a nonhomogeneous complex fluid, which exhibits non-Newtonian properties.^{6, 7, 8, 9}

Early dynamic rheological measurements that showed a non-Newtonian behavior of human blood were performed by Thurston^{10, 11} and Lessner et al.¹² using a cylindrical tube and a Couette geometry, respectively. Such non-Newtonian properties, like viscoelasticity, thixotropy, and shear-thinning behavior, arise mainly as a consequence of the deformability of RBCs as well as their tendency to interact with each other forming aggregates.^{6, 13} Indeed, at low shear rates, in a process that depends on the concentration of plasma proteins, red blood cells may form aggregate structures (rouleaux), causing an increase in blood viscosity.¹⁴ On the other extreme, when the deformable RBCs are flowing at high velocities (or high shear rates), these structures are broken and the individual RBCs tend to be elongated, leading to a decrease in the shear viscosity.¹⁵ In addition, rheological measurements show that blood exhibits a yield stress.¹⁶ This property is notoriously difficult to quantify since it requires precise measurements at very low shear rates, and as a consequence there is a wide variability in reported values.¹⁶ Nevertheless, the reported values for blood yield stress are very small, ranging from about 0.005 to 0.01 N∕m² depending on the hematocrit—at high RBC concentration, the rouleaux structures are more cohesive and therefore the yield stress tends to be higher.

Despite the extensive evidence for the complex rheology of blood,^{6, 17} the vast majority of research on hemodynamics assumes that blood behaves as a Newtonian fluid. When flowing in large vessels, such as arteries (diameter∼4 mm),¹ this assumption is usually reasonable. However, even in large vessels, non-Newtonian effects may become important due to the pulsatile (i.e., time-dependent) nature of the blood flow.⁴ More importantly, in small vessels typical of the microcirculation system, e.g., arterioles (diameter∼50 μm) and capillaries (diameter∼6 μm),¹ where the characteristic times of the flow and the fluid become comparable, blood presents a viscoelastic behavior.⁶ Furthermore, non-Newtonian effects can be enhanced when the flow vessel presents geometric features such as contractions∕expansions, taper, or bifurcations. Two important physiological examples are stenoses, an abnormal narrowing in the blood vessel due to the accumulation of cells, usually fatty material, and aneurysms, which are local abnormal dilations of the blood vessels. An interesting study about the effect of the geometry on the hemodynamic variables is reported in Tovar-Lopez et al.,¹⁸ in which blood itself is used and it is considered that it exhibits a Newtonian behavior. The authors studied platelet aggregation dynamics in blood flow through different contractions∕expansions representing diseased blood vessels with different stenosis levels in order to generate strain rate conditions similar to those in human vessels. Their flows are always characterized by Reynolds numbers on the order of hundreds.

Different constitutive equations, relating the stresses with the strain history, have been proposed and used to describe the rheological properties of human blood. To illustrate and model the inelastic shear-thinning behavior of the shear viscosity, equations such as the power-law,^{19, 20} the Casson,²¹ and the Carreau model²² are among the most widely used in the context of generalized Newtonian constitutive equations. Nevertheless, other time-independent as well as time-dependent viscosity models have been used (e.g., Yilmaz and Gundogdu),⁴ but to a lesser extent.

A comprehensive characterization of blood rheology and its flow dynamics is indeed very important in order to predict cardiovascular diseases, to plan vascular surgeries, to understand the transport of drugs through the circulatory system, and for the development of cardiovascular equipment as, for example, blood pumps, heart valves, and stents.⁴ However, the manipulation of whole blood is not a straightforward task and may not always be practical primarily due to safety reasons. As such, blood analog solutions are widely used for in vitro experiments as they exhibit several advantageous characteristics such as nontoxicity, low cost, and transparency.²³ These fluids present rheological characteristics similar to human blood and are typically based on polymer solutions. The earliest works that used blood analogs considered a suspension of 1 μm polystyrene spheres in a mixture of water, Dextran 70 and calcium chloride to stimulate the aggregation process,²⁴ and a suspension of disk-shaped, biconcave particles in Dextran 70.²⁵ In addition, other analogs have been used, namely, aqueous solutions of a polyacrylamide (PAA) and a xanthan gum (XG)^{13, 20, 23, 25} in which the addition of glycerine was used to tune the blood rheology at different hematocrit levels.^{2, 26} Gray et al.²⁰ studied the flow through a simplified arterial junction corresponding to a distal anastomosis in a femorodistal bypass using a Newtonian and two different non-Newtonian xanthan gum based blood analogs (with and without glycerine). In their experiments, the authors considered a time-dependent flow to reproduce the pulsation of the cardiac cycle and showed that the wall shear stresses obtained for the Newtonian fluid flow are very different from those obtained when non-Newtonian fluids with a shear-thinning behavior are used. Lerche et al.²⁷ and Vlastos et al.¹³ compared the rheology of PAA and XG solutions at different concentrations for the preparation of blood analog solutions. In particular, Vlastos et al.¹³ performed a combination of steady and oscillatory shear tests and found a similar rheological behavior between the human blood and the analog solutions, at concentrations of 125 ppm (w∕w) for the PAA and 500 ppm (w∕w) for XG, particularly at low shear rates. However, at high shear rates the blood analogs tended to exhibit higher viscosity and elasticity than blood.¹³

Since blood rheology is extremely complex, it is difficult to develop analog fluids that yield a complete description of all the rheological properties of blood and these fluids are typically chosen based on their density and shear viscosity. In this work, we aim to show that the elastic characteristics of the fluids (such as the relaxation time) should also be taken into account, in particular when considering conditions equivalent to those found in microcirculation. At these small scales, the role of fluid elasticity is significantly enhanced beyond what can be achieved at the macroscale, without being overwhelmed by inertial effects. For this purpose, we use microscale hyperbolic contractions to generate a quasihomogeneous and strong extensional flow to assess the elasticity level of two well-established blood analogs [an aqueous solution of a polyacrylamide at a concentration of 125 ppm and an aqueous solution of a xanthan gum at a concentration of 500 ppm (w∕w) as proposed by Vlastos et al.¹³ and Thurston²³] and test their capability of adequately representing the rheological and flow behavior of whole blood. Microscale geometries with sizes similar to capillaries were chosen to enhance the elasticity of the flow, since in more conventional macroscale geometries the blood analog fluids would essentially behave as inelastic fluids given their small relaxation times (of the order of milliseconds) and, therefore, would be nearly useless for the purpose of assessing the elasticity level of blood analogs in small blood vessels and lab-on-chip devices. The results obtained in this work clearly demonstrate that, despite having similar shear rheology, the two polymer solutions that are currently accepted as reliable blood analogs indeed exhibit different elasticity levels and show a distinct behavior in microscale flows that are typical of microcirculation, and, as such, care should be taken in their use.

EXPERIMENTAL TECHNIQUES

Microchannel fabrication and geometry

The flow of the blood analog solutions was investigated in microchannels with dimensions comparable to small human vessels, which include in their design contractions and expansions with hyperbolic and abrupt shapes. The hyperbolic shape was chosen in order to provide a nearly constant strain rate of the fluid flow along the centerline of the microgeometry.^{28, 29} The combination of geometry and reduced lengthscale characteristic of microfluidics makes it possible to study the response of the fluid under strong accelerations, in the absence of significant inertial effects, for controlled extensional flow conditions. The dimension of the narrow gap of the microgeometries is typical of small vessels such as arterioles (internal diameter of ∼50 μm), venules (internal diameter of ∼40 μm), and capillaries (internal diameter of ∼6 μm).¹

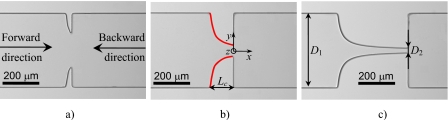
The planar microgeometries were fabricated in polydimethylsiloxane (PDMS) (Sylgard 184, Dow Corning), from an SU-8 reusable mold, using standard soft-lithography techniques.^{30, 31} Three different configurations were used as shown in the microscopy images of Fig. 1.

Figure 1.

Micrograph of the geometries studied: (a) microchannel S₁, (b) microchannel S₂, and (c) microchannel S₃. In (b) the shape of the quasihyperbolic walls is marked in red.

Independent of the configuration, the inlet∕outlet width, D₁, of the microchannels was kept constant and equal to 400 μm. The minimum width of the contraction, D₂, and the hyperbolic contraction length, L_c, were varied in order to obtain different values of the total Hencky strain (ε_H). The total Hencky strain experienced by a fluid element moving along the centerline of a planar contraction is given by ${\epsilon }_H={\int }_0^t\dot{\epsilon }dt=\text{ln}\left(D_1∕D_2\right)$.³² In Table 1 we present the values of D₂ and L_c for each geometry as well as the corresponding value of the Hencky strain. The hyperbolic walls were designed assuming the hyperbolic function y=±200∕[1+0.05(x+L_c)] (with x, y, and L_c in micrometers) valid for −L_c≤x≤0. The final PDMS microchannels obtained by replication in the SU-8 mold were imaged in the microscope set-up, and the real shape of the microchannels was slightly different and followed accurately the curve y=±200∕[1+0.05(x+L^*)−2.5×10⁻⁵(x+L^*)²] with the characteristic length L^* presented in Table 1. The corner features of the final geometries were not as sharp as printed on the chrome mask, a limitation of the fabrication techniques used, but had a radius of curvature of about 5–10 μm. Moreover, the real value of the depth of the microchannels is actually lower than the projected value (as shown in Table 1).

Table 1.

Values of the Hencky strain and dimensions of the microchannels used.

Projected (chrome mask)				PDMS microchannel
Channel	εH	D2 (μm)	Lc (μm)	εH	D2 (μm)	L* (μm)	h (μm)
S1	1.0	147	34.4	0.76	187.1	33	47
S2	2.0	54.1	128	1.86	62.4	123	45
S3	3.0	19.9	382	2.75	25.5	373	44

In addition to the benefits described above, the geometries of the microchannels used in this work are also interesting as they may be considered simplified representations of different intensity stenoses typical of diseased microcirculatory vessels.

Flow visualization

Visualizations of the flow patterns were carried out using streak photography with exposure times of the order of 1 s. For this purpose, the fluids were seeded with 1 μm fluorescent polystyrene tracer particles (20 ppm w∕w, Nile Red, Molecular Probes, Invitrogen, Ex∕Em: 520∕580 nm, density: 1.05 g∕mL) and, in the case of the blood analog solutions, sodium dodecyl sulfate (0.05 wt. %, Sigma-Aldrich) was added in order to reduce the adhesion of the particles to the channels walls. A syringe pump (PHD2000, Harvard Apparatus) was used to inject the fluid and control the flow rate in the microchannels. Syringes with different volumes (50 μl−10 ml) were used, according to the desired flow rate, and were connected to the microgeometries using Tygon tubing. The microgeometries were placed on an inverted epifluorescence microscope (DMI 5000M, Leica Microsystems GmbH) and were continuously illuminated by a 100 W mercury lamp. A filter cube (Leica Microsystems GmbH, excitation filter BP of 530–545 nm, dichroic of 565 nm, and barrier filter of 610–675 nm) was used to filter the multichromatic light into the excitation light which reaches the microgeometries containing the seeded fluid via a microscope objective (10×, NA=0.25). The light emitted by the fluorescent tracer particles was imaged through the same objective onto the camera (DFC350 FX, Leica Microsystems GmbH) in order to capture the particle trajectories. All streak images presented here are centered at the midplane of the microchannel. The flow visualization experiments were carried out at room temperature (T=293.2±1.5 K) for a wide range of flow rates (1≲Q≲70 ml h⁻¹ for de-ionized water and 0.001≲Q≲70 ml h⁻¹ for blood analogs).

Microparticle image velocimetry

Measurements of the velocity field were carried out using microparticle image velocimetry (μPIV). For that purpose, the fluids were seeded using fluorescent Nile Red polystyrene microspheres of 0.5 μm in diameter (90 ppm w∕w, Molecular Probes, Invitrogen, Ex∕Em: 520∕580 nm, density: 1.05 g∕mL). The generic imaging set-up used is similar to that described in Sec. 2B except for the microscope objective and light source. In this case, two different objectives were employed: a 20× objective (NA=0.4) in order to capture the particle displacement in a wide field of the microchannel and a 40× objective (NA=0.55) in order to improve the accuracy of the results within the contraction region, where the width is much smaller and the velocity is considerably higher. The light source used for μPIV is a doubled pulsed Nd:YAG (yttrium aluminum garnet) laser (Dual Power 65-15, Dantec Dynamics) with a wavelength of 532 nm. The time interval between pulses was adjusted in the range of 1≤Δt[μs]≤10⁴, such that particle displacement was about 25% the size of the interrogation area, which was selected according to the velocity of the flow and the objective used. For each flow rate, 150 pairs of images were acquired using a digital camera (Flow Sense 4M, Dantec Dynamics) with a resolution of 2048×2048 pixels and running in double frame mode. The images were postprocessed to obtain the velocity vector map using DYNAMIC STUDIO V2.3 software (Dantec Dynamics) based on averaging the 150 pairs of images. All images were acquired at the midplane of the microchannel.

For the optical set-up used in microfluidics, it is well known that the depth of field (δz) underestimates the actual depth over which there is a contribution of unfocused particles to the velocity field determined by μPIV and, thus, the measurement depth provides a more correct estimate of the depth of the image plane,³³

$$\delta z_m=\frac{3n{\lambda }_0}{{\left(\text{NA}\right)}^2}+\frac{2.16d_p}{\text{tan\hspace{0.17em}}\theta }+d_p,$$ (1)

where n is the refractive index, λ₀ is the wavelength of the light (in vacuum), NA is the numerical aperture of the microscope objective, and d_p is the particle diameter. Table 2 lists the depth of field and the total measurement depth for the range of objectives used for μPIV with our optical set-up.

Table 2.

Depth of field and total measurement depth for the present optical set-up.

Objective	δzf (μm)	δzm (μm)
20×	4.55	13.9
40×	2.25	7.89

Pressure-drop measurements

Pressure-drop measurements were performed connecting the two pressure taps of the microchannels, which are located far upstream (x=−2.8 mm) and far downstream (x=2.8 mm) of the test section, to a differential pressure transducer (Honeywell, model 26PC series). This pressure sensor was chosen based on the range of measurable differential pressure (ΔP_max=6.89 kPa). A 12 V dc power supply (Lascar electronics, PSU 206) was used to power the sensor, which in turn was connected to a data acquisition card (NI USB-6218, National Instruments) interfaced with LABVIEW V7.1. The output voltage of the sensor was previously calibrated in terms of pressure difference using a static column of water.

FLUID COMPOSITION AND RHEOLOGY

Two different viscoelastic fluids, which have a shear rheology behavior similar to that of human blood,^{13, 23} were used. The blood analog solutions are aqueous solutions of a xanthan gum (Sigma-Aldrich) with a concentration of 500 ppm (w∕w) and of a polyacrylamide (Sigma-Aldrich; average molecular weight, M_w=1.8×10⁷ g mol⁻¹) at a concentration of 125 ppm (w∕w), as suggested by Vlastos et al.¹³ A Newtonian fluid, de-ionized water, was also used for comparison purposes. The densities (ρ) of the XG and PAA solutions at 293.2 K are ρ=998.0 kg m⁻³ and ρ=998.2 kg m⁻³, respectively.

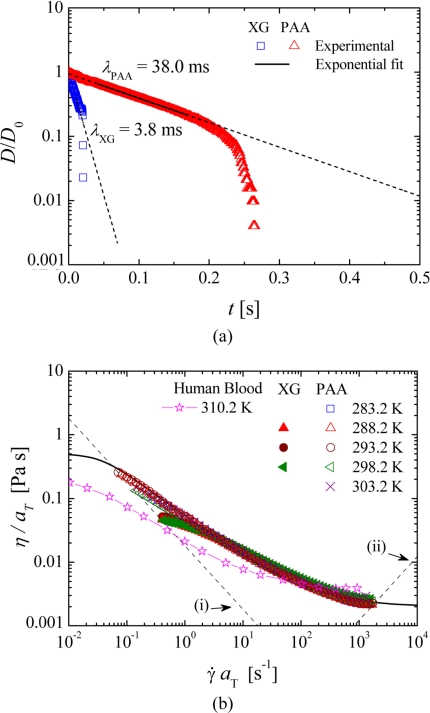
The rheology of the fluids was characterized with a rotational rheometer (MCR301, Anton Paar) and a capillary break-up extensional rheometer (Haake CaBER 1, Thermo Scientific) was used to determine the relaxation time of the fluid in extensional flow. This property was measured at the reference temperature (T₀=293.2 K) in extensional flow using two circular plates with a diameter (D_p) of 6 mm. Moreover, the geometrical configuration used for both fluids was such that the initial height was set to h_i=1.99 mm, which corresponds to an initial aspect ratio of Λ_i=h_i∕D_p=0.33. The final height was varied in a number of exploratory tests, and the best results were obtained using h_f=8.36 mm and h_f=9.10 mm for the XG and PAA solutions, respectively. Consequently, the final aspect ratio used in the measurements, which is defined as Λ_f=h_f∕D_p, was Λ_f=1.39 and Λ_f=1.52 for the XG and PAA fluids, respectively. The evolution of the filament thinning monitored in the CaBER experiments is illustrated in Fig. 2a as log[D(t)∕D₀] versus time (where D₀ is the radius of the filament at time t=0). The relaxation time (λ) was determined by fitting the experimental data in the linear region of the semilog plot to the equationD(t)∕D₀∝exp[−t∕(3λ)] resulting from the elastocapillary balance.³⁴ The determined relaxation time for the blood analog solution composed of xanthan gum was 3.8 ms while for the blood analog composed of PAA was 38.0 ms, which is one order of magnitude greater than the relaxation time of the XG solution.

Figure 2.

(a) Time evolution of the midpoint diameter of the fluid thread in a CaBER experiment at 293.2 K. The symbols represent the experimental data and the lines represent the exponential fit to the experimental data. (b) Master curves of the steady-shear viscosity for the XG and PAA blood analog solutions (symbols) and fit to the GNF model used in the numerical calculations (line). The steady-shear data for human blood at 310.2 K reported in Chien (Ref. ¹⁵) are also shown for comparison purposes. (i) Minimum measurable shear viscosity determined from 20× the minimum measurable torque of the rheometer. (ii) Onset of secondary flow due to Taylor instabilities for the 75 mm, 1° cone-plate geometry.

The steady-shear rheology was measured in the temperature range of 283.2≤T[K]≤303.2 using a cone-plate geometry (75 mm, 1° angle) under shear-rate control $\left(0.1\le \dot{\gamma }\left[{\text{s}}^{-1}\right]\le 5\times {10}^3\right)$ and the time-temperature superposition method³⁵ was used to obtain the master curve. Details of the method used and corresponding shift factors are given in supplementary material³⁶ (Sec. A). Figure 2 summarizes the resulting master curves for both blood analog solutions as well as the predicted values for a generalized Newtonian fluid model which will be described in detail in Sec. 4.

It is appropriate here to refer that to the best of our knowledge there are no archival publications with data on the elongational properties of blood. However, we are aware of the preliminary work by Poole et al.,³⁷ who attempted the measurement of blood relaxation time using a CaBER. The relaxation times measured by Poole et al.³⁷ were on the order of 100 ms for hematocrit 48%<Hct<52%, which is in excess of the relaxation time of both blood analogs used here. As such, we would expect a more pronounced elastic behavior (namely, in terms of vortex size upstream of the contraction and pressure drop) for real blood than what was observed here for either blood analogs. However, a complete comparison must be left until a more detailed study with blood is performed and∕or published.

NUMERICAL METHOD AND COMPUTATIONAL MESHES

The flow of the reference Newtonian fluid (de-ionized water) was simulated numerically in order to compare the flow patterns and velocity field with the experimental results and consequently validate the measurement techniques. In addition, we performed numerical simulations using a generalized Newtonian fluid (GNF) model, which considers shear-thinning viscosity but no memory effects (viscoelasticity). We have also fitted the rheological data to a modified Phan-Thien–Tanner (MPTT) model,³⁸ which includes both shear-thinning and elastic behavior. More precisely, it corresponds to a standard PTT model³⁹ having a shear-rate dependent viscosity coefficient. Details of this model, as well as the fitted parameters, are given in supplementary material³⁶ (Sec. B). This model was chosen because it can accurately represent the viscoelastic shear-thinning rheological behavior of the blood analog solutions used. However, the MPTT model was not used in the numerical simulations, given the three-dimensional nature of the microfluidic channel, and the high Deborah numbers attained in the experiments that would lead to highly demanding three-dimensional (3D) simulations and the inherent numerical difficulties to obtain mesh-independent solutions.⁴⁰ Nevertheless, the comparison of the numerical GNF calculations with the experimental results allows us to indirectly assess the effect of elasticity on the observed experimental results.

We assume that the flow is laminar, isothermal, and incompressible. Therefore, the equations that need to be solved are those of conservation of mass and momentum,

$$\nabla \cdot \mathbf{u}=0,$$ (2)

$$\rho \left(\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot \nabla \mathbf{u}\right)=-\nabla p+\nabla \cdot \mathbf{\tau }+{\eta }_{\text{s}}{\nabla }^2\mathbf{u},$$ (3)

where u represents the velocity vector, t the time, p the pressure, and η_s the solvent viscosity. For the calculations using the Newtonian fluid the polymeric extra stress tensor is neglected (τ=0), while for the generalized Newtonian fluid calculations the two last terms in Eq. 3 are replaced by ∇⋅[η(∇u+∇u^T)] and we use a Carreau model to describe the shear-thinning behavior of the shear viscosity,

$$\eta ={\eta }_{\text{s}}+\frac{{\eta }_0-{\eta }_{\text{s}}}{{\left[1+{\left(\Lambda \dot{\gamma }\right)}^2\right]}^{\left(1-n\right)∕2}},$$ (4)

where η₀ is the zero shear-rate viscosity, Λ is a time constant, and n is a power-law like index. For the PAA fluid, the parameters of the Carreau model are η₀=0.5 Pa s, η_s=0.002 Pa s, Λ=29 s, and n=0.33.

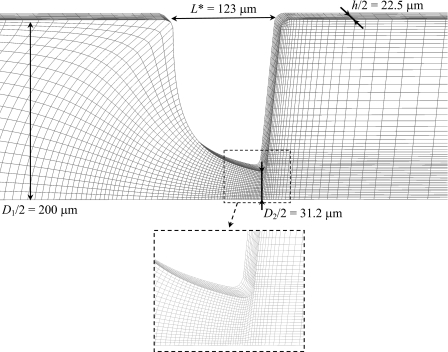
The governing equations were solved using a fully implicit finite-volume method with a time-marching pressure correction algorithm, which is described in detail in Oliveira et al.⁴¹ and Alves et al.⁴² and, consequently, are not explained here. The numerical simulations are 3D and the meshes used to represent the computational domain are block-structured, composed of nonuniform control volumes. The mesh characteristics, such as the total number of cells (NC) and the normalized minimum cell spacing (Δx_min∕D₂, Δy_min∕D₂, Δz_min∕D₂), are listed in Table 3 and an exemplifying mesh used in the simulations (corresponding to microchannel S₂) is shown in Fig. 3. Symmetry was enforced at the two center planes (x=0 and z=0), which means that only a quarter of the full domain was mapped, reducing significantly the memory requirements and the computational times.

Table 3.

Characteristics of the meshes used in the numerical simulations.

Mesh	NC	Δxmin∕D2	Δymin∕D2	Δzmin∕D2
MS1	49 920	8.03×10−3	7.29×10−3	5.04×10−3
MS2	50 080	2.09×10−2	2.04×10−2	2.12×10−2
MS3	66 720	2.14×10−2	2.50×10−2	1.90×10−2

Figure 3.

Zoomed view of the mesh used in the numerical simulations of the flow in microchannel S₂.

Regarding the boundary conditions, we imposed a uniform velocity profile (average velocity U₁) at the entrance, no-slip conditions at the solid walls, and at the outlet vanishing gradients for velocity components and linear extrapolation of pressure are imposed. The inlets and outlets were positioned far from the constriction in order that fully developed flow conditions were attained prior to the contraction region.

FLOW PATTERNS

Newtonian fluid

The flow of a Newtonian fluid (de-ionized water) was studied for all microgeometries in order to validate the experimental technique and simultaneously investigate the influence of inertia on the flow patterns in the absence of elasticity. The Reynolds number (Re) is defined as Re=ρU₂D₂∕η, where U₂ is the average velocity in the narrowest gap of the contraction, with width D₂ [cf. Fig. 1b]. The Reynolds number can also be expressed in terms of the flow rate as Re=ρQ∕(ηh).

Figure 4 compares the flow patterns predicted numerically and captured experimentally at the center plane of the microchannel S₂ for the two flow directions and at different Reynolds numbers in order to highlight the effect of inertia. For both flow directions, the Newtonian fluid flow behavior is found to be qualitatively similar for all microgeometries studied. Moreover, the appearance of recirculations downstream of the expansion (either abrupt or smooth) brought about by inertia occurs in an analogous way for the two flow directions, even though higher Reynolds numbers are required in the backward direction. At low Reynolds numbers, the fluid is pushed toward the centerline as it moves through the contraction and no flow separation is observed except near the far corners of the expansion, where small Moffatt vortices exist [cf. Fig. 4(a1) and (a2)]. Increasing the flow rate leads to the onset of flow separation downstream of the expansion due to the flow being driven against an adverse pressure gradient, leading to flow separation. First, lip vortices appear close to the reentrant corners [Fig. 4(b1) and (c2)] and eventually these vortices enlarge to the far corner with increasing Re. As inertia is further increased, the vortices grow in size in the downstream direction [Fig. 4(c1)]. With further increases in the flow rate (not attained in the experiments) the flow will eventually become asymmetric, with recirculations downstream of the expansion plane having different sizes, as found by Oliveira et al.²⁹ for abrupt microfluidic expansions and by Cherdron et al.,⁴³ among others, for planar expansions at macroscale. The experimental flow features, including the onset of vortex formation and vortex growth, are well captured by the numerical predictions.

Figure 4.

Effect of inertia on the Newtonian fluid flow patterns obtained experimentally (photograph) and predicted numerically (solid lines) for microchannel S₂. The left-hand side column corresponds to flow through the hyperbolic contraction followed by the abrupt expansion (forward direction) and the right-hand side column corresponds to the flow through the abrupt contraction followed by the hyperbolic expansion (backward direction).

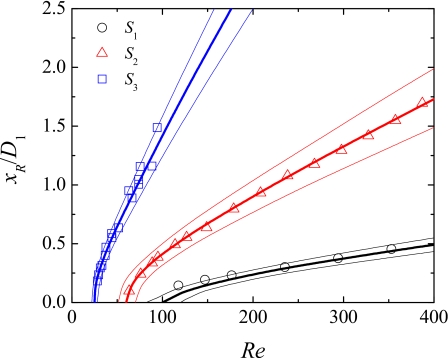
In Fig. 5 we compare the dimensionless vortex length x_R∕D₁ [cf. Fig. 4(c1) for x_R definition], predicted numerically and measured experimentally from the flow visualizations for a range of Reynolds numbers, and for the three microgeometries investigated. For all cases, a vortex increase is observed as inertial effects are enhanced, and this effect is more intense for the higher Hencky strain geometries. Good agreement between experiments and numerical simulations is observed, and considering a deviation of 3 μm in the depth of the channel is enough to explain any of the small differences observed.

Figure 5.

Influence of Reynolds number on the length of the recirculations formed downstream of the abrupt expansion for the Newtonian fluid (forward flow). The symbols represent experimental data obtained for channels S₁, S₂, and S₃ and the thick solid lines represent the corresponding numerical predictions using the depth of the channel (cf. Table 1). The thin solid lines represent the numerical predictions when the depth of the channel is varied at ±3 μm (upper line: h+3 μm; lower line: h–3 μm).

The values of Re at which the different flow patterns arise depend on the geometry used. For geometries with higher Hencky strain, the onset of lip vortices [cf. Fig. 4(b1)] and subsequent development of corner vortices [cf. Fig. 4(c1)] occurs at lower Re, and the vortices exhibit a more elongated shape. For the backward flow direction, recirculations emerge downstream of the hyperbolic expansion at higher values of Re than for the corresponding forward flow direction (cf. Fig. 4). This behavior is expected since in the forward direction, the fluid is flowing through an abrupt expansion, in which the adverse pressure gradient is higher, as compared with the smooth expansion flow, where the adverse pressure gradient is weaker.

Blood analog fluids

In order to characterize the viscoelastic fluid flow, we use the Deborah number, here defined as De=λU₂∕(D₂∕2). The Reynolds number definition presented in Sec. 5A is also used, but the shear viscosity η is evaluated at a characteristic shear rate ${\dot{\gamma }}_2=U_2∕\left(D_2∕2\right)$. The range of estimated shear rates achieved with the different geometries is shown in Table 4 for the range of flow rates tested experimentally.

Table 4.

Range of flow rates and estimated shear rates used in the experiments with the blood analogs.

Channel	Min Q (ml h−1)		Max Q (ml h−1)		Min ${\dot{\gamma }}_2$ (s−1)		Max ${\dot{\gamma }}_2$ (s−1)
	PAA	XG	PAA	XG	PAA	XG	PAA	XG
S1	1.0×10−2	1.0×10−2	10	60	3.37	3.37	3.37×103	2.02×104
S2	2.0×10−3	5.0×10−2	1.0	30	6.34	158	3.17×103	9.51×104
S3	1.0×10−3	1.0×10−2	0.6	20	19.5	195	1.17×104	3.89×105

In Fig. 6a we show the flow patterns obtained experimentally for the PAA blood analog solution flowing in the forward flow direction of microgeometry S₂. At very low flow rates (and consequently low De), the flow patterns are Newtonian-like [cf. Fig. 6(a1)] and on increasing the flow elasticity, or in other words, on increasing De, symmetric lip vortices develop upstream of the contraction and grow to the far corners [cf. Fig. 6(a2)]. The formation of corner vortices upstream of a microfluidic hyperbolic contraction has also been discussed by McKinley et al.⁴⁴ for the flow of a 0.3 wt. % polyethylene oxide (PEO) aqueous solution. Increasing further the flow rate, and consequently the elastic effects, leads to a large increase of the vortex size [cf. Fig. 6(a3)] until a critical Deborah number is reached. Above this critical De, the flow becomes unsteady and asymmetric due to an elastic instability, and the size of the upstream vortices varies in time [cf. Fig. 6(a4), where the instantaneous flow field is clearly asymmetric]. An important characteristic to bear in mind is that inertial effects remain insignificant since the values of Re in these experiments are small. These results demonstrate that the PAA fluid flow is highly elastic, and that viscoelasticity leads to the formation of strong upstream vortices, in contrast to flow inertia that leads to downstream separation. The PAA fluid flow behavior is similar for all microchannels studied and the results for the other geometries are not shown for conciseness.

Figure 6.

Experimental flow patterns at the center plane of the microgeometry S₂ for the (a) PAA and (b) XG blood analog solutions flowing in the forward flow direction.

In the case of the XG blood analog solution, the elasticity-driven flow transitions upstream of the contraction are similar to those observed with the PAA solution, but the vortex growth is weaker and occurs at significantly higher flow rates due to the lower value of the XG fluid relaxation time. Consequently, the flow is markedly different from that observed with the PAA solution, upstream and downstream of the expansion, because the inertial effects become relevant as the flow rate is increased, as shown in the streak images of Fig. 6b acquired for the XG solution in the same microgeometry (S₂). At low flow rates, Newtonian-like flow patterns are observed (not shown here) and increasing the flow rate leads to the appearance of symmetric vortices upstream of the contraction [cf. Fig. 6(b1)] that increase in size with the flow rate due to the enhancement of elastic effects. When the flow rate is increased further, inertial effects also become important and symmetric vortices are observed downstream of the abrupt expansion as for the Newtonian fluid flow. Small corner vortices and lip vortices appear near the reentrant corner of the expansion plane [cf. Fig. 6(b2)] and eventually merge forming large corner vortices [cf. Fig. 6(b3)]. For high flow rates, the flow becomes unstable [cf. Fig. 6(b4)] with the corner vortices varying in size periodically. Comparing the viscoelastic and the Newtonian fluid flow (Fig. 4) at similar Re, we conclude that these downstream vortices are smaller for the viscoelastic fluid than for the Newtonian fluid, since elasticity is responsible for the development of normal stresses in shear, which are known to lead to jet swelling and consequently to a reduction of the size of downstream recirculations.⁴⁵

In Fig. 7 we present the flow patterns obtained experimentally for both fluids flowing in the backward direction in microgeometry S₂. For the PAA fluid the flow features in the two flow directions are similar, but take place at different flow conditions [lower Q or De for the backward flow direction—cf. Figs 6a, 7a]. For the XG fluid flow in the backward direction, and for the range of flow rates measured, inertial effects were not observed [cf. Fig. 7b] possibly due to the fact that the recirculations downstream of the smooth expansion appear at higher flow rates than in the opposite forward flow direction, as was seen for the Newtonian fluid flow (cf. Sec. 5A).

Figure 7.

Experimental flow patterns at the center plane of the microgeometry S₂ for the (a) PAA and (b) XG blood analog solutions flowing in the backward flow direction.

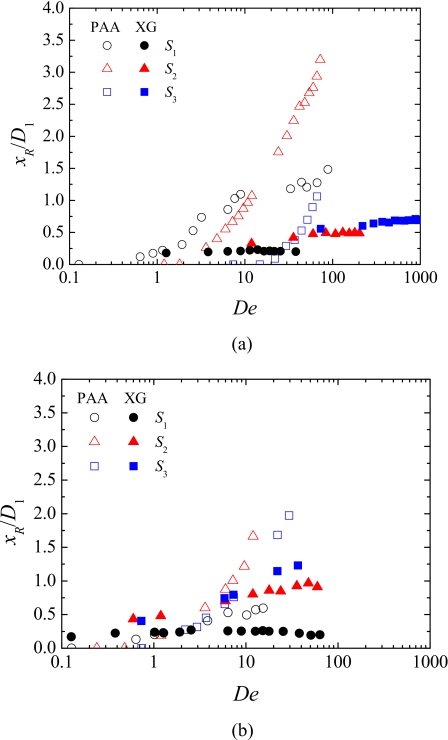
The upstream (elastic) vortex length corresponding to geometries S₁, S₂, and S₃ is plotted in Fig. 8 as a function of the Deborah number. For all cases, the vortex size increases significantly with De, but much more intensively for the PAA solution. In the case of backward flow, the results in terms of vortex size are qualitatively similar to forward flow, but for the higher Hencky strain geometry the vortices appear for lower values of De and these exhibit a more elongated shape. The increase of the vortex size with De is qualitatively different for the two polymers, with the growth regime for XG being qualitatively similar to that observed by Gulati et al.⁴⁶ for a DNA solution (of concentration c=4c^*, with c^* being the overlap concentration) in flows through 2:1 abrupt contractions. Furthermore, despite the differences in geometry (Gulati et al.⁴⁶ used a 2:1 abrupt contraction with a larger aspect ratio, i.e., a deeper microdevice), the range of vortex sizes reported by Gulati et al.⁴⁶ is comparable to those obtained here with the XG solution. These similarities are rather interesting, and may be associated to the fact that both DNA and XG are rigid rod-like molecules.

Figure 8.

Effect of De on the upstream vortex size obtained experimentally for PAA and XG solutions flowing through geometries S₁, S₂, and S₃: (a) forward direction and (b) backward direction.

In summary, markedly different flow behavior was found for the two viscoelastic fluids in these obstructed ducts, with the PAA solution showing stronger viscoelastic effects, even though both fluids are considered blood analogs and exhibit similar rheological characteristics in steady-shear flow.

VELOCITY FIELD

The velocity field at the center plane (z=0) was measured using μPIV for the flow of the Newtonian and the PAA blood analog solution. These experiments were conducted using microchannel S₂ with the fluids flowing through the hyperbolic contraction followed by the sudden expansion (forward direction only). In addition, for validation purposes the experimental results obtained for the Newtonian fluid case are compared with the corresponding numerical predictions.

Inertial effects

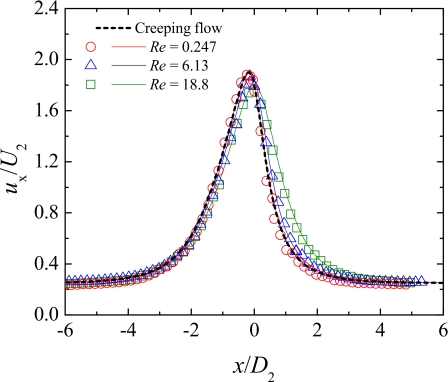
Figure 9 shows the dimensionless axial velocity profiles along the centerline measured for the Newtonian fluid at different flow rates. Moreover, a comparison between experimental and numerical results is presented in order to validate the μPIV experimental measurements. The axial velocity profile predicted for the Newtonian fluid flowing at creeping-flow conditions (Re→0) is also included in Fig. 9.

Figure 9.

Experimental (symbols) and numerical (lines) dimensionless axial velocity profiles at the centerline of the microchannel S₂ for the Newtonian fluid flow. The solid lines represent the numerical predictions for each Re and the dashed line represents the numerical predictions for creeping flow.

It is clear that as the fluid approaches the hyperbolic contraction, the axial velocity starts to increase due to entrance effects. After passing through the contraction, the fluid decelerates until the flow redevelops downstream of the abrupt expansion. For the lower flow rate, inertia is not important and the axial velocity profile coincides with that predicted numerically for creeping flow (Re→0). As the flow rate increases, fully developed conditions are reached gradually farther downstream of the expansion due to inertial effects, in agreement with the results of Oliveira et al.,²⁹ and the profiles are pushed toward the downstream direction. In addition, it is clear from Fig. 9 that the experimental results are in excellent agreement with those predicted numerically, thus validating the μPIV measurements.

Elastic effects

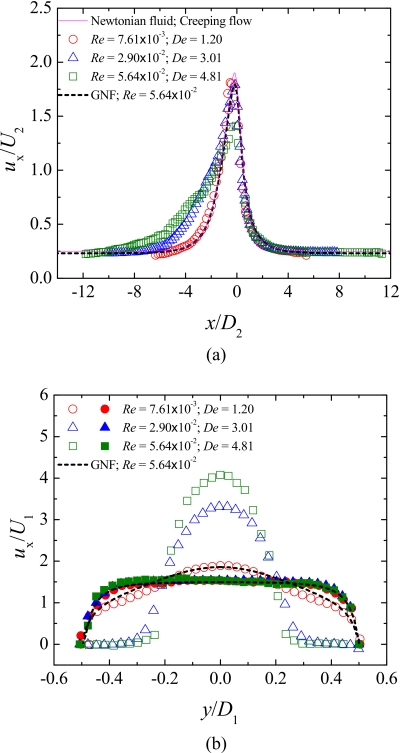
In order to highlight the effect of elasticity on the flow kinematics, Fig. 10 presents axial velocity profiles obtained at different flow rates (or Deborah numbers) for the PAA blood analog solution in channel S₂. As shown in Sec. 5B, using the PAA solution we are able to probe for elastic effects while minimizing inertial effects. In Fig. 10a, we report the axial velocity profiles obtained along the centerline and in Fig. 10b those obtained along the spanwise direction (y-direction) for different axial locations corresponding to x∕D₁=−0.63 (just upstream of the contraction region) and x∕D₁=1.64 (far downstream of the contraction region). Additionally, the axial velocity profiles predicted numerically for a Newtonian fluid under creeping-flow conditions, and for a GNF fluid described by the Carreau model fitted to the PAA shear rheology, are shown in Fig. 10 for comparison purposes. This GNF simulation corresponds to the highest flow rate achieved in the measurements with the PAA solution.

Figure 10.

Dimensionless axial velocity profiles in the microchannel S₂: (a) along the centerline (y=0) and (b) along the spanwise direction (for x∕D₁=−0.63 and x∕D₁=1.64). The symbols represent the experimental data obtained for the PAA blood analog, the solid lines represent the numerical predictions for the Newtonian fluid flow under creeping-flow conditions, and the dashed lines represent the numerical predictions for a generalized Newtonian fluid (Carreau model).

At the lowest flow rate (and De) for which μPIV measurements were performed, the axial velocity profile along the centerline in Fig. 10a is analogous to that obtained numerically for the Newtonian fluid under creeping-flow conditions, which is the limiting case when both Re and De vanish. Increasing the flow rate leads to significant changes of the normalized axial velocity profiles upstream and in the hyperbolic contraction region, as expected from the flow visualizations presented in Sec. 5B. In fact, the upstream recirculations observed for higher De act as an extension of the contraction, and as a result, the fluid at the centerline starts to accelerate further upstream in the channel [Fig. 10a], an effective way to reduce the strain rate and consequently the flow resistance for strain-hardening fluids.

The dimensionless axial velocity profile along the centerline obtained numerically using the GNF model, which takes into account the shear-thinning behavior but not the elasticity of the fluid, is similar to that found for the Newtonian fluid, except in the microchannel throat, where its value is lower than for the Newtonian fluid due to shear-thinning effects [Fig. 10a]. The GNF prediction is also similar to the results obtained in the experiments with the PAA solution at the lowest flow rate, where elasticity is at a minimum and only shear-thinning matters [Figs. 10a, 10b]. Comparing the experimental results obtained for the viscoelastic fluid at the higher flow rates with the corresponding GNF predictions, it is possible to observe significant differences in the velocity profiles particularly upstream and in the contraction region [cf. profiles in Fig. 10a and profiles at x∕D₁=−0.63 in Fig. 10b], revealing once again the strong elastic character of the flow of the PAA solution through this type of microgeometry that is enhanced when strong velocity gradients are observed.

PRESSURE-DROP MEASUREMENTS

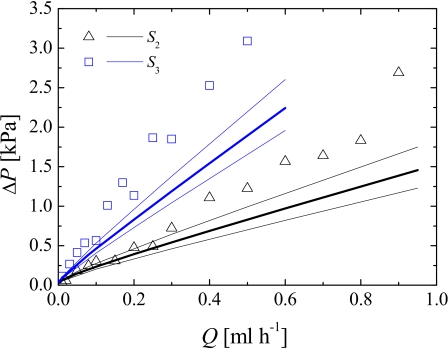
We measured the pressure drop across the test sections using the PAA blood analog for microgeometries S₂ and S₃. Figure 11 shows the pressure drop obtained as a function of the flow rate for the forward flow direction.

Figure 11.

Pressure drop of the PAA blood analog solution, measured for the forward flow direction, as a function of the flow rate for microchannels S₂ and S₃. The symbols represent the experimental data and the solid lines represent the numerical predictions using the Carreau model. The thick solid lines represent the numerical predictions using the depth of the channel and the thin solid lines represent the numerical predictions assuming a variation of ±3 μm in the depth of the channels (upper line: h–3 μm; lower line: h+3 μm).

The pressure drop increases approximately linearly with the flow rate, or Deborah number, for all microgeometries studied. As expected, for the same value of the flow rate, the pressure drop is higher for channels with higher values of the total Hencky strain, which have longer and narrower contraction regions and produce stronger extensional flows. In Fig. 11 we also show the corresponding values predicted numerically using the Carreau model. The solid thick lines represent the numerical predictions using the depth of the channel measured experimentally, while the thin lines represent the numerical predictions assuming a variation of ±3 μm in the channel depth.

As can be seen, at low flow rates, the pressure drops measured experimentally and predicted numerically using the GNF model are similar. However, above Q∼0.1–0.2 ml h⁻¹, elastic effects become increasingly relevant and the numerical predictions of the pressure drop using the GNF model, which consider the shear-thinning behavior but not the existence of elasticity, are substantially lower than the experimental results for the higher Hencky strains. We believe that the high extensional viscosity of the PAA fluid, which generates high normal stresses in the contraction region where a strong extensional flow is observed, is responsible for the distinct behavior, leading to the strong quasilinear increase of the pressure drop with the flow rate for the geometries with the higher Hencky strains.

CONCLUSIONS

The flow of two non-Newtonian fluids, commonly employed as blood analogs, through hyperbolic and abrupt contractions∕expansions revealed a considerably different behavior under strong extensional flow. Our rheological analysis confirms that both blood analogs have a shear-thinning behavior very similar to that of whole human blood but the relaxation time for both analogs differs by one order of magnitude. Moreover, the characteristics of the flow through obstructed ducts observed with the viscoelastic fluids are very different from those found with the Newtonian fluid. In the latter, inertia promotes the appearance of vortices downstream of the expansion plane. On the other hand, in the viscoelastic fluid flow case, complex flow patterns brought about by the elastic nature of the polymeric solutions are observed. When inertia is negligible, elastic-driven vortices appear upstream of the constriction, which increase in size when De is increased. Oppositely, when inertial effects are significant, downstream vortices appear, which increase with Re and result in a decrease of the size of the upstream vortices. The PAA blood analog solution revealed a stronger elastic nature than the XG blood analog, with the flow eventually becoming unsteady even in the absence of significant inertial effects. In contrast, in the flow of the XG blood analog solution, both elastic and inertial effects are observed before the flow becomes unsteady. The pressure drop measured with PAA solution in the forward direction was found to increase quasilinearly with the flow rate due to the presence of elastic effects, which compensate for the shear-thinning effects that act to slightly reduce the pressure drop as shown by the GNF simulations. Hence, it is possible to conclude that comparing the flow of human blood with the Newtonian fluid flow at the microscale is a rough oversimplification. Moreover, taking into consideration only the shear viscosity in order to manufacture a blood analog solution with a viscoelastic character is not adequate, as demonstrated by the markedly different results obtained in a strong extensional flow using two common blood analog solutions.