Microscopic mechanism of nanocrystal formation from solution by cluster aggregation and coalescence

Abstract

Solute-cluster aggregation and particle fusion have recently been suggested as alternative routes to the classical mechanism of nucleation from solution. The role of both processes in the crystallization of an aqueous electrolyte under controlled salt addition is here elucidated by molecular dynamics simulation. The time scale of the simulation allows direct observation of the entire crystallization pathway, from early events in the prenucleation stage to the formation of a nanocrystal in equilibrium with concentrated solution. The precursor originates in a small amorphous aggregate stabilized by hydration forces. The core of the nucleus becomes crystalline over time and grows by coalescence of the amorphous phase deposited at the surface. Imperfections of ion packing during coalescence promote growth of two conjoint crystallites. A parameter of order and calculated cohesive energies reflect the increasing crystalline order and stress relief at the grain boundary. Cluster aggregation plays a major role both in the formation of the nucleus and in the early stages of postnucleation growth. The mechanism identified shares common features with nucleation of solids from the melt and of liquid droplets from the vapor.

INTRODUCTION

The microscopic mechanism of homogeneous nucleation from solution remains elusive. One aspect not yet understood is the role of prenucleation solute clusters in the formation of precursors of the solid phase. A number of studies have suggested the presence of clusters in unsaturated aqueous solutions at ambient conditions, and their role in nucleation and crystal formation has been discussed. Raman spectroscopy has provided evidence of ion clusters in sodium nitrate solutions, and it was suggested that crystallization is initiated by clusters coalescence as the concentration reaches saturation.¹ Other studies have suggested the presence of hydrogen-bonded polymerlike species in several dihydrogen orthophosphates, and their implication in crystallization and fast directional growth has been discussed.² Prenucleation clusters during crystallization of glycine have also been detected with a combination of NMR, and x-ray and neutron scattering methods.³ Recently, analytical ultracentrifugation and ion-selective electrode data have provided evidence of large ion clusters in unsaturated solutions of calcium carbonate.⁴ It was suggested that these clusters are the relevant species that initiate precipitation of the solid phase, an amorphous aggregate that evolves into a particular polymorph depending on the pH of the solution.

These nucleation mechanisms differ from the classical view in which a nucleus grows continuously by monomer attachment once it reaches a critical size.⁵ Detailed investigations of alternative crystallization pathways are a recent development, motivated mainly by studies on biomineralization, the process by which organisms form crystalline or amorphous minerals from aqueous environments.^{6, 7} During the last decade evidence has accumulated that nucleation from solution may be far more complex than traditionally thought and that both classical and nonclassical mechanisms may operate simultaneously during the early phases of crystallization. One mechanism identified from these studies is oriented attachment,^{8, 9} in which nanoparticles aggregate into an iso-oriented array from which a single crystal emerge upon coalescence. Another mechanism involves the self-assembly of coated nanoparticles into mesocrystals with scattering properties similar to single crystals, but with different mechanical properties.⁹ Although progress has been made in controlling these mechanisms,^{10, 11} microscopic insight is still incomplete, even for structurally simple systems, such as uni-univalent electrolytes.

In a recent study in situ transmission electron microscopy has allowed for the first time direct observation of individual nucleation trajectories in real time with nanometer resolution.¹² Suspended platinum nanoparticles with a broad size distribution evolved toward a monosdisperse suspension of single nanocrystals. Classical and nonclassical pathways were observed: Nanocrystals formed by the classical route increased in size continually and showed single crystal characteristics throughout the growth. Nanocrystals formed by the nonclassical route emerged by random aggregation of particles into polycrystals of nonuniform shapes, which evolved toward single spherelike crystals as coalescence slowly set in.¹²

The atomic events that take place during nucleation and the early postnucleation period are difficult to probe experimentally due to the short length and time scales involved. Impurities are also difficult to eliminate completely, which may complicate the interpretation of experimental data. Thus, atomistic insight has been obtained primarily from computer simulations. These studies have most frequently dealt with nucleation and crystallization of a solid from the melt, a type of nucleation of traditional theoretical interest as well.¹³ The first observation of a nucleation event in a dynamics simulation was in a Lennard-Jones (LJ) fluid,¹⁴ where the nucleated phase was identified as a metastable bcc instead of the thermodynamically stable fcc structure. Subsequent studies showed that the structure of the nucleus depended critically on the form of the potential^{15, 16, 17}: e.g., liquid rubidium always displayed bcc order, but the truncated rubidium potential, as well as LJ and its truncated form, all showed fcc order; soft-core potentials adopted both bcc and fcc structures. Despite these structural discrepancies, there was a general agreement that nucleation follows essentially a classical mechanism, with critical nuclei containing ∼40–70 atoms. Increasingly sophisticated simulations have allowed a more detailed study of the morphology and anatomy of these nuclei and the dynamic behavior of the growing crystals. For example, simulations of 10⁶ LJ particles¹⁸ showed that many nuclei, containing ∼10–20 atoms, formed simultaneously when the system was subjected to sudden supercooling. These nuclei showed either bcc or fcc structures, but only those with fcc order grew into larger crystals. Further simulations at moderate supercooling¹⁹ revealed a more complex picture for these LJ systems: precritical nuclei with bcc order formed initially, but as time progressed their cores became fcc ordered, while their surfaces still retained the metastable bcc order. More recent simulations in LJ-like fluids have shifted the focus toward the structural properties of the liquid before nucleation takes place. It was suggested that formation of a critical nucleus is promoted by transient, medium-range, high structural order in the supercooled fluid.²⁰

Nucleation of a liquid from its saturated or supercooled vapor was one of the first mechanisms studied by nucleation theory.⁵ Like nucleation from the melt, computer simulations of droplets formation from gases have also been reported. Simulation of LJ particles at varying degrees of supercooling²¹ have shown that freezing follows a typical nucleation pathway at moderate quenches, but a spinodal regime gradually sets in as the degree of supercooling increases. These results have been confirmed by a series of independent simulations,²² where the mechanism of nucleation near the gas–liquid spinodal was elucidated. It was suggested that growth of a nucleus follows a mechanism of coalescence of small liquidlike subcritical clusters.²²

Unlike the cases of melts and gases, dynamics simulations of nucleation and crystallization of a solid from a solution have been less common. Long trajectories and relatively large systems are typically needed to observe nucleation events, unless high oversaturation is used. Simulations of electrolytes are particularly challenging because a minimum of three kinds of particles are required (water and two ion species). Thus, computational demands and quality of the energy function have prevented a systematic study of crystallization from solution. Earlier dynamics simulations of a saturated solution were carried out at 27 ºC and 0.77 kbar, using a LJ model of a two-component system, one representing the solvent and the other the precipitating solid.²³ More recently, very early events of nucleation of a supersaturated aqueous NaCl solution were studied at ambient conditions using a fully atomistic force field. Such level of modeling, arguably most realistic, is computationally demanding, so a special technique was used to sample the phase space more efficiently.²⁴ Small ion clusters were observed that were interpreted as stable precursors of NaCl nanocrystals.

The goal of this paper is to investigate the microscopic mechanisms that operate during homogeneous nucleation and nanocrystallization from an aqueous solution of a solute that forms prenucleation clusters. The problem is here studied in an aqueous NaCl electrolyte at ambient conditions, using submicrosecond dynamics simulations of a fully atomistic, physically realistic model of ions and water. Saturation is achieved gradually by adding small amounts of salts to the equilibrated solution, thus mimicking a typical biomineralization process in nature. The time scale of the simulations allows direct observation of the complete crystallization pathway, from early events in the prenucleation stage to the formation of a nanocrystal in equilibrium with concentrated solution. The atomistic model confers directionality to the hydrogen bonds, and thus allows investigation of the specific role of hydration forces on the formation and stabilization of the critical nucleus.

SIMULATION METHOD

The simulation was carried out in the isothermal–isobaric (NPT) ensemble, at 25 ºC and 1 atm, in a cubic cell with periodic boundary conditions. The all-atom (PARAM22) representation of the CHARMM force field (version c33) was used.²⁵ Long-range electrostatic forces were treated with particle-mesh Ewald summation,²⁶ using parameters optimized for simulations of liquids²⁷: width of the Gaussian function used for summation on the reciprocal space was set at 0.34 Å⁻¹; 48 grid-points were used in each direction for the fast Fourier transform; five unit-cell images were added in each direction, and complimentary error functions were calculated with B-spline interpolation of order 6. A shift function was used to shut off electrostatic and van der Waals interactions between 10 and 12 Å, and a 14 Å cutoff was used for the nonbonded list update. A CHARMM-optimized TIP3P water model was used to represent the aqueous phase; Lennard-Jones parameters for the Na⁺ and Cl⁻ ions were taken from the literature.²⁸ The quality of this model and a comparison with other major force fields was discussed in detail in Ref. 28. Bond lengths and angles were constrained with the SHAKE algorithm.²⁹ The leapfrog integrator with a 2 fs time-step was used to solve the equations of motion. Pressure was maintained with the Langevin piston method,³⁰ as implemented and optimized in CHARMM: the piston mass and the collision frequency were set at 400 amu and 20 ps⁻¹ for both equilibration and production dynamics. Constant temperature conditions were maintained with the Hoover thermostat,³¹ using a mass of 10³ kcal mol⁻¹ps² (scaled units). The side length of the simulation cell was initially set at ∼4.7 nm and filled with pure water (3491 molecules), yielding an average density of ∼0.993 g∕cm³ after equilibration.

Biomineralization in nature occurs at different rates and through different mechanisms. For example, magnetite nanocrystals formation in magnetotactic bacteria is relatively fast, while deposition of calcium phosphate on kidney stones or soft tissues occurs at much lower rates. In these cases saturation is gradually achieved by intake of solutes from the environment. To mimic these processes in a computer simulation a practical criterion is needed to add salt in a controlled manner. In these simulations the system is driven to supersaturation gradually by replacing randomly-selected water molecules with equal amounts of Na⁺ and Cl⁻ (one ion per water) in small concentration δc of NaCl molecules every δt ∼10 ns. This time interval has been estimated in previous studies^{28, 32} as the minimum necessary for the ions subsystem to reach a steady distribution of clusters. These studies addressed the concentration range between ∼0.5 and ∼3 M in an isothermal–isochoric (NVT) ensemble, i.e., well below the measured saturation concentration of NaCl at ambient conditions (∼6.3 m). An injection rate r_e = δc∕δt is used here, which guarantees near-equilibrium conditions at each step of the crystallization process. For rates lower than r_e the main results are expected to be independent on the injection rate (cf. Sec. 4). The process of gradual saturation starts from an initial concentration of ∼3 m (3125 water molecules and 183 fully dissociated NaCl molecules, i.e., 183 Na⁺ and 183 Cl⁻ ions randomly distributed throughout the simulation cell) up to a maximum of ∼7.4 m (2759 H₂O and 366 NaCl). The increment δc used here corresponds to 30 NaCl molecules per injection, or an average δc ∼0.75 m (see labels on the time axis of Fig. 1 for details). Each new injection of ions is followed by a short equilibration of ∼5 ps to allow local relaxations of the liquid before new data are collected. When the concentration reaches the maximum of ∼7.4 m the simulation is continued for another ∼0.1 μs to explore the structural relaxation within the crystal. All simulations were carried out with a parallel version of CHARMM, using eight 2.8 GHz Opteron processors in a Beowulf cluster.

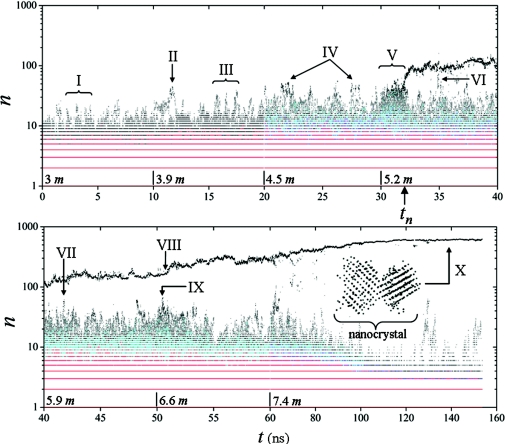
Figure 1.

Contour map of ρ(n, t): ρ = 1 is in black, ρ = 2 is in cyan, ρ = 3 is in blue, and ρ > 3 is in red. The quantity n is the number of ions in the clusters and represents the cluster size. Ions are injected every 10 ns, starting with a concentration of ∼3 m up to a maximum of ∼7.4 m (∼17% oversaturation); concentrations after each injection are indicated on the time axis. Major events along the trajectory are labeled from I to X (see text). The nucleus emerges at t_n ∼32 ns and grows irreversibly into a “poly”-nanocrystal in equilibrium with concentrated solution. The nanocrystal is composed of two conjoint crystallites separated by a grain boundary, as shown in the inset of the lower panel (the dots represent Na⁺ or Cl⁻ ions forming two interpenetrating fcc structure characteristic of a macroscopic NaCl crystal). The time scale changes for t > 60 ns.

RESULTS AND DISCUSSION

Statistical, kinetic, and dynamic properties of the cluster subsystem can be described by the density distribution ρ(n, q, t, c), defined as the number of clusters of n ions and charge q, at time t and concentration c, per unit volume.²⁸ A precise definition of ion cluster is given in Ref. 32 and adopted here. In this study q is of no immediate interest and c depends on t through the rate of injection δc∕δt, so a reduced distribution ρ(n, t) is obtained, which is plotted in Fig. 1. Neutron scattering experiments conducted at ambient conditions have shown that pairing of Na⁺ and Cl⁻ ions is consistent with diffraction patterns even at modest concentrations.³³ Additional evidence of cluster formation in aqueous NaCl solution has been provided by dynamic light scattering and other computational studies (reviewed in Ref. 28). The present simulation shows that, at ∼3 m, about half of the electrolyte is fully dissociated, i.e., present in the form of hydrated Na⁺ and Cl⁻ ions (monomers), while the rest of the ions form clusters (dimers, trimers, …, n-mers). A detailed study of the statistics, structure, kinetics, and dynamics of clusters in the canonical ensemble has been reported.^{28, 32} At ∼3 m, cluster populations are very similar to those observed at ∼3 M in these previous studies. Likewise, short-range structural order can be detected within the smaller clusters,²⁸ although substantial structural variations are also apparent. At these concentrations clusters are typically small and unstable, but fluctuations involving the reaction of several clusters within a short period of time may lead to the formation of unusually large aggregates, containing up to ∼25 ions (I in Fig. 1). These clusters tend to decay within a few picoseconds, but their cores usually remain stable for a longer period of time, which allows them to react with multiple clusters, as discussed previously.²⁸ The first injection of ions at ∼10 ns stabilizes temporarily one of these clusters. The cluster then begins to grow (II), almost doubling its size to ∼45 ions within ∼0.5 ns, which is followed by a rapid decay. The system reaches equilibrium following a pattern similar to that observed at ∼3 m, i.e., with large, unstable clusters emerging periodically (III). Increasing the concentration at ∼20 ns triggers a period of fast reactions and multiple cluster interconversions. The average cluster size increases, and amorphous aggregates containing up to ∼55 ions emerge more often than at lower concentrations (IV).

Further addition of salt at ∼30 ns induces a regime of maximum instability (V), i.e., the coexistence of many large and medium-sized clusters in rapid interconversions, which leads to abrupt changes in cluster sizes and shortened lifetimes. Out of the noisy background a small cluster begins to grow irreversibly at t_n ∼32 ns by attachment of clusters and monomers. To understand the conditions leading to the formation of this nucleus, individual ion trajectories are traced back in time to the prenucleation stage. Snapshots at regular time intervals along this pathway are shown in Fig. 2a. The sequence illustrates a possible physical mechanism operating during nucleation of a solute that forms prenucleation clusters: Early in the process several small clusters start collecting in the liquid (a). The number of local clusters soon increases (b); one cluster at the center of the group begins to grow by addition of monomers and clusters nearby (c). The number of clusters in this group begins to decrease while their sizes increase (d and e); at this time the group contains the largest clusters in the simulation cell. As time progresses the number of ions in the central cluster reaches n ∼45 (f), while the surrounding clusters begin to dissolve away, decreasing in size and number (g). The central cluster becomes stable, while the surrounding clusters have largely vanished (h). An isolated, hydrated nucleus containing ∼65 ions remains in the liquid (i), with a stable core of ∼55 ions (in red), which is the precursor of the nanocrystal. From the time it first emerges at t_n the core of the nucleus remains stable long enough to undergo internal structural relaxations and become a compact ion aggregate. Some of the ions in the core have six nearest-neighbor of opposite charge, each ion type forming a loose fcc lattice. Only the core of the nucleus (in red in i–k) is cohesive enough to provide stabilization and avoid dissolution, while the rest of the nucleus is labile and forms its amorphous phase (in white in i–k). Ions are exchanged frequently between the solution and this amorphous interfacial region, either as monomers or as small clusters. As a result the amorphous phase is recycled completely between (j) and (k). As time progresses the nucleus becomes more compact, while the core grows slowly by coalescence of the amorphous phase. The nucleus continues to grow by aggregation of monomers and clusters, and reaches a steady size before a new addition of salt at 40 ns.

Figure 2.

(a) Snapshots of the cluster buildup along the pathway leading to the formation of the first stable nucleus at t_n ∼32 ns (i): frames (a)–(i) taken every ∼0.25 ns, (j) at ∼33 ns, (k) at ∼38 ns. Ions that end up forming the stable core of the nucleus are shown in red; all others ions, including those composing the amorphous phase on the nucleus’ surface, are shown in white; about a dozen monomers (fully dissociated ions) contribute to the formation of the nucleus but are not shown. (b) Low water-density maps along the nucleation pathway shown in (a). Arrows indicate the location of the emerging nucleus. The scale applies to (b) only.

The early stages of formation of the stable nucleus are similar to those observed for other clusters at lower concentrations (t < t_n), i.e., random attachment and detachment of monomers and clusters. This process typically favors dissolution because clusters split before undergoing structural relaxations that may provide cohesion. The irreversible growth of the critical nucleus results from a reversal of the process in which dissolution is delayed beyond a nonturning point. The observation that the nucleus emerges from a small, otherwise nondescript cluster at the center of a group of clusters that build up gradually in the liquid suggests that shielding from the surrounding water may play a role in its stabilization. To quantify this process, local water density is calculated as

$$\begin{array}{c}\hfill \eta (\mathbf{r},t)={⟨\delta N(\mathbf{r},t)∕\delta \nu ⟩}_{\tau },\end{array}$$

where δν is a small volume centered at r, and the brackets denote a time average over a short period of time τ centered at t; δν and τ are chosen as to reproduce the density of pure water. Figure 2b shows a three-dimensional density map enclosing regions of very low water density. The contour level is such that similar regions are not detected at lower concentrations because of rapid cluster interconversions and ions motion, which tend to smooth the spatial variations of η. However, at ∼5.2 m, scattered, well-defined low-density regions begin to appear in the liquid, which reflects the local and gradual accumulation of clusters. These regions increase in size, merge, and end up enclosing the incipient central cluster in its earliest stages of formation. This exclusion of water from the environment of the central cluster suggests that the effects of hydration, which usually contribute to ion dissociation and cluster decay,²⁸ are largely reduced. In addition, the static dielectric permittivity of the bulk solution decreases substantially at these concentrations,³⁴ which may also favor stabilization of the nucleus. Once the nucleus is established, hydration in its environment returns to normal levels, but the nucleus is already stable enough to avoid dissolution. The size distribution of clusters immediately after the nucleus is formed (∼32–34 ns) reflects the corresponding drop of ions concentration. Over time, however, larger clusters begin to form again. One particular aggregate grows to a maximum of ∼70 ions (VI), larger than the nucleus when it first emerged, but insufficiently compact to avoid decay.

Injection of ions at ∼40 ns brings the electrolyte close to the solubility limit. Cluster aggregation on the precursor results in an initial period of steady growth, lasting ∼3.5 ns, and size fluctuations afterward. A series of structural relaxations takes place during this period in which the amorphous phase coalesces into the crystalline core, which grows as a result. Large clusters, containing up to ∼60 ions, are formed transiently in the presence of the precursor (VII) but none meets the conditions for stabilization. A new injection of ions at ∼50 ns supersaturates the solution. Within the first nanosecond, several large clusters begin to form in the liquid. The size of the nucleus, however, remains unmodified until ∼51 ns (VIII), when it starts growing continually, albeit irregularly, doubling its size in just ∼5 ns. During this period of fast growth monomers and clusters of various sizes aggregate on the precursor’s amorphous phase, and the liquid is temporarily depleted of the larger clusters until they begin to form again at ∼55 ns. Monomer attachment plays only a modest role during this period of growth, while clusters containing up to ∼40 ions make important contributions. At ∼50.5 ns a ∼65-ion amorphous aggregate is formed close to the precursor (IX), with only two layers of water separating both, but soon breaks down into several small fragments. Monitoring their individual trajectories shows that ions detached from this large aggregate are not absorbed by the precursor during the period of fast growth that immediately follows. As time progresses the size of the precursor begins to stabilize. However, the crystalline core continues to grow by coalescence of the amorphous phase, which shrinks as a consequence. The degree of crystallinity is at this point ∼70% of the precursor mass, and the core has a distinct halite (rock salt) structure, i.e., two interpenetrating fcc lattices, one of Na⁺ and the other of Cl⁻ ions, and the precursor may already be considered a NaCl crystallite of irregular shape. A final injection of ions at ∼60 ns takes the solution ∼17% above saturation. After an initial period of size fluctuations, the crystallite starts growing again by addition of monomers and clusters. At ∼0.12 μs the crystallite reaches a stable size of ∼600 ions and measures ∼2 × 2 × 3 nm. It has a high degree of crystallinity (above ∼95%) and may be considered a nanocrystal. The depletion of clusters at long times observed in Fig. 1 may be a consequence of the small size of the simulation cell combined with the periodic conditions imposed at the boundaries. Thus, a nanocrystal of comparable size may require higher oversaturation if a larger cell was used.

An order parameter based on combinations of spherical harmonics has been proposed to identify local orientational order and polymorphism in liquids and glasses.³⁵ In this simulation detection and identification of the ordered phase is not a problem, so a more direct approach is followed by defining a parameter

$$\begin{array}{c}\hfill {\mathbf{\Psi }}_i\left(t\right)=3+\Sigma {\delta }_{kl}\left|\cos {\theta }_{kl}\left(t\right)\right|\end{array}$$

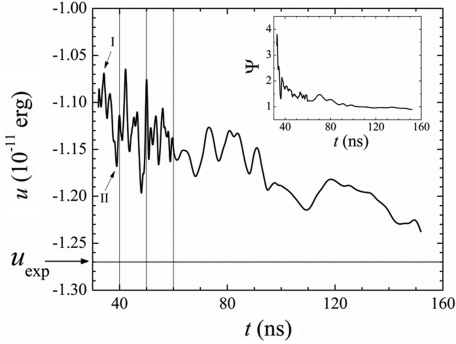
for each ion i in the core of the particle, which provides a quantitative measure of the local departure from ideal crystalline order as a function of time. The term particle refers here to the amorphous nucleus (nucleation stage), to the semicrystalline precursor (early postnucleation), or to the nanocrystal (late postnucleation), depending on the time regime considered. For the halite lattice, the summation (k ≠ l) runs over the six nearest-neighbors of i with opposite charge, and θ_kl is the angle k–i–l; δ_kl is −1∕2 if k and l are at opposite sides of the ring formed by the other four ions, and +1∕2 otherwise. In a perfect crystal Ψ_i is zero for all i, but increases as the local orientational order of the Na⁺–Cl⁻ “bonds” decreases. The parameter Ψ_i is related to the centrosymmetry parameter P used to identify defects in solids,³⁶ although Ψ_i in such context would measure the elastic deformations of the lattice. The calculations for t > t_n show that Ψ_i becomes smaller as time progresses, demonstrating the increasing crystalline character of the particle’s core. At long times Ψ_i approaches zero for all but a few ions. Further analysis shows that the nanocrystal is actually composed of two conjoint crystallites separated by a grain boundary, as shown in the inset of Fig. 1 (X). For ions at the boundary Ψ_i is relatively large due to poor orientational order, and decreases with time at a lower rate than for ions in the crystallites. The formation of this defect can be traced back to the earliest stages of formation of the precursor, and originates in subtle imperfections of ion packing during the periods of coalescence. It appears that, despite the controlled addition of ions, the injection rate was still too high, so new amorphous phase was deposited before ions were sufficiently fused with the growing lattice. This behavior is captured by the time evolution of the average of Ψ_i (cf. inset of Fig. 3). Immediately after formation of the nucleus at t_n the lattice is highly disordered but relaxes rapidly. Transient jumps originate in newly absorbed ions that have not yet fused but become more ordered with time. The slow decay at long times reflects not only the increasing order within the crystallites but also the relaxation of the grain boundary.

Figure 3.

Particle’s cohesive energy per ion pair, u, and parameter Ψ(t) = ⟨Ψ_i(t)⟩ of the particle’s compact core (inset) along the crystallization pathway. Calculations were performed every 0.2 ns (for t < 60 ns) and 1 ns (t > 60 ns). The particle was neutralized by randomly removing ions from the amorphous phase; the signal was smoothed by adjacent-data averaging.

Internal relaxation processes are also evidenced by the particle’s cohesive energy per ion pair,³⁷ calculated as u = 2(u_coul + u_vdW)∕n, where u_coul and u_vdW are the Coulomb and van der Waals potential energies, respectively. The decay of u with time shown in Fig. 3 reflects the increasing order and compactness of the particle at different time regimes. The underlying mechanism of nucleation and growth is apparent: immediately after the nucleus is formed, the amorphous phase grows faster than the crystalline core, so cohesion of the particle decreases (I); as relaxation of the core and coalescence set in, cohesion increases accordingly (II). This behavior is observed for each new addition of ions: the amorphous phase grows first by random addition of monomers and clusters, which decreases compactness and overall crystallinity of the particle. With time, the crystalline core grows at the expense of the amorphous phase and cohesion per particle increases accordingly. After the last injection of ions at ∼60 ns, the particle contains limited amount of amorphous material. In this case, the decay of u with time reflects internal structural ordering of ions within the crystallites and stress relief at the grain boundary. After ∼0.12 μs the size of the crystal no longer changes and the crystallites are well-defined interpenetrating fcc lattices, so the decay of u with time can be attributed mainly to structural relaxations of the boundary. At longer time scale the cohesive energy converges slowly to values comparable to the cohesive energy of a macroscopic NaCl crystal, u_exp ∼−1.27 erg∕ion pair.³⁷

CONCLUSIONS

Results from a single trajectory should be viewed with caution due to limited statistics. Although a single trajectory cannot rule out alternative crystallization pathways, this study demonstrates that nucleation and crystal growth by cluster attachment and coalescence is clearly possible. In particular, the fundamental role of cluster aggregation, both in the formation of the nucleus and during crystal growth is unlikely to be limited to this single trajectory. Cluster aggregation is observed continuously, in the pre- and the postnucleation stages, during the entire length of the simulation, thus statistically significant. Likewise, the process of coalescence is observed at every stage along the crystallization pathway, independently of the particle size. The slow growth of the crystalline core at the expense of the amorphous phase is then expected to be a general observation, independent of the trajectory. Different runs may lead to polycrystals with different numbers of crystallites, or single crystals, depending on how the amorphous phase coalesces onto the crystalline core. Similarly, the onset of nucleation (time t_n; cf. Fig. 1) may change in different simulations, and is probably injection rate dependent. Nonetheless, these are all physically expected changes that do not affect the mechanism reported here or the discussion of the relaxation processes of the particle (cf. Sec. 3 and Fig. 3). The physical nature of the series of events leading up to the stabilization of the nucleus, in particular the role of hydration [Fig. 2b], may however be sensitive to the particular trajectory, so a systematic study would be required. This is a rare event typically described as random. The results reported here suggest the possibility that a specific, transient hydration process may stabilize small clusters that would otherwise dissolve away. Therefore, in aqueous solution, size and morphology, as well as the hydration context of the incipient nucleus, are all important factors for nucleation and nanocrystallization. The mechanism identified here may be common in other systems known to form clusters in unsaturated conditions, such as certain minerals and salts.^{4, 28} For example, the hypothesized pathway connecting the pre- and postnucleation periods during crystallization of calcium carbonate in Ref. 4 (cf. Fig. 4 therein) may indeed be a combination of cluster aggregation and coalescence, although in this case the prenucleation clusters are stable. Particle aggregation and coalescence may also be the common theme in both the classical and nonclassical pathways observed during crystallization of platinum nanoparticles in Ref. 12, possibly involving clusters of different size scales. The mechanism described here also shares common features with nucleation of solids from melts and liquids from vapors. For example, coalescence processes have been observed during nucleation of droplets in supersaturated gases²² and in nucleation and crystallization of solids from supercooled melts.¹⁹ The mechanism of nucleation and nanocrystal growth identified here bares a closer resemblance to the collision–coalescence mechanism proposed for nanocrystal growth in aerosols.³⁸