Calibrated Measures for Breast Density Estimation

Abstract

Rationale and Objectives

Breast density is a significant breast cancer risk factor measured from mammograms. Evidence suggests that the spatial variation in mammograms may also be associated with risk. We investigated the variation in calibrated mammograms as a breast cancer risk factor and explored its relationship with other measures of breast density using full field digital mammography (FFDM).

Materials and Methods

A matched case-control analysis was used to assess a spatial variation breast density measure in calibrated FFDM images, normalized for the image acquisition technique variation. Three measures of breast density were compared between cases and controls: (a) the calibrated average measure, (b) the calibrated variation measure, and (c) the standard percentage of breast density (PD) measure derived from operator-assisted labeling. Linear correlation and statistical relationships between these three breast density measures were also investigated.

Results

Risk estimates associated with the lowest to highest quartiles for the calibrated variation measure were greater in magnitude [odds ratios: 1.0 (ref.), 3.5, 6.3, and 11.3] than the corresponding risk estimates for quartiles of the standard PD measure [odds ratios: 1.0 (ref.), 2.3, 5.6, and 6.5] and the calibrated average measure [odds ratios: 1.0 (ref.), 2.4, 2.3, and 4.4]. The three breast density measures were highly correlated, showed an inverse relationship with breast area, and related by a mixed distribution relationship.

Conclusion

The three measures of breast density capture different attributes of the same data field. These preliminary findings indicate the variation measure is a viable automated method for assessing breast density. Insights gained by this work may be used to develop a standard for measuring breast density.

1. Introduction

Breast density measured from mammograms is a significant breast cancer risk factor (1–4). The association between breast density and breast cancer has been explored for many years, spawned by the pioneering work of Wolfe (5, 6). The earlier work in breast density used an observational four/five category rating of mammograms based on patterns of increasing risk developed by Wolfe. These earlier pattern measures of risk were virtually supplanted by the percentage of breast density (PD) measure developed by these researchers (7, 8). More recently, the pattern analysis has gained attention using a different approach in comparison with the earlier observational methods. Rather than investigating the raw data directly, mammographic patterns (or projected breast structure) have been investigated with various textural related measures. For the most part, these are summary measures that include fractal analysis, features generated from applying various filtering methods, and co-occurrence features, as both investigated and reviewed by these researchers (9). Some of these measures show associations with breast cancer similar to that of the standard PD measure.

There are various methods used to assess breast density as previously reviewed (10). The operator-assisted PD measure has demonstrated repeatedly to correlate well with breast cancer without considering the x-ray imaging acquisition influences (2). Another approach involves calibrating for the inter-image acquisition technique variation (11–15) to produce normalized data representations. There is little published work showing the efficacy of calibrating mammograms for breast cancer risk assessments using breast cancer status as the endpoint comparison. Some work indicates that calibration measures do not produce stronger breast cancer associations than that of the standard operator-assisted PD measure (16, 17). Other work indicates calibration may be useful for describing the information captured by the PD measure and for automating its measurement (18). If calibration can be optimized to improve the precision with which breast density is measured, a more accurate estimate of the magnitude of association between breast density and breast cancer may be obtained. It may be too early to assess whether these methods are viable because calibration represents a newer paradigm in breast density analysis that has not been studied in great depth.

We investigated the spatial variation in mammograms that were calibrated to account for the x-ray acquisition technique differences using full field digital mammography (FFDM). The calibration method was developed previously (12, 19–22). The calibration adjusts for variations in the target/filter combination, x-ray tube voltage, radiation exposure, and compressed breast thickness to produce a normalized pixel value representation referred to as percent glandular (PG) that is equivalent to a normalized effective x-ray attenuation coefficient representation spanning this pixel value range (0–100). The calibration can be applied at the pixel or local level, which supports analyzing the calibrated pixel distribution characteristics within a given image.

2. Materials and Methods

To meet our study objectives, we performed a matched case-control study. These three breast density measures and their association with breast cancer were compared: (a) the average of the calibrated mammograms [the PG measure], (b) the standard deviation of the calibrated mammograms [the PG_sd variation measure], and (c) the standard PD measure derived from the raw data (no calibration) using an operator-assisted labeling approach. We also investigated the measurement correlation with (projected) breast area and the inter-measure correlation. Breast area was used as a surrogate for breast size. The empirical probability distributions for the calibrated fibroglandular (abbreviated as glandular hereafter) and adipose tissue components were constructed. These component distributions were used to develop a statistical relationship between the three measures of breast density using a mixed distribution model.

2.1 Study population

A description of the study population is provided. All study images were acquired with one FFDM system. Controls were individually matched on age, hormone replacement therapy (HRT), and screening history to control for possible confounding influences. Breast cancer cases (n=123) were identified from the pool of women attending the breast clinics at the H. Lee Moffitt Cancer Center. To be included as cases in the study, women had to have been diagnosed with a first-time unilateral breast cancer (September 2007–July 2010). For the purpose of matching controls to cancer cases, three groups of cases were considered based on their screening history. Group-1 was comprised of women that screened normal within 30 months prior to their breast cancer diagnosis (n₁ = 107). Group-2 was comprised of women who had a history of normal screening that fell outside of the group-1 parameters, such as a woman who had a screening in 2007 but not again until 2010 at which time she was diagnosed with cancer (n₂ = 12). Group-3 was comprised of women who were just beginning screening and were diagnosed at their baseline mammogram (n₃ = 4). Case data and images were either located by retrospective records review (n = 40) for those women with images archived on the study FFDM unit or recruited, consented, and imaged for the study (n = 83). The recruited case patients were those women found to have breast cancer at screening clinics in the surrounding area that were referred to the Moffitt Center for diagnostics or patients that were found to have breast cancer at the Moffitt Center that did not have mammograms archived on the study FFDM unit. Recruited case participants were given a standard screening type mammogram with the study FFDM unit before their treatment commenced. Cancer status was histologically verified for all cancer cases. Height, weight, and HRT usage were abstracted from patient records.

Controls (n=123) were identified from the pool of women undergoing breast cancer screening mammography at the H. Lee Moffitt Cancer Center with the study FFDM unit. Controls were age matched (±2 years), HRT usage/duration matched, and screening history matched with the cancer cases using the three screening categories discussed above. For HRT matching, non-users were defined as those women who never used HRT as well as those that stopped using HRT two years or more prior to when their study mammograms were acquired. For current users, HRT usage duration (± 1 year) was used as a control matching variable. All control data and images were located retrospectively by records review over the same timeframe as the cases and restricted to women with screening mammograms available on the study FFDM unit. These archived mammograms were used as study images. Height, weight, and HRT usage were abstracted from patient records.

In this report we used two statistically similar datasets derived from the same patients for the various explorations. We refer to these as the cancer side and non-cancer side datasets. In the cancer side dataset, the cancerous breast of a given case was matched with the ipsilateral breast of the control. In the non-cancer side dataset, the non-cancerous breast of a given case was matched with the ipsilateral breast of the control. The combined dataset consisting of both the cancer side and non-cancer side datasets is referred to as the expanded dataset below. The expanded dataset was used for the correlation and distribution modeling investigations. The study protocol and informed consent process were approved by the local Institutional Review Board (IRB). This protocol is reviewed annually.

2.2 Imaging system

One General Electric Senographe 2000D FFDM system was used for this work. This mammography unit is used for routine breast cancer screening at this facility. This system has a 100 μm digital spatial resolution. A more detailed description of the detector specifics and the system can be found elsewhere (23, 24). Craniocaudal (CC) views were used in this analysis to reduce chest muscle interference. The system produces both raw data and processed data for clinical display use. Raw data was used in the analyses (not processed data for clinical viewing). The system processed images (clinical display images) were used as raw image surrogates to provide display illustration examples. The raw image data is not useful for display purposes without considerable manipulation.

2.3 Calibrated breast density measures

We applied the PG calibration automatically at a lower resolution by averaging over 10×10 pixel regions to reduce unwanted variation. The PG and PG_sd measures were determined by calculating the average and standard deviation of the calibrated pixel values within the breast area (defined below) for each image. Related work showed that eroding the breast area produces an image coincident with where the breast was in contact with the compression paddle (21). The breast area was first segmented from the background automatically by setting all pixels within the breast area =1 and setting all other pixels to zero. A radial coordinate system origin was positioned at the side of the image (chest wall position- left side in a left CC view) at the vertical direction (parallel to the chest wall) centroid position estimated from the segmented binary image. The breast area was then eroded by 25% of the distance measured from the radial coordinate system origin to the breast perimeter along a given radial direction. The calibration requires an accurate spatial assessment of the compressed breast thickness and therefore does not apply in the region where the breast is not in contact with the compression paddle because the thickness is unknown in this region. The erosion operation produces the portion of the image that approximates the region where the compressed breast thickness is defined and known. Figure 1 (top) shows three raw image surrogates. The corresponding eroded segmented images are shown in the middle row of Fig. 1. Both the average PG and PG_sd measures were calculated from the region in the calibrated mammograms corresponding to eroded area. The respective calibrated (eroded) image examples are shown in the bottom row of Fig. 1

Figure 1.

Image examples. From left to right, the top row shows three processed images created by the study FFDM unit used as raw image surrogates for display purposes only. The middle row from left to right shows the corresponding segmented and then eroded breast image areas. The bottom row shows the corresponding percent glandular (PG) calibrated images. As in film mammograms, larger pixel values imply greater x-ray attenuation and greater breast density. For the bottom row from left to right, the measured (PG, PG_sd ) values for each image were: (14.3, 5.8), (27.5, 5.4), and (14.9, 5.1), respectively.

2.4 Operator-assisted breast density measurements

The standard PD measurements were generated with the Cumulus3 (CM) software (University of Toronto) using the batch file procedure operating on the raw (non-processed images) FFDM images. The dataset consisting of all cases-control images (left and right CC view images) were first de-identified and randomized. The CM operator was blinded to the case-control status and original image identifiers. To avoid operator fatigue, the PD labeling was performed in multiple reading sessions (490 images were labeled). Hereafter, we use PD measure to refer to the standard breast density measurement derived from the CM labeling.

2.5 Statistical analysis

Conditional logistic regression was used to assess the association between the three measures of breast density and the case-control status. A standard quartile analysis was used for the odds ratio (OR) comparisons, where the control breast density distribution was used to determine the cutoff value for each measure. The first quartile of breast density for each measure served as the reference group for the second-fourth quartiles. The quartile analysis also provided a means for comparing the inter-measure OR distributions. We adjusted for body mass index (BMI) measured in kg/m² and breast area (pixel units) in the analyses as continuous variables. The area under the receiver operator characteristic curve (Az) metric was also used for predictive capability comparisons. This analysis was performed with the SAS software package (SAS Institute Inc., NC).

Linear regression analysis was used to investigate the inter-breast density measurement association and their relationship with the projected breast area. All relationships were fitted to the y=mx+b standard form. The full projected breast area (un-eroded breast area) was used in the analysis. This regression analysis was stratified by case-control group for comparisons of the calibrated measures using the expanded dataset.

2.6 Breast density statistical model

To develop a model that explains the relationships between the three measures of breast density, the empirical probability distributions (estimates) for the combined case-control glandular and adipose tissue components were constructed and investigated (expanded dataset). These two components were used to formulate a mixed distribution that connects the standard PD, PG and PG_sd breast density measures. It was shown previously (18) that a PD-like measure (PD_c) of breast density can be generated from the calibrated PG representation (eroded) images automatically by first applying a data transform. We let pg(x, y) = PG(x, y) /100, where PG(x, y) is the calibrated image pixel value located at the (x, y) spatial coordinates. We note, the pg(x,y) pixel values are constrained to this range (0,1). The normalized attenuated x-ray exposure representation image is then defined as

$$\text{A}(\text{x},\text{y})=\text{k}(1.0-exp[-\text{pg}(\text{x},\text{y}){\text{t}}_{\text{s}}]),$$ (1)

where t_s is the system compressed breast thickness readout quantity expressed in cm for each image, and k =5000 is an arbitrary constant. Using A_c = 3200 as a static threshold, pixel values within the eroded breast region meeting this condition A(x,y) ≥ A_c were counted as glandular pixels (the d_n count), whereas pixel values meeting this condition A(x,y) < A_c were counted as adipose regions (the a_n count). For a given image, the PD-type measure is given by ${\text{PD}}_{\text{c}}=\frac{{\text{d}}_{\text{n}}}{\text{N}}\times 100\%$ with N = d_n + a_n. We have shown previously (18) that the PD_c with breast cancer is similar to that of the PD measure when analyzing the same dataset. For this work, we generated the PD_c labeled images as an intermediate step to construct the component distributions. These binary labeled PD_c images were then used as overlays for their respective PG representation images. For a given pair of PD_c and PG images, regions (pixel values) in the PG image corresponding to the regions in the PD_c image labeled as d_n were assembled into an array. This process was carried out for every PG and PD_c image pair in the extended dataset resulting in one array containing all PG pixel values corresponding to the d_n labeling. The same process was carried out for the a_n labeled regions resulting in another array. Normalizing each histogram of these arrays separately to unity gives an approximation for the respective ensemble probability distribution for each tissue type. These two component distributions were used to formulate a mixed distribution relationship for each mammogram. For a two component mixture, the mixed distribution for a given image can be expressed as

$$\text{p}(\text{z})=\text{c}\times {\text{p}}_1(\text{z})+(1-\text{c})\times {\text{p}}_2(\text{z}),$$ (2)

where p_i represents the component distributions (derived from the two arrays referenced above) with i =1 for the glandular component and i = 2 for the adipose component, c is the two-component mixing proportion, and z = PG (calibrated pixel values). For a given image, the mean can be expressed as

$$\text{m}=\text{c}\times {\text{m}}_1+(1-\text{c})\times {\text{m}}_2,$$ (3)

where m₁ and m₂ are the respective means determined from the component distributions. Likewise, the variance for a given image can be expressed as

$${\sigma }^2=\text{c}\times ({\sigma }_1^2+{\text{m}}_1^2)+(1-\text{c})\times ({\sigma }_2^2+{\text{m}}_2^2)-{\text{m}}^2,$$ (4)

where σ_i represents the respective standard deviations calculated from the component distributions, and m was defined in Eq. (3). Equations (3–4) redefine the PG and PG_sd breast density measures respectively and show the theoretical connection between the three breast density measures. The relationship with PD follows from Eq. (3). For a given image, c × 100% is an approximation of the PD measure. The mixing proportion, c, theoretically accounts for the fraction of pixels within the breast area that would be labeled as dense breast tissue by the standard PD measure. We calculated (m₁, m₂, σ₁, σ₂) from the respective component distributions. These quantities were the used with Eqs. (3–4) to estimate the mixing coefficient breast density measure, c, for each image using the respective PG and PG_sd measures as substitutes for m and σ. A brief analysis of the PD_c and the mixing coefficient measures of breast density was provided to demonstrate the validity of (a) the methods used to generate the component distributions, and (b) the Eq. (4) approximation.

3. Results

3.1 Breast density measurement comparisons

Demographic and risk factor distributions are provided for the breast cancer cases and controls in Table 1. Associations between the three breast density measurements (PD, PG_sd, and PG) and breast cancer are summarized in Table 2 (left-side) for the cancer side dataset. In this table, the OR associations and Az quantities were adjusted for BMI and the simultaneous adjustments for both BMI and breast area (i.e., the mammogram-based two-dimensional measure of breast size). For all three measures, the ORs and Az quantities increased (increased magnitude of association) when controlling for area. Both the PD and PG_sd measures showed significant magnitude of association with breast cancer for all non-referent quartiles (i.e., the left side OR confidence intervals are greater than unity). In contrast, the confidence intervals for the PG measure included unity for most quartiles. The PG_sd measure showed greater magnitude of association with breast cancer when comparing its quartile ORs with the other measures, and the PD measure showed greater association than the PG measure. The PG_sd and PD measures produced similar Az values that were larger than that produced by the PG measure.

Table 1.

Patient Characteristics. The number (n) of patients and percentages are provided for the breast cancer cases and controls stratified by hormone replacement therapy (HRT) usage and duration by years (yrs) of usage. The parenthetical entries cites current HRT users as defined in section 2.1 The mean body mass index (BMI), age, and breast area are given for each group. The associated standard deviations (SDs) for the BMI, age, and breast area distributions are also provided.

Characteristic	Case, n	Case mean / SD or %	Control, n	Control mean / SD or %
Age	123	59.4 / 9.7	123	59.2 / 9.6
HRT
Never-used	62	50.4%	68	55.3%
1–5 yrs	24(4)	19.5%	21(4)	17.1%
6–10 yrs	15(5)	12.2%	15(5)	12.1%
11–15 yrs	9(5)	7.3%	7(4)	5.7%
> 15 yrs	13(7)	10.6%	12(8)	9.8%
BMI (kg/m2)	123	27.1 / 5.1	123	25.7 / 4.7
Breast area (pixel)	123	1548303 / 69476	123	1310576 / 443321

Table 2.

Breast density measurements in association with breast cancer. This shows the association with breast cancer for the percentage of breast density (PD), the average calibrated (PG), and the calibrated standard deviation (PG_sd ) measures of breast density. The odds ratios (OR), OR confidence intervals (CI), and area under the receiver operator characteristic curve (Az) values are shown. The findings for the cancer-sided (left column) and non-cancer side (right column) are shown separately. *One case image and one unrelated control image were not usable; therefore two case-control pairs were discarded. All measures were either adjusted for body mass index (BMI) measured in kg/m² and for BMI and area (pixel units), simultaneously.

Breast density measure	Cancer Side OR (95% CI)	Case	Az	*Non-cancer Side OR (95% CI)	Case	Az
PD
BMI adjusted			0.623			0.647
1	1.00 (Ref.)	23		1.00 (Ref.)	17
2	2.16 (0.91 – 5.15)	35		2.74 (1.18 – 6.37)	35
3	3.25 (1.41 – 7.53)	30		3.12 (1.20 – 8.08)	33
4	2.85 (1.18 – 6.91)	35		4.88 (1.66 – 14.36)	36
BMI, area adjusted			0.693			0.676
1	1.00 (Ref.)	23		1.00 (Ref.)	17
2	2.33 (0.93 – 5.84)	35		2.39 (0.99 – 5.73)	35
3	5.55 (2.12 – 14.49)	30		3.65 (1.35 – 9.87)	33
4	6.52 (2.19 – 19.39)	35		6.48 (2.09 – 20.09)	36
PGsd
BMI adjusted			0.616			0.651
1	1.00 (Ref.)	18		1.00 (Ref.)	19
2	1.97 (0.93 – 4.25)	33		3.41 (1.41 – 8.24)	38
3	1.73 (0.76 – 3.94)	29		2.56 (1.02 – 6.43)	29
4	3.03 (1.30 – 7.06)	43		4.78 (1.68 – 13.59)	35
BMI, area adjusted			0.696			0.691
1	1.00 (Ref.)	18		1.00 (Ref.)	19
2	3.48 (1.40 – 8.66)	33		4.75 (1.84 – 12.26)	38
3	6.25 (2.04 – 19.16)	29		4.32 (1.56 – 11.97)	29
4	11.25 (3.54 – 35.69)	43		8.25 (2.62 – 25.92)	35
PG
BMI adjusted			0.589
1	1.00 (Ref.)	23
2	1.99 (0.89 – 4.44)	35
3	1.60 (0.71 – 3.64)	31
4	2.22 (0.93 – 5.29)	34
BMI, area adjusted			0.661
1	1.00 (Ref.)	23
2	2.35 (0.99 – 5.59)	35
3	2.30 (0.94 – 5.61)	31
4	4.42 (1.62 – 12.08)	34

To assess whether the presence of breast abnormalities in the cancer side breast was responsible for the positive associations between breast cancer and the PG_sd measure, the associations were investigated using the non-cancer side dataset. For comparison purposes, the non-cancer side analysis was performed for the PD measure for internal control comparisons. The findings are shown in Table 2 (right-side). The OR associations and Az values decreased for both measures in comparison with the cancer-side dataset, but the inter-measure relationships remained similar. Because the breast area for the cancer cases was larger than that of the controls (Table 1), a subgroup analysis was performed by ordering the cancer-side case samples by ascending breast area. Starting with the case-sample with the largest breast area, each case and associated control were removed from the 123 pairs one pair at a time until the case and control group breast areas were statistically similar. A paired t-test was used to compare the remaining case-control pair breast areas after discarding a given pair. When the set was reduced to between 100–110 matched pairs, the t-test began to lose significance. Our choice of 100 matched pairs (P=0.87) was arbitrary (104 case/control pairs would work as well). When these case-control pairs (n = 23) were excluded from the analysis, similar results were observed (data not shown).

3. 2 Correlation Comparisons

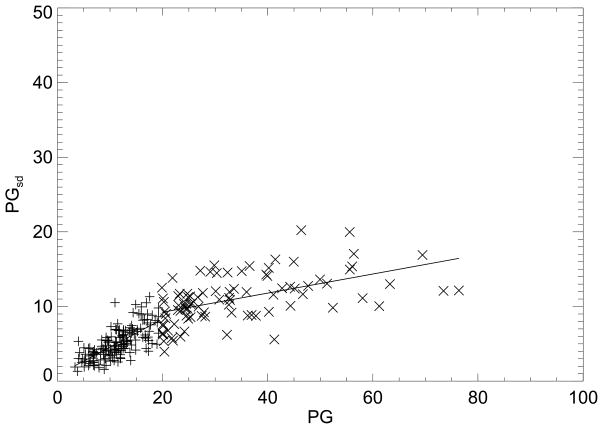
The (PG, PG_sd ) regression plot for the cancer cases is shown in Fig. 2. Because of the apparent nonlinear trend, the analysis was divided into (PG, PG_sd) pairs that were either (a) equal to, or above, the case PG distribution mean, or (b) below this mean. A similar analysis was performed for the control (PG, PG_sd) pairs using the control PG measure distribution mean as the breakpoint. The regression plot for the controls is not shown due to close similarities with Fig. 2. The regression analysis is summarized in Table 3. Comparisons of the regression parameters and linear correlation coefficients indicate the cases and controls exhibit similar behavior. The overall correlation without considering the break also showed that the cases and controls behave similarly (last column Table 3). The correlation between the PD and PG measures was R = 0.76, and the correlation between PD and PG_sd measures was R = 0.78, as determined with the extended dataset (not shown).

Figure 2.

Percent glandular breast density measure and percent glandular standard deviation breast density measure regression analysis. This shows the percent glandular (PG) and PG standard deviation (PG_sd) ordered pairs and fitted lines (solid) for the case samples (Table 3). The regression analysis was split into two parts for above (×) and below (+) the case PG distribution mean.

Table 3.

Regression parameters for cases and controls. This shows the two-part regression analysis summary fit to the form y=mx+b. The x-y pairs are shown in the first column. PG is the calibrated average measure, PG_sd is the PG standard deviation measure, and area is the projected (not eroded) breast area. The distribution mean value of × was used as the breakpoint for each pair. The linear correlation coefficient (R) is shown for each line segment and the combination (Comb) correlation is cited in the last column, derived without the breakpoint. The PG distribution mean and standard deviation (mean, SD) for the cases and controls were: (19.8, 13.9) and (18.5, 13.7), respectively. The breast area summaries are provided Table 1.

x-y		below the mean			above the mean			Comb
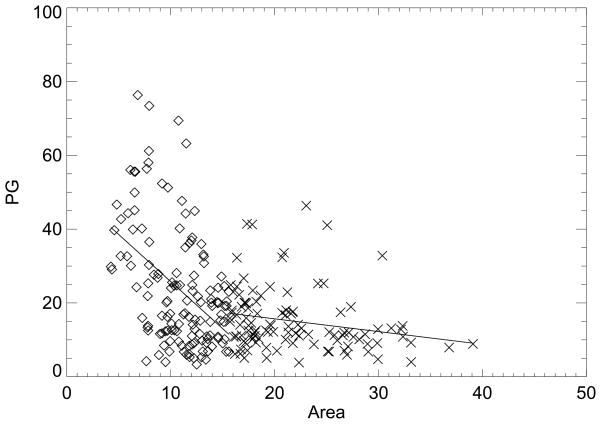
		m	b	R	m	b	R	R
PG - PGsd	Case	0.37±0.03	0.81	0.71	0.13±0.02	6.68	0.53	0.81
	Control	0.37±0.03	0.72	0.69	0.11±0.02	6.37	0.48	0.77
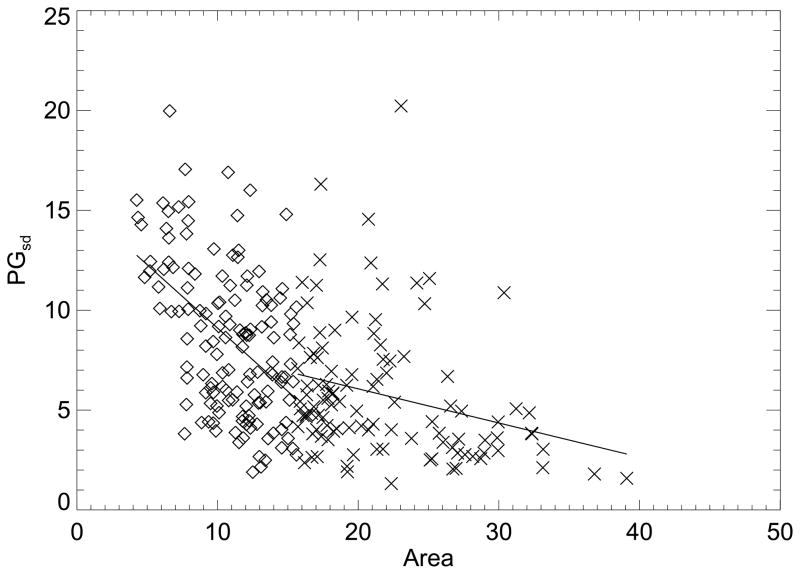
area - PGsd	Case	−0.63±0.10	15.4	−0.48	−0.17±0.06	9.48	−0.27	−0.48
	Control	−0.78±0.12	15.6	−0.48	−0.29±0.08	9.83	−0.34	−0.56
area - PG	Case	−2.55±0.43	51.3	−0.46	−0.35±0.15	22.6	−0.22	−0.41
	Control	−2.61±0.54	44.8	−0.35	−0.95±0.28	29.8	−0.30	−0.43

The correlation between the breast density measurements and breast area was investigated Figure 3 shows the (area, PG) regression plot for the cancer cases. This analysis was also divided into (area, PG) pairs using the same format as above that were (a) either equal to, or above, the case breast area distribution mean, or (b) below this mean (Table 1). Figure 4 shows the (area, PG_sd) regression plot using the same mean area break point. The two measures show similar correlation with area. A similar analysis was performed for the control PG and PG_sd measures with breast area using the control area distribution mean as the break point (not shown). The breast density measurement and breast area regression analysis findings are summarized in Table 3. The correlations and relationships were stronger and more similar across case-control group for the below mean-area groups. Using the extended dataset with no break point, the (area, PD) correlation was R = −0.39. The degree of the negative correlation between the breast density measures and breast area suggests that area should be controlled for in the association analysis as shown in Table 2.

Figure 3.

Breast area and percent glandular breast density measure regression analysis. This shows breast area (area) expressed in 10⁵ pixel units and percent glandular measure (PG) ordered pairs and fitted lines (solid) for the case samples (Table 3). The regression analysis was split into two parts for above (×) and below (diamond) the case breast area distribution mean.

Figure 4.

Breast area and percent glandular standard deviation breast density measure regression analysis. This shows the breast area (area) expressed in 10⁵ pixel units and the percent glandular standard deviation measure (PG_sd ) ordered pairs and fitted lines (solid) for the case samples (Table 3). The regression analysis was split into two parts for above (×) and below (diamond) the case breast area distribution mean.

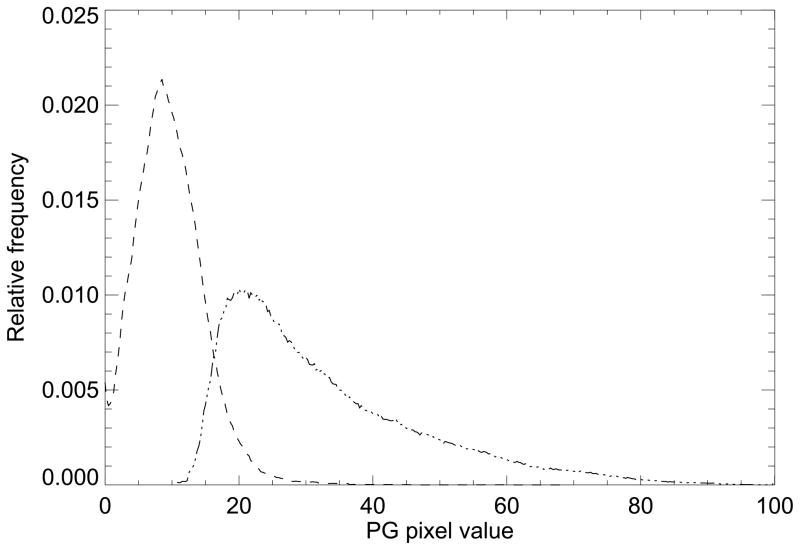
3.3 Statistical model evaluation

To explain the correlation and relationships between three breast density measures, the empirical distributions were derived from the expanded dataset for the adipose and glandular tissue types, which are shown in Fig. 5. These represent a summary of the entire dataset and they show that the total collection of PG representation images can be decomposed into two single-mode distributions. These were constructed by first generating the PD_c labeled images. For the PD_c measure, Az = 0.69 (for the cancer-side dataset adjusted for BMI and breast area), which indicates the validity of the method used to form these component distributions (Fig. 5). These distributions were used to evaluate the Eq. (4) expression relating the three breast density measures by estimating their (the distributions) respective means and standard deviations giving: (m₁, m₂) = (32.3, 9.7) and (σ₁, σ₂) = (14.6, 4.9). The mixture coefficient c [see \Eq. (3) and Eq. (4)] was derived from each image as the breast density measure (approximation for PD) to assess the Eq. (4) approximation. The c measure quartile associations with breast cancer (cancer side dataset) and Az were similar to that of PD (Table 2) when adjusting for breast area and BMI [odds ratios: 1.0 (ref.), 2.6, 3.5, and 5.5, and Az = 0.67]. Although Eq. (4) shows the connection between the various measures, understanding the positive correlation between m and σ, theoretically, requires manipulation. We generated c_s (simulated c variable) over this range (0,1), generated Eqs. (3–4) as functions of c_s using the density quantities (m₁, m₂, σ₁, σ₂), and found the theoretical linear correlation between PG and PG_sd [i.e., correlation between Eq. (3) and square root of Eq. (4)], which gave R_T = 0.79. This theoretical correlation is in agreement with the measured correlation between the PG and PG_sd shown in Table 3 (last column). As Eq. (4) shows, PG_sd is a positive valued function of increasing c but it is not monotonic.

Figure 5.

Glandular and adipose percent glandular ensemble probability distribution functions. This shows the adipose (dash) and fibro-glandular (dot) empirical ensemble probability distribution function approximations derived from the expanded dataset. These are the component distributions used for the mixed distribution model.

4. Discussion

The analysis resulted in three important findings. First, the PG_sd measure showed greater magnitude of association with breast cancer than the other measures in a side-by-side comparison. In contrast, the calibrated PG measure was the least associated breast density measure, which agrees with other calibration investigations (16, 17). Secondly, the work provides evidence for the correlation between the measures. Connecting the image variation (PG_sd measure) with the normalized PG representation, PG measure, and the PD measure with the mixed distribution relationship is an important contribution to breast density research. This relationship shows that the three measures are characterizing different attributes of the same phenomenon and helps to explain the positive correlation between the measures. Previous work (18) showed that the calibrated PG measure can be used to explain the information captured by the PD measure. These earlier findings were reinforced by the mixed distribution formulism. There is also another condition that may contribute to the positive correlation. Although most likely non-parametric, these distributions (Fig. 5) individually exhibit skewed right tail behavior similar to that of Poisson, low-order central Chi-square, and more generally lower order gamma probability density functions for example. In these non-symmetric parametric densities, the mean and standard deviations are functions of the same parameters, implying they are related (often termed signal dependent noise). By hypothesis, our findings suggest that PD is an approximation for the PG_sd measure. These assertions will require further validation. Thirdly, the work showed that breast area may be a confounding factor for both calibrated measurements as well as for the PD measure.

The PG_sd measure magnitude of association is consistent with previous work that found low frequency Fourier features show association with breast cancer similar to that of PD (9). Because the mammograms have approximately a 1/f^β power spectrum (25, 26), the majority of the image pixel intensity variation is captured in the lower frequency portion of its Fourier power spectrum. Although we did not investigate the power spectrum of the calibrated FFDM images used in this report, the previous spectral analysis of similarly acquired FFDM images (26) holds in general for these calibrated images. For a given target/filter calibration and fixed x-ray tube voltage, the calibration mapping is linear; this linear mapping preserves the spectral functional form within a constant and scaling factor. Thus for a given calibrated image, the measured PG_sd quantity is heavily influenced by the low frequency portion of its power spectrum.

Both the choice of dataset and breast area influenced the findings. Previous work showed that choosing the cancer-side or non-cancer side breast was of little consequence in the association analyses for the PD measure (27). At this time, it is not clear if this relation holds for the PG_sd measure. We found that the PG_sd measure is more predictive in the cancer-side dataset in comparison with non-cancer-side dataset. However, the same relationship held for the PD measurements as well. Previous work showed that the left breast has a tendency to be larger than the right breast and this asymmetry is exaggerated in women with breast cancer (28), but these asymmetries do not explain the differences noted here in the case-control breast areas. The mammography type-unit used for this work was the first FDA approved FFDM unit in the US (24). This system has a smaller detector than newer FFDM systems and has a problem accommodating larger breasts in a single acquisition (24). In multiple-mammography unit facilities that have mixed detector sizes, x-ray technicians (as ascertained from technicians at this center) direct women with larger breasts (by observation) to units with larger detectors. All of the control image samples were derived from images acquired with this selection process for this FFDM unit under normal screening conditions. In contrast, a portion of our cancer cases was recruited and imaged without regard to this selection process indicating that their projected breast areas may be greater than those of the controls. The breast area distribution summaries (Table 1) show this holds. The findings for the reduced dataset indicated that this bias has negligible influences when controlled for it in the full dataset analysis. The findings indicate that controlling for breast area is as important as controlling for BMI when investigating measures of breast density. Evidence also indicates larger breasts tend to have less breast density as reviewed by these researchers (29), which agrees with the overall negative breast density measurement correlation with breast area relation found here.

There are several limitations with this study. The x-ray attenuation characteristics of the adipose breast tissue equivalent phantom (used for the calibration) composition deviates somewhat from that of adipose breast tissue, which introduces error in the mapped pixel values (18). We used the Eqs. (3–4) relationships to connect the various breast density measures, which are approximations. The theoretical PG measure expression [Eq. (3)] indicates that the maximum PG measure (average PG quantity calculated over the breast region) for a given image occurs when c = 1, which should not exceed the value of m₁. In practice, the measured values fell within this m₁ limit for approximately 87% of the case-control samples (expanded dataset) or 88% of the controls and 86% of the cases. These measured distribution quantities will vary according to the PD_c generation (changing the static threshold), which is also influenced by the adipose phantom artifact and its correction. Similarly, the extent of the erosion may also impact these quantities. The findings presented in this report will require further evaluation with larger datasets and different study populations. Nevertheless, these approximations assisted in decomposing a rather complicated problem into simpler elements.

Calibration may involve considerable initial effort to develop its infrastructure. Thus, a case must be made for its utility. Related work (16, 17) indicated calibrated measures did not produce associations with breast cancer beyond that of the PD measure. Even if calibration produced a measure with statistically equivalent breast cancer associations as the standard PD measure, it may have clinical utility given the efficiency gained from automation. The operator-assisted PD measure requires considerable effort to label large databases. We speculate that calibration may be the price paid for automated breast density measurements. Additionally, the calibration produces a normalized (effective x-ray attenuation coefficient) representation related to an intrinsic physical property of the breast that may provide some quantitative benefit. Without calibration, the relationships connecting the three measures of beast density would be difficult to discern. Insights gained from this work may be useful for developing a standardized quantitative measure of breast density, leading to a better understanding of the true magnitude of the association between breast density and breast cancer.