Automated Decision Tree Classification of Corneal Shape

Abstract

Purpose

The volume and complexity of data produced during videokeratography examinations present a challenge of interpretation. As a consequence, results are often analyzed qualitatively by subjective pattern recognition or reduced to comparisons of summary indices. We describe the application of decision tree induction, an automated machine learning classification method, to discriminate between normal and keratoconic corneal shapes in an objective and quantitative way. We then compared this method with other known classification methods.

Methods

The corneal surface was modeled with a seventh-order Zernike polynomial for 132 normal eyes of 92 subjects and 112 eyes of 71 subjects diagnosed with keratoconus. A decision tree classifier was induced using the C4.5 algorithm, and its classification performance was compared with the modified Rabinowitz–McDonnell index, Schwiegerling’s Z3 index (Z3), Keratoconus Prediction Index (KPI), KISA%, and Cone Location and Magnitude Index using recommended classification thresholds for each method. We also evaluated the area under the receiver operator characteristic (ROC) curve for each classification method.

Results

Our decision tree classifier performed equal to or better than the other classifiers tested: accuracy was 92% and the area under the ROC curve was 0.97. Our decision tree classifier reduced the information needed to distinguish between normal and keratoconus eyes using four of 36 Zernike polynomial coefficients. The four surface features selected as classification attributes by the decision tree method were inferior elevation, greater sagittal depth, oblique toricity, and trefoil.

Conclusions

Automated decision tree classification of corneal shape through Zernike polynomials is an accurate quantitative method of classification that is interpretable and can be generated from any instrument platform capable of raw elevation data output. This method of pattern classification is extendable to other classification problems.

Despite the development of sophisticated methods of mapping and visualizing corneal shape, quantitative analysis and interpretation of videokeratography data continues to be problematic for clinicians and researchers. This is primarily due to the difficulty in quantitative isolation of specific features, but also because there is disagreement among clinicians and researchers about the most meaningful features for classification and diagnosis.

Several numerical summaries of videokeratographic data exist to facilitate quantitative analysis. Most were developed for the purpose of keratoconus detection, are platform dependent, and permit only cross-sectional comparisons with respect to time.^1–12 As a result, interpretation of videokeratography data is often reduced to qualitative recognition of patterns from color coded displays of corneal curvature, or subjective comparisons of statistical indices that summarize isolated features.

Automated decision tree analysis is widely used in the fields of computer science and machine learning as a means of automating the discovery of useful features from large volumes of data for the purpose of classification. Decision tree analysis has been applied by others to medical diagnostic classification problems ranging from breast cancer detection to otoneurological disease.^13–15 This approach is especially useful where complex interactions between features are not amenable to traditional statistical modeling methods. The benefits of this automated analytical method are objective feature selection, insensitivity to noisy data, computational efficiency, and a hierarchical modeling of relevant features that are easy to interpret.¹⁶

In this study we apply automated decision tree analysis to the problem of videokeratography classification in keratoconus and compare this approach to other known methods of videokeratography classification.

Methods

In this retrospective study, we compared the classification performance of several videokeratography-based keratoconus detection methods computed for the same data set. Our sample consisted of eyes diagnosed with keratoconus and a reference group of normal eyes from patients prior to corneal refractive surgery. The study conformed to the Declaration of Helsinki and was approved by the biomedical institutional review board at The Ohio State University.

Patient Selection

All patients selected for this study were identified with Keratoconus in at least one eye by ICD-9 diagnosis codes between August 1998 and January 2000. Their diagnostic classification was confirmed by chart review, applying criteria established by the Collaborative Longitudinal Evaluation of Keratoconus (CLEK) study.¹⁷ The ocular findings that defined keratoconus include: (1) an irregular cornea determined by distorted keratometry mires, distortion of the retinoscopic or ophalmoscopic red reflex (or a combination of these); (2) at least one of the following biomicroscopic signs: Vogt’s striae, Fleischer’s ring of greater than 2 mm arc, or corneal scarring consistent with keratoconus. Both eyes of each patient were included in this sample.

A comparison group of normal patients were sequentially selected from all patients that were examined for the surgical correction of refractive error during the same time interval—August 1998 to January 2000. This comparison group included both eyes from patients that had myopia with or without astigmatism, had videokeratography examination data, and had no other documented ocular disease.

We excluded eyes from either patient group that did not have full videokeratography data over the region of study (central 7 mm) or cases where the videokeratography data contained obvious artifacts due to obstruction of the corneal surface by the eyelids. All other eligible cases were included.

Data Preprocessing

We exported videokeratography data from a single image consisting of raw elevation, angle and radial position coordinates from the Keratron corneal topographer (v3.49, Optikon 2000, Rome, Italy). Elevation data were distances referenced from the corneal vertex plane and were not residual deviations from a sphere. The data from each examination consisted of up to 6,912 individual points in a 3-dimensional polar coordinate gird. In addition to the elevation data we collected the axial curvature value associated with each individual point.

To model the corneal surface we computed a 7th order expansion of Zernike polynomials over the central 7 mm from the exported elevation data using methods described by Schwiegerling et al.¹⁸ We limited our area of analysis to the central 7 mm to insure complete data over the area of analysis for all eyes in this sample. We transformed the Zernike coefficients of all left eye maps to represent right eyes before combining the data for analysis. This was done by inverting the sign of specific Zernike coefficients using the following rules:

$$\begin{array}{l}\mathit{\text{for all}}{C}_{n,m}\mathit{\text{if}}n=\mathit{\text{even and m}}<0\to C_{n,m}=-(C_{n,m})\hfill \\ \mathit{\text{for all}}{C}_{n,m}\mathit{\text{if}}n=\mathit{\text{odd and m}}>0\to C_{n,m}=-(C_{n,m})\hfill \end{array}$$ [1]

where m = angular frequency and n = polynomial order according to Optical Society of America conventions.¹⁹

Although Zernike polynomials are frequently used to represent the magnitude of optical wavefront aberrations of the eye, it is important to note that these same polynomials were instead used to model the surface features of corneal shape in this study. We did not attempt to infer the impact of these surface features on the optical performance of the eye in this study.

Decision Tree Classification

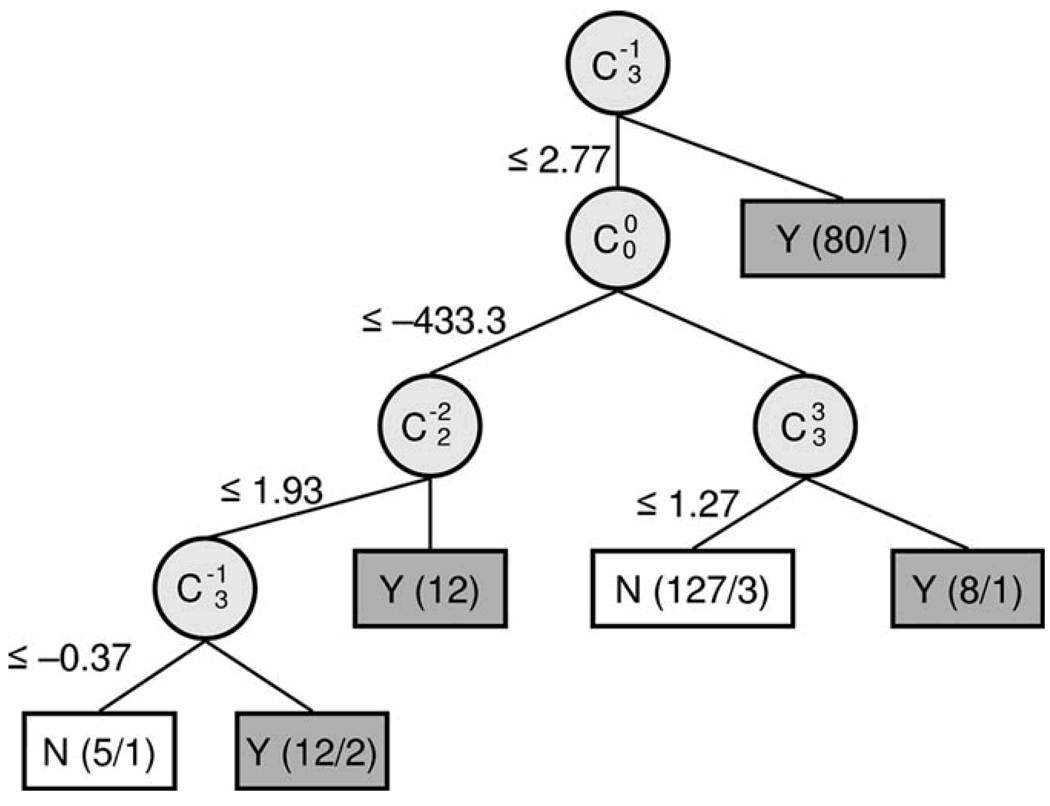
A decision tree is a collection of “if → then” conditional rules for assignment of class labels to instances of a data set. Decision trees consist of nodes that specify a particular attribute of the data, branches that represent a test of each attribute value, and leaves that correspond to the terminal decision of class assignment for an instance in the data set (Figure 1).

Figure 1.

Decision Tree Classification of Keratoconus. Decision Tree generated with C4.5, an automated induction algorithm. Classification attributes (circles) are labeled as double indexed Zernike polynomial coefficients using Optical Society of America conventions. The split criteria values label the branches of the decision tree in units of micrometers. Terminal nodes of the tree (boxes) are labeled with class assignments (Y = Keratoconus, N = Normal) and the number of records assigned to this class (correct / incorrect); total n = 244; Keratoconus n= 112; Normal = 132.

We used C4.5, an automated decision tree induction algorithm, to construct a classifier for our data set.^{20, 21} The data were structured as rows of records for each eye (records) and columns of Zernike coefficients (attributes). We selected Zernike polynomial coefficients to represent corneal surface features and used the magnitude of these coefficients as a basis to discriminate between normal and keratoconus records in our record set. A benefit of classification by decision tree induction is automated selection of the Zernike coefficients that best separates the given records as well as discovery of the coefficient magnitude necessary for optimal class discrimination. Each record of the data set was labeled with a known class assignment from the chart review.

We have previously described our decision tree induction methods and results from optimization experiments and provide additional details regarding the logic and computational methods in the appendix.²² In summary, we used WEKA (version 3.4),^* a Java based implementation of C4.5 release 8.²³ The algorithm was set to overfit the data generating trees of maximal complexity with pruning criteria set to a minimum of four records per leaf.²³ Our objective was to develop a decision tree classifier from training data that would perform well on unseen test data and to accurately estimate the true error rate for this classifier on new data. To accomplish this, we used a technique known as 10-fold cross-validation–a method that makes more efficient use of the available data than traditional hold-out methods and provides more accurate estimates of the true error rate.²⁴ We explain the details of this validation method below.

Other Videokeratography Classification Methods

Using the same videokeratography data, we computed five additional keratoconus classification indices including: Modified Rabinowitz–McDonnell Index (RM),³ KISA%,¹⁰ Keratoconus Prediction Index (KPI),⁶ Z3,²⁵ and Cone Location and Magnitude Index (CLMI).²⁶ These indices were calculated from published formulas and computed from the appropriate curvature or elevation videokeratography data.

Modified Rabinowitz–McDonnell Index

This index is calculated from a combination of the simulated keratometry value (SimK) > 47.2 D and the inferior–superior dioptric asymmetry value (ISvalue) > 1.4 D.^{3, 10} These indices were written for analysis of data from the TMS videokeratography instrument (CDB Ophthalmic, Phoenix, AZ). We adapted these published algorithms to analyze data from the Keratron videokeratography system.

KISA%

The KISA% index is derived from summary indices there were originally written to analyze data from the TMS videokeratography system. However, one of the benefits of this index is that it can be computed for data from other videokeratography systems and therefore has greater platform independence. The KISA% index is calculated from a combination of four videokeratography summary values: Kvalue,²⁷ which is an average paracentral corneal power, ISvalue,²⁷ a measure of inferior-superior asymmetry in paracentral corneal powers, corneal toricity (Cyl) and SRAX,^{10, 28} a measure related to non-orthogonal corneal toricity. This index is calculated from the following formula:

$$\mathit{\text{KISA}}\%=\frac{(\mathit{\text{Kvalue}}\times \mathit{\text{IS value}}\times \mathit{\text{Cyl}}\times \mathit{\text{SRAX}}\times 100)}{300}$$ [4]

The published threshold value for keratoconus classification is KISA% > 100.

KPI

The keratoconus prediction index (KPI) is derived from eight other videokeratography summary indices as described by Maeda et al.⁶ The keratoconus prediction index is the primary determinant of keratoconus pattern classification using the Keratoconus Classification Index. The KCI is an expert system that combines KPI along with four other indices (simK2, OSI, DSI, and CSI) to further categorize corneal topography as either non-keratoconus patterns, central steepening keratoconus, or peripheral steepening keratoconus. ⁶ Since each of these summary indices was originally developed for analysis of data from the TMS videokeratography system, we again adapted published algorithms to analyze data from the Keratron videokeratography system. The published threshold criterion for identification of keratoconus-like patterns using this classifier is KPI ≥ 0.23.

Z3

The Z3 index was originally derived from the central 6 mm diameter of TMS videokeratography elevation data by Schwiegerling et al.²⁵ This index is computed from the net third order Zernike polynomial coefficient magnitude defined as:

$$C_{n,\pm m}=\sqrt{{(C_{n,m})}^2+{(C_{n,-m})}^2}$$ [5]

These net coefficient values are then used to compute the distance of each record from the mean value of normal records. This Z3 distance metric is defined as:

$$Z3=\sqrt{{(C_{3,\pm 1}-0.00129)}^2+{(C_{3,\pm 3}-0.00058)}^2}$$ [6]

Keratoconus classification is assigned to records more than three standard deviations above the mean of normal records (Z3 > 0.00233).

CLMI

The Cone Location and Magnitude Index is calculated from axial curvature values. Details of the calculation of this index are described elsewhere.²⁶ In summary, this index is computed in four steps. First, C1 is located as the circular (1 mm radius) region of greatest area corrected axial curvature within the central 3 mm radius region. Second, M1 is computed as difference between the area-corrected power in C1 and the area corrected power in the entire central 3 mm radius region that is not C1. Third, M2 is calculated in the same manner for the 1 mm radius region located 180° opposite C1. Finally, if M1 is within the central 1.25 mm radius region, then CLMI = M1, or else CLMI = M1 – M2. Mahmoud et al. previously reported that a CLMI index of 3.0 or greater was positively associated with keratoconus.²⁶

Data Analysis

The true error of the decision tree classifier was estimated by stratified 10-fold cross validation performed in the following manner. The eyes of each diagnostic category (normal and keratoconus) were first stratified to insure that there would be a proportional representation of eyes from each category in any subgroups formed. This was accomplished by randomly dividing the eyes of each category (normal or keratoconus) into 10 approximately equal sized partitions (20 total partitions). One partition from each patient group was then combined to form a total of 10 final partitions.

In cross-validation, 9 of the 10 stratified partitions served as training data to generate a decision tree classifier. The remaining partition was held aside as the test set to estimate the error rate for the decision tree. Next, one of the previous training partitions was substituted for the test data. The previous test partition was then rotated into the training data. This substitution and rotation was repeated until each of the 10 partitions had served as the test data. In each iteration, the classifier is trained and subsequently tested on non-overlapping partitions of the data. Accuracy for the induced decision tree classifier was defined as the overall number of incorrect classifications for all 10 iterations divided by the total number of cases in the dataset. This procedure makes efficient use of the available data and provides stable and honest estimates of the true error rate since the induced classifier is tested on unseen data in each iteration.^{16, 24}

Three common metrics derived from the 2 × 2 classification table were used to evaluate the quality of each classifier: sensitivity, specificity, and accuracy (Table 1). In the context of this study, sensitivity is defined as the proportion of keratoconic eyes correctly identified in the sample. Specificity is the proportion of normal eyes correctly identified in the sample. Accuracy is the proportion of total correct classifications of both classes out of all eyes in the sample. In this study, we calculated the sensitivity, specificity and accuracy of each classifier using the published recommended thresholds for each classification method.

TABLE 1.

The confusion matrix

	Predicted Class
True class	Positive	Negative
Positive	A	B
Negative	C	D

Accuracy = (A + D)/(A + B + C+ D).

Sensitivity = A/(A +B).

Specificity = D/(D + C).

The accuracy, sensitivity and specificity of any classification method depend in large part upon the threshold criteria for categorizing each record. A useful way to compare classification methods that is criterion-free, is to show the tradeoff between sensitivity and specificity over the continuum of all possible classification threshold criteria. This is accomplished graphically by plotting sensitivity as a function of (1 – specificity). This plot is known as the Receiver Operating Characteristic Plot, or ROC curve. The area under the ROC curve provides a single metric that can be used to judge the overall discriminative ability of a classification method. An area of 0.5 indicates no discrimination, between 0.7 and 0.8 indicates acceptable discrimination, between 0.8 and 0.9 indicates excellent discrimination, and greater than 0.9 indicates outstanding discrimination.²⁹ This value can also be used as a quantitative metric for statistical comparisons between classifiers. We computed the area under the ROC curve for each classification method and then compared the area under the ROC curve for these classifiers after adjusting for multiple comparisons using a method known as multiple comparisons of the best.^{30, 31}

Results

Our sample consisted of 244 total eyes: 132 normal eyes from 92 patients (51% female) and 112 eyes from 71 patients diagnosed with keratoconus (49% female). Four eyes were excluded from the keratoconus sample due to incomplete videokeratography data over the 7 mm diameter central region.

Decision Tree classification

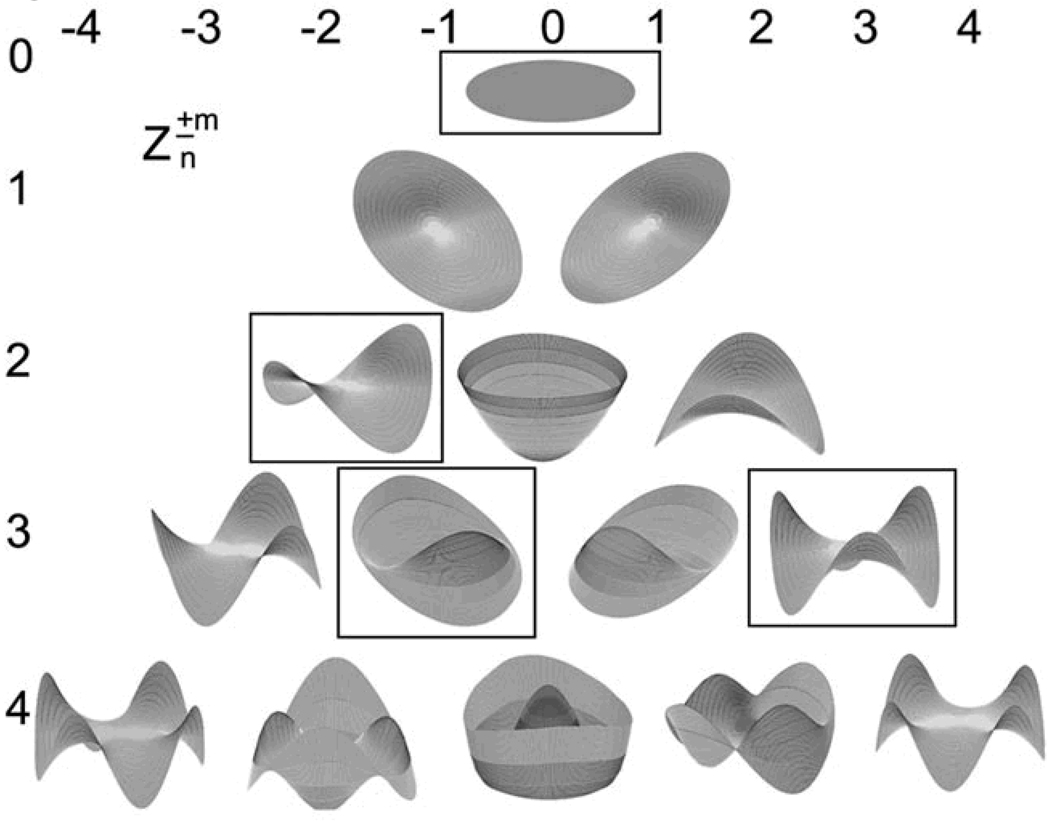
The decision tree resulting from cross-validation training and testing with the C4.5 algorithm is shown in Figure 1. The value of each Zernike polynomial coefficient that provided the best separation of the two classes at each node labels the branches of the decision tree. The resultant subset of attributes (Zernike polynomial modes) selected by the decision tree induction algorithm to discriminate between keratoconic and normal eyes are the nodes of the decision tree and their geometric correspondence is shown in Figure 2.

Figure 2.

Individual geometric modes of a 4^th order Zernike polynomial expansion. Color is used to indicate modes selected as classification attributes by the automated decision tree. Polynomial coefficients are labeled using double index notation according to Optical Society of America standards; polynomial order (n) is indicated on the vertical axis, azimuthal component (± m) is indicated by the horizontal axis.

The Zernike polynomial modes identified by the decision tree algorithm as most useful for discriminating between normal and keratoconic corneal shape (Figures 1 and 2) correspond with vertical coma (C_3,−1), mean surface height (C_0,0), with-the-rule toricity (C_2,−2), and trefoil (C_3,3).

Standard Classifier Performance Comparisons

We show the accuracy, sensitivity, and specificity of each classification method using the published classification thresholds in Table 2. We found that accuracy was best for our decision tree classification method. The CLMI classification method also had excellent accuracy that was comparable to our decision tree method. The CLMI classifier had exceptional specificity that was greater than any other classifier studied. The Z3 classification index had excellent specificity, very good sensitivity and overall classification accuracy that was comparable with the C4.5 decision tree method. The modified Rabinowitz-McDonnell classification method had excellent sensitivity, very good specificity and overall accuracy. The KISA% classification method had acceptable sensitivity, and was highly specific. This resulted in overall classification accuracy that was very good. The KPI index had excellent sensitivity but poor specificity and relatively low accuracy compared to the other classifiers evaluated.

TABLE 2.

Comparison of standard classifier performance metrics (n = 244)

Classifier	Cut point (≥)	Sensitivity (%)	Specificity (%)	Accuracy (%)
C4.5*	1	92	93	93
CLMI	3.00	79	99	90
Z3	0.00233	86	92	89
RM (D)†	47.2 (1.4)	91	81	86
KISA%	100	71	95	83
KPI	0.23	92	59	74

Selected cut points are published values recommended by the author of each classification method.

^*C4.5 classifier performance is estimated by 10-fold cross validation.

^†Reported RM cut points are K-value and (I-S values), respectively.

C4.5, decision tree classifier21; CLMI, Cone Location and Magnitude Index; RM, Modified Rabinowitz–McDonnell Index10; KISA%, K-value, IS-value, and Astigmatism Index10; Z3, third-order Zernike

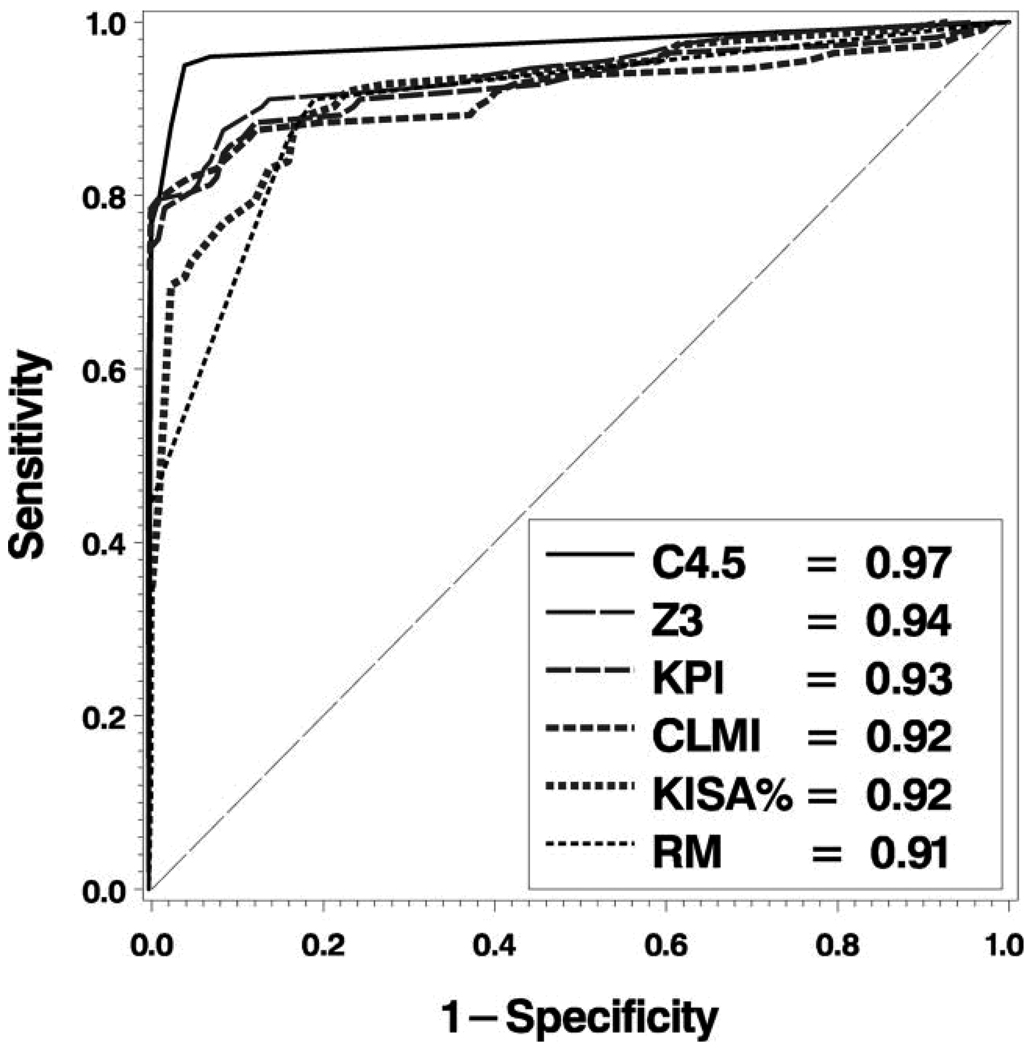
ROC Curve Analysis

In Figure 3, we plot the ROC curves for each of the classifiers. All of the classifiers studied had outstanding discrimination (area under the ROC curve > 0.90.) After controlling for multiple comparisons, we found that our C4.5 decision tree based classifier was not measurably better than the Z3 classification method of Schwiegerling et al, but both of these methods were significantly better than the remaining classification methods (Table 3; all P > .05).

Figure 3.

ROC Analysis. ROC curves and associated area under curve (see legend) for each of the 6 classification methods: C4.5 = Decision tree classifier; CLMI = Cone Location and Magnitude Index; RM = Modified Rabinowitz–McDonnell Index;¹⁰ KPI = Keratoconus Prediction Index;⁶ Z3 = 3^rd order Zernike Polynomial Index;²⁵ KISA% = K-value, IS-value, and Astigmatism Index.¹⁰

TABLE 3.

Statistical comparison of area under the receiver operating characteristic (ROC) curve for keratoconus classifiers using multiple comparisons with the best method (n = 244)

Classifier	ROC Area	Comparison	Difference	95% Confidence Interval
C4.5	0.972	C4.5 – max	0.031	−0.003–0.064
Z3	0.940	Z3 – max	−0.031	−0.0640–0.003
KPI	0.925	KPI – max	−0.047	−0.090–0.000*
CLMI	0.916	CLMI – max	−0.056	−0.101–0.000*
KISA%	0.916	KISA% – max	−0.056	−0.101–0.000*
RM	0.906	RM – max	−0.066	−0.104–0.000*

^*Statistical significance (p < 0.05).

C4.5, decision tree classifier₂₁; CLMI, Cone Location and Magnitude Index; RM, Modified Rabinowitz–McDonnell Index¹⁰; KPI, Keratoconus Prediction Index⁶; Z3, third-order Zernike Polynomial Index³¹; KISA%, K-value, IS-value, and Astigmatism Index.¹⁰

Discussion

In this study we described an automated and objective way to quantify videokeratography features based upon a Zernike polynomial transformation of exported instrument data. This method has excellent accuracy with high sensitivity and specificity. Furthermore, our decision tree method of classification had statistically greater area under the ROC curve than all but one of the keratoconus classification methods that we evaluated.

The Zernike polynomial modes identified by the decision tree algorithm as most useful for discriminating between normal and keratoconic corneal shape (Figures 1 and 2) correspond with vertical coma (C_3,−1), mean surface height (C_0,0), with-the-rule toricity (C_2,−2), and trefoil (C_3,3).

The vertical coma term (C_3,−1) was the most important attribute for classification of keratoconic surfaces. These results have clinical face validity and are in agreement with the findings of Schwiegerling et al. who describe a method of classification based on of a combination of third order Zernike polynomial coefficient magnitudes.²⁵ The RM, KISA% and KPI classifiers also capture elements of this same feature by quantifying the amount of vertical asymmetry as the ISvalue.

The second level attribute of the hierarchical decision tree corresponds to C_0,0. This Zernike mode describes the mean height of the fitted surface and selection of this attribute reflects the difference in sagittal depth between the surfaces fit in each patient group, which we would expect to be greater among keratoconic eyes. Corneal toricity that is more steeply curved in the vertical meridian is consistent with previous clinical observations and other indices such as the modified Rabinowitz-McDonnell index and KISA% that use vertically asymmetric curvature as an element for classification.

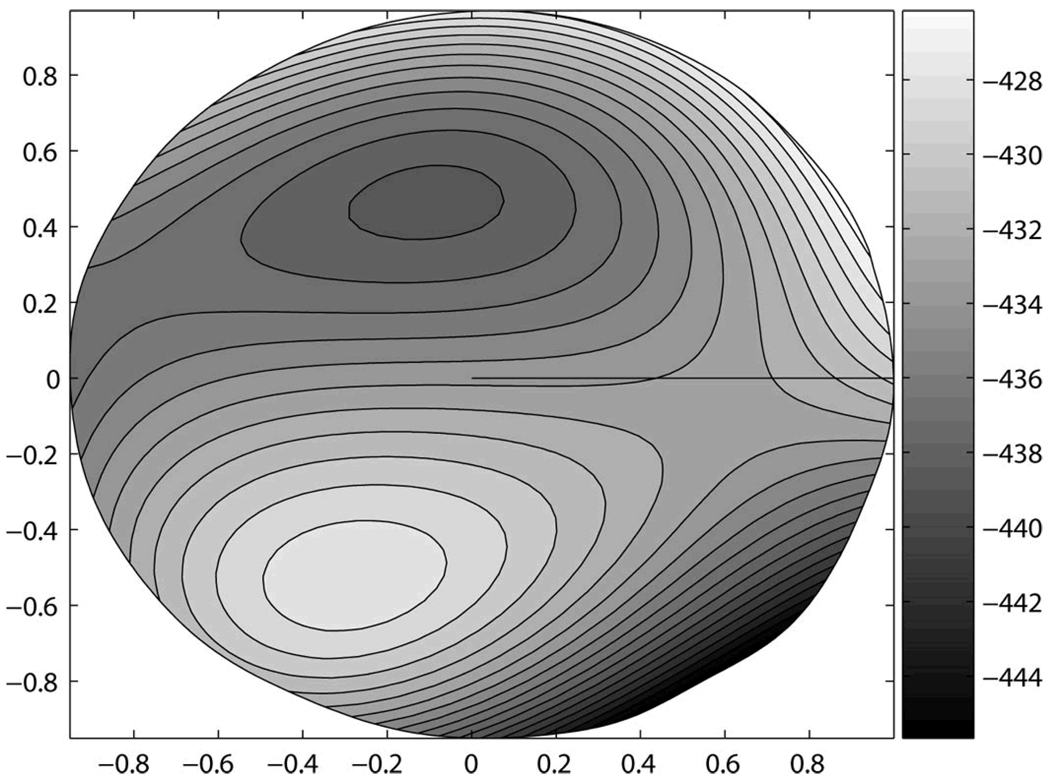
The final element of the tree, trefoil, is more difficult to visualize as a dominant feature in the combined surface features (Figure 4). This element likely contributes to differences in the location of the steepest inferior region, or the apex of the cone. When combined with the other attributes, this mode is interacting with them to modulate the location and magnitude of inferior steepening. It is apparent from Figure 4 (right eye representation) that the quantitative features represented in this surface correspond to a cone apex located in the inferior-temporal quadrant.

Figure 4.

Decision Surface. Three-dimensional, right-eye representation of corneal surface features at the boundary between eyes with keratoconus and normal eyes. This surface was constructed from the Zernike polynomial coefficients (3.5 mm radius fit) and their associated values derived from the C4.5 decision tree; total n = 244; Keratoconus n = 112; Normal = 13

With respect to interpretability, the decision tree results may be visualized in several ways. Figure 1 provides the most direct quantitative result. This hierarchical tree shows which attributes are most important for correct classification—items higher on the tree—as well as the magnitude of each attribute. While useful, this result may not be simple to visualize. As a supplementary aid we show the shapes of the corresponding Zernike polynomial modes for each coefficient in Figure 2. This too may be useful, but not intuitive. As a further means of showing what attributes distinguish the two classes of patients studied, we can construct a surface from the Zernike polynomial modes (nodes of the decision tree) in proportion (values labeling the branches of the decision tree) to their contribution to each class. The resulting surface is a quantitative spatial representation of the features that best discriminate between the two classes (Figure 4).

With respect to the performance of our proposed method in comparison to others, there has been debate among researchers regarding the best method for discriminating between normal and abnormal videokeratographic examination results,^{9, 10, 27} and the proper methods for estimation of classifier performance. Past approaches for estimating classifier performance have used the classic hold-out method, where the data are arbitrarily or randomly divided into mutually exclusive test and training sets. These separate portions of the data are then used for development of a classification method (training set), or for estimating the generalization error of the trained classifier (testing set). While valid, this approach uses the available data inefficiently compared with more modern methods such as cross-validation—the method of estimating classification performance we used for the decision tree classifier. For a detailed explanation of cross-validation and its validity, we refer the interested reader to a seminal paper on this topic by Kohavi.^24†

The shared objective has been to accurately classify normal and abnormal videokeratography test results. The fundamental dilemma is a tradeoff between sensitivity (the need to correctly identify abnormal cases) and specificity (the need to correctly identify normal cases). Our data nicely illustrate this tradeoff in Table 2 where the KISA% classifier is highly specific, but less sensitive and the KPI classifier is highly sensitive, but less specific. Nonetheless, these two classification methods achieve accuracy that differs by less than 10%. As a result, debates about which classification method is best are not easily resolved. If sensitivity is the most desirable criteria one may be dissatisfied with a classifier that is specific, yet insensitive. Figure 3 also illustrates how the tradeoff between sensitivity and specificity depends upon the separability of the sample studied with respect to diagnostic test results and the classification threshold selected. In cases where there are only 2 possible classes (e.g. disease or normal) the classification threshold value determines which class assignment to make for a given diagnostic test result. If the threshold value for classification is changed, the ratio of sensitivity and specificity will change accordingly.

Another set of criteria used to evaluate the utility of disease screening are positive and negative predictive values. When the frequency of disease in the general population is low, as in keratoconus, the positive predictive value of a test—the proportion of cases classified with disease that are truly diseased—will be correspondingly low even with a classification scheme that is highly sensitive and specific.

To address this limitation, we evaluated each classifier based on ROC curve analysis, which describes the performance of a classifier over the range of all possible combinations of sensitivity and specificity. This allowed us to compare the fundamental discriminative ability of each classifier in a fair fight, independent of any pre-defined classification thresholds, bias related to the sample studied, or confounding related to our derivation of TMS indices from Keratron data. To our knowledge, we are the first to apply ROC analysis to evaluate the fundamental discriminative ability of these different videokeratography classifiers on the same data set. While all ROC curve areas were 0.90 or better (outstanding discrimination) on this dataset, these results show that the C4.5 based decision tree classification method is better than four of the five classification methods we evaluated (significantly greater area under the ROC curve, P < .05). The Z3 index had equivalent performance to the decision tree method by ROC curve area comparisons. We believe that discrimination of these two diagnostic groups based on third-order Zernike polynomial coefficients alone is only marginally different when additional polynomial modes are included in our decision tree algorithm. Furthermore, best discrimination for each classifier was not achieved with the published recommended classification threshold criteria.

Our purpose was to develop an objective method to quantify videokeratography data that could support clinical decision making. The decision tree method described accomplished this objective well. This decision tree method has excellent sensitivity, specificity, and accuracy. Since this method is based on decision tree induction, the approach has additional advantages including faster computational speed than other machine learning methods such as neural networks, scalability for analysis of large data sets, and interpretability.^{16, 20, 21, 32}

Klyce et al. have criticized comparisons of the KISA% index with RM, KPI, and other classifiers suggesting that current techniques have evolved beyond the simplicity of these earlier methods.³³ Neural network methods described by these same authors have not been widely adopted.^{7, 9} Carvalho et al. have also recently used Zernike polynomials as input features for a neural network to classify corneal shape.³⁴ Their purpose was to use features that are available from most instrument platforms (Zernike polynomials) that would permit accurate classification of corneal shape. We argue that the potential advantage of greater classification accuracy by neural networks or any other approach that does not reveal the basis for classification is subordinate to several clinical pragmatic clinical constraints. First, diagnostic aids must be interpretable to be useful. This is not an advantage of neural networks since the basis of classification by neural networks remains a “black box.” Second, we were pleased to find that our decision tree classifier consisted of only four Zernike coefficients, all of which were third or lower-order terms making this approach both simple and more interpretable. Third, computational complexity and instrument platform restrictions limit use of these methods. Useful analysis routines should be simple, fast, and portable. Our approach differs from most previous classifiers, which are based on numeric indices derived from corneal curvature values. Since this classifier is based upon Zernike polynomials calculated directly from videokeratography elevation data, this classification method may be applied easily to data from most clinical videokeratography instruments. Finally, any machine learning method should add information that extends the knowledge and analytic power of the user thereby providing useful decision support for clinicians. We demonstrate that our approach is capable of discriminating corneal shape very well and that the results can be used to generate an intuitive and familiar spatial representation of the basis for classification that provides more useful information to the clinician than a categorical classification decision.

Limitations of this study include sampling bias, simulation of TMS indices for calculation from Keratron data, and computation of Zernike polynomials over a limited (7 mm) region. Our retrospective sample of keratoconus eyes is biased against inclusion of incorrect clinical diagnostic codes. Our sample is also potentially biased towards inclusion of more severe or progressive disease since these patients are examined more frequently. Replication of these results by others will help to interpret the potential impact of these potential biases on this classification method.

A fundamental limitation of studies that evaluate classification performance is that they depend on a disease definition and once defined, no classification method can exceed the performance of the standard—in this study, ICD-9 codes and the CLEK definition of disease in at least one eye. We selected this disease definition as one of the least ambiguous and most defensible definitions of keratoconus that was not dependent only upon videokeratographic signs to define the disease. Other definitions of disease could be used that may produce different results.

Like most previous studies in this field, our records included both eyes from a single subject in many instances. Correlation in shape between the two eyes of a single subject will reduce the variance of our data and possibly improve the separability of our records.^{35, 36} Nonetheless, conditional statistical modeling methods were not used to account for these affects, which may have influenced our results with every classifier evaluated. Although keratoconus is often bilateral, we elected to analyze our bilateral data as independent because this disease is frequently asymmetric in severity.³⁷ By including both eyes our sample represents a spectrum of disease severity from disease suspect with no videokeratographic signs, to CLEK-defined keratoconus with obvious videokeratographic signs of disease. As expected the sensitivity of each classification method is relatively high in our sample of keratoconus. Yet there were differences and the decision tree method performed better in this comparison. Similarly, we would expect the performance of each classification method to be poorer and that the relative performance of these classifiers may also be different if only early cases of disease were included.

It is possible that the lower performance of some classifiers may be attributed to inherent differences in the videokeratography instruments. Although measurement principles are similar between some instruments, alignment methods, spatial resolution of data, and other potentially important differences exist that could impact results computed from different instruments. Proprietary algorithms of each instrument translate a captured Placido image to the curvature and elevation data that we analyzed in this study. Algorithm differences and calibration factors could account for a systematic bias that explains why indices performed better on their native platforms as previously published. Additional studies comparing the repeatability of these measurements on eyes under clinical measurement conditions and across instrument platforms are needed as this may affect how these classification methods compare across instrument platforms.

Although we have adapted the computation of TMS indices for data exported from the Keratron as faithfully as possible, and our formulas are a very close approximation to the TMS output, this translation introduces another possible source of error to confound our study results. For example, our calculation of the KISA% and KPI indices are approximations. This is due to the fact that scaling constants and normalization constants are used in several formulae. We are separately evaluating the methods we used to translate each of these indices across platforms through comparisons with original indices. Nonetheless, the ROC curve analysis used minimizes the impact that this limitation may have on our results.

Calculation of Zernike polynomials over a 7 mm corneal diameter will impact these results in several ways. First, our selection criterion for full data over this region will likely bias the sample towards early to moderate disease. Second, this criterion will have a direct effect on the magnitude of the Z3 index that was originally computed for over a 6 mm diameter. Third, the magnitude of higher order Zernike polynomials could become increasingly important features for distinguishing the two classes (normal and keratoconus) studied here. If true, the decision tree induction algorithm would select a different group of coefficients to discriminate between these two groups.

The clinical dilemma of keratoconus diagnosis is rarely decided as a binary classification exercise; likewise diagnostic decisions rarely involve isolated analysis of a single clinical test result. Application of these analytical methods to the problem of keratoconus classification is a useful test bed to demonstrate the benefits of this approach. Although much of what we learn by classification of videokeratography data is supported by findings from other clinical tests, clinical interpretation of videokeratography remains an important clinical dilemma, e.g. in the context of patient screening prior to corneal refractive surgery.

The goal of a user friendly platform independent quantitative method of videokeratography analysis that provides interpretable clinical decision support is far from achieved. Our work is intended as an additional step towards the need for more accessible methods of quantitative analysis that can be easily implemented across instrument platforms.

There are several benefits to our decision tree approach to classification. First, we are not restricted to the use of videokeratography data. Decision trees can easily accommodate other data types that may be important, but are not easily included in other classification methods. Examples of other attributes that we could add to a decision tree include: categorical variables indicating disease risk-factors such as co-morbidities, family history, and demographic characteristics, or other continuous variables such as corneal thickness. Our future work will consider these other characteristics in addition to videokeratographic data to determine whether or not the detection of early disease can be facilitated by including other disease risk factors. Additional work on normative comparisons and longitudinal analysis are needed as well.

Aside from this binary classification of biomedical image data, there are potentially many other useful applications for these methods to the analysis of other clinical data that do not easily conform to traditional statistical modeling.

APPENDIX

The C4.5 algorithm is a supervised machine learning method in which information about a record’s true class assignment is known during construction of the classifier. The logic of the C4.5 decision tree induction algorithm is represented by the pseudocode in Appendix Table A1. The algorithm begins with all records in a single pool, a heterogeneous collection of both normal and keratoconus records. The C4.5 algorithm then iteratively selects individual attributes and values to determine a best separation of the records. A measure known as information gain is the basis for attribute selection and splitting citeria.20–23 The objective of splitting the records within a node of the decision tree is to reduce the dissimilarity of known class labels that exist within the pooled data by dividing it into two separate more homogenous groups of records. Entropy reduction is the quantitative metric used to calculate information gain. In the field of information theory, entropy is defined as the impurity of a collection of records, in which greater entropy is associated with multiple class labels.22 Entropy is defined mathematically as:

$$\mathit{\text{Entropy}}(s)\equiv {\displaystyle \sum _{i=1}^c-p_i{\mathit{\text{log}}}_2{p}_i}$$

where S represents the data sample, c is the number of possible classes represented in the sample, p is the proportion of records of class i. By this relationship, the entropy of a sample S with c possible classes is a function of the proportion of S that belong to class i multiplied by base two logarithm of all possible class values. In simpler terms, the entropy of a sample is determined by the homogeneity of classes found in the sample. A more homogenous sample consisting of nearly all records of one class would have low entropy. The objective of the decision tree induction algorithm is to find the set of features that provides the best separation of records with respect to class, thereby minimizing entropy of the sample at each level of the tree. Information gain is calculated as the difference between the entropy in the original sample and the entropy of the subsets that would result from splitting the records on a particular attribute. The information gain ratio provided by splitting the dataset S based on attribute A is defined as the ratio of the entropy of the resulting subsets relative to the entropy in the original set. Mathematically, this is defined as:

$$\mathit{\text{Information Gain}}(S,A)\equiv \mathit{\text{Entropy}}(S)-{\displaystyle \sum _{j\in \mathit{\text{Values}}(A)}\frac{S_j}{S}\mathit{\text{Entropy}}(S_j)}$$

where the information gain of a sample S split on attribute A is a function of the entropy of the original pool of records less the expected entropy resulting from the split. The expected entropy is the sum of entropy for each subset weighted by the proportion of records in each subset.²² This recursive process of calculating information gain to select splitting attributes and dividing records within nodes to reduce entropy continues until a complete classification model is constructed for the given set of records. Choosing the attribute that provides the greatest amount of information gain at each level of the tree minimizes the information required to classify the remaining records and results in simple classifiers.²²

TABLE A1.

Pseudocode representation of a recursive decision tree algorithm

1 Create the root node of the tree S

2 if all instances belong to the same class C then

3 S= leaf note labeled with class C

4 if attribute list (A l) is empty then

5 S= leaf node labeled with the majority class

6 Otherwise

7 Select test attribute (A t) from A l with the greatest information gain

8 Label node S as A t

9 For each possible value v i of A t

10 grow a branch from S where the test attribute A t = v i

11 Let S v be the subset of S for each value of Attribute A t = v i

12 if S v is empty then

13 label the node S v as a leaf with the most common class

14 Else below this branch add the subtree node