Brain Fiber Architecture, Genetics, and Intelligence: A High Angular Resolution Diffusion Imaging (HARDI) Study

Abstract

We developed an analysis pipeline enabling population studies of HARDI data, and applied it to map genetic influences on fiber architecture in 90 twin subjects. We applied tensor-driven 3D fluid registration to HARDI, re-sampling the spherical fiber orientation distribution functions (ODFs) in appropriate Riemannian manifolds, after ODF regularization and sharpening. Fitting structural equation models (SEM) from quantitative genetics, we evaluated genetic influences on the Jensen-Shannon divergence (JSD), a novel measure of fiber spatial coherence, and on the generalized fiber anisotropy (GFA; [1]) a measure of fiber integrity. With random-effects regression, we mapped regions where diffusion profiles were highly correlated with subjects' intelligence quotient (IQ). Fiber complexity was predominantly under genetic control, and higher in more highly anisotropic regions; the proportion of genetic versus environmental control varied spatially. Our methods show promise for discovering genes affecting fiber connectivity in the brain.

1 Introduction

Diffusion profiles of brain white-matter fibers are intermediate phenotypes that can be causally related to more basic biological measures, such as genetic variations across subjects, and to more high-order cognitive processes, such as intellectual performance. They serve as a valuable link in the quest to find genes that influence cognition and disease, as fiber integrity may be associated with genetic variation using quantitative genetic modeling, and with cognitive scores (such as intelligence quotient or IQ).

In this paper we analyzed the high angular resolution diffusion imaging (HARDI) data of 90 twin subjects. Studies of identical and fraternal twins – who share all or half of their genes respectively - are informative for understanding the genetic control of brain structure and function. We measured the regional complexity of diffusion orientation distribution functions (ODF) by applying statistics to high-dimensional HARDI data in appropriate Riemannian manifolds. We visualized associations between diffusion profiles and genetic and environmental factors, and with IQ, by fitting structural equation (SEM) and random-effects regression (RRM) models at each voxel. To our knowledge, these are the first 3D maps of genetic influences on HARDI, and reveal that HARDI signals that are genetically controlled, to some extent, are also correlated with intelligence.

2 Methods

2.1 Subject Description and Image Acquisition

HARDI data were acquired from 22 pairs of monozygotic (MZ; 20 males/24 females; age = 25.1±1.5 years) and 23 pairs of dizygotic twins (DZ; all same-sex pairs; 20 males/26 females; age = 23.5±2.2 years) on a 4T Bruker Medspec MRI scanner using an optimized diffusion tensor sequence [2]. Imaging parameters were: 21 axial slices (5 mm thick), FOV = 23 cm, TR/TE 6090/91.7 ms, 0.5 mm gap, with a 128×100 acquisition matrix. 30 images were acquired: 3 with no diffusion sensitization (i.e., T2-weighted images) and 27 diffusion-weighted images in which the gradient directions were evenly distributed on the hemisphere [2]. The reconstruction matrix was 128×128, yielding a 1.8×1.8 mm² in-plane resolution. Total scan time was 3.05 minutes.

2.2 DTI Registration

For each subject, diffusion tensor (DT) images (denoted by D_ij, 1≤ i, j ≤3) were computed from the HARDI signals using MedINRIA software (http://wwwsop.inria.fr/asclepios/software/MedINRIA). One diagonal component image (D₁₁) was manually stripped of nonbrain tissues, yielding a binary brain extraction mask (cerebellum included). The masked image was then registered to the ICBM53 average brain template with a 12-parameter linear transformation using the software FLIRT [3], and resampled to isotropic voxel resolution (dimension: 128×128×93 voxels, resolution: 1.7×1.7×1.7 mm³). The resulting transformation parameters were used to rotationally reorient the tensor at each voxel [4], and then affine align the tensor-valued images based on trilinear interpolation of the log-transformed tensors [5]. All affine-registered DT images were then registered to a randomly selected subject's image (a MZ subject), using an inverse-consistent fluid registration algorithm that minimizes the symmetrized Kullback-Leibler divergence (sKL-divergence) of the two tensor-valued images [6].

2.3 HARDI Processing and Registration

Orientation distribution functions (ODF) for water diffusion were computed voxelwise from the HARDI signals using the Funk-Radon Transform (FRT) [1]. We used Descoteaux's method [7], which expands the HARDI signals as a spherical harmonic (SH) series, simplifying the FRT to a linear matrix operation on the coefficients. To estimate the SH coefficients, we set the order of the SH series to 4, and added a Laplacian smoothing regularizer to reduce the noise level, and also a Laplacian sharpening regularizer to help detect the peaks of the ODF, as in [7]. The estimated ODF was normalized to unit mass, creating a diffusion probability density function (PDF) parameterized by spherical angle.

Images of the diffusion ODFs were registered to the target subject by applying the corresponding DTI mapping (both affine and fluid mappings) in the previous section. To keep the direction of the diffusion ODFs oriented with the direction of the underlying fibers, ODFs were reoriented using the Preservation of Principal Direction (PPD) method [4], where the principal direction of the ODF was determined by principal component analysis [8]. A generalized fractional anisotropy (GFA) map was constructed from the registered ODF ψ [1]:

$$\mathit{GFA}\sqrt{n\sum _{i=1}^n{(\psi \left({\mathbf{u}}_i\right)-\langle \psi \rangle )}^2/\left[(n-1)\sum _{i=1}^n\psi {\left({\mathbf{u}}_i\right)}^2\right]}.$$ (1)

Here u_i, 1 ≤ i ≤ n, are n gradient directions, and 〈ψ〉 is the mean of the ODF with respect to spherical angle.

Spatial interpolation of HARDI ODFs is a new issue, and is required when the registration mapping falls on non-lattice points. We addressed this by taking the square root of the ODF: the Riemannian manifold for the square root of a PDF is isomorphic to a unit sphere and there are closed form expressions defining the geodesic distance, exponential and inverse exponential mappings [9]. The interpolated square-rooted ODF (sqrt-ODF)ϕ at point (x, y, z) was then constructed by finding the weighted Karcher mean of its 8 diagonal neighbors ϕ_i in 3D at lattice points (x_i, y_i, z_i), which minimizes the square sum of the geodesic distance d:

$$\varphi =\text{argmin}{\Sigma }_{i=1}^8{w}_{i}d{(\varphi ,{\varphi }_i)}^2.$$ (2)

Here w_i is the trilinear interpolation weight defined as w_i = (1 − |x − x_i|)(1 − |y − y_i|)(1 − |z − z_i|). The weighted Karcher mean ϕ was computed using a gradient descent approach as in [9].

2.4 Measuring Regional Complexity of Diffusion

We defined the regional complexity of diffusion using the generalized Jensen-Shannon divergence (JSD) [10]. JSD measures the dissimilarity of n probability distributions, given by:

$${\mathit{JSD}}_w(\mathbf{p},\dots ,{\mathbf{p}}_n)=H\left({\Sigma }_{i=1}^n{w}_i{\mathbf{p}}_i\right)-{\Sigma }_{i=1}^n{w}_{i}H\left({\mathbf{p}}_i\right).$$ (3)

Here ${\mathbf{p}}_i=\left\{p_{ij},1\le j\le k\mid {\Sigma }_{j=1}^k{p}_{ij}=1\right\}$, and $w=\left\{w_i,1\le i\le n\mid {\Sigma }_{j=1}^k{w}_i=1\right\}$. H(•) is the Shannon entropy, defined as $H\left(\mathbf{p}\right)=-{\Sigma }_{j=1}^k{p}_j\text{log}{p}_j$. ${\mathit{JSD}}_w(\mathbf{p},\dots ,{\mathbf{p}}_n)=0$ if and only if all p₁,…, p_n are equal. The complexity of diffusion at voxel x was defined as the JSD for the ODF at x and its contiguous 26 ODFs. We adopted an equal weight of 1/n for simplicity.

2.5 Statistical Analysis of Structural Models for Twins

To analyze genetic and environmental correlations in twins, structural equation models (SEM; [11, 12]) can evaluate contributions of additive genetic (A), shared environmental (C) and random environmental (E) components to the covariances of the observed variables (y) for MZ and DZ twins, according to the following model:

$$y_j=a{A}_j+c{C}_j+e{E}_j,$$ (4)

where j = 1 or 2 for the first or second twin in the same pair. Since A, C, and E are unobservable variables, their weights θ = (a, c, e) were estimated by comparing the covariance matrix implied by the model, Σ(θ), and the sample covariance matrix of the observed variables, S, using maximum-likelihood fitting:

$$F_{\mathit{ML},\theta }=\text{log}\mid \Sigma \left(\theta \right)\mid +\mathit{trace}\left({\Sigma }^{-1}\left(\theta \right)\mathbf{S}\right)-\text{log}\mid \mathbf{S}\mid -p,$$ (5)

where p = 2 is the number of observed variables. Under the null hypothesis that the population covariance matrix of the observed variables equals Σ(θ), and the n-sample data y are multivariate normal, T_ML,θ = (n−1)F_ML,θ follows a χ² distribution with p(p+1)−t degrees of freedom, where t is the number of free model parameters. Acceptance of the null hypothesis (p > 0.05) indicates a good fit for the model.

Parameter fitting based on the above χ² distribution may be biased if the sample data are non-normal. To free SEM from distributional assumptions, we used permutation methods to determine goodness of fit [13]. At each voxel, the GFA or JSD of the diffusion ODFs served as the observed variable, with the subject's age regressed out. We computed T_ML,θ using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method [14] to minimize F_ML in (5) in the original sample, as well as in 2000 permuted samples in which the twin pairs' MZ or DZ labels were randomly shuffled. In each permutation relabeling, four null hypotheses with different θ were evaluated, for fitting the E:θ = (e), CE: θ = (c, e), AE: θ = (a, e), and ACE: θ = (a, c, e) models, and the p-values, p_E, p_CE, p_AE, and p_ACE, were determined separately by comparing T_ML,θ in the true labeling to the permutation distribution. Since the permutation distribution of the χ² statistic T_ML,θ may differ from its original distribution, we rescaled the sample data using the Bollen-Stine transformation for each null hypothesis [13]:

$$\mathbf{Z}={\mathbf{YS}}^{-1∕2}{\Sigma }^{1∕2}\left(\theta \right).$$ (6)

Here Y is an n×2 matrix of the observed variables for the n twin pairs. Matrix square roots were computed by Cholesky factorization. The rows of Z instead of Y were permuted.

The four permutation p-values, p_E, p_CE, p_AE, and p_ACE, were compared at each voxel and the voxel was assigned to one of E, CE, AE, and ACE models if the p-value for that model was greater than the other three and also greater than 0.05. Color-coded maps visualized the optimal model fitted at each voxel, with E coded as blue, CE as green, AE as red, and ACE as yellow. For better visualization, we defined “model clusters”, i.e. sets of connected (26-neighborhood) voxels where the same model fitted, for each of the four models, and displayed only clusters of more than 10,000 voxels.

2.6 Linkage of Diffusion Anisotropy or Complexity with Cognitive Function

We used random-effects regression models (RRM) [15] to measure correlations between the full-scale intelligence quotient (FSIQ) and GFA or JSD. Ordinary regression methods are inappropriate because observations are clustered within twin pairs, violating the assumption that observations must be statistically independent. In RRM, the lack of independence is addressed by adding a random variable α_i, to incorporate the clustering of the observed variables within the ith pair, into the ordinary regression equations:

$${\mathbf{y}}_i={\mathbf{X}}_i\beta +1_i{\alpha }_i+{\epsilon }_i.$$ (7)

Here y_i = the 2×1 vector of observed variables (GFA or JSD) within the ith pair, β = a (q+1)×1 vector of unknown regression coefficients, X_i = a known 2× (q+1) covariate matrix, 1_i = a 2×1 vector of ones, and ε_i represents the 2×1 error vector. q was set to 1 for subjects' FSIQ score as the covariate. We assumed that α_i and ε_i, and thus y_i, were normally distributed, with ${\alpha }_i\sim \mathrm{N}(0,{\sigma }_{\alpha }^2)$, $\epsilon \sim \mathrm{N}(0,{\sigma }^2{\mathbf{I}}_2)$, and ${\mathbf{y}}_i\sim \mathrm{N}({\mathbf{X}}_i\beta ,{\sigma }_{\alpha }^2{1}_i{1}_i^{\mathrm{T}}+{\sigma }^2{\mathbf{I}}_2)$, where I_m represents an m×m identity matrix. Estimation of these unknown parameters $(\beta ,{\sigma }_{\alpha }^2,{\sigma }^2)$ was based on maximum marginal likelihood (MML) methods detailed in [15].

We applied RRM to each voxel and tested the significance of the correlations by comparing the full (β = [β₀, β_IQ]^T; β₀ is a constant) and the reduced (β = β₀) models, which gave a significance P-value based on Wilks' lambda distribution [16]: $\Lambda =\mid {\Sigma }_{\mathit{full}}\mid /\mid {\Sigma }_{\mathit{reduced}}\mid \sim \Lambda (p,vH,vE)$, where Σ is the estimated covariance matrix of y_i. p = 2 is the number of subjects in each pair, νH = 1 is the difference in the number of parameters between full and reduced models, and νE = n-q-1, where n is the number of twin pairs. Overall significance was assessed using the positive false discovery rate (pFDR) method [17]. A pFDR value < 0.05 was considered to be significant.

3 Results

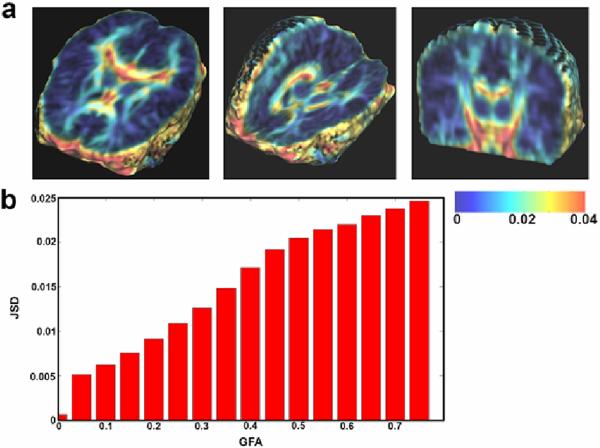
Fig. 1 displays the spatial distribution of the average JSD (averaged across all 90 subjects). The average JSD increases with GFA, suggesting that JSD is sensitive to the complexity of ODFs in major white matter fibers with high diffusion anisotropy, especially in regions where anisotropy values vary over a small spatial neighborhood.

Fig. 1.

(a) The color-coded map shows that the JSD, a measure of fiber complexity, is greater in regions of high diffusion anisotropy (e.g., the corpus callosum), especially at interfaces between high and low anisotropy. This trend is clear when plotting JSD against the GFA (b). This property of JSD is useful because in DTI/HARDI studies, diffusion properties are more informative in highly anisotropic regions, where fiber structures are highly resolved.

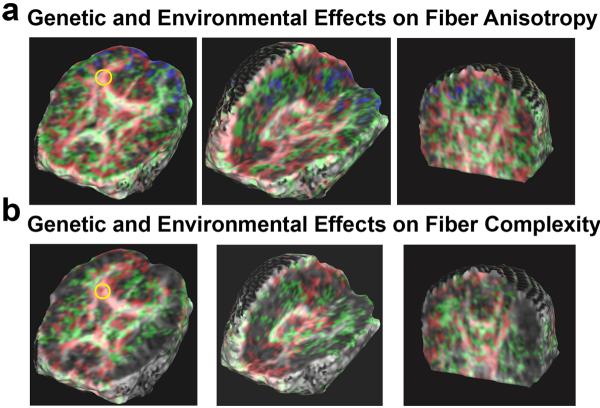
Fig. 2 shows the covariance structure fitting for GFA and JSD maps in the 90 twins. When the AE model fits best, variation in GFA or JSD values is more attributable to genetic influences, i.e., the covariance structures are best accounted for by additive genetic (added effect of genes) and random environmental effects (random experimental error is also lumped into the E term). When the CE model fits best, the variation in the observed measures is more due to environmental influences shared by twins reared in the same family [11]. The full ACE model, where all terms fit at once, could not be fitted for either GFA or JSD. For both GFA and JSD measures, more voxels had AE as the best-fitting model than CE or any other model, indicating that diffusion properties are more genetically influenced than environmentally influenced, in most brain regions.

Fig. 2.

The color-coded map shows which model fits best for the covariance matrices of (a) GFA, a measure of fiber integrity, and (b) JSD for fiber complexity, at each voxel. Voxels where the E model fits best are coded as blue, CE as green, and AE as red. For GFA and JSD, major fiber structures, such as the corpus callosum, cingulum, and internal capsules, are optimally fitted using the AE and the CE models. Model fitting is visibly asymmetrical in the cingulum fibers: the AE model fits in the right cingulum (yellow circles in (a) and (b)), while the CE model fits better in the left cingulum.

Fig. 3 shows that GFA is positively correlated with FSIQ scores in the corona radiata, corpus callosum and internal capsule (pFDR = 0.04). The correlations of JSD with FSIQ scores were not significant (pFDR = 0.21; figures not shown). Fiber measures were highly genetically controlled, especially in regions of high diffusion anisotropy. We also found that higher diffusion anisotropy is correlated with better intellectual performance in specific WM regions. Based on these measures and algorithms, future studies may be able to detect individual genes contributing to fiber architecture, and relate white matter integrity to cognition.

Fig. 3.

Correlations of GFA with the FSIQ score based on random-effects regression, visualized as maps of (a) regression coefficients (β_IQ) and (b) P-values. Higher diffusion anisotropy is associated with higher IQ in the left anterior region of the corona radiata, cingulum, and internal capsule.