Age-Independent and Age–Dependent Neural Substrate for Single-Digit Multiplication and Addition Arithmetic Problems

Abstract

The present study examined developmental differences in event-related potentials between second graders and adults in arithmetic. Consistent with previous literature in adults, multiplication for both children and adults produced a greater left anterior negativity from 400 to 900 ms, whereas addition produced a greater right posterior negativity from 400 to 900 ms. Adults showed larger left anterior negativities in the time window suggesting that adults rely more than children on a verbal processing system for solving these problems. Children showed larger right posterior negativities in the time window suggesting that they rely more on quantitative manipulation for solving these problems.

INTRODUCTION

Children acquire arithmetic facts typically by using two types of strategies: procedures involving quantitative manipulation and verbal memory (e.g., Dehaene & Cohen, 1997; Roussel, Fayol, & Barrouillet, 2002; Zhou et al., 2007). Procedural strategies include counting, transformation (e.g., 6+7=6+6+1, 9+7=9+1+6), and repeated addition (3×4=3+3+3+3), and so on. The use of procedural strategies can be a driving force in the development of the mental number line that is a visuo-spatial layout of Arabic digits representing magnitude. With the verbal memory strategy, people repeatedly recite arithmetic facts so that these facts are stored in memory as phonological associations between digit pairs and their answers. Schoolchildren are usually taught to use procedural strategies for simple addition and subtraction, but to use the verbal memory strategy to memorize multiplication facts (e.g., Dehaene & Cohen, 1997; Roussel et al., 2002; Zhou et al., 2007). These differential strategies during the acquisition of arithmetic facts may play an important role in shaping their mental representations (e.g., Siegler & Shipley, 1995). It is possible that mental representations of addition and subtraction facts have greater reliance on the manipulation of numerical magnitude and supportive visuo-spatial processes than those for multiplication facts, and the latter have greater reliance on the verbal memory than the former (e.g., Zhou et al., 2007).

Previous neuropsychological, event-related potential (ERP) and functional magnetic resonance imaging (fMRI) studies have shown a neural dissociation of brain regions involved in multiplication versus addition and subtraction problems. Neuropsychological studies have found that injury to parietal cortex produces larger deficits in addition and subtraction than in multiplication. In contrast, patients with lesions in left perisylvian language areas and those with low verbal fluency have more difficulty in multiplication than in addition and subtraction (e.g., Dehaene & Cohen, 1997; Delazer & Benke, 1997; Pesenti, Seron, & van der Linden, 1994). Using the ERP technique, Zhou et al. (2006) also showed neural dissociation among addition, subtraction, and multiplication. Compared with addition and subtraction, multiplication elicited a greater negativity at the left frontal electrodes peaking around 320 ms. Previous studies on language processing have found similar left anterior negative potentials during verbal or phonological processing tasks, such as phonological judgment (Rugg, 1984), synonym generation (Altenmüller et al., 1993), word or sentence decision with homophonic target (Niznikiewicz & Squires, 1996), and verb generalization (Rowan et al., 2004). Using the fMRI technique, Zhou et al (2007) found that addition problems were associated with greater activation in right intraparietal sulcus, whereas multiplication had greater activation in the language processing areas, including precentral gyrus, supplementary motor areas, and posterior and anterior superior temporal gyrus in the left hemisphere (Zhou et al., 2007). Altogether, these studies support the argument that left perisylvian language areas support verbal processing in multiplication tasks, whereas right parietal cortex supports quantitative manipulation in addition and subtraction tasks.

Although adult studies have shown a neural dissociation of multiplication versus addition and subtraction problems, it remains unclear how these two neural systems develop. Only two neuroimaging studies have examined developmental differences in the neural systems involved in arithmetic problems. Kawashima et al. (2004) asked children (9–14 years old) and adults (40–49 years old) to mentally perform addition, subtraction and multiplication problems. They found that adults had greater activation than children in right intraparietal cortex during subtraction and multiplication, and greater activation in supplementary motor cortex during subtraction. No developmental differences were found for addition problems and children did not show greater activation in any brain region. In a study of simple arithmetic (Rivera, Reiss, Eckert, & Menon, 2005), only addition and subtraction were investigated. Developmental increases (8- to 19-year-olds) in activation were reported in left supramarginal gyrus/intraparietal sulcus and left lateral occipito-temporal cortex (collapsed across addition and subtraction problems). Developmental decreases in activation were found in bilateral middle frontal gyri and left inferior frontal gyrus (Rivera et al., 2005). Several studies have examined developmental differences in the neural correlates of numerosity (arrays of dots) or numerical magnitude processing (Ansari, Garcia, Lucas, Hamon, & Dhital, 2005; Cantlon, Brannon, Carter, & Pelphrey, 2006). The developmental studies seem to converge on developmental increases in the engagement of intraparietal sulcus in tasks involving quantitative manipulation.

The current study examines age-independent and –dependent neural activities between Chinese children and adults when solving addition and multiplication problems. As mentioned earlier, two different types of strategies, procedural strategies involving quantitative manipulation and verbal memory strategies, are taught in schools to learn arithmetic facts. In China, the differential use of these two strategies for different arithmetic facts is especially clear. For addition and subtraction, a variety of procedures are used (e.g., transforming “4+7=3+7+1=11”), but for multiplication, Chinese children are required to use exclusively the verbal memory strategy (Zhou et al., 2007). The multiplication facts (with only smaller-operand first entries) are organized as mnemonic formulas, expressed with simple Chinese number words (e.g., 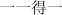, means “one one is one”, 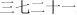, means “three seven twenty-one”). Since the collection of these formulas is very similar to rhyme, the verbalized multiplication table is also called “” (nine-factor song, literally). After acquiring basic addition in the first grade, Chinese children start to memorize the multiplication table during the second semester of the first grade or the first semester of the second grade (as compared to the third grade in the U.S.). It takes about 4 months for students to learn all multiplication facts. The Chinese children in the current study were in the end of the first semester of their second grade, and they had just finished the formal learning of addition procedures and multiplication facts.

The current study aims at determining if children (second graders) show a dissociation in cortex between multiplication and addition as do adults, and if there are developmental differences in the development of the verbal processing system involving left perisylvian language areas that has been implicated in multiplication tasks and the quantitative manipulation system involving intra-parietal cortex that has been implicated in addition tasks. We expect that second graders would show a dissociation in their event-related potentials between addition and multiplication due to one-semester (about four months) of verbal drilling on the multiplication table. Specifically, children and adults should have larger left anterior negativities for multiplication relative to addition. Moreover, because previous fMRI studies have shown that addition has greater activation in right parietal cortex and because ERP studies have shown greater right posterior negativities for mental rotation tasks (e.g., Heil & Rolke, 2002; Yoshino, Inoue, & Suzuki, 2000), we expect that addition should have greater negativities than multiplication at the right posterior electrodes. We also expect our event-related potential results to support behavioral studies that argue for a developmental decrease in the involvement of the quantitative manipulation system and a developmental increase in the involvement of verbal memory due to gradual familiarity with simple arithmetic (e.g., Geary, Nugent, Hoard, & Byrd-Craven, 2007).

METHOD

Participants

Twenty-two second graders (14 boys and 8 girls) were recruited from two primary schools in Beijing, China. Twenty-two undergraduate students (8 males and 14 females) were recruited from Beijing Normal University. The average age of children participants was 7.8 years, ranging from 7.2 to 8.1 years. The average age of the adult participants was 21.5 years, ranging from 18.0 to 26.3 years. All participants were right-handed and self-reported to have normal or corrected-to-normal vision. They had not participated in any experiments similar to the present one (i.e., involving simple arithmetic tasks of addition and multiplication) during the past year. Children's parents and adult participants gave written informed consent before the experiment. Children attended the experiment on a Saturday or Sunday from December, 2007 to January, 2008. After the experiment, children were given story books or stationery items (totaling RMB 30 yuan) as compensation for their time, and parents were given RMB 30 yuan as transportation fee and compensation for their time. Each adult participant was paid RMB 40 yuan.

Two participants (one child and one adult) had to be deleted for data analysis due to too many artifacts during EEG recording. Thus, finally 21 children (13 boys and 8 girls) and 21 adults (8 males and 13 females) were included for data reporting in current study.

Materials

Twenty-eight single-digit addition problems from 2+3 to 8+9 and 28 single-digit multiplication problems from 2×3 to 8×9, with an exception of “tie” problems, were used. “Tie” or repeated-operand problems (e.g., 3 + 3 and 3 × 3) were excluded because they involve special problem encoding and solution-retrieval (e.g., Campbell and Gunter, 2002). Problems with 0 and 1 as an operand (e.g., 1 + 5, 0 + 5, 1 × 5, 0 × 5) were also not used because they are rule-based problems (e.g., LeFevre et al., 1996). For the multiplication problems, only the smaller-first operand problems (e.g., 3×7) were suitable to use because the Chinese samples only memorized the smaller-first operand problems (Zhou et al., 2007). Due to these constraints and the need to have a balanced set of problems across operations, there were only 28 problems we could use for each operation. These problems with their answers were presented as true arithmetic equations. The participants in the current study were asked to determine whether the arithmetic equation was true or false. Thus, we also generated some false arithmetic equations.

From the 28 addition and 28 multiplication problems, four were randomly selected from each participant to form false arithmetic equations. This yielded a total of 32 addition and 32 multiplication problems. For the false arithmetic equations, false answers were generated by adding 1 to or subtracting 1 from one of the two operands and then adding or multiplying the two operands for addition and multiplication, respectively. In addition, false answers had to have the same number of digits (either one or two digits) as the true answers. With these constraints, false answers closely resembled true answers. Previous research has shown that participants might use plausibility judgment for arithmetic-equation verification (e.g., Lemaire & Fayol, 1995), so our use of false equations with solutions very close to true solutions should reduce plausibility judgment.

To allow for enough trials for the ERP recording, we had to present each problem 4 times, totaling 256 trials or problems (i.e., 32 problems × 4 times × 2 arithmetic operations). Of which, the 224 problems that had true answers were the target problems of present study, including 112 addition problems and 112 multiplication problems. Previous studies have shown that a small number of repetitions has only a limited effect on the cognitive processes involved in arithmetic. For example, the problem size effect (i.e., larger problems are more difficult than smaller problems) is typically stable even when the same one-digit multiplication problems are repeated three times (LeFevre & Liu, 1997).

Procedure

Participants were asked to determine whether an arithmetic equation was true or false. They only needed to respond when the equation was false. The true equations were our targets for ERP analysis. The design was expected to avoid the superimposition of other components elicited by the motor-related response. Half of the participants responded with their left hand, the other half with their right hand. Participants used just one hand rather than alternating hands to respond to reduce the mental load induced by a switch of response hand. Participants were encouraged to respond as accurately and quickly as possible. No responses were required for true equations to simplify the processes during the arithmetic-equation verification.

Participants were seated 105 cm away from the computer screen in a dimly lit, sound-attenuated room. All stimuli were presented visually in white against black background at the center of the screen. For each trial, an fixation “*” was first presented for 500 ms. Then, an equation was presented for 2000 ms, followed by a blank screen for 1000 ms. Each digit for the operands and solution was 0.9 × 1.3 cm in size. The operation sign “+” or “×”was 1.2 × 1.2 cm in size. The `=” sign was 1.2 × 0.6 cm. During the presentation of the arithmetic equations and the blank screen, participants would perform addition and multiplication and make a judgment by pressing a key if they judged the equation to be false. If they judged the equation to be true, they just waited for the next trial.

We used a verification task rather than a production task in the ERP experiment for two reasons. First, in verbal-production tasks, tongue movement and muscle activity are likely to add artifacts to the EEG recording. For this reason alone, many other similar studies have used verification tasks (e.g., Galfano, Mazza, Angrilli, & Umiltà, 2004; Niedeggen & Rosler, 1999; Szücs & Csépe, 2004). Second, multiplication problems generally involve larger numbers as their answers (ranging from 6–72) than do addition problems (5–17). Consequently, verbal production might result in more verbal processing for multiplication than for addition.

Previous research has shown strong evidence of interference among arithmetic operations when participants have to switch between them (e.g., Campbell & Oliphant, 1992). To reduce such interference, problems were presented in separate blocks. Each type of operation had two blocks (about 4 minutes each). Each problem was presented twice in a block. Problems were randomly presented within a block, with the constraint that consecutive problems did not have a common operand or the same solution. At the beginning of each block, the arithmetic operation to be performed was cued on the screen. Participants had a 1-minute rest between blocks.

Before the formal test, there were practice trials with problems with 0 and 1 as one of the operands (e.g., 0 × 2, 1 × 2). During the practice, participants were instructed to avoid eye-blinks. Participants were given feedback if they made two many eye blinks or response errors, took too long to respond, or had obvious head movement.

Electroencephalography (EEG) Recording and Analysis

Scalp voltages were recorded by an EGI dense-array system (Electrical Geodesics Inc., Eugene, OR, USA), using the 128-channel geodesic sensor net 200. Stimuli were presented with E-Prime (©Psychology Software Tools), which sends coded trigger pulses to the EEG system to mark stimulus onset. The sampling rate was 500 Hz. Impedances were kept below 50 kΩ. Data recording was constrained by 0.1 Hz high-pass and 100 Hz low-pass online filters, with the vertex electrode (Cz) as a reference.

The EEG data were analyzed offline with the Net Station Waveform Tools (a component of Net Station, EGI). We followed the data-analysis path recommended in the Net Station Waveform Tools Technical Manual (EGI, 2006). Data were firstly digitally processed by a 30 Hz low-pass filter, and then the continuous EEG data were segmented into epochs from 200 ms prestimulus (i.e., 200 ms before the onset of arithmetic equations) until 2000 ms poststimulus. The 200 ms prestimulus served as the baseline. After the segmentation, artifact detection was conducted on the entire segmentation. That is, if the amplitude difference (max-min) during a segmentation was larger than 400 μV, the segment was marked bad. A channel was marked bad if more than 30% of the recording was marked bad. Then, the data in bad channels were replaced with data interpolated from the remaining channels, using spherical splines. This approach never perfectly re-created a channel. The resulting waveform was only an approximation of the signal that was present at that location on the scalp during recording. Next, ocular artifacts were automatically inspected and removed with a blink slope threshold 14.00 μv/ms. After ocular artifact removal, the same artifact detection and bad channel replacement were conducted again, with the exception that the amplitude difference for bad segment marking was 200μV and a channel was marked bad if more than 20% of the recording was marked bad. Next, data were averaged over 2200 ms from −200 ms to +2000 ms relative to the onset of the presentation. The percentages of valid trials used for averaging were more than 80% for each condition. Pre-stimulus baseline correction was applied on average waveforms. Then, the average waveforms were re-referenced with average referencing. Grand average waveform was calculated on average waveforms for all participants.

Event-related potentials were time-locked to the onset of arithmetic equations. To examine amplitude differences among conditions across the whole scalp, representative nine electrode positions over anterior, central, and posterior regions of both hemispheres and the midline were defined: left anterior electrodes (electrode numbers: 27, 28, 33, 34 and 39), medial anterior electrodes (10, 11, 15, 16, 18 and 19), right anterior electrodes (1, 2, 121, 122 and 123), left central electrodes (41, 42, 46 and 47), medial central electrodes (7, 32, 55, 81 and 107), right central electrodes (103, 104, 109 and 110), left posterior electrodes (58, 59, 64,65, 69 and 90), medial posterior electrodes (72, 76, 77 and 82) and right posterior electrodes (89, 90, 91, 92, 96 and 97). The potentials were averaged over the four, five or six electrodes of each electrode position. The averaged potentials over the 9 representative electrode positions were submitted to analysis of variance (ANOVA) with Greenhouse-Geisser corrections. Scalp topographies were visualized with EEGLAB (http://sccn.ucsd.edu/eeglab/).

RESULTS

Behavioral Data

Participants in present experiment were asked to press a key only for false arithmetic equations. Thus, reaction times were calculated only for false arithmetic equations. Incorrect responses occurred when participants pressed the key for true arithmetic equations or did not press the key for false arithmetic equations. Children took 1508 (±206, standard deviation) ms and 1496 (±144 ) ms to solve the addition and multiplication problems (i.e., false arithmetic equations), respectively. The corresponding error rates were 27.6% (±18.3) and 20.3 (±17.8) for the false arithmetic equations. Adults took 1060 (±164) ms and 1085 (±141) ms. The error rates were 7.8%(±8.7) and 5.7%(±7.1). The ANOVA with arithmetic operation as the within-participant factor and age as the between-participant factor showed a significant effect of age for reaction time, F(1, 40)=110.07, p<.001, and for error rates, F(1, 40)=24.29, p<.001. There were no main effects or interactions involving operation.

For the true arithmetic equations, children's error rates were 4.7% (±3.6) and 3.9% (±4.0) for addition and multiplication problems. Adult's error rates were 1.8% (±1.9) and 1.3% (± 1.5). The ANOVA showed a significant effect of age, F(1, 40)=5.70, p=.02. There were no main effects or interactions involving operation.

Analysis of Event-Related Potentials Data

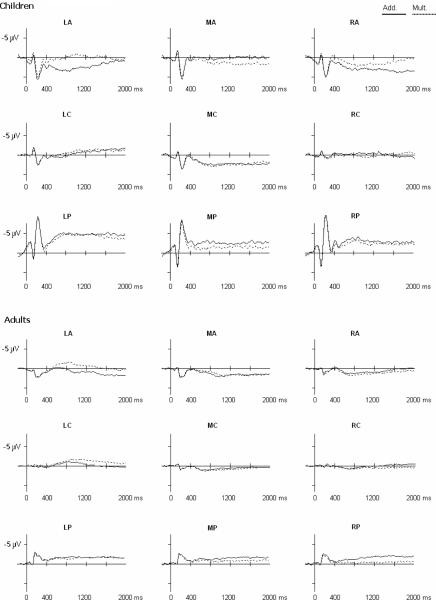
The grand mean waveforms for operation (addition and multiplication) by age are displayed in Figure 1. According to the grand mean waveforms, there are salient P1, N1, and long slow potential components. We report the statistical analyses on these components.

Figure 1.

Event-related potentials for single-digit addition and multiplication at 9 typical electrode positions over scalp in the time window from 200 ms prestimulus to 2000 ms poststimulus. Data are for all problems. The 9 electrode positions come from left, medial, to right by anterior, central to posterior, that is, left anterior(LA, the same below), medial anterior(MA), right anterior(RA), left central(LC), medial central(MC), right central(RC), left posterior(LP), medial posterior(MP), and right posterior(RP). The top panel is for children, and the bottom panel is for adults. “Add” means “Addition”, “Mult” means “Multiplication”.

Posterior P1 and N1

The P1 and N1 occurred only at posterior electrodes. To examine early differences associated with perceptual processing, we examined operation and age effects of the peak amplitude and latency of the posterior P1 and N1, using a 2 group (adults, children) × 2 operation (multiplication, addition) × 2 laterality (left, right) analysis of variance (ANOVA). The peak amplitude and latency for P1 were detected in the time window 100–150 ms, and for N1 were detected in the time window 150–220 ms.

The peak of posterior P1 showed a significant interaction of age and laterality, F(1, 40)=8.62, p=.005. Further simple effect tests showed that children had a larger posterior P1 than adults at left electrodes, F(1, 40)=5.62, p=.02; and at right electrodes, F(1, 40)=25.33, p<.001. No lateralization effect was found for adults, but children had larger P1s at right electrodes than at left electrodes, F(1, 40)=17.86, p<.001. Only a main effect of age was found for latency of P1, that is, children had longer latency than adults, 126 (±6) vs. 115(±5) ms, F(1, 40)=13.61, p<.001. Only a main effect of age for the peak of N1 component was found, that is, children had larger peak amplitudes, F(1, 40)=34.34, p<.001. Children also had longer latencies of the N1 than adults, 208 (±5) vs. 184(±10) ms, F(1, 40)=28.47, p<.001.

Slow potential components

Following the P1 and N1 components, there were slow potential components in all electrodes. Mental processing associated with the access and retrieval of representations for arithmetic facts could be reflected in the slow potential component. We analyzed the operation effect and developmental effect in the time window of 400–900 ms because this time window covered the deflections of the slow potential components for both children and adults and for both addition and multiplication. To examine the time course of these effects, we also divided the slow potential component into smaller time windows, each lasting 100 ms, that is, 400–500, 500–600, 600–700, 700–800, and 800–900 ms.

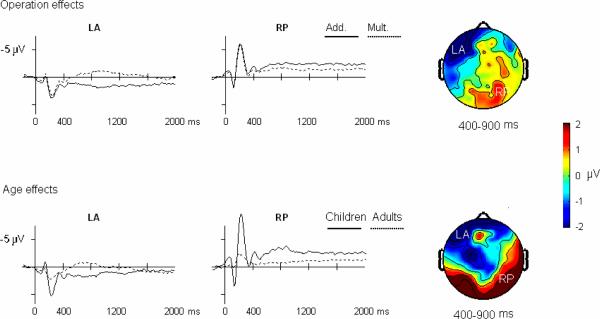
We conducted a 2 age (children, adults) × 2 operation (multiplication, subtraction) × 5 time window (400–500, 500–600, 600–700, 700–800, 800–900) × electrode position (9 positions) ANOVA on the mean amplitude. First, we observed a two-way interaction of operation and electrode position, F(8,320)=4.57, p=.002 (see Figure 2). Further simple effect tests showed that multiplication had larger negativities than addition at left anterior electrodes, F(1,40)=11.54, p=.002, whereas addition problems produced a greater negativity at right posterior electrodes, F(1,40)=4.34, p=.04. Second, there was the interaction of age and electrode position, F(8,320)=5.48, p<.001 (see Figure 3). Further simple effect tests showed that adults had large negativities than children at left anterior electrodes, F(1,40)=5.42, p=.025, and at central median electrodes, F(1,40)=8.97, p=.005; but children had greater negativity at left posterior electrodes, F(1,40)=12.11, p=.001, and at right posterior electrodes, F(1,40)=9.60, p=.004. There were no other significant interactions. Additionally, there was not a main effect of time window.

Figure 2.

Operation effects (multiplication versus subtraction, collapsed across age) in the top panel and age effects (adults versus children, collapsed across operation) in the bottom panel. The left includes the waveform at left anterior electrodes (LA) and the waveform at right posterior electrodes (RP), both from −200 ms to 2000 ms. The right refers to the topographies of difference waveforms for multiplication – addition and for adult– children in the time windows 400–900 ms. Add.: Addition, Mult.: Multiplication.

DISCUSSION

The goal of present study was to examine developmental differences in event-related potentials (ERPs) between second graders (7.8 years old) and adults (21.5 years old) in simple arithmetic (addition and multiplication). Previous studies in adults have suggested that multiplication problems rely more on a verbal processing system involving left perisylvian language areas for accessing math facts (e.g., Dehaene & Cohen, 1997; Delazer & Benke, 1997; Pesenti et al., 1994; Zhou et al., 2006, 2007), whereas addition problems rely more on a quantitative manipulation system involving visuo-spatial processing cortex (e.g., bilaterial intra-parietal sulcus) to calculate magnitude (Zhou et al., 2007). Consistent with previous literature in adults, multiplication problems for both children and adults produced a greater left anterior negativity from 400 to 900 ms, whereas addition problems produced a greater right posterior negativity in that time window. In terms of developmental differences, adults showed larger left anterior negativities from 400 to 900 ms for both addition and multiplication suggesting that adults rely more than children on a verbal processing system for solving these problems. Children showed larger right posterior negativities in that time window for both addition and multiplication suggesting that they rely more on quantitative manipulation for solving these problems. Altogether, our study suggests that, (1) adults and children share a similar dissociation of arithmetic facts, and (2) there is a developmental shift from reliance on a quantitative manipulation system to a reliance on a verbal processing system for solving simple arithmetic problems.

In current study, responses were only required for false problems in the arithmetic verification task and only 32 of 256 problems were false. Consequently, the response time measure was based on few trials, so this measure might be insensitive to operation effects. However, the lack of operation effects for both adults and children is a replication and extension of our previous study. In this study, undergraduates were asked to press keys to true and false single digit addition and multiplication problems (Zhou et al., 2007).

Differential Brain Organization for Addition and Multiplication

The first major finding regarding operation effects was that, relative to addition, multiplication produced greater left anterior negativity. This operation effect replicates results of our previous study (Zhou et al., 2006). In that study, participants were asked to first generate a solution to a given arithmetic problem (e.g., 2+3) and then to judge if their solution matched the presented answer (e.g., 5). Results showed a greater N300 component at left anterior electrodes for multiplication than for addition and subtraction during solution generation. The operation effect in our previous study occurred about 300 ms, but in the present study it was observed at about 400 ms. The later operation effect might be due to the longer exposure (2000 ms) to problems in present study. In our previous study, the problems were presented for only 200 ms, followed by a 1300 ms blank screen.

Previous studies on language processing have found a left anterior negativity during verbal or phonological processing (Altenmüller et al., 1993; Rowan et al., 2004; Rugg, 1984). These negative potentials were typically in fronto-central regions and were greater over the left than right hemisphere. Depending on task, they have been found to peak at around 300 ms (Niznikiewicz and Squires, 1996) or continue as a slow cortical potential from 1 to 3 seconds (Rowan et al., 2004). Greater potentials for multiplication from 400 to 900 ms in left frontal electrodes in the present study support the claim that multiplication involves more verbal processing than addition. The notion that multiplication facts are represented as phonological codes is consistent with previous neuropsychological findings (e.g., Dehaene & Cohen, 1997; Delazer & Benke, 1997; Present et al., 1994).

Rowan et al. (2004) examined the brain source of the lateralized slow cortical potential with the fMRI technique. They suggested that multiple brain regions contributed to the amplitude deflection, in particular, left inferior temporal, superior temporal, and inferior frontal cortices. The source analysis of the operation effect in our previous ERP study localized its source in left anterior brain areas (Zhou et al., 2006). Our fMRI study on simple arithmetic further demonstrated that compared to addition, single-digit multiplication elicited greater activation in language processing areas, including precentral gyrus, supplementary motor association cortex, and posterior and anterior superior temporal gyrus in the left hemisphere (Zhou et al., 2007). Combining these results, it is reasonable to conclude that greater activation for multiplication in brain areas involved in language, including superior temporal gyrus and inferior frontal gyrus in the left hemisphere, contribute to the greater left anterior negativities in the present study.

The second major finding regarding operation effects was that, relative to multiplication, addition produced greater negative potentials at right posterior electrodes. This result is consistent with our fMRI finding that addition had greater activation than multiplication in intraparietal sulcus and middle occipital gyrus in the right hemisphere, and superior occipital gyri in both hemispheres (Zhou et al., 2007). Previous studies have suggested that bilateral IPS is important for the manipulation of symbolic and non-symbolic numerical magnitude (e.g., Dehaene, Spelke, Stanescu, Pinel, & Tsivkin, 1999; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). The greater activation in IPS for addition relative to multiplication in the present study could reflect access and the manipulation of the magnitude information during addition.

Number representation has been claimed to have strong visuo-spatial properties (see a review by de Hevia, Vallar, & Girelli, 2008). The SNARC effect, faster response to small numbers with the left hand and faster response to larger numbers with the right hand (e.g., Dehaene, Bossini, & Giraux, 1993), suggests that numbers are encoded in a linear format in the human brain. Zorzi, Priftis, and Umiltà (2002) found that right-brain-damaged patients with persistent left neglect always had right-shift errors when they were asked to bisect a numerical interval (e.g., 11–19). These findings suggest that the mental number line may be functionally isomorphic to a physical line. The mental number line, possibly the left-to-right spatial layout of Arabic-form images, should be more involved during manipulations of magnitude in the addition task in the present study; and this may be the reason for greater activation for addition in brain regions associated with visuo-spatial processing. According to ERP studies on mental rotation, greater negative potentials at parietal electrodes have been interpreted as greater visuospatial processing (e.g., Heil & Rolke, 2002; Yoshino et al., 2000). Thus, greater negative potentials for addition in right posterior electrodes for the present study could be interpreted as greater demands on visuo-spatial processing to support numerical magnitude processing for addition as compared to multiplication. These regions have been implicated in visual perception, visual mental imagery, visuo-spatial working memory, and spatial attention (e.g. Corbetta et al., 1998; LaBar, Gitelman, Parrish, & Mesulam, 1999).

The present study found that children showed a similar dissociation of brain organization for simple arithmetic (i.e., addition and multiplication) as did adults. The dissociation is presumably related to the application of quantitative manipulation strategies for addition and the application of verbal memory strategies during multiplication. Although children were in the early acquisition of arithmetic, they had just finished formal learning of addition and multiplication facts in the context of classroom instruction. They had undergone extensive practice on the single-digit arithmetic with the differential learning strategies.

Developmental Changes in Brain Organization for Arithmetic Processing

The P1 is a positive deflection that is typically observed over occipital electrodes around 100 ms post stimulus onset. The P1 is sensitive to physical stimulus characteristics (e.g. visual contrast, luminance, size) and has a neural source in striate and extrastriate visual areas (e.g., Dale et al., 2000). The N1 followed the P1, with a latency of around 140–220 ms post stimulus onset (e.g., Bentin, Mouchetant-Rostaing, Giard, Echallier, & Pernier, 1999). Unlike the P1, the N1 may be category-specific, with larger amplitude to words or word-like stimuli (e.g. letter, pseudofont strings) by comparison with nonsense strings (e.g. icons, symbols) (e.g., Bentin et al., 1999). The N1 for word processing was left-lateralized and seemed to have a neural source in occipito-temporal cortex (e.g. in the visual word form area [VWFA]), related to extracting visual invariants of words or word-like stimuli (e.g. Brem, et al., 2006). Developmental studies on visual word processing (e.g., Grossi, Coch, Coffey-Corina, Holcomb, & Neville, 2001; Holcomb, Coffey, & Neville, 1992) have reported developmental decreases in the amplitude of the P1 and N1 as children get older. The present study also found the age-related decreases in amplitude as well as latencies of the P1 and N1. The larger P1 and N1 with delayed peak latency for children could be interpreted as less automatic and robust processing of Arabic digit forms. The P1 and N1 were not sensitive to operation (i.e. multiplication and addition) and therefore these components likely reflect low level processing.

The major developmental findings of the present study were that adults had larger left anterior negativities than children from 400–900 ms post-stimulus, and children showed larger left and right posterior negativities in that time window. These developmental shifts seemed to be specific to arithmetic processing and not due to general developmental changes because previous ERP studies on the neural development of attention and memory showed different age-related changes (e.g., Friedman, Ritter, & Snodgrass, 1996; Perchet & Garcia-Larrea, 2005).

Behavioral models of arithmetic development suggested that acquisition is marked by increasing reliance on the memory of the associations between digit pairs and their answers (Geary & Hoard, 2002). Our finding that adults showed larger left anterior negativities for addition and multiplication could be interpreted as greater verbal reliance by adults on retrieval of addition and multiplication facts. The interpretation is based on the conclusion that the left anterior negativities observed in previous studies on language processing is associated with verbal processing (e.g., Altenmüller et al., 1993; Rugg, 1984). Our previous ERP study (Zhou et al., 2006) and fMRI study (Zhou et al., 2007) on the single-digit addition and multiplication were also consistent with the notion that the left anterior negativities reflect verbal processing in simple arithmetic. Greater reliance on verbal processing by adults may have resulted from increased familiarity of arithmetic facts, as shown in the faster responses by adults to arithmetic verification in the present study.

To solve addition problems, children appeared to rely to a larger extent on the quantitative manipulation system, as suggested by larger right posterior negativities for addition during 400 to 900 ms, as compared to adults. Children also showed greater right posterior negativities compared to adults for multiplication during 400–900 ms suggesting that children relied to a greater degree on the quantitative manipulation system for multiplication. Although children could correctly recite the Chinese multiplication table, they did not have the same familiarity of multiplication facts as adults. The quantitative manipulation during children's addition and multiplication could be due to the use of back-up strategies for the simple arithmetic problems. Previous studies have shown that children during the acquisition of simple arithmetic rely on various strategies (e.g., counting procedures for addition, counting by n for multiplication) before they retrieve most of the multiplication facts from long-term memory (e.g., Ashcraft, 1982; Lefevre et al., 1996).

Ours was the first neuroimaging study to show a developmental shift from reliance on a quantitative manipulation system to reliance on a verbal processing system for solving simple arithmetic problems. This developmental shift is consistent with training studies of arithmetic. After training on various arithmetic problems (e.g. subtraction and multiplication), studies have shown that untrained items produce greater activation than trained items in parietal regions (e.g., bilateral intra-parietal sulci), whereas trained items (only multiplication) produce greater activation than untrained items in bilateral superior temporal gyri/angular gyri (e.g., Delazer et al., 2003). Qin et al. (2004) examined the effect of learning algebra problems in children (12- to 15-year-olds). They found decreasing activation in left parietal cortex, and increasing activation in bilateral supramarginal gyrus with practice. As with our developmental study, these training studies suggest a shift from reliance on the quantitative manipulation system to the verbal processing system. The development shift in the present study may be due to long-term practice with simple arithmetic.

To summarize, the present study showed both age-independent and -dependent neural activities in simple arithmetic. The dissociation of addition and multiplication in children is the first evidence to show early effects of arithmetic acquisition on brain organization. Consistent with previous studies, multiplication seems to rely more on a verbal memory system in perisylvian language areas, whereas addition seems to rely more on quantitative manipulation in parietal cortex. We also provided the first evidence to show the developmental shift from reliance on magnitude manipulation to verbal memory processing for arithmetic. In order to better understand the neural development of arithmetic processing, it is necessary to examine the role of specific brain regions (e.g. intraparietal sulcus, angular gyrus) in arithmetic over development, with a higher spatial resolution techniques, such as functional magnetic resonance imaging.