Context effects on musical chord categorization: Different forms of top-down feedback in speech and music?

Abstract

A critical issue in perception is the manner in which top-down expectancies guide lower-level perceptual processes. In speech, a common paradigm is to construct continua ranging between two phonetic endpoints and to determine how higher level lexical context influences the perceived boundary. We applied this approach to music, presenting subjects with major/minor triad continua after brief musical contexts. Two experiments yielded results that differed from classic results in speech perception. In speech, context generally expands the category of the expected stimuli. We found the opposite in music: the major/minor boundary shifted toward the expected category, contracting it. Together, these experiments support the hypothesis that musical expectancy can feed back to affect lower-level perceptual processes. However, it may do so in a way that differs fundamentally from what has been seen in other domains.

1. Introduction

In the last 30 years, research in spoken language comprehension has often been compared to work in music perception. Early work in this paradigm examined auditory perception in both speech and music to test claims that low-level speech perception processes are specific to language stimuli (Burns & Ward, 1978; Cutting & Rosner, 1974; Howard, Rosen & Broad, 1992; Locke & Kellar, 1973; Pastore, Schmuckler, Rosenblum & Szcesiul, 1983; Zatorre & Halpern, 1979). This work did not ultimately support a speech-specific mode of processing, instead suggesting that such processes are domain-general. This has been extended in a number of directions, resulting in the now broadly accepted that speech and music perception may both operate by similar perceptual principles like categorical perception (Speech: Liberman, Harris, Hoffman & Griffith, 1957, Repp, 1984 for a review; Music: Locke & Kellar, 1973; Howard et al, 1992), duplex perception (Speech: Whalen & Liberman, 1987; Music: Pastore et al, 1983; Hall & Pastore, 1992; though see Collins, 1985) and context-based restoration effects (Speech: Samuel, 1981; Music: Dewitt & Samuel, 1990). Ross, Choi and Purves (2007) provide an explanation for these common principles. Their analysis of the formant structure of isolated speech suggests that the tonal structure of music may have its evolutionary origins in the acoustics of language. Thus, it should not be surprising that both operate similarly.

Deep similarities between language and music have also been pointed out at higher levels. Both are inherently temporal, requiring similar short-term memory processes (Music: Greene & Samuel, 1986; Speech: Gibson, 1999). Similar forms of implicit statistical learning are employed for streams of both tones and syllables (Music: Saffran, Johnson, Aslin & Newport, 1999; Speech: Saffran, Aslin & Newport, 1996). Links have been established between absolute pitch and speakers of tone languages (Deutsch, Henthorn and Doslon, 2004). Finally, music and speech use a phrase structure that interacts with prosodic and rhythmic properties of the signal. This is detectable by both infants (Krumhansl & Jusczyk, 1990; Hirsh-Pasek, Kemler-Nelson, Juscyzk, Cassidy, Druss, & Kennedy, 1987) and adults (Stoffer, 1985). Cognitive neuroscience has built on this with an increasing number of studies showing at least some neuroanatomical overlap between areas processing language (particularly syntax) and music (Maess, Koelsch, Gunter & Friederici, 2001; Koelsch, Gunter, von Cramon, Zysset, Lohmann & Friederici, 2002).

Despite the magnitude of research demonstrating similarities, there are also clear differences. There’s not a clear musical analogue to semantics, nor does language have a vertical, harmonic structure (Besson & Schön, 2001). There are cortical regions that respond selectively to music or speech, as revealed by imaging techniques (reviewed in Zatorre & Binder, 2000) and neuropsychological work (Peretz & Coltheart, 2003). Discrepancies can also be seen in more subtle measures. Besson and Schön (2001), for example, demonstrate differences in Event Related Potentials (ERP) measures of expectancy violation in sung music: an N400 arises for linguistic violations in meaning, and a P600 for violations of musical structure. This argues for differences in the neural generators of these components (and perhaps the cognitive processes), but it also reveals a common principle, expectation formation and violation. Thus, while music and speech are by no means identical processes, the comparison of the two provides a paradigm in which to understand the broader principles of perceptual categorization and temporal organization that may apply across possibly different (specialized) brain areas (Lynch, Eilers & Bornstein, 1992; McMullen & Saffran, 2004; Patel, 2003). This is particularly the case in the auditory domain since music represents the only domain that approaches the complexity or temporal structure of speech.

The present experiments were intended to extend this approach by examining the way in which perceptual expectations formed by musical context influence the process of categorizing pitches into notes and chords. That is, how do those listeners’ inferences about potential upcoming musical events shape the perception of those events?

Similarly to recognizing phonemes in speech, recognizing a chord requires a listener to map a range of the continuous input-space onto chord categories (e.g. Locke & Kellar, 1973). In both domains this mapping is relative: the acoustic properties of speech must be interpreted relative to factors like the speaker’s rate or vocal tract shape and size; likewise the acoustic properties of a note or chord must be interpreted relative to the scale and key of the piece as well as the temperament of the instrument. Thus, context must play a critical role in solving this problem. Work on context effects in speech has shown that expectations for a specific category can alter the mappings between continuous inputs and the resulting categories (Ganong, 1980; McClelland, Mirman & Holt, 2006 for a review). However, while it is well known that musical context can create expectations for specific categories (e.g. Bharucha & Stoeckig, 1986), there is only a limited amount of work on how these expectations interact with perceptual categorization processes (e.g. DeWitt & Samuel, 1990; Desain & Honing, 2003; Wapnick, Bourassa & Samson, 1982). These studies, however, have not been conducted in domains of music that permit an ideal comparison with speech perception.

We start with an overview of work on musical expectancy, showing that musical context creates expectancies for chords, and can prime their processing during online recognition. This has been framed in terms of interactive activation (Bharucha, 1987), an architecture that has also been applied to speech. We will discuss this analogous work in speech to generate predictions for the present experiments, and then outline the logic of the present work. Finally, we present two experiments examining the effects of musical context on major/minor chord identification.

1.1 Context and Expectancy in Music Perception

Much of the work on listeners’ interpretation of melody and tonality in music has been framed by the notion of expectancy. Expectancy is broad; ranging from the specific expectations about how melodies are completed (e.g. after hearing the first four or five notes of Happy Birthday virtually all American listeners know exactly what note is coming next), to broader expectations about what notes are “allowed” in a given key, to even more broad expectations about the contour of a melody.

A primary focus of work on melodic or harmonic expectancy has been to establish what people expect. Some of the most influential models (Narmour, 1992; Schellenberg, 1996) make use of a small number of heuristic rules that largely ignore tonal structure to predict upcoming melodic elements. Such principles have done surprisingly well at describing listeners expectations during musical passages (Cuddy & Lunny, 1995; Schellenberg, 1996; 1997); however, it is also clear that tonality and key exert considerable additional influence of on expectancy (Cuddy & Lunny, 1995; Krumhansl, 1995; Schellenberg, 1996).

Krumhansl and her colleagues (Krumhansl and Kessler, 1982; Krumhansl, 1990 for a review) have unpacked listeners’ expectations with respect to key. They demonstrate that after short musical passages (scales or chords) the strength of listeners’ expectations to each of the 12 notes in the chromatic scale correlates well with traditional Western scale structure (forming a “tonal hierarchy”), and with frequency counts of notes used in actual music. This representation of key can be roughly seen as first-order expectancy—the class of notes that a listener might expect if he or she knew only the key.

Listeners’ expectations due to tonality and those due to contour may ultimately derive from the same processes. Pearce and Wiggins (2006), suggests both can be derived on the basis of the statistical structure in a corpus of music. Moreover, they are not static, even during the short time scales of perception. Toiviainen and Krumhansl (2003) demonstrate this quite clearly in a study in which listeners rated the goodness of each of the notes of the chromatic scale while they listened to a musical passage. Analysis of these rating with respect to the tonal hierarchy demonstrated that expectations develop rapidly, are graded and partial, and that within some passages there are periods of time in which they are diffuse and non-distinct. However, at certain points in time (e.g. the end of a phrase) these expectations are powerful and quite distinct.

Thus, musical context can create the sort of expectations that may interact with perceptual processes. However, these studies ignore the continuous nature of the stimulus (as a collection of pitches of various frequencies), and the demands of categorizing these pitches into notes and chords—the perceptual categorization problem of primary concern here. More importantly, by largely focusing on what listeners expect to hear, they also ignores what they actually do with those expectations in the moment while they are listening to music.

Bharucha and Stoekig (1986) addressed this by examining listeners’ latencies to make simple perceptual decisions (major/minor or in-tune/out-of-tune) after a short musical context. Listeners responded faster for chords that were expected (given the initial sequence), than for chords that were unrelated to the context. Thus, expectancy operates implicitly as well as explicitly. Tillman, Janeta, Birk and Bharucha (2003) later compared the melodic priming effect to a baseline condition (in which there was no clear key), demonstrating significant priming against this new standard. This suggested that priming is facilitory—expectancy builds activation for upcoming chords online, during music perception. They also tested subdominant as well as dominant chords (e.g. IV and V) and found significant priming (though less than that of tonics). This suggests 1) that priming is a general result of expectancy, and is not restricted to highly expected dominant-tonic sequences; and 2) that expectancy (and the resulting activation) is fundamentally graded. As a whole, this literature suggests an implicit, online view of expectancy in which musical context builds activations for potential subsequent material so as to facilitate their perceptual and musical processing.

Bharucha (1987) proposed an interactive activation account of this process. Their interactive activation network has nodes representing specific tones, chords and keys. Chord notes are connected to their component tones, and keys to their component chords (and Tillman, Bharucha & Bigand, 2000, suggest that the necessary connectivity can be learned from the statistical structure of a musical corpus). After hearing a given note (or sequence of notes). activation feeds back and forth along these connections, activating the appropriate tones, chords and keys. Over time, this network settles on an optimal interpretation of the stimulus—damping activation for irrelevant keys and chords, and ramping up activation for the correct interpretation. The process is dynamic and graded, so that activation from a currently active chord can spread (through keys and back) to activate related or expected chords before or as they are heard. This then serves as a primary mechanism for explaining these priming effects.

A critical property of interactive activation models is that activation unfolds over a characteristic timecourse. In particular, across a range of models, it has been shown that bottom-up perceptual information tends to dominate during the earliest moments of processing, while top-down contextual information plays a larger role later. This effect has been shown behaviorally in a number of domains, validating interactive models of visual comparison (Goldstone & Medin, 1995) and word recognition (Pitt & Samuel, 2006). Tekman and Bharucha (1992) present evidence that similar processes apply to music. They compared two types of prime chords—acoustically similar chords that were not harmonically related to the target, and acoustically dissimilar chords that were more harmonically related to the target—at two stimulus-onset-asynchronies (SOAs). They found that at short SOAs, listeners showed priming for the acoustically similar chords, but at longer SOAs only harmonically related chords were primed. This provides critical support for interactive activation as a mechanism by which melodic expectancy could influence online musical processing (and via comparison with Pitt & Samuel, 2006, further evidence that speech and music share common processing principles).

Our present questions concern the way expectancy affects the categorization of continuous (pitch) information into musical chords. The interactive activation framework provides a crucial bridge between this process and work in speech perception where it is an important explanatory tool that makes clear predictions about the role of context in perception.

1.2 Context Effects in Speech Perception

In speech perception, as in music, interactive activation models have been central to understanding the way that context affects the categorization of phonemes. Models such as TRACE (McClelland & Elman, 1986) use a similar hierarchical structure of elements to Bharucha’s (1987) model. In this case, TRACE uses layers for features, phonemes and words, and activation can spread both upward (from features to phonemes to words) and downward (from words to phonemes or features). This feedback allows lexical information to affect phonemic levels of representation in order to activate phonemes that are consistent with the broader lexical context. Much like in interactive accounts of music perception, high level knowledge (in this case words, not keys) is constructed on the basis of bottom-up perceptual information (phonetic features instead of notes). As it accumulates, this knowledge feeds back to affect perceptual processing. In a sense, then, lexical context serves to create expectancy for phonemic input (although most accounts suggest that lexical context can bias the perception of prior phonemes as well).

Interactive activation has been posited to explain a variety of context effects in speech categorization. One example of this is the phoneme restoration effect of Warren (1970; see also Warren & Warren, 1970). In this paradigm, a segment of running speech is completely excised and replaced with a noise-burst or cough. When listening to such stimuli, the missing phoneme is perceptually restored and listeners report a vivid perceptual experience. Crucially, the particular phoneme that is heard is consistent with the lexical (or semantic) context.

This paradigm demonstrates that sentential and lexical context can produce vivid phonemic percepts: activation at these levels can reach lower perceptual levels. However, it does not directly address the question of how contextual cues interact with incoming perceptual information. In this case, context does not affect the perception. Rather contextual information fills in for completely absent bottom-up information¹.

Ganong (1980) demonstrated that even when bottom up information is available, context affects speech categorization. He created sets of speech continua in which one endpoint was a word and one a non-word. For example, one ranged from duke to tuke (a non-word in American English), and a matching one ranged from doot to toot. The subjects’ task was to categorize the initial phoneme as /d/ or /t/. A shift in the category boundary between the two continua was seen, with the boundary shifting so that more of the tokens would be identified as consistent with the lexical endpoint. Importantly the cues to the initial consonant (d/t) were identical in each continuum, leaving lexical status as the only factor that could influence identification. In a sense, lexical context caused the category that was consistent with it to expand to account for more of the phonetic space.

This effect has been extensively replicated with lexical contexts (e.g. Fox, 1984; McQueen, 1991; Pitt, 1995) and extended to sentential ones. Miller, Green and Schermer (1980), for example showed that the perceptual boundary on a bath/path continuum was shifted by sentences like “She needs hot water for the b/path” or “She likes to jog along the b/path”. Thus, contextual information at multiple levels of representation can influence phoneme categorization (see also Borsky, Tuller & Shapiro, 1998; Connine, Blasko & Hall, 1991; van Alphen & McQueen, 2001). This work suggests a paradigm in which to address our core questions concerning the relationship between musical expectancy and the process of categorizing pitches into notes and chords. Similarly to speech, we can assess the mapping between the continuous input and categories, and how it changes as a function of context.

Subsequent work on lexical context effects has addressed the underlying mechanism behind these effects. Specifically, it has launched an intense debate about whether such effects arise out of either direct feedback from higher-level processing (as predicted by interactive activation mechanisms), or whether they derive from a post-perceptual mechanism (e.g. Norris, McQueen & Cutler, 2000; McClelland et al., 2006 for competing reviews). However, recent work has shown that lexically-biased phonemes can in turn affect the perception of neighboring phonemes (Elman & McClelland, 1988; Magnuson, McMurray, Tanenhaus & Aslin, 2003; Samuel & Pitt, 2003, but see Pitt & McQueen, 1998). This rules out a post-perceptual account—feedback is a legitimate property of the system. Interactive activation models like TRACE (McClelland & Elman, 1986) provide a compelling account of this feedback mechanism (McClelland et al, 2006, for a review) since the underlying phonemic percept is changed by lexical status (and could then interact with neighboring phonemes)². Moreover, recent research suggests lexical feedback may play additional roles, beyond simply biasing the perception of a single phoneme. McMurray, Munson & Gow (submitted) demonstrate that lexical feedback can interact with perceptual processes like parsing that influence the perception of multiple phonemes, even across word boundaries.

Thus, the interactive approach to lexical effects on phoneme categorization argues that context effects are an integral part of online language processing, one that permits the system to use contextual information to make inferences about upcoming material and resolve prior ambiguity. This data is best fit by interactive accounts that posit feedback from higher-level representations. This interactive activation approach to speech is analogous to what has been proposed for chord priming. Although Bharucha’s (1987) model does not attempt to model the process of mapping continuous pitches onto notes, it can easily scale down to these processes, as part of a general interactive activation framework. Such scaling framework has been applied to speech and language with the same general assumption: TRACE I (Elman & McClelland, 1986) maps the signal onto features or phonemes; TRACE II (McClelland & Elman, 1986) maps features to words; and MacDonald, Pearlmutter and Seidenberg (1994) show how interactive activation can build off lexical activation to account for structural and thematic decisions in parsing. Thus, this class of networks can easily be extended to multiple levels of representation, and inferences about the behavior of the network at one level are generally valid for other levels.

The present work applies this paradigm to music. Work on chord priming has clearly shown that listeners build activation for upcoming chords online as they listen to music. We ask whether these inferences could alter the process of identifying chords from their component frequencies (analogously to the way lexical activation can shift phoneme boundaries).

Consistent with these models, then, one hypothesis is that musical context builds activation for higher level representations of chords and keys. This expectancy would result in a number of possible expected chords being active. This can then feed back to affect the lower level processes that categorize pitches into notes. Here, as in the Ganong effect in speech, if a major chord is expected (and hence activated), it will activate its corresponding notes. While bottom-up information may be ambiguous (e.g. not quite a major third or a minor third), this top-down component would boost activation for the major third, and result in the chord being perceived as major. The result of this process is that ambiguous chords would be treated as consistent with the context, and the major/minor boundary will shift accordingly.

As an alternative account, unlike speech, the pitches of chords may be more stable with regards to context than phonemes. For example, while acoustic signatures of a /t/ can vary significantly with surrounding phonetic context, the pitch relationships in a chord may remain fairly constant in different musical contexts (particularly for highly expected chords)³. Thus, it is also possible that, unlike speech, chord categories are entirely perceived using feed-forward, bottom-up processes and are immune to contextual effects.

1.3 Chord Categorization

Testing these hypotheses requires an experimental design that would directly assess this perceptual categorization process and the way it interacts with context. Our design assessed the way in which a short musical context alters perception of a major or minor chord. In Western music, chords are typically composed of three notes: the root (the note from which the chord takes its name), the third (either 4 or 5 semitones above the tonic) and the fifth (7 semitones above the tonic). These triads have either a major or minor quality, determined by the third. If the third is 4 semitones above, the triad has a minor quality, a somber or sad affect. If the third is 5 semitones above the root, it is a major triad with more positive affect. Importantly, while the root defines the chord (e.g. C, A), the third alone determines the major or minor quality. This fact, makes it is simple to manipulate the pitch of the third to create a continuum of triads ranging from major to minor and anywhere in between. Thus, we can adopt a design similar to Ganong (1980) and Miller et al (1980) in which context effects are assessed by looking for a shift in the category boundary along a continuum. The interactive approach predicts such a shift continuum: listeners should identify more items from this continuum as major when the context predicts a major chord. This approach, however, makes the assumption that chord categories are analogous to phoneme categories (and that chord continua are analogous to speech continua). A body of research has shown that this is a reasonable assumption.

A large number of studies have examined such continua in speech (see McQueen, 1996, for an annotated bibliography). Typically, when subjects categorize each token along a speech continuum, their identifications exhibit a very sharp category boundary (e.g., Liberman et al, 1957), suggesting that most of the phonetic space is reliably and unambiguously mapped onto sharp categories. Moreover, when subjects are asked to discriminate neighboring continuum steps, they are quite poor unless the two steps straddle the category boundary, implying that continuous variation within a given category may not be accessible to higher-level cognition, a phenomenon termed categorical perception.

Locke and Kellar (1973) adapted this technique to major/minor identification (see also Burns & Ward, 1978 for an example with intervals). They created a continuum of triads ranging from major to minor and presented them to musically trained and untrained listeners. While untrained listeners exhibited poor identification functions, musically trained listeners showed the sharp boundaries and discrimination peaks that are characteristic of categorical perception. Howard et al, (1992) replicated this with a continuous measure of musical ability and showed a strong correlation between the slope of the identification (the sharpness of the categories) and musical ability. Thus, for musically trained listeners, chord categories may be analogous to phoneme categories.

Categorical speech perception was later shown to be largely an artifact of task (Carney, Widden & Viemeister, 1977; McMurray, Tanenhaus & Aslin, 2002; McMurray, Aslin, Tanenhaus, Spivey & Subik, in press; Schouten, Gerrits & Van Hessen, 2003), but work in music perception has not examined the sorts of task manipulations that might reveal this (although Wapnick, Bourassa & Sampson, 1982, and the fact that expressive changes in the tuning have noticeable effects on perception provide some evidence). For the present purposes, it is sufficient to note the analogy between triad and phoneme identification: Both require mapping a continuous dimension onto complex categories, and both exhibit a similar behavioral profile. If chords are categorized via a similar process, this supports the viability of the hypotheses generated by the interactive activation approach applied to music.

DeWitt and Samuel (1990) took advantage of these analogical levels of processing to examine context effects in music perception by applying the phoneme restoration paradigm (Warren, 1970; Samuel, 1981) to music. Subjects heard passages in which either one of the tones was excised and replaced by noise, or one of the tones was played with noise superimposed. Subjects had to determine whether the tone was present or absent. If subjects perceptually restored the tone this discrimination would be difficult and discrimination would be at chance. However, if there was no restoration, this would be easy.

In the first three experiments, short unharmonized melodies were used as context. Evidence for restoration was found, but restoration was weaker with more familiar melodies and with melodies with higher expectancy (in contrast to the predictions of interactive-activation accounts). The authors concluded that melodic information was aiding the perceptual analysis and improving discrimination, but it was not building sufficient expectancy to drive restoration. However, in Experiments 4 and 5, the authors used passages that implied key much more strongly (either a scale or a sequence of chords). Here they found that these highly expectant sequences yielded more restoration, and that the particular note restored was generally consistent with the key or the expectation.

These findings are generally consistent with a dual-process account that includes interactive activation, although there must also be a mechanisms by which context facilitates perceptual analysis. Short melodic sequences do not build up sufficient expectancy to activate upcoming material and create the restoration effect. However, they do provide enough material to aid perceptual processing. More key-defining sequences (particularly those with chords), on the other hand, offer a rich enough stimulus to engage interactive activation mechanisms and drive restoration.

Even within this account, however, it is not clear if the enhanced perceptual processing (as opposed to restoration) arises out of a core-property of the system that interprets music, or whether it is a somewhat secondary task that is engaged by the perceptual discrimination task. Thus, it is crucial to address these questions about the integration of context and perception using a task that is perhaps more central to core music processes. There is considerable debate about what the “goal” of music perception is and what constitutes musical “meaning”. However, given the important role of a chord’s major/minor status in determining key, creating expectancy, and even building affect, identifying a chord as major or minor seems more integral to the musical meaning of a piece than detecting whether they are in- or out-of-tune (a common technique in the chord priming literature), or whether a noise-burst + tone is discriminable from a noise-burst alone.

1.4 Summary

Thus, the present experiments used sequences of chords to generate expectancies for either a major or minor chord. Such sequences were shown by DeWitt and Samuel to create strong expectancies and drive restoration. After hearing this context, subjects were immediately presented with a token from a major or minor continuum and were asked to identify it. We identify two hypotheses. First, the interactive activation account that explains results in both chord priming and speech perception predicts that the major/minor boundary found in this procedure will shift such that more chords will be identified as consistent with context. Under this view, musical expectancy expands the frequency-space occupied by the expected chord. The alternative hypothesis is that, unlike speech, musical chords are typically quite unambiguous, and as a result they are categorized by a bottom-up feed-forward process that is relatively immune to context effects.

2. Experiment 1

Experiment 1 tested listeners in a major/minor decision task after contexts that predicted either a major or minor chord.

2.1 Methods

2.1.1. Participants

Thirteen University of Iowa undergraduates served as participants in this study. All participants were music majors who were enrolled in their second or fourth semester of the music school’s music theory sequence. Music majors at the University of Iowa receive extensive ear training on triad and interval identification as part of their theory instruction, so participants had at least two semesters of ear training prior to participation. Informed consent was administered in accordance with the guidelines of the American Psychological Association, and subjects were paid $8 for their participation.

2.1.2 Stimuli

Stimuli consisted of two sets of three chord contexts followed by 4 major/minor continua. Triangle waves were used for all of the stimuli to create a richer, more musical timbre and a stronger context. These were synthesized ⁴ by adding sine waves whose frequencies were the first 25 odd numbered harmonics, and whose relative amplitudes were the inverse of the harmonic number squared. Harmonic components were in phase with each other both within a note and across a chord (e.g. each started at 0 at the onset of a note). Each sequence was constructed from three chords lasting 900 ms, with 100 ms of silence in between them. The target chord lasted 1500 ms. Chords were constructed from an equal tempered tuning system.

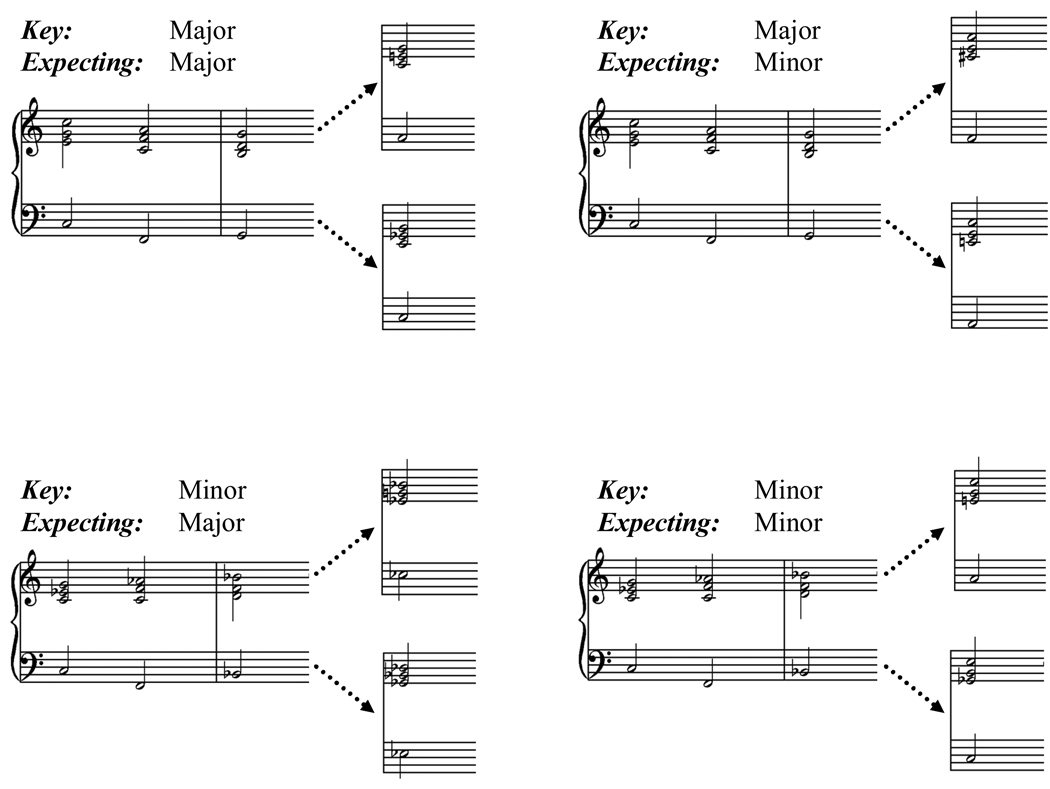
Two context sequences were constructed from these triangle-waves, one in a major key and one in a minor key. The sequences of chords are provided in Table 1 and the notation in Figure 1. Since we wanted to minimize predictability between the context sequence and the major or minor response (e.g. if C E G always biased a major chord), each sequence was used twice: once resolving to the tonic, and a second time resolving to an alternative. The use of each context twice in this way ensured that expectancy as a factor could be contrasted within identical context sequences. For the major sequence, this meant that one sequence would resolve to C major (the tonic), and one to A minor (a deceptive cadence which falls on the relative minor). For the minor sequence, one resolved to C minor (the tonic) and the second sequence resolved to the Eb major (the relative major). Additionally, in the minor sequence the dominant was not used so that there would be no ambiguity about whether it should resolve to major or minor. Instead, the seventh was used as the fifth (when the tonic was expected) and that same chord (the seventh) served as fifth for the major chord.

Table 1.

Overview of the conditions tested in Experiments 1 and 2.

Condition	Key	Expectancy	Context Sequence	Expected Chord
Maj – Maj	Major	Major	I  IV   V C    F    G	I C major
Maj – Min		Minor	I  IV   V C    F    G	vi A minor
Min – Maj	Minor	Major	i  iv   VII Cm Fm Bb	i Cm
Min – Min		Minor	i  VI   VII Cm Fm Bb	III Eb

Figure 1.

Score used in each of the four conditions in Experiment 1. Note that within a key (rows), the context sequence was identical, the only difference was in the root of the chord continuum.

Each context sequence consisted of a three note triad with a repetition of the tonic in the lower register (to help establish the tonal center). We did not attempt to use all root-position chords in these sequences as that would have led to poor voice-leading and, potentially, less musical expectancy. Instead, different voicings were used to maintain good voice-leading, with the exception that no unisons were permitted. This restriction led to small violations of standard voice-leading practice (for which we apologize to our music theory professors). However, Poulin-Charronnat Bigand and Madurell (2005) have shown that while such violations do slow processing, they do not alter patterns of expectancy (as measured by a priming paradigm).

Major-minor continua were constructed using the same triangle-wave synthesis as was used for the context. Each item in the continua consisted of all three notes of the triad with an additional root in the bass register which defined every chord as one in root position. A single note (the third) was changed in 10 equal steps to create an 11 step continuum ranging from major to minor.

Three such continua were constructed (C-major to C-minor; A-major to A-minor; and Eb-major to Eb-minor). Each continuum step was individually appended to a context sequence to create the final stimulus (11 sequences for each context). For each of the two contexts (the major-key context and the minor-key context) it was important to counterbalance the expectancy (whether the listener expected a major or minor chord). We wanted to avoid any association between the key and the expected chord. Thus, each context was used twice, once resolving to the tonic, and once resolving to the relative minor/major. The C continuum was used for both the major and minor sequences (as the tonic, though with different expectancies). The A continuum was appended to the major sequence (since it was in the key of C, A was the relative minor). The Eb continuum was appended to the minor sequence (since it was in the key of C-minor, Eb was a possible major completion). This led to 44 possible stimuli (2 keys × 2 expectancies × 11 continuum steps).

2.1.3 Task

After informed consent was administered, subjects were instructed that they were going to hear a series of musical sequences and that their task was to determine whether the final chord in the sequence was major or minor. Subjects then underwent a brief practice during which they identified each of the endpoint (unambiguous) chords in isolation. This was intended to familiarize them with the response keys, and with the overall sound of the chords while not giving them any experience with the expectancy-generating sequences.

After this short practice session, the test period began. On each trial subjects heard a complete context sequence followed by one token from the appropriate major/minor continuum. At the conclusion of the auditory stimulus a visual prompt cued them to the response keys and subjects pressed the “z” key to indicate a major chord and the “m” key to indicate a minor chord. Subjects heard each stimulus through a pair of Sennheiser HD-570 headphones, amplified by a Samson CQue8 headphone amplifier. Subjects were permitted to adjust the volume (on the amplifier) to a comfortable level.

2.1.4 Design

There were two context sequences (major and minor) crossed with two expectancy relationships (major and minor). These were combined with an 11step continua to yield 44 trials in a single repetition of the complete design. This was repeated 9 times to yield 396 trials. Completing this required approximately one hour. Trials were blocked such that all of the major key contexts appeared together in one block and minor key contexts in a second blocks. Note that within each key, however, both expectancies were equally likely. The order of the blocks was counterbalanced across subjects.

We predicted a main effect of expectancy, with major-expecting sequences yielding a shift in the boundary such that ambiguous tokens were categorized as major (and the inverse for minor-expecting passages). Key was varied in order to demonstrate that the perceptual effects can be seen in both types of passages. However, we did not hypothesize any effect of key, nor an interaction of key and expectancy. That is, listeners’ category boundaries should not shift for major or minor keys, and the magnitude of the shift due to expectancy should be the same in both keys.

2.2 Results

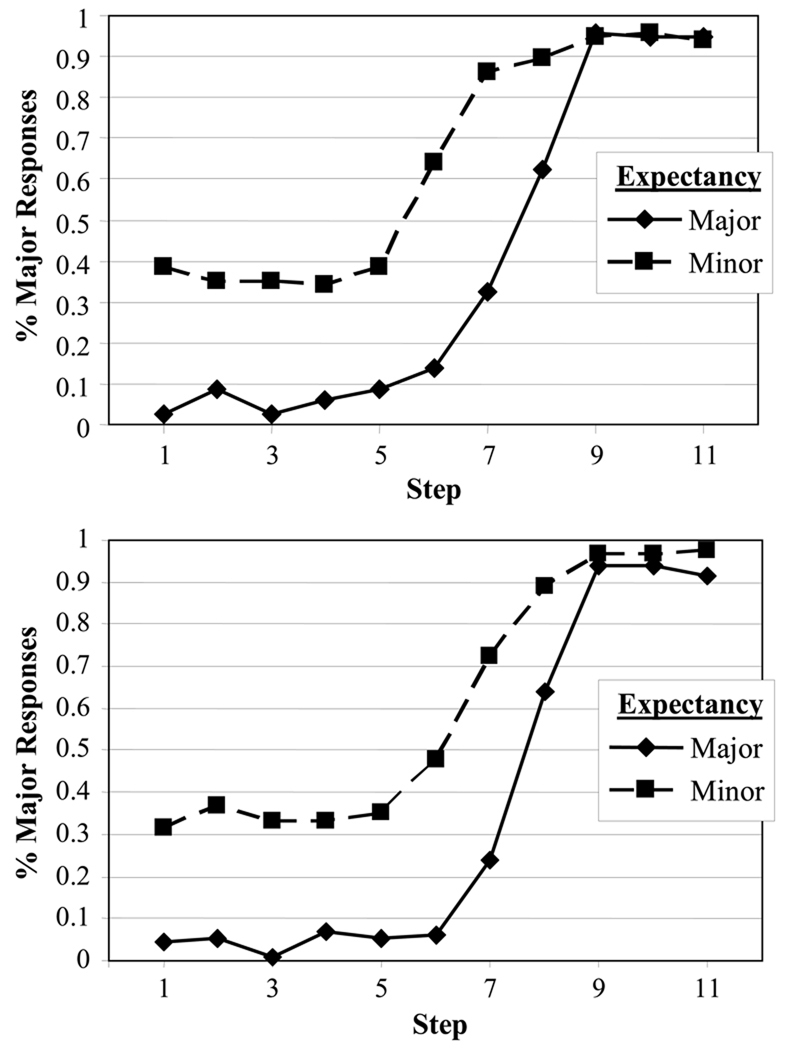
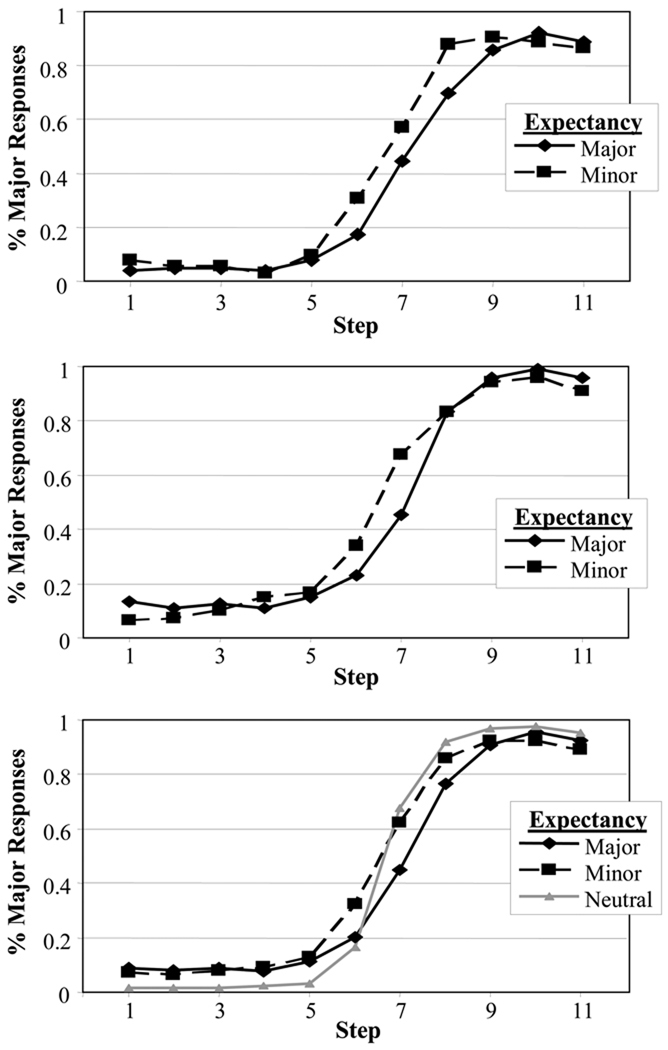
Figure 2 displays the proportion of major responses as a function of continuum step (ranging from minor to major) and expectancy. Panel A displays responses for the major-key context sequences; Panel B shows the same for the minor-key contexts. Overall, subjects showed a characteristic logistic pattern in their responses, particularly for contexts favoring major chords. For contexts expecting minor chords, however, there was a significant bias to report major. This bias was significantly non-zero even at step 1 (fully minor) in both conditions (At step 1, major expectancy: T(12)=3.8, p=.002; Minor: T(12)=2.7, p=.01). This bias prevented the use of a standard two-parameter logistic regression fitting slope and category boundary.

Figure 2.

Identification results of Experiment 2. A) Percentage of major responses as a function of step and expectancy for major keys. B) The same for minor keys.

Thus, to analyze these results, each subjects’ data was fit to a four-parameter logistic function, allowing us to determine the slope of the function and the category boundary (as in standard logistic regression) as well as the upper and lower asymptotes (standard logistic regression assumes these to be 0 and 1). These logistic parameters were estimated for each subject separately for each of the four conditions (two keys × two expectancies). These parameters (category boundary and bias in particular) then served as the dependent variable in a set of ANOVA’s. Overall the data fit the logistic models quite well, with a mean R² of .889 (SD=.196) across the thirteen subjects.

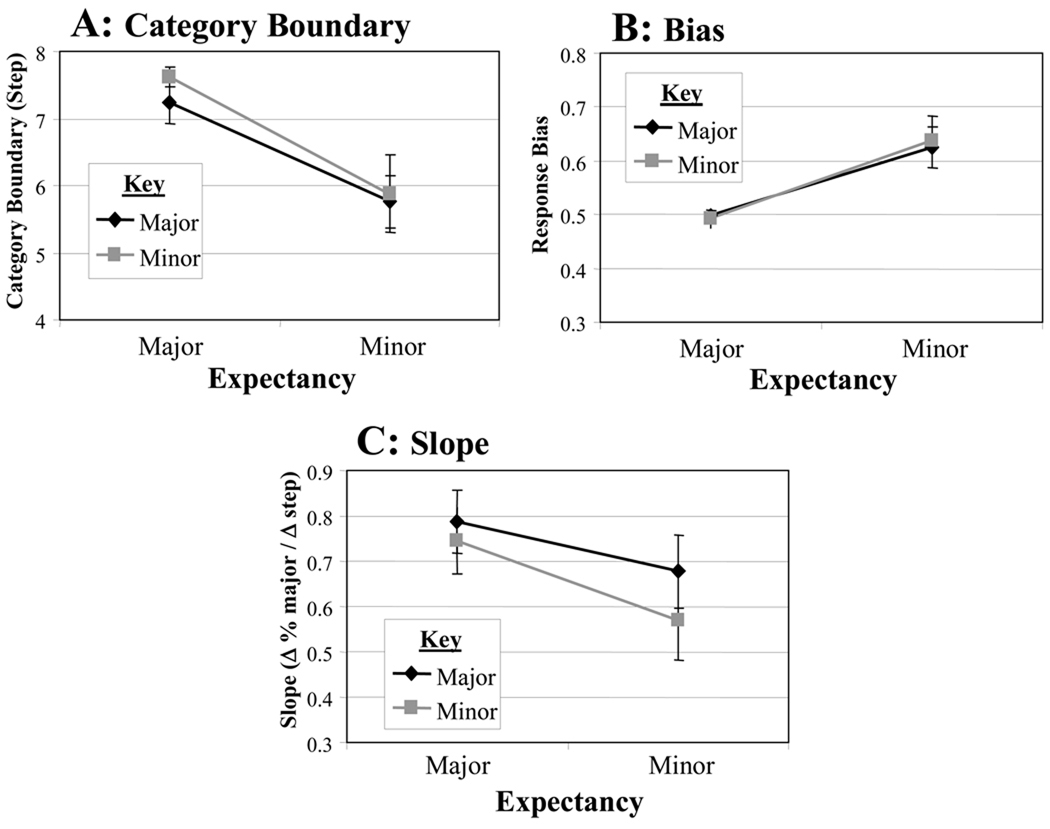
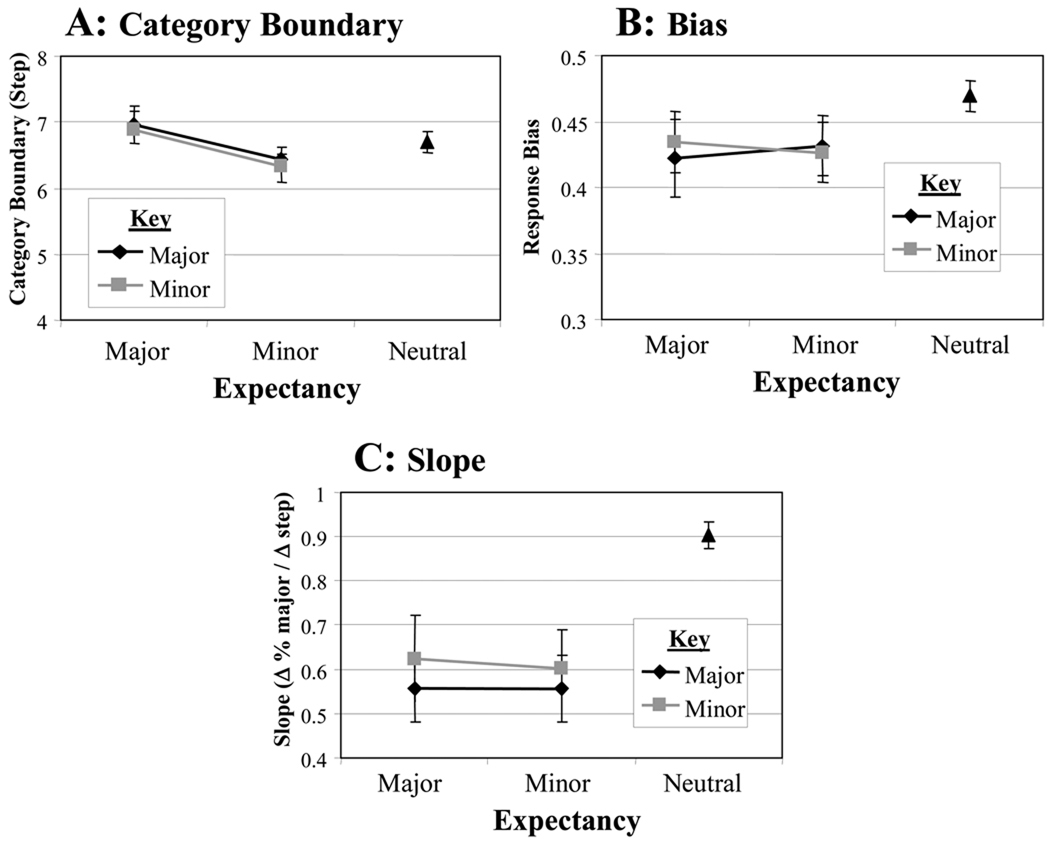
The first analysis examined the effect of expectancy and key on category boundary. Our predictions were that category boundary would shift as a function of melodic expectancy (but not as a function of key), such that there were more major responses in contexts in which a major chord was expected and more minor responses when a minor chord was expected. A 2 (key) × 2 (expectancy) repeated measures ANOVA was run using the obtained category boundaries as the dependent variable (Figure 3a). As expected, no effect of key was seen (F<1), suggesting that the major and minor keys did not show different boundaries. There was a main effect of expectancy (F(1,12)=17.4, p=.001). However, the direction of this effect was the reverse of our predictions: after a major-expecting sequence, category boundaries shifted toward the major end of the continuum, resulting in fewer major responses. This effect did not interact with Key (F<1).

Figure 3.

Key logistic parameters as a function of expectancy and key in Experiment 1. A) Category Boundary (continuum step). B) Bias (proportion). C) Slope (change in proportion per step).

The second analysis looked at bias. While we did not a priori predict any effect on overall bias, it is possible that expectancy shifts the overall response bias (towards major or minor) independently of the particular step or the boundary. Figure 3 confirms that this was the case. This 2 (key) × 2 (expectancy) ANOVA used the average of the lower and upper asymptotes as the dependent variable (Figure 3b). As in our prior analysis, there was no effect of key (F<1). However, there was, as before, a significant main effect of expectancy (F(1,12)=11.4, p=0.01). Major-expecting sequences were relatively unbiased (M=.49, SD=.004) while minor-expecting sequences were significantly major-biased (M=.63, SD=.009). Thus, as in our analysis of category boundary, bias shifts as a function of expectancy, but away from the expected chord. This effect did not interact with key (F<1), suggesting it was similar for both major- and minor-key contexts.

The final analysis examined slope, an indicator of the sharpness of the category (Figure 3c). Here, there was no effect of key (F(1,12)=1.2, p>0.2). A marginally significant effect of expectancy was seen (F(1,12)=3.7, p=0.08), in that major expectancies resulted in categories that exhibited a slightly steeper slope than minor expectancies. The two factors did not interact (F<1).

2.3 Discussion

The results of Experiment 1 showed an unexpected effect of musical expectancy. Rather than biasing the perception of ambiguous tokens towards the expected triad, expectancy biased perception away from the expected chord. This was a surprising result that we shall consider in more depth shortly. However, before making a firm conclusion, we must still consider the overall major-bias seen in the results of Experiment 1, a bias seen even in perfectly unambiguous minor chords. In particular, this bias, by raising the overall likelihood of a major response, could counteract any context effects, particularly near the category boundary where perceptual representations may be more ambiguous. Thus, Experiment 2 was designed to remove this bias and validate the effect seen in Experiment 1.

3.0 Experiment 2

One hypothesis for the source of the major bias seen in Experiment 1 derives from the timbre of the stimuli. Our stimuli were constructed from triangle waves consisting of the odd numbered harmonics. This includes the 5^th harmonic—which is very close to an equal-tempered major third. As shown in Figure 4, this effect was heightened by our use of a tonic in the bass register—the fifth harmonic of a C-minor chord (for example) appeared as the major third directly above the triad. This effect led to our minor chords containing conflicting cues: a minor third and a harmonically created major third. This seemed a plausible source of the bias observed in Experiment 1, so Experiment 2 attempted to replicate this design using stimuli constructed from sine waves (which have no harmonics).

Figure 4.

Harmonic structure of the stimuli in Experiment 1.

In addition to this change, three additional factors were modified to create a more balanced design. First, the bass note was dropped to simplify the sequences. Second, the major/minor continua were redesigned so that in all four conditions the final chord (the member of the continuum) was in root position (in the prior experiment, minor expecting contexts ended with a first inversion triad if the bass note is ignored). Finally, in order to compare the effect of each context to a baseline, we added a block of neutral trials in which each triad was presented in isolation.

3.1 Methods

3.1.1 Participants

Fourteen University of Iowa undergraduates served as participants in this study. All participants were music majors who were enrolled in their second or fourth semester of the music theory sequence. Informed consent was administered in accordance with the guidelines of the American Psychological Association, and subjects were paid $8 for their participation.

3.1.2 Stimuli

As in Experiment 1, stimuli consisted of two context sequences followed by 4 major/minor continua. All of the stimuli were synthesized using a single sine wave for each note. The timing of the chords was the same as Experiment 1.

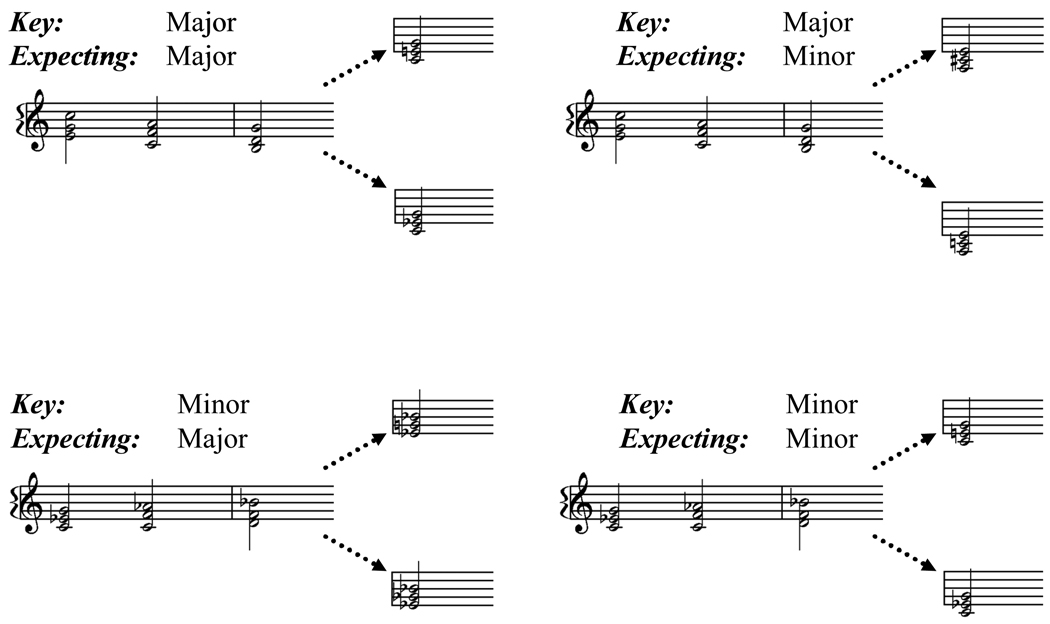
The same two context sequences as were used in Experiment 1 were constructed from these sine-waves: one in a major key and one in a minor key (Figure 5). Each context sequence consisted of a three note triad with no tonic in the lower register. Onto each of these continua we added a token chord from a major/minor continuum, constructed similarly to Experiment 1 (though out of sine-waves). These continua were all first inversion (although the context sequences were not) with nothing in the bass register. A single note (the third) was changed in 10 equal steps to create an 11 step continuum ranging from major to minor.

Figure 5.

Melodic sequences used in Experiment 2.

3.1.3 Task

The task was identical to Experiment 1.

3.1.4 Design

The design was largely identical to Experiment 1. The only addition was a block of 99 additional trials in which each triad was presented in isolation (11 steps × 9 reps). These were completed at the end of the experiment for all subjects and added an additional 10 minutes to the total time.

3.2 Results

Figure 6 shows the pattern of responding in Experiment 2 as a function of context and step. Importantly, the overall major bias was dramatically reduced in this experiment. Nonetheless, an effect of expectancy (in the same direction as Experiment 1) can still be seen.

Figure 6.

Identification results of Experiment 2. A) Percentage of major responses as a function of step and expectancy for major keys. B) The same for minor keys. C) Percentage of major responses (grouped across keys) as a function of expectancy.

Since the neutral context had neither key nor expectancy it could not be included in the any analyses that used both key and expectancy. Thus, initial analyses used a 2 (key) × 2 (expectancy) ANOVAs, while subsequent analyses collapsed across keys to determine the effect of expectancy relative to the neutral condition. As before, we predicted no main effect of key, but an effect of expectancy on the category boundary.

The first analysis examined category boundary (Figure 7). As in Experiment 1, no effect of key was found (F<1). However, a significant effect of expectancy was seen (F(1,13)=6.3, p=0.03): contexts with major expectancies resulted in a boundary shifting to favor fewer major chords. No interaction between key and expectancy was seen (F<1).

Figure 7.

Key logistic parameters as a function of expectancy and key in Experiment 2. A) Category Boundary (continuum step). B) Bias (proportion). C) Slope (change in proportion per step).

Since there was no interaction, our next analysis collapsed across key to compare major and minor melodic expectancies with the neutral context. This one-way ANOVA found a significant main effect of expectancy (F(2,26)=5.0, p=0.01). Planned comparisons showed that this effect was driven by a marginal difference between the neutral (M=6.7) and minor (M=6.4) expectancies (F(1,13)=4.6, p=0.051), and no difference between neutral and major (M=6.9) expectancies (F(1,13)=2.8, p=0.12). Thus, the major and minor expectancies are roughly on either side of the neutral, with more movement for the minor expectancies.

The next set of analyses examined bias. Here, no effects or interactions were seen (all F’s <1). This suggests that the results for the bias parameter in Experiment 1 were due to an overall major bias which was created by the upper harmonics, and modulated by context. When this bias was eliminated with sine-wave stimuli, only effects on the boundary were seen.

The final analyses examined slope. Here, no effect of key nor expectancy was found (F<1), and the interaction was non-significant (F<1). A subsequent analysis averaged across key in order to include the neutral condition. We found a main effect of expectancy (neutral, major minor) (F(2,26)=9.8, p=0.001), which was driven by the fact that the neutral condition showed a much steeper slope than either of the other two (vs. Major: F(1,13)=11.2, p=0.005; vs. Minor: F(1,13)=12.8, p=0.003). This suggests that musical expectancy creates less distinct categories.

3.3 Discussion

Experiment 2 demonstrated two things. First, the overall major bias seen in Experiment 1 was clearly due to the major third provided by the upper harmonics of the bass note. When this conflicting cue was eliminated, the major bias disappeared. This suggests (perhaps expectedly) that the spectrum of a given note can interfere with tonal and harmonic processes. It remains to be seen, however, if this effect is big enough to scale up to more realistic timbres or if it is only visible in the relatively bare timbres used here.

Second, and more importantly, when this confound was removed, the effect of expectancy seen in Experiment 1 was unchanged: contexts creating a major expectancy resulted in fewer tokens being identified as major. This provides evidence that expectancy can bias the categorization of triads. However, it is in opposition to the typical patterns of results seen in analogous work in speech perception and to the predictions of the interactive activation approach. This would apparently suggest that musical context can shrink the category of the expected chord. However, 2AFC data of this kind would also suggest that in addition to the expected category shrinking, the unexpected category must also expand. This seems counterintuitive and unlikely, as this would probably not be beneficial for normal music perception.

An alternative, however, is that subjects are treating this as a one-alternative task. A number of studies have demonstrated that minor chords are less stable than major chords (Krumhansl, Bharucha & Kessler, 1982; Bharucha & Stoeckig, 1987). If so, the minor chord may not be well represented or easily accessible. As a result, in the present experiments, subjects may have adopted a one-alternative, major vs. not-major strategy to complete the task. If this is the case, then the contraction of the major category (given appropriate context) could occur without necessarily affecting a minor category.

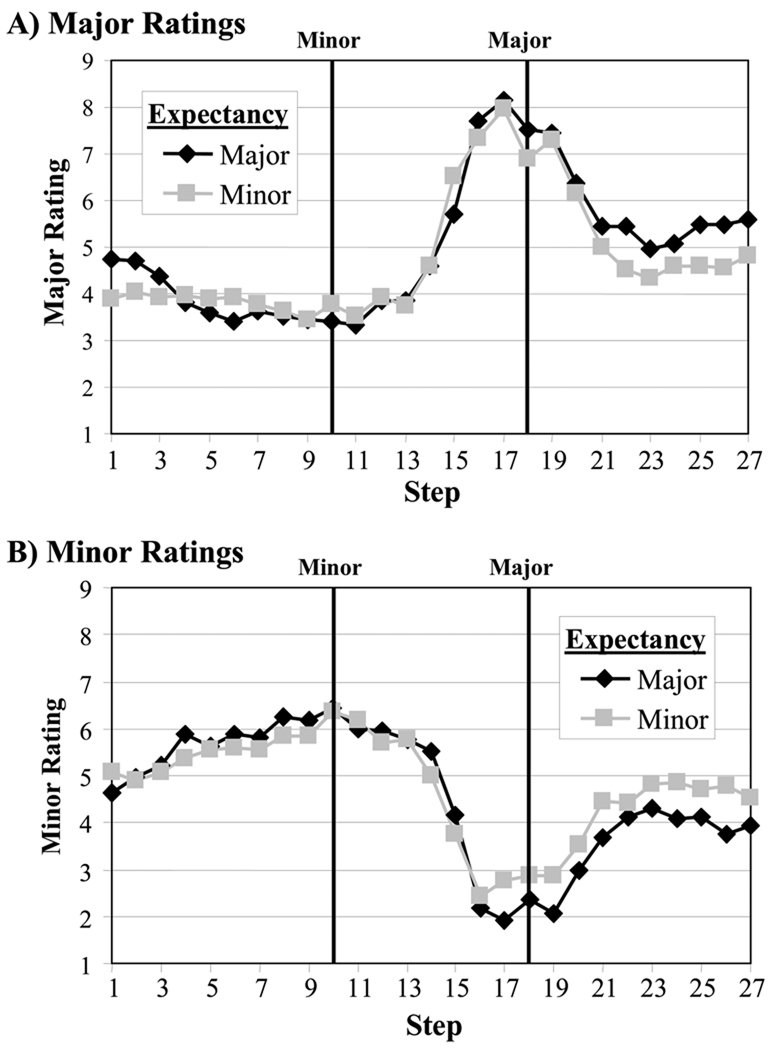
Such an interpretation is supported by a series of in progress studies using a rating task to assess the role of melodic context on major and minor categories (McMurray, Dennhardt & Struck-Marcel, in preparation). This study used the same stimuli as in Experiment 2, although the continuum was extended beyond the present range to include the 2^nd and 4^th (SUS2 and SUS4 chords). After hearing each stimulus, subjects were asked to rate how major or minor the final chord was (on a 7 point scale), similarly to work in speech perception (e.g. Miller & Volaitis, 1989; Miller, 2001 for a review). This task, was intended to allow a response in which subjects could attend only to a stimulus’ membership in a single category (rather than the either/or task).

Figure 8 shows goodness ratings over the entire continuum for major (Panel A) and minor (Panel B) ratings. In both cases, a graded structure can be seen, centered at the appropriate continuum step. However, the major category had more specific definition, and received generally higher ratings than the minor category. At the prototypical major and minor steps, the major prototype was rated a much better exemplar (of a major chord) than the minor was of a minor chord (M_major=7.44, SD_major=1.03; M_minor=6.46, SD_minor=1.34; T(1,16)=2.95, p=.009) across both keys and expectancy contexts.

Figure 8.

Preliminary major and minor ratings as a function of continuum-step and expectancy for the entire range of stimuli in McMurray et al (in preparation) Panel A: Major Ratings. Panel B: Minor Ratings. Steps corresponding to prototypical major and minor triads are marked with vertical lines.

The minor category also extended over a much greater range, suggesting it was more diffuse and less specific. For each subject, the size of the category (in steps) was computed by determining the number of tokens that were 75% of that subjects’ maximum rating (for each of the two categories). The major category (M=6.2 steps, SD=2.8) was quite a bit smaller than the minor category (M=12.9 steps, SD=4.9) (T(16)=4.5, p<.001). Thus, across two measures, the major category was rated as better and more compact. The minor category never achieved the same degree of specificity or goodness.

In fact, as Figure 8 suggests, the most unambiguous minor ratings occurred at steps 16–19 (the major prototype), and these were unambiguously small. This suggests that subjects’ major category was contributing significantly to their minor ratings. Each subjects’ correlations between their major and minor ratings were computed (across steps). Six subjects had correlations less than −.90 and the mean within-subject correlations of the major and minor ratings (across steps) was −.81. This was significantly different from zero (T(16)=28.6, p<.001). The strength of these correlations, coupled with the relative weakness of the minor category suggests that subjects were partially taking advantage of their considerably more robust major categories to complete the minor ratings.

This data, while preliminary, supports our overall picture of the results of Experiment 2. Expectancy provided by context causes the major category to shrink. Since subjects are treating this as a major/not-major task, this results in the concurrent expansion of the minor category.

4.0 General Discussion

This series of experiments examined the relationship between musical expectancy and the perceptual categorization processes behind major/minor triad identification. Surprisingly, we found the opposite pattern of results from what would be predicted by a standard interactive activation account (and the analogous experiments in speech perception): expectancy shrinks the expected category.

However, before discussing these findings, we will briefly summarize a number of additional findings. First, the difference between Experiments 1 and 2 demonstrates that the harmonics or timbre of a stimulus can contribute to perception of its tonal or harmonic properties – pitch and timbre are not completely independent. This should not be surprising since both take advantage of similar information in the signal. However, it does suggest subtle and interesting interactions that could be of interest compositionally and theoretically.

Second, Experiment 2 and the preliminary results from McMurray et al (in preparation) demonstrates that the minor chord is significantly less well perceived and represented than the major chord. The best exemplar of a minor chord was rated as less good than the best exemplar of the major chord, and the minor category extended over a much broader region of the continuum. We also found evidence that when rating minor chords, subjects were most certain in the prototypically major region of the continuum (where they were certain it was not-minor). This may arise out of psychoacoustic factors (the major third is lower on the harmonic series, than the minor third), and the importance of harmonics in explaining the differences between Experiments 1 and 2 would support this. It may also derive from an exposure effect—minor chords are somewhat less common than major chords in many musical styles.

Interestingly this parallels work in visual categorization examining the difference between logically related categories (e.g. A vs. not-A; Goldstone, 1996; Pothos, Chater & Stewart, 2004). For example in Goldstone’s (1996) study, Experiment 3 assessed the effect of making an A/not-A decision, as opposed to an A/B. Observers were trained to categorize a series of novel visual stimuli as members of a category or not (an A/not-A task). From trial to trial one or more diagnostic features (features which were criterial for the decision) or non-diagnostic (features that were present for both categories) were varied. Interestingly, observers appeared to use non-diagnostic features for positive exemplars of the category, but down-weighted them when identifying negative exemplars. When the same stimuli were classified in terms of membership in two categories (A/B) this was not seen. This suggests that deciding that a stimulus is not a member of the category may engage only criterial features, while positive members may make use of a broader range of stimuli. This may offer an important insight in to this music categorization task, since triads consist of both diagnostic features (the third, which differentiates major and minor chords) and non-diagnostic features (the first and the fifth, which are common to both). Thus, subjects may be relying on different feature sets in this task (for different stimuli) than would be assumed by a major/minor task.

With regards to our most important questions about expectancy, both experiments demonstrated evidence for a peculiar effect. In speech perception (and see Goldstone, 1995 for an example from vision), expectancy typically results in the inclusion of ambiguous stimuli in the expected category. However, effects here were in the opposite direction. In the present experiments, expectancy caused the expected category to contract and resulted in ambiguous stimuli being excluded from the category.

This result was found despite an experimental design that could have minimized subjects’ use of context. Subjects heard every context paired with both minor and major chords over the course of an hour. Thus, they may have learned that context was no longer predictive of chord membership. This should have reduced the ability of the contexts to drive expectations. Moreover, the target chords were fairly long (1500 ms.) and presented without noise—subjects could have adopted the simple strategy of ignoring context and categorizing the final chords in isolation. Thus, the fact that the major-contraction effect was seen despite these suggests this effect is either big enough to survive these strategic factors, or that they did not play a large role in our experiment.

It is possible that these results were biased by the fact that for all four experimental contexts, the expected 3^rd (either major or minor) was heard in the prior context, while the unexpected 3^rd did not appear. We chose to use the tonic and/or relative minor as the final (expected) chord since this chord would have the strongest expectancy of any in the series. However, this choice made it difficult to avoid using the third while respecting musical convention, since the third is necessary to establish key. However, we point out that the prior occurrence of notes like the third are a normal part of musical expectancy. Indeed, frequency counts of notes in longer pieces of music are highly correlated with listeners’ expectations (e.g. Krumhansl, 1990). Additionally, this critique has been thoroughly examined in the literature on priming by melodic expectancy. Bharucha and Stoekig (1987) compared priming of chords when the prime shared frequency components (but not notes) with the target and when it did not and found no difference in priming. More recently, Tekman and Bharucha (1998) have demonstrated that psychoacoustic effects on chord priming only last 50 ms (far shorter than the time between repeated notes in any of our stimuli) while expectancy effects can be seen at 500 ms or later. Thus, it seems unlikely that a purely psychoacoustic account could account for the results seen here. Rather, context must be influencing chord judgments at a musical level of representation.

While the present results do not support the version of feedback implemented by interactive activation models, they do implicate some sort of feedback between higher-level processes and perception. However, it is logically possible that these findings could be the result of some sort of post-perceptual decision bias (as has been posited and ruled-out in speech perception). However, we point out that the contraction of the category is not consistent with such an account. If subjects were adopting such a strategy it seems more likely that they would label ambiguous stimuli as consistent with context (that is what all such proposals for speech predict) resulting in the expansion of the expected category. Thus, a decision-bias account seems unlikely—some type of information flow from higher-level expectancies to low-level categorization mechanisms is the preferred explanation.

Our results, however, also appear to conflict with those of DeWitt and Samuel (1990) who used a chord restoration paradigm (similar to the phoneme restoration paradigm of Warren, 1970 and Samuel, 1981) Our melodic contexts are most similar to the ones used in their Experiments 4 and 5. These experiments found evidence for restoration, suggesting an expansion of the category. We found the opposite. Two differences may explain the discrepancy. First, DeWitt and Samuel (1990) assessed restoration for single notes, while our study examined chords. This seems an unlikely locus of the difference, since chords are built from individual notes. A second, more plausible explanation derives from the behavioral paradigm. Stimuli in the restoration paradigm are characterized by the absence of any bottom-up information whatsoever. Our stimuli, on the other hand, had conflicting information about the third. Thus it is possible that in music, expectancy can expand the category if there is no bottom-up information, but contract it (perhaps to improve perceptual analysis) when there is conflicting information.

Interestingly, our finding of contraction is consistent with the literature on in-tune/out-of-tune detection. Wapnick, Bourassa and Sampson (1982), for example, showed that listener’s ability to detect out-of-tune chords was significantly improved when these chords were presented in melodic context. In this study, it was possible that listeners were using context to simply establish the system of possible notes—any set of notes would do. However, as a part of a study on the interaction of pitch and timbre, Warrier and Zatorre (2002) found that melodic context also facilitated subjects’ ability to detect out-of-tune chords over and above the facilitation provided by a random string of notes (although the random string did facilitate performance). Thus expectancy specifically enhances the ability detect frequencies that deviate from the expected pitch (or range of pitches). Such a finding has also been peripherally seen in the chord priming literature where in-tune/out-of-tune judgments have been used as a measure of priming (Bharucha & Stoeckig, 1986; Arao & Gyoba, 1999). The general finding across this work is that melodic context facilitates these decisions—subjects are better able to detect out of tune chords when the chords are expected than when they are unexpected.

Our findings suggest a possible mechanism for these effects. Melodic expectancy acts to sharpen chord categories. As a result out-of-tune notes are easier to detect since they do not strongly activate either category. Given subjects’ apparent adoption of a major/not-major task, out-of-tune notes are less major (and therefore minor). This is partially supported by Goldstone’s (1996) work on diagnostic and non-diagnostic features in visual categorization. An interpretation of these results in light of this work would suggest, the major chord may rely on more independent features while the minor (not-major) may be defined solely with respect to the major chord. Thus, when the major chord contracts (due to subjects use of in-tune/out-of-tune task), it can drag the not-major category along for the ride.

This task-based explanation for our effect makes sense when considering music and speech perception more broadly. The acoustics of speech are highly variable and the system is under pressure in using whatever information is available to extract meaning (e.g. Lindblom, 1996). Thus, context will be weighted heavily, and the listener will be under pressure to form a coherent interpretation of any given segment in terms of this context. Tonality, on the other hand, does not impose such pressure. With respect to tonality, music is a relatively invariant system—chords quality in particular can be identified without any context whatsoever. Moreover, there is little cost to miscategorizing a chord as major or minor, and some musical styles (e.g., the blues) explicitly seek ambiguity along this dimension. Lacking this pressure, determining whether a chord is in or out of tune may in fact be the more important task.

Work on context effects on rhythm may support this. Desain and Honing (2004) built on prior demonstrations of categorical perception for rhythm (Schulze, 1989) examined context effects on rhythm categories. They tested listeners’ interpretations of ambiguous rhythmic sequences when preceded by contexts that favored either a 3/4 or 4/4 interpretation. Their results opposed ours—ambiguous sequences were identified as consistent with context. This may make sense in our task-based explanation. Rhythm is crucial in organizing incoming tonal information, and listeners are heavily biased to expect (and make use of) a consistent rhythm (at least with respect to the number of beats per measure). Thus, like speech, it may be imperative to categorize each rhythmic sequence, and the system may greedily exploit context as an additional cue. Importantly, it suggests that the relevant difference seen in the present may not be speech vs. music but rather, may arise from the interaction of the goals of the perceptual system and the structure of a given perceptual domain.

This task-based explanation helps fit our own work on melodic expectancy with the literature on tuning and rhythm. However, it does not provide a computational description of the feedback mechanism – it does not fit with the predictions of the interactive activation and we have no alternative. The apparent presence of this alternative form of context driven feedback mechanisms represents an interesting new twist for computational accounts of perception.

Connectionist and dynamical systems concepts such as graded activation, competition, feedback and online dynamics present an attractive set of tools for understanding effects like these. However, their instantiation in interactive models does not appear capable of modeling such effects. Interactive activation models typically incorporate some type of attractor dynamics in which ambiguous stimuli are gradually pushed into one category or another. Feedback from context acts to further this process. Our data suggest that feedback can also inhibit it (at least in music)—by contracting the expected category. Thus, there may be other types of dynamics available to such systems.

Attractor accounts of cognition have grown in importance in recent years (e.g. Schutte, Spencer & Schoner, 2003; Spivey, 2007). This has been motivated in part by the wide-spread application of interactive-activation dynamics in explaining word recognition (McClelland & Elman, 1986), word production (Dell, 1986), syntactic parsing (MacDonald et al, 1994), visual comparison (Goldstone & Medin, 1995), visual categorization (Goldstone, 1996), figure/ground segregation (Vecera & O’Reilly, 1998), and music perception (Bharucha, 1987). The results here suggest that the world of feedback dynamics may be more complex than can be accounted for by interactive-activation formalisms. It is crucial to elaborate on this potential alternative form of feedback and to look for evidence for it across these domains.