Treatment of Batch in the Detection, Calibration, and Quantification of Immunoassays in Large-scale Epidemiologic Studies

Abstract

Background

Many laboratory assays measure biomarkers via a 2-stage process. Direct measurement yields relative measures that are subsequently transformed to the unit of interest by using a calibration experiment. The calibration experiment is performed within the main experiment and uses a validation set for which true values are known and relative values are measured by assays to estimate the relation between relative and absolute values. Immunoassays, polymerase chain reaction, and chromatographic approaches are among assays performed in this manner.

Methods

For studies with multiple batches, data from more than a single calibration experiment are available. Conventionally, calibration of assays based on the standard curve is performed specific to each batch; the calibration experiment from each batch is used to calibrate each batch independently. This batch-specific approach incorporates batch variability but, due to the small number of calibration measurements in each batch, may not be best suited for this purpose.

Results

Mixed-effects models have been described to address interassay variability and to provide a measure of quality assurance. Conversely, when interbatch variability is negligible, a model that does not incorporate batch effect may be used to estimate an overall calibration curve.

Conclusion

We explore approaches for use of calibration data in studies with many batches. Using a real data example with biomarker and outcome information, we show that risk estimates may vary depending on the calibration approach utilized. We demonstrate the potential for bias when using simulations. Under minimal interbatch variability, as seen in our data, conventional batch-specific calibration does not best utilize information available in the data and results in attenuated risk estimates.

INTRODUCTION

Many laboratory assays measure biomarkers via a 2-stage process; direct measurement of the biomarkers yields a relative measure (eg, optical density [OD]) that subsequently must be transformed to the unit of interest through use of a calibration experiment. Regression calibration (RC) has been well described in other contexts.^1,2 Similarly for biomarker assays, the calibration experiment uses a validation set for which the true values are known. These known concentration values in combination with the assay measurements may be used to estimate the link function between the assay measurements and the desired unit. This relationship is then used to convert assay measurements to units of concentration. Such an approach affects quantification of assay results as well as the effective detection limits.^3,4 Many assays use calibration techniques for quantification. These include chemiluminescence techniques such as enzyme-linked immunosorbent assay (ELISA) and similar antibody–antigen capture systems, chromatographic approaches, and real-time polymerase chain reaction, among others. In this paper, we focus our discussion on multiplex immunologic assays for assessment of protein concentrations in a sample.

A large and rapidly growing number of multiplexing assays are available for detection and measurement of ligands. These assays allow simultaneous assessment of more than 1 ligand and are performed in multiwell plates, with each well containing 1 of the calibrator standards or study subject samples to be analyzed. When there are more samples to be analyzed than available wells, multiple batches must be utilized. When this is the case and more than 1 batch is processed, data from more than a single calibration experiment are available. Conventionally, the calibration of relative assay results into a unit of concentration based on the standard curve is performed in a batch-specific fashion; the calibration experiment and assay quantitation are performed for each batch independently. The results of each calibration experiment are used to estimate the shape and range of 1 calibration curve for each separate batch. When using some approaches, quantitation is limited to only those values in the linear range of the calibration curve, such that the assay quantification limits are essentially established during this step.

The availability of larger calibration datasets in large-scale studies raises the question of how best to utilize these data. The batch-specific approach for estimating calibration curves incorporates batch variability but may not be best suited for this purpose. Batch-specific calibration—using calibrator data from each assay for calibrating unknowns only from that assay—relies on limited calibration measurements in each batch, resulting in imprecise estimation of the calibration curve and making it difficult to differentiate measurement error from batch variability. A mixed-effects model estimating fixed and random effects has been described for addressing interassay variability that may arise for a variety of reasons—true assay variation, experimental conditions including weather, laboratory technician variability, among others—and, in measuring deviations from fixed effects within each batch, have the benefit of providing a measure of quality assurance.^5–9 Conversely, when there is negligible interbatch variability, a model that does not incorporate batch effect may be used to estimate an overall calibration curve.

In this paper, we explore various approaches for utilization of calibration data in large-scale studies with many batches and make comparisons with conventional laboratory approaches. We utilize log base 10–transformed observed ODs and known concentration values for the calibration experiments for the cytokine granulocyte colony–stimulating factor (GCSF) from a large study in which 24 batches were used. We consider linear and curvilinear calibration models in a batch-specific fixed-effects manner, mixed-effects models that incorporate batch effects as random effects, and linear models that collapse across batches (ie, do not account for a batch effect). Each of these approaches is evaluated in calibration models with the known concentration as the dependent variable as in RC¹⁰ and alternatively, with observed ODs as the dependent variable—inverse regression calibration (IRC). We apply these approaches to a dataset of cytokine levels measured in 943 women in a case-control study of miscarriage and 1) compare each approach; 2) evaluate factors that result in disagreement between the approaches; and 3) compare estimates from logistic regression models of miscarriage by using each of the proposed calibration approaches. Additionally, results of a simulation study are presented. Using a 4-parameter logistic model to generate data, as has been described in the literature,^11,12 we evaluate the effect of choice of calibration approach on risk estimates under a range of conditions.

METHODS

Study Population

Participants were selected from the Collaborative Perinatal Project (CPP) cohort. The CPP was a multisite prospective study of early childhood outcomes, conducted from 1959 to 1974, that enrolled participants at presentation for prenatal care and is described in detail elsewhere.¹³ Serum samples were collected at entry to the CPP and at subsequent bimonthly visits and stored at −20°C. Gestation was estimated using self-reported date of last menstrual period. Miscarriage was defined as involuntary loss of a clinically recognized intrauterine pregnancy at less than 140 days of gestation. Participants with serum samples collected fewer than 10 days prior to miscarriage (n = 355) or for whom serum samples were unavailable (n = 36) were excluded. After exclusions, 462 serum samples from cases of miscarriage and 481 serum samples from nonmiscarriage controls were selected for this study. These samples were used for assessment of GCSF, among other cytokines, to evaluate the relation between levels of inflammatory markers in early pregnancy and adverse pregnancy outcomes, including miscarriage and preterm delivery.

GCSF Assessment

Serum GCSF levels, along with other assayed cytokines, were measured using the multiplex Fluorokine MAP Human Cytokine detection system (R&D Systems, Inc., Minneapolis, MN) as previously described.¹⁴ Briefly, the assays use 96-well plates with 50 μg of sera in duplicates in a sandwich ELISA-based approach. The solid phase consists of fluorescent beads covalently linked with cytokine-specific monoclonal antibodies, allowing capture of each cytokine and corresponding biotinylated antibody. After addition of streptavidin-phycoerythrin, intensity is measured using the Luminex 100 IS system (Luminex Corp., Austin, TX). Utility of these assays for evaluation of serum cytokine levels in samples from the CPP repository has been previously been described.^14,15 Cytokine measurement was observed with high test–retest reliability, and cytokine levels measured in frozen CPP samples selected from the repository for these investigations were similar to those observed in freshly collected serum samples. Running 40 samples in duplicate per batch, a total of 24 separate assays were performed and analyzed. Each plate included 8 standards run in duplicate to generate calibration curves, including a diluent-only blank and 7 serial dilutions. Samples were randomly ordered by case status and batches were organized by gestational age at sample collection. Case samples and matched controls were analyzed in the same batch. Because specimens had been collected previously and identifying information had been removed, the Office of Human Subjects Research at the National Institutes of Health and the institutional review board at the University of Florida determined this study was exempt from full institutional review board review.

Statistical Analysis

Information from the calibration series on the evaluated cytokines was used to assemble the calibration data, which in turn was used to generate the calibration curves that model the relation between the calculated concentration of each cytokine in picogram-per-milliliter units and the relative fluorescence units (RFUs) produced by the assays, as quantified by the Luminex system. A total of 6 approaches for creating calibration models were evaluated. Simple linear regression models were run that disregarded the batch information, as:

$$y_{ij}^{\mathit{cal}}={\beta }_0+x_{ij}^{\mathit{cal}}{\beta }_1+\epsilon$$ (1)

where batch is i =1 to 24, y⃗^cal is a vector of log₁₀-known concentrations for the j^th standard (j=1 to 7) that are fixed across batches and with corresponding measured optical density $x_{ij}^{\mathit{cal}}$, the log₁₀ -observed light intensities in RFUs for each of the standards. A batch-specific fixed-effects model was fit including a batch–biomarker interaction and can be represented as:

$$y_{ij}^{\mathit{cal}}=({\beta }_0+{\delta }_i)+x_{ij}^{\mathit{cal}}({\beta }_1+{\gamma }_i)+\epsilon$$ (2)

where the δ_i are the batch-specific deviations from the overall intercept β₀ and the γ_i are the batch-specific deviations from the overall slope β₁.

Similarly 2 random effect models were evaluated. One incorporated a random intercept term b_0i along with a fixed slope term. The other model included a random intercept b_0i and slope b_1i; in this model, the random effects characterize the deviations of the batches from the overall fixed effects, and have mean zero and variance B as:

$$y_{ij}^{\mathit{cal}}=({\beta }_0+b_{0i})+x_{ij}^{\mathit{cal}}({\beta }_1+b_{1i})+\epsilon .$$ (3)

Each of these approaches was also explored assuming a higher-order polynomial rather than a simple regression relationship. Quadratic models were fit with square terms to allow for a curvilinear relation between known picograms per milliliter and measured RFUs. All mixed models included the same number of fixed and random terms; linear mixed models included fixed terms for intercept and slope; quadratic mixed models also considered fixed and random square terms.

Each of the aforementioned models was run with the known concentrations of the calibration standards, y⃗^cal, as independent (RC) and as dependent (IRC) variables. For either approach, the calibration models were used to relate known concentration to observed assay measurements. Subsequently, calibration model estimates were used to calibrate the unknowns, that is, estimate concentration of a sample from its measured OD. For the curvilinear models with a square term (quadratic models) with the IRC approach, we used the larger/positive root from the quadratic formula in calibration.

After generating each calibration model, parameter estimates were used to calibrate data for participant samples according to the previously described approaches. Agreement between methods was evaluated graphically, and overall goodness of fit was evaluated using -2 log likelihood and the Akaike information criterion. A case-control study analysis was performed to illustrate the effect of the choice of calibration approach on risk estimation. Concentration data generated by each method were used to model risk of miscarriage by logistic regression. Odds ratios (OR) and 95% confidence intervals (CIs) were estimated for each approach and compared.

ANALYSIS RESULTS

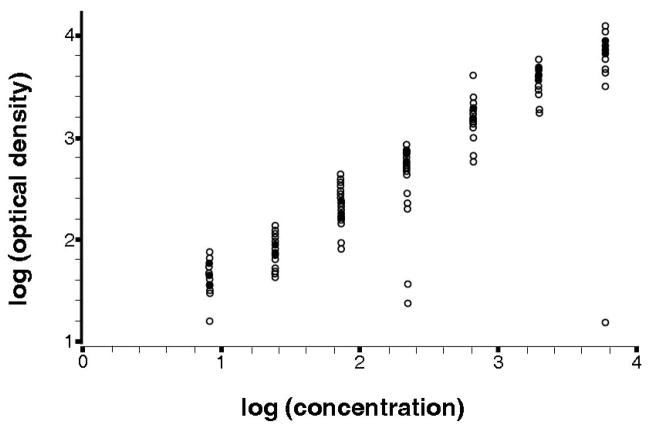
A scatter plot of the data from the calibration experiment for all 24 batches is shown in Figure 1. Log base 10 transformation of both signal and response results in an approximately linear relation between the variables. Several clearly visible outliers resulted from a few of the experiments. Specifically, 1 replicate of the fourth standard (true concentration = 222.2 pg/mL) in batches 21 and 24, and 1 replicate of the most concentrated standard (true concentration = 6000 pg/mL) were discrepant from the majority of points within those batches; however, concentrations were assigned to those points, which factored into the mean across replicates. Analysis was also performed after removal of the 3 outlying points, and the influence of the outliers on analysis is further discussed later.

Figure 1.

Scatter plot of the log₁₀ calibration data from 24 batches, each with 14 data points with known concentration and observed OD.

eTable 1 (available in the electronic version of this article) displays the parameter estimates averaged across batches for linear and quadratic calibration models, strictly for purposes of illustration. In linear RC models, the mean of the estimates from the batch-specific (intercept = −1.05; slope = 1.24) and mixed-effects models (intercept = −1.04; slope = 1.23) were similar to each other and similar to the estimates from the collapsed model (intercept = −0.98; slope = 1.21). On the other hand, quadratic model parameters were observed to differ between the collapsed (intercept = 0.79; slope = 1.06; square term = 0.13) and batch-specific models (intercept = −1.02; slope = 0.17; square term = 0.002). The curvilinear mixed model was inestimable due to a singular variance matrix for the random effects. In part, this may have occurred due to the minimal curvature in the calibration curves, which would result in a near-zero variance estimate for the quadratic random effect term.

eTable 1.

(available online only). Average parameter estimates from regression calibration (RC) and inverse regression calibration (IRC) models.

Calibration approach		Average parameter estimates			Model fit characteristics
Model	Shape	Intercept	Slope	Square	−2LL	AIC
RC
Collapsed	L	−0.9813	1.2090	N/A	−220.0	−218.0
Batch specific	L	−1.0521	1.2351	N/A	−293.3	−291.3
Mixed models	L	−1.0428	1.2312	N/A	−375.1	−367.1
Collapsed	CL	−0.7882	1.0574	0.0274	−216.1	−214.1
Batch specific	CL	−1.0167	0.1667	0.0025	−243.1	−241.1
Mixed models*	CL	~	~	~	~	~
IRC
Collapsed	L	0.8709	0.8021		−349.3	−347.3
Batch specific	L	0.8651	0.8029		−382.6	−380.6
Mixed models	L	0.8657	0.8031		−492.0	−484.0
Collapsed	CL	0.8847	0.7882	0.0029	−341.9	−339.9
Batch specific	CL	0.7675	0.8153	−0.0076	−341.5	−339.5
Mixed models*	CL	~	~	~	~	~

^*Inestimable due to singularity of covariance matrix.

Abbreviations: L, linear; CL, curvilinear, -2LL, -2 log likelihood; AIC, Akaike Information Criterion.

Among linear IRC models, mean parameter estimates from the batch-specific fixed-effects models and mixed models were approximately equal to those of the collapsed, with an intercept of 0.87 and a slope of 0.80. Differences in parameter estimates were observed for curvilinear models, although the differences were minimal. The mixed-effects IRC model was estimable up to the square term as random effects. Examining different RC and IRC models separately, mixed models had the lowest values of the Akaike information criterion, followed by collapsed and then the batch-specific interaction model.

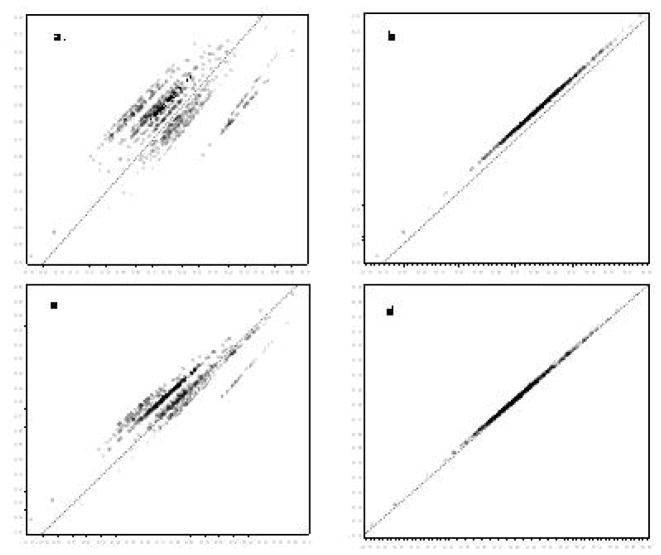
The agreement between a subset of the different approaches taken to calibration is illustrated in the panels of Figures 2 and 3. The top left panel shows collapsed RC models against batch-specific RC models. The data fall along several distinct roughly 45° lines, reflecting method agreement within batch but systematic differences between batches. Conversely, the top right panel comparing the collapsed model against mixed models illustrates a single line off the 45° line and with a nonzero intercept, which illustrates a strong correlation between the methods, but systematically higher levels determined by the collapsed approach. In the left lower panel comparing IRC collapsed to batch-specific models, a greater degree of agreement is apparent in comparison with the RC models; however, certain batches display discrepant classification related to the effect of the estimated square term. The bottom right panel displays similar overall agreement between the collapsed and mixed-model calibrated data, but those batches with outliers in the calibration series illustrate systematic differences. Inverse regression calibration adds leverage to the outlying calibrator replicates in the middle of the RC regression. As Figure 3 illustrates, removal of these few outlying points substantially affects the agreement between methods for data calibration.

eFigure 2.

(available online only). Agreement between different calibration approaches in 943 serum samples from the Collaborative Perinatal Project: GCSF concentration in picograms per millileter.

The top panels show linear RC models for collapsed compared with batch-specific fixed effects models (panel a) and compared with mixed models (panel b). The bottom panels show curvilinear IRC models for collapsed compared with batch-specific fixed-effects models (panel c) and compared with mixed models (panel d). The solid diagonal line reflects perfect agreement.

eFigure 3.

(available online only). Agreement between different calibration approaches in 943 serum samples from the Collaborative Perinatal Project after elimination of three outliers from the calibration experiment data: GCSF concentration in picograms per millileter.

The top panels show linear RC linear models for collapsed compared with batch-specific fixed-effects models (panel a) and compared with mixed models (panel b). The bottom panels show IRC fit curvilinear models for collapsed compared with batch-specific fixed-effects models (panel c) and compared with mixed models (panel d). The solid diagonal line reflects perfect agreement.

Results of logistic regression models of spontaneous abortion are shown in eTable 2. Estimates for the effect of log base 10 GCSF concentrations, as determined by each of the previously described approaches, are shown with 95% CIs on the OR. Point estimates were observed to vary widely by the calibration approach, although CIs largely overlapped. Estimates and their 95% CIs varied in regard to inference; among models in which GCSF levels were determined from RC models, those from collapsed calibration were statistically significant, whereas CIs for all others crossed the null. Among models in which GCSF levels were determined from IRC models, estimates and 95% CIs were similar for the collapsed and mixed models, with ORs ranging from 0.37 to 0.50 and 95% CI endpoints as low as 0.15 and as high as 0.95. Odds ratio estimates from batch-specific calibrated data were closer to the null and had CIs crossing the null. Importantly, we note that all CIs are conditional on the values of the assay and do not account for measurement error.

Table 2.

Logistic regression parameter estimates from models of miscarriage and log₁₀ GCSF as determined by each of the different approaches to regression calibration to convert observed RFUs into concentration in units pg/mL – comparison of data calibrated using all calibration experiment data, or with outliers eliminated from the calibration experiment dataset

Calibration models		As observed		Outliers removed
		OR	95% CI	OR	95% CI
RC
Collapsed	linear	0.338	(0.127, 0.901)	0.271	(0.101, 0.730)
Batch specific	linear	0.73	(0.457, 1.166)	0.605	(0.332, 1.103)
Mixed model	linear	0.666	(0.389, 1.141)	0.564	(0.299, 1.064)
Collapsed	curvilinear	0.214	(0.054, 0.843)	0.250	(0.087, 0.714)
Batch specific	curvilinear	0.812	(0.569, 1.16)	0.977	(0.934, 1.021)
Mixed model	curvilinear	~ a		~ a
IRC
Collapsed	linear	0.369	(0.150, 0.909)	0.282	(0.108, 0.737)
Batch specific	linear	0.629	(0.356, 1.111)	0.582	(0.316, 1.073)
Mixed model	linear	0.427	(0.193, 0.943)	0.53	(0.275, 1.022)
Collapsed	curvilinear	0.370	(0.151, 0.909)	0.287	(0.111, 0.740)
Batch specific	curvilinear	0.864	(0.530, 1.408)	0.666	(0.383, 1.157)
Mixed model	curvilinear	0.502	(0.266, 0.948)	~ a

Abbreviation: GCSF, granulocyte colony–stimulating factor.

^aInestimable due to a near singular variance matrix for the random effect variance matrix.

SIMULATION STUDY

A simulation study was conducted to assess further the effects various methods/models have on risk estimation–based data from multiple batches of biomarker measurements. Data were generated for the simulated study participants in a case-control study (lognormally distributed) with differing levels of true risk as well as for the calibration series data. For the latter, 7 replicate measures of calibration points were generated for every simulated batch. Variability parameters in the calibration function, as well as the functional shape parameters, were based on the observed variability in the case-control data.

Simulated calibration data were created using a 4-parameter model to describe the true overall relation between the relative ODs and the concentration in picogram-per-milliliter units. The 4-parameter logistic describes a sigmoidal function that has been shown to fit similar functional data well.^11,12 The 4-parameter logistic models concentration as a function of OD, making it an inverse regression approach. Random batch variability was added to simulate varying conditions over batches; at each known, fixed calibration concentration, random measurement error was added to the corresponding true OD for that batch resulting in the 14 points, 2 per concentration, used for the batch calibration curve. Additionally, laboratory failures affecting measurement of the calibrator series were simulated. Simulated true concentration data, ODs, and case-control status were simulated as described in the Appendix.

The simulated calibration data were used to estimate calibration curves by using each of the previously described methods after applying a simple log-log transformation. Case and control ODs were converted to the log scale and to log concentration “measurements” based on each method. The OR was then estimated from these simulated log concentrations by using logistic regression models with the form:

$$\text{logit}(\text{P})={\theta }_0+{\theta }_{1}Y$$

where Y is “measured” concentration and OR = exp{θ₁}.

Results of Simulation Study

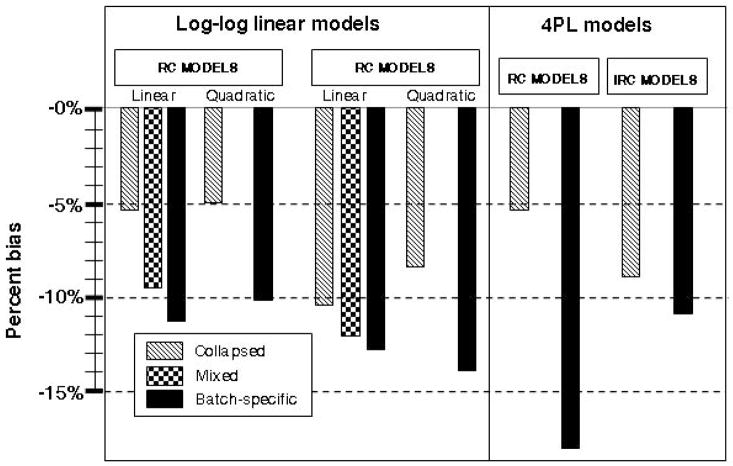
Figure 4 displays empirical bias as a percentage of the true OR for sample size n = 800 and true OR = 1.65. Standard error for estimates was similar across approaches (range from 0.22 for linear RC collapsed to 0.28 for linear IRC batch-specific models). Root mean square error was primarily determined by bias and is not displayed. With RC models, not accounting for the batch effect (collapsed) resulted in less negative bias (attenuation) than either the batch-specific fixed-effects or the mixed-effects model. Bias was similar between the linear and curvilinear models. Parameter estimates from the mixed-effects calibration model were similar to the batch-specific model. The largest bias was seen in the batch-specific calibrated data, as great in magnitude as 14% for the linear model with true OR of 1.65.

Figure 4.

Results of simulation study—percentage of bias by calibration modeling approach for true OR = 1.65 and n = 800.

On the left of the figure, percentages of bias to estimated ORs are shown for biomarker data calibrated using RC log-log linear approaches—collapsed models in light gray, mixed models in dark gray, and batch-specific fixed-effects models in black. On the right, percentages of bias for select 4-parameter logistic (4PL) models are shown.

A similar pattern was observed for IRC models, although bias was generally larger for these approaches than for RC models. Collapsed models again had the lowest bias of those evaluated, whereas the mixed models and batch-specific models resulted in similarly biased estimates of the OR. There was less variability in estimates between approaches among the IRC models,. Both linear and curvilinear batch-specific calibration models resulted in underestimates of effect. To illustrate the impact of the use of the log-log-linear calibration models, percentage of bias is also shown for the 4-parameter logistic models in Figure 4. The collapsed IRC and collapsed IRC and batch-specific IRC models had similar biases to the log-log linear models. For all evaluated scenarios, percentage of bias increased with increasing true risk and was not decreased with increasing sample size.

eTable 3 shows the bias in OR estimates when biomarker quantification is based on a 7-point calibration experiment compared with that of a 14-point calibration experiment using the four-parameter logistic model to fit the calibration data. Collapsing across batches and batch-specific models were considered. Bias was uniformly reduced under the expanded 14-point calibration experiment; however, the reduction in bias was small. The factor with the greatest impact on bias was the true OR, showing that measurement error in the calibration experiment was not eliminated under any of the approaches evaluated.

eTable 3.

(available online only). Risk estimation based on calibration curves with 7 versus 14 standards

OR	Approach	7-point curve		14-point curve
		OR estimate	% bias	OR estimate	% bias
1.05	no error	1.052	0.15%	1.052	0.15%
	collapsed linear	1.048	−0.21%	1.050	0.01%
	collapsed curved	1.048	−0.17%	1.051	0.11%
	batch-spec linear	1.042	−0.80%	1.044	−0.56%
	batch-spec curved	1.042	−0.74%	1.045	−0.47%
1.15	no error	1.150	0.04%	1.150	0.04%
	collapsed linear	1.131	−1.64%	1.135	−1.31%
	collapsed curved	1.134	−1.41%	1.138	−1.01%
	batch-spec linear	1.115	−3.00%	1.119	−2.67%
	batch-spec curved	1.118	−2.78%	1.123	−2.39%
1.65	no error	1.655	0.32%	1.655	0.32%
	collapsed linear	1.532	−7.16%	1.544	−6.42%
	collapsed curved	1.562	−5.33%	1.578	−4.39%
	batch-spec linear	1.460	−11.49%	1.472	−10.78%
	batch-spec curved	1.483	−10.12%	1.497	−9.28%

DISCUSSION

A wide range of immunoassays are used in the quantification of biomarkers in epidemiologic investigations; these assays rely on calibration experiments to convert the relative measures corresponding to light intensities produced in the assay into data in units of concentration. This calibration experiment is conventionally run repeatedly for each individual assay performed, even in large-scale studies that may entail a large number of assays to account for interbatch variability. The calibration data within an individual batch are frequently utilized independently of those of other batches. In this study we evaluated alternatives to this approach to determine best use for calibration data. We compared conventional batch-specific calibration with 2 alternatives: 1) considering all calibration data as a single calibration experiment, and; 2) using mixed models to estimate fixed effects corresponding to the overall with random, batch-specific estimates of the deviation of each batch from the overall. Using these approaches for calibration of GCSF from a case-control study of spontaneous abortion, we observed not only differences between the methods in the calibrated data, but also found substantial differences in the estimates derived from logistic regression models based on these different approaches. Our findings suggest that the calibration approach utilized has the potential to change the conclusions of investigators of epidemiologic investigations.

The problem of calibration is not a new one. Approaches for calibrating data by using a validation set have been well described in the literature.^1,2,10,16 In the context of laboratory assays, calibration has also received a substantial amount of attention.^{5–8, 17–19} Considering the conditions for performing immunoassays in large-scale studies, various investigators have advocated use of mixed models.^5,6 Such an approach has been suggested to address sources of random error including technician variability, variability by lot number, and conditions that may affect receptor–ligand binding such as temperature and light exposure.⁸ Moreover, by combining data from multiple assay runs, one may use the deviations estimates, in combination with other information, to perform quality assurance.^5,6 In comparison with fixed-effects batch-specific models that make no assumptions regarding the relation between batches, use of mixed models implies the existence of an overall relation with batch-specific deviations as the random effects; the assumption of an overall relation is explicit in models collapsed across batches. The assumption of batch exchangeability is important for determining whether estimates of an overall relation are valid, and approaches for testing this source of variability have been proposed.⁸ This assumption of independence between batch and concentration is important; investigators should take care when allocating specimens to batches to achieve a random distribution of factors that may affect concentration (eg, case status or time of sampling).

We evaluated models utilizing a RC-based approach ^1,2,10 and IRC models to reflect calibration curve fitting as is conventionally done in laboratory science, and that previously used in the literature.^5–9,18 We noted several interesting observations in comparing these approaches. Regression calibration—modeling the concentration as a function of OD in both the calibration and unknown measurement phases of the experiment—models the relationship of interest for calibrating the data but is inconsistent with many of the model assumptions and resulted in issues with the response distribution for calibration. With only 7 (or 8, if the blank is included) fixed values in replicates for all batches, there are major limitations in estimating more complex models; both collapsed and batch-specific models were estimable with quadratic (and cubic) regression but only linear mixed models converged.

Inverse regression calibration—modeling OD as a function of concentration and calibrating the data to concentration—corrects the violation of assumptions in the fixed-dependent variable RC models and solved the problem of nonconvergence. Certain outlying points on the regression line with minimal leverage in the RC models increased leverage in the IRC model and affected the estimated parameters. These effects were evident in plots from collapsed compared with mixed-effects RC models and collapsed compared with mixed-effects IRC models; in the latter, a batch effect is apparent for several batches with outlying points from a discrepant single replicate in the middle of the curve. Similarly, plots of collapsed compared with batch-specific approaches illustrate that the latter approach appears to actually add batch variability in some circumstances. Predominantly, these occur with flaws in the calibration experiment and might be remedied by rejecting the assay for tolerance violations, and rerunning. In multiplexing, multiple analytes are simultaneously measured, and failure of measurement of a single one may not justify the expense of repeating the experiment.

The results of simulations further illustrate the performance of each of the approaches when studies with large numbers of biospecimens—and accordingly larger calibration datasets—are conducted. We generated data with a true underlying calibration function, batch variability, and sources of error chosen to reflect the real data we observed. Under these conditions, batch-specific fixed-effects calibration performed decidedly worse than other evaluated approaches. Additionally, models based on modeling OD as the response variable—IRC models—resulted in increased bias to risk estimates in comparison with RC models. By estimating calibration model parameters in the same orientation as the calibration model is to be used for calibrating the unknowns, random error in the calibrated data was reduced. The IRC approach appears highly sensitive to outlying points and overmodels batch variability. In the real data example, removal of a small number of outlying points had substantial consequences to risk estimates, illustrating the sensitivity of results to mismeasurement in the calibration series. Investigators are cautioned to take heed of the importance of a good calibration experiment.

Despite the presence of interbatch variability, models that collapse over batches (ie, do not incorporate batch effect) resulted in less bias to risk estimates than did batch-specific calibration. Although counterintuitive on the surface, the benefit of collapsing comes from its exploiting the availability of a large dataset to model the underlying relation between optical density and concentration, and preventing true batch variability being swamped by uncertainty from attempting to model a relation per batch based on only 7 replicated points in each batch. Use of the collapsed model is premised on a relatively small batch-to-batch variation across batch-specific calibration curves.

In our simulations, the estimates of association (log OR estimates) were attenuated for all calibration methods; we evaluated the source of this systematic underestimation through additional simulations. We initially considered model misspecification. The 4-parameter model was chosen to maintain the complexity displayed in the real data, whereas the linear RC models were utilized for purposes of illustration, relative simplicity, and thus increased likelihood of being practically employed using standard statistical software. Regardless, in comparing use of log-log models and 4-parameter models, we did not observe significant differences for any of the models evaluated. Rather than misspecification of the model, the source of the underestimation appears to be related to the number of data points available for the calibration experiment. We compared risk estimates based on data calibrated from a standard 7-point curve with those of a curve with additional dilutions and found bias reduced in the latter. The reduction in attenuation with an increased number of points on the calibration curve may be because we do not explicitly account for the measurement error associated with the concentration levels. Future research could focus on incorporating this measurement error into the logistic regression modeling. For this paper, we have focused on the impact of the calibration approach on risk estimation and illustration of the potential variability thereof. We have not described other issues that may affect calibration, such as heteroscedasticity in the calibration regressions ^9,20,21 and serial dilution error.¹⁹ In addition to the issue of minimal variance in the known concentrations of the calibrator data, the problem of serial dilution error may arise when a laboratory error in dilution is propagated in subsequent dilutions, resulting in a nonindependence among the calibrator series. Although the use of micropipettes for volumetric dispensing is very precise, errors in preparation of the calibrator series can adversely affect calibration inference.¹⁹

A comparison of multiple approaches to calibrating data from immunoassays illustrates that the resulting differences may lead to important differences in conclusions of models of risk. We used a batch-specific approach that is used conventionally for laboratory sciences, along with alternatives including a mixed-effects model for generating concentration information for GCSF measured in multiplex assays to use in logistic regression models of spontaneous abortion; OR estimates for batch-specific approach ranged from 0.63 to 0.86 with all 95% CIs crossing 1.0, whereas statistically significant protective OR estimates were observed for alternatives. Simulation study results further illustrate the differences between calibration approaches. These observations support previous investigators who have advocated for more comprehensive use of the data from multiple calibration experiments performed within studies that entail multiple assays.^6,7 Investigators of epidemiologic studies that include similarly measured biomarkers should consider use of these data to greater advantage than convention. Failure to do so may contribute to failures to detect small effects in epidemiologic studies of complex disease.

Appendix

Simulations were conducted to assess various techniques for the utilization of calibration data to achieve the best estimation. For each method a calibration curve was generated. Then, using each curve, simulated ODs were converted into biomarker levels. We next estimated ORs (for a 1-unit change in transformed data) by using the biomarker levels from each method and calculated bias, standard error, and root mean square error over B = 2000 iterations to compare the estimators. Various parameter scenarios were investigated, OR = 1.05, 1.15, and 1.65, using several sample sizes of biomarker levels n = 400, 800, and 2000, where each batch consists of 40 measurements resulting in m =10, 20, and 50 batches, respectively.

Two phases of random data were implemented. First, n lognormally distributed “true” biomarker values, y^t, were randomly generated. Next, case and control status were simulated based on a logistic regression model where

$$\text{logit}(\text{P})={\beta }_0+{\beta }_{1}Y$$

where Y is the biomarker concentration generated in the first stage and OR = exp{β₁}.

The second phase started with a “true” overall 4-parameter logistic model

$$f(x,\beta )={\beta }_2+\frac{({\beta }_1-{\beta }_2)}{(1+{(x/{\beta }_3)}^{{\beta }_4})}$$

that models OD as a function of concentration. The parameters β = (0.000, 1.025, 8.841, and 9.698) were based on cytokine values in the CPP dataset and used as the true underlying calibration curve. From here, batch variability was introduced to create m sets of “true” batch-specific curves by randomly samplingβ_i, i = 1,…,m, from a multivariate normal distribution centered at the true β, parameters are drawn to establish “true” batch-specific calibration curves. From these “true” batch-specific curves, “true” ODs, x→*^t, were generated batch wise for the “true” biomarker measurements, y^t, from step 1.

Next, 7 fixed calibrating concentrations x = (6000, 2000, 666.67, 222.22, 74.07, 24.69, and 8.23) and the “true” batch-specific calibration curve were used to get corresponding ODs, $x_{ij}^{\ast \mathit{cal}}=f(y_{ij}^{\mathit{cal}},{\overrightarrow{\beta }}_i^{\ast })$, j = 1,…,7. Random error was then added to) these ODs such that replicate variability (measurement error) is introduced on the log scale to each of the 2 calibration measurements per fixed concentration, y_ijk = exp{log(y_ij)+ε_ijk}, where k = 1,2 and ε_ijk ~ N(0,σ_ε = 0.25). The level of replicate error used was based on the cytokine measures in the CPP dataset and introduced through a power function as suggested by Zeng and Davidian.⁷ Using these replicate measures, $x_{\mathit{ijk}}^{\ast \ast \mathit{cal}}$, at fixed concentration, $y_{ij}^{\mathit{cal}}$, each of the calibration modeling techniques described in the paper is applied and those estimated calibration curves are used to convert the biomarker ODs, x^t, into “measured” biomarker concentration levels, y^m. Disease status along with the y^m biomarker “measurements” are then used to estimate ORs based on each technique. These estimators are the unit of comparison for the various techniques.