Physical oncology: a bench-to-bedside quantitative and predictive approach

Abstract

Cancer models relating basic science to clinical care in oncology may fail to address the nuances of tumor behavior and therapy, as in the case, discussed herein, of the complex multiscale dynamics leading to the often observed enhanced invasiveness paradoxically induced by the very anti-angiogenic therapy designed to destroy the tumor. Studies would benefit from approaches that quantitatively link the multiple physical and temporal scales from molecule to tissue in order to offer outcome predictions for individual patients. Physical oncology is an approach that applies fundamental principles from the physical and biological sciences to explain certain cancer behaviors as observable characteristics arising from the underlying physical and biochemical events. For example, the transport of oxygen molecules through tissue affects phenotypic characteristics such as cell proliferation, apoptosis, and adhesion, which in turn underlie the patient-scale tumor growth and invasiveness. Our review of physical oncology illustrates how tumor behavior and treatment response may be a quantifiable function of marginally stable molecular/cellular conditions modulated by inhomogeneity. By incorporating patient-specific genomic, proteomic, metabolomic, and cellular data into multiscale physical models, physical oncology could complement current clinical practice through enhanced understanding of cancer behavior, thus potentially improving patient survival.

Introduction

Advances in multiscale modeling and dynamical systems theory, supported by emerging computational power, have now reached a stage where mathematics and numerical simulation could be productively applied to address the urgent need for nonlinear analysis of cancer behavior. Nonlinearity means that the behavior of cancer as a system may be greater or less than the simple “linear combination” (e.g., addition) of effects of its individual components. Founded on biophysics and nonlinear mathematics, physical oncology strives to link patient-specific genetic/phenotypic/microenvironmental information at the molecular/cellular scales to a quantitative prediction of tissue behavior at the critical patient scale, i.e., tumor growth, invasion, drug transport and pharmacodynamics (see[1] for applications to breast and brain cancers). This approach enables the study of cancer as a complex heterogeneous system, which typically spans seven orders of physical magnitude (from genes to tissue, 10⁻⁹–10⁻²m) and many orders of temporal magnitude (from the sub-second scale to tens-of-years).

A key feature of cancer progression is instability—dynamic changes in individual cell (epi)genetics, mitotic and metabolic rates result in heterogeneous cellular/microenvironmental domains within the central tumor mass, which in turn influence diffusion rates, local oxygen/nutrient consumption and supply, as well as less easily measurable inhomogeneities in pH, extracellular-matrix forces, toxic cell debris, and growth factors. Dynamic instability and tumor mass inhomogeneities likely play major roles in tumor progression, and occur on multiple scales with distinct timeframes.

Current clinical practice

The current clinical strategy of treating cancer with a combination of surgery, radiotherapy, and drugs based on clinical and molecular staging may be less targeted than is required for curative intent. Furthermore, detection methods are at present relatively crude not only for cancer screening, but also for gauging metastatic spread. These practices, while pragmatic and based on “best evidence” (evidence where it exists and eminence-based opinion) are limited.

Individualization of therapy is probably best exemplified in breast cancer, where clinicians currently evaluate patient features (age, menopausal status, family history), tumor characteristics (size, histology, histological grade, node metastasis, lymphovascular invasion), and cancer biology (expressions of ER, estrogen receptor, and HER2, human epidermal growth factor type 2) together with transcriptome measurements (Oncotype Dx[2], Agendia 70 gene signature[3], and disease-specific arrays). Models combining specific risk factors (see “Adjuvant! Online” program[4]) are used clinically to indicate subgroup risks of recurrence and death and to guide therapeutic decision-making. Through extensive and ongoing clinical trials, these strategies have generally benefited patient subpopulations. Except for a small subset of tumors responsive to HER2 inhibitory antibodies[5], however, the quantitative contribution of each of the known parameters in progression and therapy response (morphology, histopathology, invasion, and associated molecular phenomena) remains elusive.

Histopathology is the “gold-standard” for cancer diagnosis and has developed diagnostic criteria useful in prognostics. In the case of glioma these criteria may seem simplistic: necrosis, hemorrhage, palisading, nuclear and cytoplasmic atypia and increased cellularity. Histologic patterns of increased vasculature interspersed between necrosis and bounded by palisading malignant cells are a common diagnostic feature of the more aggressive glioblastoma multiforme.—a glial brain tumor with no known cure that usually results in death within 15 months of diagnosis. Because gliomas arise where no basement membrane restricts invasion, they grow radially, often along neuronal fiber tracts. However, tissue and cellular histologic patterns are lacking in molecular and mechanistic detail. Histopathology opens the door to new questions that could be answered by physical oncology. One question is whether this modeling enables a leap from the extensive and reliably predictive value of histopathologic patterns to identify the missing mechanisms and molecular derangements as potential therapeutic targets.

Physical modeling overview

Mathematical modeling and numerical simulation have been employed to provide insight into the complex interactions in cancer, with the ultimate goals to aid in the development of individualized therapy, further the understanding of experimental and clinical observations, and enable targeted experimental design[6].

Most models are either discrete or continuum, based on how the tumor tissue is represented. Discrete models represent individual cells according to a specific set of bio-physical and -chemical rules, which is particularly useful for studying carcinogenesis, natural selection, genetic instability, cell-cell and cell-microenvironment interaction[6]. Analyses of cell population dynamics have also been employed to study biological characteristics applying to cells in a particular population, such as therapy response.

Continuum models treat tumors as a collection of tissue, drawing upon principles from continuum mechanics to describe cancer-related variables as continuous fields by means of partial differential and integro-differential equations[6]. Variables may include cell volume fractions and substrate concentrations such as oxygen and nutrients. Multiphase (mixture-theory) continuum models are capable of describing detailed interactions among multiple solid cell species, extra-cellular and intra-cellular liquids. Solid tumors are described as a saturated medium, comprising at least one solid (cells, extracellular matrix) and one liquid (water) phase.

A third modeling category consists of a hybrid approach using both continuum and discrete representations of tumor cells and microenvironment components. This methodology aims to develop multiscale models where the discrete scale can be directly fitted to molecular and cell-scale data, and then upscaled to inform the phenomenological parameters of continuum models, which lump multiple information in each parameter. These models can be directly and accurately informed from the small scale and thus could be used for clinically relevant predictions of tumor size, spread, and drug transport and response[6].

Recent reviews include[6-13]—owing to space limitations we only mention a fraction of recent work; details can be found in the references therein. In addition to avascular growth, recent models have focused on stem cells[14], intra-cellular pathways[15], tumor-induced angiogenesis and vascular growth[16,17,18], invasion and metastasis[19], and treatment[20,21,22]. The development of more sophisticated and quantitative individual-based models coupled with an increase in computational power has paved the way for more realistic multiscale models, where multiple spatial and temporal scales are tightly coupled in one unified framework[7,17,18]. Hybrid models representing the tumor tissue at both single-cell and tissue levels have also been recently developed[23].

Illustration of quantitative and predictive physical oncology

Building upon a formulation of classical tumor models[6], a nonlinear modeling of complex tumor morphologies[24] predicted that highly vascularized tumors would stay compact and without invasive fingering, even while growing unbounded, implying that invasiveness is associated with vascular anisotropy and other microenvironmental inhomogeneties (oxygen diffusion gradients, metabolic activity, local differences in oxygen consumption). Employing a continuum model, morphology was predicted to be determined by the competition between heterogeneous diffusion-modulated cell proliferation and migration, driving shape instability and invasive tumor morphologies, and stabilizing mechanical forces (cell-cell adhesion). Subsequent work further elaborated this “morphological instability” hypothesis[25]. Using computer simulations and in-vitro experiments[26], evidence was provided that tumor-scale invasion could be suppressed by spatially homogeneous oxygen and nutrient supply because these conditions act both by decreasing gradients and promoting phenotypic stability, and, therefore, the mechanical forces maintaining a well-defined boundary. Interestingly, avascular tumor growth stability was also investigated in discrete models with similar results[27].

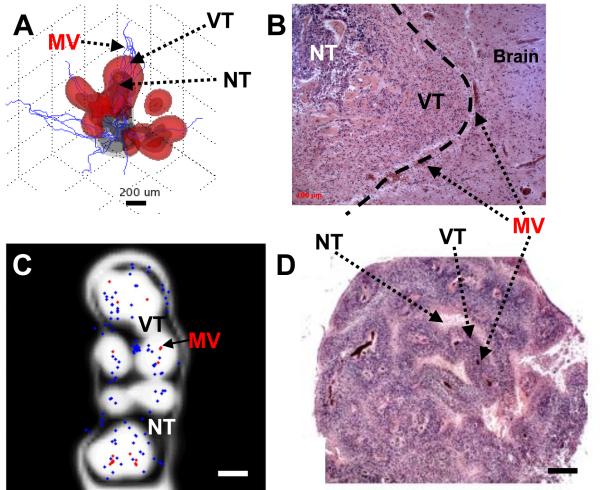
Another important advance has been the application of multiphase computational models to simulate multiple solid (cell) species and extra-/intra-cellular liquids. This work has facilitated the representation of solid tumor growth in 3D[6], which combined with models for tumor-induced angiogenesis[28], was successfully compared to patient histopathology, thus further suggesting that tumor-scale growth and invasion may be predictable processes driven by diffusion gradients and regulated by heterogeneity in genotypic, phenotypic, and microenvironmental parameters[29] (Figure).

Figure.

Physical modeling predicts tumor behavior and morphology as a quantifiable function of inhomogeneous environmental conditions modulated by diffusion gradients in cell substrates (VT:viable-tumor; NT:necrotic-tumor; MV:vessel). A:Invading and detached clusters are predicted to migrate up cell substrate gradients when cell-cell adhesion is sufficiently low. B:Glioblastoma histology shows invading cluster (left) invading into more normal brain (dashed line:tumor/brain margin). Vascularization at margin (darker spots) implies that cell substrate gradients drive collective cell infiltration via proliferative growth. C:Histology predicted by the model reveals viable tissue surrounding blood vessels, and peripheral necrosis. Tissue is within 100-200μm of blood-conducting intra-tumoral vessels and of brain parenchyma (red:vessels-conducting; blue:non-conducting). Diffusion gradients (not-shown) indicate higher oxygen/nutrient near blood-conducting vessels and lower otherwise, thereby determining viable regions. D:Glioblastoma histology reveals viable cells cuffing blood vessels, and necrosis in inter-vessel zones. Cuff thickness corresponds to oxygen/nutrient diffusion gradients. Bar,200 μm. [A,B:From Cancer Research, Vol. 69, Bearer et al., p. 4496,4499, Copyright (2009), with permission from the American Association for Cancer Research. C,D:From NeuroImage, Vol. 37, Frieboes et al. [30], p. S65, Copyright (2007), with permission from Elsevier].

This physical modeling provides evidence that tumor behavior in-vivo may for some cancers be a quantifiable function of marginally stable molecular/cellular conditions influencing and in turn influenced by inhomogeneities in nutrients, oxygen, and growth factors. Recent cancer therapy models have shown that dramatically decreasing microenvironment oxygenation (as in anti-angiogenic treatment), or inducing large-scale cell death, not only tends to promote tumor fragmentation and invasion[25], but can also increase drug resistance[22]. Conversely, increasing oxygen/nutrient supply in the microenvironment may enhance the tumor response[21]. Since such strategies may also increase chemotherapeutic agent access, these analyses may offer a more quantitative approach for targeted anti-angiogenic therapy adjuvant to chemotherapy or resection.

For glioblastomas, physical oncology has provided answers to basic biological questions of tumor behavior. The modeling found that as new clones arise, those with more survival capabilities invade the original tumor as well as adjacent tissue[29]. These aggressive clones replace original tumor cells, which are more likely to die as growth rate increases and oxygen levels decrease. This sequence produces an “engine” of instability, and results in further inhomonegneities in cellular behavior and architecture, metabolic consumption, oxygen levels, extracellular matrix fluidics/tension/density, and vascular permeability. Moreover, the physical modeling suggests that oxygen/nutrient gradients are a major driver of malignant progression. Cells that can escape and survive at low oxygen tension likely have increased invasive and mitotic potential[29]. This prediction preceded results from bevacizumab (Avastin, Genentech) therapy, where therapy withdrawal results in rapid tumor regrowth. Avastin is a monoclonal antibody against VEGF, which blocks VEGF-induced neovascularization and thus decreases tumor oxygenation. Avastin may thus exert a selective pressure promoting survival of the most malignant cells. We are currently testing this model in more depth.

The nonlinear interaction among various determinants representing cell and tumor phenotype at multiple scales is a unifying theme of these modeling results. The synergy/antagonism of combined therapeutic strategies depends heavily upon this interaction. By quantifying the patient-specific links between tumor growth/regression and the underlying phenotype, physical oncology may become a tool for more targeted study of cancer response to therapy.

Conclusion

The goal of physical oncology is to provide information about tumor behavior in predictive, diagnostic and therapeutic domains by integrating information from individual or multiple specimens across many variables from genetic alterations to mitotic rates, tumor size, and vascular parameters; and across multiple dimensions, from molecular distribution, dynamic diffusivity to cellular organelle and cell body shape and behavior, to tumor growth dynamics, to whole body physiology. This modeling can provide a system in which parameters for tumor behavior at various physical scales can be evaluated as targets for diagnosis and therapeutics, and also tested for efficacy without the expense and pain of clinical trials. This effort promises to enhance the knowledge gained from experiments and clinical observations by transforming cancer from a biological challenge into an engineering problem.

In order to attain this goal, physical modeling will need to incorporate ever-increasing amounts of laboratory and clinical knowledge at multiple temporal and physical scales, thus continuously evolving to a more accurate multiscale representation of the underlying connection between the biological/clinical “complexity” and the tumor behavior of individual patients. To sharpen predictivity, model parameters need to be uniquely constrained by values measured from independent datasets. Experiments need to be designed to be conducive to the measurement of parameters co-localized in space and along successive timepoints. An expanded dialogue and collaboration between biologists, physical scientists, and clinicians will be indispensable for the advancement of physical oncology as a practical bench-to-bedside quantitative and predictive approach.