Abstract
A vexing question in the biological sciences is the following: can biological phenotypes be explained with mathematical models of molecules that interact according to physical laws? At the crux of the matter lies the doubt that humans can develop physically faithful mathematical representations of living organisms.
We discuss advantages that synthetic biological systems confer that may help us describe life’s distinctiveness with tractable mathematics that are grounded on universal laws of thermodynamics and molecular biology.
1. Mathematical Models in Physical Sciences
Mathematical models are indispensible tools in all physical science and engineering disciplines. They are widely used to capture and understand the essential aspects of systems, processes and phenomena of interest. Founded on universally accepted laws of physics and chemistry, mathematical models provide insight that is key to designing, optimizing and controlling these systems, processes and phenomena.
Models in the physical sciences are often cast in the form of differential equations. It is then probably a platitude to state that the invention of differential and integral calculus in the 1660s was a remarkable accomplishment. Indeed, much of progress in the physical sciences can be credited to mathematical models that are based on the pioneering work of Newton and Leibnitz.
We can identify two different ways calculus enhanced the unaided human brain:
The first enhancement category is extrapolation, which is related to innate human computing capacities. This type of enhancement of human capacities is typically exemplified with instruments like the telescope or the microscope. These inventions enable visual detection beyond the range of the human eye. Similarly, the argument of a quantitative improvement in abilities can be made for calculus. As a methodological tool it extrapolates the capacities of the human brain.
The second category of human capacity enhancement is augmentation. Augmentation is well exemplified with nuclear magnetic resonance instruments. There is no a priori human ability to detect the resonance of nuclear magnetic moments to an external magnetic field. NMR equipment gives humans instrumental access to physical phenomena beyond our unaided capacities. Analogously, calculus provides access to tractable mathematics and analytical solutions previously inaccessible to the human brain. Augmentation can then be considered as a qualitative shift in abilities. With results attainable only with calculus, the foundation can be solidly laid for theories that capture and explain physical phenomena. The development of gravitational theory, electromagnentic theory, or quantum mechanical theory, is now possible, resulting, in turn, in tectonic changes in the human mindset.
Of course, with calculus, analytical models became tractable only for linear, deterministic problems. For non-linear or probabilistic phenomena, the invention of computational mathematics has introduced an equivalently distinctive set of scientific methods. Paul Humphreys has best presented convincing arguments that computational science extrapolates and augments human understanding abilities in his wonderful book entitled “Extending Ourselves”.1
Physical systems are often non-linear or stochastic; they also often possess an overwhelming number of variables. Consequently, although in principle these systems can be described with the mathematical tools of calculus, in practice their behavior cannot be predicted or satisfactorily explained because of the intractability of analytical solutions. The determination of statistical mechanical properties of matter is a strong case in point. There are insurmountable mathematical difficulties to develop analytical, predictive models of the thermodynamic properties of high density, or multicomponent systems.
Computer simulation methods provide the much needed tractable mathematics. Because analytical solutions are too complex, if not impossible to obtain, computer models and simulations that are solidly founded on physical principles can extrapolate and augment the unaided human brain’s capacities to describe, explain and predict physical phenomena.
2. Mathematical Models in Biological Sciences
The preceding discussion begs the question: what is the state of mathematical modeling in biological sciences? Arguably, mathematical models are not as indispensible a tool in the biological sciences as they are in the physical sciences. Focusing on models that are founded on established physicochemical principles, the absence of models as guides providing insight into the mechanisms of biological systems is even more glaring.
There is certainly remarkable progress in developing and using reliable models in all areas of biology: in molecular biology there are powerful models to capture the relationship between sequences, structures and functions of biomolecules;2–7 there are accurate models to determine how molecules interact, in terms of the structure of the complex or the strength of binding.8–13 Increasing the length and time scales of interest, in important areas of cellular biology, such as protein interaction networks, metabolism or development, astonishing successes have been reported.14–18
Yet there is no complete mathematical description that is based on the laws of statistical mechanics, thermodynamics, or reaction kinetics, that explains phenotypic complexity in terms of chemicals interacting in space and time. And before expanding further, and in order for the discussion to become tractable, let us focus on single cell bacterial organisms. Cells are the important functional units of all living organisms, and we can thus limit ourselves to cellular phenotypes. These phenotypes can be broadly defined as the set of biological functions in a cell, which can, in turn, be reduced to a set of concentrations of all molecular species inside a cell.
The absence of models that reduce phenotypes to soups of chemicals interacting in accord with physicochemical laws can be ascribed to two main reasons:
First, the overwhelming number of involved variables. Biological systems are composed of very many molecular components: proteins, DNA, RNA, lipids, metabolites, water, ions. In turn, each one of these molecules has very many internal degrees of freedom: conformational, orientational, chemical. Consequently, although in principle these systems obey physical laws, there are insurmountable mathematical difficulties to develop meaningful, tractable models that represent these laws. For example, if a biological system is at thermodynamic equilibrium with its environment at constant temperature and pressure, the Gibbs free energy of the system will attain a minimum value. This is an unambiguous, universal principle of statistical thermodynamics. Yet, there is no tractable mathematical model that we can use to compute and minimize the free energy for any but the very simplest of biological systems.
A second reason for the difficulty to reliably adopt mathematics in biology is that biology is a discipline in history: Theodore Dobzhansky’s dictum that “Nothing in biology makes sense except in the light of evolution” casts a long shadow on mathematical models of phenotypic complexity. Because, how exactly can we integrate thermodynamics with evolution? And billions of years of competition aside, the context and the environment any organism thrives in defines the organism as powerfully as its own nature. Mathematical models of biological systems that neglect this biological context may quickly become irrelevant.
Is there then any hope that mathematics will ever be considered as indispensible a tool in the biosciences as in the physical sciences? We believe there is. Herein, we will argue that a synthetic biology may unlock our modeling potential.
3. Synthetic biology as a catalyst for the development of mathematical models
Synthetic biology is a quest to engineer new functions in living organisms. Synthetic biology shares principles, tools, and objectives with biological and engineering sciences.19–27 Its goal is the construction of new DNA or RNA sequences that give rise to new biological behaviors, usually in the form of predefined temporal and spatial expression of proteins. This expression profile is what we hencetoforth call ‘dynamic phenotype’ in this proposal.
The building blocks used in synthetic biology applications are the components of molecular biology processes: e.g., promoter sequences, operator sequences, ribosome binding sites, termination sites, reporter proteins, and transcription factors, such as activator and repressor proteins. With inexpensive DNA synthesis (it now costs $0. 50/base to chemically synthesize DNA) and manipulation technologies it is becoming possible to engineer physical assemblies of biological building blocks and create arbitrary gene regulatory relations. Thus, numerous synthetic gene circuits have been created in the past decade, including bistable switches, oscillators, and logic gates.19–27
A significant challenge is to determine how to construct a synthetic system given a desired dynamic phenotype. In other words, what are the molecular components and how are they to be assembled for a particular temporal and spatial protein expression profile to be realized? For example, if we want to engineer an oscillating gene regulatory network in E. coli, or a metabolic pathway to produce ethanol from sugars, how do we choose the DNA sequence that will give rise to these precise phenotypic behaviors? This is a typical forward engineering problem: assembling components to a functional whole.
Certainly, the task of connecting DNA sequences to dynamic phenotypes can best be performed by experts in molecular biology. Yet, this task can become rational if mechanistic explanations of complex biological phenomena are available in terms of biomolecular interactions, which can, in turn, be connected to DNA sequences. Indeed, with knowledge of the molecular species involved and of their interactions, including the thermodynamic and kinetic rules of these interactions, a rational conceptual design of synthetic gene networks is conceivable.
Notably, the goal to provide mechanistic explanations of complex biological phenomena in terms of biomolecular interactions is commonly shared by both systems biology and synthetic biology. Indeed, systems biology and synthetic biology are the two sides of the same coin: synthetic biology is a forward engineering approach, whereas systems biology is a reverse engineering one. The former attempts to assemble components into a new whole. The latter attempts to capture the behavior of existing biological systems in a holistic way. Their paths are complementing: systems biology generates information on components and interactions that can be used in synthetic biology applications. Synthetic biology can be employed to probe mechanisms and provide mechanistic insight on how phenotypic complexity emerges from interacting molecules. Importantly, their ultimate goals overlap: efforts in both synthetic and systems biology are aimed at understanding and engineering complexity of biomolecular systems.
How can synthetic biology catalyze the development of mathematical models that are well grounded in physicochemical laws and which explain complex phenotypes in terms of interacting biomolecular ensembles?
Synthetic biological systems confer three advantages that may indeed help us make a plausible case for so ardent a vision, as to render mathematics an indispensible tool in biosciences: a) they are small and well-defined enough to be captured by universal yet tractable mathematical models; b) they are modular enough to string together and build logical and informational architectures that are the essence of living systems; c) they are human designs, not nature’s, avoiding some of the difficulties of historical explanations and contextual dependencies.
What is distinctive then is that instead of a top-down approach, with synthetic biology we start from the bottom and go up: designing small synthetic biological systems affords the luxury of knowing components and their interactions well enough to develop mechanistic models and test whether reductionism applies to biology. Furthermore, combining these systems together can result in the logical and informational architectures that Paul Nurse considers as the missing link between chemical molecules and the miracle of life.28
Again, in this discussion, we will limit ourselves to bacterial species. Synthetic biology efforts are currently being expended in more complex organisms, like yeast or mammalian cells. But the knowledge of biomolecular mechanisms, although far from perfect, is more complete for bacterial species. Consequently, it would be far more challenging to try to link phenotypic complexity to biomolecular interactions in more complex organisms, where the molecular biology mechanisms are under vigorous investigation.
In the rest of the manuscript we will explain biological phenotypes in terms of biomolecular interaction networks that obey laws of statistical thermodynamics and principles of molecular biology. We will discuss the development, testing and validation of mathematical descriptions that span multiple levels of organization from molecules to logical architectures.
4. A general modeling approach for synthetic biology
Recently we presented SynBioSS Designer, a standardized algorithmic process for generating models of synthetic gene regulatory networks that is applicable to any synthetic construct and is suitable for automation.29 Designer is a web-based tool, available at www.synbioss.org. It is part of the Synthetic Biology Software Suite,30 a software suite with which users can build models of synthetic constructs, simulate these constructs in time and optimize components and their interactions in order to achieve a targeted dynamic phenotype.
SynBioSS Designer makes use of Monod and Jacob’s postulate that observed responses of organisms to stimuli can be explained in terms of the interactions of gene regulatory networks.31,32 A user needs only to enter in SynBioSS Designer the DNA sequence of a synthetic biological construct, and SynBioSS Designer will follow closely the molecular biology dogma and represent all gene expression molecular level events with reactions of all the known biomolecular interactions involved in bacterial transcription, translation, regulation, and induction.
Following the sequence of biomolecular steps, Designer will generate reaction networks to model any DNA sequence that contains the necessary ingredients: promoters, operators, ribosome binding sites, coding regions, terminators. The user will add these necessary components in the Designer interface, one at a time and a functional annotation is necessary for Designer to generate a complete reaction network. The reaction network can be saved in any of a number of formats, such as SBML.
A schematic of how SynBioSS Designer works is shown with the help of screenshot in Fig. 1. A more detailed tutorial-like description of the required steps to build models of simple synthetic constructs, such as bistable switches, oscillators, logic-AND gates is discussed in ref. 29.
Figure 1.
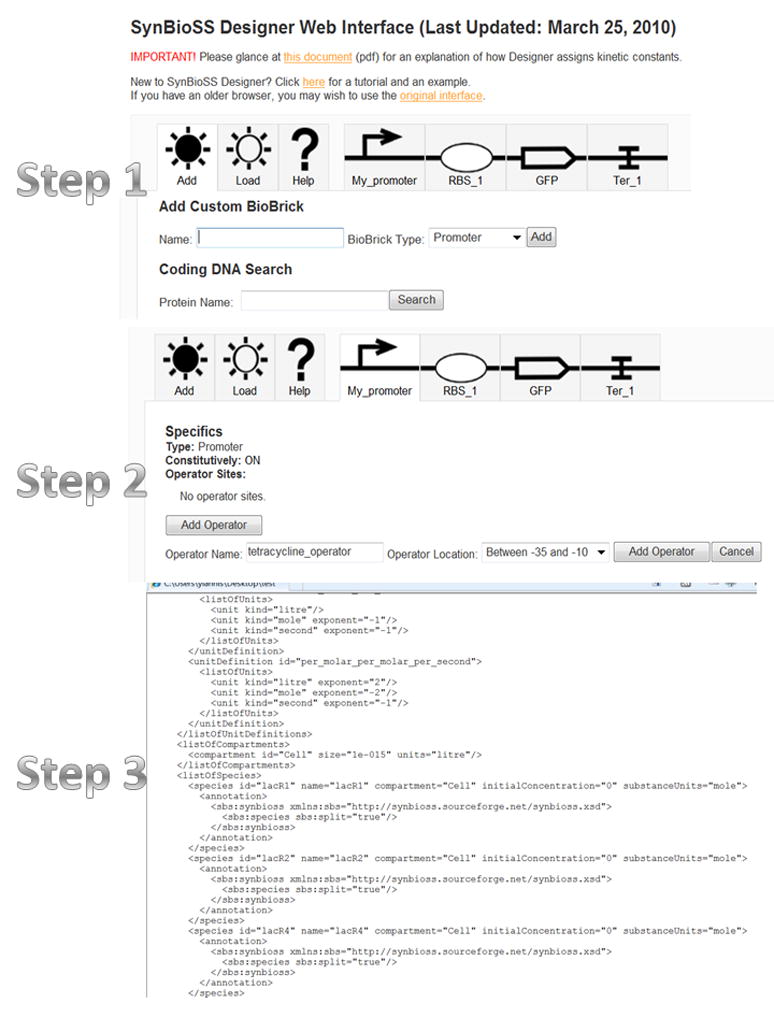
Screenshots of steps a user takes in SynBioSS Designer to build a model. Users may enter the DNA sequence of molecular components in their synthetic construct (Step 1), enter biomolecular interactions information (Step 2) and save the reaction network Designer generates automatically in SBML format (Step 3).
These reaction networks can be simulated in time to obtain dynamic phenotypes. The synthetic engineer may then decide whether the synthetic construct components will result in the targeted phenotype and make appropriate changes to the DNA sequence.
This modeling formalism was validated, by combining mechanistic-kinetic models with in vivo genetic engineering to build and test a synthetic, bio-logical AND gate.23 This device is composed of elements of the tetracycline (Tet), lactose (Lac), and λ-phage promoters and is responsive to the commonly-used inducers IPTG and aTc, producing GFP as an output signal (Fig. 2).
Figure 2.
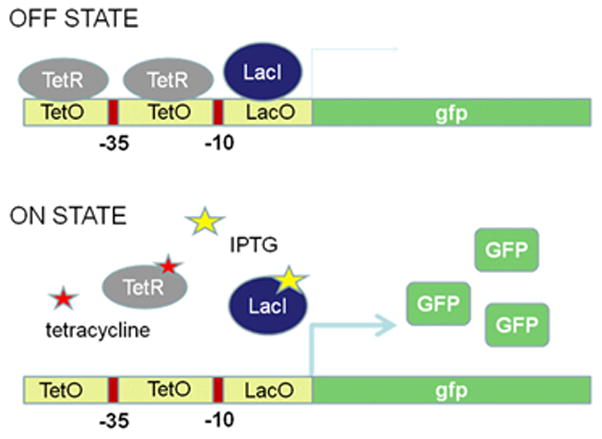
Schematic representation of the synthetic logic-AND gate promoter.
The quantitative behavior of the AND gate phenotype was studied both numerically and in vivo as a function of promoter topology. The model was constructed from kinetic data obtained from the literature, using Designer. It is a set of approximately 60 reactions that model transcription, translation, regulation, degradation, and induction. The model yields clearly-defined ON/OFF logical behavior at realistic inducer concentrations.
These behaviors were matched well to observed in vivo data obtained through fluorescence-activated cell sorting.27 Experimentally, an in vivo synthetic, hybrid system was constructed consisting of multiple operators within a single promoter. The operator sequences employed are derived from three unrelated natural regulatory elements: Lac, Tet, and λ-phage operons arranged logically within a single transcriptional unit.
In Fig. 3, the results from the experiments and the simulations are summarized for a promoter with three operators: two tetracycline operators and a lactose operator. As evidenced by the figure, this work illustrated how mathematical modeling can provide mechanistic explanations of biomolecular phenomena and guide the design of synthetic biological constructs. Using the steps described above, numerous other synthetic biological systems have also been modeled and simulated. The repressilator was modeled, a three gene network with oscillating protein expression profile, and identified the biomolecular interactions that are important for oscillations.33 A simulated annealing method to optimize the strength of key biomolecular interactions in order to obtain oscillations of certain frequency was then developed.34 Two types of bio-logical AND gates have been modeled with this formalism: ones that emerge from gene regulatory relations,27 and a second type that emerges from protein modular devices.35 Moreover, inducible systems have been modeled, such as bistable switches and tetracycline-inducible gene networks, studying the dynamic behavior and the influence of gene network topology on the dynamic phenotype.36–38
Figure 3.
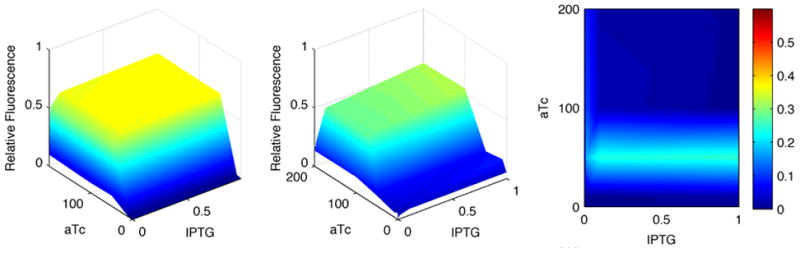
Comparison of model (1st panel) and experimental results (2nd panel) for the TTL AND gate. The x and y axes form a grid of inducer concentrations: aTc (0–200ng/ml) and IPTG (0–1mM). The color scheme reflects the average strength of fluorescence from the experiments or the average number of GFP molecules in the simulations, scaled by the maximum strength/number of GFP molecules. The third panel shows the difference between experiments and simulations. In all cases, behavior is depicted 6 hours after induction. The plotted model values are the means of 1,000 independent stochastic kinetic simulations, whereas experimental values are the means of 100,000 FACS observations.
There are numerous disadvantages in modeling biological systems in high molecular resolution, or, in other words, attempting to include all known biomolecular interactions. We were only able to validate our approach with components of the tetracycline and the lactose operons, arguably the two best studied biochemical systems. Attempting to build models for any other system currently faces insurmountable difficulties, because of the absence of kinetic or equilibrium constants. Another important difficulty stems from the assumption that the molecular biology dogma will be precisely followed. The universal validity of this assumption is questionable at best. There are molecular biology steps that may go beyond the sequence of transcription, translation, etc. Furthermore, an important postulate in SynBioSS is that the reaction network is context and environment independent. We know this is not true. For example, we have observed that in certain E. coli strains, inclusion body formation is induced early on, resulting in inaccurate representations of amounts of protein in the cell.
On the other hand we can discuss a few major advantages. SynBioSS Designer follows a general method for constructing models of synthetic biological systems, in principle applicable to any synthetic gene regulatory network. These models provide a detailed mechanistic picture of the dynamic behavior of biological systems. To our knowledge, this is the first attempt at the systematic modeling of. This approach certainly challenges established molecular biology and in the absence of agreement between models and experiments it poses new questions and requires new avenues of investigation.
Furthermore, this modeling formalism has a strong predictive character, enabling rational engineering of regulatable gene transcription systems. Rational design principles come in terms of molecular components, the kinetics and the thermodynamics of their interaction. With simply built models, alternative designs can be tested and a detailed picture can emerge of how each piece of the construct influences the synthetic network behavior. Sensitivity analysis and optimization can be conducted to determine key components and decide on network topologies. Computer simulations make possible exhaustive searches of different network connectivities and molecular thermodynamic/kinetic parameters, greatly advancing the development of design principles through the mapping of interaction strengths on specific DNA mutant sequences.
This approach is also well-suited for synthetic biology. Although numerically challenging, it always remains tractable, not hampered by the significant size and complexity of naturally occurring biological systems.
With this modeling formalism, all synthetic biological constructs are reduced to networks of biomolecular reactions. The dynamic behavior of these systems can then be simulated numerically. In the following Section, we discuss algorithms to simulate numerically cascades of biomolecular reactions.
5. Multiscale simulations of synthetic biological systems
Typically, networks of reactions may be modeled using ordinary differential equations describing the reaction rate laws. The underlying assumption that the reaction network may be modeled with ODEs is that the system is at the thermodynamic limit, that is the number of molecules of reactants and products is so large that their concentration can be thought of as a continuous variable and, importantly, there are precise numbers of reaction events per unit time per unit volume.
Of course, biomolecular systems can be far from the thermodynamic limit with reactants/products numbering only very small numbers of molecules in the system. This hinders the application of traditional mathematical models for modeling kinetic and thermodynamic processes in living organisms. Using deterministic-continuous, ordinary differential equations for simulating the reaction kinetics of these systems can produce distinctly false results. The need arises for stochastic models that account for inherent thermal noise, which is manifested as phenotypic probability distributions.
Certainly, this is not news, with the work of McQuarrie and Oppenheim developing decades ago the necessary theoretical framework for modeling reacting systems away from the thermodynamic limit.39–42 More recently, pioneering work by Gillespie, Gibson, Bruck, Rawlings and Petzold, among others,43–48 has resulted in powerful algorithms and methods to model stochastic chemical reacting systems with applications in biology.
It should be stressed though, that when simulating biological interaction networks, the need emerges quickly to improve computational efficiency, because of the multiple time scales present in these networks. Indeed, from infrequent events, such as transcription initiation, to very frequent ones, such protein-protein interactions, or metabolic reactions, values of kinetic constants may span multiple orders of magnitude. A model that includes these various types of biomolecular events will inevitably be stiff, substantially diminishing the computational efficiency of any simulation.
Various theoretical methods and algorithms have been developed to simulate biomolecular systems, which are not close to the thermodynamic limit, and contain interactions that have kinetic constants spanning multiple time scales. For example, a hybrid stochastic-discrete, stochastic continuous method was developed combining Gillespie’s discrete-stochastic kinetic Monte Carlo method,49 with a chemical Langevin equation representation of stochastic-continuous reaction events.
These along with other algorithms are incorporated in Hy3S and SynBioSS, two open software suites, made available on sourceforge.net.50–54
We should stress that there are numerous software packages with algorithms to simulate gene regulatory networks. A review of these available packages is beyond the scope of the current work. Interested readers may begin at a number of thorough published reviews.55–58
6. Concluding Remarks
Admittedly, because biological phenomena are very complex, mechanistic explanations will be fragmentary and approximate. With the Babel of sequences and structures that all living organisms are, it is difficult to anticipate that we will possess as detailed and accurate a picture of biomolecular systems as we do for physical or chemical systems. Nevertheless, the careful collection, management and dissemination of hard-earned, experimental information on biomolecular processes may advance the generation of mechanistic explanations in a way that is fit for analysis and design.
Herein we discussed a modeling methodology that may help scientists and engineers to construct complex synthetic biological systems. Sophisticated mathematical models are developed of synthetic biological systems that connect the targeted biological phenotype (what we want the synthetic biological system to do) to the DNA sequence (that we need to physically construct to realize the synthetic biological system). These models then represent a significant first step toward a broader objective: to develop theoretical and computational models that describe how the physical interactions of molecules lead to complex biological phenotypes.
Acknowledgments
This work was supported by a grant from and a grant from the National Institutes of Health (American Recovery and Reinvestment Act grant GM086865), the National Science Foundation (CBET-0425882 and CBET-0644792), and the University of Minnesota Biotechnology Institute. Computational support from the Minnesota Supercomputing Institute (MSI) is gratefully acknowledged. This work was also supported by the National Computational Science Alliance under TG-MCA04N033.
References
- 1.Humphreys P. Extending Ourselves. Oxford University Press; Oxford: 2004. [Google Scholar]
- 2.Schwede T, Peitch MC. Computational Structural Biology: Methods and Applications. World Scientific; 2008. [Google Scholar]
- 3.Broglia RA, Serrano L, Tiana G. Protein Folding and Drug Design (International School of Physics Enrico Fermi) IOS Press; 2007. [Google Scholar]
- 4.Becker OM, Karplus M. Guide to Biomolecular Simulations (Focus on Structural Biology) Springer; 2005. [Google Scholar]
- 5.Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat Struct Biol. 2002;9(9):646–52. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 6.Pastor RW, Venable RM, Feller SE. Lipid bilayers, NMR relaxation, and computer simulations. Acc Chem Res. 2002;35(6):438–46. doi: 10.1021/ar0100529. [DOI] [PubMed] [Google Scholar]
- 7.Harris SA. Modelling the biomechanical properties of DNA using computer simulation. Philos Transact A Math Phys Eng Sci. 2006;364(1849):3319–34. doi: 10.1098/rsta.2006.1906. [DOI] [PubMed] [Google Scholar]
- 8.Wong CF, McCammon AJ. Protein simulation and drug design. Adv Protein Chem. 2003;66:87–121. doi: 10.1016/s0065-3233(03)66003-1. [DOI] [PubMed] [Google Scholar]
- 9.Duan YH, Reddy BVB, Kaznessis YN. Physicochemical and residue conservation calculations to improve the ranking of protein-protein docking solutions. Prot Sci. 2005;12(2):316–328. doi: 10.1110/ps.04941505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bolintineanu D, Hazrati E, Davis HT, et al. Antimicrobial mechanism of pore-forming protegrin peptides: 100 pores to kill E. coli Peptides. 2010;21(1):1–8. doi: 10.1016/j.peptides.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Warshel A, Parson WW. Dynamics of biochemical and biophysical reactions: insight from computer simulations. Q Rev Biophys. 2001;34(4):563–679. doi: 10.1017/s0033583501003730. [DOI] [PubMed] [Google Scholar]
- 12.Adcock SA, McCammon JA. Molecular dynamics: survey of methods for simulating the activity of proteins. Chem Rev. 2006;106(5):1589–615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chipot C, Phorille A. Free Energy Calculations. Springer; 2007. [Google Scholar]
- 14.Ricklin D, Hajishengallis G, Yang K, Lambris JD. Complement: a key system for immune surveillance and homeostasis. Nat Immunol. 2010;11(9):785–97. doi: 10.1038/ni.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mastellos D, Andronis C, Persidis A, Lambris JD. Novel biological networks modulated by complement. Clin Immunol. 2005;115(3):225–35. doi: 10.1016/j.clim.2005.03.012. [DOI] [PubMed] [Google Scholar]
- 16.Stephanopoulos G, Aristidou AA, Nielsen J. Metabolic Engineering: Principles and Methodologies. Academic Press; 1998. [Google Scholar]
- 17.Smolke C, editor. The Metabolic Pathway Engineering Handbook: Fundamentals. CRC Press; 2009. [Google Scholar]
- 18.Gilbert SF. Developmental Biology. Sinauer Associates; 2010. [Google Scholar]
- 19.Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 20.Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 21.Kaern M, Blake WJ, Collins JJ. The engineering of gene regulatory networks. Annu Rev Biomed Eng. 2003;5:179–206. 29. doi: 10.1146/annurev.bioeng.5.040202.121553. [DOI] [PubMed] [Google Scholar]
- 22.Andrianantoandro E, Basu S, Karig DK, Weiss R. Synthetic biology: new engineering rules for an emerging discipline. Mol Syst Biol. 2:2006.0028. doi: 10.1038/msb4100073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Keasling J. The promise of synthetic biology. Bridge Natl Acad Eng. 2005;35:18–21. [Google Scholar]
- 24.Alon U. Biological networks: the tinkerer as an engineer. Science. 2003;301:1866–1867. doi: 10.1126/science.1089072. [DOI] [PubMed] [Google Scholar]
- 25.Serrano L. Synthetic biology: promises and challenges. Mol Syst Biol. 2007;3:158. doi: 10.1038/msb4100202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Drubin DA, Way JC, Silver PA. Designing biological systems. Genes Dev. 2007;21:242–54. doi: 10.1101/gad.1507207. [DOI] [PubMed] [Google Scholar]
- 27.Ramalingam KI, Tomshine J, Maynard JA, Kaznessis YN. Forward Engineering of Synthetic Bio-Logical AND Gates. Biochemical Engineering Journal. 2009;47(1–3):38–47. [Google Scholar]
- 28.Nurse P. Life, logic and information. Nature. 2008;454:424–6. doi: 10.1038/454424a. [DOI] [PubMed] [Google Scholar]
- 29.Weeding E, Houle J, Kaznessis YN. SynBioSS designer: a web-based tool for the automated generation of kinetic models for synthetic biological constructs. Brief Bioinform. 2010;11(4):394–402. doi: 10.1093/bib/bbq002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hill AD, Tomshine JR, Weeding EM, Sotiropoulos V, Kaznessis YN. SynBioSS: the synthetic biology modeling suite. Bioinformatics. 2008;24:2551–3. doi: 10.1093/bioinformatics/btn468. [DOI] [PubMed] [Google Scholar]
- 31.Jacob F, Monod J. Biochemical and genetic mechanisms of regulation in the bacterial cell. Bull Soc Chim Biol (Paris) 1964;46:1499–532. [PubMed] [Google Scholar]
- 32.Jacob F, Monod J. Genetic regulatory mechanisms in the synthesis of proteins. J Mol Biol. 1961;3:318–56. doi: 10.1016/s0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
- 33.Tuttle L, Salis H, Tomshine J, Kaznessis YN. Model-Driven Design Principles of Gene Networks: the Oscillator. Biophys J. 2005;89:3873–83. doi: 10.1529/biophysj.105.064204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tomshine J, Kaznessis YN. Optimization of a stochastically simulated gene network model via simulated annealing. Biophys J. 2006;91:3196–3205. doi: 10.1529/biophysj.106.083485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Salis H, Kaznessis YN. Computer-aided design of modular protein devices: Boolean AND gene activation. Phys Biol. 2006;3:295–310. doi: 10.1088/1478-3975/3/4/007. [DOI] [PubMed] [Google Scholar]
- 36.Sotiropoulos V, Kaznessis YN. Synthetic tetracycline-inducible regulatory networks: computer-aided design of dynamic phenotypes. BMC Syst Biol. 2007;1:7. doi: 10.1186/1752-0509-1-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Salis H, Kaznessis YN. Stochastic Simulations of Gene Regulatory Modules. Computers in Chemical Engineering. 2005;29:577–588. [Google Scholar]
- 38.Kaznessis Y. Multi-Scale Models for Gene Network Engineering. Chem Eng Sci. 2006;61:940–953. [Google Scholar]
- 39.McQuarrie DA. Stochastic approach to chemical kinetics. J Appl Probab. 1967;4:413–447. [Google Scholar]
- 40.Oppenheim I, Shuler KE. Master equations and Markov processes. Phys Rev. 1965;138:1007–1011. [Google Scholar]
- 41.Van Kampen NG. Stochastic Processes in Physics and Chemistry. Revised and enlarged. Amsterdam: Elsevier; 2004. [Google Scholar]
- 42.Gardiner CW. Chemistry and Natural Sciences. 3. Berlin: Springer; 2004. Handbook of Stochastic Methods for Physics. [Google Scholar]
- 43.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comp Phys. 1976;22:403–434. [Google Scholar]
- 44.Gillespie DT. Exact Stochastic Simulation of Coupled Chemical Reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 45.Haseltine EL, Rawlings JB. Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J Chem Phys. 2002;117:6959–6969. [Google Scholar]
- 46.Gibson MA, Bruck J. Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. J Phys Chem. 2000;104:1876–1889. [Google Scholar]
- 47.Cao Y, Li H, Petzold L. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J Chem Phys. 2004;121:4059–4067. doi: 10.1063/1.1778376. [DOI] [PubMed] [Google Scholar]
- 48.Chatterjee A, Mayawala K, Edwards JS, Vlachos DG. Time accelerated Monte Carlo simulations of biological networks using the binomial {tau}-leap method. Bioinformatics. 2005;21:2136–2137. doi: 10.1093/bioinformatics/bti308. [DOI] [PubMed] [Google Scholar]
- 49.Salis H, Kaznessis YN. Accurate Hybrid Stochastic Simulation of a System of Coupled Chemical or Biochemical Reactions. J Chem Phys. 2005;122:054103, 1–13. doi: 10.1063/1.1835951. [DOI] [PubMed] [Google Scholar]
- 50.Salis H, Kaznessis YN. An equation-free probabilistic steady state approximation: Dynamic application to the stochastic simulation of biochemical reaction networks. J Chem Phys. 2005;123:214106. doi: 10.1063/1.2131050. [DOI] [PubMed] [Google Scholar]
- 51.Sotiropoulos V, Kaznessis YN. An adaptive time step scheme for a system of SDEs with multiple multiplicative noise. Chemical Langevin equation, a proof of concept. J Chem Phys. 2008;128:014103. doi: 10.1063/1.2812240. [DOI] [PubMed] [Google Scholar]
- 52.Sotiropoulos V, Contou-Carrere M-N, Daoutidis P, Kaznessis YN. Model Reduction of Multiscale Chemical Langevin Equations: A Numerical Case Study. IEEE/ACM Trans Comp Biol Bioinf. 2009;6:470. doi: 10.1109/TCBB.2009.23. [DOI] [PubMed] [Google Scholar]
- 53.Kaznessis Y. Models for Synthetic Biology. BMC Systems Biology. 2007;1:47. doi: 10.1186/1752-0509-1-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Salis H, Sotiropoulos V, Kaznessis YN. Multiscale Hy3S: Hybrid Stochastic Simulations for Supercomputers. BMC Bioinformatics. 2006;7:93. doi: 10.1186/1471-2105-7-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hoops S, Sahle S, Gauges R, Lee C, Pahle J, Simus N, Singhal M, Xu L, Mendes P, Kummer U. COPASI — a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–74. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- 56.de Jong H. Modeling and simulation of genetic regulatory systems: a literature review. J Comput Biol. 2002;9:67–103. doi: 10.1089/10665270252833208. [DOI] [PubMed] [Google Scholar]
- 57.Goutsias J, Lee NH. Computational and experimental approaches for modeling gene regulatory networks. Curr Pharm Des. 2007;13(14):1415–36. doi: 10.2174/138161207780765945. [DOI] [PubMed] [Google Scholar]
- 58.Stelling J, Gilles ED. Mathematical modeling of complex regulatory networks. IEEE Trans Nanobioscience. 2004;3(3):172–9. doi: 10.1109/tnb.2004.833688. [DOI] [PubMed] [Google Scholar]


