Determination of Nucleic Acid Hydration Using Osmotic Stress

Abstract

Understanding the role water plays in biological processes requires detailed knowledge of the phenomena of biopolymer hydration. Crystal structures have identified exact sites occupied by the water molecules in immediate hydration layers. NMR and molecular modeling have provided information on dynamics of water molecules occupying these sites. However, these studies give little information on the thermodynamic contribution of water molecules to conformational equilibria and recognition affinity. This unit describes probing of nucleic acid hydration using osmotic stress, a method that provides thermodynamic information complementary to crystallography, NMR and molecular modeling. Osmotic stress monitors the depression of melting temperature upon decreasing the water activity and calculates the number of thermodynamically unique water molecules associated with the double helix and released from the single strands upon melting.

INTRODUCTION

Water is a natural solvent. Understanding the role water plays in biological processes requires detailed knowledge of the phenomena of biopolymer hydration. Water molecules are critical to nucleic acid structure and recognition by proteins and small ligands. Thus, understanding the hydration of nucleic acids is a significant problem in biochemistry of DNA and RNA. Atomic resolution crystal structures have identified exact sites occupied by the water molecules in immediate hydration layers. NMR and molecular modeling have provided further information on dynamics of water molecules occupying these sites. However, these studies give little information on the thermodynamic contribution of water molecules to conformational equilibria and recognition affinity. This unit describes probing of nucleic acid hydration using osmotic stress, a method that provides thermodynamic information complementary to crystallography, NMR and molecular modeling.

Osmotic stress (Parsegian et al. 1995; Robinson and Sligar 1995) probes the changes in hydration that accompany biologically relevant equilibria from the dependence of the equilibrium constant on water activity (osmotic pressure). Just as the dependence of equilibrium constant on temperature gives an entropy, on pH gives a number of released protons, and on salt activity gives a number of released ions, similarly, the dependence of equilibrium constant (K) on water activity gives the number of water molecules released in the reaction. For nucleic acids, osmotic stress monitors the depression of melting temperature (t_m is temperature at which K = 0.5) upon decreasing the water activity and calculates the number of thermodynamically unique water molecules (Δn_W) associated with the double helix and released from the single strands upon melting (Fig. 7.14.1, free water molecules are shown as spheres; Spink and Chaires 1999). The water activity is changed by addition of small neutral organic compounds (co-solutes). The calculation of Δn_W is done using a simple formula derived by Spink and Chaires (1999):

$$\mathrm{\Delta }{\mathrm{n}}_{\mathrm{W}}=(-\mathrm{\Delta }\mathrm{H}/\mathrm{R})[\mathrm{d}({T_m}^{-1})/\mathrm{d}({\text{lna}}_{\mathrm{w}})],$$

where R is the universal gas constant (1.986 cal/mol/K). The melting enthalpy (−ΔH) and the dependence of melting temperature on water activity (d(T_m⁻¹)/d(lna_w)) are the two experimentally determined variables. Osmotic stress has been used to study hydration of native nucleic acids (Spink and Chaires 1999; Rozners and Moulder 2004) and their analogues having modifications in heterocyclic bases (Rozners et al. 2005; Li et al. 2007; Hwang et al. 2009), sugars (Watts et al. 2010) and phosphate backbone (Kolarovic et al. 2009).

Figure 7.14.1.

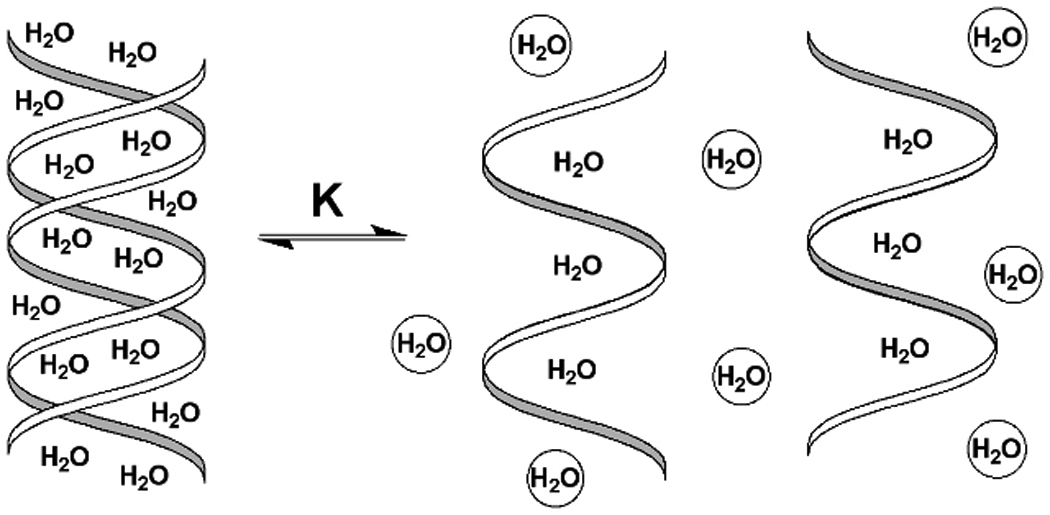
Melting of a nucleic acid double helix releases Δn_W water molecules.

STRATEGIC PLANNING

UV Thermal Melting

Choice of oligonucleotide sequence

The accuracy of osmotic stress data (Δn_W) depends on the quality of UV thermal melting curves. It is important to choose an oligonucleotide sequence that will give a sharp two-state (duplex to single strands) UV melting curve with well-defined base lines. Broad melting transitions make it difficult to define the base lines before and after melting and cause large errors in melting temperatures that propagate large errors in final Δn_W. It is difficult to predict the shape of the melting curve, and selection of the best sequences is an empirical process. We have obtained high quality data using self-complementary DNAs: 5’-GCGAATTCGC, 5’-(TA)₆ and 5’-(CG)₃ (Rozners and Moulder 2004) and 5’-CG(TA)₅CG (Kolarovic et al. 2009) and RNAs: 5’-GCGAAUUCGC, 5’-(UA)₆ and 5’-(CG)₃ (Rozners and Moulder 2004; Kolarovic et al. 2009), 5’-GGCUGGCC (Rozners et al. 2005) and 5’-GCGUACGC and 5’-CGCGAAUUCGCG (Rozners et al., unpublished data). Meanwhile, structurally similar 5’-d(CGCTAATTGGCG) and 5’-r(GCGUAUACGC) did not yield good melting curves in our hands. Others have reported successful osmotic stress experiments with modified 5’-d(GCGTACACATGCG)/3’-d(CGCATGTGTACGC) (Hwang et al. 2009), 5’-d(GCTATAATGG)/3’-r(CGAUAUUACC) and 5’-r(GCUAUAAUGG)/3’-r(CGAUAUUACC) (Watts et al. 2010).

Choice of UV-Visible spectrometer

The UV-Visible spectrometer for osmotic stress must be equipped with 1) a multi-cell Peltier temperature controller and 2) a software package for nucleic acid thermal analysis that allows programmable temperature ramp, absorbency measurement (preferably at several wavelengths at the same time), and processing of the data. The osmotic stress experiment involves measurement of melting temperatures in five different buffers of decreasing water activity. It is highly desirable to measure all five samples simultaneously; thus, the Peltier temperature controller should be at least five-position. The temperature range of the Peltier should be 0 to 100 °C. Reliable cooling and efficient nitrogen purging of the sample chamber is important to obtain good data below 15 °C. The software package should allow van’t Hoff calculations to yield t_m, ΔH, ΔS and ΔG.

We have used two UV-visible spectrometers for osmotic stress studies.

1. Varian Cary Bio 100 UV-Visible spectrometer (year 2001 model) with six-position Peltier temperature controller. The main advantage of Cary Bio 100 is the excellent software that allows 1) multiple runs to be programmed and performed without operator’s input for several days and 2) full van’t Hoff analysis of the melting curves to yield t_m, ΔH, ΔS and ΔG. The disadvantage is the relatively large cell volumes (we are using 1 cm light path cells that require 0.6 mL of sample). We have also found that Cary Bio 100 does not have effective nitrogen purging of the cell chamber and suffers from water condensation on cell windows at temperature below 10 °C.

2. Shimadzu 800 UV-visible spectrometer (year 2009 model) with eight-position Peltier temperature controller. The advantages of 800 are 1) small cell volumes of 120 µL, 2) effective nitrogen purging of cell chamber that allows easy work down to 0 °C and 3) cell closing that allows heating up to 110 °C. We have found the extended temperature range 0 to 110 °C very useful. The main disadvantage of 800 is the limited software capabilities that allow t_m but not ΔH, ΔS and ΔG calculations. The instrument cannot be programmed to do more than a single run and must be restarted manually. The 800 uses a single-piece eight-position cuvette, which is easy to clean and use but fragile and expensive to replace.

Basic Protocol 1

UV THERMAL MELTING FOR OSMOTIC STRESS STUDIES

The task of UV melting for osmotic stress studies is to establish the dependence of melting temperature on water activity. This is achieved by performing several (preferably simultaneous) UV melting experiments at different concentrations of co-solutes, small organic molecules that do not interact with the analyte, in our case, the nucleic acid duplex. Because organic molecules used to lower water activity may have some interaction with the analyte, a common practice is to perform osmotic stress studies using several different co-solutes. Although the numbers obtained with different co-solutes may vary to some extent, the presence of common trends within series of co-solutes allows reliable conclusions about the changes in hydration.

This protocol describes the UV melting experiments using three co-solutes: ethylene glycol, glycerol and acetamide. Detailed steps are given for a general UV-Visible spectrometer with specific tips for Varian Cary Bio 100 and Shimadzu 800 instruments, however, the steps may need to be modified for different instruments. Determination of the melting enthalpy and analysis of the data including calculations of Δn_W are described in the next two protocols. In the present protocols, we illustrate the osmotic stress method by determining the hydration of modified RNA sequence 5’-r(^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpA), where ^MeU_2’-F is 2’-deoxy-2’-fluoro-5-methyluridine residue, using acetamide as the organic co-solute.

Materials

• Aqueous buffer (CNE 0.3) containing 10 mM sodium cacodilate (pH 7.4), 300 mM NaCl and 0.1 mM EDTA.

• Solutions of ethylene glycol, glycerol and acetamide (see Table 7.14.1) in cacodilate buffer.

• Stock solution of oligonucleotides (we are using 0.24 mM); it can be either single self-complementary oligonucleotide or two stock solutions of the complementary strands.

• UV-visible spectrometer with multi-position Peltier temperature controller.

  Microsoft Excel software for statistical data analysis.

Table 7.14.1.

Water activity (lna_W) of co-solute buffers^a

Buffer	Co-solute concentration g/mLb	lnaW
CNE 0.3 onlyc	-	0.0104
5% ethylene glycol in CNE 0.3	0.0516	0.0248
10% ethylene glycol in CNE 0.3	0.1002	0.0392
15% ethylene glycol in CNE 0.3	0.1510	0.0541
20% ethylene glycol in CNE 0.3	0.2078	0.0665
5% glycerol in CNE 0.3	0.0508	0.0204
10% glycerol in CNE 0.3	0.0992	0.0311
15% glycerol in CNE 0.3	0.1499	0.0433
20% glycerol in CNE 0.3	0.1998	0.0569
5% acetamide in CNE 0.3	0.0500	0.0250
10% acetamide in CNE 0.3	0.1006	0.0399
15% acetamide in CNE 0.3	0.1510	0.0551
20% acetamide in CNE 0.3	0.2026	0.0686

^aThe water activities were determined experimentally by Spink and Chaires (Spink and Chaires 1999).

^bSolutions were prepared by directly weighing the precise amount of co-solute in a volumetric flask and diluting to desired volume with CNE 0.3 buffer.

^c10 mM sodium cacodilate (pH 7.4), 300 mM NaCl and 0.1 mM EDTA

1. Start up the UV spectrometer and set the desired wavelength. Default wavelength for UV melting is 260 nm, which is close to the maximum absorption of most oligonucleotides.

   • Shimadzu 800 allows measurement at three wavelengths in the same experiment. We have found that some G rich sequences give better melting curves at 280 nm, which may be used as the second wavelength.
2. Zero the UV spectrometer

   • For Varian Cary Bio 100, place pure buffer and the solutions of co-solutes (0.6 mL each) in appropriate cuvettes and position them in the temperature controller. Typical osmotic stress experiments measure five samples simultaneously: pure buffer, and 5, 10, 15 and 20% of the co-solute (see Table 7.14.1). Make sure Multi Zero option is selected in the Setup before zeroing the instrument.
   • For Shimadzu 800, the multi zero option is not available; 800 can be zeroed on any position of an empty eight-position cuvette.
3. Place the sample solutions in spectrometer’s cells.

   • For Varian Cary Bio 100 add 5 µL of nucleic acid stock solution to each buffer directly into the cuvettes; 0.24 mM stock makes a sample of 2 µM in strands concentration (the small dilution by stock solution volume is ignored).
   • For Shimadzu 800, the small volume of cuvettes makes direct addition impractical. Premix each buffer (360 µL) and stock (3 µL) in a separate tube and add 120 µL to appropriate position of the eight-position cuvette. The rest of the sample is stored in a fridge (just above freezing) and is used to reload the cells when the solution evaporates (on average, after 3 to 5 cycles).

4. Check the absorption at the wavelength to be monitored; it should be in the range of 0.2 to 0.8 and similar at all positions. For short or long oligonucleotides the absorption may fall out of range and the concentration may need to be adjusted. We have found that short sequences give better results at 4 µM in strands concentration.

5. Program the Peltier temperature controller according to the operator’s manual to perform the desired heating (0.5 °C per minute) and cooling (2 °C per minute) cycles. Acquire the data every 0.5 °C during the heating cycles (Fig. 7.14.2).

   • For Varian Cary Bio 100, start with a cooling cycle from well above the expected melting temperature and program the desired number of cycles.
   • For Shimadzu 800, start with manual heating (5 °C per minute) and cooling (2 °C per minute) cycle. Program single run (0.5 °C per minute) to acquire the data.

6. Analyze the data using the instrument’s software to obtain melting temperature.

7. Repeat the experiment (heating-cooling cycle) several times to obtain at least five good melting curves. Transfer the data to Microsoft Excel to calculate the average t_m for all five co-solute concentrations (for an example of data collection, see Table 7.14.2). The standard deviation of t_m data points should be ±0.5 °C or, preferably, better; more experiments (typically 8–12) are needed if the data are less consistent.

Figure 7.14.2.

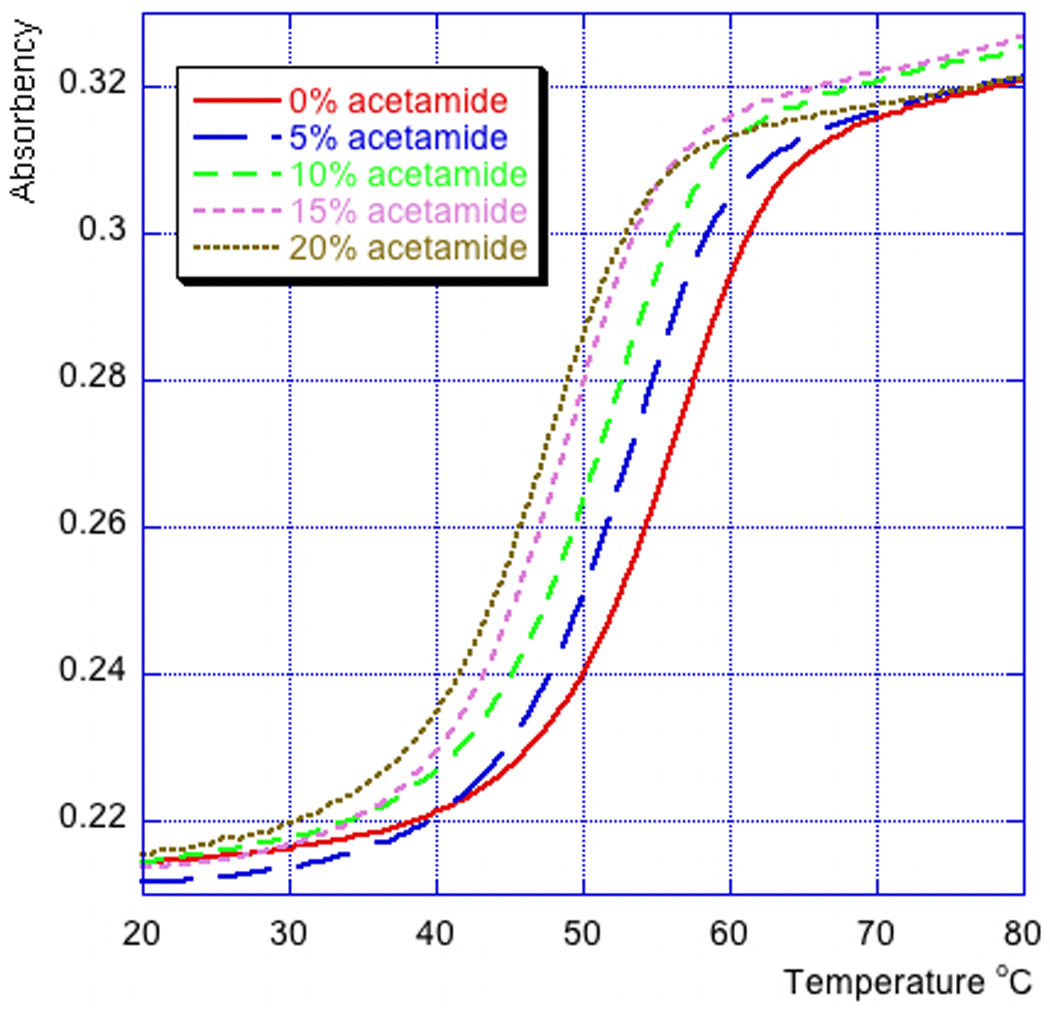
Melting curves of 5’-r(^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpA) in acetamide buffers.

Table 7.14.2.

Experimental UV thermal melting data of 5’-r(^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpA) in acetamide buffers.

	Acetamide in CNE 0.3 buffer					Derivative α curve			Van't Hoff plot
Experiment	0%	5%	10%	15%	20%	T1	T2	ΔH cal/mol	ΔH cal/mol	ΔS eu
es050a	55.4	52.3	50.8	48.5	47.4	49.02	62.45	81559	86700	237.8
es050b1	55.3	52.4	50.9	48.3	47.2	49.01	62.26	82618	85700	235.1
es050b2	55.3	52.2	50.8	48.4	47.1	49.17	62.30	83424	85600	234.5
es050b3	55.1	52.2	50.9	48.5	47.2	49.08	62.30	82833	74500	201.1
es050c1	55.3	52.1	50.9	48.5	46.7	49.11	62.14	84009	85900	235.6
es050c2	55.1	52.1	50.8	48.7	47.0	48.92	62.37	81393	72000	192.9
es050d	55.2	52.0	50.8	48.5	47.4	48.91	62.33	81563	74400	200.5
es050e1	55.3	52.4	50.9	48.6	47.3	48.99	62.43	81486	79700	216.5
es050e2	55.3	52.5	50.9	48.6	47.4	48.94	62.97	78173	80100	217.6
es050e3	55.5	52.5	51.0	48.7	47.5	48.95	62.88	78715	78700	213.3
es050f1	55.5	52.7	51.0	48.6	47.5	49.09	62.54	81477	78200	211.9
es050f2	55.7	52.6	50.9	48.7	47.3	48.99	63.08	77878	81200	220.8
es050f3	55.6	52.5	50.8	48.6	47.4	49.27	62.86	80760	79300	215.6
Average	55.4	52.3	50.9	48.6	47.3	48.8	62.5	80194	81200	221.4
Stand. Dev.	0.2	0.2	0.1	0.1	0.2	0.4	0.3	2937	4100	12.5

Basic Protocol 2

DETERMINATION OF MELTING ENTHALPY FOR OSMOTIC STRESS CALCULATION

The preferred method for determining the enthalpy of nucleic acid melting is by Differential Scanning Calorimetry (DSC). DSC provides model independent enthalpy that is not affected by assumptions about the melting transition and the quality of melting curves. Detailed description of DSC protocol has been published in UNIT 7.4 (Pilch 2000). Below we provide a short protocol we use in our osmotic stress studies. If a differential scanning calorimeter is not available or the amount of the nucleic acid is not sufficient for the calorimetric measurement (see step 5 below), the melting enthalpy can alternatively be determined from UV thermal melting curves (step 9) or from concentration dependence of melting temperatures (step 10). It is advisable to compare the enthalpy values obtained using different techniques, because good fit (within 10 to 20%) is evidence for a two-state (duplex to single strands) melting process.

Materials

• Aqueous buffer containing 10 mM sodium phosphate (pH 7.4) and 300 mM NaCl.

• Phosphate buffer is preferred for DSC studies because of its high thermal stability and small change in pH with temperature. In practice, this is important to obtain stable and reproducible base lines.

• Stock solution of oligonucleotides. We are using the same stock (0.24 mM) as in the UV melting studies.

• Differential scanning microcalorimeter suitable for biopolymer studies. We are using the TA Instruments NanoDSC equipped with 0.3 mL capillary cells.

• Oil free vacuum pump, vacuum desiccator and stirring plate for degassing.

• Thermal analysis software for calculations of van’t Hoff enthalpy from melting curves.

• KaleidaGraph software for graphical fitting of data and Microsoft Excel software for statistical data analysis.

Steps

1. Make sure the cells are clean (if necessary clean cells according to manufacturer’s recommendations).

2. Degas 3–4 mL of phosphate buffer. Place the buffer in a scintillation vial with small stirring bar and stir under moderate vacuum (ca. 80 torr) for 20–30 min. Place the degassed buffer in both sample and reference cells. We attach two 1 mL pipette tips to cell outlets using short silicon tubing and load the buffer using a 1 mL pipettor. The buffer is rocked back and forth to make sure all air bubbles are removed from the capillary cells.

3. Condition the DSC cells by performing single heating-cooling cycle 0 to 130 °C at 1 °C/min.

4. Replace the buffer in both sample and reference cells with a freshly degassed (see Step 2) buffer. Program the desired temperature limits and record 8 to 12 base line runs at 1 °C/min until stable and reproducible base lines are obtained. If base lines are not reproducible, replace the buffer and try again; clean the cells and repeat steps 1–3, if the base lines are still not satisfactory.

5. Place the desired amount of stock solution in a round bottom cryo-vial and evaporate in a speed-vac. We have found that 140 nmols of self-complementary strands (583 µL of 0.24 mM stock) provides a reasonably strong signal and a good enthalpy estimate.

6. Dissolve the dried nucleic acid in 1 mL of phosphate buffer. Dialyze the solution against the phohphate buffer (3 × 300 mL) using a Flot-A-Lyzer G2 (100–500 D, Spectrum Laboratories) or similar dialysis bag. The first dialysis buffer is replaced after 4 hours, then again after another 4 hours and the last dialysis is done overnight.

7. Degas and load the nucleic acid solution in the sample cell and the last dialysis buffer in the reference cell of the calorimeter (see step 2). Perform several heating and cooling cycles at 1 °C/min using the desired temperature limits. Record three to five reproducible heating curves with good base lines.

8. Analyze the data using instrument’s software to obtain ΔH of melting transition.

9. To obtain ΔH from melting curves in pure CNE 0.3 buffer perform the following:

   • Using the instrument’s software (Cary Bio 100) convert the experimental absorbance vs. temperature curves into fraction of strands remaining hybridized vs. temperature curves (α curves) by fitting the melting profile to a two-state transition model, with linearly sloping lower and upper base lines.
   • Construct the van’t Hoff plot of lnK vs. T_m⁻¹. For a bimolecular transition of self-complementary strands the equilibrium constant K = α/[2C(1−α)²] where C is the total strand concentration (C = 2 × 10⁻⁶ M). The van't Hoff plot (lnK vs. T_m⁻¹) is linear with - ΔH/R as the slope and ΔS/R as the intercept (R is the universal gas constant, 1.986 cal/mol/K) (Breslauer 1995). All the above steps are performed in an interactive mode using the Cary Bio 100 software that gives the final ΔH and ΔS (Table 7.14. 2, van’t Hoff plot)
   • Using the instrument’s software (Cary Bio 100) convert the α curves into differentiated melting curves (δα/δ(T_m⁻¹) vs. T_m). The width of the differentiated melting curve at the half-height is inversely proportional to the van't Hoff transition enthalpy (Breslauer 1995). For a bimolecular transition calculate ΔH = 10.14/(T₁⁻¹ − T₂⁻¹) where T₁ and T₂ are the lower and upper temperatures (in K) at one-half of δα/δ(T_m⁻¹) (Table 7.14.2, derivative α curve).

10. To obtain ΔH from concentration dependence of melting temperatures perform melting experiments in pure CNE 0.3 buffer over a concentration range of 1 to 64 µM of oligonucleotides. It is convenient to use smaller 1 and 2 mm light pass cells for the high concentration samples. For a bimolecular association of self-complementary strands T_m⁻¹ = (R/ΔH)lnC + ΔS/ΔH where R is the universal gas constant (1.986 cal/mol/K) and C is the total strand concentration 1 × 10⁻⁶ to 64 × 10⁻⁶ M (Breslauer 1995). Obtain ΔH by linear fitting the plot of T_m⁻¹ vs. lnC using KaleidaGraph software; R/ΔH is the slope of the plot.

Basic Protocol 3

CALCULATION OF THE NUMBER OF WATER MOLECULES RELEASED UPON MELTING

The final protocol uses the experimentally determined dependence of melting temperature on water activity (Protocol 1) and the melting enthalpy (Protocol 2) to calculate the number of water molecules released upon melting of oligonucleotide duplex. The errors of the final Δn_W are estimated using the standard error propagation calculations (Bewington and Robinson 1992).

Materials

• KaleidaGraph software for graphical fitting of data and Microsoft Excel software for statistical data analysis.

Steps

1. Enter the values of lna_w from Table 7.14.1 and the values of t_m obtained in Basic Protocol 1 in KaleidaGraph data table. Convert t_m to T_m⁻¹ using the KaleidaGraph Formula Entry tool: T_m⁻¹ = 1/(t_m+273.13).

2. Construct a plot with lna_w as the X axis and T_m⁻¹ as the Y axis (Fig. 7.14.3). Perform linear Curve Fit of the data. The slope of the linear fit (0.0012673 in Fig. 7.14.3) is the d(T_m⁻¹)/d(lna_w).

3. Using Microsoft Excel calculate Δn_W = (−ΔH/R)[d(T_m⁻¹)/d(lna_w)], where R is the universal gas constant (1.986 cal/mol/K), −ΔH is the melting enthalpy (Protocol 2) and d(T_m⁻¹)/d(lna_w) is the dependence of melting temperature on water activity calculated in step 2 above. For the example in Table 7.14.2 and Figure 7.14.3 the calculation gives Δn_W = (80194/1.986) × 0.0012673 = 51.2.

4. Estimate the uncertainties of the d(T_m⁻¹)/d(lna_w) plot by constructing alternative linear fits using error bars (standard deviations of T_m⁻¹) as the data points. Two alternative plots were obtained by linear fits through T_m⁻¹ plus or minus standard deviation at 0% and 5% and minus or plus at 15% and 20% of co-solute. The fit of T_m⁻¹ plus standard deviation at 0% and 5% co-solute and T_m⁻¹ minus standard deviation at 15% and 20% co-solute gave one alternative, and the fit of T_m⁻¹ minus standard deviation at 0% and 5% co-solute and T_m⁻¹ plus standard deviation at 15% and 20% co-solute gave the other alternative (Fig. 7.14. 4). The deviations of both alternative plots from the original plot were averaged to give σslope = ((0.0013388 − 0.0012673) + (0.0012673 − 0.0011959))/2 = 0.000071 as the uncertainty of the plot. Thus, the dependence of melting temperature on water activity is d(T_m⁻¹)/d(lna_w) = 0.0012673 ± 0.000071.

5. Calculate the error limits of Δn_W using the error propagation approach σΔn_W = Δn_W[(σΔH/ΔH)² + (σslope/slope)²]^0.5 where σΔH is the standard deviation of enthalpy from Table 7.14.2 and slope = d(T_m⁻¹)/d(lna_w) (Bewington and Robinson 1992). σΔn_W = 51.2 × [(2937/80194)² +(0.000071/0.0012673)²]^0.5 = 3.4. The final result is Δn_W = 51 ± 3.

Figure 7.14.3.

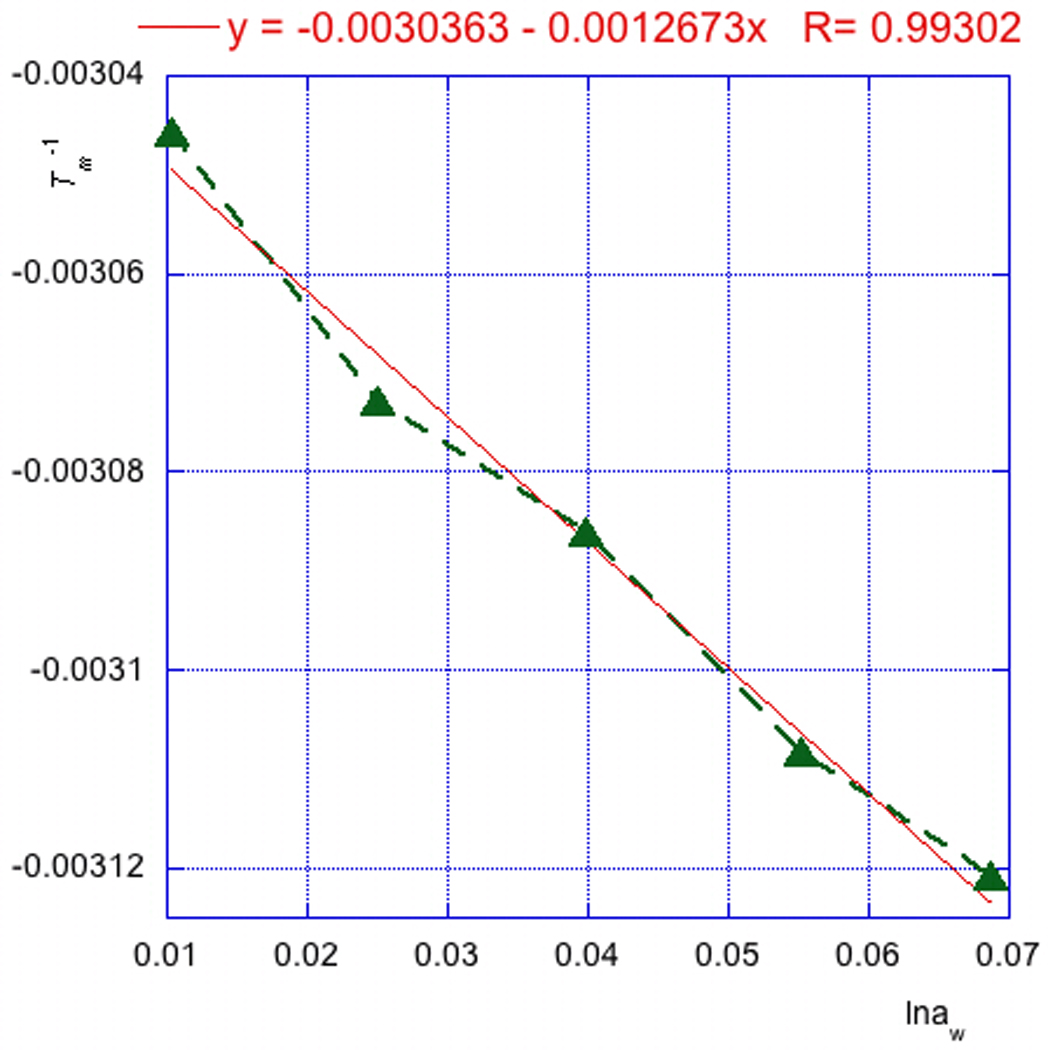
Dependence of melting temperature (T_m⁻¹) on water activity (lna_w) for 5’-r(^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpA) in acetamide buffers.

Figure 7.14.4.

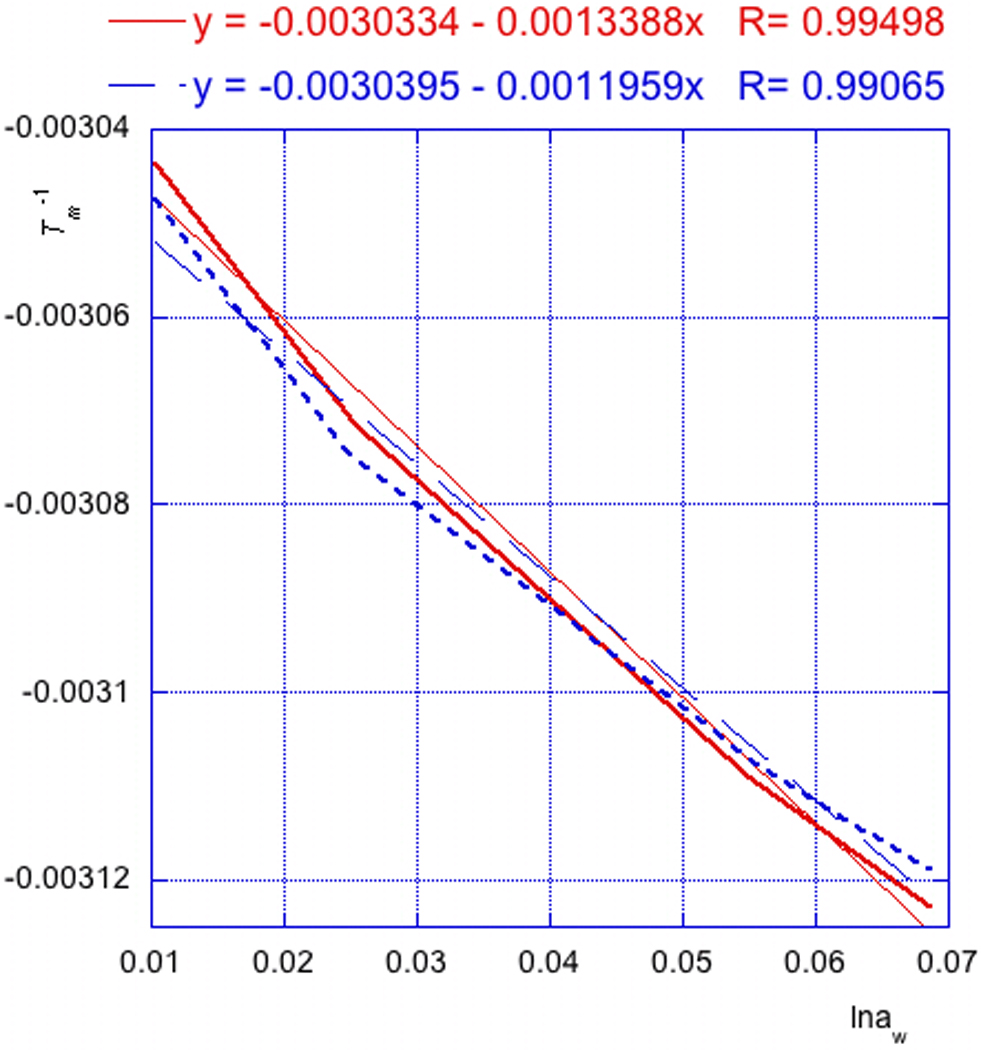
Error estimate plots of d(T_m⁻¹)/d(lna_w) for 5’-r(^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpAp^MeU_2’-FpA) in acetamide buffers.

COMMENTARY

Background Information

Osmotic stress is a relatively new method that was developed to study the changes in hydration upon conformational transitions in proteins (Parsegian et al. 1995; Robinson and Sligar 1995). Spink and Chaires pioneered the application of osmotic stress to study the hydration of DNA (Spink and Chaires 1999). Using osmotic stress Qu and Chaires found that water was an important participant in the formation of DNA intercalation complexes where binding of some intercalators was accompanied by an uptake of as many as 30 water molecules (Qu and Chaires 1999; Qu and Chaires 2001). We and others adopted osmotic stress method to probe the hydration of chemically modified nucleic acids (Rozners and Moulder 2004; Rozners et al. 2005; Li et al. 2007; Hwang et al. 2009; Kolarovic et al. 2009; Watts et al. 2010).

An equilibrium that involves changes in the number of water molecules associated with the biopolymer (e.g., dissociation of a DNA double helix) is sensitive to changes in water activity. Osmotic stress probes hydration using the dependence of the equilibrium constant on osmotic pressure (water activity). The water activity is changed by addition of small neutral organic compounds (co-solutes), which in solution are excluded from the immediate vicinity of the biopolymer. Osmotic stress assumes that the excluded co-solutes do not interact with the biopolymer, so therefore, changing the concentration of such co-solutes can be used to change the water activity without directly affecting the macromolecule. A straightforward calculation, Δn_W = (−ΔH/R)[d(T_m⁻¹)/d(lna_w)], gives the number of water molecules that are uniquely bound to the double helix, but are released upon melting (Spink and Chaires 1999).

However, the inertness of the excluded co-solutes has been questioned. Timasheff has proposed that the effect of added co-solutes on macromolecules is better described using the concepts of crowding and preferential hydration, which suggest that the exclusion depends on size, geometry, and chemical nature of the co-solute (Timasheff 1998). In other words, the experimentally determined Δn_W may deviate from the true absolute numbers if the co-solutes are not completely excluded from the vicinity of the biopolymer. Record and co-workers (Courtenay et al. 2000) found that several small solutes (including glycerol) are not completely excluded from the vicinity of proteins causing an underestimation of the Δn_W in osmotic stress experiments. We typically observe different numbers of Δn_W when using different co-solutes; acetamide gives somewhat higher numbers than ethylene glycol and glycerol. Although the physical basis of the exclusion phenomenon is still under debate, the various studies agree that osmotic stress gives correct estimates of the trends in hydration changes (Timasheff 1998; Parsegian et al. 2000). We have found that the results of osmotic stress qualitatively correlate very well with the hydration patterns seen in high-resolution crystal structures (Li et al. 2007; Kolarovic et al. 2009). It should be noticed that in most cases different co-solutes give similar trends and mutually support the qualitative discussion.

The main advantage of osmotic stress is that the method is experimentally simple, fast and does not require sophisticated equipment. The simplicity and accessibility outweigh the limitations (uncertainty in absolute numbers) and osmotic stress can be easily adopted by a wide range of laboratories specializing in organic, bioorganic and nucleic acid chemistry. The method does not require special expertise in advanced physical chemistry. We have found that osmotic stress is particularly useful to understand the effect of chemical modifications on nucleic acid hydration (Li et al. 2007; Kolarovic et al. 2009). Others have also used osmotic stress to probe changes in hydration caused by modifications in heterocyclic bases (Hwang et al. 2009) and sugars (Watts et al. 2010). In conclusion, osmotic stress is a straightforward method for rapid probing of nucleic acid hydration and changes therein caused by chemical modifications and non-covalent interactions.

Critical Parameters and Troubleshooting

The critical parameters required for osmotic stress calculations are melting temperatures at different co-solute concentrations and melting enthalpy. The quality of the melting curve determines the accuracy and reproducibility of the melting temperatures. Finding an oligonucleotide sequence that gives a sharp melting transition and stable and linear base lines (before and after the melting transition) is largely empirical and may require some time investment. It is important that both non-modified and modified oligonucleotides give good melting curves, because the final result will typically be comparison of the two Δn_W values. We have found that modifications that stabilize duplex structure typically give excellent melting curves, as is the case for formacetal internucleoside linkages (Kolarovic et al. 2009) and the 2’-fluoro modification presented herein (Fig. 17.4.2). Chemical modifications that strongly disturb the double helical structure may not give reliable two-state melting transitions at all and may not be suitable for osmotic stress study.

When probing the effect of chemical modification, it is preferable to maximize the modified units in a given duplex. This is important to bring out the effect of the modification on the background of the native nucleic acid. For example, the self-complementary 5’-r(UA)₆ has allowed us to study the effect of 12 formacetal linkages (between each U and A) on the background of 10 phosphates (between each A and U) (Kolarovic et al. 2009). However, if the modification strongly stabilizes or strongly destabilizes the double helix, the melting temperatures may be shifted out of the range that can be measured accurately (>85 or <15 °C). For example, we have not been able to use osmotic stress to study formacetal modified 5’-d(TA)₆ because the t_m < 10 °C (Kolarovic et al. 2009) and 2’-fluoro modified 5’-CCCCGGGG because of tm > 90 °C (unpublished results). A potential solution is redesign of the sequence (increasing or decreasing the number of C-G base pairs) or changing the number of modifications.

In most cases, we have obtained good quality melting curves using self-complementary DNAs 5’-GCGAATTCGC, 5’-(TA)₆ and 5’-(CG)₃ (Rozners and Moulder 2004) and 5’-CG(TA)₅CG (Kolarovic et al. 2009) and RNAs 5’-GCGAAUUCGC, 5’-(UA)₆ and 5’-(CG)₃ (Rozners and Moulder 2004; Kolarovic et al. 2009), 5’-GGCUGGCC (Rozners et al. 2005) and 5’-CGCGAAUUCGCG (Rozners et al., unpublished data). Meanwhile, structurally similar 5’-d(CGCTAATTGGCG) and 5’-r(GCGUAUACGC) did not yield good melting curves in our hands. We have extensively used self-complementary sequences containing 5’-UA (or 5’-TA) dimer because it is easy to incorporate modified internucleoside linkages between U and A and it allows maximum number of modifications in a self-complementary oligonucleotide (Kolarovic et al. 2009). Another advantage of self-complementary sequences is their internal symmetry, which simplifies other structural studies, such as NMR restrained molecular modeling. Thus, a modified UA dimer allows preparation of a variety of sequences not only for osmotic stress (5’-(UA)₆ and 5’-CG(UA)₅CG) but also for NMR (5’-GCGUACGC) and crystallographic (5’-GCGUAUACGC) studies (Kolarovic et al. 2009).

Although the use of self-complementary sequences simplifies synthesis and sample preparation, a potential problem may be competing hairpin formation. A melting transition involving both duplex and hairpin intermediates cannot be treated as two-state, even if it does not have a visibly distorted melting curve. It is recommended that in the test phase melting experiments are done at various nucleic acid concentrations (1 to 64 µM). For a two-state duplex to single strands transition the plot of T_m⁻¹ vs. lnC of oligonucleotide should be linear (please note, this is the same plot that is used to obtain ΔH). Deviation from linearity is evidence for competing hairpin structures. For a two-state hairpin to single strand transition the plot of T_m⁻¹ vs. lnC of oligonucleotides is horizontal, e.g., the melting temperature does not depend on oligonucleotide concentration. To avoid complications from competing hairpins and to improve the quality of the UV melting curves, it may be advantageous to prepare two different complementary strands. Others have reported successful osmotic stress experiments with modified 5’-d(GCGTACACATGCG)/3’-d(CGCATGTGTACGC) (Hwang et al. 2009), 5’-d(GCTATAATGG)/3’-r(CGAUAUUACC) and 5’-r(GCUAUAAUGG)/3’-r(CGAUAUUACC) (Watts et al. 2010).

It is recommended to determine the enthalpy of melting transition using several different methods (Protocol 2). Comparison of results gives an evaluation of the two-state melting behavior. The preferred method is by Differential Scanning Calorimetry (DSC). DSC gives model independent ΔH that does not depend on any assumptions on two-state vs. multistate melting transition (for more discussion, see UNIT 7.4). However, the DSC instruments are expensive and may not be available to all academic laboratories. Another limitation of the calorimetric method is the relatively large amount of nucleic acid required for calorimetric experiment (>100 nmols) compared to single UV-melting experiment (1–2 nmols). If determination of ΔH using calorimetry is complicated, good alternatives are 1) concentration dependence of melting temperatures, which also checks for possible hairpin-duplex competition and 2) van’t Hoff analysis of melting curves. For the latter, analysis of the differentiated curve is preferred because it is less impacted by distortions of pre- and post-melting base lines. Because the ΔH values may be different depending on the method used, it is important to use the same method for the comparison of various oligonucleotides.

Anticipated Results

Usually, good UV melting curves yield relatively accurate melting temperatures within ± 0.5 °C. Depending on the method, the estimates of ΔH may have uncertainties between 5 to 10%. The melting curves of 2’-fluoro modified 5’-r(UA) used to illustrate osmotic stress in Figure 7.14.2 are among the best we have observed and yield excellent t_m and ΔH estimates (Table 7.14.2) which propagate in a relatively accurate estimate of Δn_W = 51 ± 3. For this example, we used ΔH determined from analysis of differentiated melting curves (Table 7.14.2) to facilitate the comparison with the non-modified sequence studied earlier (Rozners and Moulder 2004).

As discussed above, the absolute number (51 for acetamide) may differ depending on the co-solute used. Therefore, we recommend using the quantitative data obtained in osmotic stress to support qualitative conclusions about changes in hydration. For example used herein to illustrate osmotic stress, we conclude that the 2’-fluoro modification, which gives Δn_W = 51 ± 3 causes statistically significant loss of hydration compared to the non-modified RNA, which gave Δn_W = 67 ± 6 in our earlier study (Rozners and Moulder 2004). However, the absolute numbers and exact value of the change (ΔΔn_W = 16) will depend on the co-solute used and should be used with extreme caution to avoid misleading conclusions.

Time Considerations

Measurement of one melting curve for each buffer (assuming five samples are measured simultaneously) requires two to three hours. Acquisition of a set of five to eight melting curves requires up to two days. Thus, a complete osmotic stress study of one oligonucleotide sequence may take a week or two to accomplish. Although this may seem like a long experiment, it is not labor extensive because the majority of the time is required for the relatively slow (0.5 °C per min) UV-melting experiments. Sample preparation and experimental set up is straightforward and usually does not require more than an hour for each set of co-solute melting curves. The analysis of the melting curves may take several hours depending on the quality of the curves.