Pharmacokinetic Modeling of Tumor Bioluminescence Implicates Efflux, and Not Influx, as the Bigger Hurdle in Cancer Drug Therapy

Abstract

In vivo bioluminescence imaging is a powerful tool for assessing tumor burden and quantifying therapeutic response in xenograft models. However this technique exhibits significant variability as a consequence of differences in substrate administration, as well as the tumor size, type, and location. Here we present a novel pharmacokinetic (PK) approach that utilizes bioluminescence image data. The sample data are taken from mice implanted with a melanoma tumor cell line that was transfected to express the firefly (Photinus pyralis) luciferase gene. At 5, 7 and 10 days post-implant, IP injections of D-luciferin were given to monitor the uptake into the tumor, and the tumor volume was measured using ultrasound. A multi-compartment PK model was used to simultaneously fit all experiments for each mouse. We observed that the rates of luciferin transport in and out of the tumor exhibited a clear dependence on the tumor volume. Also, the rate of tumor influx increased faster than did the efflux, resulting in a shortening of the time to peak luciferin concentration as the tumor grows. The time of the peak concentration correlated poorly with the tumor volume, but the peak bioluminescence signal and the area under the curve both exhibited a dependence on the tumor surface area. These results agree with Starling’s hypothesis relating the higher interstitial fluid pressure in the tumor with flux across the boundary, and suggest that drug transport may depend more strongly on the surface area of the tumor than its volume. These observations provide a quantitative physical rationale for molecular targeting of therapeutics that enhance trapping and overcome the accelerated efflux kinetics.

Major Findings

By combining detailed pharmacokinetic modeling with bioluminescence imaging, quantitative assessments of the relationship between tumor growth and drug uptake kinetics are possible. Much of the variability that arises from standard bioluminescence measurements is accounted for in this pharmacokinetic model, and the net result is a clear scaling relationship between drug transport kinetics, drug levels within the tumor and the tumor volume. These results illustrate how bioluminescence imaging of xenograft models, particularly in longitudinal studies of tumor load or therapy intervention, could benefit from the addition of pharmacokinetic modeling utilizing image-based readouts for individualized metrics of drug delivery and efficacy.

Quick Guide to Equations and Assumptions

$$\begin{array}{c}\frac{{\mathit{\text{dL}}}_{\mathit{\text{ip}}}}{\mathit{\text{dt}}}=-k_a{L}_{\mathit{\text{ip}}}\hfill \\ \frac{{\mathit{\text{dL}}}_b}{\mathit{\text{dt}}}=-(k_{\mathit{\text{bt}}}+k_{\mathit{\text{el}}})L_b+k_{\mathit{\text{tb}}}{L}_t+k_a{L}_{\mathit{\text{ip}}}\hfill \\ \frac{{\mathit{\text{dL}}}_t}{\mathit{\text{dt}}}=k_{\mathit{\text{bt}}}{L}_b-k_{\mathit{\text{tb}}}{L}_t\hfill \end{array}$$ Equation 1

These equations describe the mass balance of luciferin in peritoneum L_ip, blood L_b and tumor L_t. The first equation describes the intraperitoneal (IP) delivery where k_a is the first order rate constant describing the absorption of luciferin from the peritoneum into the blood. The second equation describes the change in luciferin levels in the blood with four separate components: k_btL_b describes passage from the blood to the tumor, k_tbL_t is reverse transfer from the tumor back to the blood, k_aL_ip describes adsorption from the peritoneum, and k_elL_b is the rate of elimination from the body. The rate constants vary between individual mice and may also change as the tumor grows.

Major assumption

This model ignores the specific contributions of other tissues in the body, however a three compartment model results in the nearly identical parameter values, thus this simplification is justified.

$$\frac{\mathit{\text{dP}}}{\mathit{\text{dt}}}=V_o{L}_t$$ Equation 2

This equation describes the rate of photon emission from the tumor. The reaction of luciferin with the luciferase expressed by the tumor cells should follow Michaelis-Menten kinetics because it is enzyme mediated; however we are in a regime in which the substrate concentration (luciferin) is much less than the measured K_M value for luciferin-luciferase, this linear approximation is valid (see text for more details). V_o is the conversion factor that relates the photon emission rate to the level of luciferin.

Major assumption

Since each cell expresses luciferase, we assume that the concentration of luciferase in growing tumor remains constant over the time of experiment.

Introduction

Bioluminescence imaging (BLI) is a powerful, non-invasive tool for localizing tumors, quantifying their growth properties, and monitoring the effects of therapy (1–8). The use of tumor cells expressing luciferase from firefly or other species have been of particular utility since they provide a very sensitive signal with a short acquisition time that can be adapted for high-throughput techniques. The substrate, D-luciferin, is administered by intraperitoneal (IP) or intravenous (IV) injection, and is oxidized by the endogenous luciferase when it reaches the tumor cell, resulting in photon emission.

Although there are clear advantages for tumor characterization with this technique, several challenges and drawbacks exist. First, the time course of light emission exhibits significant variability depending on the size and location of the tumor, as well as the tumor cell line used in the xenograft (1, 4, 5, 9, 10). Furthermore, the method of luciferin administration (e.g., IP vs. IV), can affect both the sensitivity and reproducibility of the results (4). Finally, although many previous studies present analyses of the bioluminescent signal suggesting that tumor volume is correlated to the peak signal or the area under the curve (AUC), some studies have found the BLI signal to be roughly linear with volume (5, 11) while others have found relationships that are sublinear or nonlinear in nature (1, 2, 4).

Here, we present a quantitative analysis of D-luciferin pharmacokinetics in a series of bioluminescence studies of luciferase-expressing tumors in mice. With the use of a two-compartment pharmacokinetic (PK) model, we can accurately describe and replicate the biodistribution of luciferin as well as the growth kinetics of the tumor. Further, this method captures the intrinsic variability present in intraperitoneal delivery, and through application of a novel simultaneous fitting algorithm, we arrive at a more accurate set of PK parameters than could be achieved through more conventional solutions to PK modeling. Our method demonstrates a clear scaling relationship between the bioluminescent signal and the tumor volume. Furthermore, unanticipated and surprising insights into tumor transport kinetics emerge from the quantitative analysis suggesting that accelerated efflux rather than reduced influx could be a limiting factor for drug therapy in these types of experimental models, offering a physical rationale for molecular targeting in tumor therapy.

Materials and Methods

Experimental Details

Albino female mice (B6(CG)-TYRC-2J/J) on a B6 background were obtained from Jackson Laboratories (Bar Harbor, ME). Animals were housed in a temperature-controlled room under a 12-hour light/dark cycle with regular mouse chow and water ad libitum. The care and treatment of animals in this study follows protocols approved by the Animal Studies Committee at Washington University. Mice (n=6) were subcutaneously implanted with 1×10⁶ B16F10-luc cells (12) in the inguinal region. These cells were obtained from and authenticated by ATCC (Manassas, VA) and were transfected to express luciferase with the pGL3 vector from Promega (Madison, WI). All cells were in culture less than six months.

On days 5, 7, and 10 post-implantation, the animals were imaged every 5 minutes for 60 minutes with an IVIS Spectrum (Caliper Life Sciences, Hopkinton, MA) after intraperitoneal injection of 150 mg/kg D-Luciferin in sterile saline (Figure 1). To prepare for imaging, the fur in the tumor region was removed by shaving followed with surgical depilatory cream. Data were analyzed offline with Living Image Software v3.1 (Caliper Life Science, Hopkinton, MA) by drawing regions of interest (ROIs) around the tumor masses to derive total photon flux, which is the radiance in each pixel summed or integrated over the ROI area (cm²)x4π giving units of photons/sec. Mice 5 and 6 were sacrificed on day 7 and mice 1–4 at the termination of the experiment in order to excise, measure and weigh the tumors and thereby confirm our ultrasound measurements.

Figure 1.

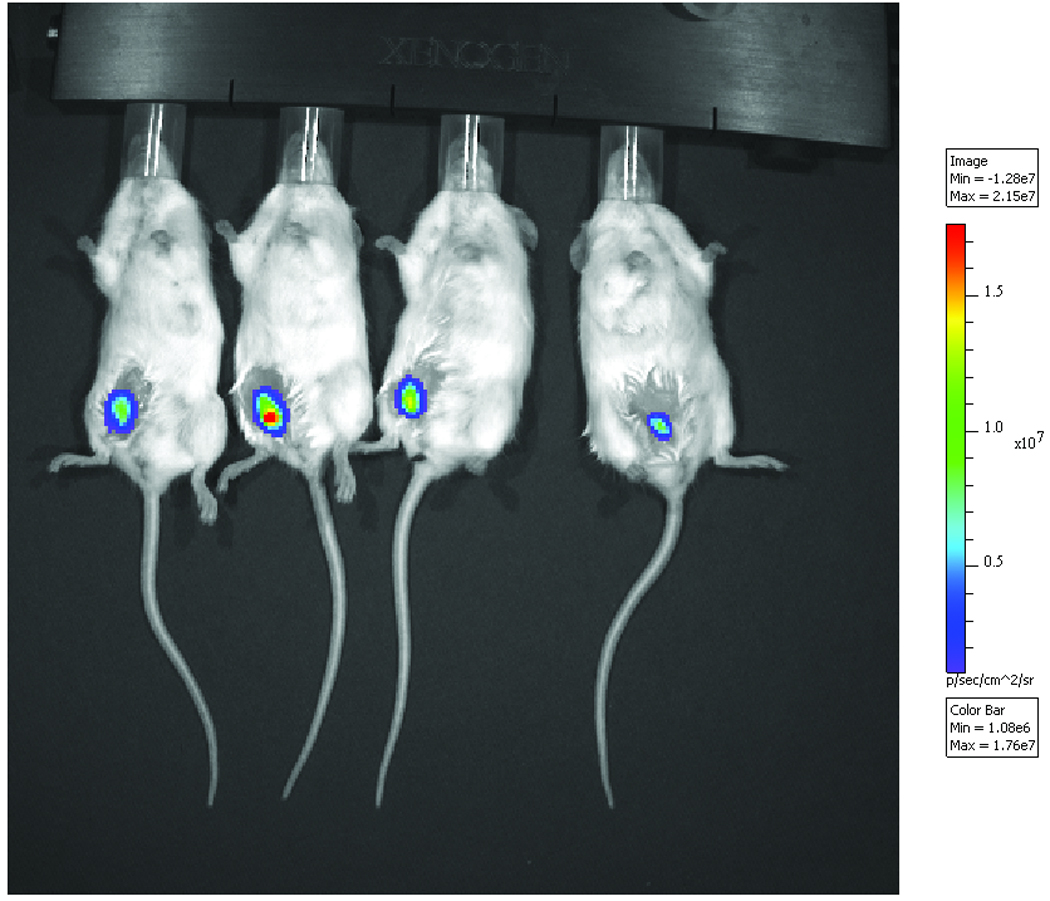
Representative bioluminescence image superimposed on a photograph of tumor-bearing mice seven days post transplantation.

For tumor volume determination, a Vevo 660 ultrasound system (VisualSonics Inc., Toronto, Ontario) with an RMV-703 35 MHz probe was used to image the animals. The Vevo 660 was modified to output analog radiofrequency (RF) signals, which were digitized using a Gage CS 12400 12-bit digitizer at 200 megasamples/sec. These data were used to compute the backscattered energy along each RF line, which was converted to grayscale values for display. The probe was affixed to a gantry, which was translated across the tumor in 100 µm steps. In this way, a sequence of frames was acquired over the entire tumor, permitting the complete tumor volume to be reconstructed from the backscattered RF data. Image formation and analysis was performed using open source software (ImageJ, W. S. Rasband, National Institutes of Health, Bethesda, MD). ROIs were drawn around the tumor cross-sections for each imaging plane, and the scaled tumor volume was computed by multiplying each ROI area by the scan step size (100 µm) and summing these values for all planes in the scan.

To test if the placement and orientation of the mice would affect the BLI signal as suggested in (9), five animals were implanted with the same tumor cell line as in the initial experiments. On day 10, the mice were all placed in the imaging chamber and injected with D-luciferin. Gauze wedges were fashioned to alter the position of the two animals on the outer left (M1) and outer right side (M5) of the group (see Figure S3 in supplemental data). The gauze tilted animal 1 to left slightly and tilted animal 5 to the right slightly. Images were taken every 5 minutes after injection of the substrate, first with the gauze in place, then with the gauze removed. The elapsed time to reposition animals between the two image acquisitions was approximately one minute.

Pharmacokinetic Model

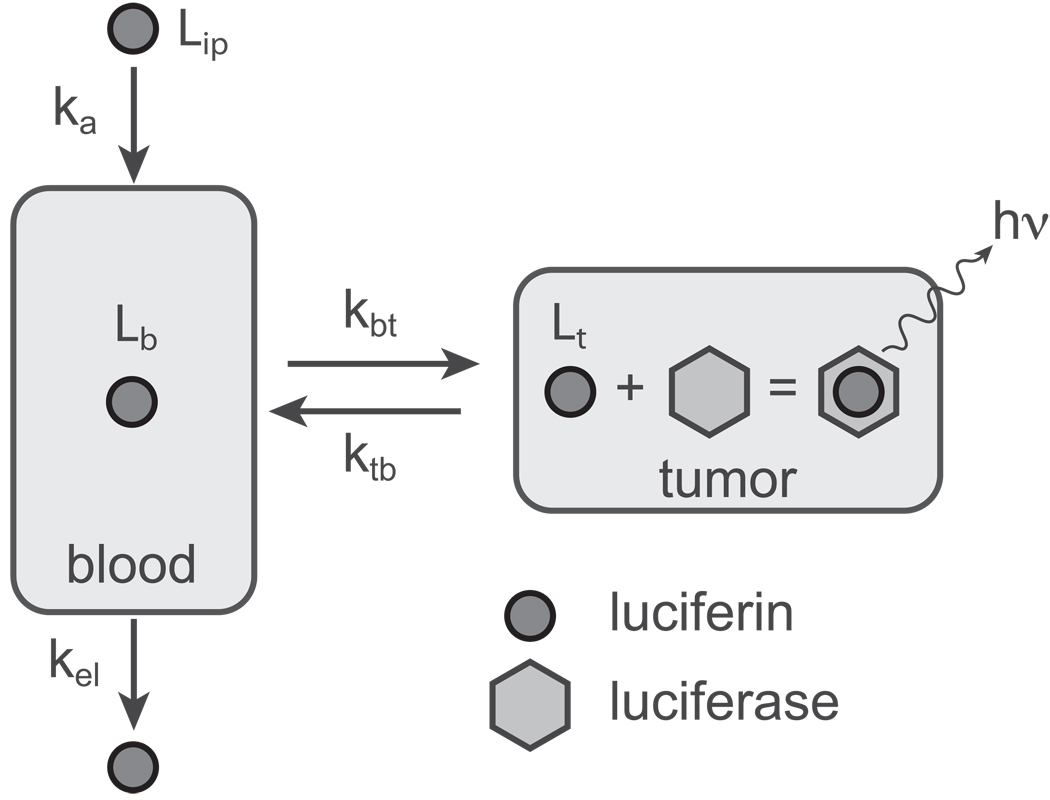
We developed a two-compartment open PK model as shown in Figure 2. To capture the nature of intraperitoneal delivery, we included a first-order kinetic term describing transit into the blood stream from the peritoneum (the k_aL_ip term in Equation 1). We also included the luciferin-luciferase reaction kinetics because the rate of reaction corresponds directly to the bioluminescence signal that we measure. This reaction should follow standard Michaelis-Menten kinetics, however the experiment is conducted in the low substrate concentration limit ([S] << K_M), allowing us to adopt the simpler, linear form shown in Equation 2. All other rate constants, k_bt, k_tb and k_el, describe standard first-order reactions.

Figure 2.

The open two-compartment pharmacokinetic model used for our analysis. Luciferin is administered via IP injection and passes into the bloodstream with first-order kinetics (k_a). Once in the bloodstream, luciferin can move into the tumor (rate constant k_bt) or be eliminated from the body (rate constant k_el). In the tumor, luciferin is passed back into the bloodstream (rate constant k_tb) or it interacts with the luciferase expressed in the tumor resulting in photon emission.

Parameter Fitting

To determine the PK parameters for each mouse/experiment, we used the simultaneous fitting procedure implemented within the public domain program NanoPK that was developed in our laboratory (13). We found little variability in the elimination rate (k_el) and fixed this parameter for each individual mouse. However k_ip was made variable to reflect the subtle differences in each IP injection, and k_bt and k_tb were allowed to change since the biodistribution clearly is altered as the tumor grows. The BLI curves for days 5, 7 and 10 were then simultaneously fit for each individual mouse using a Particle Swarm Optimization (PSO) technique based on the least squares fit between the model prediction and the BLI data. The relative light unit (V_o) in Eq. 2 was set the same value (9.07×10¹⁴) for all data. The PSO method is ideal for searches in high-dimensional spaces, and we performed 100 independent searches to ensure that we had found the optimal parameter set. The sum of square residuals (SSR) between the model solutions and the BLI curves was used as the “cost function” for the search. The top parameter set (i.e. the solution with the smallest SSR) was used as a starting point for another 100 PSO runs and the PK parameters from these 100 solutions were averaged to come up with the parameters in Table 1. The area under the curve for 60 minutes (AUC_0–60) and bioluminescence at peak (BL_peak) were obtained from the time profile after parameterization. The scaling relationships with tumor volume shown in Figure 4 and the corresponding p values were determined using nonlinear regression in R (14). Details on parameter sensitivity are shown in Figure S1.

Table 1.

Pharmacokinetic parameters from simultaneous fitting of the BLI data and the corresponding tumor volumes as measured by ultrasound. The errors are the standard deviation calculated from 100 independent parameterization runs (see Methods).

Mouse	Day	kbt (x10−4 min−1)	ktb (x10−2 min−1)	ka (x10−2 min−1)	kel (x10min−1)	Volume (mm3)
1	5	9.0 (1.7)	7.9 (1.4)	8.1 (1.4)	1.34 (0.13)	12.7
	7	102 (10)	29.9 (2.6)	3.13 (0.27)		60.9
	10	319 (49)	37.5 (7.1)	3.56 (0.28)		444
2	5	4.0 (1.4)	3.15 (0.59)	6.0 (1.9)	1.39 (0.28)	9.94
	7	25 (11)	4.5 (1.2)	12.9 (3.7)		59.3
	10	181 (25)	17.9 (3.8)	3.66 (0.33)		416
3	5	2.27 (0.63)	2.70 (0.71)	11.1 (1.7)	1.27 (0.09)	3.43
	7	25.1 (2.0)	8.76 (0.30)	10.2 (5.3)		43.4
	10	122 (8.4)	21.6 (1.5)	3.8 (2.5)		327
4	5	0.437 (0.046)	2.07 (0.25)	34.0 (5.5)	0.61 (0.13)	3.56
	7	5.5 (1.1)	7.5 (1.1)	7.9 (1.5)		15.8
	10	15.5 (4.2)	11.2 (1.1)	11.3 (1.9)		112
5	5	2.68 (0.75)	3.78 (0.53)	12.9 (2.0)	2.43 (0.33)	5.98
	7	82.2 (8.5)	41.8 (9.6)	2.11 (0.03)		22.7
6	5	0.88 (0.23)	1.51 (0.36)	8.4 (1.9)	1.45 (0.19)	3.91
	7	3.60 (0.43)	4.34 (0.26)	16.3 (1.9)		12.8

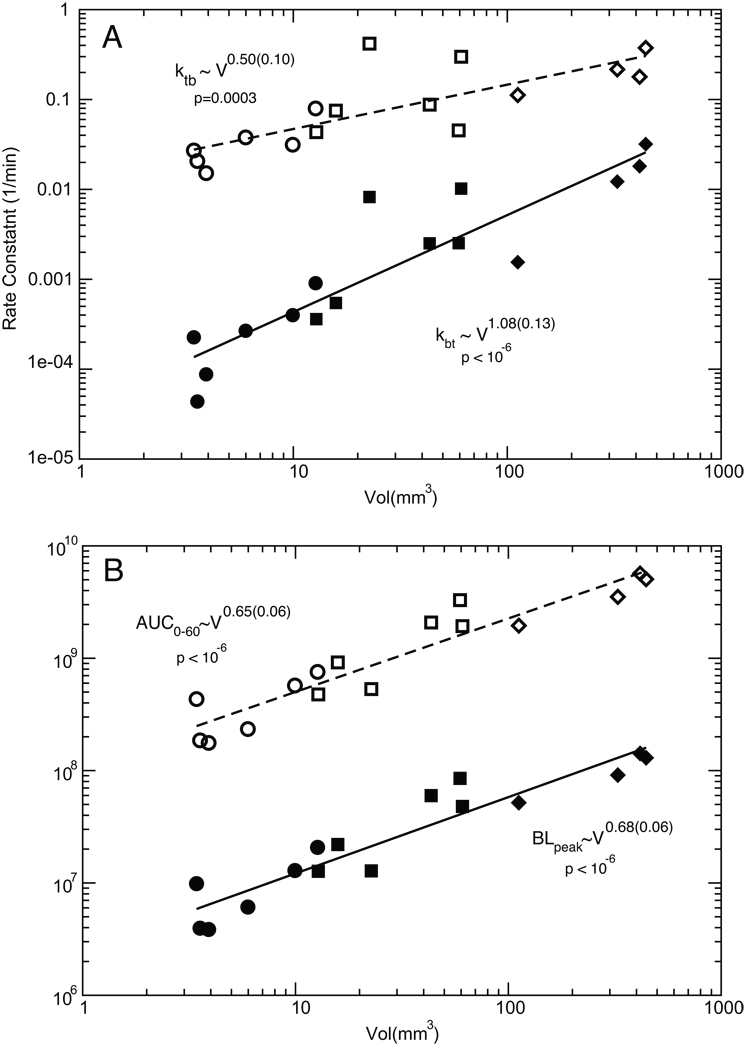
Figure 4.

Scaling behavior of PK parameters with tumor volume. (A) Both k_bt (filled symbols) and k_tb (open symbols) increase with tumor volume, although they scale differently. (B) AUC_0–60 (open symbols) and BL_peak (filled symbols) exhibit very similar scaling relationships with the tumor volume. The circle, square and diamond data points represent measurements made on days 5, 7 and 10 respectively. The scaling exponents and p values were determined with nonlinear regression.

Results and Discussion

BLI Results

On days 5, 7 and 10 following tumor implantation, BLI data was acquired for each animal every five minutes after administration of D-luciferin for a total of sixty minutes. Figure 1 shows a sample BLI acquired on day 7 with the IVIS Spectrum. Analysis of the data shows the total tumor signal increased, as expected, and the time to peak signal decreased as days post implantation increased. Ultrasound imaging of the animals also demonstrated an increase in tumor volume over the course of the experiment.

Fitting the BLI data

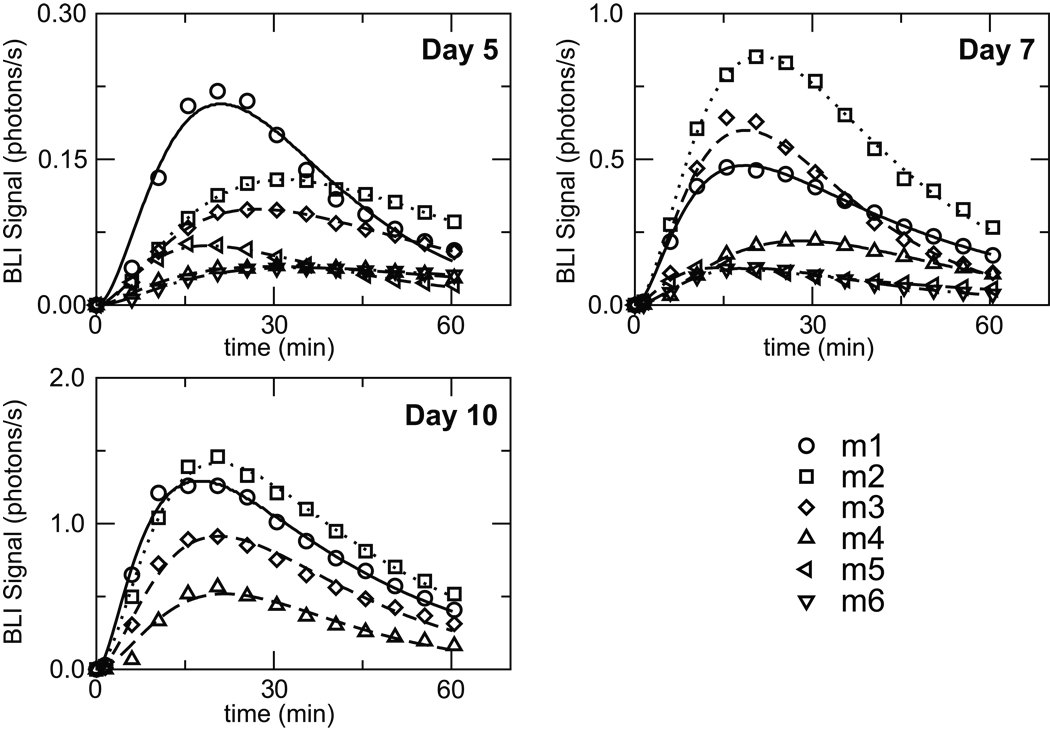
The BLI data for luciferin levels in the tumors were fit for each individual mouse using our two-compartment PK model (Figure 2). The resulting set of PK parameters is listed in Table 1 and the corresponding fits are shown along with the raw data in Figure 3. The overall fit between the experimental data and the model predictions, as measured by the sum of square residuals, is excellent and the parameter values are consistent between the individual experiments. One of the challenges noted in previous studies of this type has been the inherent variability of luciferin transit into the blood stream after IP injection (4, 5). In our studies we do observe values for k_a that range from 0.02–0.34 min⁻¹ and this does highlight the difficulties with exact reproducibility. Lower rates of transit result in a longer time-to-peak value, but this variability is not an issue here given that our PK treatment models the full system and therefore naturally adapts and compensates for these changes in administration. The elimination rate, k_el, exhibited much less variability from mouse to mouse, and because it appeared to be independent of the tumor volume, we utilized the same value in all experiments for a given mouse. Conversely, the parameters for luciferin transfer between the blood and tumor (k_bt and k_tb) were allowed to vary for each experiment because they manifested a significant dependence on tumor volume.

Figure 3.

BLI data obtained for 6 mice measured on days 5, 7, and 10 following tumor implantation. Note that the scale for the vertical axes changes for each panel. The D-luciferin dose was 150 mg/kg in each case, administered via IP injection. The lines represent the best-fit curves resulting from our PK modeling.

PK dependence on tumor volume

The size of the tumor was measured by ultrasound on days 5, 7 and 10 following implant of the xenograft. From fitting this data, we confirmed that the tumors exhibited an exponential growth with a doubling time of 1.28 days. The rate of distribution of luciferin between blood and tumor was clearly dependent on tumor size. We hypothesize that as the tumor grows, its blood supply and flow will increase resulting in the larger k_bt value that we register. However the efflux from tumor back into blood pool, k_tb, increases at the same time. Figure 4A shows how k_bt and k_tb correlate with the measured tumor volume. As one might naively expect based on simple mass balance, k_bt increases roughly linearly with the tumor volume (k_bt ~ V^1.08), but the increase of k_tb is somewhat slower (k_tb ~ V^0.5). The tumor volume increases more than 100 fold over the course of the experiment and both parameters show linear behavior over this range. Histology of our tumors excised at day 10 show healthy tumors without any signs of necrosis or hypoxia (see Figure S2), however we might anticipate in longer-term experiments that the scaling relationships could change if the viable portion of the tumor undergoes necrosis in response to drug therapy or growth itself.

Transport into the tumor

Apart from differences in luciferin administration, it has been established that the level of the bioluminescence peak correlates with tumor burden (1–5, 11, 15). However the exact dependence of this relationship has never been clearly defined. To test this in our model, we calculated both the peak luciferin level (BL_peak) as well as the area under the curve over the 60 minutes following luciferin administration (AUC_0–60). Figure 4B shows the scaling relationship between these variables and the tumor volume revealing similar behavior in both quantities: AUC_0–60 ~ V^0.65 and BL_peak ~ V^0.68.

It has long been postulated that the high interstitial fluid pressure within a tumor acts as a barrier to transcapillary transport and thus renders drug delivery into the tumor difficult (16). Starling’s Hypothesis states that the fluid flux J across a permeable boundary is given by J = L_p×S×ΔP where L_p is the hydraulic conductivity of the boundary, S is the surface area and ΔP is the pressure difference across the boundary (17). The bioluminescence levels that we observe in the tumor could be considered a surrogate for any transportable drug, as measured by either BL_peak or AUC_0–60. Both of these quantities increase roughly as V^2/3, and this scaling is intriguing since if we imagine a spherical tumor of volume V, the surface area S of the tumor would also increase as V^2/3, in agreement with Starling’s Hypothesis. Interestingly, we observe a very similar behavior if we go back and take the ratio of our PK rate constants k_bt and k_tb. In this case we again see that the equilibrium partitioning between the blood and tumor would increase as k_bt / k_tb ~ V^1.08 /V^0.5 = V^0.58 or approximately the 2/3 power of the volume. This is consistent with our other measurements, and it also illustrates how we might improve upon simple passive delivery. Because the influx into the tumor increases linearly with volume, transporting compounds into the tumor does not appear to be an issue; however efflux now is also greater with larger tumor sizes and eventually becomes the determining factor in the drug biodistribution. This scenario confirms the anticipated utility of molecular targeting whereby we might significantly increase drug levels in the tumor by decreasing the efflux through compound trapping or active targeting.

Variability in BLI measurements

Despite offering a powerful tool for diagnosis and monitoring, BLI manifests significant intrinsic variability as one of its primary limitations (9, 10). Differences in the BLI signal naturally arise from changes in the type or location of the tumor (9, 10), the size of the tumor (5), and the method and regimen of luciferin administration (4, 5). Signal differences could also possible as a result of how the animal is positioned on the stage (9), although we found that tilting the mice produced a very minor change in the BLI level and the resulting PK parameters (Figure S3). All of these variable elements make it difficult to provide quantitative assessments based on single measurements, but these factors are easily and properly dealt with in a comprehensive PK model. By considering all aspects of the luciferin (or drug) dynamics (administration, absorption, biodistribution, reaction and clearance), more quantitative and comprehensive modeling of drug levels and tumor transport kinetics is possible, and this could facilitate individualized therapeutics with the use of image-based metrics of pharmacodynamics and pharmacokinetics.