Abstract
Dihydrofolate reductase from Mycobacterium tuberculosis catalyzes the NAD(P)H dependent reduction of dihydrofolate, yielding NAD(P)+ and tetrahydrofolate, the primary one carbon unit carrier in biology. Tetrahydrofolate needs to be recycled so that reactions involved in dTMP synthesis and purine metabolism are maintained. In this work, we report the kinetic characterization of the MtDHFR. This enzyme has a sequential steady-state random kinetic mechanism, probably with a preferred pathway with NADPH binding first. A pKa value for an enzymic acid of approximately 7.0 was identified from the pH dependence of V, and the analysis of the primary kinetic isotope effects revealed that the hydride transfer step is at least partly rate limiting throughout the pH range analyzed. Additionally, the determination and analysis of solvent, and multiple kinetic isotope effects was conducted, and equilibrium isotope effects were measured on the equilibrium constant. D2OV and D2OV/K[4R-4-2H]-NADH were slightly inverse at pH 6.0, and inverse values for D2OV[4R-4-2H]-NADH and D2OV/K[4R-4-2H]-NADH suggested that a pre-equilibrium protonation is occurring before the hydride transfer step, indicating a stepwise mechanism for proton and hydride transfer. The same value was obtained for DkH at pH values of 5.5 and 7.5, reaffirming the rate-limiting nature of the hydride transfer step. A chemical mechanism is proposed based on the results obtained here.
Keywords: Folate Metabolism, DNA synthesis, Kinetics, Kinetic Isotope Effects, Pre-steady-state kinetics, Tuberculosis
TB is a global health concern. It is estimated that one third of humanity is infected with TB, and that 1.7 million deaths occur each year (1). Despite global efforts to contain the disease, the number of TB cases is still increasing, and the appearance of strains resistant to first line drugs (MDR-TB), and to both first and second line drugs (XDR-TB) has intensified the search for new and more effective antibacterial agents (2).
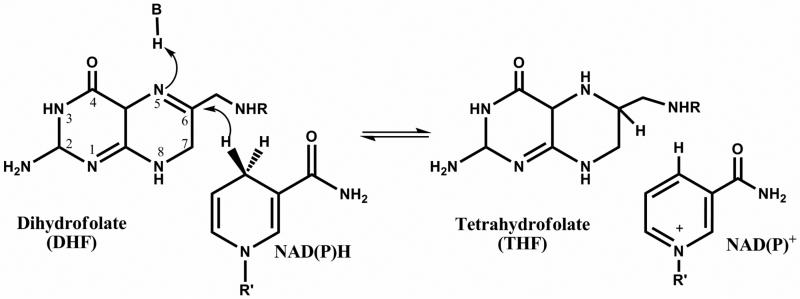
Dihydrofolate reductase (DHFR) catalyzes the NADPH-dependent reduction of dihydrofolate (DHF), yielding tetrahydrofolate (THF), an important reaction in the folate cycle, which supplies one-carbon units for the biosynthesis of deoxythymidine monophosphate (dTMP), and for reactions involved in the biosynthesis of purines (Scheme 1). Inhibition of the folate cycle interrupts the supply of dTMP, halts DNA synthesis, and consequently, cell proliferation. Drugs that inhibit DHFR have been used for decades to treat cancer (methotrexate, pemetrexate), bacterial infections (trimethoprim) and malaria (pyrimethamine) (3). Recently, a series of structure-based inhibitors were designed for the DHFR from M. tuberculosis (MtDHFR) (4-6), but a preliminary assessment of the chemotherapeutic potential of those compounds reveals that they lack the solubility, potency, and specificity required for a new drug targeting this enzyme.
Scheme 1.
Reaction catalyzed by DHFR.
The chemical mechanism of the DHFR-catalyzed reaction continues to be debated, especially the order of the protonation and hydride transfer steps, the identity of the group whose pKa value is observed in the V pH profiles, and the involvement of a water molecule in the protonation step, even though DHFR's from numerous prokaryotic and eukaryotic organisms have been studied for the past 50 years. The majority of the experimental and theoretical data favors the protonation step preceding the hydride transfer step in the EcDHFR catalyzed reaction, and that a network of water molecules linked to a general acid would be promoting the protonation (7-9). Alternatively, some authors argue that protonation at O4 would facilitate hydride transfer to C6 and the subsequent N5 ring nitrogen protonation (8, 10, 11). Recently, work conducted with DHFR from Thermotoga maritima (TmDHFR) suggested that the two steps (N5 protonation and C6 hydride transfer) were occurring in a concerted manner (12), suggesting diversity in terms of chemical mechanism for the same enzyme catalyzed reaction.
In this work the kinetic and chemical mechanisms of the MtDHFR were investigated using initial velocity and pH-rate profiles studies, measuring kinetic isotope effects under steady-state and pre-steady state conditions, as well as equilibrium isotope effects. A chemical mechanism is proposed based on the results obtained.
EXPERIMENTAL PROCEDURES
Materials
All chemicals were of analytical or reagent grade and were used without further purification. Deuterium oxide (99.9 atom % D) was from Cambridge Isotope Laboratories..
Purification of MtDHFR
Competent E. coli BL21 (DE3) cells (Novagen) were transformed with the recombinant plasmid pET28a(+):dfrA, and the expression and purification of MtDHFR followed the protocol previously reported (13). Protein concentration was determined by using the theoretical value ε280 = 40,450 M-1cm-1, or ε340 = 6,220 M-1cm-1 due to bound NADPH (14).
Preparation of MtDHFR-NADP+
Due to the fact that the MtDHFR is present in a complex with NADPH after its purification, and that this tightly bound NADPH could not be removed by extensive dialysis, a form of the enzyme that had NADP+ instead of NADPH was generated. MtDHFR-NADPH was immobilized onto a Ni-NTA resin, and 10mL of 100 mM NADP+ were passed through the column, to form the MtDHFR - NADP+ form of the enzyme. The enzyme was eluted with 500 mM imidazole, dialyzed against 2 × 2L of 100 mM HEPES, pH 7.5, and frozen at -80 °C. Attempts to generate the apoenzyme were unsuccessful, since the enzyme obtained after denaturation and refolding was less active and prone to precipitation.
Preparation of [4R-4-2H]NAD(P)H
[4R-4-2H]NADH was prepared using formate dehydrogenase and deuterated formic acid (15); [4R-4-2H]NADPH was prepared using alcohol dehydrogenase from Thermoanaerobium brockii, and isopropanol-d8 (16). All pyridine nucleotides, including commercially available NADH and NADPH to be used in isotope effects experiments were purified with a Mono-Q column equilibrated with water, using a linear gradient of 1 M sodium bicarbonate for elution (at 0.66%/mL). Fractions with an absorption ratio of 260/340 nm ≤ 2.3 were pooled, fast frozen, and lyophilized.
Enzymatic Assay for MtDHFR
Assays were performed under initial rate conditions at 25 °C and 100 mM HEPES, pH 7.5, unless stated otherwise. Measurements were performed at least in duplicate. The reaction was started by the addition of 10 nmol of MtDHFR, and the decrease in absorbance due to NAD(P)H oxidation and DHF reduction was measured at 340 nm, at 25° for 1 min. A combined molar extinction coefficient value of 11,800 M-1 cm-1 was used (17).
Initial Velocity and product inhibition patterns
Apparent kinetic constants were determined by fixing the concentration of one substrate at saturating levels, and varying the concentration of the other substrate. An appKNADPH of < 1 μM was estimated, too low to allow NADPH to be varied in initial velocity studies, and NADH was used instead. Initial velocity studies were conducted using five fixed concentrations of DHF while varying NADH concentrations. Product inhibition experiments were carried out at varying concentrations of one substrate, fixed subsaturating concentrations of the other substrate, and different fixed concentrations of THF or NADP+.
pH-Rate Profiles
To investigate the role of acid base catalysis in the MtDHFR catalyzed reaction, the pH dependence of the kinetic parameters was determined by measuring initial rates at varying concentrations of one substrate and saturating concentrations of the other. The experiments were conducted throughout the pH range of 5.5-8.5, employing a mixed buffer system containing citric acid, HEPES, and TAPS. The pH stability of the enzyme was tested by incubating the enzyme in the desired buffer and conducting the standard assay using HEPES, pH 7.5.
Kinetic isotope effects
Primary kinetic isotope effects (KIEs) were measured using [4R-4-2H]NADH or [4R-4-2H]NADPH, and DHF as substrates, with the same mixed buffer system used for the pH-rate profiles. A study of the dependence of DV/K on the concentration of the co-substrate was conducted by using five fixed concentrations of DHF while varying the concentration of NADH or [4R-4-2H]-NADH. Solvent kinetic isotope effects (SKIEs) were measured in either H2O or 91 atom% D2O, and initial velocities in the presence of fixed concentration of one substrate and varying concentrations of the co-substrate were obtained. Viscosity effects were evaluated by comparing the rates obtained in H2O, and 9% glycerol, which mimics the viscosity increase caused by D2O (ηr = 1.24) (18). Multiple KIEs (MKIEs) were determined by measuring the SKIE using [4R-4-2H]NADH as the substrate. To rule out that any change in velocity was being caused by pH fluctuations in the SKIE and MKIE measurements, citrate buffer pL 6.0 was used since this value is located in a plateau region identified in the pH-rate profiles studies.
Equilibrium isotope effects (EIE)
Equilibrium isotope effects were determined in water or D2O (D2OKeq), and using NADH or [4R-4-2H]-NADH as substrates (DKeq) (19). Each reaction contained 100 μM DHF and 100 μM of NADH or [4R-4-2H]NADH in citrate buffer, pH 6.0. The initial absorbance was recorded, and after that 20 nM MtDHFR was added (changing the reaction volume by no more than 1%), and the reaction was followed until the equilibrium was reached, usually for less than 1 hour. The concentration of products and substrates in equilibrium was calculated by using the combined ε=11,800 M-1 cm-1, and using the initial and final absorbancies. Each value is the average of at least 3 measurements. All solvents and buffers were purged with argon before each measurement to delay THF oxidation (20)
Stopped-flow measurements
To better evaluate the rate limiting nature of the chemical step, KIEs were measured under single turnover conditions using the MtDHFR-NADP+ form of the enzyme. All measurements were conducted on a SX-20 stopped-flow spectrophotometer (Applied Photophysics) under pseudo-first order conditions with at least a 5-fold excess of MtDHFR over the limiting substrate (DHF). Assays contained 1μM of DHF, 100 μM of NADPH or [4R-4-2H]NADPH, and varied concentrations of MtDHFR, to assure that binding is not contributing to the rates observed. Measurements were performed at pH values of 5.5 and 7.5 using the same mixed buffer system employed in previous experiments.
Data analysis
All data were fitted to the appropriate equations using the nonlinear regression function of SigmaPlot 2000 (SPSS, Inc.) or Origin 7.0 (OriginLab, Inc).
Initial velocity kinetic data with one substrate fixed at a saturating concentration and varied concentrations of the other substrate were fitted to eq.1.
| (1) |
Data for an intersecting initial velocity pattern were fitted to eq. 2, which describes a sequential mechanism.
| (2) |
Inhibition results were fitted to eq. 3, describing competitive inhibition, or eq.4, for noncompetitive inhibition.
| (3) |
| (4) |
For eq. 1-4, V is the maximum velocity, A and B represent substrate concentration, Ka and Kb are the Michaelis constants for substrates A and B, respectively, and Kis and Kii are the slope and intercept inhibition constants, respectively.
pH-rate profiles were fitted to eq. 5, where y is the kinetic parameter, C is the pH-independent value of y, H is the proton concentration, and Kb is the apparent basic dissociation constant for ionizing groups.
| (5) |
The pH dependence of the kinetic isotope effects data were fitted to eq. 6, where YL and YH are the limiting values at low and high pH, respectively, and Ka is the dissociation constant for ionizable groups (21)
| (6) |
The kinetic isotope effect data were fitted to eq. 7, which describes the effects on V/K and on V. The D(V/Kapp) measured with five fixed concentrations of NADH or [4R-4-2H]-NADH, and varying concentrations of DHF (50 points in total) were simultaneously fitted to eq. 8, which assumes isotope effects on V, V/Ka, V/Kb, and Kia. For equations 7 and 8, Fi represents the fraction of isotopic label, and EV/K and EV are the isotope effects minus one on V/K and on V, respectively.
| (7) |
| (8) |
The notation utilized to express isotope effects is that of Northrop (22).
Single turnover experiments were fitted to a single exponential curve, represented by eq. 9, where y0 is the y offset, A1 is the amplitude, and k is the observed rate constant.
| (9) |
The kobs values obtained with different concentrations of enzyme were reploted as a function of enzyme concentration, and fitted to eq. 10 (23), where kobs is the observed rate constant after the single exponential fitting at different concentrations of enzyme, kH is the rate obtained with NADPH was used as substrate, E is the concentration of enzyme, and Kd is the dissociation constant for the enzyme and the limiting substrate.
| (10) |
The isotope effect on the hydride transfer step (DkH) was obtained by dividing kH/kD, using the values obtained after fitting with eq. 10.
RESULTS AND DISCUSSION
Initial Velocity and product inhibition patterns
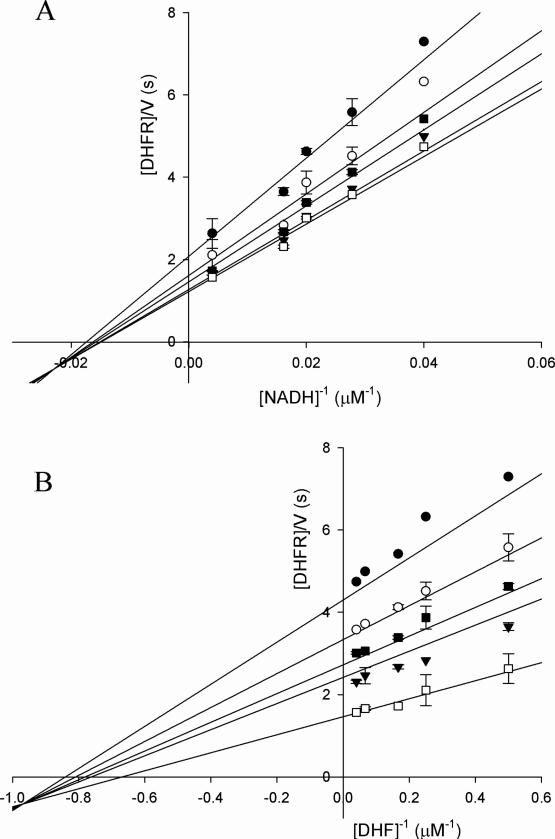
The analysis of the initial velocity pattern obtained using NADH and DHF as substrates reveals that the MtDHFR-catalyzed reaction has a sequential kinetic mechanism, with the formation of a ternary complex, as observed for DHFRs from other organisms (Figure 1). Since all lines intercept at the left of the y axis, a rapid-equilibrium ordered mechanism was ruled out. A kcat = 1.6 ± 0.1 s-1 was determined, being very similar to the appkcat = 2.3 ± 0.1 s-1 obtained when NADPH and DHF were used as substrates. Those values are one order of magnitude lower than those for the Escherichia coli (EcDHFR), and human (HsDHFR) enzymes (17, 24), and almost 20 times lower than the Streptococcus pneumoniae and mouse DHFRs (25, 26) The Km values for both NADPH and DHF are very low, with KDHF = 1.6 ± 0.4 μM, and KNADPH < 1 μM. It is common for DHFRs from other organisms to have at least one substrate with a Km value in the low micromolar or sub-micromolar range. A higher value was obtained for KNADH = 69 ± 7 μM, demonstrating the important contribution of electrostatic interactions between the 2’-phosphate group and cationic side chains in the nucleotide binding pocket of the enzyme that differentiate between the two cofactors (27). Folate was tested as a substrate at concentrations up to 1mM, but no NAD(P)H consumption was observed, in contrast to LcDHFR, EcDHFR, and HsDHFR, which are capable of reducing folate (28, 17). The product inhibition studies revealed a pattern identical to the ones previously reported for EcDHFR, with THF and NADP+ behaving as noncompetitive inhibitors when DHF is the varied substrate, and as competitive inhibitors when NADH is varied (Table 1). In combination with the initial velocity results, this argues against a classic steady-state ordered mechanism with either pyridine nucleotide or DHF binding first. The analysis of the dependence of DV/Kapp on the concentration of the co-substrate, which provides insight into the mechanism, is discussed below.
Figure 1.
Initial velocity pattern showing lines intersecting to the left of the y axis. (A) NADH as variable substrate, and fixed concentrations of 2 (•), 4 (○), 6 (▲), 15 (◆), and 25 (■) μM of DHF. (B) DHF as variable substrate and fixed concentrations of 25 (•), 36 (○), 50 (▲), 62 (◆), and 250 (■) μM of NADH. Global fitting of the data to eq. 2 (solid lines) gave a kcat=1.65 ± 0.10 s-1, KDHF=1.62 ± 0.40 μM, KNADH=68.67 ± 7.70 μM.
Table 1.
Product Inhibition Patterns for M. tuberculosis Dihydrofolate reductase
| Varied substrate | Product inhibitor | Inhibition typea | Kis (μM)b | Kii (μM)c |
|---|---|---|---|---|
| NADH | NADP+ | C | 0.020 ± 0.005 | - |
| NADH | THF | C | 31 ± 3 | - |
| DHF | NADP+ | NC | 0.40 ± 0.10 | 0.10 ± 0.04 |
| DHF | THF | NC | 38 ± 5 | 13 ± 6 |
C = competitive, NC = noncompetitive.
Kis is the slope inhibition constant.
Kii is the intercept inhibition constant.
pH-Rate Profiles
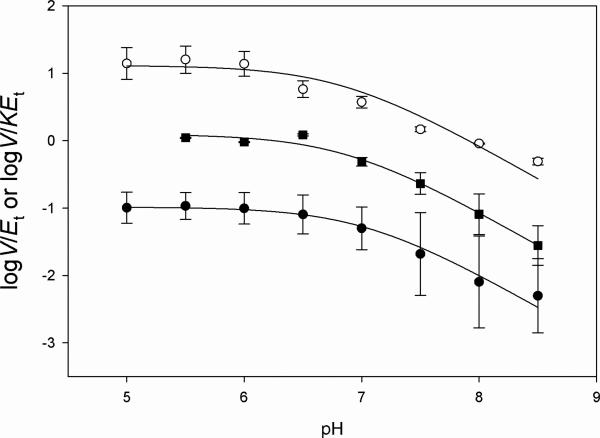
To better understand the role of acid-base catalysis during substrate binding and catalysis, pH-rate profiles were conducted in the pH range of 5.0-8.5. Two kinetic parameters were evaluated, kcat, which reports on all steps after the formation of the ternary complex capable of undergoing catalysis until the release of all products, and kcat/Km, which gives information about the binding of the varied substrate to free enzyme. The pH-dependence of kcat, kcat/KDHF and kcat/KNADH allowed the determination of pKa values of 6.8 ± 0.2, 6.9 ± 0.1, and 7.0 ± 0.1, respectively (Figure 2), suggesting that a single group needs to be protonated for maximum substrate binding and/or catalysis. A comparison of the sequences of MtDHFR with DHFRs from other organisms, suggests that this residue is a conserved aspartate (Asp27) (4), and similar pH profiles have been reported for other DHFRs, yielding similar pKa values (29). However, there is not a consensus in the literature as to the exact role Asp27 plays in the catalytic mechanism of other DHFRs, and different alternatives have been proposed (30, 31). It is clear that Asp27 cannot be directly involved in protonation of N5 of the pteridine ring of DHF since they are separated by greater than 5 Å (pdb accession code: 2CIG, 13). It has also been suggested that when DHF is bound in the EcDHFR active site, the N5 pKa increases from less than 3 when free in solution to a value of 6.0, indicating that the pKa observed for this enzyme could be reflecting the pteridine N5 pKa value, rather than Asp27 (32) We don't believe this the case for the MtDHFR, since the protonation step would have to possess a somewhat rate-limiting nature to be observed in the pH-rate profiles, which was not observed in the solvent and multiple KIE studies (see below).
Figure 2.
pH dependence of the kinetic parameters on pH. (A) pH dependence of log V/EtKNADH (○), (B) pH dependence of V/EtKDHF, (■), (C) pH dependence on V/Et (•). The lines represent fits to Eq. 5. A mixed buffer system was utilized, with 100 mM Citrate, 100 mM HEPES, and 100 mM TAPS.
Primary kinetic isotope effects
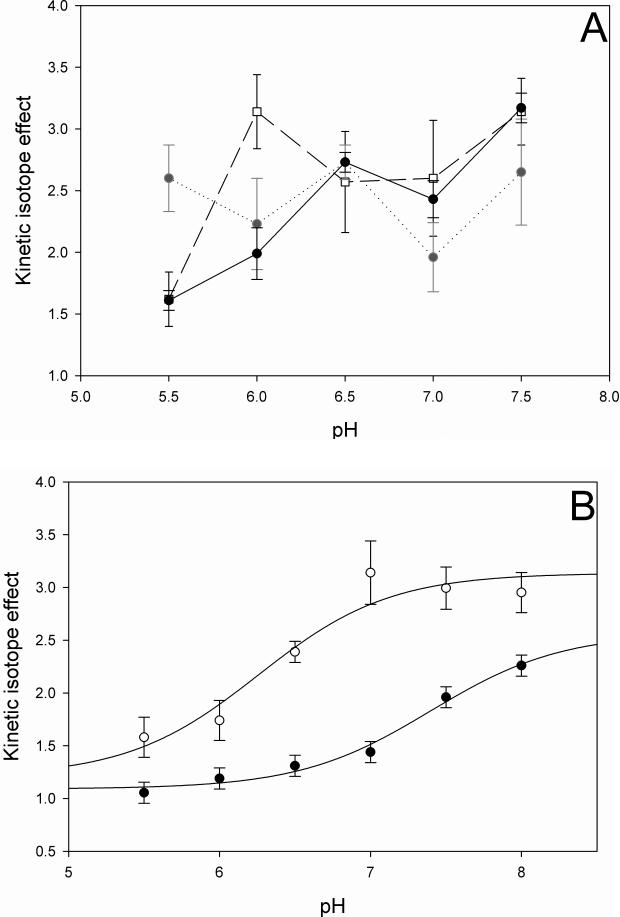
To investigate the rate-limiting nature of the chemical step, the pH-dependence of primary kinetic isotope effects was measured. It is important to note that the values obtained here are observed KIEs, and it is unlikely that these values represent intrinsic KIEs. In the case of MtDHFR, intrinsic KIEs report uniquely on the hydride transfer step, and these values are often masked by commitment factors in the forward and reverse directions. The forward commitment (cf) represents the tendency of the enzyme complex capable of undergoing catalysis to continue forward as opposed to its tendency to dissociate to free enzyme and free substrate, and the reverse commitment (cr) represents the same tendency for the reverse reaction (33). Examples of events in the catalytic cycle that raise commitment factors, consequently decreasing the magnitude of the observed KIE, are conformational changes, binding of substrates, release of products, and others (33). When [4R-4-2H]-NADH was used as substrate, the KIEs increased from DV = 1.6 ± 0.1 and DV/KNADH = 1.6 ± 0.2 at pH 5.5 to DV = 2.9 ± 0.4 and DV/KNADH = 3.1 ± 0.3 at pH 7.5, while DV/KDHF remained 2.7 ± 0.3 throughout the pH range analyzed (Table 2, Figure 3A). The observation that DV, DV/KNADH, and DV/KDHF are statistically higher than unity suggests that the hydride transfer step is at least partly rate limiting throughout the pH range analyzed (34). The classical upper limit for deuterium primary KIEs, in cases where there is no tunneling is ca. 7, and values higher than 2 can be considered partially rate limiting for hydride transfer (35). When [4R-4-2H]-NADPH was used as substrate (Table 3, Figure 3B), the KIEs increased from DV = 1.0 ± 0.1, and DV/KDHF = 1.6 ± 0.2 at pH 5.5, to DV = 2.3 ± 0.1 and DV/KDHF = 2.9 ± 0.2 at pH 8.0. Due to the low value of KNADPH, DV/KNADPH could not be reliably measured. The lower observed KIE values obtained when NADPH was used as substrate instead of NADH, suggest that NADPH is a stickier substrate than NADH. A sticky substrate is a substrate that reacts to form products faster than it dissociates from the enzyme, increasing the cf, and consequently decreasing the observed KIEs (36). Additionally, the slightly lower value of DV relative to the DV/KDHF when NADPH was the co-substrate suggests that a step after the first irreversible step, often considered to be the release of the first product, is contributing to the rate (34). In the EcDHFR (37), HsDHFR (24), and Lactobacillus casei (LcDHFR, 38) catalyzed reactions, the rate-limiting step is THF release, and the chemical step is not rate limiting at neutral pH (37). In the DHFR from Streptococcus pneumoniae (SpDHFR), it was suggested that the kcat at pH 7 was limited by a slow conformational change prior to the chemical step and the actual hydride transfer step (25), and that product release was not rate limiting at any of the pH values analyzed.
Table 2.
Kinetic isotope effects obtained with NADH as substrate
| Parameter | pH(D) | isotope effect |
|---|---|---|
| D V/K DHF | 5.5 | 2.6 ± 0.3 |
| D V/K NADH | 5.5 | 1.6 ± 0.2 |
| D V | 5.5 | 1.6 ± 0.1 |
| D V/K DHF | 6.0 | 2.2 ± 0.4 |
| D V/K NADH | 6.0 | 3.1 ± 0.3 |
| D V | 6.0 | 2.0 ± 0.2 |
| D V/K DHF | 6.5 | 2.7 ± 0.1 |
| D V/K NADH | 6.5 | 2.5 ± 0.4 |
| D V | 6.5 | 2.7 ± 0.1 |
| D V/K DHF | 7.5 | 2.6 ± 0.4 |
| D V/K NADH | 7.5 | 3.1 ± 0.3 |
| D V | 7.5 | 3.2 ± 0.1 |
| D2O V/K DHF | 6.0 | 0.9 ± 0.1 |
| D2O V/K NADH | 6.0 | 0.8 ± 0.1 |
| D2O V | 6.0 | 0.8 ± 0.1 |
| D2O V/K [4R-4-2H]NADH | 6.0 | 0.6 ± 0.1 |
| D2O V [4R-4-2H]NADH | 6.0 | 0.7 ± 0.1 |
| D K eq | 6.0 | 1.14 ± 0.08 |
| D2O K eq | 6.0 | 1.03 ± 0.01 |
Figure 3.
pH dependence of the kinetic isotope effects when (A) NADH, or (B) NADPH were used as substrates. The individual values represent fits to eq. 7, and are the average of at least two independent experiments. A mixed buffer system was utilized, with 100 mM Citrate, 100 mM HEPES, and 100 mM TAPS. (A) pH dependence of DV (•), DV/KNADH (□), and DV/KDHF ( ). (B) pH dependence of DV (•), and DV/KDHF (○). The line is a fit to eq. 6.
). (B) pH dependence of DV (•), and DV/KDHF (○). The line is a fit to eq. 6.
Table 3.
Kinetic isotope effects obtained with NADPH as substrate
| parameter | pH(D) | Isotope effect |
|---|---|---|
| D V/K DHF | 5.5 | 1.6 ± 0.2 |
| D V | 5.5 | 1.1 ± 0.1 |
| D V/K DHF | 6.0 | 1.7 ± 0.2 |
| D V | 6.0 | 1.2 ± 0.1 |
| D V/K DHF | 6.5 | 2.4 ± 0.1 |
| D V | 6.5 | 1.3 ± 0.1 |
| D V/K DHF | 7.0 | 3.1 ± 0.3 |
| D V | 7.0 | 1.4 ± 0.1 |
| D V/K DHF | 7.5 | 3.0 ± 0.2 |
| D V | 7.5 | 2.0 ± 0.1 |
| D V/K DHF | 8.0 | 3.0 ± 0.2 |
| D V | 8.0 | 2.3 ± 0.1 |
| D k H | 5.5 | 2.4 ± 0.1 |
| D k H | 7.5 | 2.7 ± 0.1 |
Furthermore, pKa values of 7.4 ± 0.1, and 6.3 ± 0.3 for DV and DV/KDHF, respectively, were observed when the pH dependence of the KIEs using NADPH as substrate was analyzed (Figure 3B). These values are comparable to the ones obtained in the pH rate profiles discussed above, suggesting that the same group that needs to be protonated for maximum binding and catalysis, is also influencing the magnitude of the observed KIEs. When the pH is low, the chemical step is faster than another step that partially limits the rate, and the observed KIEs are close to unity. As the pH increases, the hydride transfer step slows and becomes rate limiting, thus increasing the magnitude of the observed KIEs.
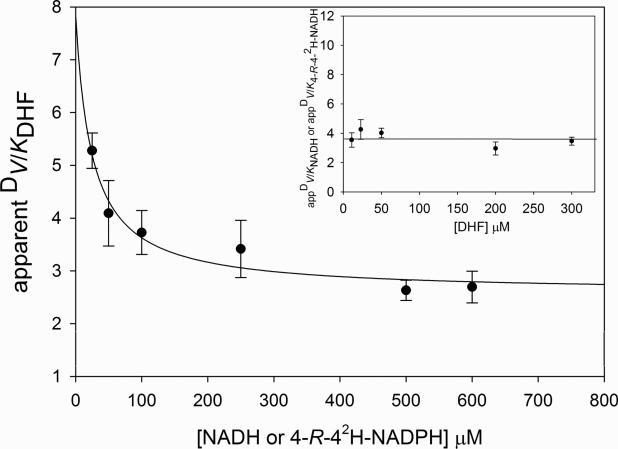
While NADPH is sticky compared to NADH, and presumably DHF, the relative stickiness of DHF and NADH was determined by the analysis of the dependence of the apparent isotope effect on V/K on the concentration of the co-substrate. Theory predicts that the magnitude of DV/Kapp will be dependent on the order of addition of substrates, and specific patterns of co-dependence are expected for a given mechanism (39). In this model, A represents the first substrate to bind in an ordered mechanism, and B is the second substrate to bind. In steady-state ordered mechanisms, D(V/Kapp)B will be independent of the concentration of A, while D(V/Kapp)A, if A is sticky, will decrease as the concentration of B is increased and become unity at infinite concentration of B. The pattern is similar in steady-state random mechanisms, but DV/Kapp for a sticky substrate will decrease as the concentration of the cosubstrate is increased and reach a finite value different than one at infinite concentration of the cosubstrate. For a nonsticky substrate, DV/Kapp will be independent of the concentration of the cosubstrate. In the case of mechanisms of the rapid equilibrium type, both ordered or random, DV/Kapp for the two substrates will be equal and independent of the concentration of the cosubstrate since all external commitment factors are zero (38).
In our case, D(V/Kapp)NADH was independent of the concentration of DHF, and exhibited a value higher than one, while D(V/Kapp)DHF decreased hyperbolically as the concentration of NADL increased, reaching a constant value greater than one at elevated concentrations of NADL (Figure 4). This pattern is characteristic of a steady-state random mechanism, as observed in other reductases, including 1-deoxy-D-xylulose-5-phosphate isomeroreductase and β-ketoacyl-acyl carrier protein (ACP) reductase, both from M. tuberculosis (40, 41). This result also indicates that DHF is a sticky substrate when the reaction occurs with NADH, and that NADH is less sticky than DHF. It is important to point out that the MtDHFR co-purifies with NADPH tightly bound, indicating that even though the free enzyme is physically capable of binding both substrates randomly, it is likely that there is a preferential pathway favoring NADPH binding first.
Figure 4.
Dependence of the apparent values of DV/K on the concentration of the co-substrate. KIEs were measured by varying the concentration of DHF at five different fixed concentrations of NADH or [4R-4-2H]-NADH. Assays contained 100mM HEPES pH 7.5 with 50 mM KCl, DHFR (10-20 nM), DHF, and either NADH or [4R-4-2H]-NADH. The solid line drawn through appV/KDHF is a fit to DV/Kapp = DV/K[NADL]→∞ + K[DV/KNADL →0 – DV/KNADL →∞]/(K + [NADL]), where K is the concentration of NADL that gives DV/Kapp = [DV/KNADL →0 – DV/KNADL →∞]/2.
Solvent and multiple kinetic isotope effects
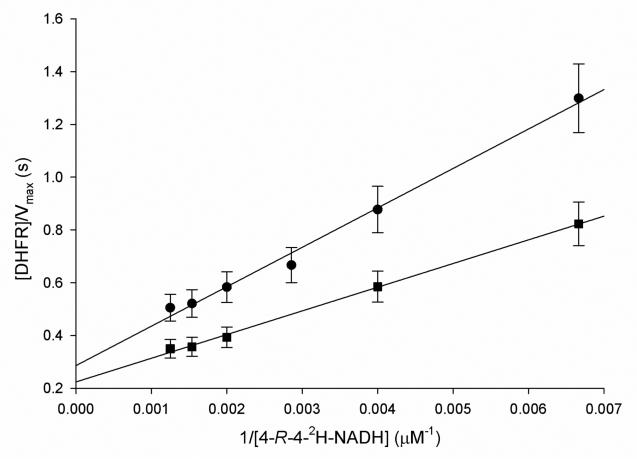
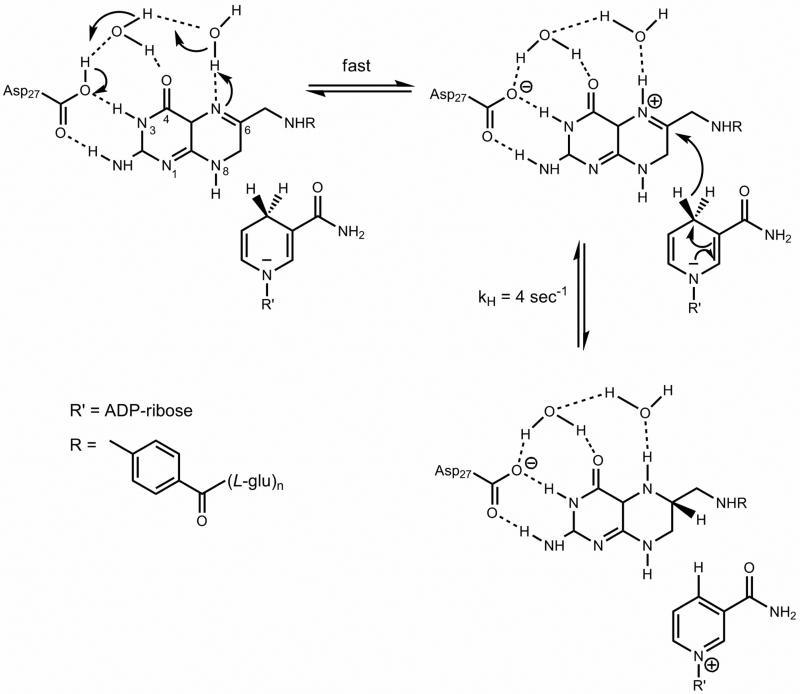
To investigate the rate limiting nature of the protonation step, solvent KIEs were measured at pH 6.0, and all values were slightly inverse (D2OV/KDHF = 0.9 ± 0.1; D2OV/KNADH = 0.8 ± 0.1; D2OV = 0.8 ± 0.1; Table 2). A viscosity study using 9% glycerol to mimic the relative viscosity of D2O was conducted, and no viscosity effect on the rate was observed (data not shown). This result shows that the protonation step is not rate limiting at this pH, when NADH and DHF are the substrates. In order to discriminate between a concerted and a stepwise mechanism for proton and hydride transfer, multiple kinetic isotope effects were carried out, measuring the solvent KIE when [4R-4-2H]-NADH and DHF were used as substrates (Figure 5). In this experiment, statistically significant inverse values of D20V/K[4R-4-2H]-NADH = 0.6 ± 0.1, and D20V = 0.7 ± 0.1 were found. According to theory (42), if protonation and hydride transfer were occurring in the same transition state, i.e., in a concerted manner, the observed multiple KIE would be of equal or higher magnitude than the solvent KIE, since the presence of deuterium in the multiple KIE experiment would increase the relative size of the energy barrier for the hydride transfer, consequently increasing the energy barrier for protonation. On the other hand, if protonation and hydride transfer were taking place in a stepwise manner, the observed multiple KIE would be smaller than the solvent KIE, since the energy barrier for hydride transfer would be higher, decreasing the observed KIE when water and D2O are compared. Hence, the results presented here suggest that the reaction follows a stepwise mechanism, and that protonation and hydride transfer are not part of the same transition state. The fact that the multiple KIE yielded an inverse value suggests that a fast pre-equilibrium protonation is occurring before the hydride transfer step (35). Because heavy water influences acid-base equilibria, D2O being more acidic than H2O, one can imagine that the presence of a fast pre-equilibrium protonation preceding the relatively slower hydride transfer step, could give rise to the observed inverse multiple KIEs due to the fact that the rapid protonation would increase the amount of an N5 protonated intermediate, which would be the true “substrate” for the hydride transfer (Scheme 2). Furthermore, inverse fractionation factors have been measured for several few amines, revealing that some solvent-exchangeable sites prefer deuterium over hydrogen, relative to solvent, which could also contribute to the inverse values obtained here (43, 44).
Figure 5.
Multiple KIEs. Curves using or [4R-4-2H]-NADH as substrate and either H2O (•) or D2O (■) were compared. The concentration of or [4R-4-2H]-NADH was varied while the concentration of DHF was kept constant at 50μM. Assays contained 100mM citrate pH 6.0 with 50 mM KCl, DHFR (10-20 nM), DHF, and [4R-4-2H]-NADH.
Scheme 2.
Chemical mechanism proposed for the MtDHFR catalyzed reaction. Asp27 is protonated as indicated by the pH-rate profiles. A conserved water molecule is shown participating in hydrogen bonds with O4 and Asp27. N5 protonation is fast and mediated by a solvent molecule. The pre-protonated intermediate is then attacked by NAD(P)H, forming the products THF and NAD(P)+.
Equilibrium isotope effects (EIE)
Even though the results presented above indicate that a fast pre-equilibrium protonation is occurring prior to the hydride transfer step, EIE (DKeq, and D2OKeq) were measured to better corroborate this mechanism. If there are isotope effects reporting on the hydride transfer step (D(V/K)NADH), the protonation step (D2O(V/K)NADH), and on both (D2O(V/K)[4R-4-2H]-NADPH), those values can be used in combination with DKeq, and D2OKeq to provide information about which one of these steps comes first. The values obtained, at pH 6.0, were DKeq = 1.14 ± 0.08, and D2OKeq = 1.03 ± 0.01. In order to distinguish between protonation preceding or following hydride transfer, the following inequality has to be satisfied:
If the two sides of this equation are equal, the two mechanisms cannot be distinguished by the analysis of multiple and equilibrium KIEs (42). Unfortunately, this is the case for the MtDHFR catalyzed reaction.
Several theoretical studies indicate that the mechanism in which protonation precedes hydride transfer is energetically favored, at least for the EcDHFR (7, 8). In this model, DHF binds the enzyme in its unprotonated form, and the enzyme facilitates protonation by exposing N5 to the solvent in a favorable orientation, in a hydrophobic pocket that locally increases the N5 pKa (9). Additionally, it was previously demonstrated by deuterium exchange experiments that the proton on N5, in the EcDHFR, comes from the solvent (7), corroborating the mechanism proposed here for the MtDHFR catalyzed reaction (Scheme 2).
Primary KIEs under pre-steady state conditions
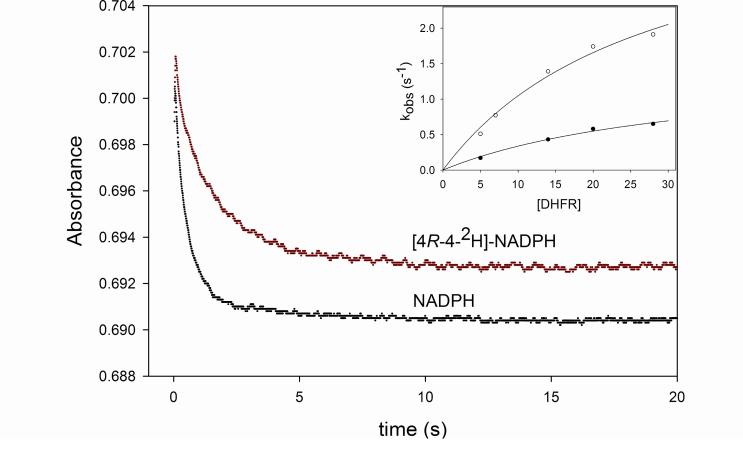
The reaction rate was measured under single turnover conditions to obtain more detailed information about the hydride transfer step. When performing single turnover experiments, the rate obtained is a combination of the rates of binding and dissociation, and forward and reverse chemical reactions. By varying the concentration of enzyme, one expects that the rate of binding becomes fast at maximum enzyme concentration, allowing the observed rates obtained with different concentrations of enzyme to be plotted as a function of enzyme concentration, yielding a hyperbola whose ymax can the interpreted as the rate of the chemical step. In the case of MtDHFR, kH will be used to describe the hydride transfer step when NADPH is used as substrate, and kD when [4R-4-2H]-NADPH is the substrate. The values obtained for kH were 8.8 ± 0.1 s-1 and 4.0 ± 0.7 s-1, at pH 5.5 and 7.5, respectively. Interestingly, the rates of kH measured here are only slightly higher than kcat, illustrating the overall rate limiting nature of the hydride transfer step in the pH range analyzed. These values are two orders of magnitude smaller than the ones for the EcDHFR, HsDHFR, and LcDHFR, at both pH 5.5 and 7.5. To rule out the possibility that a conformational change occurring prior to kH is limiting the reaction, kinetic isotope effects were measured under single turnover conditions. If a rate limiting slower step was occurring prior to kH, the values of kinetic isotope effects on the hydride transfer step (DkH) would have a decreased magnitude, due to the presence of a high cf. The value obtained for DkH at pH 5.5 was 2.4 ± 0.1, very similar to the value obtained at pH 7.5, DkH = 2.7 ± 0.3 (Figure 6). Thus, the possibility that a conformational change prior to the chemical step is determining kcat was ruled out, since the magnitude of DkH would be decreased if that were the case. These results are in contrast to what was found in the DHFR from Streptococcus pneumoniae (SpDHFR), where the kH/kD was unity at pH 6.0, and 2.4 at pH 7.0 (25), and in agreement with the values obtained for the EcDHFR-catalyzed reaction (37).
Figure 6.
KIEs under single turnover conditions. Each curve represents the average of seven traces collected with 20 μM DHFR, 1μM DHF and 100 μM of either NADPH or [4R-4-2H]-NADPH, at pH 7.5. The straight line represents a fit to a single exponential decay (eq. 9). The inset shows the replot of the observed rate constants (kobs) obtained with 5, 7, 14, 20, and 28 μM of DHFR, and either NADPH (○), or [4R-4-2H]-NADPH (•). The lines represent the fits to eq. 10.
Furthermore, the values obtained for the DkH are very comparable to all DV/K obtained at pH 7.5, when both NADH and NADPH were used as substrates. In this situation one can be tempted to interpret the value of ≈ 2.7 as the intrinsic KIE (Dkchem) for this enzyme catalyzed reaction, since DV/K and DkH can be considered equal within experimental error, as illustrated by the equation defining DV/K isotope effects shown below:
This assumption, even though plausible, must be taken with caution, since it is possible that both DV/K and DkH are being decreased from the true intrinsic value by the same factor. The intrinsic KIE was experimentally determined for the EcDHFR, being equal to 3.5 ± 0.2, and the cf then calculated to be 0.25 (45).
In this work, the kinetic mechanism of the MtDHFR catalyzed reaction was determined to be steady-state random, with a preferred pathway in which NADPH binds first. A pKa value of approximately 7.0 was identified for an enzymic acid and kinetic isotope effects revealed the partly rate limiting nature of the hydride transfer step from pH 5.5 to 8.0. Kinetic isotope effects were measured for the hydride transfer step, and EIE were measured for the first time for this reaction. A chemical mechanism including a pre-equilibrium protonation step preceding the hydride transfer step was suggested. Future studies include a complete pre-steady state analysis to better understand the catalytic cycle of the MtDHFR catalyzed reaction, as well as the study of mutants aimed at a better understanding the role of specific amino acids in catalysis.
Supplementary Material
ACKNOWLEDGMENTS
We thank Paul F. Cook (University of Oklahoma) for his valuable advice and assistance in the interpretation of the kinetic isotope effects, and Argyrides Argyrou (Glaxo Smith Kline) for his help with data analysis.
This work was supported by the NIH (AI33696).
Abbreviations
- TB
tuberculosis
- MDR-TB
multi-drug resistant tuberculosis
- XDR-TB
extensively drug resistant tuberculosis
- MtDHFR
dihydrofolate reductase from Mycobacterium tuberculosis H37Rv
- H2F
dihydrofolate
- H4F
tetrahydrofolate
- NADPH
nicotinamide adenine dinucleotide phosphate (reduced form)
- NADH
nicotinamide adenine dinucleotide (reduced form)
- NADL
NADH or [4R-4-2H]-NADH used as substrate
- dTMP
deoxythymidine monophosphate
- KIE
kinetic isotope effect
- SKIE
solvent kinetic isotope effect
- MKIE
multiple kinetic isotope effect
- EIE
equilibrium isotope effect
- EcDHFR
DHFR from Escherichia coli
- SpDHFR
DHFR from Streptococcus pneumoniae
Footnotes
Supporting Information Available
Three figures containing a multiple sequence alignment of DHFR's from several sources, a structure-based sequence alignment of the E. coli and M. tuberculosis DHFR's and a structural overlay of the E. coli and M. tuberculosis DHFR's three-dimensional structures. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1. [08/15/2010];Global tuberculosis control : epidemiology, strategy, financing : WHO report 2009. http://www.who.int/tb/publications/global_report/2009/en/index.html.
- 2.Dye C, Williams BG, Espinal MA, Raviglione MC. Erasing the world's slow stain: strategies to beat multidrug-resistant tuberculosis. Science. 2002;295:2042–2046. doi: 10.1126/science.1063814. [DOI] [PubMed] [Google Scholar]
- 3.Kompis IM, Islam K, Then RL. DNA and RNA Synthesis: Antifolates. Chem. Rev. 2005;105:593–620. doi: 10.1021/cr0301144. [DOI] [PubMed] [Google Scholar]
- 4.Li R, Sirawaraporn R, Chitnumsub P, Sirawaraporn W, Wooden J, Athappilly F, Turley S, Hol WGJ. Three-dimensional Structure of M. tuberculosis Dihydrofolate Reductase Reveals Opportunities for the Design of Novel Tuberculosis Drugs. J. Mol. Biol. 2000;295:307–323. doi: 10.1006/jmbi.1999.3328. [DOI] [PubMed] [Google Scholar]
- 5.El-Hamamsy MHRI, Smith AW, Thompson AS, Threadgill MD. Structure-based design, synthesis and preliminary evaluation of selective inhibitors of dihydrofolate reductase from Mycobacterium tuberculosis. Bioorg. Med. Chem. 2007;15:4552–4576. doi: 10.1016/j.bmc.2007.04.011. [DOI] [PubMed] [Google Scholar]
- 6.Kumar A, Siddiqi MI. Virtual screening against Mycobacterium tuberculosis dihydrofolate reductase: Suggested workflow for compound prioritization using structure interaction fingerprints. Journal of Molecular Graphics and Modelling. 2008;27:476–488. doi: 10.1016/j.jmgm.2008.08.005. [DOI] [PubMed] [Google Scholar]
- 7.Deng H, Callender R. Structure of Dihydrofolate When Bound to Dihydrofolate Reductase. J. Am. Chem. Soc. 1998;120:7730–7737. [Google Scholar]
- 8.Gready JE. Theoretical Studies on the Activation of the Pterin Cofactor in the Catalytic Mechanism of Dihydrofolate Reductase. Biochemistry. 1985;24:4761–4766. doi: 10.1021/bi00339a008. [DOI] [PubMed] [Google Scholar]
- 9.Rod TH, Brooks CL. How Dihydrofolate Reductase Facilitates Protonation of Dihydrofolate. J. Am. Chem. Soc. 2003;125:8718–8719. doi: 10.1021/ja035272r. [DOI] [PubMed] [Google Scholar]
- 10.Shrimpton P, Allemann RK. Role of water in the catalytic cycle of E. coli dihydrofolate reductase. Protein Science. 2002;11:1442–1451. doi: 10.1110/ps.5060102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Morrison JF, Stone SR. Mechanism of the reaction catalyzed by dihydrofolate reductase from Escherichia coli: pH and deuterium isotope effects with NADPH as the variable substrate. Biochemistry. 1988;27:5499–5506. doi: 10.1021/bi00415a017. [DOI] [PubMed] [Google Scholar]
- 12.Loveridge EJ, Behiry EM, Swanwick RS, Allemann RK. Different Reaction Mechanisms for Mesophilic and Thermophilic Dihydrofolate Reductases. J. Am. Chem. Soc. 2009;131:6926–6927. doi: 10.1021/ja901441k. [DOI] [PubMed] [Google Scholar]
- 13.Argyrou A, Vetting MW, Aladegbami B, Blanchard JS. Mycobacterium tuberculosis dihydrofolate reductase is a target for isoniazid. Nature Struc. & Mol. Biol. 2006;13:408–413. doi: 10.1038/nsmb1089. [DOI] [PubMed] [Google Scholar]
- 14.Pace CN, Vajdos F, Fee L, Grimsley G, Gray T. How to measure and predict the molar absorption coefficient of a protein. Protein Sci. 1995;4:2411–23. doi: 10.1002/pro.5560041120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ottolina G, Riva S, Carrea G, Danieli B, Buckmann AF. Enzymatic synthesis of [4R-4-2H]NAD(P)H and [4S-4-2H]NAD(P)H and determination of the stereospecificity of 7α- and 12α-hydroxysteroid dehydrogenase. Biochim. Biophys. Acta. 1989;998:173–178. doi: 10.1016/0167-4838(89)90270-7. [DOI] [PubMed] [Google Scholar]
- 16.Jeong S, Gready JE. A method of preparation and purification of (4R)-deuterated-reduced nicotinamide adenine dinucleotide phosphate. Anal. Biochem. 1994;221:273–277. doi: 10.1006/abio.1994.1411. [DOI] [PubMed] [Google Scholar]
- 17.Stone SR, Morrison JF. Kinetic mechanism of the reaction catalyzed by dihydrofolate reductase from Escherichia coli. Biochemistry. 1982;21:3757–3765. doi: 10.1021/bi00259a006. [DOI] [PubMed] [Google Scholar]
- 18.Karsten WE, Lai C, Cook PF. Inverse Solvent Isotope Effects in the NAD-Malic Enzyme Reaction Are the Result of the Viscosity Difference between D20 and H20: Implications for Solvent Isotope Effect Studies. J. Am. Chem. Soc. 1995;117:5914–5918. [Google Scholar]
- 19.Cook PF, Blanchard JS, Cleland WW. Primary and Secondary Deuterium Isotope Effects on Equilibrium Constants for Enzyme-Catalyzed Reactions. Biochemistry. 1980;21:4853–58. doi: 10.1021/bi00562a023. [DOI] [PubMed] [Google Scholar]
- 20.Reed LS, Archer MC. Oxidation of Tetrahydrofolic Acid by Air. J. Agric. Chem. 1980;28:801–805. [Google Scholar]
- 21.Francis K, Gadda G. Probing the Chemical Steps of Nitroalkane Oxidation Catalyzed by 2-Nitropropane Dioxygenase with Solvent Viscosity, pH, and Substrate Kinetic Isotope Effects. Biochemistry. 2006;45:13889–13898. doi: 10.1021/bi060566l. [DOI] [PubMed] [Google Scholar]
- 22.Northrop DB. Steady-state analysis of kinetic isotope effects in enzymic reactions. Biochemistry. 1975;14:2644–2651. doi: 10.1021/bi00683a013. [DOI] [PubMed] [Google Scholar]
- 23.Hiromi K. Kinetics of Fast Enzyme Reactions. John Wiley and Sons, Inc.; New York: 1979. p. 346. [Google Scholar]
- 24.Appleman JR, Beard WA, Delcampg TJ, Prendergast NJ, Freisheimg JH, Blakley RL. Unusual Transient- and Steady-state Kinetic Behavior Is Predicted by the Kinetic Scheme Operational for Recombinant Human Dihydrofolate Reductase. J. Biol.Chem. 1990;265:2740–2748. [PubMed] [Google Scholar]
- 25.Lee J, Yennawar NH, Gam J, Benkovic SJ. Kinetic and Structural Characterization of Dihydrofolate Reductase from Streptococcus pneumonia. Biochemistry. 2010;49:195–206. doi: 10.1021/bi901614m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Thillet J, Adams JA, Benkovic SJ. The kinetic mechanism of wild-type and mutant mouse dihydrofolate reductases. Biochemistry. 1990;29:5195–5202. doi: 10.1021/bi00473a028. [DOI] [PubMed] [Google Scholar]
- 27.Huang S, Appleman JR, Tan X, Thompson PD, Blakley RL, Sheridan RP, Venkataraghavan R, Freisheim JH. Role of Lysine-54 in Determining Cofactor Specificity and Binding in Human Dihydrofolate Reductase. Biochemistry. 1990;29:8063–8069. doi: 10.1021/bi00487a011. [DOI] [PubMed] [Google Scholar]
- 28.Williams EA, Morrison JF. Human dihydrofolate reductase: reduction of alternative substrates, pH effects, and inhibition by deazafolates. Biochemistry. 1992;31:6801–6811. doi: 10.1021/bi00144a022. [DOI] [PubMed] [Google Scholar]
- 29.Beard WA, Appleman JR, Delcamp TJ, Freisheims JH, Blakley RL. Hydride Transfer by Dihydrofolate Reductase. J. Biol. Chem. 1989;264:9391–9399. [PubMed] [Google Scholar]
- 30.Deng H, Callender R. Structure of Dihydrofolate When Bound to Dihydrofolate Reductase. J. Am. Chem. Soc. 1998;120:7730–7737. [Google Scholar]
- 31.Gready JE. Theoretical Studies on the Activation of the Pterin Cofactor in the Catalytic Mechanism of Dihydrofolate Reductase. Biochemistry. 1985;24:4761–4766. doi: 10.1021/bi00339a008. [DOI] [PubMed] [Google Scholar]
- 32.Chen YQ, Kraut J, Blakley RL, Callender R. Determination by Raman Spectroscopy of the pKa of N5 of Dihydrofolate Bound to Dihydrofolate Reductase: Mechanistic Implications. Biochemistry. 1994;33:7021–7026. doi: 10.1021/bi00189a001. [DOI] [PubMed] [Google Scholar]
- 33.Northrop DB. The expression of isotope effects on enzyme-catalyzed reactions. Ann. Rev. Biochem. 1981;50:103–31. doi: 10.1146/annurev.bi.50.070181.000535. [DOI] [PubMed] [Google Scholar]
- 34.Cook PF. Enzyme Mechanism from Isotope Effects. Crc Press; 1991. p. 432. [Google Scholar]
- 35.Wiberg KB. The Deuterium Isotope Effect. Chem. Rev. 1955;55:713–743. [Google Scholar]
- 36.Cook PF, Cleland WW. Enzyme kinetics and mechanism. Garland Science; New York: 2007. p. 416. [Google Scholar]
- 37.Fierke CA, Johnson KA, Benkovic SJ. Construction and Evaluation of the Kinetic Scheme Associated with Dihydrofolate Reductase from Escherichia coli. Biochemistry. 1987;26:4085–4092. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- 38.Andrews J, Fierke CA, Birdsall B, Ostler G, Feeney J, Roberts GC, Benkovic SJ. A kinetic study of wild-type and mutant dihydrofolate reductases from Lactobacillus casei. Biochemistry. 1989;28:5743–5750. doi: 10.1021/bi00440a007. [DOI] [PubMed] [Google Scholar]
- 39.Cook PF, Cleland WW. Mechanistic Deductions from Isotope Effects in Multireactant Enzyme Mechanisms. Biochemistry. 1981;20:1790–1796. doi: 10.1021/bi00510a013. [DOI] [PubMed] [Google Scholar]
- 40.Argyrou A, Blanchard JS. Kinetic and Chemical Mechanism of Mycobacterium tuberculosis1-Deoxy-D-xylulose-5-phosphate isomeroreductase. Biochemistry. 2004;43:4375–4384. doi: 10.1021/bi049974k. [DOI] [PubMed] [Google Scholar]
- 41.Silva RG, de Carvalho LPS, Blanchard JS, Santos DS, Basso LA. Mycobacterium tuberculosis β-ketoacyl-acyl carrier protein (ACP) reductase: kinetic and chemical Mechanisms. Biochemistry. 2006;45:13064–13073. doi: 10.1021/bi0611210. [DOI] [PubMed] [Google Scholar]
- 42.Hermes JD, Roeske CA, O'Leary MH, Cleland WW. Use of multiple isotope effects to determine enzyme mechanisms and intrinsic isotope effects. Malic enzyme and glucose-6-phosphate dehydrogenase. Biochemistry. 1984;21:5106–5114. doi: 10.1021/bi00263a040. [DOI] [PubMed] [Google Scholar]
- 43.Reuben J. Deuterium/Protium fractionation factors for polyfunctional organic molecules: direct determination by carbon-13 NMR spectroscopy. J. Am. Chem. Soc. 1986;108:1082–1083. [Google Scholar]
- 44.Vakonakis I, Salazar M, Kang M, Dunbar KR, LiWang AC. Deuterium isotope effects and fractionation factors of hydrogen-bonded A:T base pairs of DNA. J. Biomol. NMR. 2003;25:105–112. doi: 10.1023/a:1022211927051. [DOI] [PubMed] [Google Scholar]
- 45.Sikorski RS, Wang L, Markham KA, Pajagopalan PT, Benkovic SJ, Kohen A. Tunneling and coupled motions in the Escherichia coli dihydrofolate reductase catalysis. J. Am. Chem. Soc. 2004;126:4778–4779. doi: 10.1021/ja031683w. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.