BR-squared: a practical solution to the winner’s curse in genome-wide scans

Abstract

The detrimental effects of the winner’s curse, including overestimation of the genetic effects of associated variants and underestimation of sufficient sample sizes for replication studies are well-recognized in genome-wide association studies (GWAS). These effects can be expected to worsen as the field moves from GWAS into whole genome sequencing. To date, few studies have reported statistical adjustments to the naive estimates, due to the lack of suitable statistical methods and computational tools. We have developed an efficient genome-wide non-parametric method that explicitly accounts for the threshold, ranking, and allele frequency effects in whole genome scans. Here, we implement the method to provide bias-reduced estimates via bootstrap re-sampling (BR-squared) for association studies of both disease status and quantitative traits, and we report the results of applying BR-squared to GWAS of psoriasis and HbA1c. We observed over 50% reduction in the genetic effect size estimation for many associated SNPs. This translates into a greater than fourfold increase in sample size requirements for successful replication studies, which in part explains some of the apparent failures in replicating the original signals. Our analysis suggests that adjusting for the winner’s curse is critical for interpreting findings from whole genome scans and planning replication and meta-GWAS studies, as well as in attempts to translate findings into the clinical setting.

Introduction

Parameter estimates, such as the odds ratio (OR) for associated SNPs reported in a discovery sample are often grossly inflated as compared to the values observed in the follow-up sample. For example, in the recent GWAS of psoriasis (Nair et al. 2009), the OR estimate for rs12983316 on chromosome 19 was reduced from 1.36 in the discovery sample (1,359 cases and 1,400 controls, p = 2 × 10⁻⁵) to 1.09 in the follow-up sample (5,048 cases and 5,051 controls, p = 0.027). This phenomenon is known as the Beavis effect (Xu 2003) or the winner’s curse (Voight and Cox 2004). The magnitude of the winner’s curse in genetic studies was first demonstrated for genome-wide linkage scans (Göring et al. 2001) and subsequently for GWAS (Garner 2007). The winner’s curse is recognized as one of the major contributing factors to failed replication studies. For example, four GWAS, all published in the May 2009 issue of Nature Genetics, discussed the effect of the winner’s curse. In particular, the GWAS of severe malaria in West Africa (Jallow et al. 2009) reported “because the effect size was overestimated in initial reports (‘winner’s curse’) [among other contributing factors]…[the study] did not identify any of the well-known erythrocyte variants that have been selected by malaria, other than HbS”. More recently, Park et al. (2010) pointed out the importance of the winner’s curse adjustment in meta-GWAS analysis and in specification of risk prediction models.

Although the detrimental effect of the winner’s curse in underestimation of the necessary sample size for a successful replication study is known, statistical methods and computational tools suitable for large-scale genome-wide scans are under-developed. As a result, authors of published GWAS usually caution readers about the interpretation of the genetic effects estimated from the discovery sample (He et al. 2009), or implicate the winner’s curse as a possible explanation after a replication study has failed (Jallow et al. 2009).

Extending previous work developed for linkage scans (Sun and Bull 2005; Wu et al. 2005, 2006), we developed a bootstrap-based bias-correction method for association studies that can be applied without collecting additional data (Faye et al. 2010). In contrast to the likelihood-based approaches (e.g. Ghosh et al. 2008; Zhong and Prentice 2008), the proposed method adjusts for the effects of selection due to both the stringent genome-wide significance criterion (threshold effect) and the maximization of the association statistics over the genome (ranking effect). The ranking effect is not explicitly addressed by the likelihood approach in part due to the difficulty of specifying a correct joint likelihood for multiple correlated SNPs genome wide. However, we demonstrate below that modelling the threshold effect alone is not adequate for GWAS. Moreover, our method explicitly accounts for the differential effect of allele frequency, because the expected bias is inversely related to the power of the association test, which is influenced in turn by the frequency of the associated risk allele.

The proposed bootstrap method is conceptually straightforward, but can be computationally expensive at the genome-wide level. We implemented the method in a user friendly and efficient program, BR-squared, suitable to GWAS of either disease status or quantitative traits. We applied BR-squared to a recent GWAS of psoriasis (Nair et al. 2009), and to another of complications of type 1 diabetes in the diabetes control and complications trial (DCCT) samples (Paterson et al. 2010). In both of these studies, we observed >50% (sometimes >90%) reduction in effect estimates for many associated SNPs. We chose to focus on these two datasets because of the availability of their built-in replication/follow-up samples which provided independent estimates of the true underlying genetic effects. However, we note that the method is designed for data from the discovery stage alone when a follow-up sample is generally not available and the required replication sample size is to be determined based on the genetic effect size estimated from the discovery stage.

Materials and methods

The psoriasis dataset

Nair et al. (2009) first performed a GWAS for psoriasis using 438,670 SNPs in 1,359 cases and 1,400 controls. They then applied ranking selection without specifying a significance threshold and conducted a follow-up study of 21 promising SNPs, representing 18 independent loci, in 5,048 cases and 5,051 controls and found supporting evidence for association at 10 loci. They comment that “Owing to the `winner’s curse’, odds ratios estimated in the discovery sample were larger than those estimated in the follow-up samples” (Table 1; Fig. 1).

Table 1.

Naive, replication and bias-reduced genome-wide BR-squared OR estimates of the ten SNPs associated with psoriasis reported in Nair et al. (2009)

Chr	SNP	Pos (Mb)	MAF	Risk allele	p a	Naive ORb	Replication ORc	BR-squared ORd	SDe	Percentage reduction (%)f
6	rs12191877	31.36	0.14	T	5.73E–053	2.78	2.64	2.78	1.08	0.1
5	rs2082412	158.65	0.21	G	7.00E–010	1.56	1.44	1.39	1.07	26.4
5	rs17728338	150.46	0.06	A	1.88E–007	1.72	1.59	1.24	1.04	60.3
5	rs20541	132.02	0.22	G	5.48E–006	1.37	1.27	1.09	1.03	73.1
6	rs610604	138.24	0.32	G	1.71E–005	1.28	1.19	1.04	1.04	83.6
12	rs2066807*	55.02	0.07	C	1.53E–005	1.68	1.34	1.16	1.03	71.1
1	rs2201841	67.47	0.29	G	2.72E–007	1.35	1.13	1.13	1.04	58.6
9	rs1076160	134.8	0.46	T	2.52E–005	1.26	1.09	1.03	1.05	86.6
19	rs12983316	10.98	0.14	G	2.15E–005	1.37	1.09	1.04	1.04	88.8
2	rs397211	113.6	0.32	T	1.04E–003	1.21	1.08	1.00	1.04	100

* We replaced the imputed SNP rs2066808 with the nearby SNP rs2066807 that is in perfect LD (r ² = 1 in Hapmap phase II samples)

^aThe allelic association p value using the discovery samples (1,357 cases and 1,400 controls) from dbGaP

^bThe naive estimate of the OR using the discovery samples without accounting for the ranking effect as reported in column 7 of Table 2 of Nair et al. (2009)

^cThe OR estimated from the independent follow-up samples as reported in column 11 of Table 2 of Nair et al. (2009)

^dThe bias-reduced OR estimate provided by BR-squared using 1,000 level 1 bootstrap samples

^eSD of the BR-squared OR estimate based on 100 level 2 bootstrap samples

^fThe percentage reduction in the estimates as measured by 1-log(bootstrap.OR)/log(naive.OR)

Fig. 1.

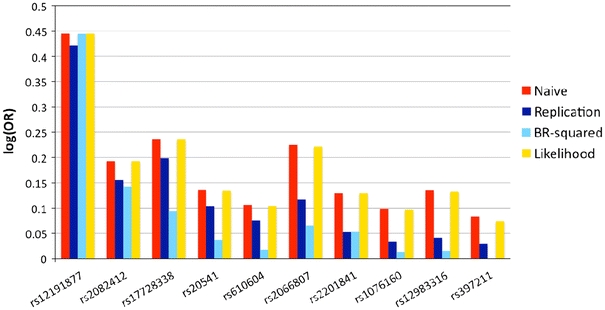
Naive (red), replication (dark blue), genome-wide BR-squared (light blue) and single-SNP likelihood (orange) estimates of the log(OR) of the ten SNPs reported in Table 2 of Nair et al. (2009). These ten SNPs were associated with psoriasis in the discovery stage and had replication p < 0.05 and the effect estimates in the same direction as the discovery stage

Moreover, despite the large sample size of the follow-up study, 9 SNPs reported in the discovery stage were not replicated (Fig. 2). Using rs2273668 as an example (naive OR 1.36 and p = 2 × 10⁻⁵ in the discovery stage; replication OR 1.07 and p = 0.12 in the follow-up stage), sample size calculation based on the naive OR estimate of 1.36 indicates that a successful replication study (α = 0.05, power = 80%) requires only ~2K:2K cases:controls. Because the actual replication study of ~5K:5K cases:controls exceeds the sample size requirement, one might conclude that rs2273668 is a false positive. However, sample size estimated using the follow-up OR value of 1.07 implies that the actual replication study was in fact drastically under-powered, and a much larger sample of ~41K:41K cases:controls (>20-fold increase) would be required to achieve 80% power at the 0.05 level (sample size calculation). Therefore, this apparent failure in replication could be explained by unsuspected low power.

Fig. 2.

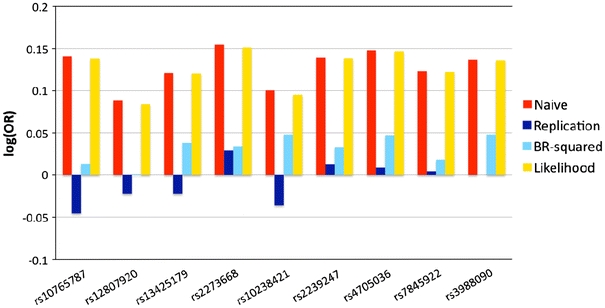
Naive (red), replication (dark blue), genome-wide BR-squared (light blue) and single-SNP likelihood (orange) estimates of the log(OR) of the nine SNPs reported in the supplementary Table 2 of Nair et al. (2009). These nine SNPs were associated with psoriasis in the discovery stage, but had replication p > 0.05 or the effect estimates in the opposite direction as the discovery stage

The HbA1c dataset

In the setting of a GWAS of longitudinal repeated measures of HbA1c in subjects from the DCCT (Paterson et al. 2010), a major locus was identified in the CONventional treatment group (n _CON = 667) near SORCS1 (10q25.1; rs1358030; p = 4.66 × 10⁻⁹) via regression analysis of the average log(HbA1c) value on SNPs with additive genotype coding (Table 2). In total, 841,342 SNPs, genotyped by the Illumina 1 M BeadArray assay, that passed a set of standard quality control criteria (Paterson et al. 2010) were assessed for association with HbA1c at α = 5 × 10⁻⁸, the genome-wide significance threshold (Dudbridge and Gusnanto 2008).

Table 2.

Naive, replication and bias-reduced genome-wide BR-squared regression coefficient (β) estimates of the significant SNP associated with HbA1c in the DCCT samples

Chr	SNP	Pos (Mb)	MAF	Risk allele	p valuea	Naive betab	Replication betac	BR-squared betad	SDe	Percentage reductionf
10	rs1358030	108.1	0.36	C	4.66E–09	0.045	0.005	0.003	0.013	93%

^aThe association p value using the 667 samples from the DCCT CON group

^bThe naive estimate of the regression coefficient beta using the 667 CON samples without accounting for the threshold effect

^cThe beta estimated from the independent 637 samples from the DCCT INT group

^dThe bias-reduced beta estimate provided by BR-squared using 1,000 level 1 bootstrap samples and with α = 5 × 10⁻⁸

^eSD of the BR-squared beta estimate based on 100 level 2 bootstrap samples

^fThe percentage reduction in the estimates as measured by 1 − bootstrap.beta/naive.beta

The naive estimate of the regression coefficient for rs1358030 is β _CON.naive = 0.045 (SD 0.008, p = 4.66 × 10⁻⁹). Based on this estimate, the associated SNP explains ~5% of the total phenotypic variation, and a successful replication study (α = 0.05, power = 80%) would require 234 samples with a single HbA1c measure (sample size calculation). However, estimates obtained from the independent INTensive treatment group (n _INT = 637) are markedly smaller: β _INT = 0.005 (SD 0.0095, p = 0.606), explaining only ~0.05% of the phenotypic variation and requiring ~15 K samples (>50-fold increase) to achieve 80% power at α = 0.05. Note that for INT, we used only measures collected at the time of screening for eligibility for the trial to exclude the treatment effect, so that the sample could be considered as a replication dataset.

The genome-wide bootstrap method

The key source of the winner’s curse is the double use of the same data for both SNP detection and effect estimation. Ideally, an unbiased effect estimate can be obtained when there are two independent data sets, one for detection and the other for estimation. A repeated sample-split approach, such as bootstrap resampling applied in the original data, can mimic the separate use of detection and estimation samples and reduce the variance of the result obtained from a single sample-split approach (Sun and Bull 2005; Faye et al. 2010). A detailed development and evaluation of the method for GWAS can be found in Faye et al. (2010). In essence, the genome-wide bootstrap estimate is constructed in the following way.

The original selection procedure (e.g. significance threshold, ranking, either or both) is repeated in B1 level 1 bootstrap samples drawn from the original dataset. For each selected SNP, the effect size is estimated in the observations in the ith bootstrap sample (β _Di) and also in the observations not included in the bootstrap sample (β _Ei, “out-of-bootstrap” sample), where i = 1,…,B1. The estimate of bias for the kth ranked SNP selected in the original sample is the average difference between β _Di and β _Ei for the kth ranked SNP selected in each bootstrap repetition, adjusted for the minor allele frequency (MAF). The bias-reduced bootstrap shrinkage estimate for the kth ranked SNP selected in the original sample is

where β _N(k) is the naive estimate for the kth ranked SNP selected in the original sample with MAF p _(k). Note that in the genome-wide setting the SNP selected in the bootstrap sample has the same rank as the SNP selected in the original data, but may or may not be the same SNP. Thus, p _i(k) is the MAF for the kth ranked SNP selected in the ith bootstrap sample. This estimator is further improved by correcting for the negative correlation between β _Di and β _Ei (Faye et al. 2010).

The standard deviation (SD) of the bootstrap estimate is estimated by obtaining B2 level 2 bootstrap samples from the original dataset to serve as a set of hypothetical “original” datasets. In each of these B2 samples, the association analysis is performed following the original selection procedure, and the same bootstrap estimation method as described above is applied to each of the j samples, j = 1,…,B2. A log transformation is applied to the level 2 shrinkage estimates to achieve approximate normality, and the SD of these estimates is used to construct a symmetric confidence interval (CI), which is then back-transformed to the original scale (Faye et al. 2010).

A single-locus bootstrap estimate may be obtained by applying the above procedure to a dataset that contains only the SNP of interest, ignoring the information provided by other SNPs correlated due to linkage disequilibrium (LD). Faye et al. (2010) show that the single-locus bootstrap and likelihood-based approaches perform similarly well, but both are outperformed by the genome-wide bootstrap method. The genome-wide bootstrap point estimate has a smaller variance and smaller root mean squared error (RMSE) than the likelihood method, and the genome-wide bootstrap CIs are narrower and achieve better coverage than the likelihood CIs.

Method implementation as BR-squared

Although the bootstrap procedure is computationally intensive, the highly efficient software package, BR-squared, that we developed can feasibly compute the bias-reduced effect estimates for typical GWAS of 1M SNPs and 2K individuals for example.

BR-squared is open-source and was developed in C++, using a small part of the PLINK (Purcell et al. 2007) code for the association tests. It is designed to be user-friendly, easy to apply and familiar to the users of PLINK, and it is portable across Linux, Windows or Mac OS environments. BR-squared contains highly optimized code and can handle arbitrarily large datasets, with similar memory requirements as PLINK. Data are read from PLINK formatted files, containing either case–control or quantitative phenotypes with or without covariates and an arbitrary number of SNPs and individuals. A variety of association tests can be specified for binary phenotypes, including allelic, trend and genotypic tests or Wald tests in the logistic model. For quantitative traits, a linear model is used.

Sample size calculation

In a case–control association study, let p.case and p. control be the allele frequencies of the risk allele in cases and controls and assume an equal number of cases and controls and an one-sided allelic test (i.e. requiring consistency of the effect direction), the sample size required for a successful replication study at α level with 1 − θ power is

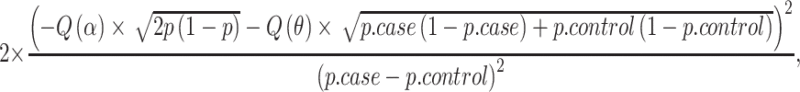where p = (p.case + p.control)/2, and 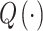is the quantile function of the standard normal distribution (Ziegler and Konig 2006). Note that p.case = OR × p.control/(OR × p.control + (1 − p.control)).

In a quantitative association study, assume that the association analysis is performed via linear regression, Y ~ β ₀ + βX, where Y is the quantitative phenotype and X is the SNP genotype coding. For notation simplicity, let β be the parameter estimate and (S _β)² the associated variance estimate. The test statistic, Z = β/S _β, is approximately normally distributed, N(μ, 1), assuming that the null and alternative variances are similar. The sample size required to achieve significance at the α level with 1 − θ power depends on

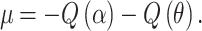Furthermore, using subscript _c for the current study and _f for the planned future replication study, and letting σ ² = Var(Y), we can show that

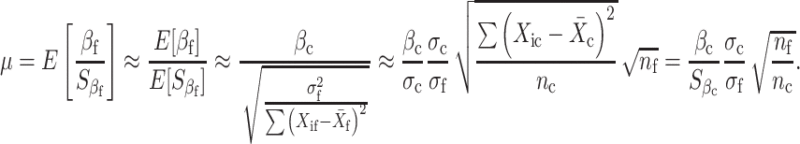Thus, the sample size required for future replication is

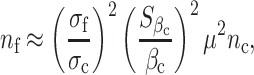1

where n _c is the sample size of the current study.

Assuming σ _f = σ _c, the sample size calculation can be simplified as

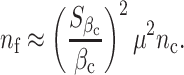2

However, if the current study used the mean of T measures of Y while the future study is to use a single measure of Y, as in the DCCT example, then

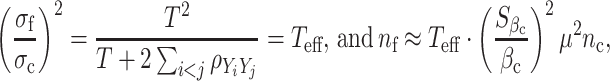3

where ρ _YiYj is the correlation between longitudinal phenotype observations, and T _eff is the effective number of observations depending on the correlation. For example, if observations are independent of each other, ρ _YiYj = 0, then T _eff = T, and the sample size required for future study using a single measure must be increased by T fold when compared with a study using the average of T measures. If observations are perfectly correlated to each other, T _eff = 1 and having more observations does not add statistical efficiency. Then, sample size calculations follow (2).

In the DCCT example (Paterson et al. 2010), the intra-class correlation coefficient between consecutive quarterly HbA1c values (in the CON group) was 0.79, falling to 0.42 for values measured 3 years apart. The estimate of T _eff was approximate 2. This value was then used for sample size calculation based on the naive estimate obtained from the CON group that had an average of 26 observations per individual. T _eff = 1 was used for sample size calculation based on the follow-up estimate obtained from the INT group since only the single measure at the eligibility time point was used for the analysis.

In general, the sample size n required for a successful replication study is inversely proportional to the effect size β such that n ~ 1/(β ²), where β is the log(OR) or the regression coefficient. Thus, if the estimate of β is reduced by 50%, the corresponding sample size is increased by approximately fourfold.

Results

GWAS of disease status: psoriasis

We obtained the Perlegen 600 K unfiltered genotype data (phg000011, phs000019.v1.p1) from dbGaP (NCBI) and the IDs of the exact 1,359 cases and 1,400 controls from Dr. Abecasis and his colleagues http://www.ncbi.nlm.nih.gov/sites/entrez?Db=gap. Because two cases are not included in the dbGaP data, our BR-squared analysis was performed on 1,357 + 1,400 samples. We excluded markers with <95% genotype call rate, MAF < 1% and HWE p < 10⁻⁶ in controls. In total, 439,496 autosomal SNPs that passed quality control criteria were used as input to BR-squared. Bias-reduced estimates were obtained for the 10 replicated SNPs (Table 1; Fig. 1) and for the nine failed SNPs (Fig. 2), using 1,000 level 1 bootstrap samples for the effect estimate and 100 level 2 samples for the variance estimate, under the ranking criterion that was used in the original discovery study. Note that BR-squared is applied to the discovery samples only, and estimates from the follow-up samples are provided in the figures and tables for comparison purposes.

Of the 10 replicated SNPs, we observed >60% reduction in OR estimates for 8 of them with the bias-adjusted estimates considerably closer to the follow-up estimates than the naive estimates (Table 1; Fig. 1). In some cases, the bootstrap method appears to be conservative. However, we note that the follow-up OR estimates as reported in Nair et al. (2009) are in fact also subject to the winner’s curse, albeit less severely, because they were reported only if supporting evidence for association had been found: p < 0.05 in the follow-up sample and direction of effect matching the discovery sample. As expected, there was not much correction for rs12191877 from chromosome 6, because it is in the well-known MHC/HLA region strongly associated with psoriasis, and was detected with extremely high power as reflected by the association test p value.

Note that for this study we modelled the ranking effect alone because the reported SNPs were mostly selected based on ranks without a statistical significance threshold (Nair et al. 2009). In such a situation, Zhong and Prentice (2010) suggested using a threshold value of 0.05 for the likelihood approaches (the likelihood method however tends to be sensitive to the choice of the threshold value). For comparison, we calculated the likelihood-based estimate that averages the conditional maximum likelihood estimate adjusting for α = 0.05 and the mean of the normalized conditional likelihood estimate proposed by Ghosh et al. (2008). This latter estimator was shown to outperform other likelihood-based estimators (Ghosh et al. 2008; Faye et al. 2010). Because it is difficult to specify a joint distribution for all GWAS SNPs simultaneously, the likelihood method must be applied to one SNP at a time. The results in Fig. 1 clearly demonstrate that the single-SNP approach is not adequate for GWAS and multiple correlated SNPs must be considered jointly at the genome-wide level as implemented in BR-squared.

Interestingly, the bootstrap method appears to be anti-conservative for the nine SNPs that were not replicated (Fig. 2) in contrast to the conservative observation made for the 10 replicated SNPs (Fig. 1). One reason is that BR-squared treats “flip-flop” estimates [change in the direction of log(OR)] as evidence for no association and forces the BR-squared estimate to be zero (Discussion). In addition, important to note is that the follow-up OR estimates in this case suffer from what we call the “loser’s curse”, because they were reported only if no supporting association evidence was found, i.e. p > 0.05 in the follow-up sample or direction of effect opposite of the discovery sample. The results of the BR-squared analysis imply that it might be premature to conclude false positives for several of the failed SNPs including rs2273668.

GWAS of a quantitative trait: HbA1c

The genome-wide BR-squared method was applied to the CONventional treatment group (n _CON = 667) with 1,000 level 1 and 100 level 2 bootstrap samples, following the original selection procedure, i.e. under a significance threshold of 5 × 10⁻⁸ for the p value of an association test in the linear regression of the average log(HbA1c) value on an additively coded SNP. In total, 841,342 SNPs with MAF > 1%, HWE p > 10⁻⁶, and not significantly associated with gender were analyzed jointly. Application of BR-squared yielded an effect size estimate, β_CON._bootstrap = 0.003 for rs1358030, the only SNP that achieved genome-wide significance in the original GWAS. While the naive estimate is β_CON.naive = 0.045, this bias-reduced effect estimate is comparable to the value obtained from independent INT group, β_INT = 0.005 (Table 2).

For comparison, we also applied the likelihood-based method to CON and obtained an estimate of 0.032. This value is similar to that obtained via the single-locus bootstrap option in BR-squared (0.037), which ignores the fact that rs1358030 not only achieved genome-wide significance, but its association test statistic was also the largest among all competing SNPs. Clearly, modelling the threshold effect alone is not adequate for GWAS, and considering all SNPs jointly can further reduce the estimation bias considerably.

Discussion

The genome-wide bootstrap is computationally intensive but nevertheless practically feasible. The total CPU time required for a typical GWAS (~2,000 individuals, ~1 M SNPs) with 1,000 bootstrap samples is less than an hour (4 Amd Opteron CPU at 2.8Ghz and 8 GB RAM), growing linearly with the number of individuals and SNPs. Estimating the variation of the estimate is more costly because it requires a two-level nested bootstrap, and the time is multiplied by the number of level 2 bootstrap samples (typically 100). For example, the psoriasis application used a total CPU time of 22 days for both point and CI estimation, and only 45 min for the point estimation alone.

To improve time efficiency, we have implemented BR-squared as a truly distributed application, so that it can utilize a single computer with multiple CPUs, a heterogeneous computer cluster or both at the same time. Therefore, application of BR-squared for a typical GWAS could be completed within a day using 20 computers in a cluster, a reasonable undertaking for most investigators. To further improve the efficiency of the bootstrap calculations, we also provide an option to use only the top ranked 5–10% of the original set of GWAS SNPs. For example, in the psoriasis application, when only the top 20 K SNPs were eligible for inclusion in the bootstrap averages, 95% of the bootstrap estimates were within 5.4% of the estimates using all the SNPs. Using the top 20 K SNPs, the total CPU time was only 22 h with 1,000 level 1 and 100 level 2 bootstrap samples as compared to 22 days using all ~440 K SNPs. Therefore, the computational time can be reduced by more than 90% with little compromise in estimation accuracy.

The bootstrap approach also has the advantage of flexibility and can be readily modified to reflect different analysis strategies as illustrated by the GWAS of psoriasis in which selection of SNPs was based on ranks only. BR-squared also allows selection of SNPs based on the minimum p value of trend and genotypic association tests as used by the GWAS of the Wellcome Trust Case Control Consortium (WTCCC 2007).

For many associated SNPs, particularly for those with p values just below the genome-wide significance threshold, we observed >50% reduction in genetic effect estimates, consistent with the value of 60% suggested by others (Ioannidis et al. 2009; Zhong and Prentice 2010). Our results lead to a minimal fourfold increase in the sample size requirement for replication studies, and also imply that many loci that appeared not to have been replicated may be in fact true positives, but failed to replicate because the replication sample sizes, and thus power, were too low. It is therefore crucial to adjust for selection bias when interpreting whole genome scan findings and planning replication and meta-GWAS studies. Our method, BR-squared, offers a practical solution to the winner’s curse in genome-wide scans.

The genome-wide bootstrap method tends to be slightly conservative for true positives, as seen in the applications herein as well as in simulation studies reported by Faye et al. (2010). A conservative effect estimate will lead to over-estimation of necessary replication sample size. Although sample size over-estimation can result in unnecessary cost, replication sample size is typically calculated under a set of ideal assumptions such as using the same ascertainment strategy as the discovery stage, samples from a homogenous population, no missing or bad quality data, etc. In practice, violation of assumptions might lead to a larger sample size necessary for successful replication study. For these reasons, slight conservativeness in effect estimation in some situations could be helpful. Xu et al. (2011) recently showed that there is no unbiased estimate conditionally on the significance of the corresponding hypothesis test. Therefore, further improvements in effect estimation likely require additional information or data. For false positives or SNPs with effect size close to the null value, the method can be anticonservative (Fig. 2) due to the “flip-flop” constraint. Lifting the constraint would improve the performance for putatively false positive SNPs, but there is a trade-off between the null and alternative cases. Practically, it is advantageous for the method to perform better for true positives: a false-positive SNP can be easily weeded out in the replication study (e.g. 95% of the time the replication p value will be >0.05 regardless of the sample size as long as the p values are calculated properly), but a truly associated SNP not replicated (say due to insufficient sample size) will not be followed up. In application, because we do not know the underlying truth between true or false positives, we impose the “flip-flop” constraint in the BR-squared implementation.

The phenomenon of the winner’s curse is not limited to association studies of main effects. In fact, the winner’s curse can affect all under-powered studies in which the same observations are used for both effect estimation and hypothesis testing, for example eQTL (Choy et al. 2008), haplotype association, G × G or G × E analyses. The winner’s curse could lead to false-positive interaction studies, for example, when a significantly associated SNP, detected in one group (e.g. a cohort or a treatment group) is tested for interaction with another group (Bailey et al. 2009). In that case, because the effect estimate is subject to the winner’s curse only in the first group, the apparent difference in the main effect estimates between the two groups could be misinterpreted as evidence for interaction. In principle, the proposed bootstrap framework can be adapted to address the problem, but the corresponding implementation is non-trivial and requires investigation of the specifics of each setting.

As we move into whole genome sequencing, the number of tests conducted will increase, but power to detect rare variants may be only modest. In this setting, the adverse effects of the winner’s curse are likely to be more severe, and methods to reduce bias, such as BR-squared are essential.

URLs: The software package, BR-squared, that provides bias-reduced estimates via bootstrap re-sampling for genome-wide association studies of either disease status or quantitative traits, is available at the website of corresponding author L.S. (http://www.utstat.toronto.edu/sun/).