A new framework for identifying cis-regulatory motifs in prokaryotes

Abstract

We present a new algorithm, BOBRO, for prediction of cis-regulatory motifs in a given set of promoter sequences. The algorithm substantially improves the prediction accuracy and extends the scope of applicability of the existing programs based on two key new ideas: (i) we developed a highly effective method for reliably assessing the possibility for each position in a given promoter to be the (approximate) start of a conserved sequence motif; and (ii) we developed a highly reliable way for recognition of actual motifs from the accidental ones based on the concept of ‘motif closure’. These two key ideas are embedded in a classical framework for motif finding through finding cliques in a graph but have made this framework substantially more sensitive as well as more selective in motif finding in a very noisy background. A comparative analysis shows that the performance coefficient was improved from 29% to 41% by our program compared to the best among other six state-of-the-art prediction tools on a large-scale data sets of promoters from one genome, and also consistently improved by substantial margins on another kind of large-scale data sets of orthologous promoters across multiple genomes. The power of BOBRO in dealing with noisy data was further demonstrated through identification of the motifs of the global transcriptional regulators by running it over 2390 promoter sequences of Escherichia coli K12.

INTRODUCTION

Identification of cis-regulatory motifs in genomic sequences represents a basic and important problem in computational genomics. Its application ranges from inference of regulatory elements for specific operons or pathways to identification of regulons responsive to particular stimuli and to the elucidation of the global transcription regulation network encoded in a prokaryotic genome. Substantial efforts have been invested into the study of this problem in the past two decades, which has led to the development of numerous computational tools for cis-regulatory motif prediction (1–9). Still, the problem remains largely unsolved, particularly for genome-scale applications (10,11).

One general issue with most of the existing motif-finding programs, if not all, is that they generally require that the majority of the input promoter sequences should contain an instance of the to-be-identified motif; and the prediction performance drops rapidly as the percentage of the input promoter sequences not containing such instances increases. While in some applications, the user of such motif-finding tools may get a set of promoter sequences of potentially co-regulated genes based on co-expression data, there is actually no guarantee that the majority of these promoter sequences would contain common cis-regulatory motifs. One way to overcome this problem is through employing the phylogenetic footprinting strategy (3,12–18), which is to identify motifs that are conserved across orthologous promoters in related genomes. However, this strategy had only limited success since orthologous promoters are often not well defined or may not even exist across prokaryotes. Basically, the most essential challenge for computational motif-finding problem remains to be the development of algorithms that are capable of detecting possibly weak signals associated with motifs embedded in promoter sequences and doing so when the motifs appear only in a small fraction of the promoter sequences.

In this article, we present a new algorithm, BOBRO, which we believe represents a substantial progress towards accomplishing the above goal. The main contribution of the work can be summarized as: we found a very effective way to reduce the search space for motif identification into a highly sparse graph in which most of the to-be-identified motifs are mapped into cliques of the graph. While the idea of finding motifs through finding cliques in a graph has been widely used by previous motif-finding programs, there are fundamental differences between our algorithm and all the previous algorithms, which we explain as follows.

Consider a matrix H = (h_ij) for a given set of promoters with the same sequence length, some of which contain the to-be-identified motifs, where each row of H represents a distinct promoter sequence and each column represents a distinct position in the promoter sequences. H has the following property: If these promoters have a total of k instances of a motif then H contains exactly k non-zero entries with h_ij being k if and only if an instance of the motif starts at the position i in the j-th promoter. Although accurate construction of the H matrix is equally challenging to the original motif-finding problem, it does provide a new way for looking at the problem and designing algorithms for solving the problem rigorously or approximately. We found that having an approximation matrix of H can lead to a good solution to the motif-finding problem. Specifically, we found a simple way to construct an approximation of the H matrix with the following properties: (i) each to-be-identified motif in the j-th promoter with its starting position at i generally corresponds to a relatively high positive value in h_i + k,j for some |k| being 0, 1 or 2; and (ii) entries with such relatively high positive values are highly sparse in the H matrix. These two properties serve as the foundation for our algorithm for motif-finding through finding and extending maximal cliques in a graph dynamically defined over a generally small vertex set corresponding to those entries with relatively high positive values in H. In addition, we have utilized a concept, ‘motif closure’ developed by the authors (1) in our algorithm to distinguish maximal cliques representing true motifs from the accidental ones, as well as to recruit additional motif elements into the motif cores represented by the identified maximal cliques.

We have assessed the prediction performance of BOBRO on large datasets, including 37 sets of co-regulated promoter sequences from a same genome and 547 sets of orthologous promoters from related genomes, against six popular motif prediction programs by other authors, namely AlignACE (19), Bioprospector (7), CONSENSUS (8), MDscan (20), MEME (21) and Weeder (4). Our assessment results showed that BOBRO outperforms each of these programs by a substantial margin on all datasets across all the measures that are typically used for assessing motif-finding programs. To further demonstrate the strengths of BOBRO in picking out a small number of conserved motifs from a large background set, we tested it on the whole Escherichia coli K12 genome with 2930 promoters (300 bp each), and predicted the regulons of 8 out of 10 most global transcription factors (TFs), namely CRP, Fur, FNR, IHF, Fis, Lrp, CpxR, ArcA, NarL and H-NS, which took one day (wall-clock time) of CPU time on a typical desk-top PC. Additional attractive properties of BOBRO include that it can automatically and reliably predict the motif lengths and that it can find multiple conserved motifs from the same promoters.

The executable code of BOBRO, written in ANSI C and tested using GCC (version3.3.3) on Linux, is available at http://csbl.bmb.uga.edu/∼maqin/motif_finding/, and a server version of the program is also available upon request.

MATERIALS AND METHODS

The basic idea of our algorithm can be explained as follows. First, the algorithm generates an approximation matrix M of the matrix H using a two-stage alignment procedure, where M(i, j) corresponds to the i-th position in the j-th promoter sequence. The procedure first generates a preliminary approximation M′ of H, where each entry of M′ represents the number of matches for the corresponding sequence segment (of a fixed length) in the (corresponding) promoter sequence with the other promoter sequences. The final approximation M of H is obtained by consolidating those potential motifs into one, each of which may represent a variation of the same motif. This consolidation process, in conjunction with a filtering step, substantially increases the signal-to-noise ratio of the to-be-identified motifs. Then the algorithm dynamically constructs an un-weighted graph to represent a list of potential motifs and their pair-wise sequence similarities. In this generally sparse graph, actual motifs typically correspond to dense subgraphs. The algorithm then identifies all the significant (maximal) cliques in this graph, each of which typically corresponds to the core part of the conserved motif we aim to find. As the last step, the algorithm employs an expansion and refinement procedure to expand the identified cliques into motif closures and ranks them based on their P-values.

Formally, the input to the algorithm is a set of m promoters 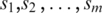of the same length (the same length constraint is used only for the simplicity of discussion and it is not really needed when implementing the algorithm) n + L − 1 (n + L − 1 = 300 bp is the default but adjustable) of a prokaryotic genome, with L being the length of the to-be-identified motif. Let 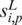denote the sequence segment of length L in promoter 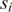starting at position p, and 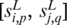be the number of matched nucleotides in the best gapless alignment between 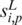and 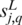. The algorithm executes the following four steps, for each possible length L of the candidate motifs, ranging from 5 to 30.

Step 1: Approximation of the H matrix

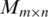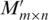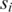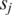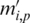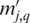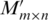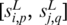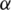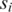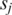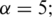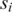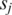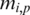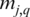(i) Initialize matrix and an auxiliary matrix to zero; for each pair of promoters and , add 1 to both elements and of if and only if is among the top such values across all the L-segment sequence alignments between and , where the default is and (ii) for each pair of promoters and , add 1 to both and of 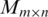if and only if

is among the top 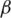such values across all the L-segment alignments between 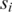and 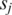, respectively, where the default is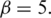

Intuitively, if 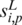and 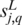are cis motifs of the same TF, the 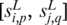value should generally be high. However, we found that sometimes the highest value is associated with one of the neighboring elements of p or q, so we use

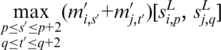instead of 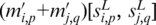to consolidate such cases and to enhance the motif signals. We now predict the motifs based on more global information through finding maximal cliques in the graph constructed below. It's worth noting that, during the pair-wise segment comparison mentioned above, the simple sequence segments, i.e. segments containing more than five consecutive A's or T's were ignored since generally they will not represent a real motif.

Step 2: Construction of graph G

For each pair of and 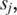solve the equation

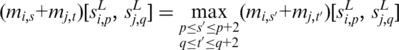for variables (s, t) under the constraint p ≤ s ≤ p + 2 and q ≤ t ≤ q + 2; if this maximum value is among the top 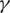across all combinations of positions p and q on 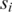and 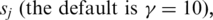then positions s and t on 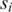and 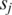are included as vertices and connected by an edge in G.

Note that the idea of finding conserved motifs through finding cliques or near cliques has been widely used in the existing motif-finding programs (22–23). However, the success has been limited mostly because of two reasons: (i) the graphs constructed for the clique-finding problem are generally quite noisy, often leading to high false positive predictions, and (ii) cliques or near cliques alone are not adequate to capture the majority of the motifs, hence leading high false negative predictions. We have addressed the issue (i) by using the above two-step procedure to ensure that our representing graph has a high motif signal-to-noise ratio; and we have addressed (ii) by decomposing the motif-finding problem into two steps: finding cliques in the representing graph and using them as the seeds of motif groups to find the ‘whole’ groups of motifs through expanding the cliques into motif closures.

Step 3: Clique finding in G

Find all disjoint maximal cliques in G using the following greedy approach: set C to be empty; choose an edge (u, v) in G with the largest with N_G(x) representing all the vertices incident to vertex x; add u and v to the current clique C; Repeat the above on the sub-graph induced by 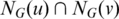until the subgraph is empty; remove the current clique from G, and repeat this step on the remaining graph for w times (the default is w = 10). Set L = L + 1 and go to Step 1 if L < 30; otherwise go to Step 4.

For a set C of motif candidates of L bp long, call their best gapless alignment as the profile of this motif set. Define a profile matrix 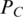of C as

where 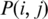is the probability of nucleotide type i appearing at position j in the alignment, and q(i) is the probability of i appearing in the background sequence. Define the match score between a candidate motif and a profile matrix as the sum of corresponding values of the matrix based on the specific nucleotide in each position of the motif, and 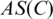the average (match) score over all the sequence segments in C. 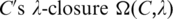is defined as the set of sequence segments in the input promoter sequences, whose match scores with C's profile matrix are at least 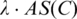(see Section 1 of Supplementary Data), where 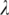is a parameter and its value is determined in Step 4. This closure definition generalizes our previous one given in Ref. (1).

We calculate the P-value 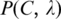of 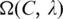as follows. Let x be a random variable denoting the number of sequence segments of length L from a set of m random nucleotide sequences, each of which has a match score with C's profile matrix at least 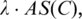p(x) be the probability distribution of x, and P(t) the accumulated probability of p(x) over x ≥ t. So 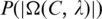represents the P-value of a motif 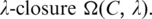While the exact calculation of 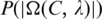is rather difficult due to the (non-independent) relationships among the sequence segments in 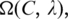our computational experiments suggest that the distribution of p(x) is very close to a Poisson distribution. So we can approximate p(x) as follows (1):

Hence the P-value of a motif 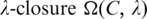can be approximated by simply summing up p(x) over 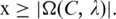The aforementioned random sequences can be generated through reshuffling the given promoter sequences. Now we can find all the desired motif groups by executing the following step.

Step 4: Expansion and evaluation

For each clique C identified in Step 3, calculate the P-value 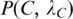of motif 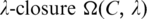after calculating the 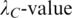from 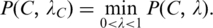Sort the motif closures in the increasing order of their P-values. Output the most significant o motif closures according to their P-values, with o being a parameter selected by the user.

RESULTS

We tested the performance of BOBRO against six existing tools on large-scale data sets, including both simulated and biological data sets, to demonstrate the advantage of our strategy. We first show the prediction results on one simulated data set to demonstrate the power of BOBRO in identifying multiple motifs simultaneously. To do so, we generated five synthetic sequence sets each containing 60 DNA sequences of length 300 bp, in which we implanted 305 motif sequences belonging to 24 hypothetic TFs. Table 1 summarizes the prediction results on this set of sequences (see Supplementary Table S1 for additional information). From the table, we can see that BOBRO outperforms the other six programs by a substantial margin.

Table 1.

Prediction performance of seven programs on sequences with multiple motifs

Program	Hypothetic TFs (24a)	Inserted motifs (305a)
	n (%)	n (%)
AlignACE	0 (0.00)	0 (0.00)
Bioprospector	10 (41.7)	83 (27.2)
CONSENSUS	7 (29.2)	74 (24.3)
MDscan	7 (29.2)	40 (13.1)
MEME	16 (66.7)	156 (51.1)
Weeder	4 (16.6)	27 (8.9)
BOBRO	22 (91.7)	201 (65.9)

^aThe numbers in brackets on the first row are the total numbers of hypothetic TFs and inserted motif segments in the whole data sets, respectively. Second and fourth columns represent the numbers of hypothetic TFs and inserted motif segments identified by the corresponding programs, respectively.

Prediction of cis-regulatory motifs in E. coli K12

We have carried out a number of large-scale predictions using BOBRO, all on the genome sequence of E. coli K12 MG1655. For each potential promoter sequence, we used the upstream region of 300-bp long from the annotated translation start site of each operon.

Identification of cis-regulatory motifs for co-regulated genes when the motif lengths are known

A common application of motif finding has been in detecting cis-regulatory motifs of a group of genes suspected to be transcriptionally co-regulated by the same TF, based on other information such as gene expression data. We extracted all the E. coli K12 TFs with at least five known cis motifs from RegulonDB (24) (see Supplementary Table S2). In these datasets, the number of promoter sequences targeted by these TFs varies from 5 to 153, and the number of known motifs ranges from 5 to 222. We ran BOBRO on these datasets, and predicted the optimum motif closure, i.e. a motif closure with the minimum P-value, as the candidate motif for each data set. The prediction results are shown in Table 2, from which we can see that BOBRO is able to identify most of the known motifs for the 37 data sets. For the purpose of comparison, we also run the other six prediction programs on these data sets. These tools were applied using the optimal parameter values based on the original papers of the tools or based on our experience of running these tools; and the best outputs by the six programs were recorded. Special care has to be taken for the Weeder program since it allows motif length ranging from 6 to 12 only, while some of the motifs are longer than 12 so we ran the program using all possible allowed motif lengths, and took the best output as the final prediction. We have used three widely used prediction criteria, sensitivity (SN), specificity (SP) and performance coefficient (PC), to assess the prediction performance: SN = |PM∩RM|/|RM|, SP = |PM∩RM|/|PM| and PC = |PM∩RM|/|RM⋃PM|, with RM representing the real motif set, and PM being the corresponding predicted motif segments set (10,22).

Table 2.

Prediction of BOBRO on E. coli K12 co-regulated promoter sequences

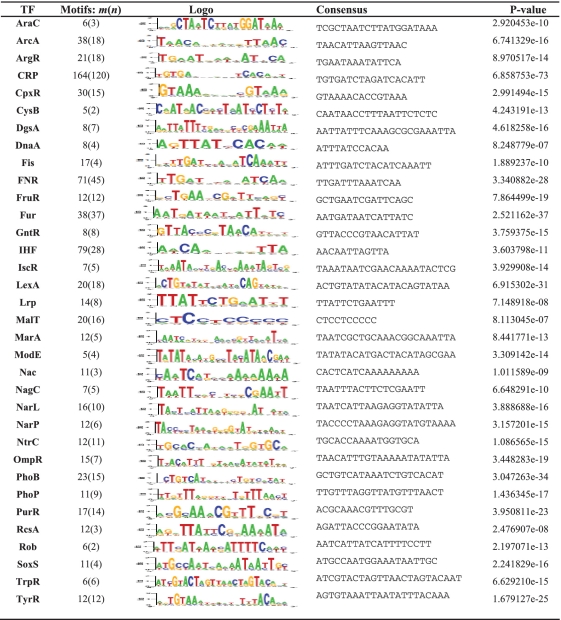BOBRO outputs 37 optimum motif closures. The names of corresponding TFs are listed in the first column of the table. In the second column, m is the number of all the predicted motifs in respective motif closure output by BOBRO, and, n the number of those in the corresponding closure that have been documented as TFBSs. The profile logos, consensus sequences, and P-values of these closures are presented in third, fourth, and fifth columns, respectively.

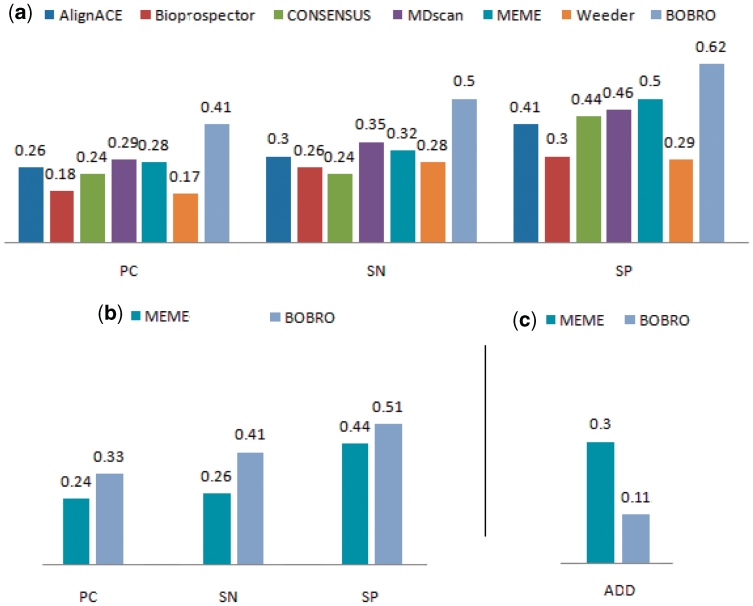
Figure 1a summarizes the prediction performance by the seven programs, with the detailed comparison results given in Supplementary Table S2. We can see from the figure that BOBRO consistently outperforms all the other six programs across all three measurements on average. It should be noted that this data set contains two TFs, H-NS and CytR, which were reported to bind to DNA in a non-sequence-specific manner (25–26). AlignACE, Weeder and BOBRO recovered four, 12 and 11 motif segments of H-Ns, respectively; and only BOBRO predicted two cis motifs of CytR with no predictions from the other programs. We have checked the sequence conservation of the identified motifs, and did find these two sets of motifs are slightly conserved in contrary to the previous report mentioned above.

Figure 1.

Comparison between BOBRO and six other programs on 37 co-regulated data sets from E. coli K12. The numbers shown in (a) and (b) are the average values of SN, SP and PC, respectively. (a) Performance comparison with motif length information. (b) Performance comparison without motif length information. (c) Comparisons of average deviation degrees (ADD) between predicted motif lengths by MEME and BOBRO.

Identification of cis-regulatory motifs for co-regulated genes without motif length information

Among the six prediction programs against which we are comparing, only MEME was designed to predict the motif length when attempting to identify a motif. So we compared the prediction performance only between MEME and BOBRO on the same 37 data sets used above. Figure 1b summarizes the comparison results between BOBRO and MEME (detailed comparisons given in Supplementary Tables S2 and S3), which shows that BOBRO outperforms MEME when no motif-length information is provided. To assess the accuracies of the predicted motif lengths, we define the degree of deviation (DD) of a predicted motif length from its actual length as the ratio of the (absolute) difference between the actual and the predicted lengths to the actual length. Figure 1c shows the average DDs for MEME and BOBRO on the set of motifs that both programs have identified, from which we can see that the predicted motif lengths by BOBRO are substantially more accurate than those by MEME that tends to over-predict the motif lengths (see Supplementary Table S3 for details). It is worth noting that BOBRO even performs consistently better with no motif-length information than the other six programs with motif-length information.

Identification of cis motifs across orthologous promoters

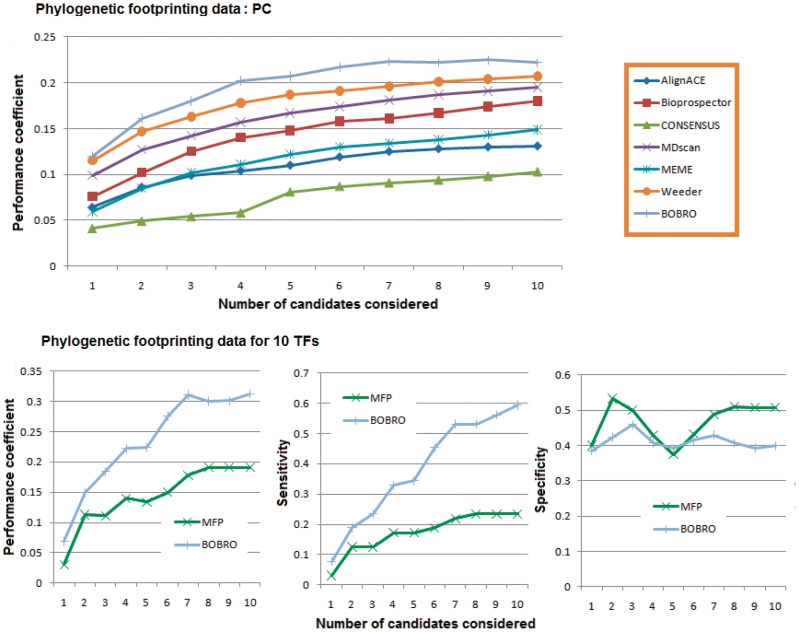
We have examined BOBRO's performance on a different type of data than the above, specifically orthologous promoters across multiple genomes in comparison with performances by the other six programs. Since there is no generally accepted benchmark set for this type of data, we generated a large collection of orthologous promoters derived from the promoters of 547 operons of E. coli K12, the minimal set of promoters containing all the 2026 known cis motifs provided in RegulonDB (details in Supplementary Data). For each of these E. coli promoters, we selected up to 12 orthologous promoter sequences from 675 complete bacterial genomes as follows: we searched for the orthologs of each (relevant) E. coli gene across the 675 bacterial genomes using the bidirectional best hit search (27), and collected their corresponding promoter regions. Twelve orthologous promoters were selected from this set after removing the promoters that are either too close or too far from the query promoter based on the sequence similarity provided by ClustalW (28), which gives rise to 547 phylogenetic foot-printing datasets. We then ran BOBRO and the other six programs on each set of orthologous promoters. Considering that an operon may be regulated by multiple TFs, we generated up to 10 different motif candidates for each set by each of the seven programs. We then compared the performance by the seven programs averaged over all the 547 data sets when considering 1 up to 10 candidate motifs for each set. When assessing the performance of a prediction, we consider a motif is predicted correctly if its sequence was covered at least 50% by one of the top k motif candidates by a prediction program, for k = 1, …, 10. The prediction performance by the seven programs is shown in Figure 2 and Supplementary Figure S1. Again BOBRO has the best performance compared to other six tools. An interesting observation is that the performance of motif finding tools on the co-regulated data and phylogenetic foot-printing data (promoters from different genomes) are quite different. For example, Weeder and Bioprospector have worse performance on the co-regulated data compared to the other tools, but obtained better results on the phylogenetic foot-printing data. BOBRO performs consistently well on both types of data.

Figure 2.

Comparison between BOBRO and other programs on orthologous promoters across multiple genomes. The top panel shows the PCs of prediction results by the seven programs on 547 E. coli promoters. The lower panels are PC, SN and SP of prediction results by BOBRO and MicroFootprinter on promoters of 10 E. coli TFs.

Considering that all the six tools used for comparison are mostly designed for co-regulated data, we further compared BOBRO with MicroFootprinter (3), which was specifically designed for motif finding on phylogenetic foot-printing data. Since the program has only a server version, we used a small set for comparison, which contains 10 TFs that regulate the most numbers of operons of E. coli, namely, CRP, Fur, FNR, IHF, Fis, Lrp, CpxR, ArcA, NarL and H-NS. Together they have 64 known binding motifs covered by RegulonDB. For these 10 data sets, we collected the prediction results of MicroFootprinter from its server and compared with those obtained by BOBRO (see the lower panels of Figure 2). From the figure, we can see that BOBRO has a performance coefficient substantially higher than that of MicroFootprinter although its specificity is lower. Note that unlike MicroFootprinter, BOBRO uses sequence information only. We believe that the performance of BOBRO could get further improved if phylogenetic foot-printing information is used like in MicroFootprinter.

Identification of motifs for global TFs at genome scale

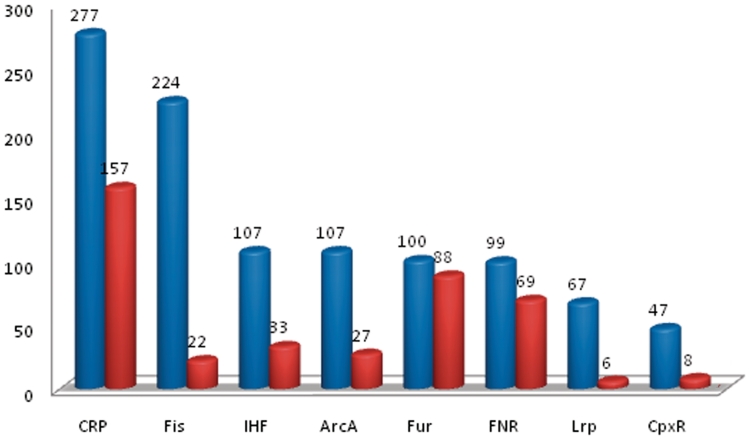
To illustrate where we are in terms of motif prediction at a large-scale, we have run the seven prediction programs on the whole genome of E. coli K12 to check how these programs can do in terms of finding the cis-regulatory motifs of the 10 largest regulons, each containing at least 25 operons, namely CRP, Fur, FNR, IHF, Fis, Lrp, CpxR, ArcA, NarL and H-NS (see Supplementary Figure S2). To carry out this prediction, we extracted 2390 promoter sequences of E. coli K12 based on the predicted operons (32–33). We ran BOBRO on these sequences, and compared the overlaps between our predictions and the known cis regulatory motifs of these regulons, where we considered only those motifs with lengths ranging from 10 to 18 bp, based on our knowledge about the motifs of these global regulons. BOBRO found motifs for 8 out of the 10 global regulons and did not find any cis motifs of NarL and H-NS. Figure 3 summarizes the key results in terms of the level of overlap between our predicted motifs and known motifs of these eight regulons. Among the 277 known motifs of the CRP regulon, our 22 top motif closures contain 157 of the 227 motifs, represented as (277, 157, 22). Similarly, we have (224, 22, 2) for Fis, (107, 33, 3) for IHF, (107, 27, 3) for ArcA, (100, 88, 10) for Fur, (99, 69, 11) for FNR and (67, 6, 1) for Lrp, (47, 8, 1) for CpxR. The detailed prediction data is given in Supplementary Figure S2 and Supplementary Table S4. For the other six prediction programs, none of them were successful in making any prediction on this large dataset. While we recognize that there is clearly a long way to go to have highly accurate identification of all the cis motifs encoded in E. coli, we believe that our study represents the first systematic effort in prediction of cis regulatory motifs of the global regulons of E. coli.

Figure 3.

Comparisons between documented and predicted cis motifs for the eight TFs. Each blue bar represents the total number of documented motifs of the corresponding regulon, and the red bar represents the correctly predicted motifs for the corresponding regulon.

Interestingly, we noted that some of our predicted conserved motifs may represent some other classes of functional elements rather than cis-regulatory motifs, such as non-coding RNAs and terminal signals of transposable elements. For example, two of our predicted motif closures have consensus sequence ‘CTTATCCGGCCTACAAA’ and ‘TGCCGGATGCGGCGTGA’, respectively, which were not included in RegulonDB. These two patterns are from the same group of sequences of 35-bp long (see Supplementary Table S5 in the supplementary). They are documented as repeat elements (REP) in the E. coli K12 genome with unknown function (http://www.ecosal.org/), and match non-coding RNAs of Mus musculus in the non-coding RNA database (http://biobases.ibch.poznan.pl/ncRNA/).

DISCUSSION

Compared to the existing popular motif-prediction programs, BOBRO has a number of unique features outlined as follows. (i) The initial selection of the (approximate) starting positions of candidate motifs led to a small set of motif candidates with high concentration and high coverage of the to-be-identified motifs, substantially reducing the difficulty in picking out true motifs from the initial candidate list. (ii) The introduction of motif closures provides a natural way to recognize actual motif length and motif itself from even those with weak sequence conservations, and to improve both prediction sensitivity and specificity. (iii) BOBRO is able to identify multiple cis-regulatory motifs embedded in same promoters if any. (iv) It is also able to output several distinct conserved motifs simultaneously while previous tools typically deal with this issue by modifying the input promoter sequences before attempting to find additional motifs after the initial motifs were predicted. BOBRO dealt with this issue by identifying those significant cliques based on the P-value of their corresponding motif closures without making any changes on the input sequences. (v) BOBRO has both a low computational complexity at O(m²n²) + O(tmn), where m is the number of input sequences, n is sequence length, and t is the number of simulations for calculation of the P-values of motif closures, and a short computing time. Note that BOBRO's running time is independent of the to-be-identified motif length. The comparison between BOBRO and other six tools about the running time against data size and motif length indicates that BOBRO has running time comparable to others (Appendix 7 in Supplementary Data). For example, BOBRO can run through the whole set of E. coli K12 of 2390 promoters, each with 300 bp and find conserved motifs within one day of wall-clock time on a typical desk-top single-processor PC station.

Among all the unique features outlined above, we believe that (i) and (ii) are the most fundamental reasons for the substantially improved performance in motif finding by BOBRO.

CONCLUSION

We presented a new algorithm BOBRO for prediction of cis-regulatory motifs for prokaryotic genomes, which improves the state-of-the-art in motif-finding as we have shown in this article. Our performance analyses of BOBRO versus other programs suggest that the program is capable of making reliable predictions of cis-regulatory motif predictions at a genome scale. Our analysis results also suggest a few directions for further improvement of the program. For example, we will consider (i) designing better strategies to approximate the H matrix; (ii) including additional information related to features of cis-regulatory motifs such as that certain motifs, particularly less conserved motifs, tend to form palindromes, into the prediction program; and (iii) improving the usage of phylogenetic information in a similar fashion to that introduced by McGuire et al. (14), to make our program more generally applicable for large-scale applications.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation (#NSF/ITR-IIS-0407204, #NSF/DBI-0542119); U.S. Department of Energy's BioEnergy Science Center (BESC) grant through the Office of Biological and Environmental Research; 61070095, 60873207 and 10631070 from National Science Foundation of China and the Taishan Scholar Fund from Shandong Province of China to G.J.L. Funding for open access charge: National Science Foundation (#NSF/ITR-IIS-0407204, #NSF/DBI-0542119); U.S. Department of Energy's BioEnergy Science Center (BESC) grant through the Office of Biological and Environmental Research.

Conflict of interest statement. None declared.