Interpreting protein/DNA interactions: distinguishing specific from non-specific and electrostatic from non-electrostatic components

Abstract

We discuss the effectiveness of existing methods for understanding the forces driving the formation of specific protein–DNA complexes. Theoretical approaches using the Poisson–Boltzmann (PB) equation to analyse interactions between these highly charged macromolecules to form known structures are contrasted with an empirical approach that analyses the effects of salt on the stability of these complexes and assumes that release of counter-ions associated with the free DNA plays the dominant role in their formation. According to this counter-ion condensation (CC) concept, the salt-dependent part of the Gibbs energy of binding, which is defined as the electrostatic component, is fully entropic and its dependence on the salt concentration represents the number of ionic contacts present in the complex. It is shown that although this electrostatic component provides the majority of the Gibbs energy of complex formation and does not depend on the DNA sequence, the salt-independent part of the Gibbs energy—usually regarded as non-electrostatic—is sequence specific. The CC approach thus has considerable practical value for studying protein/DNA complexes, while practical applications of PB analysis have yet to demonstrate their merit.

INTRODUCTION

The description of macromolecular interactions in terms of the binding constant and Gibbs energy of binding is widely used in considering protein–protein and protein–DNA complexes. However, it is far from sufficient for elucidating the nature of the physical forces acting between the partners, in particular for understanding the basis of highly tuned, i.e. specific, protein–DNA recognition, the issue of prime interest. Separation of the Gibbs energy into its enthalpic and entropic components was a key development that has not involved any substantial uncertainties, since it was based on direct calorimetric measurements of the enthalpies. However, separation of the overall binding energy into its electrostatic and non-electrostatic components remained an essential further step for describing the interactions between such highly charged macromolecules as DNA and the DNA-binding domains (DBDs) of proteins for which ionic contacts play a major role. This led to the practical issue of how the electrostatic and non-electrostatic contributions to the enthalpic and entropic components of the Gibbs energy of binding might be separately determined, so as to obtain an understanding of which forces are responsible for the affinity and, in particular, for the specificity of protein binding to DNA.

One approach, initially proposed by Manning (1,2) and implemented into the practice of studying protein–DNA complexes by Record and colleagues (3–7), assumes that the electrostatic component of the binding energy results solely from the cratic entropy of mixing the displaced DNA counter-ions with ions in bulk solution. According to this counter-ion condensation (CC) concept, the electrostatic component of the binding can be determined directly from the salt dependence of the association constant, as described by the linear equation:

(1)

where the first term accounts for the non-electrostatic interactions, the second represents the salt dependent electrostatic interactions and N is the total number of counter-ions released from the DNA on forming the complex. N is written as Zψ, where Z is the number of DNA phosphate groups that interact with protein/peptide and ψ is the number of cations associated with a phosphate group that are displaced on complex formation. Since at 1 M concentration of salt the second term drops to zero, analysing the salt dependence of the association constant leads to an extrapolated value for the non-electrostatic component of binding and, by difference from the total Gibbs energy, the electrostatic component. This concept, therefore, fully defines the electrostatic and non-electrostatic components of the binding energy and suggests an experimental procedure for their evaluation. An advantage is that from the slope of this logarithmic dependence one can estimate the total number of counter-ions released on forming the complex and thereby estimate the number of contacts between the partners forming the complex.

However, this approach has been criticized as too simplified (8–10) and indeed it was difficult to believe that the DNA counter-ions are tightly held by the DNA phosphates rather than distributed in accordance with the Poisson–Boltzmann (PB) equation for polyelectrolytes. It was supposed that by analysing the known structures of protein–DNA complexes using the non-linear PB equation one could determine all the forces responsible for their formation. However, a serious obstacle to such an analysis is the dielectric constant used in the PB equation, a quantity of uncertain meaning in a heterogeneous system such as a protein–DNA interface sitting in an aqueous environment. Nevertheless, postulating values for the dielectric constant of water at the interface, this analysis led to estimates of these forces in terms of the ion–molecule, the ion–ion and entropic ion release contributions to the free energy (8). According to this analysis, the first two free energy terms both have enthalpic and entropic components, while the third term is a purely cratic entropy. A practical problem of this approach, however, is that it does not lead to a clear procedure for the experimental evaluation of each of these terms, which is essential both for its verification and for the practical characterization of protein–DNA complexes. As an example of the PB analysis: in the DNA binding of the λcI repressor, it was calculated that the electrostatic interactions together oppose the association by about +300 kJ/mol of free energy and it is the hydrophobic effect of burying interfacial surface area, amounting to −630 kJ/mol, that principally drives the binding, although partly compensated by a number of other smaller interactions (10). Overall, the general conclusion of that work was that protein/DNA association is driven by the non-polar interactions, whereas specificity results from the electrostatic interactions that weaken binding. But how can one check the reliability of these estimates and of the general conclusions drawn?

The CC approach to protein–DNA interactions, which proposes a split into salt-dependent (electrostatic) and salt-independent (non-electrostatic) components, certainly poses questions that need to be answered in order to decide if it effectively describes the energetic basis of forming such complexes:

1. Is the salt dependency of the binding constant indeed linear on the logarithmic scale and does the slope really represent the number of released counter-ions?

2. What is the meaning of log(K^a) at 1 M salt concentration where the second term in Equation (1) drops to zero?

3. Is the electrostatic component of the binding energy indeed purely entropic?

4. What does the non-electrostatic component of binding energy represent?

These key questions are answered in this article by analysing published experimental studies of the formation of a substantial number of specific protein–DNA complexes of different types, using only structures known to atomic resolution.

• (i)Are plots of log(K^a) against log[Salt] linear and does the slope of this dependence represent how many counter-ions are released?

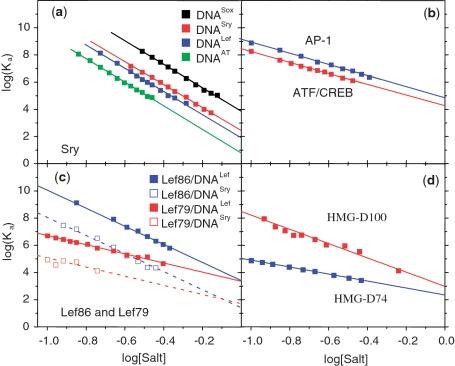
Figure 1 presents the logarithmic salt dependencies of the binding constants of several DBDs: three HMG boxes (and their modified forms) and a bZIP dimer binding to their target DNA duplexes (11,12). Over the range of salt concentrations (KCl) permitting the binding constant to be measured with accuracy (typically down to K^a values of ∼10 µM by monitoring the fluorescence anisotropy of labelled DNA), good linearity is observed, even up to 0.75 M KCl in the case of SRY binding to DNA^Sox (Figure 1a). Figure 2 presents similar data for two other major groove binders, the homeodomains from Engrailed and Antennapedia, the latter in two forms: with and without its N-terminal tail that binds in the minor groove, while the DNA recognition helix of the main fold of these DBDs enters into the major groove (13).

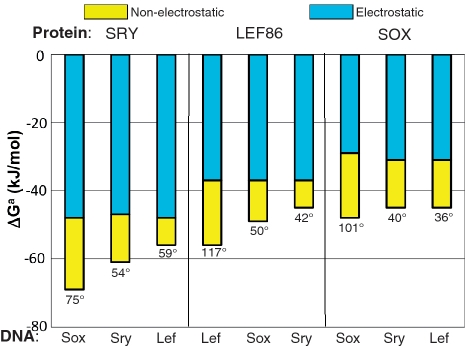
Figure 1.

The salt dependence of binding constants, K^a, (salt plots). (a) The SS HMG box from hSRY binding to its optimal target DNA (DNA^Sox) and to three other duplexes of lower affinity, one containing just a central –ATAT– sequence (DNA^AT). (b) The bZIP homodimer from yeast GCN4 binding to the AP1 (–ATGACTCAT–) and ATF/CREB (–ATGACGTCAT–) target sequences. (c) The HMG box from mLEF-1 (Lef86) and its truncated form lacking the basic C-terminal tail (Lef79) binding to DNA^Lef (–TTCAAA–) the optimal target and to DNA^Sry (–CACAAA–) a sub-optimal sequence. (d) The NSS HMG box from Drosophila HMG-D (D-100) and its truncated form (D74) lacking the basic C-terminal tail binding to DNA^Lef. Data taken from Refs (11,12,17).

Figure 2.

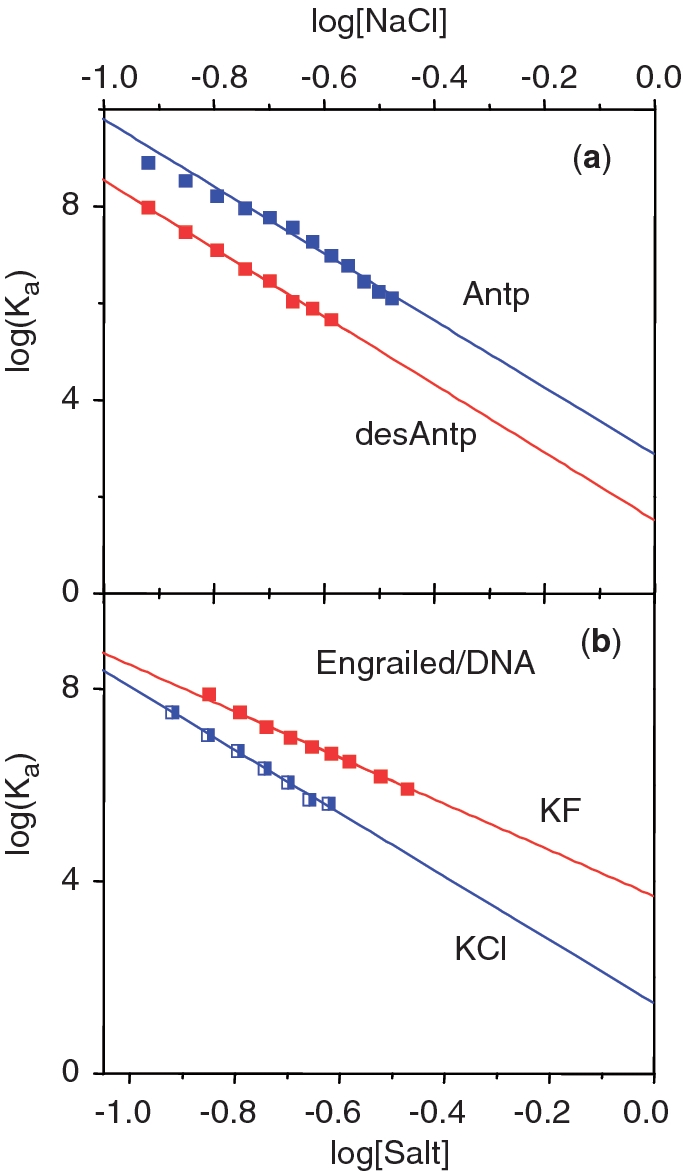
(a) Salt plots for Drosophila Antennapedia (Antp) and its truncated form (desAntp) lacking the N-terminal tail (–RKRGRQ–) that binds in the minor groove. Identical slopes indicate that the same number of counterions are displaced, i.e. the N-tail does not make electrostatic contacts with the DNA (as seen in the structure of the complex). (b) Two salt plots for the Engrailed homeodomain binding to its target DNA sequence, one using KCl (blue), the other using KF (red). The reduced slope using fluoride shows that fewer counterions are displaced than in chloride solution. Data taken from Ref. (13).

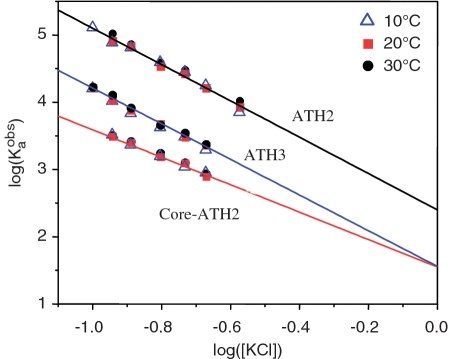
Another striking example is the DNA binding of AT-hooks (ATH), very short unfolded peptides interacting with AT-rich DNA. ATH3, the third AT-hook of the HMGA1 transcription factor, consists of a central arginine–glycine–arginine tripeptide flanked at both ends by proline residues and by pairs of positively charged residues (−PGRKPRGRPKK−): this enters into the minor groove of DNA at the PRDII site of the human β-interferon enhancer without inducing distortion (14). The core region of the closely related second AT-hook of HMGA1 (CoreATH2) is almost identical to ATH3 but contains one less basic residue since the final lysine is replaced by glycine (−PKRPRGRPKG−): this is followed in the experimental peptide ATH2 by a seven-residue extension (−SKNKGAA−) that binds across the sugar–phosphate backbone (14). As shown in Figure 3, the logarithmic salt dependencies of the binding constants of ATH3, ATH2 and CoreATH2 are perfectly linear (15). Thus three very different types of DNA-binding proteins show a linear dependence between the logarithm of the binding constant and the logarithm of salt concentration.

Figure 3.

Salt titrations for the NSS ATH from hHMGA1 binding to an AT-rich target duplex. ATH3 is the 11-residue third hook and CoreATH2 is the closely related 10-residue second hook, whilst ATH2 is an extended form of CoreATH2 having seven additional C-terminal residues. Binding constants were obtained at three temperatures, 10, 20 and 30°C. Data taken from Ref. (15).

According to the CC concept, the slope of the plots of Equation (1) represents the number, N, of condensed counter-ions (cations) released from the DNA on binding protein and this is assumed proportional to the number of ionic contacts made. As seen in Figure 3, the slopes of ATH2 and ATH3 are almost identical, showing that they both make four ionic contacts with phosphates, while the slope of Core-ATH2 is smaller, corresponding to three contacts, due to exchange of the C-terminal lysine for glycine. These numbers of contacts accord with the structural studies (14) and it follows that the extension in ATH2 makes an additional contact above the three of CoreATH2 using one of the lysine residues in the extension. Extrapolation of the logarithmic salt dependencies of the binding constants of ATH3, ATH2 and CoreATH2 to 1 M salt shows that for ATH3 and Core-ATH2 these functions focus at the same point (as expected from their closely related sequences) corresponding to their non-electrostatic Gibbs energies of −8.5 kJ/mol. However, for ATH2 the extrapolation gives a value of −12 kJ/mol, showing that its seven-residue extension contributes a further −3.5 kJ/mol to the non-electrostatic component of the binding free energy.

A similar situation is seen in the case of Antp and its truncated form, desAntp, lacking the N-terminal tail that binds in the minor groove. These two proteins exhibit the same slopes (Figure 2a), i.e. make the same number of ionic contacts. It follows that the N-terminal tail (−RKRGRQ−) makes no electrostatic contacts at all and the increased values of log(K^a) for Antp relative to desAntp (corresponding to the Gibbs energy of binding the tail) is entirely non-electrostatic—despite it containing four basic amino acids, two of which are highly conserved. This implies that the binding of short polypeptide chains containing Arg/Lys residues inside the minor groove (a common binding motif) can hardly be the consequence of an unusual electrostatic field generated by a narrowed minor groove, as recently proposed (16). It appears that the key contribution in placing Lys and Arg residues in the minor groove is played by the apolar part of their long side chains. A similar situation is found for AT-hooks in the minor groove: the atomic structure shows that the RGR triplet forms tight apolar contacts with bases deep in the AT-rich minor groove (14).

Figures 1a compares the binding of a given DBD, SRY, to different DNA sequences: to its optimal target sequence (DNA^Sox), to sub-optimal sequences and to an AT-sequence of even lower affinity. It is seen that the slopes are all the same, i.e. the same number of ionic contacts are made in the different complexes. This is also true for the binding of the bZIP dimer of GCN4 to two targets that differ in length by 1 bp (Figure 1b), and for the HMG boxes from mLEF-1 (Lef86 and Lef79) binding to DNA^Lef and to DNA^Sry (Figure 1c). In the last case, the affinity of Lef86 for DNA^Sry is two orders of magnitude less than for DNA^Lef (the optimal sequence): nevertheless, the ionic contacts (i.e. the slopes) remain unchanged. When, however, the binding of Lef86 is compared with that of the truncated Lef79 using the same target DNA (either DNA^Lef or DNA^Sry), the slope is reduced substantially due to loss of multiple ionic contacts in the C-terminal tail that are not present in Lef79. Figure 1d shows equivalent data for the non-sequence-specific (NSS) HMG box HMG-D100: removal of its long C-terminal tail to give D74 lowers the affinity in 0.1 M KCl by more than three orders, with a reduction in the slope of the salt plot from 5.8 to 2.5 (17).

Since the slopes of the salt plots give the number of displaced counter-ions, i.e. represent the number of electrostatic contacts made to the DNA, comparison of a parent HMG box with its tailless product yields the number of contacts made by the tail. For example: for the parent Lef86, the slope N = 6.8, i.e. Z ∼ 10, while for the tailless Lef79, Z is found to be ∼5, so the tail makes five ionic contacts with the DNA. This number is of interest since although the structure of the Lef/DNA complex gives details of the ionic contacts made by the globular part (Lef79), it gives only incomplete information on the conformation of the C-terminal tail. In the case of HMG-D100, the globular domain (D74) and the tail are both observed to make four ionic contacts: the figure for the tail is striking bearing in mind that its 26 residues include a total of 10 Lys/Arg residues. A better description of the DNA binding of the C-terminal tail of HMG-D100 would, therefore, be that it makes a total of four net contacts with phosphate groups (17,18). In the case of specific and non-specific DNA binding of the lac repressor (19), the atomic structures show that the non-specific complex has lost base-specific contacts and gained phosphate contacts: the higher number of electrostatic contacts in the non-specific complex is reflected in the slope of the salt plot that corresponds to 11 ionic contacts per monomer, in contrast to the specific complex that gives a slope corresponding to only six contacts (20).

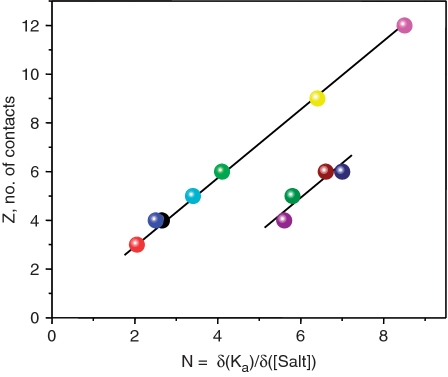
Table 1 gives values obtained for the slopes, N, of the salt plots and the numbers of ionic contacts to DNA phosphate groups, Z, observed in the atomic structures of the DNA complexes. The plot of these data in Figure 4 shows that seven cases (four HMG boxes, the bZIP dimer and two AT-hooks) exhibit a linear relationship that goes through the origin, demonstrating that the slopes (N values) are proportional to the number of electrostatic contacts made to the phosphates. The inverse slope, N/Z = ψ, equals 0.70, a value close to 0.64, that derived earlier for short duplexes (21). In contrast, the data for the four homeodomains fall close to a parallel line shifted horizontally by about 2.5 ions, i.e. 2.5 more ions are displaced than expected from the number of phosphate contacts made, a difference deriving from release of tightly bound chloride ions from the homeodomains. Figure 2(b) shows that salt titrations of the Engrailed homeodomain using KCl (NaCl acts identically) exhibit a slope N = 6.6, the value plotted in Figure 4, but when NaF is used for dissociation, the slope N is 4.5, which if ψ = 0.70, corresponds to 6 phosphate contacts, the number observed in the Engrailed/DNA complex. Since the difference between KCl/NaCl and NaF is in the anion, it follows that about two tightly bound chloride ions are lost from the Engrailed DBD when it binds to DNA. In agreement with this explanation, it was also observed (13) that chloride ions stabilise the free homeodomains, relative to fluoride, so it is to be expected that their affinities for DNA are higher in fluoride than in chloride, as seen in Figure 2(b). This additional anion loss can be formally taken into account by writing the slope of Equation 1 as: N = (Zψ + β), where β is the number of anions displaced.

Table 1.

Data for experimental values of the slope, N, of salt plots for protein/DNA complexes and the number, Z, and identity of ionic contacts reported by the authors of their atomic resolution structures determined by NMR or X-ray crystallography

Protein-DNA Complex	Slope of salt plot, N, (Ref)	No. of ionic contacts, Z	Identity of contacting residues	(Ref): PDB file
CoreATH2	−2.1 (15)	3	K7,R8,K14	(14): 2EZD
ATH3	−2.6 (15)	4	R33,K34,K41,K40	(14): 2EZF
D74	−2.5 (17)	4	R7,K24,K60,K37/R44	(34): 1QRV
LEF79	−3.4 (12)	5	K3,K14,R17,K27,R59	(35): 2LEF
GCN4	−4.1 (11)	6	R232,R234,R240,R241,R243,R245	(36): 2DGC
NHP6A	−6.4 (12)	9	K16,K22,R36,R40,K53K60,K67,K78,K85	(37): 1LWA
SRY	−8.5 (12)	12	R4,R6,R17,R21,R31,K37,K44,K51,R66,K73,K79,K81	(38): 1J47
desNK2	−5.5 (13)	4	R31,K46,R53,K55	(39): 1NK3
MATα2	−5.8 (13)	5	K46,R53,R54,K55,K57	(40): 1APL
desANTP	−7.0 (13)	6	R28,R31,R43,R52,R53,K55	(42): 9ANT
Engrailed	−6.6 (13)	6	R31,K46,R53,K55,K57,K58	(41): 3HDD

Figure 4.

The slopes, N, of the salt plots for several protein/DNA complexes (x-axis) graphed against the number of contacts, Z, between DNA phosphates and Lys/Arg residues (y-axis) reported by the authors who determined the atomic resolution structures of the complexes using X-ray or NMR methods. On the main line that goes through the origin the 7 complexes are: CoreATH2 (red), ATH3 (black), Drosophila D74 (dark blue), Lef79 (light blue), GCN4 (green), NHP (yellow), SRY (pink). The 4 homeodomains, desNK2 (purple), MATα2 (green), Engrailed (dark red), desAntp (blue) lie on a parallel line displaced by ∼2.5 ions along the x-axis. All thermodynamic data obtained in 100 mM KCl.

Release of anions specifically bound to these homeodomains upon association with DNA is not an exception and has been documented experimentally in the formation of several protein/DNA complexes (22–24). As the specific binding of certain ions to DBDs (often rather flexible domains) can significantly change their structure and thus their ability to interact with DNA, it is always necessary to test if the salt affects the state of the free protein in the absence of DNA. It follows that in cases where titration of different salts into protein–DNA complexes results in different slopes [e.g. IHF in Ref. (24)], the minimal slope must be associated with the lowest level of anion binding to the protein component.

• (ii)What is the meaning of log(K^a) at 1 M salt concentration where the second term in Equation (1) drops to zero?

Since salt addition leads to redistribution of the ionic interactions, the salt-dependent part of the binding energy can be considered as its electrostatic component. The straightforward interpretation of Equation (1) is that all electrostatic interactions drop to zero at 1 M salt concentration and so the value of K^a at this point represents the association constant resulting from only non-electrostatic forces—leading to the corresponding non-electrostatic Gibbs free energy (ΔG_nel). Loss of the electrostatic contribution at precisely 1 M salt concentration seems somewhat arbitrary but in fact simply reflects taking 1 M salt as the standard condition from which the electrostatic component of the binding energy is counted. The salt-independent part of the binding free energy, which is determined by excluding the electrostatic component from the total binding energy, can be regarded as the non-electrostatic component. Labelling the salt-independent part of the binding free energy as entirely non-electrostatic could be thought not entirely appropriate because it would include the Coulombic electrostatic effects that are independent of the salt concentration. However, the main contributions to the non-electrostatic component come from dehydration effects, van der Waals interactions and hydrogen bonding, which are typically regarded as non-electrostatic. In fact, van der Waals interactions and hydrogen bonding are also of electrostatic origin but they are not affected by changing salt concentrations: thus it is somewhat a matter of semantics to call their collective contribution non-electrostatic, bearing in mind that none of them can be separately measured.

The advantage of defining the electrostatic and non-electrostatic binding energies as the salt-dependent and salt-independent components, respectively, becomes clear on comparing the DNA binding of DBDs having N- or C-terminal tails that bind independently of the main globular domain, e.g. by comparing Lef86 with its truncated form Lef79 and using two different DNA targets, DNA^Lef and DNA^Sry (Figure 1c). Using DNA^Lef, the salt plots for Lef86 and Lef79 converge to a value of log(K^a) = 3.4 in 1 M KCl and using DNA^Sry they converge to log(K^a) = 1.5. Lef86 and Lef79 are equivalent in their non-electrostatic interactions with DNA, though not in their electrostatic contacts, so the point at which the two plots converge must be that at which all electrostatic interactions have dropped to zero—seen here to be in 1 M KCl. The same is true for the Drosophila NSS HMG box D100 and its truncated form, D74, lacking the basic C-terminal tail, which also become equivalent at close to 1 M KCl, (Figure 1d).

• (iii)Is the electrostatic component of the binding energy indeed purely entropic?

This question can also be framed in another way: is there no enthalpic component to the electrostatic part of the binding energy, i.e. are binding enthalpies totally non-electrostatic? If this is the case, the logarithmic salt dependencies of the binding constants should not depend on temperature. This is just what is observed for the AT-hooks: the salt titration of these peptides was carried out at three temperatures, 10, 20 and 30°C and it was observed that for a given peptide (ATH3, ATH2 or CoreATH2) all three titrations overlapped (Figure 3).

A further example studied in detail was the binding of the bZIP fragment from yeast GCN4 to its target ATF/CREB recognition sequence, over the temperature range from 5 to 40°C (11). Table 2 gives the variation of the total Gibbs energy of binding and its non-electrostatic and electrostatic components, separated using Equation (1). It is striking that while the non-electrostatic component of the Gibbs energy becomes substantially more negative with temperature rise, the electrostatic component shows no dependence on temperature at all. This is to be expected if the electrostatic component is purely entropic and its enthalpy is close to zero.

Table 2.

Binding of the homodimeric bZIP fragment from yGCN4 to the ATF/CREB recognition sequence in 100 mM NaCl, 30 mM Na–phosphate, pH 7.4, according to (11)

Temperature °C	ΔGa kJ/mol	ΔGanel kJ/mol	ΔGael kJ/mol
5	−42.6	−19.5	−23.1
10	−44.1	−21.0	−23.1
15	−45.5	−22.4	−23.1
20	−46.5	−23.4	−23.1
25	−47.9	−24.8	−23.1
30	−49.0	−25.9	−23.1
35	−50.0	−26.9	−23.1
40	−51.0	−27.9	−23.1

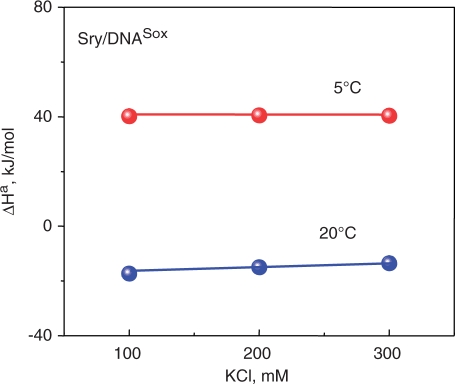
Direct calorimetric measurements of the binding enthalpies of forming a protein–DNA complex also show constancy over a substantial range of salt concentration. For example, the enthalpy of binding the SRY HMG box to its optimal DNA target sequence, DNA^Sox, was measured by ITC at 100, 200 and 300 mM KCl, a range of salt concentrations over which the binding constant drops by four orders of magnitude (Figure 1a) (12). Nevertheless, after correction for protein refolding, the binding enthalpy was found to be essentially invariant at about −20 kJ/mol at 20°C and +40 kJ/mol at 5°C (Figure 5).

Figure 5.

(a) Enthalpies of binding the SS HMG box from hSRY to its optimal target sequence, (DNA^Sox), measured by ITC in 100, 200 and 300 mM KCl at two temperatures, 5 and 20°C. Data taken from Ref. (12).

It should be noted that many DNA-binding proteins are partly unfolded when free in solution but refold upon association with DNA: ITC-measured enthalpies of binding must therefore be corrected for protein refolding (25). Furthermore, DNA-binding proteins when free may interact specifically with certain anions and this might result in changes of their state. If these anions are removed on binding to DNA, the enthalpy of DNA binding might show a dependency on the salt concentration, as seen in Ref. (24), but this salt dependence cannot be taken as indicating that the electrostatic contribution from phosphate contacts to basic amino acids is not fully entropic.

• (iv)What does the non-electrostatic component of the binding energy represent?

The several salt plots in Figure 1 make it clear that whereas the electrostatic component of binding (the slope) is independent of the DNA target sequence (optimal or sub-optimal), the non-electrostatic component, ΔG^nel, given by the extrapolated value of the association constants in 1 M KCl, log(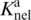), varies considerably. For example, K^a for SRY binding to DNA^AT and DNA^Sox differs by three orders of magnitude, (Figure 1a), and Lef86 binding to DNA^Lef and DNA^Sry differs by two orders of magnitude (Figure 1c): these differences can be assigned to the non-electrostatic components of binding.

Consideration of the Gibbs energies of sequence-specific (SS) HMG box binding to DNA makes it particularly clear that ΔG^nel is indeed the component that defines the specificity. Figure 6 displays the electrostatic and non-electrostatic components of the Gibbs energies of three SS HMG boxes, each binding to three different DNA sequences. The first striking fact is the extent to which the non-specific electrostatic component (in blue) dominates the total affinity, ∼70% for SRY binding to its optimal target, DNA^Sox. Despite the large magnitude and the constancy of the electrostatic component for a given HMG box over a wide range of bend angles, (from 42° to 117° for Lef86), there is considerable variation in the total Gibbs energy and it is the non-electrostatic component (in yellow) that accounts for this variation in affinity and bend angle as the DNA sequence changes from the optimal to sub-optimal. These experimental results are thus in sharp contrast with theoretical expectations that specificity results from electrostatic interactions, a contribution said to weaken binding (10).

Figure 6.

Gibbs free energies of binding SS HMG boxes to their optimal and sub-optimal DNA sequences, separated into their electrostatic and non-electrostatic components using Equation (1). The protein-induced bend angles are given below the bars. Although the electrostatic component dominates the affinity in all cases, the more tightly a given HMG box binds (the more negative the total Gibbs energy), the greater is the non-electrostatic component and the larger the bend angle. As regards the relationship to the bend angle, see also (32). The DNA sequences DNA^Lef, DNA^Sry and DNA^Sox are those previously considered optimal for binding the three HMG boxes, though SRY protein binds better to DNA^Sox. Data taken from (12).

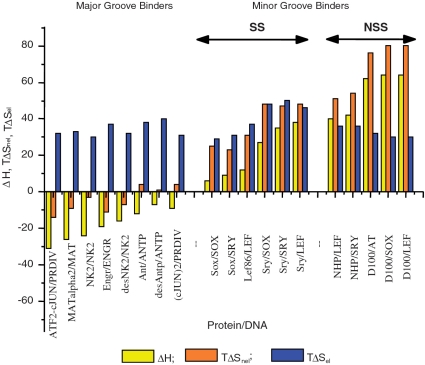
As follows from the above, the electrostatic component of the Gibbs energy of binding is totally entropic, while the salt-independent non-electrostatic component can have both entropic and enthalpic contributions. It is of particular interest, therefore, to define the degree to which the entropy of binding is non-electrostatic or electrostatic and what relationship that has with the non-electrostatic enthalpy of binding. Figure 7 compares experimental data for typical SS and NSS binders to the minor and major grooves of cognate DNAs. It shows that binding to the major groove is driven by a negative enthalpy and positive entropy, the latter mostly of electrostatic origin, i.e. both the enthalpy and entropy favour binding. In contrast, binding to the minor groove proceeds with positive enthalpy and even more positive entropy, i.e. it is completely entropy driven. It is particularly intriguing that, in contrast to the major groove, for the minor groove the driving entropy has a very large non-electrostatic component: this can arise only from dehydration. As previously discussed (26), the large positive entropy and enthalpy of binding to the minor groove might result from removal of the highly ordered stretch of water that lines this groove, which has been detected by NMR and crystallography (27–30). It is, however, essential to note that ordering of this water comes not from the apolar groups of DNA but from its hydrogen bonding to regularly arranged polar groups in the minor groove, so the entropic stabilization of binding to the minor groove cannot be classified as a classical ‘hydrophobic effect’.

Figure 7.

Enthalpies (ΔH) and entropy factors (TΔS: nel, non-electrostatic; el, electrostatic) of binding proteins to the minor and major groove of their optimal and sub-optimal DNAs. SS = sequence-specific, NSS = non-sequence-specific DNA binding domains. Each data set is labelled with the name of the protein DBD followed by the DNA designation. Data taken from: Sry, Sox, Lef, NHP, Box-B, D100, D74—(12); Antp, NK2, MATα2, Engrailed—(13); ATF2-cJun and (cJun)₂—(33). See also (32).

CONCLUSION

Honig and colleagues (8) stated that an experimental evaluation of the CC and PB theories requires a determination of the salt dependence of the enthalpy and entropy of protein binding to DNA. The experiments summarized here do that and thereby make clear that the CC theory, as initially applied to DNA by Privalov et al. (31) and then to DNA/protein complexes by Manning (1,2) and by Record (3), gives a very effective description of protein–DNA interactions. In particular, it is seen that:

1. The protein–DNA binding energy can be split unequivocally into two qualitatively different components: the salt-dependent and salt-independent parts, which can be considered as the electrostatic and non-electrostatic components of the binding free energy. At present, observation of the salt dependence of the binding constant is the only experimentally accessible approach for quantitative evaluation of these two components.

2. The enthalpy of binding is independent of the salt concentration and the effects of salt are reflected solely in the entropy of binding. Thus the electrostatic component of the binding energy is fully entropic.

3. The specificity of interactions is manifested entirely in the non-electrostatic component, despite the electrostatic component typically contributing the majority of the affinity.

4. Notwithstanding certain simplifications, the CC methodology gives reliable binding characteristics and thus has considerable practical value for elucidating the forces contributing to the formation of protein–DNA complexes.

FUNDING

National Institutes of Health (Grant RO1 A1080828).

Conflict of interest statement. None declared.