Controlling instabilities in manipulation requires specific cortical-striatal-cerebellar networks

Abstract

Dexterous manipulation requires both strength, the ability to produce fingertip forces of a specific magnitude, and dexterity, the ability to dynamically regulate the magnitude and direction of fingertip force vectors and finger motions. Although cortical activity in fronto-parietal networks has been established for stable grip and pinch forces, the cortical regulation in the dexterous control of unstable objects remains unknown. We used functional magnetic resonance imaging (fMRI) to interrogate cortical networks engaged in the control of four objects with increasing instabilities but requiring constant strength. In addition to expected activity in fronto-parietal networks we find that dexterous manipulation of increasingly unstable objects is associated with a linear increase in the amplitude of the BOLD signal in the basal ganglia (P = 0.007 and P = 0.023 for 2 compression tasks). A computational regression (connectivity) model identified independent subsets of cortical networks whose connection strengths were mutable and associated with object instability (P < 0.001). Our results suggest that in the presence of object instability, the basal ganglia may modulate the activity of premotor areas and subsequent motor output. This work, therefore, provides new evidence for the selectable cortical representation and execution of dynamic multifinger manipulation for grasp stability.

dynamic dexterous manipulation of objects is essential to everyday life, yet its cortical underpinnings remain poorly characterized. One reason is that the classical categorization of grip into power and precision grips (Napier 1956; Cutkosky 1989) and neurophysiological studies thereof applies to holding solid objects in a fixed orientation using isometric finger forces, but not to dynamical manipulation of unstable objects. The power grip is used when the pads of all of the fingers hold an object against the palm, typically with high magnitude forces to hold large or heavy objects. Conversely, the precision grip involves holding small or delicate objects between the tips of the thumb and one or more fingers using forces of lower magnitude. The regulation of precision grip force magnitude to prevent slippage has been extensively studied in the context of maintaining a constant posture of the fingers against constant or impulsive perturbation loads, or a change in orientation with respect to the gravitation field (Gordon 1991; Johansson and Cole 1992; Hepp-Raymond et al. 1996). In response to these perturbations, grip forces normal to the contact surface are known to appropriately increase and counteract slippage produced by these tangential forces (Cole and Abbs 1988; Johansson and Cole 1992; Johansson 1996; Johansson 1998; Ehrsson et al. 2003; Kuhtz-Buschbeck et al. 2001). A number of previous investigations have examined the neural correlates underlying the control of finger force magnitudes in precision grip in both human subjects and nonhuman primates. Primate investigations and functional imaging [PET, functional magnetic resonance imaging (fMRI)] studies in humans consistently reveal a network of frontal and parietal regions (including the dorsal and ventral premotor cortex, cingulate cortex, sensorimotor cortex, and parietal cortex) active during grasping and in precision grip tasks (Rizzolatti et al. 1988; Rizzolatti et al. 1996; Jeannerod et al. 1995; Sakata et al. 1995; Binkofski et al. 1999; Murata et al. 2000; Kuhtz-Buschbeck et al. 2001; Ehrsson et al. 2000; Ehrsson et al. 2001; Ehrsson et al. 2003; Tunik et al. 2005). Moreover, fMRI studies of precise force scaling in a static precision grip task demonstrate task-specific activity in sensorimotor cortex (M1/S1), supplementary and cingulate motor areas (SMA/CMA), ventral premotor cortex (PMv) and inferior parietal cortex (Kuhtz-Buschbeck et al. 2001). However, these studies demonstrating parietal cortex involvement in object manipulation examined manipulation of either stable objects or used a stable grip paradigm. Dexterous manipulation in general, however, requires the ability to not only generate and scale the magnitude of fingertip forces, but it also requires the sensorimotor ability to dynamically regulate the posture of the finger and the direction of the force vectors.

To address this gap in our knowledge of brain function for the control of stability of dexterous manipulation, we interrogate the nervous system with tasks of varying stability requirements. This allows us to test the hypothesis of whether dynamic manipulation of increasingly unstable objects is associated with the scaling of activity in sensorimotor and parietal cortex or, alternatively, is associated with increased activity in other subcortical or cerebellar networks. We have previously formalized the ability to produce a fingertip force vector of a specific magnitude as strength, and conversely, dexterity, as the ability to dynamically regulate the posture of the finger and the direction of the fingertip force vector (Valero-Cuevas 2003b; Valero-Cuevas et al. 2003a; Valero-Cuevas 2005). In this study we focus on understanding the cortical, subcortical, and cerebellar activity associated with tasks where human participants squeezed springs requiring the same amount of fingertip force magnitude, but differing dexterity requirements (i.e., different levels of instability). Our results show that control of stability in dynamic manipulation is achieved through independent and tunable networks arising from differential activity in cortical-striatal-cerebellar circuits.

MATERIALS AND METHODS

A total of 16 healthy adult right-handed human subjects (10 men, 6 women; age range = 22–54; mean age = 32) participated in this investigation. Due to congenital hand defects in one subject unknown before enrollment, data from only 15 of the subjects were included in the data analysis. All subjects gave written informed consent before the experiment using consent approved by the Indiana University Institutional Review Board.

Experimental paradigm.

To identify neural correlates of dexterity for a chosen strength level (as defined in the introduction) we employed a modified version (suitable for fMRI) of a behavioral task that quantifies the strength and dexterity requirements for precision pinch tasks (Valero-Cuevas et al. 2003a). Briefly, the Strength-Dexterity Test (S-D Test) is based on the compression of commercially available stainless steel springs (Century Spring, Los Angeles, CA) using three-point precision pinch grip between the index finger, middle finger, and opposing thumb. The strength requirement is the pinch force required to compress the spring to solid length, defined by the linear stiffness constant and free length of each spring. The dexterity requirement is the ability to prevent the spring from buckling when compressed and is mathematically defined by the material properties and slenderness of the spring. A subset of four compression springs from the S-D Test kit were chosen to have similar strength requirements (29N-34N) but different dexterity requirements ranging from the largest more stable spring 1, to the most slender and least stable spring 4 (dexterity indexes of 0.40–1.67 as defined in Valero-Cuevas et al. 2003a). The MR-compatible springs were made of high-quality austenitic stainless steel, which is neither ferromagnetic nor paramagnetic^† and is commonly used in MR-compatible devices and implants. Table 1 lists the specifications for each of the springs.

Table 1.

Specifications of the four springs used in the experiments

Spring No.	Century Stock No.	Outside Diameter (in)	Inside Diameter (in)	Free Length (in)	Spring Rate (lb/in)	Max Deflection (in)	Max Load (lb)	Solid Length	Wire Diameter (in)	Total Coils
SP1	12699	0.953	0.873	1	2.8	0.82	2.3	0.18	0.04	3.5
SP2	S-1141	0.562	0.494	1	3	0.77	2.3	0.23	0.034	5.75
SP3	70790S	0.3	0.256	1	2.6	0.56	1.4	0.16	0.022	7.25
SP4	W-42	0.219	0.167	0.94	5	0.47	2.3	0.47	0.026	18

Subjects held the springs in their dominant hand while lying supine in the MRI scanner. Before imaging, each subject practiced all experimental tasks (with each spring) by performing trials complete with the auditory and visual stimuli for ∼20 min while outside the scanner.

Subjects were instructed to grip the springs with the pads of their index and middle fingers on the top and the thumb underneath, forming a three-point precision pinch (Cutkosky 1989; Hepp-Raymond et al. 1996). The fingers were maintained in a comfortable flexed position to ensure that only the tips of the fingers contacted the spring and that no finger joint was hyperextended (i.e., locked).

The experiment involved three separate precision-grip tasks: sustained compression, cyclic compression, and rest. For the sustained compression task, subjects were instructed to smoothly compress and hold the spring at the point of maximal instability (i.e., as compressed as possible without the coils of the spring touching, i.e., full compression was not achieved). This task requires online sustained regulation of the fingertip force vector's magnitudes and directions at a nearly constant finger posture to hold a compressed length most prone to buckling. The cyclic compression task required the subject to repeatedly compress and relax each spring from free to solid length while attempting to prevent buckling; compressions were synchronized to a metronome (1 Hz). Cyclic compression requires both periodic and continuous regulation of finger motions and the cyclic scaling of force magnitudes, while also directing forces to prevent buckling. For the control case of rest periods, subjects maintained a relaxed but stable grip on the spring without active compression (all springs are inherently stable when held at minimal compression). The term ‘rest’ means that no net compression forces were exerted on the spring, but only the finger force magnitude necessary to maintain hold of the uncompressed spring.

The fMRI data were acquired using an event-related (ER) paradigm. This approach was chosen to separate out BOLD responses to the different tasks given predicted overlap in the hemodynamic response function for sustained and cyclic compression. Each experiment consisted of four separate runs, one run for each spring, the order of which was randomized among subjects. Each run consisted of a total of 150 trials of sustained compression, cyclic compression, and rest. Instructional video cues (colored squares of identical dimension and intensity presented on a black background: red = rest; green = sustained compression; blue = cyclic compression) were each presented for a duration of 3 s. During the final 0.5 s before the beginning of the following trial, the screen would clear, cueing the subject to relax his or her grip on the spring and prepare for the next task. Each of the three tasks was presented a total of 50 times with a mean inter-trial stimulus interval (ISI) of 10 s with the trials randomized. Although the auditory cue (1-Hz metronome) was used by subjects only during the cyclic compression tasks, it was presented throughout the entire run. Subjects were trained to utilize the metronome only during the cyclic compression task.

Brain imaging.

All subjects were imaged on a Siemens 3.0 T Trio MRI scanner using an eight-channel head array RF coil with a mounted mirror providing direct visualization of a screen located at the end bore of the scanner onto which were projected the visual cues. Daily quality assurance (QA) single and multislice scans were performed to assure homogeneity of the main magnetic field (β₀); the mean drift for studies of these experiments was 0.35% (range 0.30–0.80), and no studies were conducted with drift greater than 0.8^†. Following the three-plane localizer, standard three-dimensional and manual shimming was performed. High-resolution, three-dimensional sagittal MPRAGE images (isotropic 1-mm³ voxels, full brain coverage) were acquired initially for anatomical coregistration of the fMRI data. Five functional runs were then performed for each subject: one run for each of the four springs and a final run with no spring, each using the ER paradigm described above. For the functional runs, single shot Gradient Recalled Echo-Echo Planar Imaging (GRE-EPI) T2* weighted BOLD [repetition time/echo time (TR/TE) = 1,500/30 ms; 64 × 64 acquisition matrix; 90° flip angle, 22.4 cm field of view (FOV)] imaging was used to acquire a total of 316 images in 23 axial slices with a 4.5-mm slice thickness. These voxel dimensions were chosen to permit whole brain coverage to the level of the cerebellar tonsils within the TR. The short TR was chosen to capture hypothesized differences in the slope of the BOLD hemodynamic response function between tasks. Thus the anisotropic z voxel dimension permits optimal volume for BOLD contrast to noise while minimizing intravoxel frequency offsets and phase dispersion that is further compensated by orthogonal axis shimming. To correct for the minimal B₀ drift, signals from the phase correction scan that preceded each acquisition of raw image data were used to quantify the absolute B₀ field and each k-space line and multiplied with a phase factor that compensates for phase evolution during the off-resonance acquisition. Real-time prospective motion correction was additionally performed by application of the Prospective Acquisition Correction (PACE) algorithm, which uses a rigid body transformation and regridding of residual motion from the temporal series of volumes using a Fourier-based shearing method (Thesen et al. 2000).

To ensure that the sustained and cyclical compression tasks with the springs did not generate k-space phase artifacts, gradient field (β₀) mapping was performed before scanning, which revealed no phase distortions.

To verify that subjects were performing compression tasks synchronized with the paradigm and to compare motor effort across conditions, muscle activity in the hand was recorded via surface electromyography (EMG) in the MRI scanner. Muscle activity present during the compression tasks was recorded via surface electromyography (Biopac Systems: MP 150). Three 4-mm Ag/AgCl surface electrodes with carbon fiber leads and custom-fabricated cable were utilized. The two recording electrodes were placed over the thenar eminence with a dipole distance of ∼3 cm, and the ground electrode was placed over the lateral epicondyle at the elbow. The cable was passed through a 4-cm RF waveguide in the penetration panel, and data acquisition and conditioning was performed on a computer located in the scanner control room. The raw EMG signals were sampled at a frequency of 10 kHz and amplified with a gain of 1,000. A trigger pulse embedded in the EPI pulse sequence synchronized the EMG signal acquisition with the start of the fMRI data acquisition, and EMG signals were continually acquired throughout the fMRI data acquisition of 300 s. The hand, spring, and electrodes rested on pillows over the lower abdomen of the subject to allow for a comfortable arm posture that did not affect the brain imaging.

Before these experiments, phantom and single human subject (K. Mosier) testing was performed to ensure that the EMG electrodes, electrode interface, leads, or cables with and without the springs did not produce artifacts in k-space or image data.

Although the EMG system introduced no artifacts in the fMRI or image data, the switching gradients of the MR system introduced significant artifacts in the EMG signal, which were removed in post-processing using custom filtering techniques. See supplementary material (all supplementary material can be found with the online version of this article) for a complete description of methods and results.

Image processing and statistical analysis.

The raw EPI fMRI data were processed offline using Analysis of Functional NeuroImages (AFNI) (afni.nimh.nih.gov/afni). To account for system equilibration, the first eight functional images of each run were removed, and all other images were realigned to the new first image. Time-series data from the functional runs were spatially smoothed with a low-pass filter kernel of 5 mm full-width at half-maximum.

Hemodynamic response functions (HRFs) for each voxel were estimated through general linear modeling; computations were performed with the use of the AFNI function 3dDeconvolve. Included in the model for each HRF was a basis set of eleven predictor time series, each of which were delayed in time by integer multiples of the TR (1,500 ms). Time series s(n) and c(n) for the sustained and cyclic compression tasks were input into 3dDeconvolve with baseline correction, retrospective head motion correction using the three-dimensional rotational and translation motion parameters detected in the PACE algorithm, outlier correction, and detrending.

The HRF results from all 15 subjects were pooled together and a three-factor, mixed-effects, ANOVA was performed on the mean HRFs from all subjects: factor 1-springs, fixed; factor 2-tasks, fixed; factor 3-subjects, random. Several effects were examined in this group analysis, including the overall effect from each spring and compression task. With no significant difference in mean HRF between compression and rest set as the null hypothesis, peak activation corresponding to P < 0.05 (corrected) was recorded. For the group analysis, the AFNI program AlphaSim was used to compute the corrected type I error. The criteria input to AlphaSim included voxel size (3.5 × 3.5 × 4.5 mm), desired P threshold (P = 0.01), cluster connection radius (4 mm), and image dimension (32 × 64 × 23 voxels-individual hemispheres were isolated). A Monte Carlo simulation (1,000 trials) was run in AlphaSim, which output the corrected type I error (α) and minimum cluster sizes necessary to perform a cluster analysis on the functional data. Cluster analyses of all functional maps were performed using the AFNI function 3dclust. The minimum significant cluster size for each of the cluster analyses was determined by AlphaSim. The criteria for AlphaSim, in addition to the minimum cluster size, were also used as the criteria for 3dclust, to generate statistical group maps revealing activation in the brain corresponding to each of the fixed effects. Regions of interest (ROIs) generated from these group maps represent the regional brain responses. Single factor mean effect group maps were also generated to examine activation in response to individual factor levels (i.e., activation due to individual springs or individual tasks) (P < 0.01; uncorrected).

Volumetric overlap between ROIs of the mean effects was investigated using conjunction analysis: the conjunction maps display overlap between the mean effects for spring 1 and spring 4 (most stable and least stable springs, respectively), or the overlap between the two mean task effects. A common t-threshold was selected so that all activity plotted above the threshold would indicate significant activation (P < 0.01, uncorrrected). For example, in the task overlap map, all activation corresponding to the mean sustained compression effect was assigned a value of 1, whereas the cyclical compression activity was assigned a value of 2 (for spring overlap, spring 1 = 1, spring 4 = 2). The two functional mean effect maps were then summed, and all overlapping areas were thus assigned a value of 3. Finally, F-statistics were used to generate a group map, which displays ROIs significant for interactions between factors. All group map data and conjunction analysis were warped into Talairach space and coregistered with the anatomical MR images.

Connectivity analysis.

Connectivity analysis was used to detect task-dependent functional cortical networks, defined as correlated activity among individual cortical elements. To examine mutable cortical, subcortical, and cerebellar circuitry for different tasks, we tested models of effective connectivity among premotor, motor, parietal, basal ganglia, and cerebellar regions during sustained and cyclic compression tasks. Effective connectivity is an established technique to test and represent the functional connections among different brain regions for a specific task based on covariation of the BOLD signal in fMRI (McIntosh and Gonzalez-Lima 1994; Mosier and Bereznaya 2001). A neuroanatomical model was constructed based on known connections among brain regions. The analysis was restricted to those regions showing consistent activation in our study to reduce computational load. The signal intensity and volume of the clusters from each of the four springs (i.e., levels) across the sustained or cyclic compression data were subjected to Pearson's product moment correlation analysis. The resulting correlation matrix provided the weighting factors for each connection pathway. The assignment of functional weighting, or path coefficients, was accomplished through singular value decomposition of the correlation matrix. The neuroanatomical model combined with the path coefficients defines the functional model. The algorithm used to test the functional model is of the form: η = βn + ψ (the structural model), where η is the vector of variances of regional activity for the regions specified, β is the matrix that defines the network and contains the path coefficients, and ψ is the vector of residual effects (McIntosh and Gonzalez-Lima 1994; Mosier and Bereznaya 2001). The structural equations are solved through iterative fitting with the probability of the structural model to reproduce the data determined through a χ2 goodness of fit ^40–41. The structural model: Y=(I−B)−1·Φ(I−B′)−1 was employed, with a Maximum Wishart Likelihood algorithm used to fit parameters (Systat version 10.0; SPSS, Chicago, IL). Figure 4 shows the functional connections with the respective weighting (point estimates) of each path for the sustained and cyclic compression tasks. The direction of the arrow in the dependence path indicates the direction of the connection between brain regions with double-headed arrows indicating reciprocal connection. Positive or negative values for the point estimates do not imply excitatory or inhibitory neurotransmission; rather, they represent positive or negative causal inferences that reflect positive or negative inter-regional covariance in the fMRI time-series.

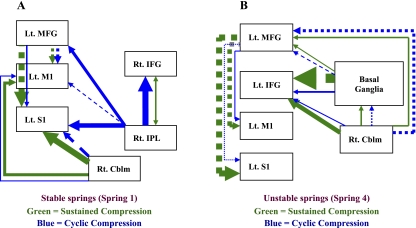
Fig. 4.

Diagrams of the connectivity models (SEM models) for sustained and cyclic compressions. The arrows represent the weighting of the point estimates (PE) and direction of correlation between brain regions. Other anatomically relevant brain regional connections were used to fit the models (i.e., other brain areas are active in both tasks); only the major significant differences between compression tasks are shown. Solid lines represent positive correlation; dashed lines represent negative correlations. Green = sustained compression; blue = cyclic compression. 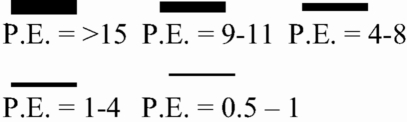. Rt, right; Lt, left; Cblm, cerebellum; IFG, inferior frontal gyrus; IPL, inferior parietal lobule.

RESULTS

Effect of changing dexterity requirement (object stability).

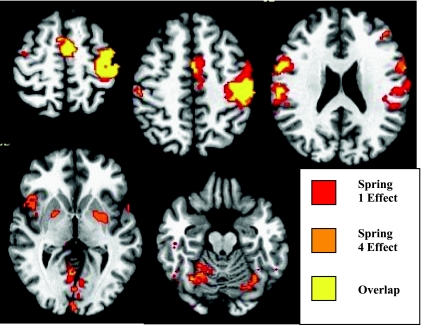
We first examined compression of each of the four springs versus rest. Compression of the springs with varying dexterity requirements resulted in consistent activation [t (56) = 2.975; P = 0.0099] in frontal and parietal cortices [left primary motor and somatic sensory cortex, the supplementary motor area (SMA; Brodmann's area 6), and bilaterally in the superior and inferior frontal gyrus, inferior parietal cortex] and subcortical areas (left putamen and bilateral cerebellum). We then examined the effects of dexterity across spring levels by performing conjunction analysis to determine the spatial overlap of activated clusters for each of the four springs. Figure 1 shows selected slices from the conjunction analysis displaying the overlap between springs 1 and 4 (lowest and highest dexterity index, respectively). Springs 2 and 3 showed overlap within the clusters shown in Fig. 1 but are omitted for clarity. Activation overlapped in the SMA, predominately in the left primary motor and sensory cortex, with lesser volume in the right primary and sensory cortex, the right middle frontal gyrus, and right cerebellum.

Fig. 1.

Conjunction activation maps showing regions of overlap in mean effect between springs 1 (lowest dexterity value; most stable) and 4 (highest dexterity value; most unstable). Conjunction maps are shown overlaid to select axial T1-weighted images from most superior slice (top left) to most inferior slice (bottom right). Images are presented in radiological coordinates: left of image is subject's right side. All spring 1 activation above a t-threshold of 2.975 (P = 0.01) is plotted in red, whereas all spring 4 activation (above t-threshold of 2.975; P = 0.01) is plotted in orange. All overlapping regions of interest (ROI) are displayed in yellow. Top row, left: ROI in bilateral supplementary motor area (SMA) and contralateral primary motor cortex (MI) and primary sensory cortex (SI). Top row, middle: ROIs in contralateral SMA, MI, SI, and ipsilateral SI. Top row, right: ROIs in bilateral ventral premotor (PMv), SI, and contralateral middle frontal gyrus and posterior parietal lobule. Bottom row, left: ROIs in bilateral PMv, putamen/globuspallidus, and thalamus, and bilateral visual areas. Bottom row, right: bilateral ROIs in cerebellum.

Clusters that did not overlap included activity in the left inferior parietal cortex and left cerebellum for spring 1, whereas spring 4 demonstrates activity in bilateral putamen, right insula, and cerebellum. These data show that precision pinch compression of springs with differing dexterity requirements (but similar strength) is associated with activity in premotor, primary sensorimotor, parietal, and cerebellar regions. With increasing dexterity index (increasing demand on dynamical regulation of fingertip force vectors), however, activity selectively increases in the basal ganglia.

Effect of changing the task (task induced stability/instability).

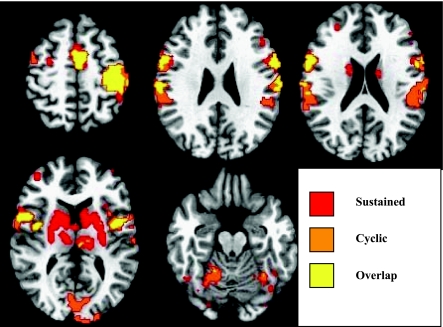
We next examined the effect of the type of compression (sustained or cyclic) versus rest. Table 2 shows the mean effect of the sustained compression task, and Table 3 shows the mean effect of the cyclical compression task. Both sustained (compress and hold at the point of maximal instability) and cyclical (repeatedly compress from free to solid length, synchronized to the metronome) compression tasks activated the sensorimotor cortex (including primary motor cortex and primary sensory cortex), SMA, inferior frontal gyrus bilaterally, and the left insula, putamen, and declive of the cerebellum. Conjunction analysis of the activation overlap for sustained and cyclic compression tasks is shown in Figure 2. Activation for the two tasks overlaps in the left sensorimotor cortex, bilateral premotor/prefrontal cortex, and cerebellum. Sustained compression is distinguished from cyclical compression by the significant bilateral activation in the basal ganglia (caudate and putamen) in contrast with cyclical compression, which shows activation in the bilateral inferior parietal lobule, superior temporal gyrus, and cerebellum.

Table 2.

Regions of interest found in the mean sustained compression effect group map

Region of Activation	Talairach Coordintes Center (X, Y, Z)	Volume (cm3)	Mean F-stat
Left hemisphere
Left thalamus	−10, −17, 10	2.416	5.332
Left medial frontal gyrus (BA 6)	−4, −3, 56	3.584	5.235
Left putamen and left caudate nucleus	−20, 0, 7	5.312	5.207
Left postcentral gyrus (BA 2)	−45, −25, 46	8.088	5.127
Left insula (BA 13)	−43, 4, 5	1.664	4.297
Left precentral gyrus	−40, −15, 51	7.024	4.202
Left inferior frontal gyrus (BA 9)	−51, 7, 30	2.408	3.337
Left cingulate gyrus (BA 24)	−5, 1, 45	0.552	3.186
Left declive	−23, −46, −14	0.680	−0.820
Right hemisphere
Right thalamus	10, −13, 9	1.560	4.694
Right medial frontal gyrus (BA 6)	4, −1, 55	1.552	4.57
Right declive	17, −56, −11	5.144	4.523
Right inferior frontal gyrus (BA 44)	54, 8, 26	2.768	4.206
Right putamen and right caudate nucleus	18, 2, 8	3.440	3.959
Right postcentral gyrus (BA 2)	56, −21, 30	2.632	3.454
Right precentral gyrus	49, 4, 12	2.936	3.23
Right fusiform gyrus (BA 19)	25, −57, −9	0.544	1.614

Table 3.

Regions of interest found in the mean cyclic compression effect group map

Region of Activation	Talairach Coordintes Center (X, Y, Z)	Volume (cm3)	Mean F-stat
Left hemisphere
Left medial frontal gyrus (BA 6)	−4, −6, 57	2.272	7.055
Left postcentral gyrus (BA 2)	−46, −24, 47	10.720	6.25
Left inferior frontal gyrus (BA 9)	−54, 6, 29	1.624	4.793
Left putamen	−24, 0, 2	1.448	4.671
Left insula	−48, −31, 19	0.568	4.137
Left lingual gyrus (BA 18)	−3, −80, 1	4.928	3.929
Left declive	−17, −62, −10	2.312	3.468
Left precentral gyrus	−40, −13, 47	11.824	2.333
Right hemisphere
Right precentral gyrus	50, 4, 12	4.280	4.629
Right inferior frontal gyrus	54, 7, 26	2.080	3.86
Right superior temporal gyrus	58, −38, 17	0.616	3.885
Right inferior parietal lobule	59, −24, 24	2.208	3.559
Right culmen	15, −57, −9	5.600	3.487
Right lingual gyrus	12, −81, −5	6.072	3.442
Right medial frontal gyrus (BA 6)	3, −2, 56	1.048	3.051

Fig. 2.

Conjunction activation maps showing regions of overlap in mean effect between the sustained compression task and the cyclic compression task. Conjunction maps are shown overlaid to select axial T1-weighted from most superior slice (top left) to most inferior slice (bottom right). Images are presented in radiological coordinates: left of image is subject's right side. All sustained compression activation above a t = 2.975 (P < 0.01) is plotted in red, whereas all cyclic compression activation above t = 2.975 (P < 0.01) is plotted in orange. All overlapping regions of interest are displayed in yellow. Top row, left: overlap of activation in bilateral SMA and contralateral MI and SI. Top row, middle: bilateral overlap in ventral premotor areas (PMv) and SI. Top row, right: overlap of activation in ipsilateral PMv; sustained compression (red) activation in bilateral caudate; cyclic compression (orange) activation in secondary sensory cortex (SII), anterior intraparietalsulcus (IPS). Bottom row, left: overlap of activation in bilateral PMv; sustained compression activation throughout bilateral basal ganglia (caudate nucleus and putamen) and thalamus; cyclic compression (orange) activation in visual cortex. Bottom row, right: small areas of overlap and larger areas of activation in cyclic compression in bilateral culmen of the cerebellum.

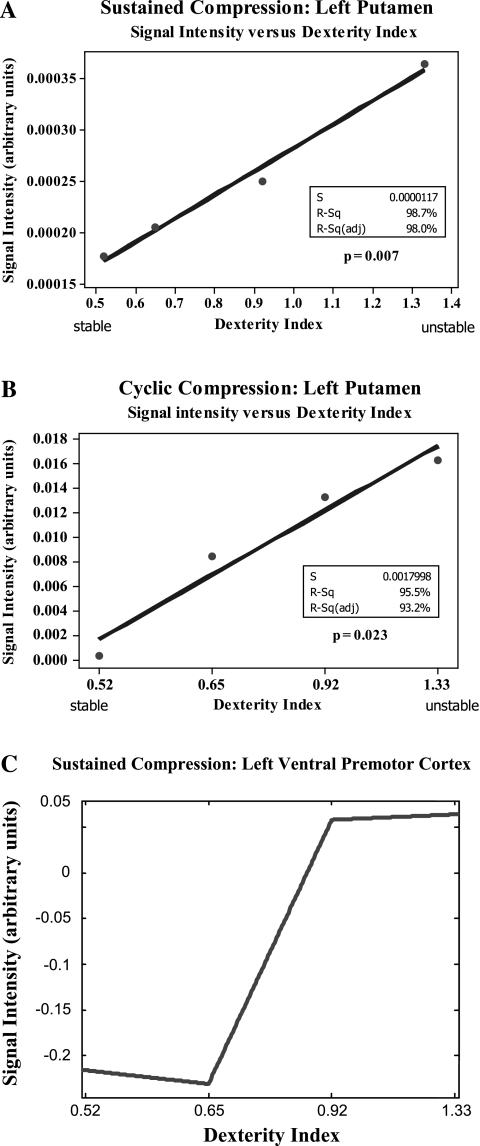
The pattern of activation of the basal ganglia from the conjunction analyses suggests a correlation between activity in the basal ganglia and levels of instability. We performed linear regression analysis to assess the linearity of the response in the basal ganglia and all other brain regions identified in the cluster analysis data. Due to the smaller volume of the basal ganglia (putamen) there was heteroskedasticity to the variance despite a normal distribution. We performed Johnson transformation on the signal intensity cluster data to correct this heteroskedasticity and performed linear regression on the transformed data. A Box Cox transformation could not be applied due to the presence of negative values. Figure 3, A and B, shows that for increasing levels of dexterity index (increasingly unstable springs) there is a linear increase in activity in the contralateral putamen for both the sustained and cyclic compression task.

Fig. 3.

A and B: linear regression analysis of the BOLD signal change in the left (contralateral) putamen for both sustained (A) and cyclic (B) compression tasks. There is a statistically significant increase in signal intensity with increasing dexterity index (more unstable springs). C: piecewise polynomial fit of regression coefficients of the BOLD signal change in the left (contralateral) ventral premotor cortex (vPM; inferior frontal gyrus). There is a significant increase in signal intensity between springs 2 and 3 (dexterity index 0.65 and 0.92), suggesting a step function type response.

Thus irrespective of in the cyclic nature of the task (sustained versus cyclic compression), there is a significant linear response in the putamen to dexterity requirement. None of the other ROIs demonstrated a significant linear response to dexterity. Specifically, the data did not support the hypothesis of a scaling of activity within the sensorimotor or parietal cortex. However, the contralateral ventral premotor cortex showed a nonlinear step type response to dexterity index under the sustained compression conditions (Fig. 3C).

Interaction effects.

Finally, we examined whether performing the sustained or cyclic compression task yielded differing activation across the four different dexterity levels (Table 4). We found a task by dexterity interaction in brain activation [F(6,168) = 4.291, p = 0.01] in four contralateral ROIs: putamen, insula, visual cortex (lingual gyrus), and the anterior inferior parietal lobule (AIP).

Table 4.

Regions of interest for interaction effects of springs and task

Region of Activation	Talairach Coordinates Center (X, Y, Z)	Volume (cm3)	Mean F-stat
Left putamen	−26, −5, −3	0.520	6.13
Left insula (BA 13)	−39, −7, 15	1.040	5.71
Left lingual gyrus (BA 18)	−18, −54, 5	0.496	4.50
Left inferior parietal lobule (BA 40)	−51, −32, 26	0.680	3.08

Correlation with EMG.

The average root mean square voltage (V_rms) of the post-processed and rectified EMG signal for the four springs was 0.123 ± 0.043. ANOVA revealed no statistically significant differences in the amplitude of the EMG signal between the four springs (P = 0.54). Thus differences in the dexterity index are not associated with differences in gross EMG activity. This validates our experimental design of holding the strength requirement of the tasks constant while systematically changing their dexterity requirements.

Although statistically significant correlation was observed between the EMG and fMRI clusters identified for each of the four springs (data not shown), there was no statistically significant correlation between the EMG and the fMRI clusters identified for the mean effect of the springs. These data suggest that there is no significant association between neural activity related to differences in dexterity requirements and the root mean square of EMG activity, and importantly, that muscle co-contraction cannot account for the neural correlates of dexterity index. Thus these results are in agreement with other evidence that the task of compressing springs is likely a sensorimotor integration task that does not rely on simply stiffening the fingers (Venkadesan et al. 2007). See supplementary material for further discussion of EMG.

Effective connectivity.

Figure 4 shows the differences in connectivity between selected brain regions for stable (spring 1) and unstable (spring 4) springs during the sustained and cyclic compression tasks.

Figure 4A shows that for stable springs during more stable compression tasks, there is predominant effect of the right inferior parietal cortex on the ipsilateral ventral premotor cortex, and contralateral dorsal premotor and primary sensory cortex (cyclic compression, blue lines). During unstable compression tasks, (sustained compression, green lines) the effect is predominately from the ipsilateral cerebellum to the contralateral primary motor and sensory cortex. In addition, during unstable compression, there is a significant negative effect from the ventral premotor cortex to the primary sensory cortex.

For unstable springs (Fig. 4B), during unstable (sustained) compression, there is a significant and predominant negative effect of the basal ganglia on the contralateral ventral premotor cortex. Moreover, there is moderate negative effect of the dorsal premotor cortex on the primary motor and sensory cortex and a moderate positive effect of the ipsilateral cerebellum on the contralateral ventral premotor cortex.

The negative effect from the basal ganglia on the inferior frontal gyrus together with the negative effect from the dorsal premotor cortex on the primary motor and sensory cortices suggests that during unstable compression tasks with unstable springs, there may be changes in the activity of direct and indirect basal ganglia circuits (Alexander and Crutcher 1990) such that there is altered facilitation or inhibition of the ventral premotor cortex and thalamus, and hence the primary motor and sensory cortices. We did not include the thalamus in the model since we did not see consistent activation in the thalamus. However, our analysis of the BOLD signal changes included only positive BOLD changes; we did not include in the analysis of negative BOLD changes, which, although an area of debate, studies have associated with cortical inhibition (Shmuel et al. 2002; Stefanovic et al. 2004). Further studies are necessary to elucidate the specific basal ganglia-thalamocortical circuitry changes in precision pinch tasks. Moreover, during sustained compression compared to cyclic compression there is a substantially increased effect of the right cerebellum on the primary motor and sensory cortex and the ventral premotor cortex and diminution of the effect from the dorsal premotor cortex.

An important limitation of the structural equation modeling (SEM) analysis is that although reciprocal connections between cortical regions, basal ganglia, and cerebellum are explicitly included in the model, this hemodynamic-based model represents only regional global hemodynamic effects. It does not capture the full character of information processing and control mechanisms contained within subcircuits or within known disynaptic pathways, for example, between the basal ganglia and cerebellum (Bostan et al. 2010; Hoshi et al. 2005). Moreover, the SEM analyses represent regional hemodynamic covariation over the entire time course of the fMRI time-series and thereby do not capture the temporal variation in cortical facilitation or suppression that occurs between premotor cortex, motor cortex, and parietal cortex during precision grip motor planning and execution (Koch et al. 2006; Koch et al. 2010). Finally, although negative point estimates from fMRI SEM analyses have been interpreted as inhibition in the context of motor planning and execution (Zhuang et al. 2005), the negative point estimates observed in our study more likely reflect regional offsets in activity.

DISCUSSION

The findings of this investigation build upon previous studies of the neural representation of precision grip by extending to dynamic manipulation. Although prior investigations addressed static and isometric precision pinch of solid objects, we used the strength-dexterity paradigm to systematically present the nervous system with a variety of dynamic manipulation tasks (Valero-Cuevas et al. 2003a; Valero-Cuevas 2005). Two building blocks of dexterous manipulation are the ability to dynamically control the magnitude (i.e., the strength requirement to compress the spring) and direction (i.e., the dexterity requirement for the spring not to buckle) of fingertip force vectors (Cutkosky 1989; Valero-Cuevas et al. 2003a; Valero-Cuevas 2005). By holding the magnitude of the fingertip force constant across springs, we were able to tease apart changes in the neural representation of tasks associated with increasing levels of the dexterity requirement (i.e., increasingly less stable springs) in the context of both nearly constant and time-varying finger postures.

Among the four springs, activity overlapped in the sensorimotor cortex, prefrontal/premotor cortex (SMA, middle frontal gyrus, inferior frontal gyrus), and cerebellum. Activity in these regions is typically observed in grasping or grip studies and has been shown to constitute part of the postulated fronto-parietal networks involved in grasping actions of the hands and in isometric and static precision grip (Rizzolatti et al. 1996; Binkofski et al. 1999; Ehrsson et al. 2000; Ehrsson et al. 2001). Thus, regardless of dexterity index, pinch compression of the springs involves a sensorimotor, prefrontal/premotor, and cerebellar network that is likely shared with isometric and precision grip tasks.

The activity in several other cortical areas, however, changed with the dexterity requirement of the task. Increases in the dexterity requirement were associated with selective increases in basal ganglia activity, whereas compression of springs with lesser dexterity requirements involved the inferior parietal cortex.

Similar to the findings across springs with different dexterity indexes, our results demonstrate activation in the sensorimotor cortex (primary motor and sensory cortex), prefrontal/premotor cortex, and cerebellum for both sustained and cyclic compression tasks. It is important to underscore that our sustained compression task is starkly different from simply holding a solid object. Simply maintaining a constant level of spring compression requires dynamical regulation of fingertip force direction because the spring deforms and could buckle. Thus it is more related to the dexterous everyday task of holding a brittle and deformable object (e.g., ripe fruit) than the task of holding a stone. These brain regions, then, constitute a common network involved in the control of finger posture and movement, which are a fundamental component of dexterous manipulation.

The selective increases in activation observed for the sustained versus cyclic compression closely parallel the activation patterns observed for unstable versus stable springs. The consistency in results between spring instability level and task is explained by consideration of the mechanics of the task. For the sustained compression task, the nervous system is consistently faced with a higher degree of instability compared with the cyclic compression task, where the nervous system is faced with the greatest instability only briefly in the part of the cycle when the spring is close to being fully compressed. Based on mathematical theories of buckling instabilities under time-varying forces (El Naschie 1990; Berglund and Gentz 2002), we speculate that the cyclic compression is stabilized because the time-scale of the cyclic compressive force is faster than that associated with the spring's instability. Although at maximal compression the spring could be unstable, the cyclic compression could lead to stability if the compressive force decreased fast enough so that the spring becomes passively stable before buckling. This does not apply to the sustained compression, where maintaining a near constant load without stabilizing control will allow for the spring's instability to grow to a point where it will buckle. Testing this explanation will require dynamic experiments with the spring.

Our results demonstrate an increase in the activity of the dorsal striatum bilaterally during compression of unstable springs, a linear response in the contralateral putamen to instability in the springs for both compression tasks, and a significant effect of the ventral premotor cortex during compression of the most unstable springs in the unstable (sustained) compression task. Together, these findings suggest there are specific striatial-cortical responses to the demands of a dexterous manipulation task. Thus our data show a strong association of dexterous manipulation of increasingly unstable objects with an increase in the amplitude of the BOLD signal in the basal ganglia. However, such an association is not found for the cerebellar-parietal network.

Numerous studies have established that the basal ganglia is involved or activated in precision grip tasks (Ehrsson et al. 2001) and play a role in grip force (Dettmers et al. 1995; Spraker et al. 2007; Vaillancourt et al. 2004). In our experiments, the mechanical specification of the springs constrained the force to a set level and the rate of force/finger motion was controlled via synchronization of movement to the metronome. Because force levels in our experiments were constrained to a narrow invariant range, the linear response of the basal ganglia to dexterity demand suggests a role for the striatum in the control of dexterity. Furthermore, the interaction effects between dexterity level of the spring and task revealed specific increases in activity of the putamen (Table 4). These results suggest that the basal ganglia may be involved in selectively controlling the direction of the applied force independently of the magnitude of the applied grip force. Desmurget et al. (2004) demonstrated spatially selective increases in basal ganglia activity for control of movement amplitude and movement direction in visually cued reaching movements. In our experiments, the magnitude of the applied fingertip force and EMG were constant while we varied the requirement for dynamical control of the applied force direction. The selective increase in basal ganglia activity we observed therefore supports independent modulation of fingertip force direction prompted by sensory input via sensorimotor integration. Neural network models of grasp and reach to grasp postulate the basal ganglia as having a gating function in updating the difference vector between the limb and target (Ulloa and Bullock 2003; Rice et al. 2006), whereas other studies have correlated basal ganglia activity with reward prediction error (Tanaka et al. 2004). Although these two hypotheses address different functions, a fundamental similarity is the postulate of the basal ganglia as having a role in updating error signals. Shadmehr and Krakauer (2008) formalized this error-update function by pointing to the comparator role of the basal ganglia in state comparison of the costs of motor commands of the task with the predicted sensory outcome (reward). In the context of our results, the basal ganglia appears capable of performing error updating independently for control of fingertip force vector direction and amplitude.

Under task conditions where the sensitivity to motor error is high (precision grip of unstable springs with task instability), the basal ganglia generates a significant effect on the ventral premotor area, and a moderate effect of the ventral premotor area on the motor cortex. Although ventral premotor cortex excitatory facilitation of motor cortex in limb movements and grasp is well established (Cerri et al. 2003; Jeannerod et al. 1995), transcranial magnetic stimulation studies (rTMS) suggest that contralateral premotor cortex plays a role in suppressing prepared but unselected movements of the hand in a grip task (Koch et al. 2006). The ventral premotor cortex has been shown to select the type of grasp or grip and that during precision grip, input from the ventral premotor cortex to the primary motor cortex is selectively facilitated (Umilta et al. 2007; Davare et al. 2008). Input from the ventral premotor cortex to M1 during unstable dexterous manipulation may serve to constrain the movement of the fingers or alternatively to constrain the degrees of freedom. In agreement with other results the level of EMG activity was not associated with the increase in dexterity requirements (Venkadesan et al. 2007), suggesting that stiffening of the fingers via co-contraction is not the dominant strategy to compress an unstable spring. This result differs from the findings of a recent study for the whole arm, where stiffness increase was used to counter the externally applied destabilizing force on the arm (Selen et al. 2009). Future studies should investigate the reason for differences between control of the hand and the arm in the face of external instabilities.

Both for springs with less severe dexterity requirements and the cyclic compression task, we observed selective increases in activation in the inferior parietal lobule and cerebellum. The parietal cortex, and in particular the inferior parietal lobule and regions lining the intraparietal sulcus (AIP, LIP), are established brain regions involved in predicatively shaping the hand for grasping (Sakata et al. 1995; Tunik et al. 2005), and it is hypothesized to be one of several brain regions involved in the anticipatory modulation of grip force (Ehrsson et al. 2003). The increased activity we observed in the inferior parietal cortex together with activity observed in the cerebellum suggests a role for cerebellar-parietal circuitry in coordination of the 12 joint angles across and within fingers required for the cyclic compression task. Other studies of cerebellar deficits have also identified a critical role for the cerebellum in coordination across joints during complex tasks (Bastian et al. 1996; Topka et al. 1998; Cooper et al. 2000). In the case of less challenging, inherently stable springs like springs 1 or 2, a predominantly predictive strategy of hand shaping likely suffices for successful spring compression since these springs are robust to errors in finger motions and force, thus not requiring careful sensory monitoring. Therefore, based on well established results that predictive hand shaping for grasping (Sakata et al. 1995; Tunik et al. 2005) and predictive grip force modulation (Ehrsson et al. 2003), both activate the parietal cortex, and in particular the inferior parietal lobule and regions lining the intraparietal sulcus (AIP, LIP), we speculate that predictive (i.e., memory trace, internal models, etc.), multi-joint, multi-finger coordination is principally governed by the cerebellar-parietal circuitry identified by our study.

The interaction effects revealed four significant areas of activation: the contralateral (left) anterior intraparietal area (AIP; in the inferior parietal lobule), insula, visual cortex, and putamen. These areas of activation represent those brain areas in which activity moderates those brain areas active for the different springs or the two compression tasks. In our study, the interaction areas are those involved with coordinating the sensory input with motor output. The visual cortex activity (in the lingula) likely reflects the specific visual cue (color) associated with rest periods and the sustained or cyclic compression tasks (Allison et al. 1993). We speculate that the activity in the AIP and putamen reflects the sensorimotor integration and coordination demands of the dexterity or compression (sustained or cyclic) requirements of the task. The insula has been implicated in tactile recognition and recall and functions as a pathway connecting somatosensory cortical areas with the cingulate and hippocampus (Augustine 1996). Moreover, activation in the insula is routinely observed for a very wide range of motor tasks. The subjects could see neither their hands nor the springs, and, when presented with the spring before scanning at the beginning of the run, often compressed the spring several times. The spring (and its particular dynamics) would therefore have to be identified on the basis of tactile and proprioceptive recognition alone. Thus, the insula may, through its connections to sensory areas and memory modules, function to compare the actual sensory feedback with the predicted sensory model of the spring dynamics.

Finally, the differences we observed in the effective connectivity suggest that during sustained compression as compared with cyclic compression, the system may be dampening sensorimotor noise or gain or may be providing some signal gating. In this sense, the basal ganglia of itself, or together with cerebellar circuits, may be operating within the context of a minimal-intervention strategy, vis-à-vis attending to errors (due to sensorimotor noise, sensory uncertainty, etc.) only when the task is more challenging as in the sustained compression.

In summary, our identification of differential cortical or subcortical activation with different dexterity requirements clearly suggests that the CNS uses a spectrum of control strategies depending on task context. The difference in cortical networks involved in tasks with greater dexterity versus those with lesser dexterity requirement suggests that control systems at the cortical level may attend to, or place greater weighting on, sensory feedback in the face of greater instability or uncertainty, and conversely, when this sensory attention or weighting is not needed, the system may rely more on internal models or memory to execute the task. Thus, by combining functional neuroanatomy with a systematic manipulation of a mechanical task, our results support the conjecture that the CNS uses a spectrum of control systems including sensory feedback, memory traces, or internal models depending on task requirements (Hinton 1984; Loeb et al. 1999).

Our experimental design permits a well-defined and focused interrogation of cortical networks and control systems and lays the foundation to systematically test and associate mathematical models of sensorimotor control with their biological implementation. For example, this approach is amenable to application in stroke populations where affected frontal, parietal, or cerebellar areas may result in failure of cortical control systems clinically presenting as over-stiff musculoskeletal plants or neuromuscular fatigue, and so on.

GRANTS

This work was supported in part by grants (to F. Valero-Cuevas) National Science Foundation (NSF) 0237258 and National Institutes of Health (NIH) HD048566 and AR050520. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS), the National Institute of Neurological Disorders and Stoke (NINDS), the NIH, or the NSF.

DISCLOSURES

F. J. Valero−Cuevas holds the patent to some of the technology used in this study.