Internal curvature signal and noise in low- and high-level vision

Abstract

How does internal processing contribute to visual pattern perception? By modeling visual search performance, we estimated internal signal and noise relevant to perception of curvature, a basic feature important for encoding of three-dimensional surfaces and objects. We used isolated, sparse, crowded, and face contexts to determine how internal curvature signal and noise depended on image crowding, lateral feature interactions, and level of pattern processing. Observers reported the curvature of a briefly flashed segment, which was presented alone (without lateral interaction) or among multiple straight segments (with lateral interaction). Each segment was presented with no context (engaging low-to-intermediate-level curvature processing), embedded within a face context as the mouth (engaging high-level face processing), or embedded within an inverted-scrambled-face context as a control for crowding. Using a simple, biologically plausible model of curvature perception, we estimated internal curvature signal and noise as the mean and standard deviation, respectively, of the Gaussian-distributed population activity of local curvature-tuned channels that best simulated behavioral curvature responses. Internal noise was increased by crowding but not by face context (irrespective of lateral interactions), suggesting prevention of noise accumulation in high-level pattern processing. In contrast, internal curvature signal was unaffected by crowding but modulated by lateral interactions. Lateral interactions (with straight segments) increased curvature signal when no contextual elements were added, but equivalent interactions reduced curvature signal when each segment was presented within a face. These opposing effects of lateral interactions are consistent with the phenomena of local-feature contrast in low-level processing and global-feature averaging in high-level processing.

the inner workings of the visual system create a subjective impression of reality with stunning resolution (e.g., Morgan 1992). This is remarkable considering the fact that neural responses are subject to random noise arising from multiple sources and that noise could potentially accumulate in downstream visual areas through feed-forward connections (e.g., Faisal et al. 2008). As the saying goes, “seeing is believing.” However, how much of what we see reflects physical reality, and how much of it reflects internal factors such as the nature of feature coding, hierarchical processing, lateral interactions, and internal noise? To elucidate the role of these internal factors in pattern perception, we investigated how internal representations of feature signals and noise were influenced by image crowding, long-range lateral interactions, and level of visual processing.

We examined visual pattern perception under conditions of brief viewing because, in these circumstances, perception is especially susceptible to the effects of intrinsic processes. For example, when a slightly tilted target Gabor patch was briefly presented either alone or among multiple vertical Gabor patches, the orientation of the target appeared to be randomly shifted from its veridical orientation on any given trial (Baldassi et al. 2006). Notably, observers were more confident when they reported a larger tilt, even in error, suggesting that random shifts in reported orientation were due to noise in the orientation processing mechanism rather than due to guessing. It has also been shown that the aspect ratio of a briefly flashed ellipse appears to be randomly deviated from its veridical aspect ratio despite being clearly visible (e.g., Regan and Hamstra 1992; Suzuki and Cavanagh 1998), suggesting that perception of aspect ratio is also susceptible to internal processing noise. In addition, Suzuki and Cavanagh (1998) reported that perceived aspect ratios were systematically exaggerated under brief viewing; that is, tall ellipses appeared taller than they actually were, and flat ellipses appeared flatter than they actually were. Thus random feature perturbations (indicative of internal feature noise) have been implicated in the processing of orientation and aspect ratio, and systematic feature exaggeration (indicative of an internal enhancement of feature signal) has been implicated in the processing of aspect ratio.

These random and systematic effects of internal feature processing under brief viewing can be quite large (Baldassi et al. 2006; Suzuki and Cavanagh 1998). Furthermore, brief viewing is common in everyday life because people frequently make saccades with only brief fixations between them (with a mode of ∼300 ms per fixation, Yarbus 1967). Random feature perturbation and systematic feature exaggeration are thus relevant to typical visual experience. We therefore conducted behavioral experiments using briefly presented stimuli to investigate how feature signal and noise are regulated in different levels of pattern processing and how they are influenced by spatial interactions including crowding and lateral interactions (at noncrowding distances).

We focused on perception of curvature because curvature is a salient feature (e.g., Wolfe et al. 1992) that is relevant to figure-ground segregation (e.g., Kanizsa 1979; Pao et al. 1999) as well as to extraction of two- (2-D) and three-dimensional (3-D) properties of surfaces and objects (e.g., Attneave 1954; Biederman 1987; Hoffman and Richards 1984; Poirier and Wilson 2006; Stevens and Brookes 1987). Curvature is also a feature that is coded in both low- and intermediate-level processing in nonhuman primates (e.g., Pasupathy and Connor 1999, 2001, 2002) and in humans (e.g., Gallant et al. 2000; Gheorghiu and Kingdom 2007; Habak et al. 2004) and integrated in high-level coding of complex features.

A curved segment presented alone is presumably coded in low-to-intermediate-level processing such as in V1 or V2 (e.g., Hegdé and Van Essen 2000, 2007) and V4 (Hegdé and Van Essen 2007; Pasupathy and Connor 1999, 2001, 2002) as the population activity of neurons tuned to different curvature values. In contrast, when a curved segment is presented within a face context (e.g., as the mouth), it is integrated into a global feature of facial expression processed by high-level visual neurons tuned to facial features (e.g., Freiwald et al. 2009; Hasselmo et al. 1989; Hoffman and Haxby 2000; Streit et al. 1999; Sugase et al. 1999). Behavioral studies have demonstrated that the presence of a face context engages global configural processing while disrupting processing of individual component features (e.g., Farah et al. 1995; Goolsby et al. 2005; Mermelstein et al. 1979; Suzuki and Cavanagh 1995; note that because our task did not require face recognition, any face configuration effect that we obtain would not be confounded by decisional factors; e.g., Richler et al. 2008; Wenger and Ingvalson 2002). We thus compared the magnitudes of internal curvature signal and noise when curved segments were presented alone (presumably engaging low-to-intermediate-level curvature processing) and when they were embedded within a face context (presumably engaging high-level face processing).

Methodologically, we combined brief stimulus presentations with a visual search paradigm for the following reasons. First, objects are typically seen in the context of other objects (rather than in isolation), and people often look for an object of interest when attending to a visual scene. Second, the perceptual effect of internal feature noise is enhanced in a search paradigm compared with presentation of one stimulus at a time (Baldassi et al. 2006). This enhancement is consistent with a simple biologically plausible model of feature search (e.g., curvature search), which assumes that search items are concurrently processed by local populations of feature-tuned (e.g., curvature-tuned) neurons, and the observer selects the population yielding the maximum magnitude of feature output (e.g., maximum curvature) as the target (e.g., Baldassi et al. 2006; Green and Swets 1966; Verghese 2001). Crucially, fitting behavioral data with this model allowed us to estimate the magnitudes of internal curvature signal and curvature noise.

The specific model we used to analyze our behavioral data is based on previous modeling of orientation search (e.g., Baldassi et al. 2006) and is grounded on simple and plausible assumptions. Suppose that a slightly curved (upward or downward) segment is briefly presented among multiple straight segments (see Fig. 1A for an example). The observer's task would be to find the curved segment and report both the magnitude and direction of its curvature. We assume that the curvatures of all segments are initially processed in parallel by sets of local “curvature channels” tuned to different curvatures (with each channel consisting of a neural population broadly tuned to a specific curvature). The perceived curvature of each segment is then coded as a central tendency (e.g., Deneve et al. 1999; Lee et al. 1988; Vogels 1990; Young and Yamane 1992) of the population activity of those local curvature channels. Because neural responses are noisy, local-channel responses to the same stimulus curvature vary from trial to trial. It is reasonable to assume that neural response variability is approximately Gaussian-distributed at the level of population activity relevant to perception (e.g., Faisal et al. 2008; Stocker and Simoncelli 2006). We thus model the central tendency of local curvature-channel population activity in response to each stimulus as a random sampling from a Gaussian distribution defined along an upward-downward curvature dimension (see Fig. 2A for an example). The mean of this Gaussian output distribution represents the magnitude of the internal curvature signal, and its standard deviation represents the average magnitude of the internal curvature noise. In a curvature search context, the channel population responding to the curved segment would have a Gaussian output distribution with its mean corresponding to the magnitude of the internal curvature signal elicited by the curved segment (a larger positive or negative mean signaling greater curvature; e.g., Fig. 3A). The remaining channel populations responding to the straight segments would have Gaussian output distributions centered at 0 (plus or minus any potential perceptual bias; see below).

Fig. 1.

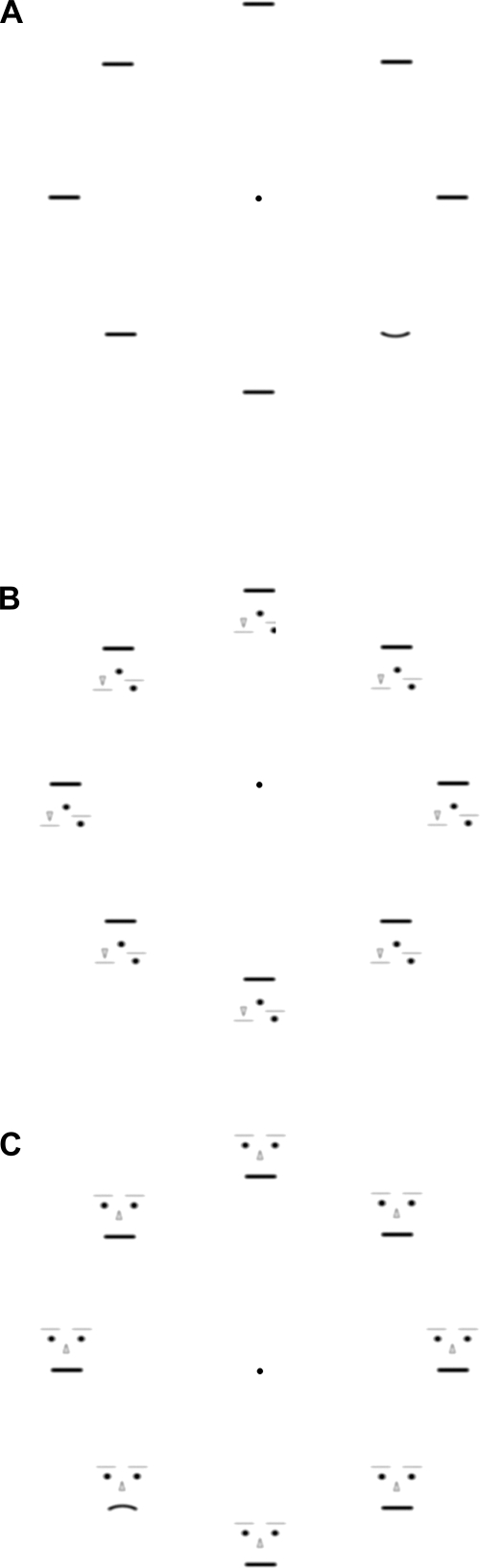
A: a no-context array with 7 straight segments and 1 upward-curved segment (an example of a curvature-present trial). B: an inverted-scrambled-face array with all straight segments (an example of a curvature-absent trial). C: a face-context array with 7 straight segments and 1 downward-curved segment (an example of a curvature-present trial).

Fig. 2.

A: the curvature-matching screen. Observers indicated the perceived curvature by selecting among the 10 displayed curvatures (top row) the 1 that most closely matched the perceived target curvature and pressing the corresponding button. The buttons were labeled “1” (corresponding to largest downward curvature) through “10” (corresponding to largest upward curvature). For clarity, a scale with negative values assigned to downward curvature and positive values assigned to upward curvature (bottom row) was used for data analyses. The assigned curvature values are proportional to the vertical stretch of the curved segments. B: the confidence-rating screen. Observers rated their confidence in the curvature judgment from little confidence to very confident by pressing 1 of the 5 buttons.

Fig. 3.

Gaussian probability distributions of local curvature-channel population outputs with their means (peaks) indicating average curvature signals and standard deviations (widths) indicating average noise magnitudes used in our model to simulate curvature search. On each simulated curvature-search trial, these populations produce randomly sampled outputs (indicated by filled circles) in parallel, and the observer selects the channel population yielding the largest curvature output and reports that value; in the illustration, the observer selects the population for which the filled circle is most deviated from null curvature (indicated by the vertical lines). A: example of a curvature-present trial (from the no-context condition in experiment 1). The Gaussian mean is shifted for the channel population responding to the upward-curved segment due to curvature signal; the Gaussian means are virtually 0 for all other local channel populations responding to the straight segments (indicating little perceptual bias). In this example, the channel population responding to the curved segment produced the largest output (indicated by the circle shifted farthest away from null curvature represented by the vertical line). A response error occurs when the largest curvature output happens to be generated (due to noise) in the opposite direction by a channel population responding to a straight segment. B: example of a curvature-absent trial. The Gaussian means are near 0 for all channel populations because all stimuli are straight and there is little coding bias. The channel population most strongly perturbed by curvature noise leads the observer to report a downward-curved segment of the corresponding curvature. Note that in these illustrations, the Gaussian channel-output distributions have been drawn in proportion to the estimates of average curvature signal and noise obtained in experiment 1.

For simplicity, we assume that outputs from all channel populations responding to the straight segments have the same standard deviation; that is, we assume that all channel populations responding to the straight segments have the same average noise magnitude. We, however, allow the possibility that the population response to a curved segment may have a different standard deviation than the population response to a straight segment, motivated by neurophysiological results. Curvature-tuned neurons, as a population, respond more strongly to a curved than to a straight contour in macaque V2 and V4 (Hegdé and Van Essen 2007; Pasupathy and Connor 1999, 2001) and inferotemporal cortex (Kayaert et al. 2005), and variability in neural response tends to increase with increased firing rate in low-level (e.g., Gur et al. 1997; Softky and Koch 1993) and high-level (e.g., Averbeck and Lee 2003; Freiwald et al. 2009; Hurlbert 2000; Lee et al. 1998a; Tolhurst et al. 1983) visual areas. These results suggest that curvature-tuned neurons should respond with more variability to curved than to straight segments. By including separate standard deviations for channel-population responses to curved and straight segments in the model, we were able to evaluate the potential behavioral consequence of increased neural response variability to curved than to straight segments.

We assume that, when asked to look for a curved segment among straight segments and report its curvature, observers compare the curvature outputs from all responding channel populations (e.g., Fig. 3A), select the population yielding the largest curvature output (regardless of upward or downward direction), and report that maximum curvature including direction (e.g., Baldassi et al. 2006). On curvature-absent trials, observers still search for a curved segment and select the target based on the channel population yielding the largest curvature output (e.g., Fig. 3B); note that all curvature outputs are due to internal noise on curvature-absent trials.

If curvature search operates in this way, we should be able to probabilistically simulate the perceived curvatures reported by each observer using the simple algorithm described above. In other words, given that appropriate means and standard deviations (free parameters of the model) are chosen for the Gaussian output distributions of the local curvature-channel populations responding to the curved and straight segments (e.g., Fig. 3), the frequency distributions of behaviorally reported curvatures should be well-fit by the simulated distributions of maximum-curvature outputs generated by the model. If the simulated distributions fit the behavioral data well, we would be able to estimate the magnitude of the internal curvature signal representing the curved segment, as the optimum Gaussian mean for the channel population responding to the curved segment. We would also be able to estimate the magnitudes of the internal curvature noise for processing of the curved and straight segments, as the optimum standard deviations for the channel populations responding to the curved and straight segments, respectively.

We randomly presented a trial with an upward-curved segment, a downward-curved segment, or no curved segment (all straight segments) with equal probability. Observers were told that a curved segment would be presented on every trial and were instructed to find it and report its curvature using the scale shown in Fig. 2A. Curved and straight segments were presented in three configurations: 1) with no context (Fig. 1A), to engage low-to-intermediate-level curvature processing; 2) each embedded within a face as the mouth (Fig. 1C), to engage high-level face processing; and 3) each embedded within an inverted-scrambled face (Fig. 1B), to engage low-to-intermediate-level curvature processing but controlling for crowding within the face context. This stimulus design, combined with the model fitting (see methods for details), allowed us to determine how the magnitudes of internal curvature signal and noise depended on image crowding and the level of pattern processing. We also intermixed trials with only one stimulus in experiment 2 to investigate potential effects of long-range spatial interactions among local curvature-channel populations. If each local population responded independently, curvature signal and noise estimated from single- and eight-stimulus trials would be equivalent. Any systematic differences in these estimates would elucidate the characteristics of spatial interactions across local channel populations.

Of particular interest were questions of whether internal curvature noise was increased by image crowding (0.6° to the nearest crowding element), whether internal curvature noise accumulated in higher-level pattern processing, whether the curvature signal was intrinsically exaggerated, how the magnitude of the curvature signal depended on image crowding and level of pattern processing (e.g., is curvature signal enhanced when a curved segment is embedded within a face as the mouth?), and how noncrowding spatial interactions (across 4.2° interstimulus distance) affected curvature signal and noise in low- and high-level processing.

EXPERIMENT 1

Methods

Observers.

Thirty-six participants including 12 graduate students and 24 undergraduate students from Northwestern University gave informed consent to participate in the experiment. They all had normal or corrected-to-normal visual acuity and were tested individually in a dimly lit room. An independent review board at Northwestern University approved the experimental protocol. We tested both graduate and undergraduate groups to ensure the stability of our results. Because the pattern of results was statistically equivalent across the two groups, we combined them in the analyses. We note that all reported effects were separately significant for each group.

Stimuli.

Each search array consisted of eight line segments evenly spaced along the circumference of an imaginary circle (5.50° radius) centered at the fixation marker (Fig. 1). On a curvature-present trial, one of the line segments was curved [upward or downward, subtending 0.80° (horizontal) by 0.14° (vertical) of visual angle], whereas the rest of the line segments were straight [subtending 0.86° (horizontal) by 0.06° (vertical)]; the curved and straight segments were of the same length. On a curvature-absent trial, all line segments were straight. The curvature of the curved segment was small (“5” or “6” in the curvature scale shown in Fig. 2A), allowing us to measure any perceptual exaggeration of curvature with high sensitivity.

The search array was presented in three different conditions. In the no-context condition, each line segment was presented with no additional contextual elements (Fig. 1A). In the face-context condition, a pair of small circles as the eyes, a pair of horizontal lines as the eyebrows, and a triangle as the nose were added to each line segment, which served as the mouth. Face-tuned neurons have been shown to respond well to schematic faces such as these (e.g., Freiwald et al. 2009). Each face subtended 1.15° (horizontal) by 1.49° (vertical) of visual angle. The contextual elements were presented with lower contrasts to reduce potential lateral masking effects. The curved and straight line segments generated different facial expressions; an upward-curved segment generated a happy expression, a downward-curved segment generated a sad expression, and a straight segment generated a neutral expression (Fig. 1C). The inverted-scrambled-face configuration was designed to control for the crowding induced by the elements added to create the face context. The geometric configuration of the added elements and their proximity (shortest distance of 0.6°) to the crucial line segment were identical for the face and inverted-scrambled-face stimuli except that the locations of the nose, eyes, and eyebrows were exchanged in the inverted-scrambled-face stimuli so that they did not look like faces (Fig. 1B). Disrupting the configuration of facial features has been shown to substantially reduce the response of high-level facial-feature-tuned neurons (e.g., Freiwald et al. 2009; Perret et al. 1982). The retinal eccentricity of the line segments was identical across all three stimulus conditions (no-context, inverted-scrambled-face, and face-context conditions). The line segments (9.6 cd/m²) and contextual elements (20.6 cd/m²) were drawn with dark contours and presented against a white (94.0 cd/m²) background.

The no-context, inverted-scrambled-face, and face-context conditions were run in separate blocks (each preceded by 6 practice trials) with block order counterbalanced across observers. Within each block of 48 trials, ⅓ contained an upward-curved segment, ⅓ contained a downward-curved segment, and ⅓ contained no curved segment, with these trials randomly intermixed. On trials containing a curved segment, its location was equiprobable among the 8 locations. All stimuli were presented on a 19-in. cathode ray tube (CRT) monitor at a viewing distance of 100 cm.

Procedure.

Each trial began with the presentation of a fixation marker for 1,000 ms. A search array then appeared for 100 ms, and the fixation marker disappeared after 200 ms. Observers were told that a curved segment would be presented in every array, and they were instructed to find it and report its curvature using a curvature-matching screen (Fig. 2A) presented at the end of each trial. Observers selected the curvature that most closely matched the perceived curvature by pressing the corresponding number on a button pad. To encourage subtle curvature discriminations, the curvature-matching screen did not contain an option to report a straight segment. Note that the model simulation was subjected to the same response constraint (see Modeling below). On response, a confidence-rating screen appeared, prompting observers to rate their confidence in the preceding curvature judgment on a scale of 1–5 with 1 indicating “little confidence” and 5 indicating “very confident” (Fig. 2B). Confidence ratings were used to verify that internal noise acted like a curvature signal rather than simply causing perceptual uncertainty (e.g., Baldassi et al. 2006) by demonstrating that even on curvature-absent trials (where any perceived curvature must be generated by internal noise), observers were more confident when they reported a larger curvature.

Modeling.

The logic and assumptions underlying the model we used to estimate internal curvature signal and noise from behavioral magnitude-estimation data are described above in the Introduction.

To estimate the internal curvature bias and noise, we first simulated the histogram of the behavioral curvature responses from the curvature-absent trials separately for each observer and condition (no context, inverted-scrambled-face, and face-context). We used the mean and standard deviation of the Gaussian-shaped curvature-channel population-output distribution (assumed to be the same for each local curvature-channel population) as the fitting parameters. Each trial was simulated by 1) randomly sampling 8 times from the population-output distribution (simulating parallel outputs from the 8 local curvature-channel populations responding to the 8 straight segments), 2) selecting the largest sampled curvature output (either upward or downward), and 3) recording this maximum curvature as the behaviorally reported curvature.

In our experimental design, observers matched their perceived curvature to the closest value among a set of discrete response choices. In other words, observers binned continuous values of perceived curvature into the categories on the response screen. We incorporated this aspect of our behavioral design into our simulation by binning the continuous curvature values generated by the model into the discrete response choices (e.g., model output values between 0 and 1 would be binned as a perceived value of 0.5; see the coding of behavioral response shown in the bottom row in Fig. 2A). Our observers and simulation were thus subjected to the same response constraints. We simulated 20,000 curvature-absent trials to construct the probability distribution of curvature responses and assessed the goodness of fit by computing the sum of squared errors between the simulated and behavioral histograms of curvature responses. Using a gradient descent method with iterative 20,000-trial simulations, we determined the optimum values of the mean and standard deviation of the Gaussian population-output distribution that minimized this error, and those values respectively provided estimates of the magnitudes of curvature bias and curvature noise in response to a straight segment for each observer for each stimulus condition.

In the rare cases where an observer only used 2 adjacent response choices (e.g., “5” and “6”) and used them equally frequently, any noise standard deviation below a certain value would fit the response distribution equally well. This occurred for 2 out of 36 observers in this experiment (and 2 out of 12 observers in experiment 2) and only in the no-context condition and could have occurred because these observers only perceived straight segments. For these observers, we entered both the upper-limit value and 0 (i.e., the full potential range of estimated noise) as their noise standard deviations for the no-context condition for analyses. In results (both for this experiment and experiment 2), we only present the analyses based on the upper-limit values from these observers unless statistical inferences differed depending on which value was used. Note that because the mean estimated noise was always lowest in the no-context condition (compared with the inverted-scrambled-face and face-context conditions; see results), using the upper-limit values for the no-context condition made our analyses of the effects of the stimulus conditions on curvature noise conservative.

After estimating the bias and noise for the channel populations responding to the straight segments based on the curvature-absent trials, we similarly estimated the curvature signal and noise elicited by the curved segment by simulating the histogram of behavioral curvature responses from the curvature-present trials.

To attempt to fit the behavioral data with a minimal set of fitting parameters, we assumed that the magnitude of the internal curvature signal was the same for the upward- and downward-curved segments. To confirm that this assumption was reasonable, we calculated the mean ratings from the upward- and downward-curvature trials relative to the bias obtained from the curvature-absent trials. In this way, we estimated the difference in the perceived curvature magnitude for the upward- and downward-curved segments. Neither the upward nor downward curvature was consistently rated larger in magnitude across conditions, and the small numerical differences did not reach statistical significance. Given that there were no consistent magnitude differences, we felt that assigning separate fitting parameters to the upward- and downward-curvature trials might overfit the data by fitting spurious variability across observers. Second, as shown in the supplemental figures (available in the data supplement online at the Journal of Neurophysiology web site), the model fits are already very good, indicating that any fitting improvement with the extra free parameter would be inconsequential.

We also assumed that the bias additively contributed to the signal from the curved segment. In other words, we assumed that the Gaussian-output mean for the local channel population responding to a curved segment was the sum of the internal curvature signal (a fitting parameter) and the bias estimated from the curvature-absent trials (for each condition and observer). Note that because the biases were much smaller than the curvature signals (see the results sections), violation of the assumption of linear summation would have little consequence on our conclusions. The same bias estimate was also used as the Gaussian-output mean for the local channel populations responding to straight segments.

Neurophysiological results suggest that response noise may be greater when the neural population involved in curvature coding responds to a curved compared with a straight stimulus (see the Introduction). We thus included the Gaussian-output standard deviation for the local channel population responding to a curved segment as a second fitting parameter. For the Gaussian-output standard deviation for the local channel populations responding to straight segments, we used the value estimated from the curvature-absent trials (for each observer and condition). In this way, we fit both the curvature-present and -absent trials using two free parameters.

To simulate each curvature-present trial, we 1) randomly sampled once from the Gaussian population-output distribution for the curved segment [with its mean (minus the bias) and standard deviation as the fitting parameters] and 7 times from the Gaussian population-output distribution for the straight segments (with their means and standard deviations derived from the curvature-absent trials), 2) selected the largest sampled curvature output (either upward or downward), and 3) recorded this maximum curvature as the behaviorally reported curvature. We simulated 20,000 such trials (10,000 trials for each of the 2 curvature directions, taking into account the bias) to construct the histogram of curvature responses and assessed the goodness of fit by computing the sum of squared errors between the simulated and behavioral histograms of curvature responses. Using a gradient descent method with iterative 20,000-trial simulations, we determined the optimum values for the mean (minus the bias) and standard deviation of the Gaussian output distribution for the channel population responding to the curved segment that minimized this error, and those values provided estimates of curvature signal and noise in response to a curved segment for each observer for each condition.

Note that by randomly sampling from each Gaussian population-output distribution in our simulation, we assumed that local curvature-channel populations (responding to the 8 stimuli) were independent in terms of their response variability. Neurophysiological results have shown that neural noise is relatively independent across neighboring neurons in V1 (Gawne et al. 1996; Reich et al. 2001; van Kan et al. 1985), V5/MT (Zohary et al. 1994), inferotemporal cortex (only 5–6% correlation; Gawne and Richmond 1993), perirhinal cortex (Erickson et al. 2000), supplementary motor cortex (Averbeck and Lee 2003), and parietal cortex (Lee et al. 1998a), suggesting that uncorrelated noise is a general principle of cortical organization (Gawne et al. 1996). This assumption has also been used to successfully model orientation search (Baldassi et al. 2006; see discussion for details). Even if noise was uncorrelated across channel populations, curvature signals might still be influenced by long-range interactions across the channel populations in the context of our search task. This possibility was investigated in experiment 2.

Results

The histograms of behavioral curvature responses from the curvature-absent and -present trials were both well-fit by the model for all stimulus conditions: no context, inverted-scrambled-face, and face-context (Supplemental Fig. S1, A–F). These good fits support the assumptions of the model and justify its use for estimating the internal curvature bias, signal, and noise within the population activity of curvature channels and for determining how the signal and noise depend on crowding and facial organization.

Fitting the curvature-absent trials to estimate the internal curvature bias and noise for a channel population responding to a straight segment presented among other straight segments.

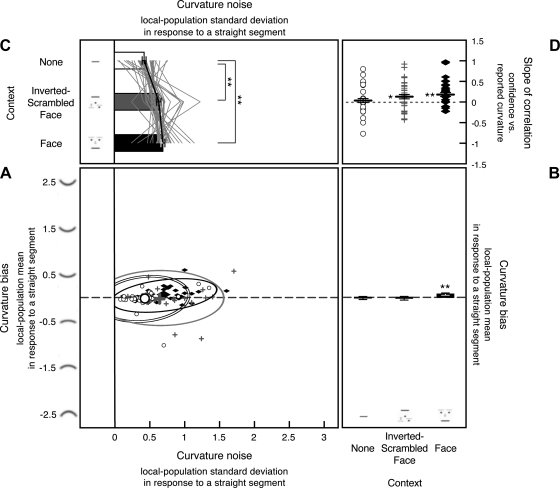
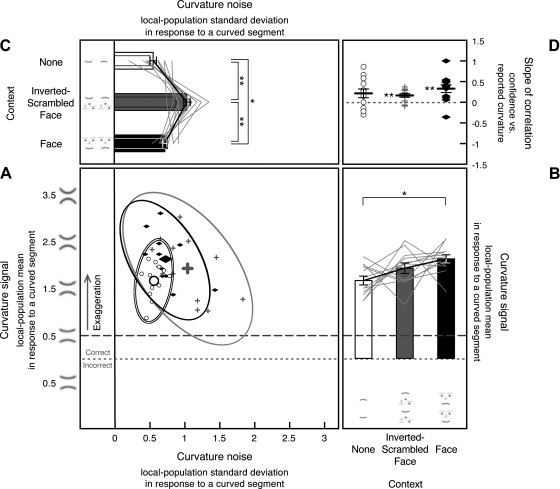
For each observer, we fit the model to his or her behavioral response histogram from curvature-absent trials to estimate the internal curvature signal (in this case, bias because all stimuli were straight segments) and curvature noise for each stimulus condition (see Supplemental Fig. S1, A–C, for the goodness of model fits). The scatterplot presented in Fig. 4A shows the estimates of bias and noise for each observer for each condition. Each open circle represents the curvature bias (y-value) and noise (x-value) from one observer for the no-context condition. Similarly, each gray plus symbol and each filled black diamond represent the bias and noise from one observer for the inverted-scrambled-face and face-context conditions, respectively. The large circle, plus symbol, and diamond represent the group means with the ellipses indicating the 95% confidence limits.

Fig. 4.

Internal curvature bias (i.e., the Gaussian mean of the curvature-channel population output) and noise (i.e., the Gaussian standard deviation of the channel-population output) in response to a straight segment estimated from 8-stimulus curvature-absent trials in experiment 1, shown along with the slopes for the correlation between reported curvature and confidence. A: scatterplot showing each observer's internal curvature noise (x-axis) and curvature bias (y-axis) from each condition, with open circles showing estimates for the no-context condition, gray “plus” symbols showing estimates for the inverted-scrambled-face condition, and filled black diamonds showing estimates for the face-context condition, with corresponding 95% confidence ellipses. Large circles, plus symbols, and diamonds indicate the group means for the 3 stimulus conditions. The dashed horizontal line indicates no curvature bias. Note that, although the scatterplot shows data for all observers, the consistent effect of stimulus conditions on the magnitude of curvature noise is obscured by the relatively large individual differences in the baseline levels of noise (see main text for details). B: the y-dimension of the scatterplot (estimated internal curvature bias). Because there was little perceptual bias across all stimulus conditions, only the group means (bar graphs) are presented with the error bars representing ±1 SE. C: the x-dimension of the scatterplot (estimated internal curvature noise) presented as a line graph per observer with each observer's overall mean aligned to the group mean to show the consistent condition effects. The accompanying bar graphs show the group means with the error bars representing ±1 SE (adjusted for repeated-measures comparisons). For the 2 observers whose noise magnitudes could not be precisely determined for the no-context condition, we used the maximum noise estimates (see methods for experiment 1 for details). D: slope of the correlation between reported curvature and confidence shown for each observer for each stimulus condition (note that incidences of similar slopes produced overlapping symbols, giving the impression of missing data). The black horizontal bars indicate the mean slopes with the error bars representing ±1 SE. For A–D, **P < 0.01, and *P < 0.05.

This 2-D scatterplot is informative in that it shows the estimates of curvature bias and noise for all observers for all conditions. However, the consistent effects of stimulus conditions on the magnitude of curvature noise are obscured because the scatterplot includes the relatively large baseline differences in noise across observers that are orthogonal to evaluating the condition effects. Thus, in Fig. 4C, we show the x-dimension of the scatterplot (noise estimates), where each line graph represents the estimated noise magnitudes for the three conditions for one observer, with the line graphs for different observers aligned so that the overall mean of each line graph coincides with the grand mean (thus effectively subtracting the baseline differences across observers). These line graphs show (along with statistical analyses) that the three stimulus conditions produced consistent effects on the internal curvature noise across observers.

Image crowding increased internal curvature noise; the estimated noise significantly increased in both of the crowded conditions (the inverted-scrambled-face and face-context conditions) compared with the no-context condition [t(35) = 4.044, P < 0.001, d = 0.674 for the inverted-scrambled-face condition vs. the no-context condition, and t(35) = 5.668, P < 0.001, d = 0.945 for the face-context condition vs. the no-context condition]. The face context, however, did not increase curvature noise compared with the crowding-matched control [t(35) = 1.063, not significant (n.s.), d = 0.177 for the face-context condition vs. inverted-scrambled-face condition]. These results suggest that image crowding increases curvature noise. The results are also consistent with the idea that noise does not accumulate in high-level face processing compared with low-to-intermediate-level curvature processing.

There was no bias in perceived curvature for the no-context condition [t(35) = 0.445, n.s., d = 0.074] or the inverted-scrambled-face condition [t(35) = 0.465, n.s., d = 0.078]. In the face-context condition, there was a small but significant bias [t(35) = 2.976, P < 0.01, d = 0.496] so that straight segments tended to be seen as upward-curved (average biases shown in Fig. 4B). Because this bias occurred only in the face-context condition, it is likely generated in high-level face processing, perhaps indicating a happy bias. We have no explanation for this small bias, but it is tangential to the primary goal of the study.

We used confidence ratings to confirm that the variability in the reported curvature was due to internal noise in curvature processing rather than to guessing (as was previously confirmed for orientation search; Baldassi et al. 2006). Because all stimuli were straight on curvature-absent trials, any variability in the reported curvatures on those trials must have been either due to curvature perception generated by noise or to guessing from uncertainty.

Anecdotally, during the postexperiment debriefing, observers were surprised to find that some trials did not contain curved segments, suggesting that they actually saw curved segments on curvature-absent trials. If the curvatures reported on curvature-absent trials were generated by internal curvature noise, observers should have been more confident in reporting a larger noise-generated curvature because they would have actually perceived a larger curvature in that case. Confidence ratings should then be positively correlated with the magnitude of reported curvature. In contrast, if reported curvatures on curvature-absent trials were due to random guessing, there should be no systematic relationship between reported curvatures and confidence ratings.

We thus computed the slope for the linear correlation between reported curvature and confidence rating on curvature-absent trials for each observer for each condition. Outliers beyond the 95% confidence ellipse were eliminated before computing the correlation for each observer in this and all other correlation analyses. The correlation slopes from all observers are shown for each stimulus condition in Fig. 4D. The mean slopes were significantly positive for the inverted-scrambled-face condition [t(35) = 2.409, P < 0.05, d = 0.401] and the face-context condition [t(35) = 3.725, P < 0.001, d = 0.629] but not for the no-context condition [t(35) = 0.717, n.s., d = 0.119].

These results support the assumption of our model that internal curvature noise contributes to curvature perception (see Baldassi et al. 2006 for a similar correlation between reported orientation and confidence in orientation search) at least for the inverted-scrambled-face and face-context conditions. We cannot confirm, however, that internal noise generated curvature perception in the no-context condition because of the nonsignificant reported-curvature-vs.-confidence correlation. It is thus possible that our estimates of noise in the no-context condition may reflect noise in the decision stage rather than the curvature coding stage. Alternatively, it is also possible that we did not obtain a significant reported-curvature-vs.-confidence correlation for the no-context condition because the response variability was relatively small in that condition. Regardless, the results clearly suggest that image crowding (in the inverted-scrambled-face and face-context conditions) increases noise compared with the no-context condition and that the increased noise arises in the curvature coding process.

Fitting the curvature-present trials to estimate the internal curvature signal and noise for a channel population responding to a curved segment presented among straight segments.

For each observer, we fit the model to his or her behavioral response histogram from curvature-present trials to estimate the internal curvature signal and curvature noise for each stimulus condition (see Supplemental Fig. S1, D–F, for the goodness of model fits). As above, the scatterplot (Fig. 5A) shows estimates of curvature signal (y-values) and noise (x-values) for all observers for each stimulus condition. As mentioned above, the stimulus condition effects are obscured in the scatterplot because it includes the baseline individual differences in the overall levels of curvature signal and noise. To reveal the consistent condition effects on curvature signal and noise unconfounded by the baseline individual differences, Fig. 5B shows the y-dimension (signal estimates), and Fig. 5C shows the x-dimension (noise estimates), both with the baseline individual differences removed (see above).

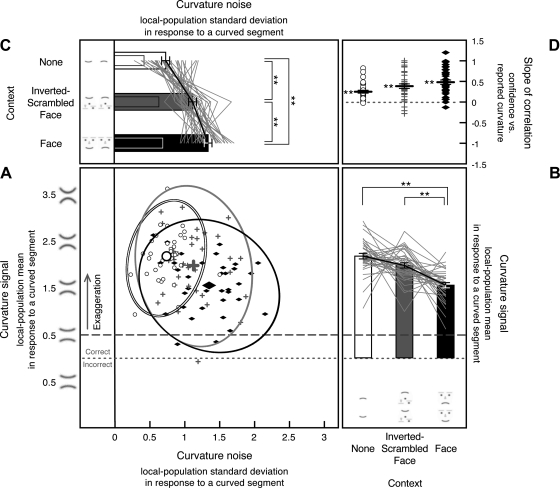
Fig. 5.

Internal curvature signal (i.e., the Gaussian mean of the curvature-channel population output) and noise (i.e., the Gaussian standard deviation of the channel-population output) in response to a curved segment estimated from 8-stimulus curvature-present trials in experiment 1, shown along with the slopes for the correlation between reported curvature and confidence. A: scatterplot showing each observer's internal curvature noise (x-axis) and curvature signal (y-axis) from each condition, with open circles showing estimates for the no-context condition, gray plus symbols showing estimates for the inverted-scrambled-face condition, and filled black diamonds showing estimates for the face-context condition, with corresponding 95% confidence ellipses. Estimates of curvature signal are collapsed across trials containing an upward-curved segment and those containing a downward-curved segment so that the values on the y-axis reflect the absolute magnitude of reported curvature independent of direction (see methods for experiment 1). Estimates of internal curvature signal above the dotted line indicate correct encoding of curvature direction, and those below the dotted line indicate incorrect encoding of curvature direction. Estimates of internal curvature signal above the dashed line (the veridical curvature magnitude) indicate exaggeration. As in Fig. 4, the scatterplot shows data for all observers, but it obscures the consistent effects of stimulus conditions on the magnitudes of curvature signal and noise because of the relatively large individual differences in the baseline levels of internal curvature signal and noise. B: the y-dimension of the scatterplot (estimated internal curvature signal) presented as a line graph per observer with each observer's overall mean aligned to the group mean to show the consistent condition effects. The accompanying bar graphs show the group means with the error bars representing ±1 SE (adjusted for repeated-measures comparisons). C: the x-dimension of the scatterplot (estimated internal curvature noise) presented as a line graph per observer with each observer's overall mean aligned to the group mean to show the consistent condition effects. The accompanying bar graphs show the group means with the error bars representing ±1 SE (adjusted for repeated-measures comparisons). The internal curvature noise in response to a straight segment (reproduced from Fig. 4C) is shown for comparison as overlapping narrow bars. D: slope of the correlation between reported curvature and confidence shown for each observer for each stimulus condition (note that incidences of similar slopes produced overlapping symbols, giving the impression of missing data). The black horizontal bars indicate the mean slope with the error bars representing ±1 SE. For A–D, **P < 0.01.

The estimated internal noise in response to a curved segment increased with crowding and further increased with a face context (Fig. 5C). Internal noise was greater for the inverted-scrambled-face condition [t(35) = 6.132, P < 0.0001, d = 1.022] and the face-context condition [t(35) = 8.841, P < 0.0001, d = 1.473] compared with the no-context condition. Internal noise was also greater for the face-context condition than for the inverted-scrambled-face condition [t(35) = 4.080, P < 0.001, d = 0.680]. The amount of noise increase due to face processing (from the inverted-scrambled-face condition to the face-context condition), however, was small relative to the amount of noise increase due to crowding (from the no-context to the inverted-scrambled-face condition), t(35) = 1.711, P < 0.09, d = 0.285 (Fig. 5C). Moreover, face processing did not increase noise for responses to straight segments (Fig. 4C) nor did face processing increase noise for responses to curved or straight segments in experiment 2. Thus, whereas crowding in a curvature search context consistently increased curvature noise (across all conditions in this study), engaging face processing overall had little impact on curvature noise.

When the results from the curvature-present and -absent trials are compared, we find that the estimated internal noise increased when a channel population responded to a curved segment compared with when it responded to a straight (null-curvature) segment. The increase was multiplicative in that, although the internal noise in response to a straight segment (estimated from the curvature-absent trials) differed across the three conditions (Fig. 4C, and reproduced as overlapping narrow bars in Fig. 5C), the percentage of noise increase in response to a curved segment was equivalent for the three conditions [131% increase for the no-context condition, SE (adjusted for repeated-measures comparisons) = 32%, t(35) = 4.069, P < 0.001, d = 0.678, 119% increase for the inverted-scrambled-face condition, SE = 17%, t(35) = 6.867, P < 0.0001, d = 1.146, and 138% increase for the face-context condition, SE = 24%, t(35) = 5.743, P < 0.0001, d = 0.957] with no significant difference among the conditions, F(2,70) = 0.1996, n.s., η_p² = 0.006.

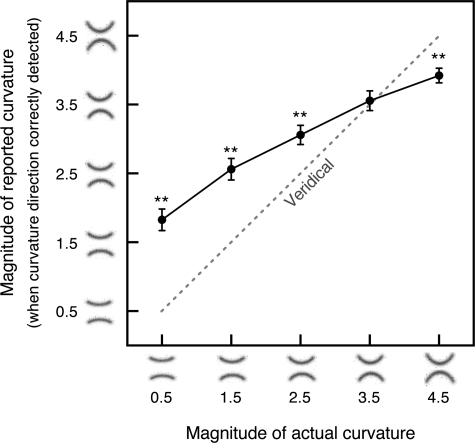
The estimated curvature signal was exaggerated in all three conditions. If perception of curvature were veridical, the channel-population-output mean in response to the curved segment would equal 0.5 according to the scale we used (Fig. 2A). In contrast, the obtained population-output mean for a curved segment was substantially greater than 0.5 for all three conditions [t(35) = 19.742, P < 0.0001, d = 3.290 for the no-context condition, t(35) = 12.596, P < 0.0001, d = 2.099 for the inverted-scrambled-face condition, and t(35) = 10.869, P < 0.0001, d = 1.811 for the face-context condition; Fig. 5B].

Image crowding did not influence the magnitude of curvature signal [t(35) = 1.930, n.s., d = 0.322 for the no-context condition vs. the inverted-scrambled-face condition]. In contrast, the face context significantly reduced curvature signal compared with the crowding-matched inverted-scrambled-face condition, t(35) = 4.444, P < 0.0001, d = 0.741, and compared with the no-context condition, t(35) = 6.170, P < 0.0001, d = 1.028. These results suggest that in a curvature search context, briefly presented curvatures are substantially exaggerated in the internal representation and that the magnitude of curvature signal is unaffected by image crowding but reduced in high-level face processing.

The magnitude of reported curvature was positively correlated with confidence on curvature-present trials in all three conditions, indicated by significantly positive slopes (Fig. 5D), t(35) = 7.133, P < 0.0001, d = 1.188 for the no-context condition, t(35) = 6.941, P < 0.0001, d = 1.157 for the inverted-scrambled-face condition, and t(35) = 9.039, P < 0.0001, d = 1.507 for the face-context condition. This confirms that internal curvature noise alters the perceived curvature of a curved segment in addition to inducing perceived curvature on straight segments.

The results from this experiment suggest that the model we used appropriately describes concurrent processing of curvature at multiple locations in a curvature search context, thus providing estimates of internal bias, signal, and noise in curvature processing. With respect to the question of how image crowding and level of processing influence signal and noise in curvature processing, the results suggest 1) that curvature noise increases with crowding but does not substantially increase in high-level face processing, and 2) that curvature signal is exaggerated in brief viewing with its magnitude unaffected by crowding but reduced in high-level face processing. We replicated and extended these results in experiment 2.

EXPERIMENT 2

In the previous experiment, search displays always contained eight stimuli. Thus at least some portion of the estimated curvature signal, especially exaggeration, and curvature noise could have been generated by spatial interactions across the local curvature-channel populations that responded to the eight stimuli. To address this issue, we randomly intermixed trials in which only one stimulus was presented. We then compared the curvature signal and noise estimated from eight-stimulus trials with those estimated from single-stimulus trials.

If the channel populations activated by the eight stimuli responded independently, the noise magnitudes estimated from eight-stimulus trials should be equivalent to those estimated from single-stimulus trials. If the channel populations influenced one another through excitatory (or inhibitory) interactions, the noise magnitudes estimated from eight-stimulus trials would be larger (or smaller) than those estimated from single-stimulus trials.

As for the perceptual exaggeration of curvature obtained in experiment 1, it could be the result of a feature-contrast effect between the curved segment and straight segments. Similar contrast effects have been reported for perception of orientation and spatial frequency, known as “off-orientation looking” and “off-frequency looking” (Losada and Mullen 1995; Mareschal et al. 2008; Perkins and Landy 1991; Solomon 2000; Solomon 2002). If the curvature exaggeration obtained in experiment 1 was solely due to this type of feature-contrast effect, perceived curvature should not be exaggerated when only one curved stimulus is presented. In contrast, if perceptual exaggeration is an integral part of brief curvature coding, perceived curvature should still be exaggerated on single-stimulus trials.

Methods

Observers.

Twelve undergraduate students from Northwestern University gave informed consent to participate in the experiment. They all had normal or corrected-to-normal visual acuity and were tested individually in a dimly lit room. An independent review board at Northwestern University approved the experimental protocol.

Stimuli, procedure, and modeling.

The stimuli and design were identical to those used in experiment 1 except that on half of the trials, only 1 stimulus (either an upward-curved, downward-curved, or straight segment with an equal probability) was presented randomly at 1 of the 8 positions. The single- and 8-stimulus trials were randomly intermixed within each block of 96 trials. As in experiment 1, the no-context, inverted-scrambled-face, and face-context conditions were run in separate blocks (each preceded by 6 practice trials) with block order counterbalanced across observers. The modeling and fitting procedures were the same as in experiment 1.

Results

The histograms of behavioral curvature responses from both curvature-absent and -present trials and both eight- and single-stimulus trials were well-fit by the model for all stimulus conditions: no context, inverted-scrambled-face, and face-context; see Supplemental Fig. S2, A–F, for eight-stimulus trials and Supplemental Fig. S3, A–F, for single-stimulus trials. These good fitting results (as in experiment 1) confirm that the model is appropriate for estimating the internal curvature signal and noise for the perception of single and multiple stimuli. We determined how the estimates of curvature signal and noise as well as their dependence on crowding and facial context differed between eight- and single-stimulus trials.

Fitting the eight-stimulus curvature-absent trials to estimate the internal curvature bias and noise for a channel population responding to a straight segment presented among other straight segments.

As in experiment 1, we fit the model to each observer's behavioral response histogram from eight-stimulus curvature-absent trials to estimate the internal curvature bias and noise for each stimulus condition (see Supplemental Fig. S2, A–C, for the goodness of model fits). The scatterplot presented in Fig. 6A shows estimates of curvature bias (y-values) and noise (x-values) for all observers for each stimulus condition. To illustrate the condition effects on curvature noise unconfounded by the baseline individual differences, the line graphs in Fig. 6C show the x-dimension (noise estimates) with the baseline individual differences removed (see experiment 1 results for details). Average biases are shown in Fig. 6B.

Fig. 6.

A–D: internal curvature bias (i.e., the Gaussian mean of the curvature-channel population output) and noise (i.e., the Gaussian standard deviation of the channel-population output) in response to a straight segment estimated from 8-stimulus curvature-absent trials in experiment 2, shown along with the slopes for the correlation between reported curvature and confidence. The formats and labels are identical to those in Fig. 4, which presents similar data from experiment 1.

There was little bias in perceived curvature for the no-context condition [t(11) = 0.871, n.s., d = 0.251] or for the inverted-scrambled-face condition [t(11) = 1.351, n.s., d = 0.39] as in experiment 1. The small happy bias that we obtained in experiment 1 for the face-context condition (i.e., straight segments tending to appear upward-curved) was not significant in this experiment [t(11) = 0.890, n.s., d = 0.260; Fig. 6B].

As in experiment 1, image crowding increased internal curvature noise [greater noise in the inverted-scrambled-face condition compared with the no-context condition, t(11) = 2.427, P < 0.05, d = 0.701, and greater noise in the face-context condition compared with the no-context condition, t(11) = 2.619, P < 0.05, d = 0.756], but the face context did not further increase noise [equivalent noise for the face-context and inverted-scrambled-face conditions, t(11) = 1.459, n.s., d = 0.421; Fig. 6C]. It may appear in Fig. 6C that two observers yielded atypically strong effects of crowding (no-context vs. inverted-scrambled-face). However, the statistical results remain the same even if we remove these observers from the analysis; image crowding still significantly increased curvature noise [t(9) = 2.417, P < 0.05, d = 0.698 for inverted-scrambled-face vs. no-context, and t(9) = 2.346, P < 0.05, d = 0.677 for face-context vs. no-context] with no further increase in noise due to face context [t(9) = 1.064, n.s., d = 0.307 for face-context vs. inverted-scrambled-face]. These results support the conclusions from experiment 1 that image crowding increases curvature noise, but this noise does not accumulate in high-level face processing compared with low-to-intermediate-level curvature processing.

We also replicated the positive correlations between the magnitude of reported curvature and confidence ratings, confirming that responses on the curvature-absent trials reflected perceived curvatures generated by internal noise rather than random responses due to uncertainty, at least in the inverted-scrambled-face and face-context conditions. The slopes were significantly positive for the inverted-scrambled-face condition, t(11) = 2.464, P < 0.05, d = 0.711, and for the face-context condition, t(11) = 2.294, P < 0.05, d = 0.662, but not significant for the no-context condition, t(11) = 0.873, n.s., d = 0.252 (Fig. 6D). Thus, as in experiment 1, our estimates of noise in the no-context condition may reflect noise at the decision stage and not the curvature coding stage. As with experiment 1, however, relatively low variability in the reported curvature in the no-context condition could have made a correlation difficult to detect. Note that on curvature-present trials, the correlation slopes were significantly positive for all stimulus conditions as in experiment 1, t(11) = 3.700, P < 0.01, d = 1.068 for the no-context condition, t(11) = 5.344, P < 0.0001, d = 1.543 for the inverted-scrambled-face condition, and t(11) = 6.881, P < 0.0001, d = 1.986 for the face-context condition (Fig. 7D), confirming that internal curvature noise alters perceived curvature of a curved segment in addition to inducing perceived curvature on straight segments.

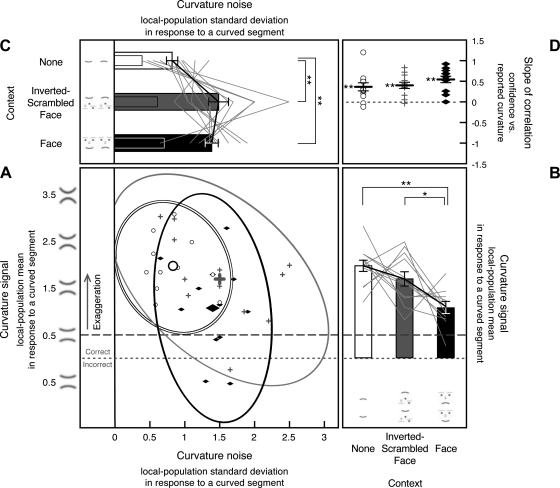
Fig. 7.

Internal curvature signal (i.e., the Gaussian mean of the curvature-channel population output) and noise (i.e., the Gaussian standard deviation of the channel-population output) in response to a curved segment estimated from 8-stimulus curvature-present trials in experiment 2, shown along with the slopes for the correlation between reported curvature and confidence. The formats and labels are identical to those in Fig. 5, which presents similar data from experiment 1. For A–D, **P < 0.01, and *P < 0.05.

Fitting eight-stimulus curvature-present trials to estimate the internal curvature signal and noise for a channel population responding to a curved segment presented among straight segments.

We fit the model to each observer's behavioral response histogram from eight-stimulus curvature-present trials to estimate the internal curvature signal and noise for each stimulus condition (see Supplemental Fig. S2, D–F, for the goodness of model fits). The scatterplot presented in Fig. 7A shows estimates of curvature signal (y-values) and curvature noise (x-values) for all observers for each stimulus condition. To illustrate the condition effects on curvature signal and noise unconfounded by the baseline individual differences, the line graphs in Fig. 7B show the y-dimension (signal estimates), and those in Fig. 7C show the x-dimension (noise estimates), both with the baseline individual differences removed (see experiment 1 results for details).

The estimated internal noise in response to a curved segment increased with crowding, but it did not further increase with a face context (Fig. 7C). Internal noise was greater for the inverted-scrambled-face condition [t(11) = 3.161, P < 0.01, d = 0.912] and the face-context condition [t(11) = 5.459, P < 0.001, d = 1.576] compared with the no-context condition, but noise was not greater in the face-context condition compared with the inverted-scrambled-face condition [t(11) = 0.438, n.s., d = 0.126].

As in experiment 1, a comparison between the results from the curvature-absent and -present trials shows that the estimated internal noise increased when a channel population responded to a curved segment compared with when it responded to a straight segment (estimated from the curvature-absent trials), and the percentage of increase was equivalent for the three conditions [139% increase for the no-context condition, SE (adjusted for repeated-measures comparisons) = 41%, t(11) = 3.386, P < 0.01, d = 0.977, 199% increase for the inverted-scrambled-face condition, SE = 50%, t(11) = 3.997, P < 0.01, d = 1.154, and 184% increase for the face-context condition, SE = 56%, t(11) = 3.274, P < 0.01, d = 0.945] with no significant difference among the conditions, F(2,22) = 0.374, n.s., η_p² = 0.031 (Fig. 7C; the overlapping narrow bars show noise in response to a straight segment reproduced from Fig. 6C). Thus, as in experiment 1, the estimated curvature noise increased multiplicatively when the curvature-channel population responded to a curved segment compared with when it responded to a straight segment.

Also as in experiment 1, the estimated curvature signal was exaggerated in all three conditions; the obtained channel-population-output mean for a curved segment was substantially greater than the veridical value of 0.5 for the no-context condition [t(11) = 8.784, P < 0.0001, d = 2.536], the inverted-scrambled-face condition [t(11) = 4.460, P < 0.001, d = 1.287], and the face-context condition [t(11) = 1.988, P = 0.072, d = 0.574; Fig. 7B]. Importantly, image crowding did not influence the magnitude of curvature signal [t(11) = 1.117, n.s., d = 0.322 for the no-context condition vs. the inverted-scrambled-face condition], but face context significantly reduced curvature signal compared with both the no-context condition [t(11) = 5.228, P < 0.001, d = 1.509] and the crowding-matched inverted-scrambled-face condition [t(11) = 2.596, P < 0.05, d = 0.749], replicating experiment 1.

Fitting the single-stimulus curvature-absent trials to estimate the internal curvature bias and noise for a channel population responding to an isolated straight segment.

We fit the model to each observer's behavioral response histogram from single-stimulus curvature-absent trials to estimate the internal curvature bias and noise for each stimulus condition in the absence of interstimulus interactions (see Supplemental Fig. 3, A–C, for the goodness of model fits). The scatterplot presented in Fig. 8A shows estimates of curvature bias (y-values) and noise (x-values) for all observers for each stimulus condition. To illustrate the condition effects on curvature noise unconfounded by the baseline individual differences, the line graphs in Fig. 8C show the x-dimension (noise estimates) with the baseline individual differences removed (see experiment 1 results for details). Average biases are shown in Fig. 8B.

Fig. 8.

A–D: internal curvature bias (i.e., the Gaussian mean of the curvature-channel population output) and noise (i.e., the Gaussian standard deviation of the channel-population output) in response to a straight segment estimated from single-stimulus curvature-absent trials in experiment 2, shown along with the slopes for the correlation between reported curvature and confidence. The formats and labels are identical to those in Figs. 4 and 6, which present similar data for 8-stimulus trials.

There was little bias in perceived curvature for the no-context condition [t(11) = 1.724, n.s., d = 0.497] or for the inverted-scrambled-face condition [t(11) = 1.408, n.s., d = 0.406], but there was a trend for a happy bias for the face-context condition (i.e., straight segments tended to appear upward-curved), t(11) = 2.032, P = 0.067, d = 0.587 (Fig. 8B).

Image crowding increased internal curvature noise [greater noise in the inverted-scrambled-face condition compared with the no-context condition, t(11) = 3.454, P < 0.01, d = 0.997], but the face context did not further increase noise relative to the crowding-matched control condition [equivalent noise for the face-context and inverted-scrambled-face conditions, t(11) = 0.659, n.s., d = 0.190; Fig. 8C]. One may notice in Fig. 8C that one observer appears to be an outlier (atypically low noise in the no-context condition and atypically high noise in the face-context condition). With this observer removed, image crowding still increased internal curvature noise [t(10) = 3.336, P < 0.01, d = 0.962], but the face context actually reduced noise relative to the crowding-matched control condition [t(10) = 2.413, P < 0.05, d = 0.696] and did not increase noise relative to the no-context condition [t(10) = 1.373, n.s., d = 0.396]. Thus, when a single stimulus is presented, engaging face processing may improve curvature perception by reducing noise. In either case, these results support the conclusions from the analyses of eight-stimulus trials, suggesting that whether a single stimulus or multiple stimuli are presented, crowding each stimulus with proximate (0.6°) elements increases curvature noise, but this noise does not seem to accumulate in high-level face processing compared with low-to-intermediate-level curvature processing.

The slopes of the correlations between the magnitudes of reported curvature and confidence ratings were not significantly positive for any of the three conditions [t(11) = 1.0, n.s., d = 0.288 for the no-context condition, t(11) = 1.481, n.s., d = 0.427 for the inverted-scrambled-face condition, and t(11) = 1.511, n.s., d = 0.436 for the face-context condition; Fig. 8D]. We thus cannot confirm that internal noise influenced curvature perception on the single-stimulus curvature-absent trials on the basis of the response-vs.-confidence correlations; it is thus possible that our estimates of internal noise from the single-stimulus trials may reflect decision noise instead of curvature-processing noise. We note, however, that the curvature noise estimated from the single-stimulus curvature-absent trials here (Fig. 8C) depended on image crowding and face context in a manner similar to the curvature noise estimated from the eight-stimulus curvature-absent trials in this experiment (Fig. 6C) and in experiment 1 (Fig. 4C) where the significant reported-curvature-vs.-confidence correlations provided evidence of curvature-processing noise. In all cases, the estimated noise was increased by crowding, but it was not further increased by a face context (although there was some variability in the effects of face context; see above). This consistent dependence of estimated curvature noise on the stimulus conditions would be unlikely if response variability in the single-stimulus curvature-absent trials primarily reflected random decision noise unrelated to curvature perception.

Fitting the single-stimulus curvature-present trials to estimate the internal curvature signal and noise for a channel population responding to an isolated curved segment.

We fit the model to each observer's behavioral response histogram from single-stimulus curvature-present trials to estimate the internal curvature signal and noise for each stimulus condition (see Supplemental Fig. S3, D–F, for the goodness of model fits). The scatterplot presented in Fig. 9A shows estimates of curvature signal (y-values) and curvature noise (x-values) for all observers for each stimulus condition. To illustrate the condition effects on curvature signal and noise unconfounded by the baseline individual differences, the line graphs in Fig. 9B show the y-dimension (signal estimates), and those in Fig. 9C show the x-dimension (noise estimates), both with the baseline individual differences removed (see experiment 1 results for details).

Fig. 9.

Internal curvature signal (i.e., the Gaussian mean of the curvature-channel population output) and noise (i.e., the Gaussian standard deviation of the channel-population output) in response to a curved segment estimated from single-stimulus curvature-present trials in experiment 2, shown along with the slopes for the correlation between reported curvature and confidence. The formats and labels are identical to those in Figs. 5 and 7, which present similar data for 8-stimulus trials. For A–D, **P < 0.01, and *P < 0.05.

The estimated internal noise in response to a curved segment increased with crowding, but there was no further increase with a face context (Fig. 9C). Internal noise was greater for the inverted-scrambled-face condition [t(11) = 5.094, P < 0.01, d = 1.471] and the face-context condition [t(11) = 2.694, P < 0.05, d = 0.777] compared with the no-context condition. Interestingly, a face context decreased the estimated internal noise compared with the crowding matched inverted-scrambled-face condition [t(11) = 4.476, P < 0.01, d = 1.292].

Unlike the case with eight-stimulus trials, on single-stimulus trials, the estimated internal noise did not significantly increase when a curvature-channel population responded to a curved segment compared with when it responded to a straight segment [19% increase, SE = 15%, t(11) = 1.448, n.s., d = 0.418 for the no-context condition, 31% increase, SE = 15%, t(11) = 2.052, n.s., d = 0.592 for the inverted-scrambled-face condition, and 14% increase, SE = 14%, t(11) = 1.045, n.s., d = 0.302 for the face-context condition].

Consistent with the results from eight-stimulus trials, the estimated curvature signal was exaggerated in all three conditions on single-stimulus trials. The obtained channel-population-output mean for a curved segment was significantly greater than the veridical value of 0.5 for all three conditions [t(11) = 10.982, P < 0.0001, d = 3.170 for the no-context condition, t(11) = 7.451, P < 0.0001, d = 2.151 for the inverted-scrambled-face condition, and t(11) = 10.801, P < 0.0001, d = 3.118 for the face-context condition; Fig. 9B]. As with eight-stimulus trials, image crowding did not significantly influence the magnitude of curvature signal on single-stimulus trials [t(11) = 1.415, n.s., d = 0.408 for the no-context condition vs. the inverted-scrambled-face condition]. Unlike eight-stimulus trials, however, the face-context condition did not reduce curvature signal compared with the crowding-matched inverted-scrambled-face condition [t(11) = 1.119, n.s., d = 0.323]; rather, the face-context condition significantly increased curvature signal compared with the no-context condition [t(11) = 3.202, P < 0.01, d = 0.924].

Thus it appears that when a single stimulus is presented, engaging face processing enhances curvature discriminability by both reducing noise (Fig. 9C) and increasing signal (Fig. 9B). This result is consistent with previous demonstrations of “face-superiority effects” where a facial configuration improved pattern detection and discrimination (e.g., Gorea and Julesz 1990; Tanaka and Farah 1993). Because facial expression is a highly behaviorally relevant visual feature encoded by expression-tuned neurons (e.g., Hasselmo et al. 1989; Sugase et al. 1999) and mouth curvature is an important part of facial expression, it is plausible that feedback from high-level face processing to lower-level retinotopic processing enhances signal-to-noise ratio for local curvature processing. Note that when multiple stimuli were simultaneously presented (on the 8-stimulus trials), engaging face processing no longer reduced noise (Figs. 4C and 6C) and even decreased curvature signal (Figs. 5B and 7B). A potential explanation is that presenting an emotional face among neutral faces results in within-receptive-field averaging (see discussion), which weakens responses of expression-tuned neurons, thus eliminating the facilitative feedback. Within-receptive-field averaging also reduces the magnitude of encoded expression (e.g., Sweeny et al. 2009), which in turn might reduce encoded mouth curvature in low-level curvature processing through feedback (see discussion).

The curvature-response-vs.-confidence correlation slopes were significantly positive on curvature-present trials for the inverted-scrambled-face [t(11) = 3.796, P < 0.01, d = 1.096] and face-context [t(11) = 3.477, P < 0.01, d = 1.004] conditions and were tending to be significantly positive for the no-context condition [t(11) = 2.033, P = 0.067, d = 0.587; Fig. 9D]. This provides evidence that internal noise altered perceived curvature of a curved segment even on single-stimulus trials.

Differences in the estimates of curvature signal and noise between eight- and single-stimulus trials reveal the characteristics of spatial interactions among the putative local curvature-channel populations. These estimates are thus systematically compared in the next section.

Spatial interactions among local curvature-channel populations.

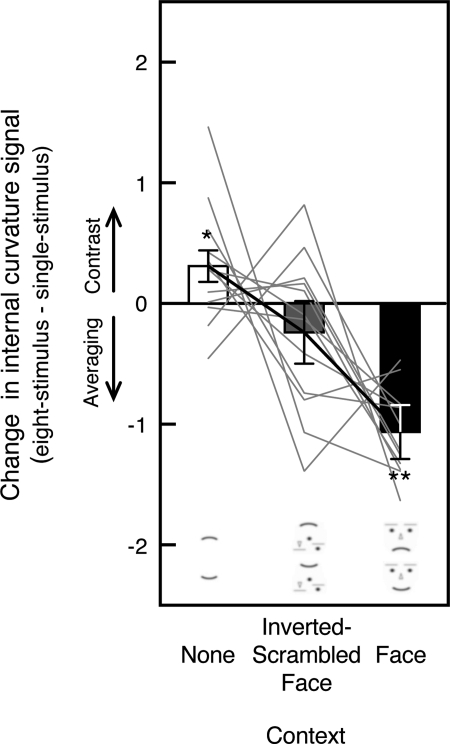
If local curvature-channel populations do not interact, the estimates of curvature signal and noise should be the same whether only one stimulus is presented (single-stimulus trials) or multiple stimuli are simultaneously presented (8-stimulus trials). Consistent with this no-interaction hypothesis, the estimated noise for a curvature-channel population responding to a straight segment did not significantly change between single- and 8-stimulus trials (compare Figs. 8C and 6C), t(11) = 1.792, n.s., d = 0.517 for the inverted-scrambled-face condition and t(11) = 0.352, n.s., d = 0.102 for the face-context condition; for the no-context condition, curvature noise either did not change [t(11) = 1.065, n.s., d = 0.307 using the minimum noise estimates for the 2 observers with ambiguous estimates; see methods for experiment 1] or decreased [t(11) = 3.466, P < 0.01, d = 1.000 using the maximum noise estimates for the same 2 observers] on the 8-stimulus trials compared with the single-stimulus trials. Thus our results provide little evidence of spatial interactions among the curvature-channel populations when they responded to homogenous straight segments.

In contrast, the noise in response to a curved segment increased when a curved segment was presented among straight segments compared with when a curved segment was presented alone (compare Figs. 9C and 7C), t(11) = 3.120, P < 0.01, d = 0.901 for the no-context condition, t(11) = 2.112, P = 0.058, d = 0.610 for the inverted-scrambled-face condition, and t(11) = 7.929, P < 0.0001, d = 2.289 for the face-context condition. Note that when only one stimulus was presented, the estimated noise was equivalent whether a channel population responded to a curved or straight segment (compare Figs. 8C and 9C; see above for statistical analyses).

Thus, in terms of how the estimated noise in curvature coding was affected by stimulus curvature and lateral interactions, the noise was not affected by stimulus curvature per se (no difference between a single curved stimulus and a single straight stimulus) or lateral interactions per se (no difference between a single straight stimulus and multiple straight stimuli). However, the noise was selectively increased in response to a curved segment when it represented a feature odd-ball against straight segments. Neurophysiological results suggest that a feature contrast detected in high-level visual processing modulates low-level neural responses by facilitating local responses to the feature odd-ball and/or by suppressing responses to the surrounding homogenous stimuli (e.g., Kastner et al. 1997; Lee et al. 2002; Zipser et al. 1996). Although this feedback presumably facilitates detection of a feature odd-ball, it might also contribute noise to processing of local curvature when a stimulus represents a feature odd-ball.

This odd-ball specific feedback might also explain the fact that in the eight-stimulus curvature-present condition (i.e., an odd-ball present condition), curvature noise tended to increase [F(1,46) = 3.997, P < 0.052, η_p² = 0.079] and curvature signal tended to decrease [F(1,46) = 3.049, P < 0.088, η_p² = 0.062] in experiment 2 compared with experiment 1. The only difference between the two experiments was that the eight-stimulus trials were randomly intermixed with the single-stimulus trials in experiment 2, whereas only eight-stimulus trials were presented in experiment 1. We speculate that intermixing two very different stimulus configurations might have increased variability in high-level visual processing (e.g., the single- and eight-stimulus arrays are very different from the point of view of high-level visual neurons with large receptive fields) and that this increased variability in high-level processing might have resulted in noisy feedback, which degraded the coding of odd-ball curvature (increasing curvature noise and reducing curvature signal). Intermixing the eight-stimulus trials with the single-stimulus trials might have also increased demands on attention processes (e.g., switching between searching for a curved target and responding to a single curved target), but it is unlikely that a general increase in task difficulty caused the perceptual degradation effect because curvature noise in response to straight segments (in the absence of a feature odd-ball) did not increase in experiment 2 compared with experiment 1 [F(1,46) = 0.009, n.s., η_p² = 0.0001]. Future experiments are needed to confirm these interpretations, but we note that the perceptual degradation of odd-ball curvature that occurred when the eight-stimulus trials were intermixed with the single-stimulus trials in experiment 2 (compared with experiment 1) was small (only marginally significant). In other words, the results for eight-stimulus trials in experiment 2 replicated experiment 1 for the most part.

Importantly, the effects of stimulus conditions (no-context, inverted-scrambled-face, and face-context) on curvature noise were relatively orthogonal to the effects of stimulus curvature, intermixing the single- and eight-stimulus trials, and spatial interactions. The estimated noise was increased by crowding but was not further increased by face context whether a channel population responded to a curved or straight segment and whether a single stimulus or multiple stimuli were presented.

For the estimated curvature signal, however, the effects of stimulus conditions systematically differed for single- and eight-stimulus trials. When a curved segment was presented alone, the magnitude of curvature signal increased from the no-context to inverted-scrambled-face to face-context conditions (Fig. 9B), whereas when a curved segment was presented among straight segments, the magnitude of curvature signal decreased from the no-context to inverted-scrambled-face to face-context conditions (Fig. 7B), F(2,22) = 14.073, P < 0.001, η_p² = 0.561 for the interaction. A follow-up pairwise comparison of the magnitudes of curvature signal between the single- and eight-stimulus trials within each condition indicates that 1) the presence of straight segments significantly increased curvature signal in the no-context condition [t(11) = 2.373, P < 0.05, d = 0.685], 2) the presence of straight segments made no difference in the inverted-scrambled-face condition [t(11) = 0.929, n.s., d = 0.268], and 3) the presence of straight segments significantly decreased curvature signal in the face-context condition [t(11) = 4.753, P < 0.001, d = 1.372; Fig. 10]. This seemingly puzzling pattern of results is consistent with the previously reported phenomena of feature contrast in low-level processing and feature averaging in high-level processing (see discussion).

Fig. 10.

Feature contrast in the no-context condition and feature averaging in the face-context condition. The bar graphs show the difference in estimated internal curvature signals between 8-stimulus and single-stimulus curvature-present trials for the 3 stimulus conditions. Positive values indicate feature contrast, and negative values indicate feature averaging. For the no-context condition, the presence of straight segments (on 8-stimulus trials) increased curvature signal from the curved segment compared with when the curved segment was presented alone (on single-stimulus trials), feature contrast (the left bar). For the face-context condition, the presence of straight segments reduced curvature signal from the curved segment, feature averaging (the right bar). The line graphs show individual observers' data with each observer's overall mean aligned to the group mean to show the consistent condition effects unobscured by the baseline individual differences. The error bars represent ±1 SE. **P < 0.01 and *P < 0.05 for deviations from 0 (no change in internal curvature signal due to spatial interaction).

An alternative model.

By simulating the behavioral curvature-response histograms with a model based on Gaussian-distributed noisy outputs from local curvature-channel populations, we were able to estimate the internal signal and noise in curvature coding and determine how they depended on image crowding, the level of pattern processing, and lateral interactions. We used a “find-the-maximum-feature-value (a.k.a., signed-max)” algorithm to model the process of finding a curved segment among straight segments. The algorithm is simple and biologically plausible (see methods in experiment 1), it has been successfully used to model orientation search (e.g., Baldassi et al. 2006), and it produced good fits to our behavioral data (Supplemental Figs. S1–S3). Nevertheless, there is an alternative curvature search algorithm that is also simple and plausible.

A curved segment embedded within straight segments can be detected by trying to find the maximally curved segment, a signed-max algorithm (which we used), but it could also be detected by trying to find the segment with the maximally deviant curvature, a “max-deviation” algorithm. Because both search algorithms operate on the outputs from the local curvature-channel populations, for either algorithm, greater curvature signals from the channel population responding to the curved segment would result in greater exaggeration of the reported curvature, and greater variability in channel-population outputs would result in greater variability in the reported curvature. It is thus reasonable to expect that the singed-max and max-deviation algorithms would not substantially differ in simulating our behavioral data. Nevertheless, we compared the performance of the signed-max and max-deviation algorithms in fitting the behavioral curvature response histograms from the eight-stimulus trials in experiment 2; note that no search algorithm is required for fitting single-stimulus trials. The signed-max algorithm selected the local curvature-channel population with maximum curvature output as the one representing the curved stimulus. In contrast, the max-deviation algorithm selected the local channel population whose curvature output was most deviated from the average output of all channel populations as the one representing the curved stimulus. The same fitting parameters that we used for the signed-max algorithm (see methods in experiment 1) were also used for the max-deviation algorithm.

When we pooled the fitting results across the three stimulus conditions (no-context, inverted-scrambled-face, and face-context), the root-mean-squared fitting error was significantly greater for the max-deviation algorithm than for the signed-max algorithm for fitting the behavioral responses from curvature-absent trials [F(1,11) = 8.205, P < 0.05, η_p² = 0.427], but the error was equivalent for the two algorithms for fitting the behavioral responses from curvature-present trials [F(1,11) = 0.0003, n.s., η_p² = 0.00005]. Crucially, the pattern of dependence of the estimated curvature signal and noise on the stimulus conditions (no-context, inverted-scrambled-face, and face-context) was the same regardless of which algorithm was used; the choice of algorithm (signed-max vs. max-deviation) did not interact with stimulus condition for either estimating curvature signal [F(2,22) = 0.270, n.s., η_p² = 0.024] or estimating curvature noise [F(2,22) = 1.332, n.s., η_p² = 0.108].

In summary, the signed-max algorithm produced overall superior fits to our behavioral curvature response data than the max-deviation algorithm. Importantly, our conclusions on how image crowding, facial context, and lateral interactions influence curvature signal and noise are valid regardless of whether the search algorithm uses the strategy of finding the maximum or most deviant local curvature output.

EXPERIMENT 3

In each of the preceding experiments, the curved segment always had the lowest-magnitude curvature on the magnitude-estimation scale (“5” or “6” in Fig. 2A). It is thus possible that the exaggerated curvature responses that we obtained could be attributable to a floor effect if observers first determined the direction of curvature and then evaluated its magnitude. In other words, on trials where observers correctly detected the direction of curvature, a random error in reporting the small magnitude of the curved segment could have biased the responses toward exaggerated curvature. Note that this possibility is inconsistent with the results that the estimated curvature signal significantly reduced whereas the estimated noise significantly increased in the face-context condition compared with the no-context condition. If exaggerated curvature responses arose from a floor effect operating on random response variability, this pattern of results (reduced exaggeration with increased variability) would not have occurred. Nevertheless, it is important to demonstrate perceptual curvature exaggeration in the absence of a potential floor effect.

We thus conducted a control experiment in which the magnitude of the curved segment on a given trial was randomly chosen from the full range on the matching screen (“1” through “10”). In particular, if exaggeration occurred on trials where the curved segment had an intermediate value of “3” or “8” in the middle of the response scale for each curvature direction (thus susceptible to neither a floor nor ceiling effect), such a result would confirm that the visual system exaggerates briefly presented curvature signals.

Methods

Observers.

Ten undergraduate students from Northwestern University gave informed consent to participate in the experiment. They all had normal or corrected-to-normal visual acuity and were tested individually in a dimly lit room. An independent review board at Northwestern University approved the experimental protocol.

Stimuli and procedure.

The stimuli and design were identical to those used in experiment 1 with the following exceptions. We only tested the 8-stimulus no-context condition because the magnitude of curvature exaggeration was largest in this condition. Each trial contained a curved segment with its curvature randomly selected from the entire range of magnitudes on the matching scale (Fig. 2A) with equal probability. Each of the 10 curvatures was presented once at each of the 8 locations on the screen, resulting in 80 trials.

Results

The goal of this experiment was to confirm that the curvature exaggeration obtained in experiments 1 and 2 reflected perceptual curvature exaggeration rather than a response artifact, which could have occurred if observers correctly perceived the direction of the small curvature but their random guessing of magnitudes combined with a floor effect generated exaggerated curvature responses. We thus selectively analyzed the trials on which observers correctly reported curvature directions.

As shown in Fig. 11, the curvature responses (averaged across upward and downward curves) to the low- to middle-curvature stimuli were significantly greater than the veridical values, t(9) = 8.473, P < 0.0001, d = 2.679 for the 0.5 curvature (i.e., for curves “5” and “6”), t(9) = 6.762, P < 0.0001, d = 2.138 for the 1.5 curvature (i.e., for curves “4” and “7”), and t(9) = 4.009, P < 0.01, d = 1.268 for the 2.5 curvature (i.e., for curves “3” and “8”; see Fig. 2 for the curvature coding scale). The curvature responses to the second largest (3.5) curvature (i.e., for curves “2” and “9”) were veridical [t(9) = 0.381, n.s., d = 0.121], and those to the largest (4.5) curvature (i.e., for curves “1” and “10”) were significantly smaller than the veridical value [t(9) = 5.437, P < 0.01, d = 1.719]. Thus observers underestimated the largest curvature, and this could be attributable to a ceiling effect of the range of matching curvatures we used. Importantly, the fact that observers significantly overestimated moderate curvatures including the midrange curvature affected neither by a floor nor ceiling effect demonstrates that moderate curvatures of briefly presented stimuli are exaggerated in the curvature encoding process.

Fig. 11.

Magnitude of reported curvature as a function of the actual curvature of a curved segment presented among straight segments in the no-context condition when curvature direction was correctly reported. The data are collapsed across the upward and downward curvature directions. Values above the dotted line indicate perceptual exaggeration, and values below the dotted line indicate underestimation. The error bars represent ±1 SE. **P < 0.01 for deviations from veridical curvature magnitudes (dashed line).

DISCUSSION

Previous work with briefly presented stimuli has demonstrated that internal feature processing can have a substantial impact on perception. Noise within feature processing mechanisms acts similarly to feature signals in the coding of local orientation (Baldassi et al. 2006) and aspect ratio (Suzuki and Cavanagh 1998), and feature signals are exaggerated in the coding of aspect ratio (Suzuki and Cavanagh 1998). By combining behavioral experiments with computational modeling, we determined the magnitudes of internal signal and noise in the coding of curvature, a basic feature (e.g., Wolfe et al. 1992) crucial for figure-ground segregation (e.g., Kanizsa 1979; Pao et al. 1999) as well as for perception of surfaces and objects (e.g., Attneave 1954; Biederman 1987; Hoffman and Richards 1984; Poirier and Wilson 2006; Stevens and Brookes 1987). The current study was conducted with two primary goals. Our first goal was to demonstrate that a simple model of feature coding based on the population activity of noisy local channels tuned to different feature values appropriately simulates the perception of curvature as well as orientation (Baldassi et al. 2006) in the context of a behaviorally relevant task of visual search. Our second goal was to use the model to determine how the internal curvature signal and noise change from low- to high-level pattern processing in sparse and crowded situations.

The model produced good fits to our curvature perception data across all stimulus conditions (no-context, inverted-scrambled-face, and face-context) for both curvature-present and -absent trials and for both single- and multistimulus trials (Supplemental Figs. S1–S3). This confirmed that, in addition to describing orientation coding (Baldassi et al. 2006), the model appropriately describes curvature coding. The success of the model suggests that the curvatures of search stimuli are processed in parallel by local curvature-channel populations with each population generating a noisy curvature output and that people select the population yielding the maximum curvature output as the one representing the curved target. Importantly, the success of the model allowed us to estimate the internal curvature signal and noise as the optimal values of the fitting parameters.

Crowding increased internal curvature noise (increased noise in the inverted-scrambled-face condition relative to the no-context condition; Figs. 4C, 5C, 6C, 7C, 8C, and 9C). It is typically assumed that each local curvature-coding mechanism consists of a population of neural channels that are tuned to different curvature values (e.g., Hegdé and Van Essen 2000; Pasupathy and Connor 1999, 2001, 2002) and that perceived curvature reflects some form of a central tendency of the population activity (e.g., Deneve et al. 1999; Lee et al. 1988; Vogels 1990; Young and Yamane 1992) across those curvature-tuned channels. Variability in the perceived curvature may thus reflect uncorrelated noise in the responses of various curvature-tuned channels within each curvature-coding population. Crowding might increase this variability due to short-range (in the order of 0.6° based on the proximity of the crowding elements we used) interactions between the curvature-tuned channels responding to the segment of interest and those responding to the crowding elements, with noise from channels responding to the crowding elements adding noise to the channels responding to the relevant segment. Our results, however, suggest that these interactions do not systematically affect the population-level activity (at least for our stimuli) because crowding did not change the average magnitude of perceived curvature; that is, we found little difference in the estimated curvature signal between the no-context and inverted-scrambled-face conditions (Figs. 5B, 7B, and 9B).

Although crowding increased curvature noise, estimates of noise did not increase in the face-context condition relative to the crowding-matched inverted-scrambled-face condition (Figs. 4C, 6C, 7C, 8C, and 9C). Behavioral and neuropsychological evidence suggests that a face context engages configural processing of the constituent parts even when global processing would be disadvantageous or irrelevant to performing a task (e.g., Farah et al. 1995; Goolsby et al. 2005; Mermelstein et al. 1979; Suzuki and Cavanagh 1995). Consistent with these behavioral results, neurophysiological results suggest that face processing is mediated by visual neurons with large receptive fields in high-level visual areas and that those “face-selective” neurons engage even when face perception is not explicitly required by a task. For example, some visual neurons in inferotemporal cortex respond preferentially to faces (and not to most other patterns) even when monkeys are not explicitly performing a face recognition task (Foldiak et al. 2004; Tsao et al. 2006) or are under anesthesia and immobilization (e.g., Bruce et al. 1981). It is thus likely that our estimates of curvature signal and noise in the face-context condition reflect a contribution from high-level face processing, either via a direct contribution such as forcing the relevant curved or straight segment to be processed as the mouth of a face or via an indirect contribution by influencing lower-level curvature processing through feedback connections (e.g., Lee et al. 1998b; Rockland and Van Hoesen 1994). The overall absence of an increase in noise with a face context therefore suggests that internal noise in curvature processing is not increased by engaging high-level face processing. This result is consistent with neurophysiological demonstrations of similar levels of noise in macaque V1, V2, and V4 (Hegdé and Van Essen 2007) and similar levels of baseline activity in V2 and V4 (Luck et al. 1997) with successful modeling of V2 and V4 responses under the assumption of equal amounts of noise in both areas (Reynolds et al. 1999) and with the suggestion that uncorrelated noisy signals across multiple neurons cancel out when they converge on a higher-level neuron (Gawne and Richmond 1993), thereby preventing noise accumulation.

The internal curvature signal was substantially exaggerated in all stimulus conditions (no-context, inverted-scrambled-face, and face-context). Feature exaggeration occurs in reference to a neutral feature value. In the case of aspect ratio (Suzuki and Cavanagh 1998), horizontal and vertical aspect ratios were perceptually exaggerated relative to a neutral aspect ratio (e.g., a circle). In the current investigation, upward and downward curvatures were perceptually exaggerated relative to a neutral curvature (i.e., a straight segment). In perceiving aspect ratio and curvature, the corresponding neutral values can be considered category boundaries. Thus perceptual exaggeration that occurs in brief viewing may serve to initially sharpen category boundaries in feature coding.

In considering the potential neural mechanism of initial feature exaggeration, we note that it has been suggested that a feature that includes a category boundary is primarily coded by the relative activation of neural units tuned to the opponent values (e.g., Regan and Hamstra 1992; Suzuki 2005; see Poirier and Wilson 2006 for a model of opponent curvature coding, but see Bell et al. 2009 for additional curvature coding mechanisms). There is physiological evidence for this type of “opponent coding” for intermediate-to-high-level visual features. In particular, the tuning peaks of curvature-tuned V4 and inferotemporal cortex neural populations are shifted toward large curvatures (Kayaert et al. 2005; Pasupathy and Connor 1999, 2001). For example, 91% of V4 neurons tested by Pasupathy and Connor (1999) preferred curved to straight segments, and even among neurons selected based on strong responses to straight segments, 74% made even stronger responses to curved segments. Likewise, among the neurons investigated by Hegdé and Van Essen (2007), 87% of those in V4 and 84% of those in V2 responded more strongly to curved than straight segments. Similar preferential responses to extreme (rather than average) feature values have also been found in the middle face patch (in the temporal lobe) for neurons that are tuned to different facial features (Freiwald et al. 2009). These preferential neural tunings to opponent feature values are also consistent with the psychophysical characteristics of curvature (Müller et al. 2009), aspect-ratio (e.g., Regan and Hamstra 1992; Suzuki and Rivest 1998), and face (e.g., Leopold et al. 2001; Webster and MacLin 1999) aftereffects, where adaptation to a neutral feature value produces weak (or no) aftereffects (see Suzuki 2005 for a review). Thus neurophysiological and psychophysical results converge to suggest that intermediate-to-high-level visual features that are coded with respect to a neutral value are represented by the relative activity of neural populations broadly tuned to the opponent feature directions. In addition, visual neurons generally respond especially strongly at the stimulus onset (e.g., Muller et al. 1999; Oram and Perrett 1992; Sugase et al. 1999). Thus strong initial activation of the neurons that are preferentially tuned to the presented feature value might initially strongly inhibit those tuned to the opponent feature values, thereby skewing the population response toward the presented feature value, causing perceptual exaggeration in brief viewing.

Curvature exaggeration occurred even when a single curved segment was presented, suggesting that brief curvature exaggeration is an intrinsic property of local curvature processing. Such exaggeration may be adaptive. For example, direction of local curvature may be important for figure-ground determination (e.g., Kanizsa 1979; Pao et al. 1999) and for computing surface curvature (e.g., Biederman 1987; Stevens and Brookes 1987). Exaggerating local curvature in brief viewing may facilitate rapid extraction of surface and object properties by enhancing local curvature contrasts.

The fact that curvature signal increased when a curved segment was presented among multiple straight segments suggests that a contrastive interaction between a curved segment and its straight neighbors (placed at noncrowding distances) additionally contributes to enhancing perceived curvature of the curved segment. This result is consistent with prior reports of off-orientation and off-frequency looking; that is, when a target needs to be detected on the basis of its deviant orientation or spatial frequency compared with those of the masking or contextual stimuli, the visual system optimizes target detection by utilizing orientation or spatial-frequency detectors that are tuned farther away from the values associated with the masking or contextual stimuli than the actual value associated with the target (e.g., Losada and Mullen 1995; Mareschal et al. 2008; Perkins and Landy 1991; Solomon 2000; Solomon 2002).

This contrastive spatial interaction was eliminated when crowding elements were placed around the curved and straight segments in the inverted-scrambled-face condition (Fig. 10). This suggests that lateral inhibition from intervening crowding elements (Wilkinson et al. 1997; Wolford and Chambers 1983) interferes with longer-range contrastive interactions.

A face context also influenced the magnitude of curvature signal. When a single stimulus was presented, a face context increased curvature signal presumably via facilitative feedback from facial-expression processing (see experiment 2 results). In contrast, when multiple stimuli were presented, the same face context substantially reduced curvature signal with a 21% reduction in the face-context condition compared with the inverted-scrambled-face condition in experiment 1 and a 37% reduction in experiment 2. These seemingly paradoxical results are consistent with our recent result demonstrating long-range averaging of facial expressions (Sweeny et al. 2009), which is in turn consistent with within-receptive-field averaging of visual features enacted by ventral visual neurons. When multiple stimuli are simultaneously presented in the receptive field of a ventral visual neuron, its response tends to be the average of its responses to the individual stimuli presented alone (e.g., Chelazzi et al. 1998; Kastner et al. 2001; Miller et al. 1993; Reynolds et al. 1999; Rolls and Tovee 1995; Sato 1989; Zoccolan et al. 2005).

Given the spacing between our stimuli, each stimulus would have been processed by separate small receptive fields in low-level curvature processing, but multiple stimuli would have been simultaneously processed within a large receptive field (encompassing as much as the entire visual hemifield or more) in high-level face processing (see Kastner et al. 2001; Suzuki 2005 for reviews of progressively larger receptive fields in downstream visual areas in the ventral pathway). Thus within-receptive-field averaging would have been operative primarily in the face-context condition, and this averaging would have reduced neural responses to a happy/sad expression when a happy/sad face was averaged with simultaneously presented neutral faces. The reduced activity of expression-tuned neurons might in turn synergistically decrease responses of the lower-level curvature-tuned neurons that contribute to those expressions via extensive feedback connections from high-level temporal visual areas to lower-level retinotopic visual areas (e.g., Rockland and Van Hoesen 1994; Roland et al. 2006). These interactions could explain why presenting a curved segment among straight segments reduced curvature signal in the presence of a face context. The same interactions could also explain the previous result that curvature singleton search was significantly slowed when curved segments were organized into multiple faces (Suzuki and Cavanagh 1995).

Overall, the following inferences can be drawn from the specific ways in which curvature signal depended on the contextual manipulations and set size (1 or 8). First, local curvature is intrinsically exaggerated in brief viewing, evidenced by the substantial curvature exaggeration in response to a single curved stimulus in the no-context condition. Second, local curvature signal is further increased by contrastive interactions with neighboring straight stimuli (similar to off-orientation and off-frequency looking). This contrastive interaction, however, is disrupted by crowding elements. Third, when a single curved stimulus is presented, a face context increases curvature signal (and reduces curvature noise) likely due to facilitative feedback from facial-expression processing to curvature processing. Curvature signal, however, is reduced when a curved target and straight distractors are presented as multiple faces, presumably due to influences from large-scale neural averaging that occurs in high-level face processing.

Our model included no a priori assumptions about feature contrast or averaging; there were no stages in the model where curvature channels from different local curvature-coding populations were allowed to interact. Instead, we estimated the “effective” curvature signal and noise that are directly associated with behavioral curvature responses. Because we assumed locally independent curvature coding in the model, any changes in the estimated signal and noise from single- to multistimulus trials would indicate a failure of the independence assumption, implying spatial interactions among the curvature-channel populations. We thus inferred that spatial interactions increased the curvature signal in the no-context condition but reduced the curvature signal in the face-context condition. We then speculated that spatial interactions at the level of simple curvature processing primarily take the form of feature contrast (as occurs in processing of other simple contour features), whereas spatial interactions at the level of face processing primarily take the form of feature averaging (as occurs in processing of facial expression and other complex features).

Contrastive interactions in curvature processing could be implemented in the model as mutual inhibition among the neighboring curvature channels that respond to the same curvature value, similar to spatial interactions in the coding of orientation, spatial frequency, and aspect ratio (e.g., Klein et al. 1974; Schwartz et al. 2007; Sweeny et al. 2011). In this way, the “low-to-null-curvature-tuned” channels strongly responding to the multiple straight segments would laterally inhibit the low-to-null-curvature-tuned channels responding to the curved segment, thereby shifting the population response profile for the curved segment to be more strongly dominated by channels tuned to higher curvatures. In simulating contrastive interactions, the strength of the underlying inhibitory interactions (likely dependent on interstimulus distance and/or density) would be a relevant parameter. Within-receptive-field averaging in face processing could be implemented by simulating the activity of each expression-tuned channel responding to multiple (simultaneously presented) faces as the average of its responses to the individual faces presented alone. In computing this averaging, the widths of expression tuning, the number of faces presented within the receptive field, as well as weighting of different stimuli within the receptive field (e.g., expressive faces and/or faces at lower retinal eccentricities may be more strongly weighted than neutral faces and/or faces at higher retinal eccentricities) would be relevant parameters. Because face processing is likely to influence curvature coding via feedback connections, the strength of feedback input to curvature-tuned channels would also be a relevant parameter. To nontrivially implement these contrastive, averaging, and feedback interactions in the model, future research needs to quantify parametrically the spatial and feature-based characteristics of these interactions.

In summary, our behavioral and computational results on brief curvature search have provided basic insights into the mechanisms of curvature coding and pattern coding in general. The success of the simple local-feature-processing model as applied to orientation search (Baldassi et al. 2006) and extended to curvature search (this study) suggests that sparsely distributed items are processed in parallel by noisy local feature-channel populations and that the population yielding the largest feature output is selected during search for an item possessing that feature. Our results have also confirmed that computational modeling provides a useful technique for behaviorally estimating the magnitudes of internal feature signal and noise. Image crowding (induced by irrelevant elements placed around each stimulus in close proximity) increased curvature noise without systematically affecting the strength of the curvature signal (except disrupting long-range contrastive interactions), suggesting that short-range (∼0.6°) spatial interactions among noisy curvature channels result in increased response variability but without systematically altering the central tendency of the population activity. Engagement of high-level face processing did not increase internal curvature noise, consistent with previous neurophysiological results suggesting that noise does not accumulate in high-level visual processing. The robust curvature exaggeration that we obtained across all conditions (even when a single curved segment was presented) suggests that the visual system enhances local curvature in brief viewing, potentially facilitating rapid analyses of figure-ground organization and surface curvature. In the absence of a spatial interaction, a face context improved curvature perception by both increasing curvature signal and reducing noise, implicating facilitative feedback from high-level face processing to lower-level curvature processing. Long-range spatial interactions produced two opposing effects depending on the level of processing involved. Curvature signal was increased when a curved segment was presented among straight segments, consistent with previous reports of contrastive interactions among local features in low-level processing. In contrast, when the same curved and straight segments were presented as the mouths of multiple faces, curvature signal was substantially reduced (the noise benefit of the face context obtained for a single face was also eliminated), consistent with previous reports of long-range feature averaging in high-level processing. Overall, our results have provided integrative insights into how crowding, long-range spatial interactions and level of processing influence curvature coding in the context of visual search.

GRANTS

This research was supported by National Eye Institute Grants R01-EY-018197-02S1 and EY-018197 and National Science Foundation Grant BCS 0643191.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).