Semiparametric Bayesian Inference for Multilevel Repeated Measurement Data

Summary

We discuss inference for data with repeated measurements at multiple levels. The motivating example is data with blood counts from cancer patients undergoing multiple cycles of chemotherapy, with days nested within cycles. Some inference questions relate to repeated measurements over days within cycle, while other questions are concerned with the dependence across cycles. When the desired inference relates to both levels of repetition, it becomes important to reflect the data structure in the model. We develop a semiparametric Bayesian modeling approach, restricting attention to two levels of repeated measurements. For the top-level longitudinal sampling model we use random effects to introduce the desired dependence across repeated measurements. We use a nonparametric prior for the random effects distribution. Inference about dependence across second-level repetition is implemented by the clustering implied in the nonparametric random effects model. Practical use of the model requires that the posterior distribution on the latent random effects be reasonably precise.

1. Introduction

We consider semiparametric Bayesian inference for data with repeated measurements at multiple levels. The motivating data are blood count measurements for chemotherapy patients over multiple courses of chemotherapy. In earlier papers (Müller and Rosner, 1997; Müller, Quintana, and Rosner, 2004), we considered inference for the first course of chemotherapy only. Naturally, such data do not allow inference about changes between cycles. In clinical practice, however, cancer patients receive chemotherapy over multiple courses or cycles of predetermined duration. These courses of therapy typically consist of a period during which the patient receives active drug therapy, followed by a no-drug period to allow the patient to recover for the next round of chemotherapy. Often some aspect of the treatment protocol is intended to mitigate deterioration of the patient’s performance across repeated treatment cycles. Inference related to such aspects of the treatment involves a comparison across cycles, which requires modeling of the entire data set, including data from later cycles. In this extended data set, repeated measurements occur at two levels. Each patient receives multiple cycles of chemotherapy, and within each cycle, measurements are recorded over time. Another typical example of this data structure is drug concentration measurements over repeated dosing studies of pharmacokinetics.

A standard parametric approach would base inference on conjugate distributions for the sampling model, hierarchical priors, and random effects distributions. Bayesian inference for such multilevel hierarchical models is reviewed, among many others, in Goldstein, Browne, and Rasbash (2002), who also discuss software for commonly used parametric models. Browne et al. (2002) compare Bayesian and likelihood-based methods. Heagerty and Zeger (2000) discuss likelihood-based inference for marginal multilevel models. Marginal models regress the marginal means of the outcome on covariates, rather than conditional means given random effects. A recent comprehensive treatment of multilevel models appears in Goldstein (2003).

The proposed semiparametric Bayesian inference replaces traditional normal random effects distributions with non-parametric Bayesian models. Nonparametric Bayesian random effects distributions in mixed-effects models were first introduced in Bush and MacEachern (1996). Mukhopadhyay and Gelfand (1997) construct a semiparametric Bayesian version of generalized linear models. Applications to longitudinal data models are developed in Kleinman and Ibrahim (1998a), Müller and Rosner (1997), and Walker and Wakefield (1998), among many others. Ishwaran and Takahara (2002) extensively discuss Monte Carlo algorithms for similar semi-parametric longitudinal data models. In particular, they propose clever variations of a sequential importance sampling method known as the Chinese restaurant process. Kleinman and Ibrahim (1998b) extend the approach in Kleinman and Ibrahim (1998a) to allow binary outcomes, using generalized linear models for the top-level likelihood. In each of these papers, the authors use variations of Dirichlet process (DP) models to define flexible nonparametric models for an unknown random effects distribution. The DP was introduced as a prior probability model for random probability measures in Ferguson (1973) and Antoniak (1974). See these papers for basic properties of the DP model. A recent review of semi-parametric Bayesian inference based on DP models appears in Müller and Quintana (2004). Related non-Bayesian semiparametric approaches for longitudinal data are discussed, among others, in Lin and Carroll (2001a) and (2001b). These approaches use generalized estimating equations to implement estimation in semiparametric longitudinal data models.

The main novelty in the proposed model is the construction of a nonparametric model for a high-dimensional random effects distribution for multilevel repeated measurement data. The proposed approach avoids parameterization of the high-dimensional dependence structure. We achieve this by using a mixture of nonparametric models for lower-dimensional subvectors. In the application the lower-dimensional subvector is the cycle-specific random effects vector θ_ij for cycle j and patient i, nested within a higher-dimensional patient-specific random effects vector θ_i = (θ_ij, j = 1, …, n_i). The mixture model allows us to learn about dependence without having to define a specific parametric structure in a way that is analogous to modeling a multivariate distribution as a mixture of independent kernels. Even if the kernels are independent, the mixture allows us to model essentially arbitrary dependence.

The rest of this article is organized as follows. In Section 2, we introduce the proposed sampling model. In Section 3, we focus on the next level of the hierarchy by proposing suitable models to represent and allow learning about dependence at the second level of the hierarchy. Section 4 discusses implementation of posterior simulation in the proposed model. Section 5 reports inference for the application that motivated this discussion. A final discussion section concludes the article.

2. First-Level Repeated Measurement Model

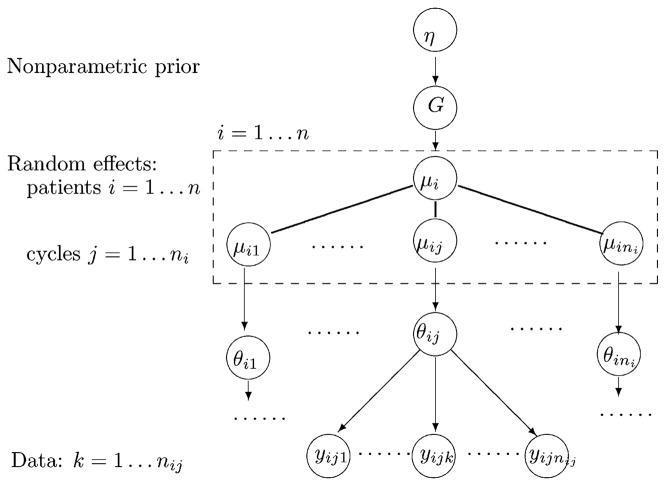
In our semiparametric Bayesian model representing repeated measurements at different levels of a hierarchy, the model hierarchy follows the structure of the data. The key elements of the proposed approach are as follows. We consider two nested levels of measurement units, with each level giving rise to a repeated measurement structure. Assume data y_ijk are recorded at times k, k = 1,…, n_ij, for units j, j = 1, …, n_i, nested within higher-level units i, i = 1, …, n. We will refer to the experimental units i as “subjects” and to experimental units j as “cycles” to simplify the following discussion and remind us of the motivating application. Figure 1 shows the overall structure.

Figure 1.

Model structure. Circles indicate random variables. Arrows indicate conditional dependence. The dashed box and the solid lines (without arrows) show how μ_i is partitioned into subvectors. The sampling model p(y_ijk |θ_ij ), the random effects model p(θ_ij, j = 1, …, n_i | G), and the nonparametric prior p(G |η) are defined in (1), (3), and (5), respectively.

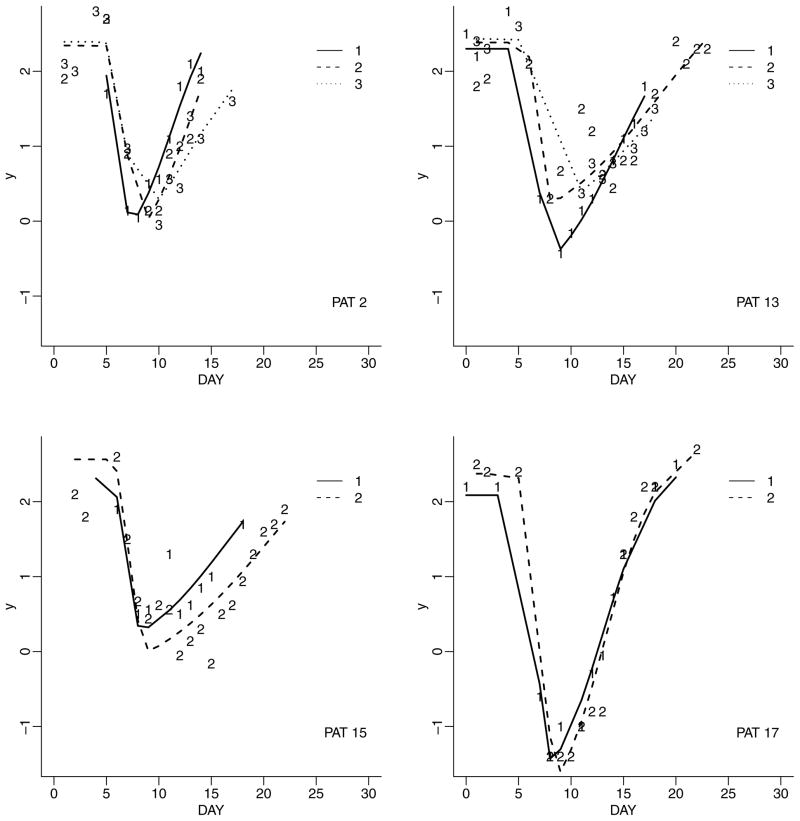
We start by modeling dependence of the repeated measurements within a cycle, y_ij = (y_ijk, k = 1, …, n_ij ). We assume p(y_ij |θ_ij, η) to be a nonlinear regression parameterized by cycle-specific random effects θ_ij. Here and throughout the following discussion, η are hyperparameters common across subjects i and cycles j. Figure 2 shows typical examples of continuous outcomes y_ijk, measured over multiple cycles, with repeated measurements within each cycle.

Figure 2.

Repeated measurements over time (DAY) and cycles. Each panel shows data for one patient. Within each panel, the curves labeled 1, 2, and 3 show profiles for the first, second, and third cycle of chemotherapy (only two cycles are recorded for patients 15 and 17). The curves show posterior estimated fitted profiles. The observed data are indicated by “1,” “2,” or “3” for cycles 1, 2, and 3, respectively.

We define dependence within each cycle by assuming that observations arise according to some underlying mean function plus independent residuals:

$$y_{\mathit{ijk}}=f(t_{\mathit{ijk}};{\theta }_{ij})+e_{\mathit{ijk}}.$$ (1)

Here f is a nonlinear regression with parameters θ_ij, and e_ijk are assumed to be independent and identically distributed (i.i.d.) N(0, σ²) normal errors. Marginalizing with respect to θ_ij, model (1) defines a dependent probability model for y_ij This use of random effects to introduce dependence in models for repeated measurement data is common practice. The choice of f(·;θ) is problem specific. In the implementation reported later, we use a piecewise linear-linear-logistic function. In the absence of more specific information, we suggest the use of generic smoothing functions, such as spline functions (Denison et al., 2002).

3. Second-Level Repeated Measurement Model

3.1 A Semiparametric Random Effects Model

We introduce a dependent random effects distribution on θ_i = (θ_i1, …, θ_ini ) to induce dependence across cycles. We will proceed with the most general approach, leaving the nature of the dependence unconstrained. We achieve this by considering a nonparametric prior for the joint distribution p(θ_i1,…, θin_i).

We first introduce a parametric model, constructed to be comparable to the nonparametric model, to clarify structure, and for later reference. Let η = (m, B, S, σ²) denote a set of hyperparameters. We use i, j, and k to index patients i = 1,…, n, cycles j = 1, …, n_i, and observations k = 1, …, n_ij.

$$\begin{array}{l}\text{Cycle}\text{effects}:p({\mu }_j\mid \eta )=N(m,B)\\ \text{Random}\text{effects}:p({\theta }_{ij}\mid \mu ,\eta )=N({\mu }_j,S)\\ \text{Data}:p(y_{ij}\mid {\theta }_{ij},\eta )=\prod _{k}p(y_{\mathit{ijk}}\mid {\theta }_{ij},{\sigma }^2).\end{array}$$ (2)

We assume independence across cycles at all levels. This implies that also posterior inference on θ_ij and posterior predictive inference is independent across cycles. We could modify (2) to include a dependent prior p(μ₁, μ₂, … | η) to allow for dependence. However, even for moderate dimension of θ_ij this is not practical. Instead, we proceed with a semiparametric extension that implements learning about dependence through essentially a mixture of independent models as in (2).

We generalize the random effects distribution for θ_i = (θ_i1, …, θ_ini ) to a mixture of normal models. Let N(x; m, S) indicate a normal distributed random variable x with moments (m, S). We assume

$$p({\theta }_i\mid G,S)=\int \prod _{j}N({\theta }_{ij};{\mu }_{ij},S)\text{d}G({\mu }_i),$$ (3)

with a nonparametric prior on the mixing measure G for the latent normal means μ_i = (μ_i1, …, μ_ini ). As usual in mixture models, posterior inference proceeds with an equivalent hierarchical model:

$${\theta }_{ij}\sim N({\mu }_{ij},S)\text{and}{\mu }_i\sim G.$$ (4)

Substituting a common value μ_i = μ₀ across all patients i, that is, a point mass G(μ) = I(μ = μ₀), shows the correspondence with the parametric model. In Section 3.2 we will introduce a prior for a discrete random measure G. Denote with ${\mu }_h^o$ the point masses of G. Implicit in the model for G will be an independent N(m, B) prior for the subvectors ${\mu }_{hj}^o$ corresponding to cycles, with independence across h and j. In other words, we generalize (2) by a mixture of independent models. The mixture allows learning about dependence in much the same way as a kernel density estimate with independent bivariate kernels can be used to estimate a dependent bivariate distribution.

3.2 The Random Probability Measure G

The probability model for G is the main mechanism for learning about dependence across cycles. We use a DP prior. We write DP(M, G^☆) for a DP model with base measure G^☆ and total mass parameter M. We complete model (1) and (4) with

$$G\sim \text{DP}(M,G^{★}).$$ (5)

See, for example, MacEachern and Müller (2000) for a review of DP mixture models as in (4).

Besides technical convenience and computational simplicity, the main reason for our choice is the nature of the predictive inference that is implied by the DP model. Assume patients i = 1,…, n have been observed. The prior predictive p(θ _n+1 |θ ₁, …, θ_n) for patient n + 1 is of the following type. With some probability, θ_n+1 is similar to one of the previously recorded patients. And with the remaining probability, θ_n+1 is generated from a baseline distribution G^☆ defined below. The notion of “similarity” is formalized by assuming a positive prior probability for a tie of the latent variables μ_i. Let k = n denote the number of unique values among μ₁, …, μ_n and denote such values by ${\mu }_1^{\ast },\dots ,{\mu }_k^{\ast }$. Let mh, h = 1, …, k, denote the number of latent variables μ_i equal to ${\mu }_h^{\ast }$, and let w_h = m_h /(M + n) and w_k+1 = M/(M + n). The DP prior on G implies

$$p({\mu }_{n+1}\mid {\mu }_1,\dots ,{\mu }_n)=\{\begin{array}{ll}{\mu }_{n+1}={\mu }_h^{\ast },\hfill & \text{with}\text{prob}.w_h(m_1,\dots ,m_k),h=1,\dots ,k\hfill \\ G^{\ast }\hfill & \text{with}\text{prob}.w_{k+1}(m_1,\dots ,m_k).\hfill \end{array}$$ (6)

The predictive distribution for μ_n+1 is a mixture of the empirical distribution of the already observed values and the base measure G^☆. The predictive rule (6) is attractive in many applications. For example, consider the application to the multi-cycle hematologic counts. The model implies that with some probability the response for the new patient replicates one of the previous patient responses (up to residual variation), and with the remaining probability the response is generated from an underlying base measure G^☆.

4. Posterior Inference

4.1 Base Measure, Kernel, and Regression

For the base measure G^☆ we use the same factorization as in (3),

$$G^{★}({\mu }_i)=\prod _{j=1}^{n_i}p({\mu }_{ij}\mid \eta )=\prod N({\mu }_{ij};m,B).$$ (7)

The advantage of this choice of base measure is that hyper-parameters η that define G^☆ only need to be defined for the random vector μ_ij instead of the higher-dimensional vector μ_i. Using a base measure with conditional independence across cycles, any inference about dependence across cycles for a future patient arises from the data-driven clustering of the imputed μ_i vectors. Clustering over locations allows modeling dependence in much the same way as a mixture of bivariate standard normals kernel can approximate any bivariate distribution, with arbitrary variance-covariance matrix, in a bivariate kernel density estimate.

As usual in DP mixture models, posterior inference proceeds in the marginal model (6), after analytically integrating out the random measure G. Choosing a conjugate base measure G^☆ and kernel p(θ_ij | μ_ij, η), such as the conjugate normal kernel and base measure used in (4) and (7), further facilitates posterior simulation. See Section 4.2 for details.

A minor modification of the model allows us to include cycle-specific covariates. Let x_ij denote a vector of covariates for cycle j of patient i. This could, for example, include dose of a treatment in cycle j. A straightforward way to include a regression on x_ij is to extend the probability model on θ_ij to a probability model on θ̃_ij ≡ (x_ij, θ_ij ). The implied conditional distribution p(θ_ij | x_ij ) formalizes the desired density estimation for as a function of x. This approach is used, for example, in Mallet et al. (1988) and Müller and Rosner (1997).

4.2 Posterior MCMC

Posterior simulation in the proposed model is straightforward by Markov chain Monte Carlo simulation (MCMC). See, for example, MacEachern and Müller (2000), Neal (2000), or Jain and Neal (2004) for an explanation of MCMC posterior simulation for DP mixture models.

We briefly explain the main steps in each iteration of the MCMC. An important feature of the model is the conditional independence of the θ_ij across cycles j given μ_i and η. This allows us to consider one cycle at a time when updating θ_ij in the Gibbs sampler. Updating θ_ij, conditional on currently imputed values for μ_i, reduces to the problem of posterior simulation in a parametric, nonlinear regression with sampling model (1) and prior (4). See the discussion in Section 5.1 for a specific example.

Next, consider updating μ_i conditional on currently imputed values for θ_i, hyperparameters η, and {μ_ℓ;ℓ ≠ i}. We use notation similar to (6), with an additional superindex⁻ indicating the exclusion of the ith element, as follows. First, reorder the indices of ${\mu }_h^{\ast }$, such that μ_i is equal to the last of the unique values, that is, ${\mu }_i={\mu }_k^{\ast }$. Let { ${\mu }_h^{\ast },h=1,\dots ,k^{-}$} denote the set of unique values among {μ_ℓ, ℓ ≠ i}, and let $m_h^{-}=\mid \{\ell :{\mu }_{\ell }={\mu }_h^{\ast },\ell \ne i\}\mid$. From this we can find the complete conditional posterior distribution for μ_i. Let Q₀ = ∫ p (y_i |θ ) dG^☆ (θ) and q₀ ∝ p(y_i |θ)G^☆ (θ).

$$p({\mu }_i\mid \dots )=\{\begin{array}{ll}I({\mu }_i={\mu }_h^{\ast })\hfill & \text{w}.\text{pr}.\propto m_h^{-}p(y_i\mid {\mu }_h^{\ast })\hfill \\ q_0({\mu }_i)\hfill & \text{w}.\text{pr}.\propto {MQ}_0,\hfill \end{array}$$

h = 1, …, k⁻. Exploiting the conjugate nature of the base measure G^☆ and the kernel p(θ_ij | μ_ij, η), we can simplify one step further. We can analytically marginalize with respect to μ_i, conditional only on the configuration of ties among the μ_i. Define indicators s_i, i = 1, …, n, with s_i = h if ${\mu }_i={\mu }_h^{\ast }$ and let ${\mathrm{\Gamma }}_h^{-}=\{\ell :s_{\ell }=h,\ell \ne i\}$ denote the set of indices with common value ${\mu }_i={\mu }_h^{\ast }$. Also let s⁻ = (s_ℓ; ℓ ≠i and y⁻ = (y_ℓ; ℓ ≠ i) Then we can replace sampling p(μ_i | …) by sampling from

$$p(s_i\mid s^{-},y^{-},y_i,\eta )=\sum _{h=1}^{k^{-}}I(s_i=h)m_h^{-}{Q}_h+I(s_i=k^{-}+1){MQ}_0,$$

with $Q_h=\int p(y_i\mid {\mu }_i={\mu }_h^{\ast })\text{d}p({\mu }_h^{\ast }\mid y_{\ell },\ell \in {\mathrm{\Gamma }}_h^{-},\eta )$. This step critically improves mixing of the Markov chain simulation (MacEachern, 1994).

As usual in DP mixture models, we include a transition probability to update ${\mu }_h^{\ast }$, conditional on currently imputed values of all other parameters. As before, { ${\mu }_1^{\ast },\dots ,{\mu }_k^{\ast }$} are the unique values among {μ_i, i = 1, …, n}. Let ${\mu }_{hj}^{\ast }$ denote the subvector of ${\mu }_h^{\ast }$ corresponding to the jth cycle. For resampling ${\mu }_h^{\ast }$, we condition on s (now again without excluding μi) and find $p({\mu }_{hj}^{\ast }\mid s,\theta ,\eta )\propto G^{★}({\mu }_{hj}^{\ast }){\prod }_{i\in {\mathrm{\Gamma }}_h}p({\theta }_{ij}\mid {\mu }_{hj}^{\ast })$.

5. Modeling Multiple Cycle Hematologic Data

5.1 Data and Model

Modeling patient profiles (e.g., blood counts, drug concentrations, etc.) over multiple treatment cycles requires a hierarchical extension of a basic one-cycle model. Models (1), (4), (5), and (7) provide such a generalization. Several important inference questions can only be addressed in the context of a joint probability model across multiple cycles. For example, in a typical chemotherapy regimen, some aspects of the proposed treatment are aimed at mitigating deterioration of the patient’s overall performance over the course of the treatment. Immunotherapy, growth factors, or other treatments might be considered to ensure reconstitution of blood cell counts after each chemotherapy cycle.

We analyze data from a phase I clinical trial with cancer patients carried out by the Cancer and Leukemia Group B (CALGB), a cooperative group of university hospitals funded by the U.S. National Cancer Institute to conduct studies relating to cancer therapy. The trial, CALGB 8881, was conducted to determine the highest dose of the anti-cancer agent cyclophosphamide (CTX) one can safely deliver every 2 weeks in an outpatient setting (Lichtman et al., 1993). The drug is known to cause a drop in white blood cell counts (WBC). Therefore, patients also received GM-CSF, a colony stimulating factor given to spur regrowth of blood cells (i.e., for hematologic support). The protocol required fairly extensive monitoring of patient blood counts during treatment cycles. The number of measurements per cycle varied between 4 and 18, with an average of 13. The investigators treated cohorts of patients at different doses of the agents. Six patients each were treated at the following combinations (CTX, GM-CSF) of CTX (in g/m²) and GM-CSF (in μg/kg): (1.5, 10), (3.0, 2.5), (3.0, 5.0), (3.0, 10.0), and (6.0, 5.0). Cohorts of 12 and 10 patients, respectively, were treated at dose combinations of (4.5, 5.0) and (4.5, 10.0). Hematologic toxicity was the primary endpoint.

In Müller and Rosner (1997) and Müller et al. (2004), we reported analyses restricted to data from the first treatment cycle. However, the study data include responses over several cycles for many patients, allowing us to address questions related to changes over cycles. We use the model proposed in Sections 2 and 3 to analyze the full data. The data are WBC in thousands, on a logarithmic scale, y_ijk = log(WBC/1000), recorded for patient i, cycle j, on day t_ijk. The times t_ijk are known, and reported as days within cycle. We use a nonlinear regression to set up p(y_ij | θ_ij, η). For each patient and cycle, the response y_ij = (y_ij1, …, yijn_ij ) follows a typical “bath tub” pattern, starting with an initial baseline, followed by a sudden drop in WBC at the beginning of chemotherapy, and eventually a slow S-shaped recovery. In Müller and Rosner (1997) we studied inference for one cycle alone, using a nonlinear regression (1) in the form of a piecewise linear and logistic curve. The mean function f(t; ) is parameterized by a vector of random effects = (z₁, z₂, z₃, τ₁, τ₂, β₁):

$$f(t;\theta )=\{\begin{array}{ll}{z}_1\hfill & t<{\tau }_1\hfill \\ {rz}_1+(1-r)g(\theta ,{\tau }_2)\hfill & {\tau }_1\le t<{\tau }_2\hfill \\ g(\theta ,t)\hfill & t\ge {\tau }_2,\hfill \end{array}$$ (8)

where r = (τ₂ – t)/( τ₂ – τ₁) and g(θ, t) = z₂ + z₃/[1 + exp{2.0 – β₁(t – τ₂)}]. The intercept in the logistic regression was fixed at 2.0 after finding in a preliminary data analysis that a variable intercept did not significantly improve the fit. This conclusion is based on comparing the posterior fitted curves E(f(·; θ_ij ) | data) with the observed responses. We did not carry out a formal test of fit.

We use model (8) and assume θ_ij ~ N(μ_ij, S), independently across patients i and cycles j. Dependence across cycles is introduced by the nonparametric prior μ_i ~ G.

We introduce two modifications to the general model to make it suitable for the application. First, we allow a different residual variance for each cycle, that is, we use e_ijk ~ N (0, σ_ij) for the nonlinear regression in (1). Second, we add a constraint to the kernel in (3). Let (τ _1ij, τ _2ij) denote the two elements of θ_ij corresponding to the change points τ ₁ and τ₂ in (8). We use p(θ_ij | μ_i, η) ∝ N (μ_ij, S)I(τ_1ij < τ_2ij).

Finally, we include a regression on covariates x_ij. We use the bivariate covariate of the treatment doses of CTX and GM-CSF in cycle j, patient i. Both doses are centered and scaled to zero mean and standard deviation 1.0 using the empirical mean and standard deviation across the n = 52 patients. Conditioning on x_ij, the mixture of normals for θ̃_ij = (x_ij, θ_ij ) implies a locally weighted mixture of linear regressions. Compare with Section 4.1.

5.2 Hyperpriors

We complete the model with prior specifications for the hyper-parameters η. For the residual variance ${\sigma }_{ij}^2$ we assume ${\sigma }_{ij}^{-2}\sim \text{Gamma}(a/2,ab/2)$, parameterized such that $E({\sigma }_{ij}^{-2})=1/b$, with a = 10 and b = 0.01. Let diag(x) denote a diagonal matrix with diagonal elements x. For the covariance matrix of the normal kernel in (3), we use S⁻¹ ~ W(q, R⁻¹/q) with q = 25 degrees of freedom and R = diag(0.01, 0.01, 0.1, 0.1, 0.1, 0.01, 1, 1). The elements of θ_ij are arranged such that the first two elements correspond to the covariate x_ij and the third through eighth elements correspond to the parameters in the nonlinear regression (8), z₁, z₂, z₃, τ₁, τ₂, and β₁. The base measure G^☆ of the DP prior is assumed multivariate normal G^☆ (μ_ij) = N (m, B) with a conjugate normal and inverse Wishart hyperprior on the moments. That is, m ~ N(d, D) and B⁻¹ ~ W(c, C⁻¹/c) with c = 25 and C = diag(1, 1, 1, 1, 1, .1, 1, 1), D = I₈, and the hyperprior mean is fixed as the average of single patient maximum likelihood estimates (MLE). Let θ̂_il denote the MLE for patient i. We use d = 1/n Σθ̂_i1. Finally, the total mass parameter is assumed M ~ Gamma(5, 1).

5.3 Posterior MCMC Simulation

We implemented posterior MCMC simulation to carry out inference in models (1), (4), (5), and (7), using the described prior and hyperprior choices. The parameters ${\sigma }_{ij}^2$, S, B, m are updated by draws from their complete conditional posterior distributions. All are standard probability models that allow efficient random variate generation. Updating the latent variables μ_i, i = 1, …, n and the total mass parameter M proceeds as described in MacEachern and Müller (2000). Finally, consider updating θ_i. Conditional on μ_i, inference in the model is unchanged from the single-cycle model. Updating the random effects parameters θ_ij in a posterior MCMC simulation reduces to a nonlinear regression defined by the sampling model (8) and the normal prior θ_ij ~ N(μ_ij, S). In particular, for the coefficients in θ_ij corresponding to the random effects parameters z₁, z₂, and z₃, the complete conditional posterior is available in closed form as the posterior in a normal linear regression model. We use a Metropolis–Hastings random walk proposal to update the elements of θ_ij corresponding to τ ₁ and τ ₂. If the proposed values violate the order constraint τ ₁ < τ ₂, we evaluate the prior probability as zero and reject the proposal.

As starting values for θ_ij, we used maximum likelihood estimates based on y_ij, substituting average values when too few responses were available for a given cycle. We then ran 200,000 iterations of the described MCMC, discarding the first 100,000 as initial transient, and saving imputed values after every 50th iteration.

We considered imputed values of the six-dimensional random effects vectors θ_ij for all cycles for the four patients shown in Figure 2 to verify convergence. We used BOA (Smith, 2005) to evaluate convergence diagnostics, and chose the diagnostic proposed in Geweke (1992), using default parameters in BOA. We evaluated the convergence diagnostics for a total number of 60 tracked parameters. The summary of the 60 diagnostics is (min, first quartile, mean, third quart, max) = (−1.94, −0.75, 0.01, 0.60, 1.92).

5.4 Results

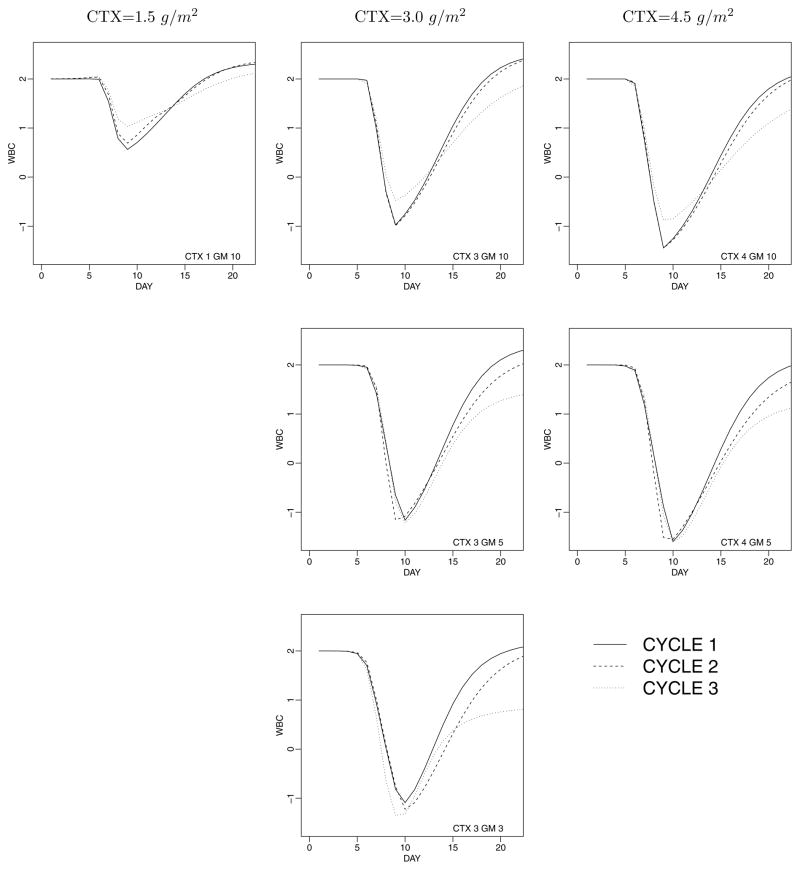
Posterior inference is summarized in Figures 3 through 5. Let 3 H(θ_i) = p(θ_i | μ_i, η) dG(μ_i) denote the nonparametric mixture model for the random effects distribution. Also, we use Y to denote all observed data. Note that the posterior expectation E(H | Y) is identical to the posterior predictive p(θ_n+1 | Y) for a new subject: p(θ_n+1 | Y ) = ∫ p(θ_n+1 | H, Y ) dp(H | Y ) = ∫ H(θ_n+1) dp(H | Y ). The high-dimensional nature of θ_ij makes it impractical to show the estimated random effects distribution itself. Instead, we show the implied WBC profile as a relevant summary. Figure 3 shows posterior predictive WBC counts for a future patient, arranged by dose x_ij and cycle j. Each panel shows posterior predictive inference for a different dose of CTX and GM-CSF, assuming a constant dose across all cycles. Within each panel, three curves show posterior predictive mean responses for cycles j = 1 through j = 3. Each curve shows E(y_n+1,jk | Y ), plotted against t_n+1,jk. Together, the three curves summarize what was learned about the change of θ_ij across cycles. Note how the curve for the third cycle (j = 3) deteriorates by failing to achieve the recovery to baseline WBC. Comparing the predicted WBC pro-files for high versus low dose of GM-CSF for the same level of CTX confirms that the growth factor worked as intended by the clinicians. The added GM-CSF improves the recovery to baseline for later cycles.

Figure 3.

Prediction for future patients treated at different levels of CTX and GM-CSF. For each patient we show the predicted response over the first three cycles as solid, dashed, and dotted lines, respectively. CTX levels are 1.5, 3.0, and 4.5 g/m² (labeled as 1, 3, and 4 in the figure). GM-CSF doses are 2.5, 5, and 10 μg/kg (labeled as 3, 5, and 10). Inference is conditional on a baseline of 2.0. Posterior predictive standard deviations are approximately 0.6.

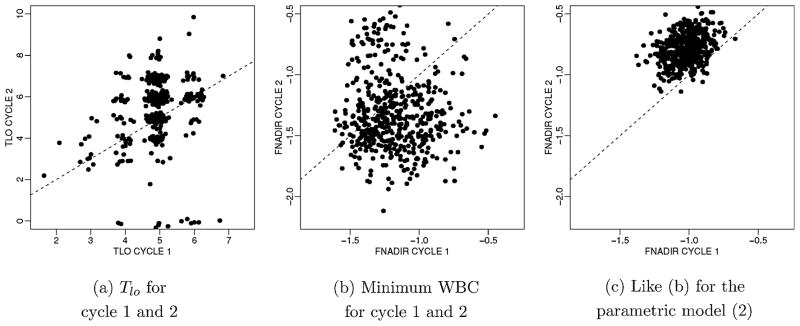
Figure 5.

Estimated H(θ). We show the bivariate marginals for cycles 1 and 2 for two relevant summaries of, for doses CTX = 3 g/m² and GM-CSF = 5 μg/kg. (a) shows the estimated distribution of T_lo, the number of days that WBC is below 1000, for the first two cycles. (b) shows the same for the minimum WBC (in log 1000). (c) shows the same inference as (b) for the parametric model. The distributions are represented by scatterplots of 500 simulated draws. For the integer valued variable T_lo we added additional noise to the draws to visualize multiple draws at the same integer pairs. For comparison, the 45 degree line is shown (dashed line).

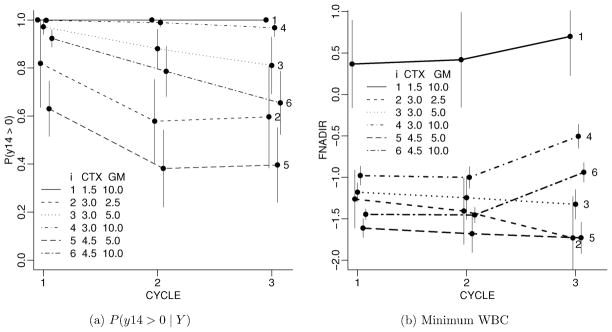
Figure 4a summarizes an important feature of G. Let p14 denote the probability of WBC above a critical threshold of 1000 on day 14, that is, p14 = p(Y _n+1,jk > log 1000 | Y ) for t_n+1,jk = 14 (we modeled log WBC). The figure plots p14 against cycle, arranged by treatment level x_n+1 (assuming constant treatment level across all cycles and denoting the common value by x_n+1). For each cycle j and treatment level the lines show the marginal posterior predictive probability of a WBC beyond 1000 by day 14. At low to moderate levels of the chemotherapy agent CTX, treatment with high level of the growth factor stimulating GM-CSF stops the otherwise expected deterioration across cycles. Even for high CTX, the additional treatment with GM-CSF still mitigates the decline over cycles. Figure 4b plots the posterior predictive minimum WBC (in log 1000) by cycle within doses of the two drugs. Short vertical line segments in both panels indicate pointwise posterior predictive standard deviations. The large posterior predictive uncertainties realistically reflect the range of observed responses in the data. Compare with Figure 5b. The numerical uncertainty of the Monte Carlo average is negligible.

Figure 4.

Clinically relevant summaries of the inference across cycles: probability of WBC > 1000 on day 14 (left panel) and estimated nadir WBC count (right panel). The left panel shows the posterior probability of WBC above 1000 on day 14, plotted by treatment and cycle. The right panel shows the minimum WBC (in log 1000) plotted by treatment and cycle. Reported CTX doses are in g/m² and GM-CSF doses are in μg/kg. The vertical error bars show plus/minus 1/2 pointwise posterior predictive standard deviation. We added a small horizontal offset to each line to avoid overlap.

Figure 5a, and 5b shows another summary of the estimated random effects model H( _i ), across cycles, for fixed doses, CTX = 3 g/m² and GM-CSF = 5 μg/kg. We select two clinically relevant summaries, the nadir WBC (fnadir) and the number of days that WBC is below a critical thresh-old of 1000 (T_lo ), to visualize the high-dimensional distributions. Both summaries are evaluated for each cycle. For each summary statistic, we show the joint distribution for cycles 1 and 2. The bivariate distributions are shown by plotting 500 random draws. One can recognize distinct clusters in the joint distribution. Figure 5c shows results for the parametric model (2). All hyperparameters were chosen identical as for the semiparametric model. The parametric model shrinks the random effects to the mean of the estimated unimodal random effects distribution. The shown summaries are highly nonlinear functions of the parameters, making it difficult to interpret the shrinkage beyond the fact that the estimated random effects distribution under the parametric model is unimodal and is significantly more peaked. We carried out similar comparisons (not shown) for Figures 2 and 3. The fit-ted profiles shown in Figure 2 remain almost unchanged under the parametric model. The predictive inference shown in Figure 3, however, changes substantially. The change in Figure 5c relative to Figure 5b shows summaries.

Finally, we carried out sensitivity analyses to investigate the robustness of the reported results with respect to changes in the prior assumptions. Results are summarized in Table 1. The columns of Table 1 report the probability of WBC count above a critical threshold in cycle 3, labeled P(y₁₄ > 0), the change in this probability from cycle 2 to 3 (ΔP), and predicted nadir count (FNADIR) in the third cycle, arranged by three different doses of GM-CSF, fixing CTX at 4.5 g/m². Reported summaries in Table 1 are with respect to the posterior predictive distribution for a future patient. The three horizontal blocks of the table report changes in the three main layers of the hierarchical model. The first three rows report inference for different choices of the prior expectation $E({\sigma }_{ij}^2)$ for the residual variances in (1). The next three lines report inference under different choices of the hyperprior on S. Recall from Section 5.2 that we use a Wishart hyperprior S⁻¹ ~ W(q, R⁻¹/q). The rows labeled r = 0.5 and r = 2.0 rescale the hyperparameter R by 0.5 and 2.0, respectively. The final set of four lines reports inference for different choices of the total mass parameter M, using fixed values of M = 1, 5, and 10. The row marked with 5* reports inference under the Gamma(5, 1) hyperprior with E(M) = 5 reported in Section 5.2. The rows marked with $E({\sigma }_{ij}^2)=0.01$, M = 5*, and r = 1.0 are identical These are the choices reported in Section 5.2. Under this wide range of reasonable hyperprior parameters, we find the reported features of the posterior inference to be reasonably robust.

Table 1.

Important inference summaries for low, medium, and high choices of three hyperprior parameters. The columns report three important summaries related to Figure 4. See the text for details. The three horizontal blocks report inference when changing hyperprior parameters related to the nonlinear regression sampling model (first block, E(σ²)), the prior on the random effects (marked with r), and the nonparametric prior (M). See the text for details.

	Dose GM-CSF
	P (y14> 0)			ΔP(y14> 0)			FNADIR
	2.5	5.0	10.0	2.5	5.0	10.0	2.5	5.0	10.0
E(σ2)
0.01	0.60	0.81	0.97	0.02	−0.07	−0.017	−1.7	−1.3	0.00
0.10	0.64	0.72	0.90	0.00	−0.27	−0.040	−1.6	−1.4	−0.54
1.00	0.62	0.58	0.97	0.04	−0.36	0.000	−1.5	−1.7	−0.34
r
0.5	0.62	0.72	0.87	−0.10	0.14	0.090	−1.7	−1.1	−0.19
1.0	0.60	0.81	0.97	0.02	−0.07	−0.017	−1.7	−1.3	0.00
2.0	0.84	0.81	0.99	−0.12	−0.12	0.010	−1.6	−1.7	−0.37
M
1	0.58	0.78	0.97	−0.09	−0.21	−0.010	−1.7	−1.4	−0.33
5	0.59	0.74	0.97	−0.08	−0.25	−0.010	−1.7	−1.5	−0.46
5*	0.60	0.81	0.97	0.02	−0.07	−0.017	−1.7	-1.3	0.00
10	0.56	0.68	0.98	−0.11	−0.30	−0.010	−1.6	−1.3	−0.40

6. Conclusion

We have introduced semiparametric Bayesian inference for multilevel repeated measurement data. The nonparametric nature of the model is the random effects distribution for the first-level random effects and the probability model for the joint distribution of random effects across second-level repetitions.

The main limitation of the proposed approach is the computation-intensive implementation. Important directions of extensions for the proposed model are to different data formats, for example, repeated binary data, and to a more structured model for the dependence across cycles. In the proposed model, dependence across cycles is essentially learned by clustering of the imputed random effects vectors for the observed patients. The approach works well for continuous responses with a nonlinear regression model (1), assuming the residual variance is small enough to leave little posterior uncertainty for the θ_ij. The model is not appropriate for less informative data, for example, binary data. Finally, the main reasons for choosing the DP prior were computational ease and the nature of the predictive rule (6). Both apply for a wider class of models known as species sampling models (Pitman, 1996; Ishwaran and James, 2003). Such models could be substituted for the DP model, with only minimal changes in the implementation.