Gelation of Covalently Cross-Linked PEG–Heparin Hydrogels

Abstract

We study PEG–heparin hydrogels to identify compositions that lead to gel formation and measure the corresponding gelation kinetics. The material consists of a maleimide-functionalized high molecular weight heparin (HMWH) backbone covalently cross-linked with bis-thiol poly(ethylene glycol) (PEG). Using multiple particle tracking microrheology, we investigate a broad composition space, defined by the number of maleimide functional sites per HMWH (f = 3.9–11.8), the molecular weight of the PEG cross-linker (M_n = 2000, 5000, and 10 000), and the concentrations of the heparin and PEG polymers. Gelation kinetics are characterized by time–cure superposition, yielding the gel time, t_c, and the critical relaxation exponent, n. Gelation times range from 5 < t_c ≤ 45 min, with the fastest kinetics occurring for the highest HMWH maleimide functionalities. t_c depends nonmonotonically on the PEG cross-linker molecular weight, suggesting that gelation is affected by the length of the cross-linker relative to intermolecular interactions between heparin molecules. The critical relaxation exponent decreases from n = 0.52 for PEG 2000 to n = 0.39 for PEG 10 000. Finally, 219 equilibrated samples taken over the entire composition space are identified as liquid or solid, defining the “gelation envelope”. The boundaries of this empirical gelation envelope are in good agreement with Flory–Stockmayer theory. In all, microrheological measurements enable characterization over a large parameter space and provide crucial insight into the gelation of complex, multifunctional hydrogelators used in therapeutic applications.

Introduction

Hydrogels are dilute, cross-linked polymer networks that do not flow once equilibrated.¹ Because of their highly varied, tunable structure and mechanical properties, hydrogels are found in a wide variety of applications, including use in foods,² personal care products,³ and therapeutic materials.^4-21 Recent work toward engineering new biocompatible hydrogel materials has exploited advances in structural biology and the quantitative understanding of biomacromolecular and cellular behavior.^{4-12,14,16,17} This enables the rational design of hydrogels that mimic biologically relevant microenvironments in tissue engineering, wound healing, and other biomedical applications,^6-8,10,11 including the ability to controllably deliver sequestered proteins,^{5,9,10,14,17-22} especially in response to environmental cues, such as changes in pH and ionic strength.^5-9,11,14 Because of their responsiveness, hydrogels can also be engineered to act as biological sensors.^12,13,23,24

Heparin-based hydrogels have properties which make them attractive for therapeutic applications, including the ability to sequester and stabilize proteins, such as growth factors.^{5,6,8,14,15,17-22,25-27} Heparin is a highly sulfated glycos aminoglycan (GAG); thus, the protein–polysaccharide interactions provided by heparin closely mimic the native structure and function of the extracellular matrix (ECM). In tissue engineering applications, growth factor delivery by the heparin scaffold generates proliferation signals to cells, while the mechanically soft gel environment coupled with material degradation enables efficient scaffold remodeling during cell migration.^6-8,22,25-28 Heparin immobilization is also used to promote controlled growth factor release and increased biocompatibility in various hydrogel systems,¹⁶ including poly(ethylene glycol) scaffolds,^17,21 polymeric micelles,¹⁹ non-sulfated glycosaminoglycans,¹⁸ and in vivo photo-cross-linkable materials.²⁰

The heparin hydrogel in this study consists of a maleimide-functionalized high molecular weight heparin (HMWH) backbone covalently cross-linked by bis-thiol poly(ethylene glycol) (PEG). PEG is a synthetic polymer that is incorporated into the hydrogel due to its resistance to protein adsorption and hydrophilicity.^25,29,30 These components create a covalently cross-linked hydrogel, which can be engineered to vary physical characteristics such as moduli and growth factor release profiles.^25,26 Passive degradation occurs via hydrolysis of the 3-mercaptoproionic acid esterified PEG molecules.

Microrheological measurements, specifically multiple particle tracking (MPT), are ideal for characterizing such emerging hydrogel materials. MPT measures the thermal motion of probe particles embedded in the material, which is related to the material rheological properties.^31-33 MPT is advantageous because it requires only a small amount of material, 20–40 μL, for each sample and provides access to a large range of relaxation time scales. Furthermore, recent developments in microrheology have shown that it is a powerful method for studying the liquid–solid transition of hydrogelators.^2,34,35 Determining the gel point of these dilute systems has proven difficult using bulk rheological measurements due to the rapid gelation kinetics and weak mechanical properties of the incipient gel, which are typically within the noise limit of the rheometer and subject to disruption by the external stress. Alternatively, measuring the Brownian diffusion of small probe particles produces less strain on the network and is more sensitive at low moduli (<1 Pa). In all, the small sample sizes, rapid acquisition times, and parallel preparation of samples make microrheology an ideal approach for studying the gelation of materials over a wide composition space.³⁶

In this work, the kinetics of the HMWH hydrogelation reaction are studied to identify both the gel time and critical gelation exponent using time–cure superposition.^34,35,37 These values vary as the PEG molecular weights are changed. Next, material assembly conditions are investigated as a function of HMWH backbone functionality, PEG cross-linker size, and total polymer concentration. The critical gelation exponent is used to identify the state of each sample, i.e., sol or gel. In each map, a unique “gelation envelope” is measured; the size and location of this region vary with each parameter studied.³⁶ The gelation envelope is compared to the predicted boundaries using Flory–Stockmayer theory.

Experimental Section

Hydrogel Materials and Sample Preparation

The hydrogel system consists of a maleimide-functionalized high molecular weight heparin (HMWH, M_n = 15 000, Sigma-Aldrich) polymer backbone covalently cross-linked with bis-thiol poly(ethylene glycol) (PEG, Sigma-Aldrich). Details of the HMWH functionalization reaction have been provided previously.²⁵ The average maleimide functionality of the HMWH, f, is determined by ¹H NMR and varies between 3.9 and 11.8. Three PEG molecular weights (M_n = 2000, 5000, and 10 000) are used to investigate the effect of cross-linker size on the hydrogel formation and gelation kinetics. Thus, the composition space of the gels studied here consists of the concentration of HMWH, the concentration of the PEG cross-linker, the HMWH maleimide functionality, and the length of the PEG cross-linker. The relevant physical length scales of the polymer molecules, including the contour length, L_c, average end-to-end length, 〈r_ee²〉 , and radius of gyration, R_g, are tablulated in Table 1. We use 0.7 nm for the Kuhn length and 0.35 nm for the segment length of PEG; these values are consistent with those obtained from light scattering.^30,38-40

Table 1. Polymer Length Scales²⁹,³⁰,^{38 a}.

polymer	Mn (g/mol)	N	Lc (nm)	〈ree2〉1/2 (nm)	Rg (nm)
PEG	2000	45	15.7	3.3	1.4
PEG	5000	114	39.9	5.3	2.2
PEG	10000	227	79.4	7.5	3.0
HMWH	15000	26	26.8	16.7	4.5

^aM_n is the number-average molecular weight, N is the number of monomer units, L_c is the contour length, 〈r_ee²〉^1/2 is the root-mean-squared end-to-end length, and R_g is the radius of gyration.

Samples are prepared first by creating 4 wt % stock solutions of both the HWMH and PEG cross-linker in 1x phosphate buffered saline (1x PBS, Invitrogen). Fluorescently labeled polystyrene probe particles (diameter 2a = 1.05 ± 0.01 μm, Polysciences) are diluted to a volume fraction ϕ ≈ 10⁻² with ultrapure water (resistivity >18.2 MΩ · 3 cm, Millipore). Probe particles are added to the HMWH precursor solution. The gelation reaction is initiated by mixing the HMWH and PEG precursor solutions. In this study, HMWH with functionalities f = 3.9, 6.3, 7.8, and 11.8 are cross-linked with 2000 and 5000 molecular weight PEG, while gels made with PEG 10 000 use HMWH with functionalities f = 4.2, 6.5, 8.3, and 11.0.

Multiple Particle Tracking Microrheology

After mixing the HMWH and PEG precursor solutions, hydrogel samples are immediately loaded into capillary tubes (0.2 × 2.0 × 50 mm, Vitrotubes), which are fixed to microscope slides (25 × 75 × 1 mm, Fisher Scientific) and sealed with UV-cured thiolene resin (NOA81, Norland Products). The sample volume required for each microrheology sample is approximately 20–40 μL.

Data are collected by video microscopy with an inverted microscope (Axiovert 200, Carl Zeiss, Inc.) at a magnification of 63x (63x water immersion objective, N.A. 1.2, 1x Optovar, Carl Zeiss, Inc.). The focal plane is positioned in the middle of the sample volume to minimize wall effects on the Brownian motion. A CMOS high-speed camera (Phantom v5.1, 1024 × 1024 pixels, Vision Research) records the movement of the probe particles at 30 frames/s with an exposure time of 1000 μs, chosen to minimize the static and dynamic particle tracking errors.⁴¹ Individual particle trajectories are generated by a brightness-weighted centroid particle tracking algorithm from the 800 frame movie.³³ At least 100 particles are tracked in each movie. The ensemble averaged mean-squared displacement (MSD), 〈Δr²(τ)〉, is calculated from the particle trajectories. The MSD of the probe particles is related to the linear viscoelastic properties of the material by the generalized Stokes–Einstein relation (GSER)

$$\langle \Delta r^2\left(\tau \right)\rangle =\frac{k_{\mathrm{B}}T}{\pi a}J\left(\tau \right)$$ (1)

where k_BT is the thermal energy, a is the probe particle radius, and J(τ) is the embedding material creep compliance.⁴²

For measurements of gelation kinetics, only one sample is studied at a time. Images are collected every 2.5 min, starting 5 min after initiation of the gelation reaction and continuing until 30 min after probe particle movement is no longer detectable by eye, ensuring that the entire gelation reaction is captured. Note that, although the microrheology data are acquired as the material is still evolving, the time scale of the reaction is (typically) significantly longer than the experimental acquisition time (≈30 s), making any changes in the material properties during the acquisition window negligible. In the current work, this applies only to materials formed from heparin with the lowest maleimide functionalities, f =3.9-4.2, since this is the only system that evolves slowly enough to ensure that each measurement is a “quasi-stationary” sampling of the probe particle dynamics during the gelation reaction.

Equilibrated samples are prepared by systematically varying the polymer concentrations, backbone functionality, and cross-linker molecular weight. Eight samples are fixed to one glass slide to increase the efficiency of data acquisition. All samples are prepared at the same time, allowing equilibration to proceed in parallel. Two hours after initiating the gelation reactions, the equilibrated samples are measured. The parallel equilibration of the samples vastly increases the throughput of the rheological measurements.³⁶

Finally, we note that we do not observe obvious signs of heterogeneity in the gelling or equilibrated materials, such as subpopulations of diffusing and trapped particles in the same sample, as is sometimes observed for materials with a large degree of heterogeneity on micrometer length scales, such as collagen⁴³ or agarose.⁴⁴

Results and Discussion

There are two principal results of our study: First, the gelation kinetics are measured as a function of HMWH maleimide functionality and PEG cross-linker molecular weight. These experiments are performed at the lowest total polymer concentration where a gel will form for the given system. Second, equilibrated samples are analyzed over the complete composition space, which includes the HMWH concentration, PEG concentration, HMWH maleimide functionality, and PEG molecular weight. These enable us to identify the compositions that lead to gel formation. The gelation kinetics will be discussed first because this provides important details regarding the interpretation of the equilibrated sample experiments.

Gelation Kinetics

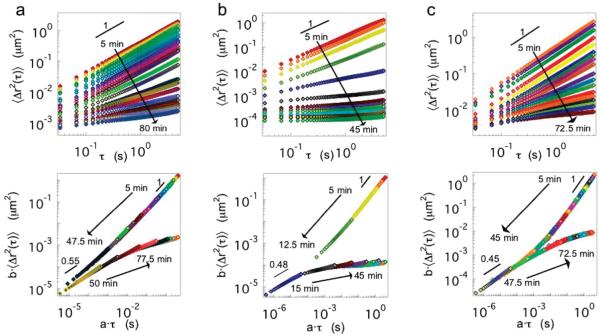
After mixing the precursor HMWH and PEG solutions, tracer particles are tracked throughout the evolution of the material from the initial liquid state to the final equilibrated solid state. Typical results are shown in Figure 1 for 4:1, 2:1, and 2.6:2.4 weight percent of high molecular weight heparin and PEG 2000, 5000, and 10 000 (1:1, 1.3:1, and 1.5:1 maleimide to thiol sites), respectively. When plotted in log–log fashion, the initial mean-squared displacement is linear, indicating that 〈Δr²(τ)〉~τ for a viscous fluid. The MSD initially decreases in magnitude as the viscosity increases. As the gelation reaction proceeds, subdiffusive dynamics first appear at short lag times, while long lag times retain the diffusive scaling. The crossover time scale between these dynamics increases, and the MSD at long lag times makes a sudden shift to subdiffusive scaling. This signals the onset of an elastic plateau and the formation of a viscoelastic solid.

Figure 1.

Gelation kinetics for maleimide-functionalized HMWH covalently cross-linked with bis-thiol (a) PEG 2000, (b) PEG 5000, and (c) PEG 10 000. The top row is the ensemble averaged mean-squared displacement, and the lower row is the shifted mean-squared displacement into pre- and postgel master curves.

The gelation kinetics are analyzed by time–cure superposition of the tracer particle mean-squared displacement.^34,35 Time–cure superposition is the superposition of viscoelastic functions for varying extents of a gelation reaction, p. Adolf and Martin first demonstrated time–cure superposition using bulk rheology data taken at various extents of reaction for an epoxy.³⁷ This enables the identification of the gel point (critical extent of reaction, p_c) and critical scaling exponents of the longest relaxation time and equilibrium modulus.

The self-similarity of the MSD curves shown in Figure 1 enables the creation of two master curves for the pre- and postgel states. The shift factor a, which scales the lag time, is related to the longest relaxation time, τ_L, and the distance from the critical extent of reaction by

$$a\sim {{\tau }_{\mathrm{L}}}^{-1}\sim {\left(\frac{\mid p-p_{\mathrm{c}}\mid }{p_{\mathrm{c}}}\right)}^y$$ (2)

Similarly, the MSD shift factor b is related to the steady-state creep compliance, $J_{\mathrm{e}}^0$, and the distance from the critical extent of reaction by

$$b\sim \frac{1}{J_{\mathrm{e}}^0}\sim {\left(\frac{\mid p-p_{\mathrm{c}}\mid }{p_{\mathrm{c}}}\right)}^z$$ (3)

In eqs 2 and 3, y and z are the critical scaling exponents of the longest relaxation time and modulus, respectively.⁴⁵ Note that, due to the nature of the hydrogelation reaction, stopping the gel formation at specific extents of reaction is not possible. Therefore, the time after the initiation of the gelation is assumed to be proportional to the extent of reaction, t ~ p. The asymptotic behavior of a and b when plotted versus time are used to determine the gel time, t_c.^34,35 It should be noted that for this analysis technique to be valid the range of lag times must be sufficiently wide in order to capture the longest relaxation time of the polymer system.

Time–cure superposition of the hydrogelation kinetics can only be performed for the lowest HMWH functionalities, f = 3.9–4.2, because these are the only conditions with gelation kinetics slow enough to yield sufficient data for meaningful analysis. Increasing the functionality of the HMWH decreases the gel time to below 10 min. This is consistent across all PEG molecular weights, as summarized in Table 2. For f ≈ 6, the gel time can be identified from the MSDs to occur between 5 and 10 min, but the low number of MSD curves acquired in the pregel state precludes analysis by time–cure superposition. For all other samples, the gel point is reached in under 5 min.

Table 2. Summary of Gel Times for all HMWH Functionalities and PEG Cross-Linkers.

HMWH functionality, f	PEG Mn (g/mol)	HMWH (wt %): PEG (wt%)	HMWH reactive sites: PEG reactive sites	gel time, tc (min)
3.9	2000	4:1	1:1	45
3.9	5000	2:1	1.3:1	15
4.2	10000	2.6:2.4	1.5:1	41
6.3	2000	3:1	1.3:1	5 < tc < 10
6.3	5000	2:1	2.1:1	5 < tc < 10
6.5	10000	2:3	1.4:1	5 < tc < 10
7.8	2000	2:1	1:1	<5
7.8	5000	2:1	2.6:1	<5
8.3	10000	2:3	1.8:1	<5
11.8	2000	2:1	1.6:1	<5
11.8	5000	2:1	3.9:1	<5
11.0	10000	2:3	2.4:3	<5

For the lowest HMWH functionalities, however, we find an interesting nonmonotonic effect of PEG cross-linker molecular weight on the gel time. Both PEG 2000 and PEG 10 000 samples have similar gel times, 45 and 41 min, respectively. In contrast, the PEG 5000 gels in ~15 min. These values are reproducible; measurements for identical compositions and samples in which the HMWH to PEG cross-linker ratio are varied give similar results. Repeating the experiment at least three times and holding the composition constant for both PEG 2000 and 5000 results in average gel times of 44.5 ± 3.8 and 14.9 ± 3.3 min, respectively. PEG 10 000 is studied through the composition space by holding the total polymer concentration (HMWH and PEG) constant at 5 wt % and varying the HMWH to PEG cross-linker ratio (HMWH (wt %):PEG (wt %) = 2.6:2.4, 2.73:2.26, 2.86:2.12, and 3:2, which are equivalent to the maleimide: thiol ratios 1.5:1, 1.7:1, 1.9:1, and 2.1:1). The average gel time for these samples is 40.6 ± 8.2 min.

The nonmonotonic dependence of the gel time on cross-linker molecular weight for the lowest HMWH maleimide functionalities may reflect the competition of several physical effects on the cross-linking efficiency, including the effective range of interaction between heparin molecules produced by the cross-link, the tendency to form loops on the same HMWH molecule, and steric constraints between cross-linking molecules as the PEG molecular weight becomes large. The relevant length scales for these molecules are summarized in Table 1. For comparison, the average distances between maleimide functional sites on the HMWH backbone, as estimated from the average placement of maleimide groups after the reaction of aminoethylmaleimide with carboxylates on the HMWH, are summarized in Table 3.

Table 3. Average Distance between Maleimide Groups d̄ on HMWH with Maleimide Functionality f.

f	d̄ (nm)
3.9	6.9
4.2	6.4
6.3	4.2
6.5	4.1
7.8	3.4
8.3	3.2
11.0	2.4
11.8	2.3

First, we consider PEG 2000. This cross-linker is fairly short, with a radius of gyration R_g ≈ 1.4 nm and the average end-to-end separation is 3.3 nm. The formation of loops by the reaction of both ends of the PEG with two sites on the same HMWH molecule is unlikely for all HMWH functionalities but f = 11. However, this also means that the effective attraction between HMWH molecules caused by the cross-linker is short-ranged compared to excluded volume of the HMWH and the potentially strong electrostatic repulsions between heparin molecules. The latter could be expected due to the large negative charge of the heparin molecule (−75e);²² however, the Debye screening length of the buffer solution is κ⁻¹ = 0.7 nm, implying that the electrostatic interactions are fairly well-screened.⁴⁶ Instead, the entropic penalty of bringing two HMWH molecules together with such a short cross-linker appears to be the main contributor to a repulsive barrier that slows the kinetics of cross-link formation and the overall rate of gelation. This makes PEG 2000 an inefficient cross-linker overall.

In contrast, the end-to-end separation of PEG 5000 is 1.6x larger than the PEG 2000 molecules, extending the range of the attraction and making the PEG long enough for attachment to two HMWH molecules to be favorable. Therefore, the PEG 5000 is the fastest and most efficient hydrogelator because it is long enough to encourage links between backbones, and the molecule’s length scale is slightly smaller than the average spacing of maleimide functional sites.

The HMWH with PEG 10 000 gels in ~45 min, a much longer time than PEG 5000 but comparable to PEG 2000. The average end-to-end separation for PEG 10 000 is 〈r_ee²〉^1/2 = 7.5 nm, which is larger than the average linear spacing of the maleimide functional sites for all HMWH functionalities. First, this implies that looping, the reaction of a single PEG with two maleimide sites on the same heparin molecule, may occur. This would reduce the effective functionality of a particular backbone molecule to f – 2. Second, it may be difficult for the larger PEG molecule to penetrate the excluded volume of the HMWH molecule, essentially giving rise to an entropic repulsion between the two molecules that slows the reaction kinetics. Finally, as the bulkier PEG chains decorate the HMWH backbones, they will contribute a steric hindrance and decrease the mobility of the heparin molecules, which may also contribute to the slower gelation kinetics.

Overall, for low numbers of cross-linkable sites on heparin, the reaction kinetics are balanced between two competing effects: the range of the effective interaction generated by the cross-linker and the steric constraints of large cross-linker molecules, both of which slow the kinetics of the reaction. With increasing HMWH maleimide functionalities, the gelation reaction proceeds at a faster rate, and is not dependent, within the accuracy of our measurements, to the size of the cross-linker.

Critical Relaxation Exponent

At the gel point, the creep compliance exhibits time-independent scaling

$$J_{\mathrm{c}}=\frac{\sin n\pi }{Sn\pi }{t}^n$$ (4)

where n is the critical relaxation exponent and S is the incipient gel strength in units Pa·sⁿ.⁴⁷ Equation 4 is equivalent to the more commonly used relationship

$$G^{\prime }\left(\omega \right)\sim G^{\prime \prime }\left(\omega \right)\sim {\omega }^n$$ (5)

which states that the storage G’(ω) and loss G”(ω) moduli exhibit a frequency-independent scaling behavior or, equivalently, that the loss tangent, tan δ = G”/G’, is constant over all frequencies at the gel point.^48,49 For microrheological measurements, the generalized Stokes–Einstein relationship gives the ensemble-averaged mean-squared displacement

$$\langle \Delta r^2\left(\tau \right)\rangle \sim {\tau }^n$$ (6)

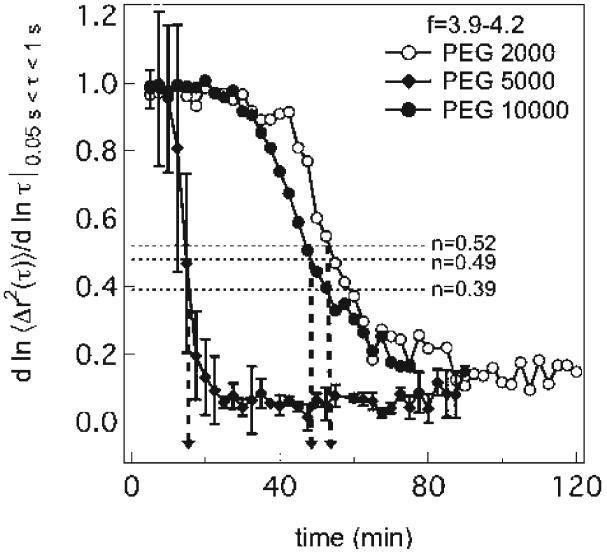
at the gel point.^34,50 Thus, from the logarithmic slope of the MSD, α = d log〈Δr²(τ)〉/d log τ, the gel point can be determined by α = n, if the value of n is known. Unfortunately, n is strongly dependent on the material, with values between 0.1 < n < 0.9 reported in the literature.^{34,35,37,47-49,51,52} Note also that the use of the logarithmic slope is approximate for t ≠ t_c because eq 6 only holds at t = t_c. Nonetheless, the local slope over a short-range of lag times still provides an accurate measure of the gel point. This will be used below to identify material compositions that lead to hydrogelation. The time–cure superposition master curves in Figure 1 are used to identify the value of n by the slope of the converging pre- and postgel master curves. An example of the MSD logarithmic slope α = d log〈Δr²(τ)〉/d log τ over the lag time range 0.05 < τ < 1 s for f = 3.9–4.2 is shown in Figure 2. After the initiation of gelation, there is a plateau where the material is becoming more viscous but is still a liquid. Then the gelation reaction proceeds rapidly until equilibrating at a final value of the terminal slope.

Figure 2.

Logarithmic slope of mean-square displacement for all cross-linkers over the entire gelation reaction.

Interestingly, n decreases as a function of increasing molecular weight of the PEG cross-linker, with n_avg = 0.52 ± 0.07, 0.49 ± 0.2, and 0.39 ± 0.04 for PEG 2000, 5000, and 10 000, respectively. This value does remain constant over the rest of the hydrogel composition space; thus, n depends primarily on the cross-linker molecular weight. From a practical standpoint, the narrow range of values does not lead to significant uncertainty when identifying the gel time, as shown in Figure 2, nor will it preclude its use in identifying gelation conditions in the following section. However, the values are of interest for comparing to theoretical predictions based on the structure and dynamics of the incipient gel.

Previous studies of gelation critical exponents using time–cure superposition microrheology reported values of n = 0.6 and 0.55 for a semiflexible self-assembled peptide hydrogel and poly(acrylamide), respectively. These values are consistent with the percolation universality class for hydrodynamically unscreened (Rouse-like) dynamics of the incipient gel.

Power law behavior of the incipient gel rheology reflects mechanical self-similarity over a wide range of time scales. It is thought that this is driven by structural self-similarity, i.e., fractal-like structure of the gel. For a monodisperse solution of polymers exhibiting Rouse dynamics (freely draining), the critical gel relaxation exponent is predicted to be⁵²

$$n=d_{\mathrm{f}}∕(d_{\mathrm{f}}+2)$$ (7)

where d_f is the fractal dimension describing the cluster radius at the gel point for a cluster mass M, R_M ~ M^d_f. For 1 ≤ d_f ≤ 3, the relaxation exponent has values 1/3 ≤ n ≤ 3/5. Correcting for polydispersity of the critical gel results in

$$n=d_{\mathrm{f}}(\tau -1)∕(d_{\mathrm{f}}+2)$$ (8)

where τ is the scaling exponent of the cluster number distribution with respect to cluster mass, N_M ~ M^−τ. This results in n = 2/3, noting that percolation theory predicts τ = 2.20 and d_f = 2.5. The influence of excluded volume is to swell clusters from the percolation prediction to d_f = 2, resulting in n = 1/2, which is in good agreement with the value for gels synthesized with PEG 2000. In addition to being affected by the stoichiometric ratio of the cross-linker to precursor, the physical characteristics of the precursor also influence n. For instance, gels formed from polycaprolactone solutions above the entanglement molecular weight exhibit lower values of n, implying that the critical gel is more elastic.⁵³ This is consistent with the value of n decreasing as the PEG cross-linker molecular weight increases in the HMWH–PEG hydrogels.

Hydrogel Assembly Conditions

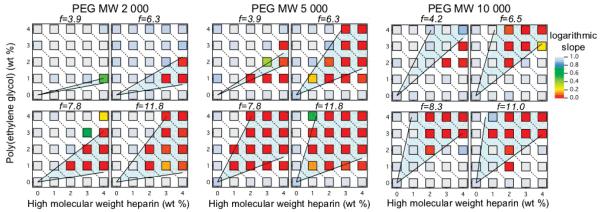
Gelation maps sampling a wide area of the compositional space are created for the heparin hydrogels to identify compositions that lead to gel formation. All 219 compositions, covering variations in the HMWH concentration, PEG concentration, maleimide functionality of the HMWH, and molecular weight of the PEG, are shown in Figure 3. The abscissa for each gelation map is the concentration of the HMWH backbone, while the ordinate is the poly(ethylene glycol) concentration. The color of each discrete point represents the logarithmic slope of the mean-squared displacement α measured with multiple particle tracking microrheology. Cool (light) colors in the figures represent samples that are liquid like, and the warm (dark) colors indicate a solid gel state. The critical gelation exponent, n, obtained from kinetic measurements, divides the data into a liquid or gel state. Therefore, the liquid state is defined by α > n and α < n indicates a gel.

Figure 3.

Hydrogel assembly conditions for all 219 samples. From left to right: PEG 2000, PEG 5000, and PEG 10 000. The data for PEG 10 000 were reported previously³⁶ and shown here for comparison.

The empirical gelation maps are compared to Flory–Stockmayer theory.^54-56 In our earlier work,³⁶ we found that Flory–Stockmayer theory provided an adequate estimate of the gelation conditions for HMWH hydrogels cross-linked by PEG 10 000. The lower and upper lines defining the “gelation envelope” correspond to the bounding conditions that lead to percolation in the sample. The lower limit of the Flory–Stockmayer theory corresponds to the condition in which there is one PEG molecule for each HMWH backbone

$$n_{\mathrm{PEG}}=\left(\frac{f}{f-1}\right)n_{\mathrm{HMWH}}$$ (9)

where f is the maleimide functionality of the HMWH backbone and n_HMWH and n_PEG are the moles of heparin and PEG, respectively.^36,54-56 This limit predicts the minimum concentrations necessary for the growing network to create an infinite cluster within the given sample. The upper limit of cross-linker attachment to the backbone occurs when there is only one functional site available for cross-linking due to backbone decoration on each heparin backbone

$$n_{\mathrm{PEG}}=(f-1)n_{\mathrm{HMWH}}$$ (10)

Flory–Stockmayer theory predicts the conditions of gelation remarkably well over the entire composition space of HMWH–PEG hydrogels, with the exception of lowest HMWH functionalities and the highest molecular weight cross-linker. In our earlier work, we noted that the disagreement at f = 4.2 for PEG 10 000 implied that a statistically significant fraction of HMWH had functionality f < 3.³⁶ This decreases the amount of HMWH available to satisfy the conditions for percolation; by Flory–Stockmayer theory, percolation is maintained only for f > 2. The results for PEG 5000 and f = 3.9 appear to be consistent with this, as the gel region is pushed to slightly higher concentrations, although it is broader than expected. The gel region for PEG 2000 is too narrow to draw any conclusions regarding the functionality of the HMWH but is consistent with the narrow range compositions leading to gelation predicted by Flory–Stockmayer theory.

Overall, the best agreement with Flory–Stockmayer theory occurs for hydrogels made with PEG 5000. This hydrogel has the largest gelation region over the measured compositional space, with boundaries that are in good agreement with Flory–Stockmayer theory. A lower total polymer concentration for gel formation is not apparent in the sample data collected but is expected to occur between 0 and 2 wt % polymer. Recall that PEG 5000 also exhibited the fastest gelation kinetics. Thus, the efficiency of this cross-linker backbone combination, apparent in the total region of gel formation, allows gels to form at the lowest polymer concentrations in the shortest amounts of time. Depending on the application, this could be a desirable property for engineering a hydrogel system. The lower total polymer concentration limit for gelation is less than 3–4 wt % for f > 3.9. This envelope is notable from the other cross-linkers because gels form at low PEG concentrations, namely 1 wt %. The modulus of hydrogel samples, measured using bulk rheology, confirms that the cross-linking efficiency of PEG 5000 is the greatest among the cross-linker molecular weights tested (unpublished data). These studies will be presented in detail in a subsequent paper.

Finally, whereas PEG 2000 and 5000 exhibit a fairly uniform region of compositions where gelation is observed, the gel boundaries for PEG 10 000 are more complicated. For instance, gelation is not observed below 3–4 wt % total polymer. For f = 11.0 in particular, the gelation occurs for 1 wt % PEG, 2 wt % HMWH (0.1:1 thiol:maleimide reactive sites), below the expected lower gel limit, but not for 4 wt % PEG, 1 wt % HMWH (1.1:1 thiol:maleimide sites). The slower kinetics measured for PEG 10 000 than PEG 5000 (for low functionalities) raised the possibility that significant steric interactions may play a role as the number of large PEG molecules decorate the HMWH backbones. The average separation between maleimide functional groups for f ≥ 6.5 is d ≥ 4.1 nm, which implies that two PEG 10 000 molecules on neighboring sites would overlap if both sites were occupied, since d̄ < 2R_g. Thus, it is unsurprising that the gelation boundaries become more complicated as the PEG molecular weight increases. Also, bulk rheological measurements (data unpublished) show good agreement with both microrheological gelation maps and the Flory–Stockmayer limits cited.

Conclusions

Engineering hydrogel material for therapeutic applications requires knowledge of the gelation kinetics and compositions that lead to gel formation. Multiple particle tracking microrheology is an essential characterization tool for these aims. Gelation kinetics measurements capture the evolution of the material rheology with time, enabling the identification of the gel time and critical relaxation exponent of the weak, incipient gel. These experiments clearly demonstrate that changing the molecular weight of the cross-linker affects the hydrogelation reaction kinetics. An optimal cross-linker molecular weight balances the repulsion between HMWH molecules, which dominates for short cross-linkers, and the repulsion between the PEG cross-linker and HMWH, which dominates at high PEG molecular weights. However, these differences are only observed for the smallest maleimide functionalities of the HMWH.

Second, the rapid data acquisition of microrheology enables the efficient collection of rheological data from 219 discrete samples of varying composition. The resulting “gelation maps”, which distinguish compositions that lead to a solid gel versus a fluid, exhibit a clear gelation envelope, which is effectively bounded by the Flory–Stockmayer theory. However, deviations from Flory–Stockmayer theory, particularly for samples cross-linked with PEG 10 000, indicate that there are complexities of the gelation reaction which Flory–Stockmayer theory does not capture. These include potential looping and the steric hindrance of cross-linking due to the large PEG molecules. Non-monotinicity of the gelation kinetics with cross-linker size and deviation from the expected Flory–Stockmayer gel boundaries emphasize the power of microrheology, in particular as a high-throughput screening method. We expect that the complexity of interactions in hydrogelators will increase with the number of components comprising a therapeutic hydrogel, including sequestered proteins, adhesion ligands, and cross-linking agents, placing predictions of gel properties well beyond simple models like Flory–Stockmayer theory. Therefore, rapid, empirical determination of gelation kinetics and conditions over a broad composition space that also conserve material is critical for future materials engineering.

Finally, the information gained in this study enhances hydrogel engineering for therapeutic applications. In previous studies, we investigated physically cross-linked hydrogels, focusing on the degradation profile and the ability to deliver proteins, such as growth factors.²⁶ Development of covalent cross-linking strategies to expand the functions of these materials has also permitted identification of compositions that control growth factor release and cellular interactions with heparinized gels.^5,25 Understanding the percolation boundaries of PEG–HMWH hydrogels enables the use of combined covalent and noncovalent cross-linking strategies. Heparin could be covalently cross-linked immediately below the percolation threshold, while additional cross-links provided by a physical cross-linker, such as a dimeric growth factor, would form the gel. This strategy will provide responsive delivery and coupled erosion via biologically relevant, ligand-exchange mechanisms while providing greater flexibility in tailoring the mechanical strength of the gel.¹⁵