Skip to main content
PMC home page
BMC Genomics logoLink to BMC Genomics
. 2011 Mar 23;12:157. doi: 10.1186/1471-2164-12-157

Alu distribution and mutation types of cancer genes

Wensheng Zhang 1, Andrea Edwards 1, Wei Fan 2, Prescott Deininger 3,✉, Kun Zhang 1,✉
PMCID: PMC3074553  PMID: 21429208

Abstract

Background

Alu elements are the most abundant retrotransposable elements comprising ~11% of the human genome. Many studies have highlighted the role that Alu elements have in genetic instability and how their contribution to the assortment of mutagenic events can lead to cancer. As of yet, little has been done to quantitatively assess the association between Alu distribution and genes that are causally implicated in oncogenesis.

Results

We have investigated the effect of various Alu densities on the mutation type based classifications of cancer genes. In order to establish the direct relationship between Alus and the cancer genes of interest, genome wide Alu-related densities were measured using genes rather than the sliding windows of fixed length as the units. Several novel genomic features, such as the density of the adjacent Alu pairs and the number of Alu-Exon-Alu triplets, were developed in order to extend the investigation via the multivariate statistical analysis toward more advanced biological insight. In addition, we characterized the genome-wide intron Alu distribution with a mixture model that distinguished genes containing Alu elements from those with no Alus, and evaluated the gene-level effect of the 5'-TTAAAA motif associated with Alu insertion sites using a two-step regression analysis method.

Conclusions

The study resulted in several novel findings worthy of further investigation. They include: (1) Recessive cancer genes (tumor suppressor genes) are enriched with Alu elements (p < 0.01) compared to dominant cancer genes (oncogenes) and the entire set of genes in the human genome; (2) Alu-related genomic features can be used to cluster cancer genes into biological meaningful groups; (3) The retention of exon Alus has been restricted in the human genome development, and an upper limit to the chromosome-level exon Alu densities is suggested by the distribution profile; (4) For the genes with at least one intron Alu repeat in individual chromosomes, the intron Alu densities can be well fitted by a Gamma distribution; (5) The effect of the 5'-TTAAAA motif on Alu densities varies across different chromosomes.

Background

Classified as a Short Interspersed Element (SINE), Alu is the most abundant mobile element in the human genome [1,2]. A full-length Alu is approximately 300 nt in length and includes two tandem monomer units separated by a poly "A" stretch [3]. Alu elements are initially inserted fairly randomly throughout genome, with 5'-TTAAAA like motifs as preferred sites, and then accumulated over time in GC-rich regions through evolutionary selection [4-9]. Alu integration polymorphisms exist among individuals of the same population [10]. It has been a general recognition that Alu repeats play an important role in genome evolution, some cellular processes, DNA methylation, and transcriptional regulation [3,11-14].

In disease biology, the importance of Alu elements is further highlighted by the potential association with genetic instability, one of the principal hallmarks and causative factors in cancer [15,16]. Alu-mediated insertional mutagenesis and recombination have been reported in a few cancer genes [17-23]. Despite the rapid advances in Alu research, the rate and scope of the contribution of Alu to the origin and progression of human cancer is still poorly quantified to date [16]. As an endeavor to address this issue, a crucial task herein is to explore the association between genome-wide-spread Alus and mutated genes that are causally implicated in oncogenesis. However, the current knowledge about the known Alu-mediated cancer events is disproportional to that of the identified cancer genes. In a recently updated cancer gene database [24,25], 428 genes are verified to contribute to cancers; in contrast, only ten genes related to Alu-mediated insertional mutagenesis and recombination are cited in the most up-to-date literature [16]. Given Alus are the most abundant retro-transposable elements in the human genome, the reported number of verified genes may account for only a small fraction of the potential cancer genes involved in Alu-mediated genetic instabilities. This fact greatly underscores the urgent need to conduct a genome wide association analysis of Alus and mutated cancer genes.

Numerous studies have been performed to investigate the distribution of Alu elements in the human genome. Some focus on how Alu repeats were integrated and spread in the human genome and the factors that may influence their distribution [2,4,9,26,27]. Others inspected the potential biological roles of these elements and their association with the genes of different functional categories in the specific chromosomes [28-30]. Because of Alus' potential contributions to genetic instability, in this paper, we attempted to investigate the effect of various Alu densities on the mutation feature based classifications of cancer genes. In order to establish more direct relationship between Alu repeats and the cancer genes of interest, "densities" were determined using genes as measurement units rather than the sliding windows of fixed length widely employed in practice [27,28,31]. Several novel genomic features, such as the density of adjacent Alu pairs and the number of Alu-Exon-Alu triplets, which may both contribute to Alu/Alu recombination rates that might influence gene function, were developed in order to extend the investigation via a clustering analysis toward more advanced biological insight. In addition, we characterized the Alu distribution with a mixture model that distinguished the genes with no Alu elements from those containing Alus. We also evaluated the gene-level effect of the predicted preferred integration site of Alus, 5'-TTAAAA, on the genome-wide Alu densities using a two-step regression analysis. These methods were especially proposed for analyzing the observed data where a large proportion of genes contain no Alus in their intron sequences. The study resulted in several important findings. In particular, we showed that recessive cancer genes are enriched with Alu elements compared to dominant cancer genes (oncogenes) and the entire gene set of the human genome.

Results

Chromosome-level Alu densities of different genome regions

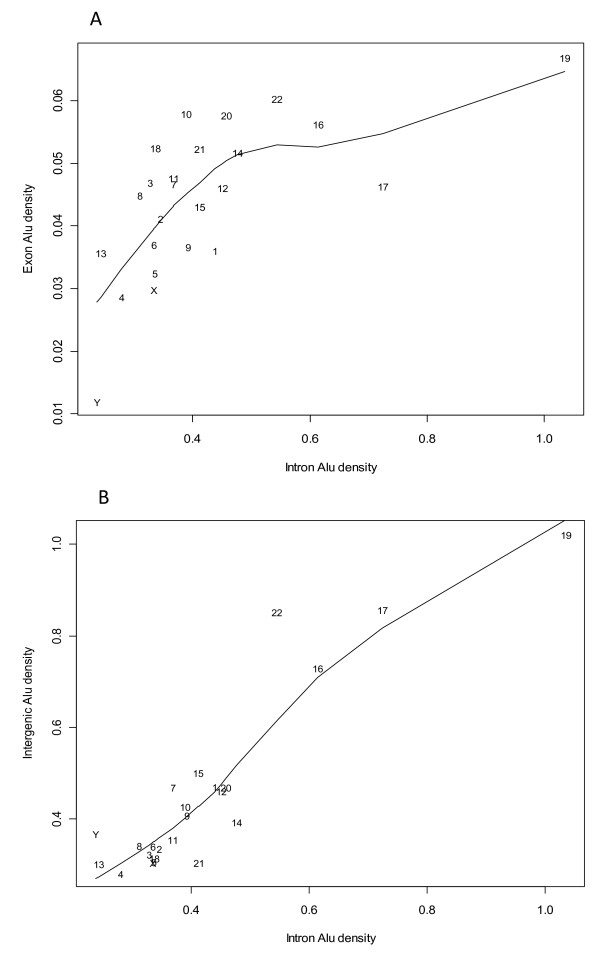
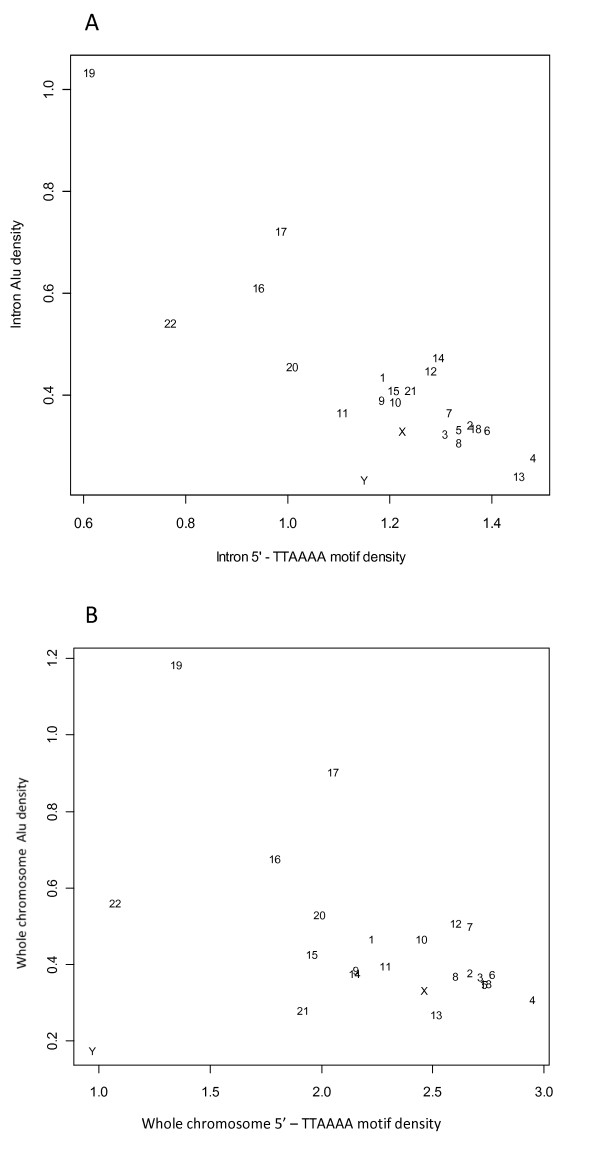
The location of Alu elements relative to genes is important in assessing their potential to contribute to gene disruption and genetic instability. Therefore, Alu densities in intron, exon and intergenic regions were calculated for individual chromosomes using the method described in the Methods section. The results were projected onto a two dimensional coordinate system (Figure 1A). Substantial variability exists across chromosomes. For example, chromosome-Y has the lowest intron and exon Alu densities, and chromosome-19 has the highest intron and exon Alu densities. The densities of intron and exon Alu elements in most of the chromosomes demonstrate a positive linear correlation if the three points corresponding to chromosome-Y, -17, and -19 are regarded as "outliers". The densities of exon Alu are approximately one order of magnitude lower than the Alu densities in introns. The intron Alu density of chromosome-19 is extremely high but its exon Alu density is comparable to those of chromosome-22 and -20. A possible explanation for this phenomenon is that exon Alu retention is under similar selective pressures on all chromosomes, while the intron Alu densities are controlled by different selective pressures. An upper limit to the chromosome-level exon Alu densities is suggested by the distribution profile. On the other hand, intergenic Alu densities and intron Alu densities are of the similar scale of magnitude. There is a strong positive linear relationship between the chromosome-level intergenic and intron Alu densities (Figure 1B). Based on this finding, we hypothesize that Alu elements in the intergenic and intron regions are under an analogous selection pressure or have not been selected in the evolution of the human genome. This, from another perspective, further highlights the distinct capability of exons from other genomic regions in retaining Alu elements.

Figure 1.

Figure 1

Open in a new tab

The variability and association of chromosome-level Alu densities in different genomic regions. The data points are labeled with chromosome IDs. The intron (exon or intergenic) Alu density is calculated by the number of intron (exon or intergenic) Alus divided by the corresponding sequence length measured in Knt (see the Methods section for details).

Distributional characterization of gene-level intron Alu density

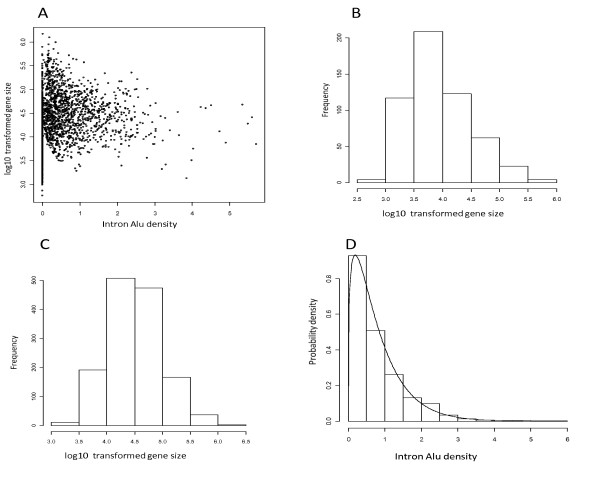
As discussed above, the number of fixed Alus in exon regions of genes is quite small compared to that in intron regions. Therefore, we focused on characterizing the distribution of gene-level Alu density in intron regions. In the UCSC gene annotation released in 2006, approximately 12% of the human genes (21461) are of single exon and have no intron sequences in the transcript(s), thus those single-exon genes were excluded. The 18856 multi-exon genes are kept for further analysis. As an illustration, with the log10 transformed gene size (sequence length) as X-axis and the intron Alu density as Y-axis, we projected 1928 multi-exon genes in chromosome-1 onto a two-dimensional coordinate system (Figure 2A). Regardless of the gene size, 28.1% of these multi-exon genes in chromosome-1 contain no Alu elements in their intron regions. We selected those genes and generated a histogram of their log10 transformed sizes (Figure 2B). Similarly, we generated the histogram for the multi-exon genes with at least one intron Alu (Figure 2C). Both profiles are largely in the shape of a normal distribution. Compared to Figure 2B, the center of Figure 2C shifts 0.5 units in logarithmic scale to the right, indicating that the geometric mean of the multi-exon genes with intron Alus is approximately three times of that of the multi-exon genes without any intron Alus. (This ratio also holds for the whole genome). Figure 2D presents the histogram of the intron Alu density of the 1386 genes with at least one Alu in their intron region(s). The curve represents a fitted Gamma probability density function with 0.615 and 1.313 as the shape and scale parameters, respectively. The rationale and formulation of the mixture model analysis of gene-level intron Alu density are discussed below. It should be noted that, gene-level intron Alu densities in the other 23 chromosomes also carry the similar Gamma distribution characteristic (see Table 1 for the estimated model parameters).

Figure 2.

Figure 2

Open in a new tab

The distributional characterization of intron Alu density in chromosome-1. A: the scatter plot of intron Alu densities versus log10 transformed lengths of gene sequences. B: The distribution of the lengths of the multi-exon genes without any Alu elements in the intron sequence(s). C: The distribution of the lengths of the multi-exon genes with at least one Alu element in the intron sequence(s). D: The distribution of intron Alu densities of the multi-exon genes with at least one Alu in the intron sequence(s). The curve represents a gamma density function with 0.615 and 1.313 as the shape and scale parameters, respectively.

Table 1.

The mixture model analysis of intron Alu density

Chr. N r θ κ
chr1 1928 0.281 1.303 0.615
chr2 1212 0.271 1.498 0.441
chr3 1036 0.248 1.398 0.459
chr4 728 0.26 1.573 0.31
chr5 837 0.238 1.406 0.42
chr6 952 0.279 1.369 0.47
chr7 893 0.308 1.157 0.735
chr8 667 0.315 1.553 0.403
chr9 734 0.342 1.656 0.411
chr10 749 0.288 1.509 0.457
chr11 1072 0.328 1.349 0.528
chr12 984 0.269 1.262 0.71
chr13 325 0.295 1.881 0.246
chr14 562 0.285 1.667 0.475
chr15 580 0.284 1.367 0.59
chr16 811 0.337 1.74 0.617
chr17 1106 0.344 1.782 0.617
chr18 262 0.214 1.694 0.329
chr19 1342 0.286 1.586 1.002
chr20 537 0.307 1.363 0.582
chr21 203 0.241 1.758 0.355
chr22 452 0.352 1.762 0.595
chrX 778 0.356 1.241 0.471
chrY 93 0.688 2.098 0.217
Open in a new tab

N: the number of genes with multiple exons in the NCBI reference sequences. r: the proportion of the multi-exon genes without any Alus. θ: the shape parameter of the fitted Gamma distribution. κ: the scale parameter of the fitted Gamma distribution.

Mixture model analysis of gene-level intron Alu density for multi-exon genes

Because of the significant number of genes without any Alu elements, the descriptive statistics, such as mean and standard deviation, are not sufficient to characterize the gene-level Alu distributions for the genes in the individual chromosome. Furthermore, the separation of the presence or absence of Alu elements from the continuous density measures may be important in the investigation of the mechanism underlying the Alu insertion and retention. Based on these considerations, we characterized the gene-level intron Alu density distribution with a mixture model that consists of a Bernoulli probability mass function and a Gamma probability density function. 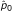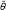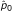The summary statistics included Inline graphic, Inline graphic, and Inline graphic. Inline graphic is the proportion of the genes without any intron Alus. 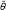Inline graphic and Inline graphic are the shape and scale parameters of the Gamma function that describes the empirical distribution of Alu densities of the genes with at least one intron Alu element. The details of the model are presented in the Methods section.

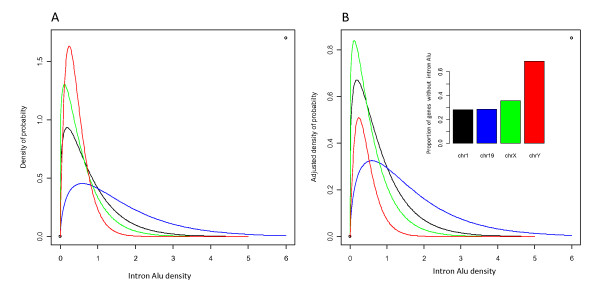
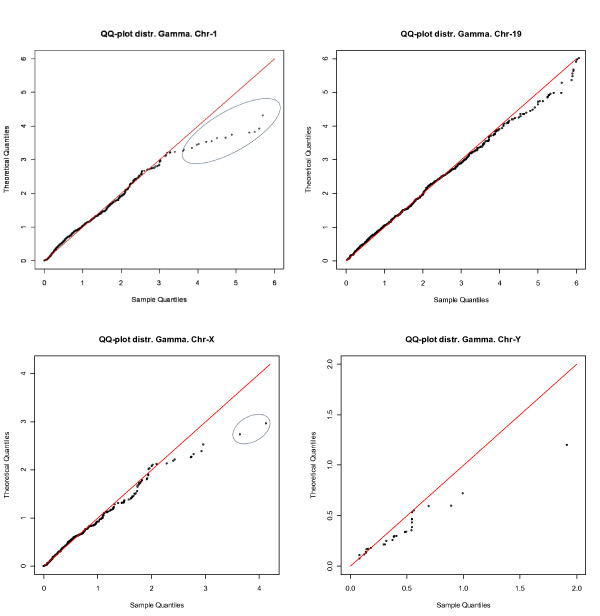
Table 1 lists the estimated model parameters for all 24 chromosomes. Using those parameters, we can clearly visualize the intron Alu distribution of each chromosome and demonstrate the differences among them. In Figure 3A, the curves represent the theoretically calculated distributions of intron Alu densities of the genes containing at least one Alu for chromosomes -1, -19, -X and -Y. In Figure 3B, the probability density is adjusted based on the proportion of the genes without any intron Alus such that, for each chromosome, the sum of 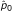Inline graphic and the area under the curve is equal to one. Figure 4 shows the Q-Q plots of the four chromosomes characterized in Figure 3. Those plots were generated to evaluate how well the estimated Gamma distributions described the observed intron Alu densities. Each dot on the plots represents a gene and the rightmost genes have the highest intron Alu density. The top left plot corresponds to the Gamma curve of chromosome-1. It is evident that, in general, the estimated Gamma curve fits the observed data except for a few outliers at the tail. The Q-Q plot for chromosome-19, the Alu-richest chromosome, is almost perfect in that nearly all points lie close to the diagonal line, indicating a good fit. Similar to chromosome-1, the plots for the two sex chromosomes have several outliers at the tails. The highest degree of deviation can be observed from the plot of chromosome-Y, which is the least Alu dense chromosome. After examining the plots for the rest of the chromosomes (Additional file 1), we can draw the general conclusion that the proposed model fit the Alu-rich chromosomes better than the Alu-poor chromosomes. For each chromosome, the overall good fitting of a right-skewed Gamma distribution to the intron Alu density of the Alu-containing genes indicated that the bulk of genes have relatively low Alu density with fewer genes retaining very high Alu densities.

Figure 3.

Figure 3

Open in a new tab

The characterization of intron Alu densities of multi-exon genes in chromosomes-1, -19, -X and -Y with a mixture model. A: the curves represent the probability density functions given the intron Alu density larger than zero. B: the probability densities are adjusted according to the proportion of the genes without Alus. For each chromosome, the sum of its proportion of genes without intron Alus and the area under the Gamma curve equals to one.

Figure 4.

Figure 4

Open in a new tab

The Q-Q plots for fitting a Gamma distribution to the gene-level intron Alu densities in chromosomes-1, -19, -X and -Y. The dots represent genes. The genes in the ovals on the plots for chromosome -1 and -X are regarded as outliers and further analyzed in Additional file 2.

The information of 47 genes on chromosomes 1,3,6,13,21 and X that apparently deviate from the diagonal lines in Q-Q plots is summarized in Additional file 2. We found that these genes cluster in a few chromosome regions and approximately one third of them have high exon Alu density which is not taken into account in the modeling. We did not note any over-represented functional groups of these genes, however, and believe that the high Alu density of these genes may be mainly influenced by their chromosomal region rather than their function.

Distributions of Alus and 5'-TTAAAA motifs

It has been widely recognized that the integration of Alu elements is initiated with its endonuclease-dependent cleavage at the 5'-TTAAAA hexanucleotide, and the variants derived by a single base substitution, particularly from A to G and T to C [4,8]. A recent publication further analyzed the effects of genomic features, including the density of 5'-TTAAAA, on the Alu density using a multiple regression method [9]. The authors divided the entire human genome into around 2400 bins with each of 1 M bases long, and measured motif and Alu densities on these sequences of fixed length. In our study, the densities were determined using genes as the units, thus our data structure and representation was quite different from that in [9]. Considering the scarcity of the retained Alu elements in the exon regions, we focused on the analysis of the motif in introns relative to Alu densities. The substantial level of genes without any Alus makes the method employed in [9] not applicable to the statistical analysis conducted here.

Figure 5 presents the chromosome-level Alu and 5'-TTAAAA motif densities in introns and in each individual chromosome, respectively. A striking negative correlation between Alu density and 5'-TTAAAA motif density can be observed from both plots regardless of the measurements performed in introns or in the whole chromosome. These data suggest that either the density of potential insertion sites is not rate limiting, or that the relative density of Alu elements is governed more by selection than by initial insertion density.

Figure 5.

Figure 5

Open in a new tab

The correlation between chromosome-level Alu density and 5' - TTAAAA motif density in introns and in the individual chromosome. The data points are labeled with chromosome IDs.

Two-step regression analysis of the gene-level effect of 5'-TTAAAA motif density on Alu density

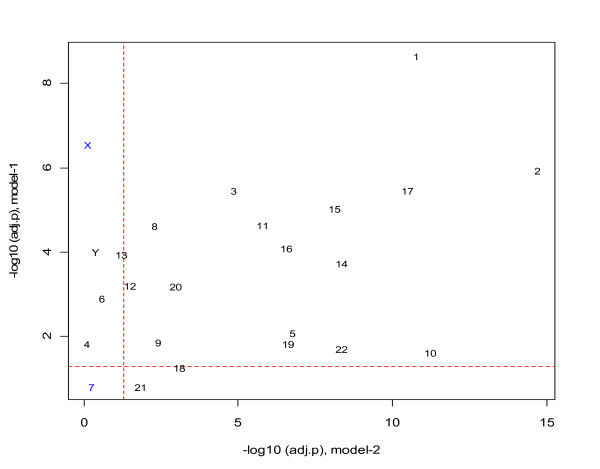
We conducted a more refined study to analyze the effect of 5'-TTAAAA motif density on intron Alu density at the gene level. Figure 6 shows the results obtained from the proposed two-step regression method (see the Methods section for details). The data points are labeled with chromosome IDs. The X- and Y- coordinates are the negatives of the log10 transformed FDR-adjusted p-values [32] from the two models, respectively. The dashed red lines correspond to 0.05 in the scale of adjusted p-values. Model-1 evaluates the effect of the motif density on the presence or absence of Alus in the gene introns. Model-2 evaluates the effect of the motif density on the intron Alu density of the genes with at least one Alu repeat in their intron regions. As shown in Figure 6, the influence of motif density on the intron Alu density is chromosome-specific. For chromosome-7, the effect is not significant as demonstrated by both models. For chromosomes -4, -6, -13, -X, and -Y, the effect is significant only in Model-1. For chromosomes -18 and -21, the effect is significant only in Model-2. The rest of the chromosomes have the adjusted p-values less than 0.05 as reflected by both models. The most significant cases are detected in chromosome-1 where the adjusted p-values are less than 1 × 10-8 and 1 × 10-10 in the two models, respectively. For chromosome-19 which has the highest genome-wide Alu density, the effect is marginally significant as measured by Model-1. The chromosome-wide gene-level positive association between Alus and the motif are suggested by the facts that all the regression coefficients β are positive in the model-1 and the coefficients β* are positive in model-2 except for chromosomes -7 and X.

Figure 6.

Figure 6

Open in a new tab

The visualization of the gene-level effects of 5'-TTAAAA intron motif density on intron Alu density obtained from the proposed two step regression method. The data points are labeled with chromosome IDs. The X- and Y- coordinates are the negatives of the log10 transformed p-values (adjusted with BH method) from the two models, respectively. The dashed red lines correspond to 0.05 in the scale of adjusted p-values. Model-1 evaluates the effect of the motif density on the presence or absence of Alus in the introns of the genes. Model-2 evaluates the effect of the motif density on the intron Alu density of the genes with at least one Alu repeat in their intron regions. All the regression coefficients β are positive in the model-1 and the coefficients β* are positive in model-2 except for chromosomes 7 and X (marked with blue).

Correlations of Alu density with the genetic classifications of cancer genes

We analyzed the effect of Alu density on the classification of 428 cancer genes collected in the recently updated (May 2010) COSMIC database [25]. The three classifications evaluated are:

(1) Dominant or recessive mutations;

(2) Somatic or germline mutations;

(3) Translocation or non-translocation mutations.

We filtered out 77 genes that either contained only a single exon or were not included in the UCSC 2006 annotation, and kept the remaining 351 genes for further analysis. In addition, 30 genes with the mutation found in both cell types were excluded from the comparison of somatic and germline mutations, and 2 genes labeled with "Rec?" in the database were excluded from dominant and recessive mutation comparison.

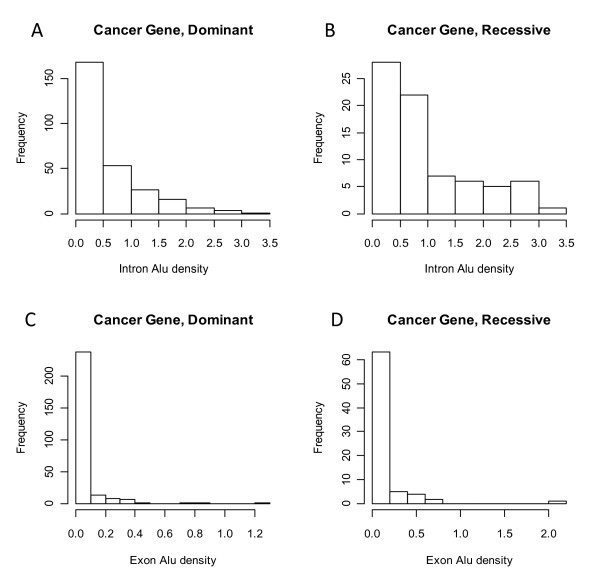
Figure 7 shows the frequency distributions of intron Alu densities (A and B) and exon Alu densities (C and D) of the cancer genes with dominant mutations (n = 274) and recessive mutations (n = 75), respectively. The class of recessive genes, also known as tumor repressor genes, has higher Alu densities. In particular, approximately 63% of recessive genes, compared to 19% of dominant genes, have intron Alu densities greater than 0.5. Statistical analysis using a logistic regression model (see the Methods section) further demonstrated that, on the dominant/recessive mutation types based classification, the effect of intron Alu density is extremely significant (p <.001) and the effect of exon Alu density is marginally significant (p < .05). The comparison of the genes with the mutations found in somatic cells (n = 285) or germline cells (n = 36) is shown in Additional file 3. The class of genes with germline mutations demonstrated higher Alu densities in that approximately 64% of germline genes, in contrast to 40% of somatic line genes, have over 0.5 intron Alu densities. On the germline/somatic classification, the effect of intron Alu density is extremely significant (p <.001) and the effect of exon Alu density is marginally significant (p < .05). In the last comparison (Additional file 4), only intron Alu density demonstrates significant effect (p = 0.013) on the translocation/non-translocation mutation types based classification. The class of genes with translocation mutations (n = 231) has lower Alu density than the genes with non-translocation mutations (n = 120). The corresponding proportions of genes with intron Alu density over 0.5 in the translocation/non-translocation mutations are 44% and 57%, respectively.

Figure 7.

Figure 7

Open in a new tab

The frequency distributions of intron and exon Alu densities of the cancer genes with dominant and recessive mutations.

Enrichment analysis of Alu elements and mutation types in cancer genes

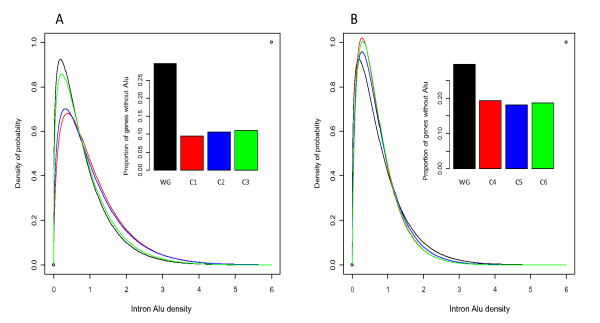
Alu mediated mutagenesis events have been widely reported in the literature and most of the studied cancer genes contain a considerable number of Alu elements in their sequences. In order to highlight the differences among the studied cancer gene classes, we used the mixture model as discussed above to visualize the observed results (Figure 8A). The distributions of the intron Alu densities of the three cancer gene classes, i.e. recessive mutation (C1, n = 75), germline mutation (C2, n = 36) and non-translocation mutation (C3, n = 120) differ from the profile of the entire multiple-exon genes (N = 18856) in the human genome in both the proportion of the genes without Alus (as shown by the column charts) and the genes with at least one Alu element (described by the Gamma curves). A logistic regression analysis shows that the association between these gene classes and Alu intron density are significant (p < 0.01). This statistical model was established with z ∈{1,0} (indicating whether or not a gene belongs to a mutation class) as the dependent variable, and the intron Alu density and log10 transformed gene size as the explainable variables.

Figure 8.

Figure 8

Open in a new tab

The comparison of estimated distributions of intron Alu densities in different cancer gene classes. The proposed mixture model method was used in this analysis. The curves represent the approximated Gamma distributions of Alu density for the genes with at least one intron Alu. The column charts represent the proportions of genes without any intron Alus. WG: the entire set of multiple-exon genes in human genome. C1: the cancer genes with recessive mutations. C2: the cancer genes with mutations found in germline. C3: the cancer genes with non-translocation mutations. C4: the cancer genes with dominant mutations. C5: the cancer genes with somatic mutations. C6: the cancer genes with translocation mutations. See Figure 7, Additional files 3 and 4 for the empirical distributions of Alu densities for the above six classes C1-C6.

Figure 8B presents the distributions of the intron Alu densities of another three cancer gene classes, i.e. dominant mutation (C4, n = 274), somatic mutation and (C5, n = 285) and translocation mutation (C6, n = 231). As demonstrated by the Gamma curves describing the genes with at least one Alu element, the distributions of these three classes are similar to the profile of the entire multiple-exon genes in human genome. Moreover, the logistic regression analysis shows that the association between these gene classes and Alu intron density is not significant (p > 0.05).

Clustering analysis of cancer genes based on Alu-related genomic features

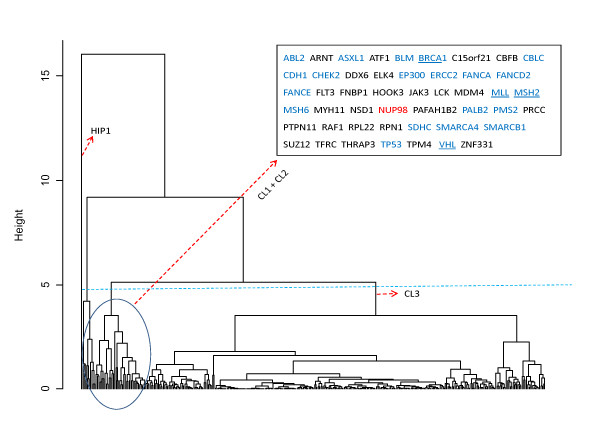
In order to further investigate the association between Alu density and mutagenesis by using other information besides intron Alu density, we conducted a clustering analysis on the 351 cancer genes as mentioned above. Figure 9 shows the dendrogram generated by applying the agglomerative hierarchical clustering algorithm to the gene set described by four Alu-related genomic features and GC content (see the Methods section for details). Based on the biological insight that can be derived from all possible groups, we chose to cut the tree at the height of 4.5 heuristically, and aggregated the 351 genes into a scalar (HIP1) and three clusters. The two smaller clusters (CL1 and CL2) contain 48 genes in total. Among them, the recessive cancer genes, also known as tumor suppressor genes, account for 45.8%. This proportion is 2.5 times of the corresponding ratio (53/302 = 17.6%) in the third cluster (CL3). Statistical analysis using Fisher's exact test demonstrates that this difference is not due to chance (p = 3.8 × 10-5). Furthermore, gene NUP98, classified as dominant mutation in the COSMIC database but located at a tumor suppressor gene region [33], is also included in this set of 48 genes. Among the seven genes with numerous Alu mediated recombination events reported [16], four genes (BRCA1, MLL, MSH2 and VHL) are contained in CL1 and CL2. Another two (MYB and MLH1) are grouped into CL3 and the remaining one (hCAD) is not among the COSMIC gene list. This suggests that the clustering analysis may provide a promising gene list for further investigation of more Alu mediated recombination events. In order to reveal the relative importance of the used genomic features in the clustering, we sorted the 351 genes in terms of the intron Alu density and visualized the results using five bar-plots (Additional file 5). It is evident that the genes within CL1 and CL2 have much higher intron Alu density (as well as intron Alu pairs) than the genes in CL3. HIP1 is distinguished from other genes due to its large number of Alu-exon - Alu triplets. On the other hand, not much differential information can be inferred from the rather comparable GC content of those cancer genes.

Figure 9.

Figure 9

Open in a new tab

The clustering analysis of cancer genes using Alu-related genome features and GC content. In the text box, 22 recessive cancer genes (tumor suppressor genes) are highlighted in blue. The BRCA1, MLL, MSH2 and VHL genes (marked with underlines) are among the seven cancer genes in which Alu mediated recombination events have been reported [16]. NUP98 (marked with red) was classified as dominant mutation in the COSMIC database but located at a cancer suppressor gene region [33]. The gene that appears as a scalar in the dendrogram is the Huntingtin interacting protein 1 gene (HIP1).

Discussion

We entered this study with the biological observation that Alu elements contribute to genetic instability by insertional mutagenesis, and then deletions/duplications through Alu/Alu non-allelic homologous recombination [16]. Based on this perception, we hypothesized that local Alu integration rate or density may have unequal significance to the mutations of different functional classes or biological groups of cancer genes that are usually predominated by one or multiple special genetic mechanisms. While our primary effort focused on bioinformatically testing this hypothesis, we also modeled the genome-wide, different-levels of relationships between the 5'-TTAAAA density and Alu distribution. The latter study is relevant in that the Alu cleavage related to this motif by the L1 endonuclease is not only a key first step in Alu integration [4], but may also help lead to DNA double-strand breaks that could contribute to Alu/Alu non-allelic homologous recombination events and genetic instability in motif-rich genes. With respect to the methodology, besides characterizing the genome-wide intron Alu density using a mixture model and analyzing the effects of 5'-TTAAAA on the Alu integration through a two-step regression approach, we devised the use of Alu pairs and Alu-exon-Alu triplets as additional means of targeting those sets of Alus that are most likely to contribute to genetic instability within genes. Moreover, the association between these Alu-related genomic features and the different types of cancer genes was studied using a logistic regression model and an un-supervised learning method. Because the impact of this genetic instability on genes is the most critical aspect to human disease, we chose to carry out all analyses on individual genes as the key unit, with a particular focus on cancer genes where genetic instability is known to be a major contributor to the disease. Through the rigorous statistical analysis, we observed the hypothesized association between the Alu density and mutation type of cancer genes. In the following, we focus on some results that require further discussion.

Exon Alu density

Exonized Alus (insertion within an intron that led to exon creation) and exonic Alus (insertion into existing exons) were summed together in the calculation. It is reasonable to assume that Alu elements initially integrating into exon sequences have led to strong negative selective pressures limiting their accumulation [11]. The overall positive linear correlation between the chromosome-level exon Alu densities as shown in Figure 1A suggests the approximately equal chance (across chromosomes) of the retention of the initially inserted Alus in exon regions. On the other hand, the observed upper limit to the chromosome-level exon Alu density may indicate that the fixation of Alu elements in the coding regions of genes is further determined by the biological tolerance. The hypothesis of the negative selection of Alus in exon regions is also supported by the simple positive linear relationship of Alu densities in intron and integenic regions (Figure 1B).

Distributional characterization of Alus

If a gene has no Alu repeats in its intron region(s), the intron Alu density of this gene will be zero. As illustrated by genes on chromosome-1 (Figure 2A), the sizes of genes without Alus nearly span all possible lengths. Due to the substantial existence (N = 5578) of multi-exon genes of such kind in human genome, we characterized the distribution of the intron Alu density with a mixture model that distinguished genes without Alu elements from those containing Alus. The main advantages of this method include: (1) it provides a more insightful summary of Alu distribution than simple statistics such as means and standard deviations for the observed data with complex structures [34]; (2) the separation of Alu presence or absence from the continuous density measures may be important in the investigation of the mechanism underlying the Alu insertion and retention. It is worth noting that we can replace the Gamma distribution with another member of exponent family, i.e. Weibul distribution. We prefer the Gamma distribution because the first and second moments (expectation and variance), which may be of interest to some researchers, can be directly calculated from the model parameters using two simple formulas, i.e. E(X ) = θκ and var(X ) = θκ2 [34]. Power law-like distributions, such as the Gamma distribution, have been widely used in describing genomic features [31,35] and empirically found to fit many basic population models [36]. Our model suggests that genes containing Alu elements have an excellent, though not perfect, fit to a gamma distribution (Figure 4), indicating a similarity between Alu distribution in genes and natural population variation. Deviations from a perfect fit might suggest that some genes either have a less than normal selection against the presence of Alu elements or have either a sequence preference for the element that leads to unusually high Alu buildup.

For multi-exon genes without intron Alus, an interesting question worth further study is why they lack this type of repeats. Is it because those genes are located in Alu-poor regions or their structures or (and) functions don't tolerate Alus after the initial insertion? A functional enrichment analysis using DAVID tool [37] showed that 64 level-5 (most specific) GO terms, of which 77% belong to the general category of biological process, are over-represented by those genes with the FDR adjusted p-values less than 0.01 (Additional file 6). The result is different from a recent study that stated that "no evidence for selective loss of these elements in any function class." [38]. We are conducting a more comprehensive investigation on this issue.

Intron Alu density and 5'-TTAAAA motif density

As specified by [4], 5'-TTAAAA is the most abundant hexanucleotide signal for the primary integration of Alus. A recent publication further reported that such motif(s) contributed to 6.1% - 26.7% of the variation in Alu density of genome sequences of fixed length, depending on the subtypes and the genome regions related to the evolution divergence of human, chimpanzee and orangutan [9]. Our study shows that the gene-level effect of the motif density on Alu density varied across chromosomes substantially in terms of statistical significance level. However, except for chromosome-7, all other chromosomes have the adjusted p-values less than 0.05 at least in one of the two proposed statistical models that evaluated the motif effects from different aspects. The (pseudo) contribution rates to the total variability are lower than 11%, in general. One exception occurred in chromosome-Y where the Alu distribution holds special importance in studying the evolution of genome. For this chromosome, the pseudo contribution rate is as high as 33% in Model-1 where the binary dependent variable indicates if a gene contains at least one Alu in its intron region(s). A possible explanation for this exception is that the redistribution of Alus on this sex chromosome was relatively delayed due to the lack of recombination between chromosome pairs [27]; therefore, the initial association between the motif and Alus has been largely retained. Here, one may be puzzled that the adjusted p-value calculated from Model-2 (indicating the gene-level effect of 5'-TTAAAA motif on intron Alu density) for chromosome Y is larger than 0.05. While the reason is still not clear, we tend to attribute the inconsistence to the fact that, in our dataset, chromosome-Y has only 29 genes containing Alus and thus the Model-2 lacks power to detect the Alu-motif association for this chromosome

Surprisingly, we also found a fairly strong negative correlation between the density of this motif and Alu element density on a chromosome basis. This suggests that either there is little correlation of the density of L1 endonuclease cleavage sites and the final density of Alu elements, or that the post-insertional selection process has largely led to the dissociation of these Alu density from its initial insertion density. Evolutionary analysis of older vs. younger Alu elements [27], as well as de novo Alu insertions in tissue culture [39-43], strongly support the latter hypothesis. It has been argued that Alu elements are selectively retained in genes of specific classes [38]. We would argue that Alus insert initially fairly randomly and there is variable selective loss by genes, but the most significant factor is likely to be that genes that are particularly sensitive to the genetic instability caused by Alu elements through recombination may retain the Alus because those elements cannot be lost through recombination. On the other hand, it is reasonable to assume that the association between the 5'-TTAAAA motif and Alu elements in these genes have been retained, leading to the positive correlation as shown at the gene-level for individual chromosomes.

Alu-enriched cancer genes

In the Result section, we firstly showed that intron Alu density has a significant impact on several binary classifications of cancer genes established on the mutation types provided by COSMIC. Then, by comparing those gene categories with the entire gene set in the human genome, we found that in each classification pair, only one class is enriched with Alus. The Alu-enriched categories (p < 0.01) include recessive mutation class (C1), germline mutation class (C2), and non-translocation class (C3). However, because about 90% of genes in germline mutation class are also recessive, we actually have two relatively independent Alu-enriched classes, i.e. C1 and C3. Furthermore, because the classification based on germinal and somatic mutations can be well explained by the classification in terms of dominant and recessive mutations [24], here we concentrate our analysis on the implications behind the associations between the Alu density and the dominant and recessive mutations.

Our findings relative to these cancer-causing genes fall largely into the distribution expected for genes influenced by genetic instability. For instance, oncogenes or dominant cancer genes are often subject to smaller mutations than those caused by Alu insertion or recombination. Alu elements more typically disrupt gene expression or cause loss of part of a gene, and this is more typical of the mode of cancer generation by the recessive cancer genes or tumor suppressors. The high density of Alu elements in tumor suppressor genes would then cause increased risk of Alu/Alu recombination leading to cancer. Although it is somewhat counterintuitive to think that Alu elements would build up in genes that have such potential sensitivity to the genetic instability that they would cause, one might explain it by considering that once an Alu is present in the gene, it is difficult to allow it to be removed by a recombination-based process. At first glance, the finding of a negative correlation between Alu elements and translocation mutations might seem surprising. Alu elements have been shown to be capable of undergoing non-allelic homologous recombination between chromosomes [44] that could contribute to such translocations. However, the vast majority of chromosomal translocations, particularly those associated with cancer, have been found to be formed by non-homologous end-joining, a process that would not be influenced by Alu elements.

As discussed above, the main message conveyed by this paper is that cancer genes have different Alu insertion (or retention) rates according to the genes' type of mutation. This is a rigorous conclusion in the sense that, prior to reaching it, we explored the potential influence of other factors on the statistical significance of the discovered association. That is, in a preliminary study, we analyzed the correlation of various genomic features, such as the gene length, exon number, exon/intron length ratio and the density of the recombination hot spots-related motif CCTCCCT [45], with the studied classifications of cancer genes. The results showed that the only significant factor is the gene length (p < 0.05), therefore we included this feature in the final statistical models as described in the Method and Result sections. Another relevant concern is that the adopted classification of cancer genes may be biased because, in the search for tumor suppressor genes, special effort has been made in genomic regions undergoing frequent losses. In this regard, we retrieved the middle coordinates of 129 documented fragile sites (FS) in human genome assembly 36 [46,47]. Based on the coordinates and the genes' locations, we calculated the distance between each studied cancer gene to its nearest FS. The subsequent statistical analysis showed that the distances did not significantly differentiate among the different gene classes (p > 0.1). This indicates that our conclusion on the association between the Alu density and mutation types of cancer genes is still valid even when the genes' physical locations relative to the unstable genome regions are considered. The mechanism behind the fairly high Alu density in recessive cancer genes is still unclear. One possible explanation is that, except for a few "dominant negative" cases such as those in TP53 [48], an Alu mediated mutation including insertion and recombination events may less likely change the protein-coding sequences (exons) such that the chances leading to novel proteins, especially those with lethal effects, may be relatively low, thus only in the homozygous status can the mutated allele produce deleterious effect.

Knowledge discovery based on Alu-related genomic features

It has been suggested that, besides the intron Alu density, the existence or absence of exon Alus, the relative location among Alus, the proximity of Alus to exons, and the GC content in the gene sequences are also important factors in the Alu mediated mutagenesis events [16]. In this study, the clustering analysis of cancer genes using these genomic features demonstrated a clear hierarchical structure as shown in Figure 9. The significant association between the clusters and the genetic classification of cancer genes is identified from the advanced statistical analysis. This result suggests that the potential merits of using these features to predict recessive cancer genes and Alu mediated recombination events. Because the majority of currently documented cancer genes are dominant, it is reasonable to assume that many recessive cancer genes remain undiscovered. Volina et al recently proposed an approach to identify the genome-wide recessive cancer genes by combining the contributions of the different types of genetic alterations to loss of functions [49]. The method was promising but without remarkable sensitivity. It is possible to extend this study by integrating the measures used in [49], i.e. amino-acid substitutions, frame-shifts and gene deletions, with the Alu-related genomic features for a more insightful exploration.

Methods

Data sources

Chromosome DNA sequences and gene annotation information (including the official symbols, orientations, and coordinates of NCBI reference gene sequences and exons) were retrieved from UCSC tables for NCBI36/hg18. Single exon genes (without any introns in the reference sequence) were excluded from further analysis because they lack information of Alu integration. The coordinates of intron Alus, exonic Alus and exonized Alus were extracted from the AluGene database [50,51], which is established by applying the RepeatMasker software to hg18 [52]. The coordinates of 5'-TTAAAA motifs were identified by using the R package "Biostrings" on hg18. The information of cancer genes was obtained from Catalogue of Somatic Mutations in Cancer (COSMIC) [25].

Density and other related calculations

Gene level densities

For each reference gene, the Alu density in its intron or exon region (or region clusters) was determined by the number of intron or exon Alus and the corresponding adjusted sequence length with the nucleotides contained in the Alus being excluded from the calculation of the sequence length. More specifically, the number of Alus in a NCBI gene reference sequence (Nt) and the number of Alus in the exon region(s) (Ne) were respectively counted. Exon Alus included exonized Alus (insertion within an intron that led to exon creation) and exonic Alus (insertion into existing exons). The number of Alus in the intron region(s) (Ni) was calculated by subtracting Ne from Nt. The adjusted intron sequence length (Si) was calculated by subtracting the total length of exon(s) and intron Alu(s) from the gene sequence length. The adjusted exon sequence length (Se) was calculated by subtracting the total length of exon Alu(s) from the total length of exon(s). Intron Alu density (Di) and exon Alu density (De) were computed by the following formulas. All sequence lengths, such as Si and Se, were measured in terms of kilo nucleotides, abbreviated as Knt.

graphic file with name 1471-2164-12-157-i4.gif (1)

For each reference gene, the 5'-TTAAAA motif density in the region (or region cluster) of intron or exon was determined by the number of the motifs and the corresponding adjusted sequence length with the nucleotides in the Alus excluded from the sequence length calculation. The details were similar to the computation of Alu densities as mentioned above.

Finally, the determined Alu (motif) densities were adapted to the gene names present in the UCSC genome browser. For a gene annotated with multiple reference sequences (transcripts) in the same chromosome and strand, the Alu (motif) densities were obtained by calculating the mean.

Gene level intron Alu-pair density

An Alu-pair forms when the distance between two adjacent intron Alu elements is less than 300 bases. The density was calculated by the number of Alu-pairs divided by the adjusted intron sequence length. The number of Alu-pairs in each reference (gene) sequence was counted individually. For a gene annotated with multiple reference sequences, we calculated the average value.

Gene level number of Alu-exon-Alu triplets

An Alu-exon-Alu triplet was defined as an exon flanked by two Alus with the distance of each interval (Alu-exon or exon-Alu) less than 300 bases. The number of such triplets in each reference (gene) sequence was counted individually. For a gene annotated with multiple reference sequences, we calculated the average triplet number.

Gene level CG content

To unbiasedly estimate the CG content that can reflect the genomic environment for Alu integration, we excluded the nucleotides contained in the Alu elements from the calculation. This is different from the common practice employed in the literature.

Chromosome level densities

For each chromosome, its intron (exon, intergentic) Alu (motif) density was calculated by dividing the total number of intron (exon, intergenic) Alus (motifs) by the adjusted total intron (exon, intergenic) sequence length. Same as the gene-level density calculation described above, all sequence lengths were measured in terms of Knt, and "adjusted" means that Alu sequences were excluded from the sequence length calculation. An intergenic sequence was approximately determined as the genome section between the two flanking transcripts of the adjacent genes in the UCSC annotation table.

Statistical analysis

Mixture model

Because of the substantial existence of genes without any Alus, a mixture model was proposed to characterize the distribution of gene level intron Alu density within each chromosome or the cancer gene class. It consists of a Bernoulli probability mass function and a Gamma probability density function [34]. Let x = {xi} represent the intron Alu densities and p0 indicates the ratio of genes without Alus, the mixture model can be expressed as follows.

graphic file with name 1471-2164-12-157-i5.gif (2)

In the implementation, we estimated p0 with r, the observed ratio of genes without Alus, and approximated the model as

graphic file with name 1471-2164-12-157-i6.gif (3)

The model parameters θ (shape) and κ (scale) were estimated using maximum likelihood method (ML) implemented in the R package MASS [53]. The fitted and empirical distributions were compared using Q-Q plots.

Two-step regression analysis

This method was specially developed to analyze the gene-level effect of 5'-TTAAAA motif on the integration of Alu elements. The motivation is that a single linear model is not sufficient to analyze the observed data where a substantial proportion (e. g. approximately 30% in human genome) of genes contains no Alu elements and, as a result, we cannot conduct the logarithm transformation of Alu densities to resemble a normal distribution. The proposed method consists of a logistic regression model and a simple linear model. Below are the mathematical expressions of these two models.

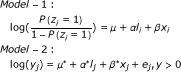graphic file with name 1471-2164-12-157-i7.gif (4)

In Model-1, z i ∈ {1,0} indicates if gene i has at least one Alu or no Alus in the intron region(s). xi is the intron motif density, and li is the log10 transformed adjusted sequence length (with Alu sequences excluded from the calculation). In Model-2, for a specific gene j, xj, yj, lj, and ej are the motif density, Alu density, log10 adjusted sequence length of this gene, and random noise, respectively. (μ,α, β) and (μ*,α*, β*) are the parameter sets of the two models. Model-1 tests the effect of the motif density on the presence or absence of Alu elements in intron regions for all multi-exon genes. Model-2 tests the effect of the motif density on the intron Alu density for the genes with at least one Alu in the intron region(s). We conducted the logistic regression analysis using the procedure lrm included in the R package "Design". The pseudo contribution rate of the intron motif to the total variability was measured as the increase of Nagelkerke R2 index [54] due to adding the density (x) to the reduced model which contained l as the only explainable variable. The simple regression analysis was conducted with the procedure lm in the R package "stats" and the contribution rate of intron motif to the total variability was measured as the increase of statistic R2 due to adding the density (x) to the reduced model. The multi-testing across chromosomes was addressed by BH method [32]. It is worth noting that in both models, gene size was included as an independent variable. This is because our preliminary study showed that gene size had a significant effect on the presence or absence of Alu in intron region(s) for most chromosomes.

The association of Alu integration and mutation types of cancer genes

The effect of Alu density on mutation feature based classification (a binary variable) was analyzed using a logistic regression model. The formula was similar to the Model-1 in equation (4) with the binary variable zi indicating the category of the cancer gene i. For example, the value of zi is 1 if the mutation type of gene i is "recessive", or 0 if the mutation is "dominant". When comparing a specific gene class with the entire gene set in the genome, we assigned 1 or 0 to zi depending on gene i within the studied class or not.

Clustering analysis

Agglomerative hierarchical clustering algorithm was used to group the multi-exon cancer genes. The used features included the intron Alu density, the exon Alu density, the density of intron Alu pairs, the number of Alu-exon-Alu triplets, and GC content (Alu sequences were excluded from the calculation). The algorithm was executed with complete linkage and Euclidean distance as the parameters. The dendrogram was cut in a heuristic way.

Authors' contributions

WZ carried out the statistical analysis and drafted the manuscript. AE, WF, PD and KZ helped with the experimental design, provided editorial comments and participated in writing. PD provided the biological interpretation. KZ supervised and coordinated the project. All authors read and approved the final manuscript.

Supplementary Material

Additional file 1

The Q-Q plots for fitting a Gamma distribution to the gene-level intron Alu densities in 20 chromosomes.

Click here for file (290.4KB, PDF)
Additional file 2

The analysis of genes deviating from the diagonal lines of the Q-Q plots for chromosomes-1, -3, -6, -13, -21, and -X.

Click here for file (9.9KB, PDF)
Additional file 3

The frequency distributions of intron and exon Alu densities of the cancer genes with somatic and germline mutations.

Click here for file (30KB, PDF)
Additional file 4

The frequency distributions of intron and exon Alu densities of the cancer genes with translocation and non-translocation mutations.

Click here for file (31.7KB, PDF)
Additional file 5

The distributions of 351 cancer genes measured by the Alu-related genomic features and GC content.

Click here for file (34.6KB, PDF)
Additional file 6

The Functional enrichment analysis of 5578 multi-exons genes without intron Alus.

Click here for file (56.1KB, PDF)

Contributor Information

Wensheng Zhang, Email: wzhang@xula.edu.

Andrea Edwards, Email: aedwards@xula.edu.

Wei Fan, Email: weifan@us.ibm.com.

Prescott Deininger, Email: pdeinin@tulane.edu.

Kun Zhang, Email: kzhang@xula.edu.

Acknowledgements

This work was supported by NIH grants (RCMI 5G12RR026260-02, NCRR P20RR016456), a Louisiana BOR award (LEQSF(2008-11)-RD-A-32) and an NSF grant EPS-1006891. We thank the reviewers for the insightful comments.

References

  1. Novick GE, Batzer MA, Deininger PL, Herrera RJ. The Mobile Genetic Element "Alu" in the Human Genome. BioScience. 1996;46(1):32–41. doi: 10.2307/1312653. [DOI] [Google Scholar]
  2. Jurka J, Kohany O, Pavlicek A, Kapitonov VV, Jurka MV. Duplication, coclustering, and selection of human Alu retrotransposons. Proc Natl Acad Sci USA. 2004;101(5):1268–1272. doi: 10.1073/pnas.0308084100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Batzer MA, Deininger PL. Alu repeats and human genomic diversity. Nat Rev Genet. 2002;3(5):370–379. doi: 10.1038/nrg798. [DOI] [PubMed] [Google Scholar]
  4. Jurka J. Sequence patterns indicate an enzymatic involvement in integration of mammalian retroposons. Proc Natl Acad Sci USA. 1997;94(5):1872–1877. doi: 10.1073/pnas.94.5.1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Jurka J. Evolutionary impact of human Alu repetitive elements. Curr Opin Genet Dev. 2004;14(6):603–608. doi: 10.1016/j.gde.2004.08.008. [DOI] [PubMed] [Google Scholar]
  6. Abrusan G, Krambeck HJ. The distribution of L1 and Alu retroelements in relation to GC content on human sex chromosomes is consistent with the ectopic recombination model. J Mol Evol. 2006;63(4):484–492. doi: 10.1007/s00239-005-0275-0. [DOI] [PubMed] [Google Scholar]
  7. Yang S, Smit AF, Schwartz S, Chiaromonte F, Roskin KM, Haussler D, Miller W, Hardison RC. Patterns of insertions and their covariation with substitutions in the rat, mouse, and human genomes. Genome Res. 2004;14(4):517–527. doi: 10.1101/gr.1984404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Zhang K, Fan W, Deininger P, Edwards A, Xu Z, Zhu D. Breaking the computational barrier: a divide-conquer and aggregate based approach for Alu insertion site characterisation. Int J Comput Biol Drug Des. 2009;2(4):302–322. doi: 10.1504/IJCBDD.2009.030763. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kvikstad EM, Makova KD. The (r)evolution of SINE versus LINE distributions in primate genomes: sex chromosomes are important. Genome Res. 2010;20(5):600–613. doi: 10.1101/gr.099044.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Wang J, Song L, Gonder MK, Azrak S, Ray DA, Batzer MA, Tishkoff SA, Liang P. Whole genome computational comparative genomics: A fruitful approach for ascertaining Alu insertion polymorphisms. Gene. 2006;365:11–20. doi: 10.1016/j.gene.2005.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Sela N, Mersch B, Gal-Mark N, Lev-Maor G, Hotz-Wagenblatt A, Ast G. Comparative analysis of transposed element insertion within human and mouse genomes reveals Alu's unique role in shaping the human transcriptome. Genome Biol. 2007;8(6):R127. doi: 10.1186/gb-2007-8-6-r127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Levy A, Sela N, Ast G. TranspoGene and microTranspoGene: transposed elements influence on the transcriptome of seven vertebrates and invertebrates. Nucleic Acids Res. 2008. pp. D47–52. [DOI] [PMC free article] [PubMed]
  13. Gu TJ, Yi X, Zhao XW, Zhao Y, Yin JQ. Alu-directed transcriptional regulation of some novel miRNAs. BMC Genomics. 2009;10:563. doi: 10.1186/1471-2164-10-563. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Stenger JE, Lobachev KS, Gordenin D, Darden TA, Jurka J, Resnick MA. Biased distribution of inverted and direct Alus in the human genome: implications for insertion, exclusion, and genome stability. Genome Res. 2001;11(1):12–27. doi: 10.1101/gr.158801. [DOI] [PubMed] [Google Scholar]
  15. Deininger PL, Batzer MA. Alu repeats and human disease. Mol Genet Metab. 1999;67(3):183–193. doi: 10.1006/mgme.1999.2864. [DOI] [PubMed] [Google Scholar]
  16. Belancio VP, Roy-Engel AM, Deininger PL. All y'all need to know 'bout retroelements in cancer. Semin Cancer Biol. 2010;20(4):200–210. doi: 10.1016/j.semcancer.2010.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Strout MP, Marcucci G, Bloomfield CD, Caligiuri MA. The partial tandem duplication of ALL1 (MLL) is consistently generated by Alu-mediated homologous recombination in acute myeloid leukemia. Proc Natl Acad Sci USA. 1998;95(5):2390–2395. doi: 10.1073/pnas.95.5.2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Viel A, Petronzelli F, Della Puppa L, Lucci-Cordisco E, Fornasarig M, Pucciarelli S, Rovella V, Quaia M, Ponz de Leon M, Boiocchi M. et al. Different molecular mechanisms underlie genomic deletions in the MLH1 Gene. Hum Mutat. 2002;20(5):368–374. doi: 10.1002/humu.10138. [DOI] [PubMed] [Google Scholar]
  19. Hsieh SY, Chen WY, Yeh TS, Sheen IS, Huang SF. High-frequency Alu-mediated genomic recombination/deletion within the caspase-activated DNase gene in human hepatoma. Oncogene. 2005;24(43):6584–6589. doi: 10.1038/sj.onc.1208803. [DOI] [PubMed] [Google Scholar]
  20. van der Klift H, Wijnen J, Wagner A, Verkuilen P, Tops C, Otway R, Kohonen-Corish M, Vasen H, Oliani C, Barana D. et al. Molecular characterization of the spectrum of genomic deletions in the mismatch repair genes MSH2, MLH1, MSH6, and PMS2 responsible for hereditary nonpolyposis colorectal cancer (HNPCC) Genes Chromosomes Cancer. 2005;44(2):123–138. doi: 10.1002/gcc.20219. [DOI] [PubMed] [Google Scholar]
  21. O'Neil J, Tchinda J, Gutierrez A, Moreau L, Maser RS, Wong KK, Li W, McKenna K, Liu XS, Feng B. et al. Alu elements mediate MYB gene tandem duplication in human T-ALL. J Exp Med. 2007;204(13):3059–3066. doi: 10.1084/jem.20071637. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Franke G, Bausch B, Hoffmann MM, Cybulla M, Wilhelm C, Kohlhase J, Scherer G, Neumann HP. Alu-Alu recombination underlies the vast majority of large VHL germline deletions: Molecular characterization and genotype-phenotype correlations in VHL patients. Hum Mutat. 2009;30(5):776–786. doi: 10.1002/humu.20948. [DOI] [PubMed] [Google Scholar]
  23. Teugels E, De Greve J. About the c.156_157insAlu BRCA2 breast cancer predisposing mutation. Breast Cancer Res Treat. 2009;116(3):621–622. doi: 10.1007/s10549-008-0188-x. [DOI] [PubMed] [Google Scholar]
  24. Futreal PA, Coin L, Marshall M, Down T, Hubbard T, Wooster R, Rahman N, Stratton MR. A census of human cancer genes. Nat Rev Cancer. 2004;4(3):177–183. doi: 10.1038/nrc1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. http://www.sanger.ac.uk/genetics/CGP/cosmic/
  26. Korenberg JR, Rykowski MC. Human genome organization: Alu, lines, and the molecular structure of metaphase chromosome bands. Cell. 1988;53(3):391–400. doi: 10.1016/0092-8674(88)90159-6. [DOI] [PubMed] [Google Scholar]
  27. Medstrand P, van de Lagemaat LN, Mager DL. Retroelement distributions in the human genome: variations associated with age and proximity to genes. Genome Res. 2002;12(10):1483–1495. doi: 10.1101/gr.388902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Grover D, Majumder PP, C BR, Brahmachari SK, Mukerji M. Nonrandom distribution of alu elements in genes of various functional categories: insight from analysis of human chromosomes 21 and 22. Mol Biol Evol. 2003;20(9):1420–1424. doi: 10.1093/molbev/msg153. [DOI] [PubMed] [Google Scholar]
  29. Lin L, Shen S, Tye A, Cai JJ, Jiang P, Davidson BL, Xing Y. Diverse splicing patterns of exonized Alu elements in human tissues. PLoS Genet. 2008;4(10):e1000225. doi: 10.1371/journal.pgen.1000225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schwartz S, Gal-Mark N, Kfir N, Oren R, Kim E, Ast G. Alu exonization events reveal features required for precise recognition of exons by the splicing machinery. PLoS Comput Biol. 2009;5(3):e1000300. doi: 10.1371/journal.pcbi.1000300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sellis D, Provata A, Almirantis Y. Alu and LINE1 distributions in the human chromosomes: evidence of global genomic organization expressed in the form of power laws. Mol Biol Evol. 2007;24(11):2385–2399. doi: 10.1093/molbev/msm181. [DOI] [PubMed] [Google Scholar]
  32. Benjamini Y, Hochberg Y. Controlling the false discover rate - A practical and powerful approach to multiple testing. J ROY STAT SOC B MET. 1995;75:289–300. [Google Scholar]
  33. Hu RJ, Lee MP, Connors TD, Johnson LA, Burn TC, Su K, Landes GM, Feinberg AP. A 2.5-Mb transcript map of a tumor-suppressing subchromosomal transferable fragment from 11p15.5, and isolation and sequence analysis of three novel genes. Genomics. 1997;46(1):9–17. doi: 10.1006/geno.1997.4981. [DOI] [PubMed] [Google Scholar]
  34. Casella G, Berger RL. Statistical inference. 2. Thmoson Learning; 2001. [Google Scholar]
  35. McCoy MW, Allen AP, Gillooly JF. The random nature of genome architecture: predicting open reading frame distributions. PLoS One. 2009;4(7):e6456. doi: 10.1371/journal.pone.0006456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Dennis B, Patil GP. The gamma distribution and weighted multimodal gamma distributions as models of population abundance. Mathematical Biosciences. 1984;68:187–212. doi: 10.1016/0025-5564(84)90031-2. [DOI] [Google Scholar]
  37. Huang DW, Sherman BT, Lempicki RA. Systematic and integrative analysis of large gene lists using DAVID Bioinformatics Resources. Nature Protoc. 2009;4(1):44–57. doi: 10.1038/nprot.2008.211. [DOI] [PubMed] [Google Scholar]
  38. Tsirigos A, Rigoutsos I. Alu and b1 repeats have been selectively retained in the upstream and intronic regions of genes of specific functional classes. PLoS Comput Biol. 2009;5(12):e1000610. doi: 10.1371/journal.pcbi.1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Gilbert N, Lutz-Prigge S, Moran JV. Genomic deletions created upon LINE-1 retrotransposition. Cell. 2002;110(3):315–325. doi: 10.1016/S0092-8674(02)00828-0. [DOI] [PubMed] [Google Scholar]
  40. Morrish TA, Gilbert N, Myers JS, Vincent BJ, Stamato TD, Taccioli GE, Batzer MA, Moran JV. DNA repair mediated by endonuclease-independent LINE-1 retrotransposition. Nat Genet. 2002;31(2):159–165. doi: 10.1038/ng898. [DOI] [PubMed] [Google Scholar]
  41. Callinan PA, Wang J, Herke SW, Garber RK, Liang P, Batzer MA. Alu retrotransposition-mediated deletion. J Mol Biol. 2005;348(4):791–800. doi: 10.1016/j.jmb.2005.02.043. [DOI] [PubMed] [Google Scholar]
  42. Sen SK, Huang CT, Han K, Batzer MA. Endonuclease-independent insertion provides an alternative pathway for L1 retrotransposition in the human genome. Nucleic Acids Res. 2007;35(11):3741–3751. doi: 10.1093/nar/gkm317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Srikanta D, Sen SK, Huang CT, Conlin EM, Rhodes RM, Batzer MA. An alternative pathway for Alu retrotransposition suggests a role in DNA double-strand break repair. Genomics. 2009;93(3):205–212. doi: 10.1016/j.ygeno.2008.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Sen SK, Han K, Wang J, Lee J, Wang H, Callinan PA, Dyer M, Cordaux R, Liang P, Batzer MA. Human genomic deletions mediated by recombination between Alu elements. Am J Hum Genet. 2006;79(1):41–53. doi: 10.1086/504600. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Myers S, Bottolo L, Freeman C, McVean G, Donnelly P. A fine-scale map of recombination rates and hotspots across the human genome. Science. 2005;310(5746):321–324. doi: 10.1126/science.1117196. [DOI] [PubMed] [Google Scholar]
  46. http://www.ncrna.org
  47. Debacker K, Kooy RF. Fragile sites and human disease. Hum Mol Genet. 2007;16(Spec No. 2):R150–158. doi: 10.1093/hmg/ddm136. [DOI] [PubMed] [Google Scholar]
  48. Baker SJ, Markowitz S, Fearon ER, Willson JK, Vogelstein B. Suppression of human colorectal carcinoma cell growth by wild-type p53. Science. 1990;249(4971):912–915. doi: 10.1126/science.2144057. [DOI] [PubMed] [Google Scholar]
  49. Volinia S, Mascellani N, Marchesini J, Veronese A, Ormondroyd E, Alder H, Palatini J, Negrini M, Croce CM. Genome wide identification of recessive cancer genes by combinatorial mutation analysis. PLoS One. 2008;3(10):e3380. doi: 10.1371/journal.pone.0003380. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Dagan T, Sorek R, Sharon E, Ast G, Graur D. AluGene: a database of Alu elements incorporated within protein-coding genes. Nucleic Acids Res. 2004. pp. D489–492. [DOI] [PMC free article] [PubMed]
  51. http://transpogene.tau.ac.il
  52. http://ftp.genome.washington.edu
  53. Ricci V. Fitting distributions with R. 2005.
  54. Nagelkerke NJD. A note on a general definition of the coefficient of determination. Biometrika. 1991. pp. 691–692. [DOI]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Additional file 1

The Q-Q plots for fitting a Gamma distribution to the gene-level intron Alu densities in 20 chromosomes.

Click here for file (290.4KB, PDF)
Additional file 2

The analysis of genes deviating from the diagonal lines of the Q-Q plots for chromosomes-1, -3, -6, -13, -21, and -X.

Click here for file (9.9KB, PDF)
Additional file 3

The frequency distributions of intron and exon Alu densities of the cancer genes with somatic and germline mutations.

Click here for file (30KB, PDF)
Additional file 4

The frequency distributions of intron and exon Alu densities of the cancer genes with translocation and non-translocation mutations.

Click here for file (31.7KB, PDF)
Additional file 5

The distributions of 351 cancer genes measured by the Alu-related genomic features and GC content.

Click here for file (34.6KB, PDF)
Additional file 6

The Functional enrichment analysis of 5578 multi-exons genes without intron Alus.

Click here for file (56.1KB, PDF)

Articles from BMC Genomics are provided here courtesy of BMC

RESOURCES