Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2011 Mar 4;7(4):890–897. doi: 10.1021/ct100605v

On the Use of Accelerated Molecular Dynamics to Enhance Configurational Sampling in Ab Initio Simulations

Denis Bucher 1,*, Levi C T Pierce 1, J Andrew McCammon 1, Phineus R L Markwick 1
PMCID: PMC3074571  PMID: 21494425

Abstract

We have implemented the accelerated molecular dynamics approach (Hamelberg, D.; Mongan, J.; McCammon, J. A. J. Chem. Phys. 2004, 120 (24), 11919) in the framework of ab initio MD (AIMD). Using three simple examples, we demonstrate that accelerated AIMD (A-AIMD) can be used to accelerate solvent relaxation in AIMD simulations and facilitate the detection of reaction coordinates: (i) We show, for one cyclohexane molecule in the gas phase, that the method can be used to accelerate the rate of the chair-to-chair interconversion by a factor of ∼1 × 105, while allowing for the reconstruction of the correct canonical distribution of low-energy states; (ii) We then show, for a water box of 64 H2O molecules, that A-AIMD can also be used in the condensed phase to accelerate the sampling of water conformations, without affecting the structural properties of the solvent; and (iii) The method is then used to compute the potential of mean force (PMF) for the dissociation of Na−Cl in water, accelerating the convergence by a factor of ∼3−4 compared to conventional AIMD simulations.(2) These results suggest that A-AIMD is a useful addition to existing methods for enhanced conformational and phase-space sampling in solution. While the method does not make the use of collective variables superfluous, it also does not require the user to define a set of collective variables that can capture all the low-energy minima on the potential energy surface. This property may prove very useful when dealing with highly complex multidimensional systems that require a quantum mechanical treatment.

Introduction

In recent years, ab initio molecular dynamics (AIMD) has emerged as a promising tool for performing accurate free energy calculations from first principles.(3) AIMD has been successfully applied to the study of a diverse variety of systems, including isolated molecules and condensed matter and solid-state systems.(4) AIMD has also been employed in a quantum mechanics/molecular mechanics (QM/MM) manifold to investigate enzymatic reactions.(5) However, the potential of AIMD to obtain accurate free energy statistics is hindered by the fact that configurational transitions or chemical reactions occur on time scales that are significantly longer than those accessible using standard AIMD methodologies. Despite the sustained and rapid increase in available computational power and the continued development of efficient simulation algorithms, AIMD simulations of even small, isolated molecules are generally limited to time scales of hundreds of picoseconds.

In the last two decades, considerable progress has been made in the development of more sophisticated methods to explore the configurational space of molecular systems more efficiently, allowing for the study of slow molecular motions and rare events. In general, these methods can be divided into two groups: The first involves the identification of transition pathways between known initial and final states. Such methods include, for example, transition path sampling,(6) targeted molecular dynamics(7) (and constrained dynamics(8) in general), and essential molecular dynamics.(9) The second group contains those methods that efficiently sample low-energy molecular conformations, allowing the rapid identification of thermodynamically dominant regions on the potential energy surface (PES). These methods include replica exchange MD(10) and metadynamics.(11)

In the specific context of AIMD, the two most popular contemporary free energy methods employed are constrained MD and metadynamics. In the constrained MD method, a series of simulations are performed using a predefined internal degree of freedom as a constraint, and the free energy profile is obtained by integrating the average constraint force over the reaction coordinate. In metadynamics, the system is destabilized along a small set of predefined collective variables (internal degrees of freedom) by adding Gaussian potentials onto the PES in a history-dependent fashion. The free-energy surface is then obtained as the negative of the total bias potential added during the simulation. Noticeably, the successful application of both these enhanced sampling methods is dependent on the appropriate definition of a reaction coordinate or a set of collective variables and therefore requires at least some a priori understanding of the underlying PES.

In this paper we explore an alternative biased potential method that has been proposed recently in the framework of classical molecular dynamics, called accelerated Molecular Dynamics (aMD).(1) In the original variant of aMD, one adds a continuous non-negative bias potential to the actual PES, while still maintaining the essential details of the underlying PES. This has the effect of raising the low-energy regions on the potential energy landscape, decreasing the magnitude of energy barriers and accelerating the exchange between low-energy conformational states. One of the favorable characteristics of this method is that one can recover the canonical average of an observable so that thermodynamic and other equilibrium properties can be accurately determined. In comparison to the other enhanced sampling methods described above, aMD does not require any prior knowledge of the underlying PES.

In the context of classical simulations, aMD has already been successfully employed to study slow time-scale dynamics in proteins, such as HIV-protease,(12) ubiquitin,(13) IKBA,(14) and H-Ras.(15) The enhanced conformational space sampled by aMD has also been shown to significantly improve the theoretical prediction of experimental NMR observables, such as residual dipolar couplings, scalar J-couplings,(13) and chemical shifts,(14) which are sensitive to dynamic averaging on the micro- to millisecond time scale.

In this paper, we explore the possibility of using the accelerated ab initio MD (A-AIMD) to study conformational transitions and enhance phase-space sampling in the condensed phase. The present work is aimed at developing the A-AIMD method for studying systems in aqueous solution, which could initiate a variety of new applications, since most biological, chemical, and industrial processes, occur in water.

After presenting briefly the formal methodology, we present our results for three test systems: First, we investigate the conformational behavior of an isolated cyclohexane molecule in the gas phase. We demonstrate how A-AIMD can be used to explore the PES, identifying different molecular conformers, and affording accurate relative free energy statistics. Next, we present the results of A-AIMD simulations performed on bulk water, where it is shown that one can accelerate rotational and translational diffusion, and hence the sampling of water conformations, while still maintaining accurate free-energy weighted structural properties of the system. We then apply the method to Na−Cl in solution, to show that one can accelerate the convergence of the dissociation free energy profile of the two ions.

Theory and Computational Details

The details of accelerated molecular dynamics have been discussed previously in the literature.1,17 Following Voter’s hyperdynamics scheme,(18) a reference boost energy Eb is defined, which lies above the minimum of the PES. At each step in the simulation, if the potential energy V(r) lies below this boost energy, a continuous non-negative bias potential ΔV(r) is added to the actual potential. The application of the bias potential raises the low-energy valleys and decreases the magnitude of energy barriers, while maintaining the essential details of the energy landscape. Explicitly, the modified potential V*(r) is defined as

graphic file with name ct-2010-00605v_m001.jpg

where the bias potential is defined as

graphic file with name ct-2010-00605v_m002.jpg

The extent of acceleration (i.e., how much the PES is raised and flattened) is determined by the choice of the boost energy (Eb) and the acceleration parameter (α). More aggressive acceleration can be achieved either by increasing Eb to flatten the potential or by decreasing the magnitude of α, which reduces the roughness of the potential. In practice, finding optimal parameters require some testing. One usually chooses parameters so that the magnitude of fluctuations in ΔV during the simulations approximate the energy barriers. In many cases, the barrier heights are not known, and optimal parameters are found by holding one of the two parameters, while allowing the second parameter to evolve until the system starts exploring new regions of the phase space.

The forces acting on the nuclei are expressed as

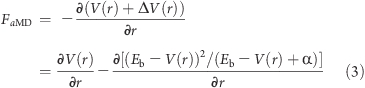graphic file with name ct-2010-00605v_m003.jpg

which can be reformulated as (for a derivation see the Supporting Information):

graphic file with name ct-2010-00605v_m004.jpg

The bias potential as defined above ensures that the derivative of the modified potential will not be discontinuous at points where V(r) = Eb.

One of the favorable characteristics of this method is that it yields a canonical average of an observable, so that thermodynamic and other equilibrium properties can be accurately determined. The corrected canonical ensemble average of any given property, <A>c is obtained by reweighting each point in the configuration space on the modified potential by the strength of the Boltzmann factor of the bias energy, exp(βΔV(r,ti)), at that particular point:

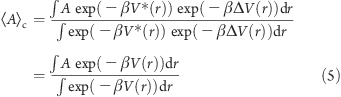graphic file with name ct-2010-00605v_m005.jpg

Computational Details

AIMD simulations were performed using the Car−Parrinello (CP) scheme,(19) and an in-house modified version of the CPMD 3.13 code.(20) The three systems studied in this work were: (i) an isolated cyclohexane molecule in the gas phase placed at the center of a cubic box of length L = 12.00 Å; (ii) a periodically repeating cubic box of length L = 12.44 Å containing 64 H2O molecules; and (iii) a periodically repeating cubic box of length L = 12.35 Å containing 62 H20 molecules, one Na+ ion and one Cl− ion. The electronic structure problem was solved with density functional theory (DFT), and in each case, the Becke (B) exchange and Lee−Yang−Parr (LYP) correlation functional were employed.(21) Although a variety of empirical corrections have been suggested to include the effect of dispersion forces in the BLYP functional, we chose to use the standard functional, which allows us to compare our results directly to previous works on these systems. For each system, a fictitious electron mass of 400 au was ascribed to the electronic degrees of freedom, and the coupled equations of motion were solved using the velocity Verlet algorithm(22) with a time-step of 4 au core electrons and were treated using the norm-conserving pseudopotentials of Troullier and Martins,(23) and the valence orbitals were expanded in a plane-wave basis set up to an energy cutoff of 80 Ry. All standard and A-AIMD simulations were performed at T = 300 K using a Nose−Hoover chain thermostat(24) on the ions with coupling frequency of 600 cm−1. In the case of cyclohexane, a thermostat was also used on the electrons, with a target kinetic energy of 0.001 au and a coupling frequency of 6000 cm−1.

Results

Conformations of Cyclohexane

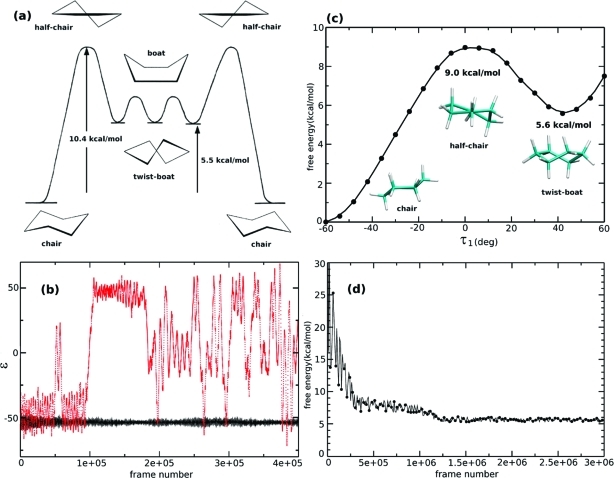
Accelerated AIMD is a highly efficient and robust conformational space sampling method. In order to demonstrate this, we performed an initial study to explore the PES of cyclohexane. Cyclohexane can exist in a variety of conformational states that have been depicted diagrammatically in Figure 1a. The most stable chemical conformation of cyclohexane is the ‘chair’ form, for which there are two geometric isomers. These isomers differ in respect to which hydrogen atoms in the ring adopt axial and equatorial positions. During the interconversion process, known as ‘ring flipping’, the axial hydrogens become equatorial and the equatorial hydrogens become axial, and the system passes through a metastable state, referred to as the ‘twist−boat’ conformation, which also possesses several geometric isomers. The transition states associated with interconversion between twist−boat isomers and the twist−boat and chair conformations are called the ‘boat’ and ‘half-chair’ forms, respectively. Experimental studies have shown that the free energy of the twist−boat conformer lies approximately 5.5 kcal/mol above that of the thermodynamically stable chair conformation in the gas phase,(25) and the free energy barrier for interconversion between the chair and twist−boat conformers has been estimated by NMR experiments to be approximately 10.4 kcal/mol.(26) The ring-flipping process is therefore very slow, occurring on the microsecond time scale at 300 K, which is inaccessible using standard AIMD methods.

Figure 1.

Figure 1

Open in a new tab

(a) Scheme representing the different conformations of cyclohexane. (b) The chair-to-chair interconversion was monitored during the simulations using a ε coordinate defined in the text. The A-AIMD simulation is shown in red (dotted line), and conventional AIMD in black (solid line), (4e + 05 frames = ∼40 ps). (c) Constrained MD was used to calculate a reference PMF and to obtain the theoretical relative free energy of the twist−boat conformation with BLYP. (d) The A-AIMD estimate for the relative free energy of the twist−boat conformation converges toward the expected value.

An initial standard AIMD simulation of cyclohexane was performed at T = 300 K starting in the chair conformation. Unsurprisingly, this initial 400 000 steps (∼40 ps) simulation confirmed that the chair conformation is very stable, and the average potential energy was −41.14 au (1 au = 627.51 kcal/mol). This value was used as the reference potential energy V0 in the subsequent A-AIMD simulations. Keeping the acceleration parameter α fixed at 0.016 au (∼10 kcal/mol), a series of short (400 000 steps) accelerated simulations were performed using different boost energies: [Eb − V0] = (0.02, 0.04, 0.06, 0.08, and 0.10). As the value of [Eb − V0] was systematically increased, enhanced conformational space sampling was observed. Inspection of the resulting trajectories revealed that the ‘optimal’ acceleration parameters for observing the ring flipping process within the time scale of the simulations were: {[Eb − V0], α} = {0.10 au, 0.016 au}.

The conformational changes occurring in the A-AIMD simulations were analyzed using geometric criteria defined by the dihedral angles of the ring (Table SI1, Supporting Information). In addition, a configuration coordinate, ε, was formulated as

graphic file with name ct-2010-00605v_m006.jpg

where τi is the internal ring dihedral angle (see Supporting Information for more details). Using this configuration coordinate, the two isomeric forms of the chair conformation correspond to ε values of approximately −60 and +60° and the twist−boat intermediate corresponds to a value of ε of approximately 0. In Figure 1b, we show the conformational space sampling afforded by the extended 400 000 step ‘optimal’ A-AIMD simulation, compared to a standard AIMD simulation performed under the same physical conditions. In comparison to the standard AIMD simulation, which remains in the initial chair conformation throughout the entire trajectory, the optimal A-AIMD simulation readily interchanges between the different conformational states. Indeed, in the course of the 400 000 step (∼ 40 ps) simulation, eight ring-flipping events were observed, and the system visited all known stable, metastable, and transition states (chair, half-chair, twist−boat, envelope, and boat, see Table SI1, Supporting Information). The efficiency of the sampling is demonstrated by the fact that even within just 100 000 steps of A-AIMD (the equivalent of 10 ps), we observe a conformational transition which according to transition-state theory (assuming a transmission coefficient of 1) would actually occur on a time scale of approximately 1 μs.

As discussed in the Theory and Computational Details Section, aMD is not only an efficient conformational space sampling algorithm but is also a robust free energy sampling method. However, obtaining accurate free energy statistics is more challenging than just exploring the conformational space: Relative free energy statistics are determined not only by the variation in the magnitude of the bias-potential but also by the density of states (i.e., the effective population) on the modified potential. Accurate free energy statistics can only be obtained if multiple transitions between the different conformational states are observed. In light of this, a second, much longer, 3 000 000 step (∼300 ps) accelerated AIMD simulation was then performed at the optimal acceleration level. The relative free energy of the twist−boast conformer with respect to the chair conformation was calculated as ΔG(twist−chair) = −kT ln(P(twist)/P(chair)), using the density of the two states after reweighting the trajectories by the strength of the Boltzmann factor of the bias [exp(βΔV(r,ti)]. In order to obtain an accurate estimate of the theoretical free energy barrier for the chair to twist−boat conformational transition, using the BLYP density functional, we employed the well-established constrained MD approach (see Supporting Information for more details). The results of this study are presented in Figure 1c. The theoretical free energy barrier was found to be 9.0 ± 0.3 kcal/mol, which is in good agreement with the experimental estimate (10.4 kcal/mol). The A-AIMD simulation determined the free energy for the twist−boat conformation to lie 5.8 kcal/mol above that of the chair conformer, which is in excellent agreement with the reference constrained MD result (5.6 kcal/mol ±0.3 kcal/mol, Figure 1c). The number of A-AIMD steps required to reach convergence in the free energy statistics was approximately 1.5 × 106 (see Figure 1d). In terms of required CPU time, this is the equivalent of ∼150 ps of standard AIMD, which is readily accessible.

In addition to obtaining the relative free energies of stable and metastable states, the magnitude of the free energy barrier can also be estimated approximately from A-AIMD simulations by measuring the amount of destabilization required to observe the conformational transition (i.e., the maximum bias potential, ΔVmax). The energy barrier for the chair-to-chair interconversion was estimated in this way by gradually increasing Eb (with α fixed) until the conformational transition was observed. A bias potential of ∼10 kcal/mol was required to leave the chair conformation, in good agreement with the reference calculation for the energy barrier and with experimental data. Taken together, these encouraging results suggest that A-AIMD represents a useful method to sample the conformational space of isolated molecules. Next, we show that A-AIMD can also be used to accelerate the sampling for systems in the condensed phase. We have chosen for this study to carry out simulations on a water box. This choice was made not only because water is important in chemistry and biology but also because water is an important system from a theoretical perspective, as it is often used to test AIMD schemes and assist the development of new DFT functionals.

Enhanced Sampling in Condensed Matter Systems: Bulk Water

The cyclohexane study described above readily demonstrates how A-AIMD simulations can be used to efficiently explore the conformational space of isolated molecules and obtain accurate free energy statistics. However, such is the versatility of this method, A-AIMD simulations can also be employed to enhance the phase-space sampling in condensed matter systems. In order to investigate this, we performed a test study on bulk water. The particular focus of this study was to identify if it is possible to enhance the phase-space sampling using A-AIMD while still maintaining an accurate (free energy weighted) representation of the structural properties of the system.

Analogous to the cyclohexane study, an initial standard AIMD simulation was performed on a cubic box containing 64 water molecules under periodic boundary conditions, for 20 ps. The average density functional energy for the system was −1098.22 au, which was used as the reference potential energy, V0. A series of five 150 000 steps A-AIMD simulations were then performed at different acceleration levels. The specific acceleration parameters, [Eb − V0], and α, are presented in Table 1. As discussed in the Theory and Computational Details Section, the level of acceleration is determined by the relative magnitude of both [Eb − V0] and α. The A-AIMD simulations performed here, which we refer to as sim1−sim5, are ranked according to the level of acceleration determined by the average magnitude of the effective bias potential (ΔVave in Table 1).

Table 1. Summary of the A-AIMD Simulations Performed for a Water Box with 64 H2O Moleculesa.

simulations Eb − V0 (au) α (au) time (ps) ΔVave (kcal/mol) ΔVmax (kcal/mol) Dacc/D τ/τacc
MD − − 20 − − 1.0 1.0
sim1 0.1 0.1 15 0.8 5.4 2.1 1.7
sim2 0.2 0.4 15 1.1 7.3 2.9 1.9
sim3 0.2 0.1 15 1.7 11.2 4.3 2.1
sim4 0.3 0.4 15 2.5 15.4 6.4 3.0
sim5 0.3 0.1 15 3.1 16.6 7.1 3.6
Open in a new tab
a

The two parameters Eb and α are used to control the level of acceleration. The difference between Eb and the average potential energy V0 of a conventional AIMD simulation is given. The average and maximum values of the effective bias potential during the simulation are shown together with the acceleration with respect to conventional simulations in the observed diffusive properties (Dacc/D) and orientational correlation times (τ/τacc).

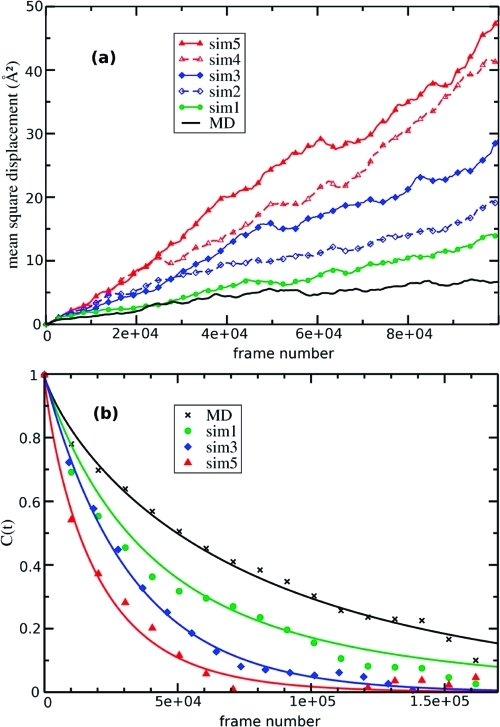
The most direct way to assess the amount of phase-space sampling in condensed matter systems is to monitor the average translational and rotational diffusion properties of the composite molecules. In Figure 2a we show the mean square displacement of water molecules (computed after correcting for the displacement of the center of mass of the box) for the standard AIMD simulation and the five accelerated A-AIMD simulations. The effect of the bias potential clearly enhances the average translational diffusion of the water molecules. Compared to the standard AIMD simulation, the mean square displacement was found to increase from two- to eight-fold from the least aggressive (sim1) to most aggressive (sim5) A-AIMD simulation. In a similar manner, the application of the bias potential also increased the observed average rotational diffusion, which was assessed by calculating the effective (unweighted) reorientational autocorrelation function of the normalized O−H bond vector, averaged over all water molecules in the system. The reorientational autocorrelation functions shown in Figure 2b describe how a water molecule on average loses memory of its orientational ‘state’ during the simulation. As reorientation diffusion in condensed matter systems is a stochastic process, the associated autocorrelation functions show an exponential decay. By definition, in the limit that the autocorrelation function approaches zero, the water molecules in the system have undergone a rotation of 2π radians on average. As can be seen in Figure 2b, even under only moderate acceleration (sim3), the reorientational correlation function approaches zero within 150 000 steps, compared to the standard AIMD simulation, where the reorientational correlation function approaches zero at step 315 000 (by extrapolation).

Figure 2.

Figure 2

Open in a new tab

Observed dynamical properties of waters in conventional AIMD and A-AIMD simulations: (a) mean-square displacement and (b) orientational autocorrelation functions for O−H vectors.

We would like to point out that during an A-AIMD simulation, the system evolves on a nonlinear time scale. Unfortunately, obtaining an accurate estimate of the time scale of the observed phase-space sampling in the A-AIMD simulations is not trivial. In light of this, we did not attempt to extract a meaningful estimate of the true translational and reorientational diffusion coefficients from the biased potential AIMD simulations. However, by comparing the effective mean-square displacements and reorientational relaxation ‘times’ (as a function of the number of MD steps), we can assess the effective enhancement in the translational and reorientational phase-space sampling compared to the standard AIMD simulation, reported in Table 1.

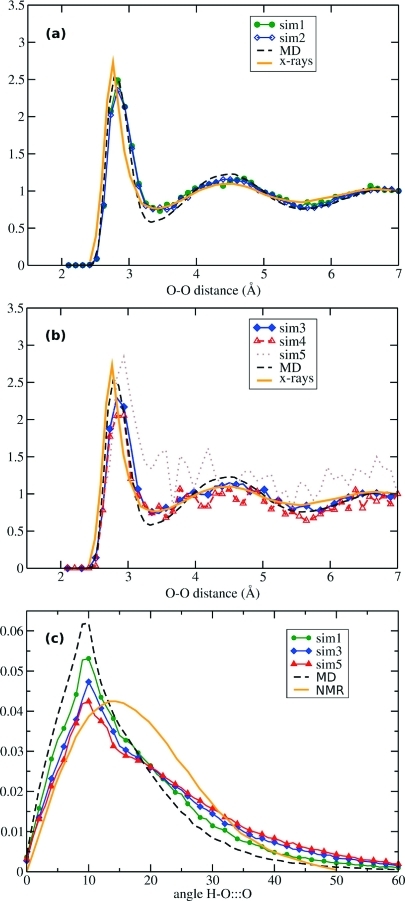
The results presented in Figure 2 clearly show that the effect of the bias potential significantly enhances the translational and reorientational diffusion properties of the system, and therefore A-AIMD simulations afford a substantial increase in the observed phase-space sampling. In order to study the structural properties of the system under the application of the bias potential, we calculated the free-energy weighted radial (O···O) and angular (H−O···O) distribution functions for all five A-AIMD simulations.

The O···O radial distribution functions are presented in Figure 3a and b along with the results obtained for both the standard AIMD simulation (20 ps) and an experimental X-ray diffraction study. Up to a moderate acceleration level (sim3), the free energy weighted radial distribution functions are in excellent agreement with the experimental X-ray diffraction data. The radial distribution functions obtained from the more aggressive accelerated simulations (sim4 and particularly sim5) appear to be less accurate, which is a direct result of the relatively short length of the simulations and the effect of enhanced statistical noise in the free energy reweighting protocol. When performing longer A-AIMD simulations at elevated acceleration levels, the noise in the free energy statistics will start to cancel out, and there may be in fact no loss in accuracy. The free energy weighted H−O···O angular distribution functions for the five A-AIMD simulations discussed here are presented in Figure 3c and compared to the standard AIMD result and experimental NMR data. Interestingly, a closer resemblance was obtained between the computed angular distribution function and the experimental NMR result as the level of acceleration (and therefore the extent of phase-space sampled) was increased. We note in passing that under more aggressive acceleration conditions, we observed proton transfer events caused by the dissociation of water (data not shown). Although we did not attempt to study water autoionization here, it suggests that an even larger boost may be useful in some cases to study these rare events. Experimentally, a single water molecule is known to undergo autoionization in ∼10 h.(29)

Figure 3.

Figure 3

Open in a new tab

Structural properties of water in conventional AIMD and A-AIMD simulations. (a and b) Showing a comparison with X-rays diffraction(27) for the O−O radial distribution functions (RDFs) and (c) a comparison with NMR(28) for the orientation of hydrogen bonds.

Potential of Mean Force (PMF) Calculation for the Dissociation of Na−Cl in Water

The results obtained from our initial study on bulk water show that the application of the bias potential allows for a significant enhancement in the phase-space sampling, while still maintaining an accurate free energy weighted representation of the structural properties of the system up to moderate acceleration levels. In light of these results, it appears that A-AIMD can be employed as an efficient method to determine thermodynamic and equilibrium properties in condensed matter systems, particularly when these properties are sensitive to the effects of time and ensemble averaging, mediated by the diffusive properties of the solvent. In order to demonstrate this, we have calculated the free energy profile for the dissociation of Na−Cl in bulk water using an extended accelerated AIMD approach. Classical MD studies of this system date to 1984.(30) However, it has been studied only recently with ab initio methods.(2)

The simulation details and setup employed in this work are identical to those of the recently published study by Timko et al. using conventional constrained AIMD simulations. In this published study, the reaction coordinate, r, was defined as the distance between the Na and Cl ions, and it was found that a simulation time of up to 6 ps was required in order to converge the average constraint force at each constraint distance. The free energy profile (or potential of mean force) for Na−Cl dissociation was then obtained by integrating the average constraint force over the reaction coordinate. In the present work, we have performed the same constrained simulations in the framework of A-AIMD, using the ‘optimal’ acceleration parameters obtained from the bulk water study presented above: {Eb − V0, α} = {0.2 au, 0.1 au}.

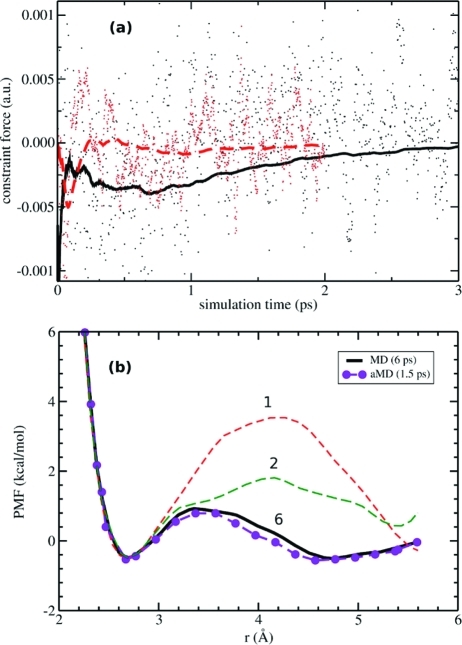
In Figure 4a we compare the convergence of the cumulative average constraint force obtained from A-AIMD to that obtained using standard AIMD for a constraint distance, r = 3.5 Å. The cumulative average of the mean force in the A-AIMD simulation (which is free energy weighted) converges to the same value as in the conventional AIMD simulation (−0.0004 au) within 15 000 steps (the equivalent of 1.5 ps of standard AIMD simulation). Using this result as a guideline, the free energy profile for dissociation of NaCl in bulk water was calculated by performing 21 constrained accelerated AIMD simulations for 15 000 steps across the entire reaction coordinate from r = 2.7 to 5.7 Å (Figure 4b). The resulting potential of mean force is in excellent agreement with the previously published results of Timko et al., who used a sampling time of 6 ps. Therefore, the application of the bias potential affords an approximate four-fold speed up in the convergence of the potential of mean force, as is readily demonstrated in Figure 4b. This four-fold speed-up is consistent with the estimated enhanced phase-space sampling results obtained from the comparative analysis of the translational and reorientational diffusion properties of bulk water (Table 1, sim3).

Figure 4.

Figure 4

Open in a new tab

Convergence of the dissociation profile of NaCl in solution: (a) Cumulative average of the mean force at a separation length of 3.5 Å between Na and Cl (after reweighting the trajectories with eq 5). The convergence is shown for A-AIMD (dashed red line) and for conventional AIMD (solid black line). (b) Potential of mean force for the dissociation of NaCl in water computed with A-AIMD (1.5 ps per point) and with conventional AIMD (1, 2, and 6 ps per point).

Conclusions

We have discussed the preliminary testing and implementation of the accelerated MD approach in the framework of AIMD. Using three simple examples, we have demonstrated that A-AIMD is a highly efficient and robust method for enhanced conformational and phase-space sampling. In particular, we have shown that the effect of the bias potential allows for the study of slow conformational transitions and rare events, such as the ring-flipping process in cyclohexane, that occurs on microsecond time scales and is inaccessible when using standard AIMD. For isolated molecules, we have shown that A-AIMD affords accurate free energy statistics that allows for the determination of thermodynamic and other equilibrium properties. In the condensed phase, obtaining converged free energy with A-AIMD may be more challenging, due to the requirement that rare events are sampled many times. However, convergence problems can be avoided by using a different free energy method that allows for the computation of the free energy along collective variables. As an example, we have shown that A-AIMD can be used in conjunction with constrained MD to accelerate the convergence of constrained MD by a factor of ∼4, for the case of 2 ions in a water box. The A-AIMD method is likely to be a useful addition to existing methods for sampling purposes and for helping to determine an optimal set of collective variables that can describe all the low-energy transformations.

As mentioned in the Introduction, one interesting feature of A-AIMD is that it can accelerate rare events while maintaining the essential details of the underlying PES. Since the ordering of minima on the PES is conserved, events that are low in energy are likely to occur first during an A-AIMD simulation. This property can be used to gain an intuitive understanding of chemical reactivity. In future applications, we plan to apply the method to study complex chemical reactions in the condensed phase.

Finally, although all the biased potential simulations presented here have been performed in the framework of Car−Parrinello MD, we would like to note that the implementation of this method in the framework of Born−Oppenheimer or Ehrenfest dynamics is equally viable. In conclusion, A-AIMD represents a highly efficient and versatile addition to existing ab initio methodologies for performing enhanced conformational space sampling and determining accurate free energies. In future works, A-AIMD could also be used to study chemical reactions in solution or applied to larger systems of biological relevance within a QM/MM framework.

Acknowledgments

This work was supported by the National Science Foundation, the National Institutes of Health, the Howard Hughes Medical Institute, the Center for Theoretical Biological Physics, the National Biomedical Computation Resource, the National Science Foundation Supercomputer Centers, and the Swiss Science Foundation (DB).

Supporting Information Available

Derivation of the formula for the forces is given, the geometrical criteria used to analyze the cyclohexane trajectories are presented, together with computational details about the constrained MD calculations. This information is available free of charge via the Internet at http://pubs.acs.org/.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ct100605v_si_001.pdf (186.6KB, pdf)

References

  1. Hamelberg D.; Mongan J.; McCammon J. A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120 (24), 11919. [DOI] [PubMed] [Google Scholar]
  2. Timko J.; Bucher D.; Kuyucak S. Dissociation of NaCl in water from ab initio molecular dynamics simulations. J. Chem. Phys. 2010, 132 (11), 114510. [DOI] [PubMed] [Google Scholar]
  3. Leone V.; Marinelli F.; Carloni P.; Parrinello M. Targeting biomolecular flexibility with metadynamics. Curr. Opin. Struct. Biol. 2010, 20 (2), 148. [DOI] [PubMed] [Google Scholar]
  4. Hutter J.; Marx D.. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, U.K., 2009; p 578. [Google Scholar]
  5. Senn H. M.; Thiel W. QM/MM Studies of Enzymes. Curr. Opin. Chem. Biol. 2007, 11 (2), 182. [DOI] [PubMed] [Google Scholar]; b Laio A.; VandeVondele J.; Rothlisberger U. A Hamiltonian electrostatic coupling scheme for hybrid Car-Parrinello molecular dynamics simulations. J. Chem. Phys. 2002, 116 (16), 6941. [Google Scholar]
  6. Dellago C.; Bolhuis P. G.; Csajka F. S.; Chandler D. Transition path sampling and the calculation of rate constants. J. Chem. Phys. 1998, 108 (5), 1964. [Google Scholar]
  7. Schlitter J.; Engels M.; Kruger P.; Jacoby E.; Wollmer A. Targeted Molecular-Dynamics Simulation of Conformational Change Application to the T-R Transition in Insulin. Mol. Simul. 1993, 10 (2−6), 291. [Google Scholar]
  8. Ciccotti G.; Ferrario M.; Hynes J. T.; Kapral R. Constrained Molecular-Dynamics and the Mean Potential for an Ion-Pair in a Polar-Solvent. Chem. Phys. 1989, 129 (2), 241. [Google Scholar]
  9. Amadei A.; Linssen A. B. M.; Berendsen H. J. C. Essential Dynamics of Proteins. Proteins: Struct., Funct., Genet. 1993, 17 (4), 412. [DOI] [PubMed] [Google Scholar]
  10. Sugita Y.; Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314 (1−2), 141. [Google Scholar]
  11. Laio A.; Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 2002, 99 (20), 12562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hamelberg D.; McCammon J. A. Fast peptidyl cis-trans isomerization within the flexible Gly-rich flaps of HIV-1 protease. J. Am. Chem. Soc. 2005, 127 (40), 13778. [DOI] [PubMed] [Google Scholar]
  13. Markwick P. R. L.; Bouvignies G.; Salmon L.; McCammon J. A.; Nilges M.; Blackledge M. Toward a Unified Representation of Protein Structural Dynamics in Solution. J. Am. Chem. Soc. 2009, 131 (46), 16968. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Markwick P. R. L.; Cervantes C. F.; Abel B. L.; Komives E. A.; Blackledge M.; McCammon J. A. Enhanced Conformational Space Sampling Improves the Prediction of Chemical Shifts in Proteins. J. Am. Chem. Soc. 2010, 132 (4), 1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Grant B. J.; Gorfe A. A.; McCammon J. A. Ras Conformational Switching: Simulating Nucleotide-Dependent Conformational Transitions with Accelerated Molecular Dynamics. PLoS Comput. Biol. 2009, 5 (3), e1000325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pierce L. C. T.; Markwick R. L.; McCammon J. A.; Doltsinis N. L.. Accelerating Chemical Reactions: Exploring Reactive Free Energy Surfaces Using Accelerated Ab Initio Molecular Dynamics. J. Chem. Phys. 2010, in press. [DOI] [PMC free article] [PubMed]
  17. Hamelberg D.; de Oliveira C. A. F.; McCammon J. A. Sampling of slow diffusive conformational transitions with accelerated molecular dynamics. J. Chem. Phys. 2007, 127 (15), 155102. [DOI] [PubMed] [Google Scholar]
  18. Voter A. F. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 1997, 78 (20), 3908. [Google Scholar]
  19. Car R.; Parrinello M. Unified Approach for Molecular-Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55 (22), 2471. [DOI] [PubMed] [Google Scholar]
  20. Car Parrinello Molecular Dynamics (CPMD); IBM Corp.: Zurich, Switzerland, 2008; http://www.cpmd.org/.
  21. a Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38 (6), 3098. [DOI] [PubMed] [Google Scholar]; b Lee C. T.; Yang W. T.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37 (2), 785. [DOI] [PubMed] [Google Scholar]
  22. Martyna G. J.; Tuckerman M. E.; Tobias D. J.; Klein M. L. Explicit reversible integrators for extended systems dynamics. Mol. Phys. 1996, 87 (5), 1117. [Google Scholar]
  23. Troullier N.; Martins J. L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 43 (3), 1993. [DOI] [PubMed] [Google Scholar]
  24. Martyna G. J.; Klein M. L.; Tuckerman M. Nose-Hoover Chains - the Canonical Ensemble Via Continuous Dynamics. J. Chem. Phys. 1992, 97 (4), 2635. [Google Scholar]
  25. a Squillacote M.; Sheridan R. S.; Chapman O. L.; Anet F. A. L. Spectroscopic Detection of Twist-Boat Conformation of Cyclohexane - Direct Measurement of Free-Energy Difference between Chair and Twist-Boat. J. Am. Chem. Soc. 1975, 97 (11), 3244. [Google Scholar]; b Offenbach J. L.; Fredin L.; Strauss H. L. Vibrational-Spectra of Twist-Boat Cyclohexane. J. Am. Chem. Soc. 1981, 103 (5), 1001. [Google Scholar]; c Gill G.; Pawar D. M.; Noe E. A. Conformational study of cis-1,4-di-tert-butylcyclohexane by dynamic NMR spectroscopy and computational methods. Observation of chair and twist-boat conformations. J. Am. Chem. Soc. 2005, 70 (26), 10726. [DOI] [PubMed] [Google Scholar]
  26. Ross B. D.; True N. S. Nmr-Spectroscopy of Cyclohexane Gas -Phase Conformational Kinetics. J. Am. Chem. Soc. 1983, 105 (15), 4871. [Google Scholar]
  27. Hura G.; Sorenson J. M.; Glaeser R. M.; Head-Gordon T. A high-quality x-ray scattering experiment on liquid water at ambient conditions. J. Chem. Phys. 2000, 113 (20), 9140. [Google Scholar]
  28. Modig K.; Pfrommer B. G.; Halle B. Temperature-dependent hydrogen-bond geometry in liquid water. Phys. Rev. Lett. 2003, 90 (7), 075502–1. [DOI] [PubMed] [Google Scholar]
  29. Eigen M.; Demaeyer L. Untersuchungen Uber Die Kinetik Der Neutralisation. Z. Elektrochem. 1955, 59 (10), 986. [Google Scholar]
  30. Berkowitz M.; Karim O. A.; McCammon J. A.; Rossky P. J. Sodium-Chloride Ion-Pair Interaction in Water - Computer-Simulation. Chem. Phys. Lett. 1984, 105 (6), 577. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct100605v_si_001.pdf (186.6KB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES