Transient Hoogsteen Base Pairs in Canonical Duplex DNA

Abstract

Sequence-directed variations in the canonical DNA double helix structure that retain Watson-Crick base-pairing play important roles in DNA recognition, topology, and nucleosome positioning. By using nuclear magnetic resonance relaxation dispersion spectroscopy in concert with steered molecular dynamics simulations, we have observed transient sequence-specific excursions away from Watson-Crick base-pairing at CA and TA steps inside canonical duplex DNA towards low-populated and short-lived A•T and G•C Hoogsteen base-pairs. The observation of Hoogsteen base-pairs in DNA duplexes specifically bound to transcription factors and in damaged DNA sites implies that the DNA double helix intrinsically codes for excited state Hoogsteen base-pairs as a means of expanding its structural complexity beyond that which can be achieved based on Watson-Crick base-pairing. The methods presented here provide a new route for characterizing transient low-populated nucleic acid structures, which we predict will be abundant in the genome and constitute a second transient layer of the genetic code.

Soon after its discovery¹, it was recognized that the DNA double helix could accommodate a range of conformations that retain Watson-Crick (WC) base-pairing². Sequence-directed variations in duplex DNA structure, shape, and flexibility have since been shown to play fundamental roles in biology including in the indirect readout of DNA sequences by recognition factors^3,4, nucleosome positioning^4,5, and formation of loops and other large-scale architectures⁶ involved in DNA packaging, replication, transcription, and recombination. DNA duplexes resiliently maintain WC base-pairing even when supercoiled and wrapped around histone octamers in nucleosomes⁷ and when adopting left-handed double-helical conformations known as Z-DNA⁸. Deviations from the WC base-pairing have so far only been observed in duplex DNA bound to proteins^9,10 and small molecule ligands^11,12 and in the context of damaged DNA^13,14, but never within naked canonical B-DNA duplexes.

Thus far, atomic resolution structural studies of the iconic DNA double helix have exclusively focused on its dominant, experimentally accessible, ground state conformation. Far less is known about other low-energy DNA conformations that may be sampled only transiently in solution. NMR relaxation dispersion experiments^15,16 provide a rare opportunity to detect and characterize such short-lived (<5 ms) and low-populated species (>0.1%), often referred to as “excited states”. This methodology has been widely used to characterize protein excited states that have been implicated in folding^15,16, recognition¹⁷, and catalysis¹⁸, culminating in the recent structure determination of a transient protein-folding intermediate¹⁹. Recent advances in carbon-based relaxation dispersion experiments combined with selective labeling schemes have addressed limitations that have hindered application of this methodology to nucleic acids, allowing detection of excited states in both RNA^20,21 and DNA^21,22. However, the structures of nucleic acid excited states remain elusive.

Relaxation dispersion reveals base-pair specific excited states in CA steps of duplex DNA

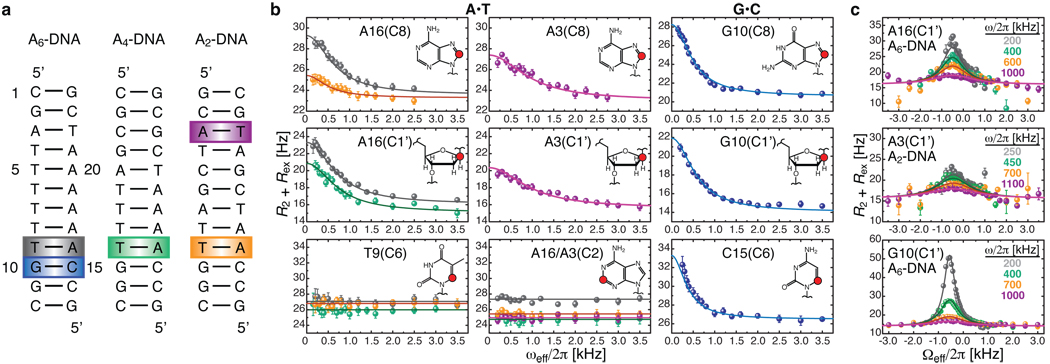
We used a recently introduced carbon R_1ρ relaxation dispersion NMR experiment that allows detection of excited states with enhanced timescale sensitivity²¹ to probe for the existence of excited states in canonical DNA duplexes (Fig. 1a). We uncovered chemical exchange processes directed towards excited states occurring specifically at A•T and G•C base-pairs in CA/TG steps (Fig. 1b), which together with TA steps are the most flexible dinucleotide steps in DNA and frequently the confluence point for local structural deformations²³. In particular, we observed significant R_1ρ relaxation dispersion, indicative of chemical exchange, at the base C8 and sugar C1’ carbons of the adenine and guanine residues, and for the C6 carbon of the cytosine residue. No relaxation dispersion was observed for the adenine base C2, the thymine residue, or the cytosine sugar C1’ sites (Fig. 1b, Supplementary Fig. 3). The exchange process is enhanced by longer 3’ neighboring A-tracts, modulated by positional context, and for the G•C base-pair, is highly pH dependent (Supplementary Fig. 2). A two-state analysis $(\mathrm{A}\underset{k_B}{\overset{k_A}{\rightleftarrows }}\mathrm{B})$ of the off-resonance relaxation dispersion data (Fig. 1c, Supplementary Fig. 2) revealed a single base-pair exchange process that is slightly faster for A•T versus G•C and that is directed towards minutely populated (p_B ~ 0.64 % and ~ 0.47 % for G•C and A•T, 26 °C) excited states that have exceptionally short lifetimes (τ_B = 1/k_B ~ 1.5 ms and ~0.3 ms for G•C and A•T, 26 °C), and that have downfield-shifted carbon chemical shifts (Δω_AB(C8) ~ 2.7 – 3.2 ppm, Δω_AB(C1’) ~ 3.1 – 3.7 ppm, and Δω_AB(C6) ~ 2.2 ppm, Supplementary Table 2).

Figure 1. Detection of base-pair specific excited states in CA/TG steps of duplex DNA.

a, DNA constructs containing varying length A-tracts with color-coded A•T and G•C base-pairs at CA/TG steps that show carbon chemical exchange. b, On-resonance ¹³C R_1ρ relaxation dispersion profiles for A•T (26.0 °C) and G•C (30.5 °C) showing CA/TG specific chemical exchange at purine base C8 and sugar C1’ and at cytosine base C6. Shown are the best base-pair global fits (solid line) to a two-state asymmetric exchange model (Supplementary Eq.1). c, Representative off-resonance relaxation dispersion profiles for corresponding C1’ sites and best global fits as in b. All error bars represent experimental uncertainty (one s.d.) estimated from mono-exponential fitting of duplicate sets of R_1ρ data.

Chemical shift and kinetic-thermodynamic assignment of excited state Hoogsteen base-pairs

What is the excited state encoded by CA/TG steps and detected by NMR relaxation dispersion? NMR imino proton exchange measurements^24,25 and computer simulations²⁶ have previously shown that WC base-pairs can spontaneously break open and access extrahelical conformations. While the forward exchange rates (k_A) measured by relaxation dispersion (~ 4 – 20 s⁻¹ at 26 °C, Supplementary Table 2) are within an order of magnitude of rates reported previously for base-pair opening (~ 40 – 400 s⁻¹ at 25 °C)²⁷, the excited states detected here are at least three orders of magnitude more populated (Supplementary Table 2) and point to more energetically favorable species. To obtain more insights into the excited state, we measured carbon R_1ρ relaxation dispersion as a function of temperature (Fig. 2a). We then used transition-state theory and van’t Hoff analysis to extract a complete thermodynamic-kinetic description of the two-state equilibria (Supplementary Table 5). Semi-logarithmic van’t Hoff plots revealed a linear dependence characteristic of a two-state process for A•T and G•C base-pairs (Fig. 2b). The analysis yielded activation free energies (~16 kcal/mol) and enthalpies (~12 – 26 kcal/mol) for the forward transition (Fig. 2c) that are comparable to values reported previously for base-pair opening (~14 – 25 kcal/mol and ~8 – 29 kcal/mol respectively)^27,28. Thus, the transition to the excited state entails disruption of stacking and hydrogen-bonding interactions in the WC base-pair. However, for both A•T and G•C, this loss in enthalpy is nearly entirely restored when the exited state is formed. In fact, the excited state is in part destabilized relative to the WC ground state by a less favorable entropy, implying a more “rigid” excited state conformation and counter to what would be expected for a flexible looped-out state.

Figure 2. Kinetic-thermodynamic analysis of ground-to-excited state transitions.

a, Representative on-resonance ¹³C R_1ρ relaxation dispersion profiles as a function of temperature for A16 (A₆-DNA and A₄-DNA), A3 (A₂-DNA), and G10 (A₆-DNA) C1’. b, Modified van’t Hoff plots showing temperature dependence of the forward (k_A) and reverse (k_B) rate constants for the two-site exchange in A•T and G•C base-pairs highlighted in Fig. 1a. Error bars represent experimental uncertainty (one s.d.) as determined from propagation of errors obtained from mono-exponential fitting of duplicate sets of R_1ρ data. c, Corresponding kinetic-thermodynamic profiles for exchange between the Watson-Crick (WC) ground state and the excited state (ES) via a transition state (‡), showing activation and net free energy (G), enthalpy (H), and entropy (TS) changes (referenced to 0).

Taken together, our data point to an excited state conformation whose creation requires complete disruption of WC base-pairs, but whose thermodynamic stability is comparable to that of a WC base-pair. One possibility is that the excited state represents an alternative base-pair. Here, the correlated nature of the exchange at purine C8 and C1’ nuclei and the large downfield carbon chemical shifts provides important clues. In particular, the magnitude and direction of Δω_AB(C8) and Δω_AB(C1’) are strongly indicative of an anti-to-syn transition, as deduced from a survey of carbon chemical shifts²⁹ and density functional theory (DFT) calculations³⁰. Remarkably, an anti-to-syn rotation of the adenine or guanine base results in creation of a Hoogsteen (HG) base-pair optimally stabilized by two hydrogen bonds (Fig. 3a). The HG G•C base-pair would require protonation of cytosine N3 (G•C⁺, pK_a(N3) ~4.2³¹), which can in turn explain the relaxation dispersion observed at cytosine C6 at neutral and acidic pH, and the downfield shifted excited state C6 chemical shift, as well as the pH dependence of dispersion measured at carbon sites in the G•C but not in the A•T base-pair (see Supplementary Discussion). HG base-pairs have widely been observed in non-canonical DNA structures, such as DNA triplexes and quadruplexes, where they are specifically recognized by proteins³². In a few cases, HG base-pairs have also been observed in duplex DNA containing alternating AT repeats³³ or in complex with ligands^11,12 and proteins, including the active site of DNA polymerase-ι³⁴ and a complex between TATA binding protein (TBP) and a mutant TATA-box DNA⁹, where HG G•C⁺ base-pairs are formed at near neutral pH. Indeed, the free energy differences measured between the ground and excited state (3.0 – 3.5 kcal/mol for A•T, 2.9 kcal/mol for G•C⁺) compare well with estimates for stability of HG base-pairs in an all-anti triplex relative to duplex WC base-pairs (3.2 – 3.7 kcal/mol for A•T, 3.1 – 4.2 kcal/mol for G•C⁺)³⁵. An excited-state HG base-pair can explain the lower enthalpy and lower entropy of the exited state relative to a base-pair open state. Its creation requires a ~ 180-degree base rotation around the glycosidic linkage and disruption of the WC base-pair, consistent with our measured transition state barriers. These excited state HG base-pairs may have evaded detection by prior solvent exchange measurements due to hydrogen-bond protection of the thymine imino proton in (A•T) and/or inaccessibility of the guanine imino proton in (G•C) in addition to slower exchange rates. For example, the observation of a non-hydrogen bonded G H1 resonance in a G(syn)•AH⁺(anti) mismatch base-pair at 20 °C inside a DNA duplex³⁶ supports the lower exchange rates with solvent.

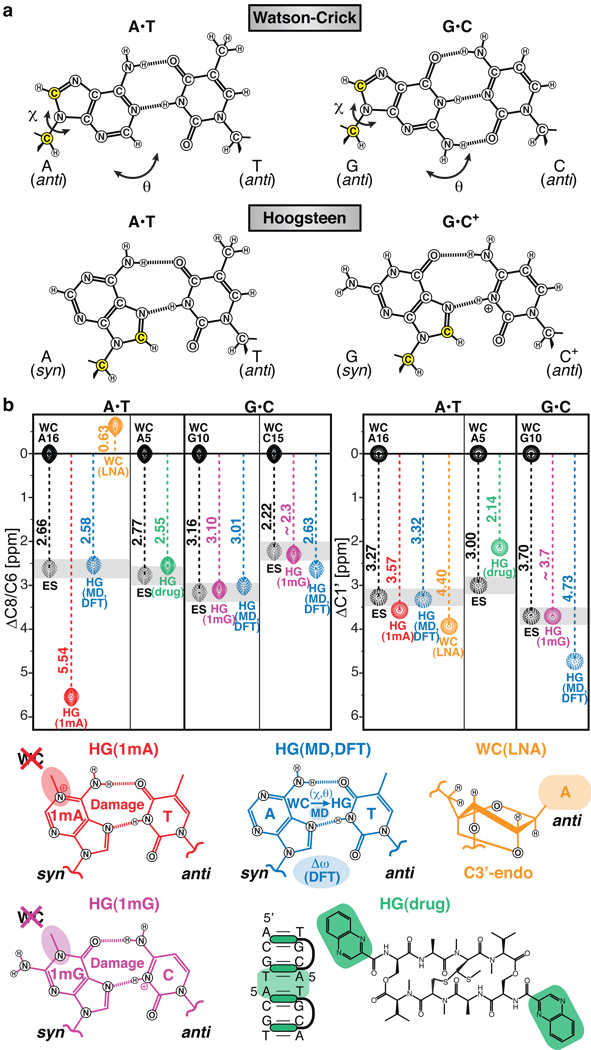
Figure 3. Chemical shift assignment of excited state Hoogsteen base-pairs.

a, Chemical structures for WC and HG A•T and G•C⁺ base-pairs. The HG geometry can be achieved by purine rotation around the glycosidic bond (χ) and base-flipping (θ), affecting simultaneously C8 and C1’ (yellow). b, Depiction of C8 and C1’ chemical shifts relative to WC for the excited state (ES, grey); an N1-methyladenine modified A₆-DNA (HG(1mA), red), an N1-methylguanine modified A₆-DNA (HG(1mG), violet), and an echinomycin-bound DNA (HG(drug), green) forming HG base-pairs; a simulated A16•T9 HG base-pair in A₆-DNA (HG(MD), blue); a C3’-endo locked A₆-DNA (WC(LNA), orange); and representative cartoons.

Trapping HG base-pairs in duplex DNA

To further test for the existence of HG base-pairs, we used chemical modifications to trap the excited state HG base-pair within duplex DNA. This allowed us to directly compare the carbon chemical shift signatures of the trapped HG base-pair with those measured for the excited state using relaxation dispersion. By installing an N1-methylated adenine (1mA), which is a common DNA lesion known to sterically impair WC base-pairs and favor HG base-pairs^13,37 at the CA step, we trapped the HG A•T base-pair in the A₆-DNA duplex as confirmed by analysis of NOE connectivity and proton chemical shifts (Supplementary Fig. 5). Though never observed previously, we also successfully trapped an HG G•C⁺ base-pair using instead the structural analog to 1mA – an N1-methylated guanine (1mG) – at the same CA step (Supplementary Fig. 5). The ability to independently trap HG A•T or G•C⁺ base-pairs is consistent with the relaxation dispersion data showing that transitions to excited state A•T and G•C HG base-pairs within CA steps are semi-independent of one another. Strikingly, the differences in carbon chemical shift measured between modified and unmodified DNA were in excellent agreement with the chemical shift differences measured between the ground and excited state by relaxation dispersion (Fig. 3b). The noticeably downfield chemical shift observed for the trapped 1mA versus the unmodified excited state HG base-pair could be attributed to changes in the electronic environment arising from introduction of the methyl group and positive charge (not present in 1mG), as supported by DFT calculations (Supplementary Information) and possibly from slight differences in the HG geometry. Conversely, resonances that showed small differences in carbon chemical shift between modified and unmodified constructs (Supplementary Table 4) exhibited little to no carbon chemical exchange (Supplementary Fig. 3). Our data rule out other non-canonical base-pairing modes involving pyrimidine base rotation or a repuckered sugar conformation from C2’-endo to C3’-endo, which yields upfield rather than downfield nucleobase carbon chemical shifts (Fig. 3b, Supplementary Fig. 4). Thus, comparison of known HG ground state chemical shifts with the excited state chemical shifts provides strong support for its assignment as an HG base-pair.

As an inverse experiment, we asked whether TA steps, which have also been observed to form HG base-pairs in duplex DNA bound to small molecule ligands^11,12, exhibit the characteristic HG exited state. We measured carbon relaxation dispersion data for a palindromic DNA sequence, which has previously been shown to form tandem A•T HG base-pairs in solution³⁸ when in complex with the bis-intercalating antibiotic echinomycin (Fig. 3b). Strikingly, we observe the same chemical exchange pattern in the TA step and carbon chemical shift differences between ground and exited state that are in excellent agreement with the differences between the free (WC) DNA and drug-bound (HG) DNA (Fig. 3b, Supplementary Fig. 6). Thus, excited state HG base-pairs are not restricted to CA/TG steps but also include TA steps, and they can be conformationally captured by recognition factors. In fact, our recent observation of chemical exchange in a TA step containing an 1,N6-ethenoadenine adduct²¹ could potentially be explained by transient anti-to-syn excursions as in the HG base-pair. Moreover, the weaker binding affinity of TBP to an HG-containing mutant TATA box, where a WC base-pair would not be tolerated, versus the wild-type sequence with all-WC base-pairing (ΔΔG ~3 kcal/mol)³⁹ could be attributed to conformational selection of a low-populated HG base-pair and could be further correlated with transcriptional regulation of gene repression⁴⁰.

NMR-informed simulations of the WC-to-HG transition

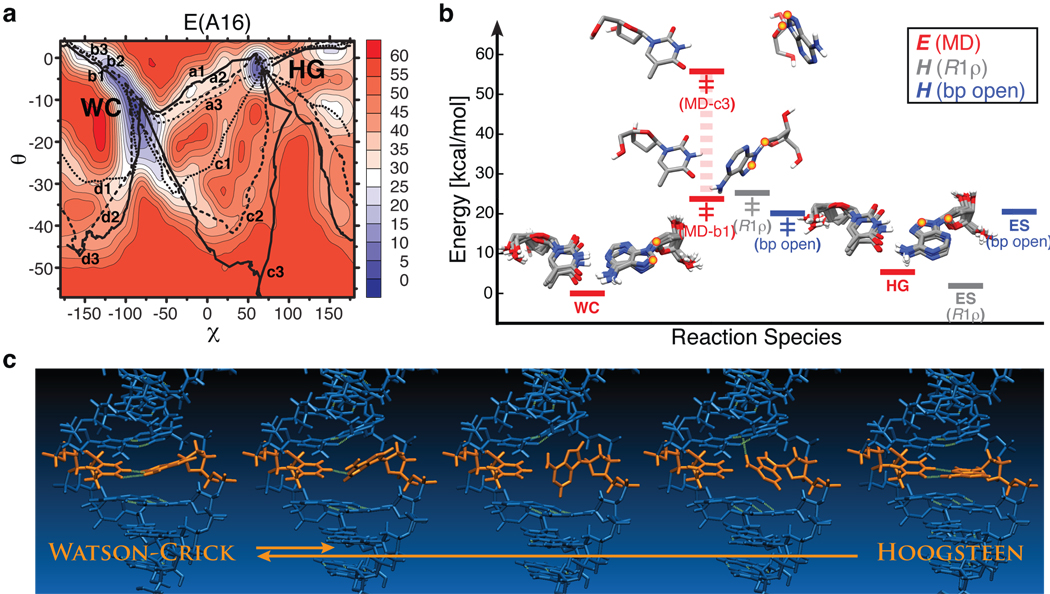
To assess the energetic and stereochemical feasibility of the proposed WC-to-HG transition, as well as obtain insights into the transition pathway, we used conjugate peak refinement (CPR)⁴¹ methods to simulate multiple transition pathways between WC and excited state HG base-pairs that sample various glycosidic (χ) and base opening (θ) angles (Fig. 4a). CPR trajectories for A16•T9 and G10•C15 in A₆-DNA showed smooth WC-to-HG transitions via anti-to-syn purine rotation around χ accompanied by minor adjustments in the complementary pyrimidine residue and neighboring WC base-pairs (Fig. 4a, Supplementary Fig. 7 and Movies). Optimal pathways feature purine base-flips at low base-pair opening angles into the major groove and transition states, which require complete disruption of WC base-pairing – this is also observed experimentally by relaxation dispersion – in which the purine base is near-orthogonal to its pyrimidine partner. This unusual geometry is well accommodated by the rather large inter-base-pair spacing in the B-form helix (i.e. base-pair rise ~3.3 Å) and its ability to mold without loss of other WC base-pairing. Although a large spread of transition barriers are sampled, the minimal energy barriers and net energy changes are within 2 kcal/mol of NMR-derived ensemble enthalpy terms (Fig. 4b). The final HG state for G10•C15 yields generally lower relative CPR energies – it is observed to adopt variable syn-guanine geometry, with either one or no optimal hydrogen bonds to the cytosine due to the lack of N3 protonation that stabilizes the ideal HG base-pair, but on occasion forming an intraresidue hydrogen bond to a backbone oxygen (Supplementary Movie 2).

Figure 4. Watson-Crick to Hoogsteen base-pair transition simulations.

a, Pseudo-free-energy (E, kcal/mol) contour plots as a function of (χ, θ) pairs for A16•T9 obtained from multiple CPR trajectories (a–d). b, Initial WC and final exited-state (ES) HG structures and representative lowest-energy (b1) and highest-energy (c3) transition state (‡) structures of A16•T9 illustrating the span of CPR transition barriers, and their relative potential energies (averaged for WC and HG) compared with enthalpies (H) derived from NMR R_1ρ relaxation dispersion for chemical exchange or NMR imino proton exchange for A•T base-pair opening²⁷. c, Snapshots from a representative CPR transition pathway (a1) for A16•T9.

The carbon chemical shifts computed for the WC and lowest-energy HG geometries using DFT also exhibited the characteristic downfield-shifted Δω_AB(C8) and Δω_AB(C1’) observed experimentally by relaxation dispersion (Fig. 3b, Supplementary Table 4). Conversely, the predicted chemical shifts revealed little and/or random variations between WC and HG base-pairs for adenine C2, thymine C6, and cytosine C1’, consistent with the lack of observable relaxation dispersion at those sites (Supplementary Fig. 8). Comprehensive DFT calculation of carbon chemical shifts for conformers sampled in various pathways between WC and HG states (Supplementary Fig. 8) yielded a small number of geometries that match the measured excited-state chemical shifts, but that could readily be excluded because they involve barrierless transitions and/or represent high-energy structures that disagree with experimentally derived enthalpies.

Our data strongly argue that the DNA double helix codes for a pre-existing WC-to-HG equilibrium, with HG base-pairs representing an accessible and energetically competent alternative to WC base-pairing that present very distinct electrostatic and hydrophobic signatures. This makes it possible to trap HG base-pairs by interactions with cellular triggers, thereby expanding the structural and functional diversity of the double helix beyond that which can be achieved based on an alphabet of only WC base-pairing. There are several examples of transcription factors including TBP⁹ and p53 tumor suppressor¹⁰ that specifically recognize HG base-pairs embedded in different WC contexts, where the modulation in binding affinity, conceivably, by an HG base-pair could even be correlated with an essential biological function⁴⁰. In addition, HG base-pairs are often trapped by oxidative and alkylation lesions¹⁴, providing unique recognition signals for repair enzymes in search of damage sites in a sea of undamaged DNA. Transient formation of HG base-pairs inside B-DNA may also serve to promote non-canonical structures such as contiguous HG motifs, especially in tandem CA and TA repeats, or more dramatic transformations to Z-DNA⁴², and may well exist in much greater abundance for native genomic DNA, which is under torsional stress in the cellular environment. The methods presented here provide a general strategy for detecting and characterizing excited states in DNA and RNA, which we predict will be abundant in the genome and constitute another transient layer of the genetic code.

METHODS SUMMARY

Detailed methods on DNA sample preparation and assignment, NMR relaxation dispersion data collection and analysis, MD/CPR simulations, and DFT chemical shift calculations can be found in Methods.

Full Methods and associated references are available in the online version of the paper at www.nature.com/nature.

METHODS

Preparation and NMR resonance assignment of unlabeled and ¹³C/¹⁵N-labeled DNA

Isotopically labeled DNA dodecamers (Fig. 1a) were synthesized by in vitro primer extension using a template hairpin DNA (IDT, Inc.), Klenow fragment DNA polymerase (NEB, Inc.), and uniformly ¹³C/¹⁵N-labeled dNTPs (Isotec, Sigma-Aldrich). Single-stranded DNA products were purified by 20% denaturing polyacrylamide gel electrophoresis (PAGE), isolated by passive elution and desalted on a C18 reverse-phase column (Sep-pak, Waters). Oligonucleotides were lyophilized and resuspended in NMR buffer (15 mM sodium phosphate pH 6.8, 25 mM sodium chloride, 0.1 mM EDTA, 10% D₂O). Complementary oligonucleotides were annealed at an equimolar ratio typically at 0.5–1.0 mM for NMR studies. Unlabeled DNA oligonucleotides were purchased from IDT, Inc. (A₂-DNA, A₄-DNA, A₆-DNA in Fig. 1a, and E-DNA in Fig. S6), Exiqon A/S (A₆-DNA^A16LNA and A₂-DNA^A16LNA in Fig. S4) and Midland Certified, Inc. (A₆-DNA^1mA16 and A₆-DNA^1mG10 in Fig. S5). Unlabeled DNA constructs including equivalent samples to ¹³C/¹⁵N-labeled DNA were prepared as described²¹ at 2.0–4.0 mM concentrations and assigned using conventional ¹H-¹H NOESY in 10% D₂O at 5 °C and/or 26 °C. The 2:1 complex between E-DNA and echinomycin (Selleck Chemicals) was prepared as previously described³⁸. All NMR experiments were performed on a Bruker Avance 600 MHz NMR spectrometer equipped with a 5mm triple-resonance cryogenic probe.

Selective ¹³C R_1ρ relaxation dispersion

Rotating frame (R_1ρ) relaxation dispersion profiles were measured at a single field (14.1 T) using a selective carbon experiment with a 1D acquisition scheme²¹ that extends the sensitivity to chemical exchange into millisecond timescales relative to conventional 2D relaxation dispersion methods. On-resonance data were recorded at variable (100 to 3500 Hz) effective spin-lock field strength (ω_eff) (Supplementary Table 1 and 3) for various sites in ¹³C/¹⁵N-labeled and unlabeled DNA constructs. For ¹³C/¹⁵N-labeled DNA samples (Supplementary Fig. 2) and E-DNA octamer (Supplementary Fig. 6), off-resonance dispersion data were collected in a temperature dependent manner at various spinlock offset frequencies (Ω_eff) and at three to four different spinlock powers (ω) (Supplementary Table 1 and 3). In each case, the following relaxation delays were used: {0, 4, 8, 12 (2X), 16, 20, 26, 32 (2X) ms} for C2/C6/C8 and {0, 4, 8, 12 (2X), 18, 26, 34, 42 (2X) ms} for C1’ in ¹³C/¹⁵N-labeled DNA constructs; {0, 40(2X) ms} for C8 and {0, 48(2X) ms} for C1’ at 17 °C, {0, 42(2X) ms} for C8 (17.0 °C) and {0, 60(2X) ms} for C1’ at 26 °C in E-DNA; {0, 30(2X) ms} for C8 (17.0 °C) in A₆-DNA^A16LNA. Data points corresponding to Hartmann-Hahn matching conditions were omitted from the data fits as previously described²¹. Data were processed using nmrPipe⁴³ and the effective transverse relaxation rates (R_2eff = R₂ + R_ex) were computed by fitting the resonance intensities with monoexponential decays using Mathematica 6.0 (Wolfram Research, Inc., Champaign, IL).

Measured relaxation dispersion profiles with on- and off-resonance data were fit by Eq.1 (below) that assumes a two-state equilibrium $(\mathrm{A}\underset{k_B}{\overset{k_A}{\rightleftarrows }}\mathrm{B})$ with asymmetric population distributions (p_A ≫ p_B)⁴⁴ using Mathematica 6.0 (Wolfram Research, Inc., Champaign, IL)

$$R_{1\rho }=R_1{\text{cos}}^2\theta +R_2{\text{sin}}^2\theta +{\text{sin}}^2\theta \frac{p_A{p}_B\mathrm{\Delta }{\omega }_{\mathit{\text{AB}}}^2{k}_{\mathit{\text{ex}}}}{{\mathrm{\Omega }}_B^2+{\omega }_1+k_{\mathit{\text{ex}}}^2}$$ (1)

, where R₁ and R₂ are the intrinsic longitudinal and transverse relaxation rates respectively (assumed to be identical for A and B species), Ω is the resonance offset from the spinlock carrier, ω₁ is the spinlock strength; Ω= tan(ω₁/ Ω_ave), Δω_AB = Ω_B - Ω_A, Ω_ave = p_AΩ_A - p_BΩ_B, where p_A (p_B) is the major (minor) state fractional population (p_A + p_B = 1); k_ex = k_A + k_B is the exchange rate constant for a two-state equilibrium, where k_A = p_Bk_ex and k_B = p_Ak_ex are the forward and reverse rate constants respectively. Similar results were obtained when fitting relaxation dispersion profiles against more complex two-state exchange models including the Laguerre approximation⁴⁵ that do not assume a skewed population distribution (data not shown) and statistical analysis implied that application of the more complex model to extract exchange parameters here was not justified. Temperature-dependent data for base/sugar resonances within the same nucleotide or base-pair were fit individually and globally with shared parameters (k_ex and p_B for each temperature) (Supplementary Table 2 and 3). The best-fit model was assessed using F-test (data not shown), which uses chi-square (χ²) and F-distribution analysis to determine the feasibility of a complicated model (i.e. individual fits) versus a more simple model (i.e. shared-parameter fits) nested inside the first model. The chemical shift difference Δω_AB was assumed to be invariant over the narrow temperature range investigated. On-resonance R_1ρ profiles were fit by a simplified two-state fast exchange expression⁴⁴ (k_ex ≫ Δω_AB):

$$R_{1\rho }=R_2+R_{\mathit{\text{ex}}}=R_2+\frac{{\mathrm{\Phi }}_{\mathit{\text{ex}}}{k}_{\mathit{\text{ex}}}}{{\omega }_1+k_{\mathit{\text{ex}}}^2};{\mathrm{\Phi }}_{\mathit{\text{ex}}}=p_A{p}_B\mathrm{\Delta }{\omega }_{\mathit{\text{AB}}}^2$$ (2)

, where all parameters are as described above.

Thermodynamic Analysis

The observed temperature dependence of the forward (k_A) and reverse (k_B) rate constants (Supplementary Table 2) was fit by a modified van’t Hoff equation that accounts for statistical compensation effects and assumes a smooth energy surface²⁷:

$$\text{ln}\left(\frac{k_i(T)}{T}\right)=\text{ln}\left(\frac{k_B\kappa }{h}\right)-\frac{\mathrm{\Delta }{G}_i^T(T_{\mathit{\text{hm}}})}{{\mathit{\text{RT}}}_{\mathit{\text{hm}}}}-\frac{\mathrm{\Delta }{H}_i^T(T_{\mathit{\text{hm}}})}{R}\left(\frac{1}{T}-\frac{1}{T_{\mathit{\text{hm}}}}\right)$$ (3)

, where k_i (i = A, B) is the rate constant, $\mathrm{\Delta }{G}_i^T\mathrm{\text{and}}\mathrm{\Delta }{H}_i^T$ are the free energy and enthalpy of activation respectively, R is the universal gas constant, T is temperature, and T_hm is the harmonic mean of the experimental temperatures computed as $T_{\mathit{\text{hm}}}=n/{\displaystyle \sum _{i=1}^n(1/T_i)}$; k_B is Boltzmann’s constant, h is Plank’s constant, κ is the transmission coefficient (assumed to be 1) in the pre-exponential factor of Eyring’s theory. The entropy of activation $(\mathrm{\Delta }{\mathrm{S}}_i^T)$ was calculated as follows:

$$\mathrm{\Delta }{S}_i^T=\frac{\mathrm{\Delta }{H}_i^T-\mathrm{\Delta }{G}_i^T(T_{\mathit{\text{hm}}})}{T_{\mathit{\text{hm}}}}$$ (4)

Semi-logarithmic plots are included in Fig. 2b and best-fit thermodynamic parameters are reported in Supplementary Table 5.

An alternative interpretation of the thermodynamic parameters is given by the phenomenological Ferry law^46,47, which incorporates a lower energy barrier with a rough enthalpic surface:

$$\text{ln}(k_i)=\text{ln}C-\frac{\mathrm{\Delta }{H}_i^T}{\mathit{\text{RT}}}-\frac{<H_i^2>}{{(\mathit{\text{RT}})}^2}$$ (5)

, where C is a constant, where $<H_i^2{>}^{1/2}$ represents the enthalpy due to ruggedness of the barrier. The maximum $<H_i^2{>}^{1/2}$ values were calculated by taking the smooth Arrhenius-like enthalpic barrier to be vanishing $(\mathrm{\Delta }{H}_i^T=0)$ and are reported in Supplementary Table 4.

Molecular dynamics simulations of WC-to-HG base-pair transition pathways

An initial duplex DNA in standard B-form with Watson-Crick (WC) base-pairing corresponding to A₆-DNA was generated using 3DNA⁴⁸. Hoogsteen (HG) base-pairs were generated at A16•T9, A3•T22, and G10•C15 positions using known X-ray coordinates^49,50, where the purine adopts a syn conformation, while the complementary pyrimidine retains an anti conformation (see Fig. 3a). Initially, all conformers with WC or HG base-pairing were equilibrated through a series of energy minimizations using the Adopted Basis Newton-Raphson (ABNR) algorithm. Canonical (NVT) ensemble MD were performed with the CHARMM27 all-atom force field⁵¹ and the generalized Born molecular volume (GBMV) implicit solvation model (GBMV II)^52–54. The velocity-Verlet algorithm was used with a time step of 2 fs. A temperature of 300 K was kept constant with a Nose-Hoover thermostat^55,56. The cutoff for non-bonded list generation was set to 21 Å, the cutoff for non-bonded interactions was set to 18 Å, and the onset of switching for non-bonded interactions was set to 16 Å. The SHAKE algorithm was used to constrain vibrations of covalent bonds to hydrogen atoms involved. To conserve the duplex DNA structure during pre-equilibration, flat-bottom distance restraints were applied, which prevented the hydrogen-bond donor from moving more than 2.0 Å. The simulations ran for a total of 6.0 ns (Supplementary Fig. 7).

For the collection and analysis of equilibrium data, the initial 1 ns simulation data were discarded. We constructed a 2D free-energy map using the following two reaction coordinates: the DNA backbone root-mean-square deviation (rmsd) and the potential energy value; the minimization of this approximate free energy surface permitted us to choose the most populated structure in the canonical ensemble. [F=−k_BT ln P(X,Y), X and Y are reaction coordinates, k_B is Boltzmann’s constant, T is the absolute temperature (Supplementary Fig. 7)]. The DNA backbone rmsd is defined by selecting the P-O5’-C5’-C4’-C3’-O3’ atoms. The reference structure was a standard B-form DNA (Twist angle Ω = 36.0°, Rise per base-pair along helix axis = 3.3 Å) without minimization. In order to probe the transition pathway between a WC and a HG base-pair conformer, we used the conjugate peak refinement (CPR) method⁴¹ applicable to the study of complex isomerization reactions including allosteric transitions in proteins and more general conformational changes in macromolecules. The resulting paths follow the adiabatic energy surface without applying any constraints and path-points between saddle-points ensure the continuity of the path, not necessarily constrained to find the absolute bottom of the energy valley. The initial WC-to-HG pathways were generated using a targeted molecular dynamics method that applied a holonomic constraint, which decreased gradually the rmsd to the final target structure. In each CPR cycle, a heuristic procedure was used to modify the path by improving, removing, or inserting one path-point, so that the new path avoids the maximum energy peak. Finally, to refine the CPR path further, we used a synchronous chain minimization method of all path-points, under the constraint that the points move within hyper-planes orthogonal to the path. The most populated structures with the WC base-pair or with the HG base-pair from the normal MD simulations corresponded to “reactant” and “product” wells, respectively, on the energy surface. In order to sample a wider range of possible transition pathways, additional putative intermediates that differed in either the flip-over or flip-out were added by modifying, respectively, the glycosidic angle, χ (O4’-C1’-N9-C4), of the purine base and a center-of-mass pseudo-dihedral angle, θ²⁸, which describes the extent to base opening. CPR data is reported in Supplementary Fig. 7.

Density functional theory (DFT) calculations of carbon chemical shifts

DFT chemical shift calculations were conducted on a high-performance computing cluster using Gaussian 03⁵⁷. DNA conformations of the target A•T and G•C base-pair that represent a range of (χ, θ) pairs were selected from each simulated WC-to-HG transition pathway and capped by 3’OH/5’OH (UCSF Chimera⁵⁸) for DFT calculations (Supplementary Fig. 8) without further geometry optimization. NMR ¹³C chemical shift calculations were conducted using the GIAO method with the B3LYP/6-311+G(2d,p) basis set. The isotropic carbon chemical shifts (σ_ISO) were referenced to TMS (σ_TMS = 182.759) using the relationship δ_ISO = σ_TMS - σ_ISO, where the structure of TMS was optimized at the same level of theory. Computed carbon chemical shifts were referenced to the most stable WC conformer in a given transition pathway and matched with NMR excited-state chemical shift differences (Δω_AB) in Supplementary Table 4. For benchmarking, similar calculations were performed on single guanosine nucleotides with anti and syn glycosidic conformations from crystal structures of Oxytricha Nova telomeric G-quadruplex (5’ (G)₄(T)₄(G)₄; PDB ID: IJPQ, 1JRN, 2GWQ, 2GWE, and 2NPR) with added hydrogen atoms (UCSF Chimera⁵⁸) and no further geometry optimization, and compared to observed NMR C8 chemical shifts for the same G-quadruplex (courtesy of Dr. Michelle Gill and Dr. Patrick Loria) (Supplementary Fig. 8).