Exact iterative reconstruction for the interior problem

Abstract

There is a trend in single photon emission computed tomography (SPECT) that small and dedicated imaging systems are becoming popular. For example, many companies are developing small dedicated cardiac SPECT systems with different designs. These dedicated systems have a smaller field of view (FOV) than a full-size clinical system. Thus data truncation has become the norm rather than the exception in these systems. Therefore, it is important to develop region of interest (ROI) reconstruction algorithms using truncated data. This paper is a stepping stone toward this direction. This paper shows that the common generic iterative image reconstruction algorithms are able to exactly reconstruct the ROI under the conditions that the convex ROI is fully sampled and the image value in a sub-region within the ROI is known. If the ROI includes a sub-region that is outside the patient body, then the conditions can be easily satisfied.

1. Introduction

The interior problem in computed tomography considers the situation that the projection data are only available to cover a region of interest (ROI) within the support of the object. The aim is to reconstruct the ROI with these truncated projections.

The interior problem has received attention of many researchers. Many researchers, for example, Natterer (1986), Maass (1992), Hamaker et al (1980) and Louis and Rieder (1989), studied the nature of the interior problem. They concluded that the interior problem is stable and one can reconstruct up to an additive almost constant function in a fairly stable way.

More recent results indicate that if additional information about the ROI is available, the interior problem is exactly solvable (Defrise et al 2006, Ye et al 2007, 2008, Kudo et al 2008). The main idea is to use the analytic continuation technique to extend the known information to the entire ROI. The numerical implementation of the analytic continuation is the iterative POCS (projection onto convex sets) technique. The image is reconstructed by first taking the derivative of the projection data; backprojecting the differentiated data into the ROI; estimating the Hilbert transform in the ROI with the iterative POCS technique and some prior information of the image in a sub-region of the ROI; and finally, performing the finite one-dimensional Hilbert transform to obtain the ROI image.

In single photon emission computed tomography (SPECT), iterative algorithms, especially, the maximum likelihood expectation maximization (ML-EM) and ordered subset expectation maximization (OS-EM), are most popular in image reconstruction. We have previously investigated the general performance of an iterative algorithm using truncated projection data (Zhang and Zeng 2007). In this paper, we investigate whether the iterative image reconstruction algorithm is able to exactly solve the interior problem if additional knowledge of the image in a sub-region of the ROI is given.

2. Theory

2.1. Attenuation-less (Radon transform) case

Without loss of generality, we formulate a two-dimensional (2D) problem as follows. The 2D object f(x, y) is compact and has a support of a unit disk. That is, f(x, y) = 0, if x² + y² > 1. A circular ROI has a radius r with 0 < r < 1. A line integral of the object=f(x, y) is denoted as p(θ, s):

$$p(\theta ,s)={\int }_{-\infty }^{\infty }f(s\overrightarrow{\theta }+t{\overrightarrow{\theta }}^{\perp })\mathrm{d}t$$ (1)

where the direction is defined as $\overrightarrow{\theta }=(\text{cos}\theta ,\text{sin}\theta )$.

For an interior problem, p(θ, s) is only available for |s| ≤ r. In other words, every line integral of f(x, y) passing through the ROI is measured and the lines do not pass through the ROI are not measured. If the imaging geometry is not parallel, we can always rebin the data into parallel-beam format to satisfy (1). Since this paper only deals with iterative reconstructions, the imaging geometry is not a concern as long as all line integrals passing through the ROI are measured. We also assume that f(x, y) is known in a sub-region Ω of the ROI. Without loss of generality, this sub-region is defined as x² + y² < ρ² with 0 < ρ < r.

Next, we formulate the iterative algorithm solution of the interior problem with f(x, y) known in a sub-region Ω. To make our analysis tractable, we only consider the noiseless situations where all projections are exact and consistent. We assume that the iterative algorithm converges to a unique zero solution (i.e., all image pixel values are zero) in the ROI if measured projections are zero. We also assume that the iterative algorithm has already converged to a solution f₁(x, y) that satisfies all measurements, that is,

$$p(\theta ,s)={\int }_{-\infty }^{\infty }{f}_1(s\overrightarrow{\theta }+t{\overrightarrow{\theta }}^{\perp })\mathrm{d}t$$ (2)

for |s| ≤ r, and the solution matches the given image values in Ω, that is, f₁(x, y) = f(x, y) in Ω. We are going to prove that f₁(x, y) = f(x, y) holds for the entire ROI, x² + y² < r².

Let

$$f_2(x,y)=f(x,y)-f_1(x,y),$$ (3)

and we will prove that f₂(x, y) = 0, if (x, y) is in the ROI, that is, x² + y² < r².

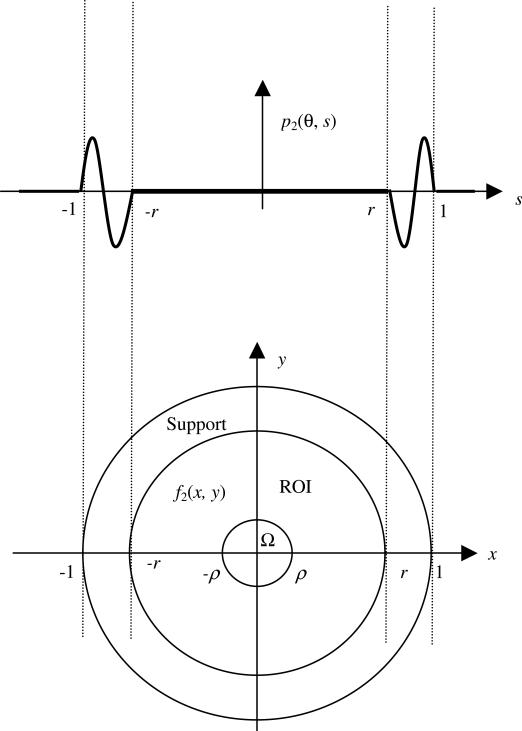
According to the projection definition (1), let the projection of f₂ (x, y) be p₂(θ, s), as illustrated in figure 1. Then p₂(θ, s) = 0, for |s| < r, because both f and f₁ satisfy the measurements according to (1) and (2).

Figure 1.

In the image domain, the objects have a finite support which is assumed to be a unit disk. The ROI is a disk with a radius r. In the sub-region Ω, which is a disk of radius ρ, the object values are known.

We also have p₂(θ, s) = 0, for |s| > 1, because the finite support of the object is a unit disk.

Now we apply the well-known filtered backprojection (FBP) algorithm (i.e. the Radon inversion formula) to reconstruct f₂(x, y) from p₂(θ, s) as follows:

$$f_2(x,y)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-1}^1\frac{1}{s-(x\text{cos}\theta +y\text{sin}\theta )}\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (4)

If we are only interested in reconstructing the image values in (−r, r) on the x-axis, (4) becomes

$$f_2(x,0)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-1}^1\frac{1}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (5)

Next, we decompose the right-hand side of (5) into two terms:

$$f_2(x,0)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-r}^r\frac{1}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s+\frac{1}{4{\pi }^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{r<\mid s\mid <1}\frac{1}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (6)

The first term on the right-hand side of (6) is zero because p₂(θ, s) = 0 when |s| < r. Let us denote the second term on the right-hand side of (6) as h(x) for |x| < r:

$$h\left(x\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{r<\mid s\mid <1}\frac{1}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (7)

In (7), |x| < r and |s| > r; thus 1/(s − x cos θ) is differentiable of any order. If we replace x by the complex variable z in (7), then h(z) defined by (7) is an analytic function in the entire z-plane with cuts along [−1, −r] and [r, 1], provided that ∂p₂/∂s is absolutely integrable, which is usually satisfied in practice.

It is known that for any x₀ in (−ρ, ρ), f₂ (x₀, 0) = 0 because f₁(x, y) = f(x, y) in Ω. From (7), h(x) = 0 in (−ρ, ρ). Using analytic continuation, we have h(x) = 0 in (−r, r). Thus, f₂(x, 0) = 0 in (−r, r).

Since the x-axis is arbitrarily chosen (that is, any line passing through the origin can be the x-axis), f₂(x, y) = 0 in the entire ROI, x² + y² < r². In other words, f₁(x, y) = f(x, y) holds for the entire ROI which means that we have an exact reconstruction on the ROI.

This analytic continuation trick was first used in ROI tomography by Defrise et al (2006). The above proof, in fact, follows step-by-step the proof in Defrise et al (2006). In Defrise's work, a special finite Hilbert transform was used in the proof. People may have an impression that in order to obtain an exact ROI reconstruction with truncated data, the finite Hilbert transform must be used. This paper shows that this is not the case. In fact, any FBP (filtered backprojection) algorithm can be used for the proof.

We must point out that the above proof does not imply that the ROI image reconstruction is via the FBP algorithm and analytic continuation. The image is reconstructed by a generic iterative algorithm such as the ML-EM or OS-EM. The FBP algorithm and analytic continuation are only used to prove that the exact solution can be obtained.

In this paper, we have made some very strong assumptions. The projection data are assumed to be consistent without noise. After the application of an iterative image reconstruction algorithm, all projections are assumed to be exactly satisfied. The result of the iterative reconstruction is assumed to be the only smooth image that satisfies all projections and matches the given image values in the sub-region in the ROI. This last assumption implies that analytic continuation has automatically been performed, because analytic continuation enforces smoothness.

2.2. Uniform attenuation (exponential Radon transform) case

In this section, we consider a simple SPECT imaging situation where the detector is at the center of rotation and the attenuation coefficient is a constant μ. We define the exponential Radon transform as

$$p(\theta ,s)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mu t}f(s\overrightarrow{\theta }+t{\overrightarrow{\theta }}^{\perp })\mathrm{d}t.$$ (8)

We now make the same assumptions as in section 2.1. The projection p(θ, s) is only available for |s| ≤ r. All weighted line integrals (8) passing through the ROI are measured. We also assume that f(x, y) is known in a sub-region Ω, x² + y² < ρ², 0 < ρ < r, of the ROI.

We also assume that the iterative algorithm has already converged to a solution f₁(x, y), all measurements are satisfied, that is,

$$p(\theta ,s)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{\mu t}{f}_1(s\overrightarrow{\theta }+t{\overrightarrow{\theta }}^{\perp })\mathrm{d}t.$$ (9)

for |s| ≤ r, and the solution matches the given image values in Ω, that is f₁(x, y) = f(x, y) in Ω. We are going to prove that f₁(x, y) = f(x, y) holds for the entire ROI, x² + y² < r².

Let

$$f_2(x,y)=f(x,y)-f_1(x,y).$$ (10)

According to the weighted projection definition (8), let the weighted projection of f₂ (x, y) be p₂(θ, s), as illustrated in figure 1. Then p₂(θ, s) = 0, for |s| < r, because both f and f₁ satisfy the measurements according to (8) and (9).

Now we apply Tretiak and Metz's FBP algorithm (Tretiak and Metz 1980) to reconstruct f₂ (x, y) from p₂(θ, s) as follows:

$$f_2(x,y)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\mathrm{e}}^{-\mu t}\mathrm{d}\theta {\int }_{-1}^1\frac{\text{cos}\left(\mu (s-(x\text{cos}\theta +y\text{sin}\theta ))\right)}{s-(x\text{cos}\theta +y\text{sin}\theta )}\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s$$ (11)

where t = −x sin θ + y cos θ. This expression is new and is equivalent to Tretiak and Metz's original expressions. If we are only interested in reconstructing the image values in (−r, r) on the x-axis, then (11) becomes

$$f_2(x,0)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\mathrm{e}}^{\mu x\text{sin}\theta }\mathrm{d}\theta {\int }_{-1}^1\frac{\text{cos}(\mu s-\mu x\text{cos}\theta )}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (12)

The differences between the FBP algorithm (4) for the Radon transform and the FBP algorithm (11) for the exponential Radon transform are that (11) has an exponential weighting factor in the backprojector, and the Hilbert transform kernel 1/s has an extra cosine function. The effect of this cosine function is to shift the Fourier transform of 1/s to the left and to the right in the frequency axis. The combination of the left and right shifted versions results in a notch in the low frequency region.

As in section 2.1, we decompose the right-hand side of (12) into two terms:

$$f_2(x,0)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\mathrm{e}}^{\mu x\text{sin}\theta }\mathrm{d}\theta {\int }_{-r}^r\frac{\text{cos}(\mu s-\mu x\text{cos}\theta )}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s+\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\mathrm{e}}^{\mu x\text{sin}\theta }d\theta {\int }_{r<\mid s\mid <1}\frac{\text{cos}(\mu s-\mu x\text{cos}\theta )}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (13)

The first term on the right-hand side of (13) is zero, because p₂(θ, s) = 0 when |s| < r. Let us denote the second term on the right-hand side of (13) as h(x) for |x| < r:

$$h\left(x\right)=\frac{1}{4{\pi }^2}{\int }_0^{2\pi }{\mathrm{e}}^{\mu x\text{sin}\theta }\mathrm{d}\theta {\int }_{r<\mid s\mid <1}\frac{\text{cos}(\mu s-\mu x\text{cos}\theta )}{s-x\text{cos}\theta }\frac{\partial p_2(\theta ,s)}{\partial s}\mathrm{d}s.$$ (14)

In (14), |x| < r and |s| > r, thus 1/(s − x cos θ) is differentiable of any order. If we replace x by the complex variable z in (14), then h(z) defined by (14) is an analytic function in the entire z-plane with cuts along [−1, −r] and [r, 1], provided that e^{μx sin θ} cos(μs − μx cos θ)∂p₂/∂s is absolutely integrable, which is usually satisfied in practice.

It is known that for any x₀ in (−ρ, ρ), f₂ (x₀, 0) = 0 because f₁(x, y) = f(x, y) in Ω. From (14), h(x) = 0 in (−ρ, ρ). Using analytic continuation, we have h(x) = 0 in (−r, r). Thus, f₂(x, 0) = 0 in (−r, r).

Since the x-axis is arbitrarily chosen (that is, any line passing through the origin can be the x-axis), f₂(x, y) = 0 in the entire ROI, x² + y² < r². In other words, f₁(x, y) = f(x, y) holds for the entire ROI which means that we have an exact reconstruction on the ROI. This proof procedure is exactly the same as that in section 2.1.

From the proof we observe that the requirement of the object being compact is not used. We can change the integrals with respect to s from [−1, 1] to (−∞,∞) and change the integrals with respect to s from r < |s| < 1 to r < |s|. Thus, our result can be extended to a general absolutely integrable object function that may not have a compact support. If the object is compact, then the interior problem of the exponential Radon transform with some known values in the ROI has been solved by Yu et al (2009). If the object is compact, then the interior problem of the regular Radon transform with some known values in the ROI has been previously solved (Defrise et al 2006, Ye et al 2007, Kudo et al 2008). However, our proofs differ.

2.3. Non-uniform attenuation (attenuated Radon transform) case

In this section, we consider a simple SPECT imaging situation where the detector is at the center of rotation and the attenuation coefficient is a non-uniform attenuator μ(x, y) which is given. We define the attenuated Radon transform as

$$p(\theta ,s)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{{\int }_0^t\mu (s\overrightarrow{\theta }+\widehat{t}{\overrightarrow{\theta }}^{\perp })\mathrm{d}\widehat{t}}f(s\overrightarrow{\theta }+t{\overrightarrow{\theta }}^{\perp })\mathrm{d}t.$$ (15)

We now make the same assumptions as in sections A and B. The projection p(θ, s) is only available for |s| ≤ r. All weighted line integrals (8) passing through the ROI are measured. We also assume that f(x, y) is known in a sub-region Ω, x² + y² < ρ², 0 < ρ < r, of the ROI.

We also assume that the iterative algorithm has already converged to a solution f₁(x, y), all measurements are satisfied, that is,

$$p(\theta ,s)={\int }_{-\infty }^{\infty }{\mathrm{e}}^{{\int }_0^t\mu (s\overrightarrow{\theta }+\widehat{t}{\overrightarrow{\theta }}^{\perp })\mathrm{d}\widehat{t}}{f}_1(s\overrightarrow{\theta }+t{\overrightarrow{\theta }}^{\perp })\mathrm{d}t$$ (16)

for |s| ≤ r, and the solution matches the given image values in Ω, that is, f₁(x, y) = f(x, y) in Ω. We are going to prove that f₁(x, y) = f(x, y) holds for the entire ROI, x² + y² < r².

Let

$$f_2(x,y)=f(x,y)-f_1(x,y).$$ (17)

According to the attenuated projection definition (16), let the attenuated projection of f₂ (x, y) be p₂(θ, s), as illustrated in figure 1. Then p₂(θ, s) = 0, for |s| < r, because both f and f₁ satisfy the measurements according to (16) and (17).

Now we apply Novikov's FBP algorithm (Novikov 2002) to reconstruct f₂(x, y) from p₂(θ, s) as follows (You et al 2005).

$$f_2(x,y)=\mathrm{Re}\frac{1}{4{\pi }^2}\left[{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-\infty }^{\infty }\frac{{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}}{s-l}\frac{\partial \left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{\partial l}\mathrm{d}l+{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-\infty }^{\infty }\frac{\partial }{\partial s}{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}\frac{\left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{s-l}\mathrm{d}l\right]$$ (18)

where s = x cos θ + y sin θ, t = −x sin θ + y cos θ, $a_{\theta }(s,t)={\int }_t^{\infty }\mu (s\stackrel{\rightharpoonup }{\theta }+\tau {\stackrel{\rightharpoonup }{\theta }}^{\perp })\mathrm{d}\tau$, $g(\theta ,s)=\frac{1}{2}\left[(\mathbf{R}+i\mathbf{HR})\mu \right](\theta ,s)$, R is the Radon transform operator H is the Hilbert transform operator.

The proof procedure is identical to those in sections 2.1 and 2.2. We first let y = 0 and only consider the image f₂(x, 0) values (−r, r) on the x-axis. We then write the expression (18) f₂(x, 0), −r < x < r, as

$$f_2(x,0)=\mathrm{Re}\frac{1}{4{\pi }^2}\left[{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{-r}^r\frac{{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}}{s-l}\frac{\partial \left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{\partial l}\mathrm{d}l+{\int }_0^{2\pi }\mathrm{d}r{\int }_{-r}^r\frac{\partial }{\partial s}{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}\frac{\left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{s-l}\mathrm{d}l\right]+\mathrm{Re}\frac{1}{4{\pi }^2}\left[{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{r<\mid l\mid }\frac{{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}}{s-l}\frac{\partial \left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{\partial l}\mathrm{d}l+{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{r<\mid l\mid }\frac{\partial }{\partial s}{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}\frac{\left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{s-l}\mathrm{d}l\right]$$ (19)

where s = x cos θ and t = −x sin θ. The first and the third terms are zero, because p₂(θ, s) = 0 when |s| < r. Let us denote the sum of the second term and the fourth term on the right-hand side of (19) as h(x) for |x| < r:

$$h\left(x\right)=\mathrm{Re}\frac{1}{4{\pi }^2}\left[{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{r<\mid l\mid }\frac{{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}}{s-l}\frac{\partial \left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{\partial l}\mathrm{d}l+{\int }_0^{2\pi }\mathrm{d}\theta {\int }_{r<\mid l\mid }\frac{\partial }{\partial s}{\mathrm{e}}^{a_{\theta }(s,t)-g(\theta ,s)}\frac{\left({\mathrm{e}}^g{p}_2\right)(\theta ,l)}{s-l}\mathrm{d}l\right].$$ (20)

In (20), |x| < r and |l| > r, thus 1/(s −l) is differentiable of any order. If we replace x by the complex variable z in (20), then h(−z) defined by (20) is an analytic function in the entire z-plane with cuts along (−∞, −r] and [r, ∞).

It is known that for any x₀ in (−ρ, ρ), f₂ (x₀, 0) = 0 because f₁(x, y) = f(x, y) in Ω. From (20), h(x) = 0 in (−ρ, ρ). Using analytic continuation, we have h(x) = 0 in (−r, r). Thus, f₂(x, 0) = 0 in (−r, r).

Since the x-axis is arbitrarily chosen (that is, any line passing through the origin can be the x-axis), f₂(x, y) = 0 in the entire ROI, x² + y² < r². In other words, f₁(x, y) = f(x, y) holds for the entire ROI which means that we have an exact reconstruction on the ROI.

This result for the attenuated Radon transform for a non-uniform attenuator is new.

2.4. Extension to more general cases

From the above almost identical derivations, we conclude that the interior problem with some known values in the ROI is exactly solvable in a general imaging problem, regardless the dimension (e.g. 2D or 3D) and the geometry (e.g. parallel-beam, fan-beam or cone-beam), as long as a closed-form reconstruction algorithm exists for non-truncated data. The closed-form image reconstruction algorithm can be an FBP type or can be other types, such as filtering the backprojection of the data, or performing the Hilbert transform of the backprojection of differentiated data. The object does not need to have a finite support.

In order to make the analytical continuation work, the filtering can only have one singularity at the point of reconstruction. The general reconstruction scheme is in the form of

$$f_2=\left(\text{data}{p}_2\text{contribution from}\mathrm{ROI}\right)+\left(\text{data}{p}_2\text{contribution from outside of}\mathrm{ROI}\right).$$ (21)

The singularity only appears in the first term on the right-hand side of (21). This first term is zero because p₂ is zero in this region. There is no singularity in the second term because we only reconstruct f₂ in the ROI.

3. Computer simulations

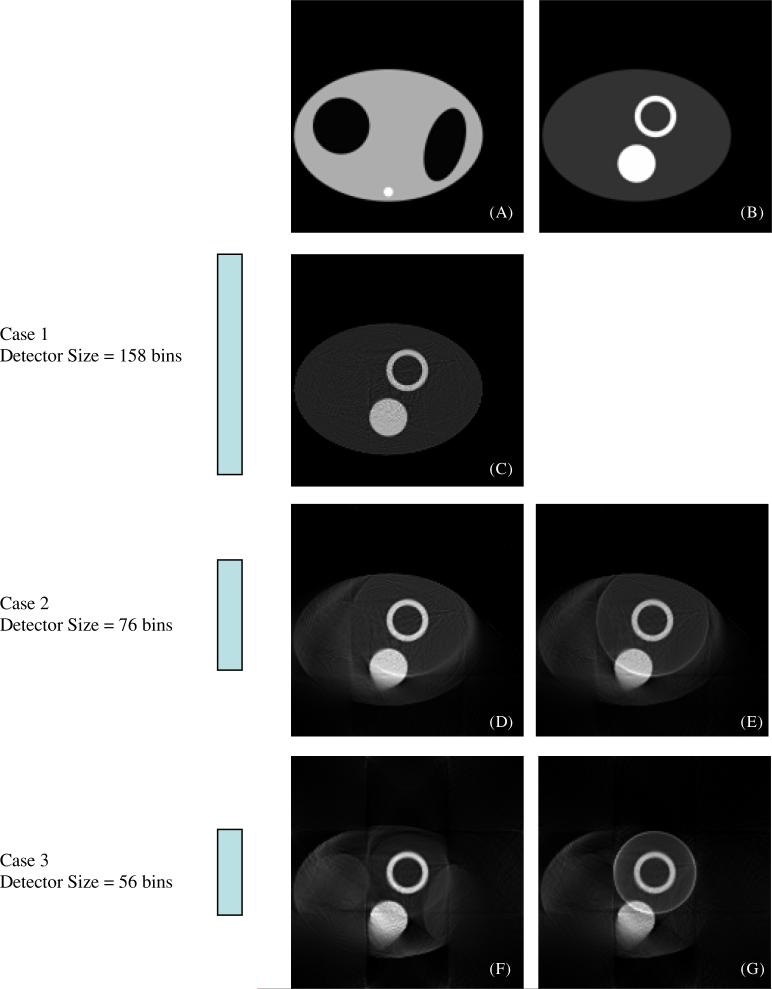
Computer simulations have been conducted to verify the proposed algorithm with truncated emission data for exact ROI reconstruction. The known non-uniform attenuator is shown in figure 2(A), where the large ellipse represents a torso with an attenuation coefficient of 0.15 cm⁻¹, the two darker ellipses represent the lungs with an attenuation coefficient of 0.04 cm⁻¹, and the small bright dot represents the bone with an attenuation coefficient of 0.22 cm⁻¹. The emission object is shown in figure 2(B), where the ring represents the heart and the disk represents the liver. The intensity of the heart and that of the liver are the same, and is five times the intensity of the background activity in the torso. The ROI is the heart. The emission data are measured with a small parallel-hole collimator, and the detector bin size is 0.5 cm.

Figure 2.

Computer simulations of ROI reconstruction. The phantom is offset so that the heart is at the center of rotation. (A) The known attenuation map. (B) The emission phantom. (C) A truncation-less reconstruction. ROI reconstructions are shown in (D, E, F and G). The ROI is the circular region containing the heart. The detector is larger in (D) and (E) than in (F) and (G). In (E) and (G), the average value of the central 6 × 6 sub-region is forced to be equal to a known value.

Three cases of the detector size are simulated. In the first case, the detector has 158 bins, the second case has 76 bins, and the third case has 56 bins. The phantom is positioned such that the heart is at the center of rotation. The projection data are analytically calculated without noise added. The image is reconstructed with 500 iterations of the ML-EM algorithm. The image is represented in a 158 × 158 array.

Figure 2(C) shows the reconstruction of the first case, where there is no data truncation.

The reconstructions for the second case are shown in figures 2(D) and (E). The difference between these two reconstructions is as follows. A regular ML-EM algorithm is used to reconstruct the image shown in figure 2(D), while a modified ML-EM algorithm is applied to obtain figure 2(E). In the modified algorithm, it is assumed that the average emission image value at a small 6 × 6 square at the center of the object is known. At each iteration, a constant is added to each image value such that the average emission image value in this 6 × 6 square matches the given value.

For the third case, the reconstructed images are shown in figure 2(F) via the regular ML-EM algorithm and 2(G) via the modified ML-EM algorithm.

Within the ROI, the reconstructed images in figures 2(D) and (E) are almost identical. In the central 6 × 6 square region, they both reach the same average value of 0.1. The second case represents a general situation that the ROI (which is also the common field of view (FOV) of the imaging system) contains a region that is outside the torso, where the image value is known to be zero. In this case, it is not necessary to know the average image value in the central 6 × 6 square region.

The average image value in the central 6 × 6 square region is 0.075 in figure 2(F), and is 0.1 in figure 2(G). The correct value is 0.1. The ROI reconstruction shown in figure 2(F) is slightly biased. This bias is very small and is difficult to visualize even with profile curves. In practical SPECT, if the ROI does not contain any region that is outside the patient body, it is difficult to obtain a region in which the emission activity intensity is exactly known. One could find a cold region and assume that the activity is zero in that region.

4. Conclusion

Nowadays many companies are developing various dedicated cardiac SPECT cameras. They use convergent imaging geometries with pinhole, fan-beam, cone-beam or scanning parallel-beam collimators to obtain higher detection sensitivity. These dedicated systems have a smaller FOV than a full-size clinical system. Data truncation has thus become the norm rather than the exception. Therefore, it is important to develop ROI image reconstruction algorithms for truncated data. This paper is a stepping stone towards this direction. The algorithm developed in this paper requires that emission image values in a small region within the ROI should be exactly known. If the ROI includes a region that is outside the patient body, then this condition is satisfied. If the ROI is completely within the patient body, the ROI may contain a background region. If the background activity is extremely low, it can be assumed to be zero. If the background activity can be somehow estimated, the exact ROI reconstruction is also possible.

This paper presents a general result for iterative algorithms in solving the interior problem with some known values within the ROI. We believe that our conclusion is not restricted to iterative algorithms, and we can apply our proof to almost any analytic image reconstruction algorithm. The proofs are essentially the same as presented in this paper except that the projection data are not assumed to be zero, and the known function within the specified small region is not zero, as treated in Defrise et al (2006), Ye et al (2007, 2008) and Kudo et al (2008). Unlike the previous work (e.g. Defrise et al 2006), we do not need to assume the object f (x, y) to be continuous; our proof only requires that ∂p(θ, s)/∂s is absolutely integrable. This condition is very easy to satisfy in practice. If the object has a finite support and ∂p(θ, s)/∂s is piece-wise continuous, then this condition is satisfied.

In this paper, the non-uniform attenuation map is assumed to be known and is not truncated. Exact reconstruction of the interior problem is still an open problem if both the transmission and emission data are truncated, however the problem has been solved for the case where the transmission data are truncated but the emission data are not (Zeng and Gullberg 2009).