Integrative Systems Models of Cardiac Excitation Contraction Coupling

Abstract

Excitation-contraction coupling in the cardiac myocyte is mediated by a number of highly integrated mechanisms of intracellular Ca²⁺ transport. The complexity and integrative nature of heart cell electrophysiology and Ca²⁺-cycling has led to an evolution of computational models that have played a crucial role in shaping our understanding of heart function. An important emerging theme in systems biology is that the detailed nature of local signaling events, such as those that occur in the cardiac dyad, have important consequences at higher biological scales. Multi-scale modeling techniques have revealed many mechanistic links between micro-scale events, such as Ca²⁺ binding to a channel protein, and macro-scale phenomena, such as excitation-contraction coupling gain. Here we review experimentally based multi-scale computational models of excitation-contraction coupling and the insights that have been gained through their application.

Overview of cardiac excitation-contraction coupling

Intracellular calcium (Ca²⁺) concentration plays a number of important regulatory roles in the cardiac myocyte. These include excitation-contraction coupling (ECC)¹, intracellular signaling², regulation of mitochondrial function³, gene expression⁴, and cell death^{2, 5}. This review article is focused on the role of Ca²⁺ in ECC in cardiac ventricular myocytes. In particular, we will review experimentally based computational models of ECC, with a specific focus on mechanisms of Ca²⁺-induced Ca²⁺ release (CICR), and the insights that have been gained through application of these models.

The nature of ECC is linked closely to both the micro-anatomical structure of the cell, and to the arrangement of contractile proteins within the cell. The basic unit of contraction in the cardiac myocyte is the sarcomere. Individual sarcomeres are bounded on both ends by the t-tubular system^{1, 6, 7}. The t-tubules are cylindrical invaginations of the sarcolemma that extend deep into the cell and approach an organelle known as the sarcoplasmic reticulum (SR). The SR is a luminal organelle located throughout the interior of the cell, and it is involved in the uptake, sequestration and release of Ca²⁺. SR can be divided into three main components known as junctional SR (JSR), corbular SR, and network SR (NSR). The JSR is that portion of the SR most closely approximating (within 12–15 nm)⁸ the t-tubules. The close proximity of these two structures forms a micro-domain known as the dyad.

Ca²⁺-sensitive Ca²⁺-release channels known as ryanodine receptors (RyRs) are preferentially located in the dyadic region of the JSR membrane. In addition, sarcolemmal voltage-gated L-type Ca²⁺ channels (LCCs) are preferentially located within the dyadic region of the t-tubules, where they are in close opposition to the RyRs. Early data from freeze fracture electron micrographs suggested that RyRs are arranged in a somewhat regular lattice⁹. The assumption that RyRs are tightly packed in dyadic junctions led to estimates of 100–300 RyRs per dyad⁸. However, more recent imaging studies have demonstrated that dyadic clefts are small, where junctions contain an average of 14 RyRs, with some clusters incompletely filled with RyRs, and with a large fraction of clusters closely spaced within 20–50 nm, suggesting that smaller clusters may act together to function as a single site of CICR^{10, 11}.

During the initial depolarization stages of the action potential (AP), LCCs open allowing for the entry of Ca²⁺. This inward flux of Ca²⁺ contributes to maintenance of the plateau phase of the AP. As Ca²⁺ concentration in the dyad increases, Ca²⁺ binds to the RyRs, increasing their open probability. Opening of RyRs leads to Ca²⁺ release from the JSR. The amount of Ca²⁺ released from the JSR is significantly more than the amount of trigger Ca²⁺ entering via LCCs¹². The ratio of release to trigger flux of Ca²⁺ is known as ECC gain. The Ca²⁺ release flux is a smooth, continuous function of trigger influx, a behavior observed originally by Fabiato et al¹³ and known as graded Ca²⁺ release. The resulting rapid, large increase in dyad Ca²⁺ concentration ([Ca²⁺]_d) leads to Ca²⁺ diffusion from the dyad into the cytosol. As cytosolic Ca²⁺ concentration ([Ca²⁺]_c) increases, Ca²⁺ binding to troponin C in the myofilaments initiates contraction of the myocyte.

Several mechanisms exist to remove trigger Ca²⁺ from the myocyte, and for re-uptake of released Ca²⁺ back into the NSR. During diastole, the Na⁺-Ca²⁺ exchanger (NCX) is believed to import three Na⁺ ions for every Ca²⁺ ion extruded, yielding a net inward charge movement¹⁴ (see¹⁵ for recently proposed alternative transport modes). It is the principal means by which Ca²⁺ is extruded from the myocyte. It can also function in reverse mode during the AP, in which case it extrudes Na⁺ and imports Ca²⁺.¹⁶ The duration of reverse mode NCX, and hence its effect on AP shape, has been shown to vary with species, heart failure, and other factors^{17, 18}. The sarcolemmal Ca²⁺-ATPase also transports Ca²⁺ out of the cell, but flux through this pathway is small (2–3%) relative to other pathways¹⁹. The major mechanism by which released Ca²⁺ is transported back into the SR is the SR Ca²⁺-ATPase (SERCA pump). Phospholamban (PLB) is normally bound to the SERCA pump, inhibiting its activity. Phosphorylation of PLB functionally up-regulates SERCA by increasing its Ca²⁺-affinity^{1, 20}. Density of the SERCA pump is highest in NSR. JSR refilling occurs via Ca²⁺ diffusion from the NSR. As each of these mechanisms restores [Ca²⁺]_c to diastolic values, Ca²⁺ dissociates from troponin C, terminating the contraction phase of the cardiac cycle.

The elucidation of CICR mechanisms has become possible with the development of experimental techniques for simultaneous measurement of L-type Ca²⁺ current (I_CaL) and Ca²⁺ transients, and detection of local Ca²⁺ release events known as Ca²⁺ sparks^{21, 22}. As indicated by Soeller and Cannell²³, the tight regulation of SR Ca²⁺ release by triggering LCC current became evident with the following observations: (1) ECC gain is ~10 in response to a voltage clamp to 0 mV^{24, 25}; (2) The magnitude of SR release is a smoothly graded function of I_CaL amplitude^{25, 26}; and (3) the bell-shaped voltage-dependence of SR release is similar to that for I_CaL, but with its peak shifted in the hyperpolarizing direction by ~ 10 mV^{25, 26}. These experimental observations gave rise to and later verified the local control theory of EC coupling. The mechanism of local control predicts that within discrete regions of the dyadic cleft, the opening of an individual LCC will trigger Ca²⁺ release from a small cluster of RyRs that reside in close proximity directly across the dyad. Tight regulation of CICR is achieved because LCCs and RyRs are regulated by [Ca²⁺]_d rather than by [Ca²⁺]_c. The amplitude and profile of the whole-cell intracellular Ca²⁺ transient results from the recruitment and temporal summation of the elementary Ca²⁺ spark release events. The recruitment of Ca²⁺ sparks via this mechanism allows for graded control of SR Ca²⁺ release²⁷.

Many advances in integrative modeling of the ventricular myocyte have resulted from quantitative modeling of these components which underlie CICR and ECC in cardiac myocytes. In this review, we will present a range of models that have been developed to understand properties of CICR and ECC in the cardiac ventricular myocyte. We have chosen to focus on development of major new functional components of CICR and ECC, their integration into whole-cell models, and the insights that have been obtained from these advances in modeling capabilities that span multiple biological scales.

Common pool models of CICR

The landmark DiFrancesco-Noble model of the cardiac Purkinje fiber²⁸ was developed from the preceding Beeler-Reuter model²⁹ (first computational model of the cardiac ventricular myocyte) and that of McAllister et al³⁰. This model was ground breaking for many reasons and was the first model to introduce descriptions of the transport of Ca²⁺ into the NSR by SERCA, extrusion of Ca²⁺ from the cytosol by NCX, diffusion of Ca²⁺ from NSR to JSR, and CICR from the JSR. This model established the conceptual framework on which all subsequent models of the myocyte have been built. While this model did reproduce graded SR Ca²⁺ release, it did so with ECC gain that was non-physiologically low.

The construction of mechanistic mathematical models of CICR which attempt to capture both high gain and graded SR Ca²⁺ release first lead to a series of “common pool” models, which, in fact, fail to capture these fundamental properties. As defined by Stern²⁷, common pool models are those in which LCC trigger Ca²⁺ enters the same Ca²⁺ pool into which JSR Ca²⁺ is released, and which controls JSR Ca²⁺ release. The rapid increase of Ca²⁺ in this pool leads to non-physiological regenerative, all-or-none rather than graded Ca²⁺ release, a situation where whole-cell SR Ca²⁺ release escapes control by I_CaL once it is initiated²⁶. An additional assumption inherent in this type of model is that the gating dynamics of the entire population of RyRs are controlled by properties of whole-cell I_CaL rather than by properties of local LCC channel gating. Stern elegantly demonstrated via the application of linear stability theory that common pool models cannot achieve both high gain and graded Ca²⁺ release²⁷.

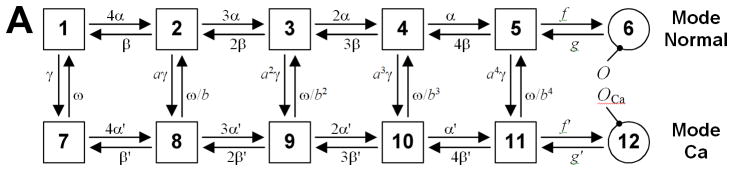
Regardless of this limitation of common pool models, many advances in cardiac myocyte modeling over the past decade have stemmed from improved descriptions of CICR in such models. The Jafri et al³¹ model of the guinea pig ventricular myocyte was the first to incorporate a Markov model of the LCC (Fig. 1A) into an integrated myocyte model with mechanistic ECC. The LCC model was based on the concept of modal gating introduced by Imredy and Yue³² based on single-LCC recordings in which Ca²⁺ induced a shift in LCC gating dynamics into a low open probability mode. The model contains subsets of states which reproduce channel behavior prior to (mode-normal), and following (mode-Ca) the occurrence of Ca²⁺ dependent inactivation (CDI). Openings are rare in mode-Ca, effectively inactivating the channel. Successive LCC models have incorporated the concept of modal gating in Markov models for describing LCC inactivation^33–35 as well as other modes such as phosphorylation³⁶. The Jafri et al³¹ model was also first to implement a “restricted subspace”, a single compartment representing the total volume of all dyads into which all Ca²⁺ flux through RyRs and LCCs is directed. This model made a number of predictions regarding mechanisms of CICR and Ca²⁺ cycling (reviewed in³⁷). A major prediction of this model was that experimentally measured interval-force (transient) and frequency-force (steady-state) relationships could be explained by the interplay between RyR inactivation and SR Ca²⁺ load dynamics. This Ca²⁺-subsystem was modified for canine in the model of Winslow et al³⁸ from which a model of heart failure was developed based on data obtained from myocytes isolated from dogs with tachycardia pacing-induced heart failure³⁹. The model predicted that in heart failure, down-regulation of the SERCA pump and up-regulation of NCX decreased JSR Ca²⁺ load, Ca²⁺ release via the RyRs, and the strength of I_CaL CDI. The resulting increase in I_CaL acted to prolong AP duration (APD), a characteristic phenotype of heart failure. The model predictions were subsequently validated by experimental studies^{40, 41}, thereby demonstrating that negative feedback on LCCs by Ca²⁺ release from RyRs can exert significant control of AP properties. Furthermore, the heart failure model could produce early after depolarizations (EADs), a cellular arrhythmia believed to be a possible trigger for arrhythmia at the whole heart level. Upon introduction into a model of the ventricles, the EADs in the heart failure model quickly led to degeneration of electrical propagation into a cardiac arrhythmia, whereas the control myocyte model yielded normal coordinated ventricular activation during pacing.⁴²

Figure 1.

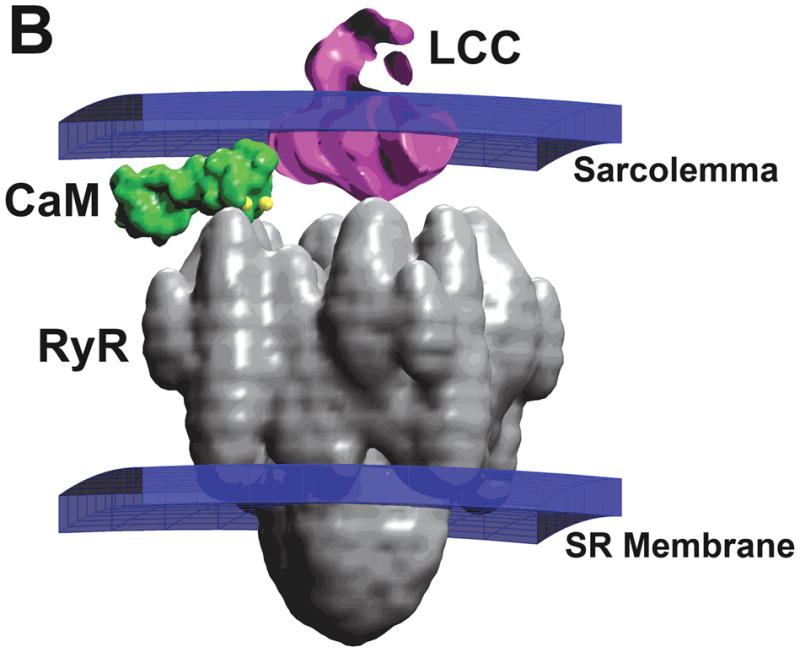
(A) Markov state model for gating of the LCC as proposed by Jafri et al.³¹ CDI occurs as a result of downward transitions from model-normal to mode-Ca. VDI is described by an independent Hodgkin-Huxley type gate (not shown). (B) Structure of a region of the dyad containing one LCC opposed to a single RyR, and one CaM molecule tethered to the LCC⁷³.

Despite the fact that these common pool models were not able to reproduce graded SR Ca²⁺ release, they were able to reproduce and predict many important behaviors of the cardiac ventricular myocyte, raising the question of whether capturing the mechanisms of graded release is of primary importance. One way to circumvent this issue is to model SR Ca²⁺ release flux as a phenomenological function of LCC influx and/or membrane potential. Doing so removes the positive feedback effect inherent to common pool models. Models incorporating a phenomenological mechanism of CICR have been successful in describing many myocyte behaviors (including the widely utilized models of Rudy and colleagues^{43, 44}). However, as with any phenomenological model, care must be taken when interpreting results of these models that pertain to Ca²⁺ release. The critical relationship between SR Ca²⁺ release and APD^{38, 40, 41}, and the recognition that the feedback of SR Ca²⁺ release on LCCs occurs locally in discrete Ca²⁺ spark events²¹ suggested that capturing the mechanisms of local interaction between LCCs and RyRs would be essential. Furthermore, experimental data were emerging that supported the idea that LCC inactivation was dominated by CDI rather than voltage-dependent inactivation (VDI)^45–47. Strong CDI in combination with weak/incomplete VDI causes instability in common pool models³⁴ (which were therefore typically formulated with strong VDI and weak CDI) because all-or-none SR Ca²⁺ release induces fast whole-cell CDI which eliminates the late phase of I_CaL and destabilizes the AP plateau (see Fig. 10C of ref34). This made it clear that in order to fully capture the core mechanisms of ECC, a model in which LCCs locally control RyR function was needed.

Local control of SR Ca²⁺ release

In 1992, Stern²⁷ formulated idealized models of “local control” of CICR, and in doing so advanced the local control theory of ECC which underlies how the microscopic properties of CICR translate into macroscopic physiologic phenomena observed in experiments. The approach was to recognize that the non-physiologic positive feedback loop inherent in common pool models of CICR must be broken by separating Ca²⁺ released from the SR from the trigger Ca²⁺ influx. This was accomplished by noting that LCCs and RyRs reside in close apposition on opposite sides of the dyadic cleft, which would effectively grant Ca²⁺ ions permeating an LCC privileged access to the Ca²⁺ binding sites on nearby RyRs. Importantly, the assumed structural separation of individual clefts⁸ means that released Ca²⁺ would not generally act as a trigger to RyRs in distant dyads (though recent studies suggest neighboring RyR clusters may have a functional role in ECC^{11, 48}). Stern’s “calcium-synapse” model, in which each dyad was assumed to contain a single LCC and a single SR release channel, captured these ideas in an elegantly simple way, demonstrating that high gain and graded SR release arise from the local correlation in stochastic LCC and RyR gating due to their communication via a common local Ca²⁺ signal. In this model, graded release is achieved by statistical recruitment of elementary SR Ca²⁺ release events. This fundamental idea of local control of SR release spurred a number of modeling studies, some of which focused on detailed dynamics of Ca²⁺ distribution within the dyadic junction, some of which focused on mechanisms of Ca²⁺ release termination, and a small handful of which developed fully integrative models that relate macroscopic cellular properties of ECC to the function of independent, locally controlled Ca²⁺ release units.

Due to the small size of the dyad, it became clear that understanding the spatial and temporal profile of [Ca²⁺]_d would be an important step in elucidating the mechanistic details of local CICR. Langer and Peskoff⁴⁹ developed one of the first detailed models to numerically simulate the time course of dyadic Ca²⁺. The model predicted that a single typical LCC opening led to ~ 1 mmol/L [Ca²⁺]_d near the mouth of the LCC. The presence of sarcolemmal buffering sites slowed the decay of the local Ca²⁺ transient (such that it remained highly elevated long after LCC closure) as compared to the dynamics in the absence of buffers, a finding which was inconsistent with the idea that LCC gating imposes tight control on RyR activity. Soeller and Cannell⁵⁰ formulated a dyad model which introduced the electrostatic effects of ion movement which predicted that [Ca²⁺]_d actually changes more rapidly in response to LCC gating. In this model, [Ca²⁺]_d was approximately proportional to unitary LCC currents over a wide range of current amplitudes. The model yielded predictions of [Ca²⁺]_d profiles during JSR release, which peaked as high as 300 μmol/L near the center of the dyad. The decay in dyadic Ca²⁺ occurred in ~ 2 ms following termination of SR release (but this was sensitive to the dyad boundary condition). The high speed of the response of dyadic Ca²⁺ to LCC and RyR gating in this model helped to explain how tight local control of SR release by LCCs can be achieved.

With the growing acceptance of local control theory of CICR and that Ca²⁺ sparks are the elementary events underlying SR Ca²⁺ release (for a review see51), mathematical models of Ca²⁺ sparks were developed. The summation of Ca²⁺ sparks could explain the characteristic properties of CICR, ECC gain, and whole-cell Ca²⁺ transients, therefore the analysis of models of single Ca²⁺ sparks and ensembles of Ca²⁺ sparks provided a wealth of information. Local control of CICR requires that SR release be stable, which suggests that Ca²⁺ sparks, which are locally regenerative, must be terminated rapidly by a robust mechanism. While the mechanisms of Ca²⁺ spark termination still remain unclear, a number of models have helped elucidate how possible mechanisms may contribute to termination of SR Ca²⁺ release.

Stern²⁷ originally described three mechanisms that can terminate SR release in a cluster of RyRs: (1) RyR inactivation is a time-dependent process which may be initiated by Ca²⁺ binding to an inactivation site on the RyR or may occur “fatefully” following opening of the channel. The observed inactivation process has been described as classically inactivating (leading to absolute refractoriness of CICR)⁵² or taking on the complex properties of adaptation⁵¹. (2) Depletion of locally releasable JSR Ca²⁺ will occur as the result of RyR activity. The emptying of the cisternal Ca²⁺ store reduces the Ca²⁺ gradient across the RyRs, and hence the Ca²⁺ flux. This will diminish the local feedback that underlies regenerative release in a cluster of RyRs, allowing them to close. (3) “Stochastic attrition” occurs as a result of the non-zero probability that all RyRs in a cluster are simultaneously closed. Since Ca²⁺ diffuses rapidly out of the dyad, the simultaneous closure of all RyRs would lead to a rapid reduction in [Ca²⁺]_d below the level which sustains RyR activity. Active RyR clusters would therefore gradually cease gating spontaneously. This mechanism can only be effective on a reasonable timescale if very few RyRs are activated during a Ca²⁺ spark, and it does not provide for a mechanism of refractoriness. The stereotypic nature of Ca²⁺ spark properties suggested that spark generation and termination are likely controlled by regulatory feedback mechanisms and cannot be described by a simple stochastic mechanism alone²³. An additional mechanism proposed recently is RyR regulation by luminal SR Ca²⁺. RyR sensitivity to [Ca²⁺]_d can be altered by the level of JSR luminal [Ca²⁺] via the interaction of the Ca²⁺ buffer calsequestrin with RyR accessory proteins triadin and junction within the JSR⁵³. The decrease in RyR open probability with JSR depletion likely contributes to termination of Ca²⁺ release.

In 1999, Stern et al³³ developed a stochastic model of cardiac ECC. The model consisted of a cardiac dyad in which the Ca²⁺ concentration profile was simulated by solving equations governing diffusion and Ca²⁺ binding reactions in the cleft. LCCs and RyRs were represented by Markov state models, which were simulated as part of a stochastic system in which the state of each individual channel was tracked. The behavior of six different RyR gating schemes was analyzed in the context of local control of ECC. This study revealed that local control, in a realistic setting of dyad geometry, number, and location of channels, could explain graded release, when the RyR was represented by a simple phenomenological four-state gating scheme which included inactivation (Ca²⁺-dependent or fateful). This success has led to continued development of this RyR model in more recent work^{54, 55}. However, RyR channel gating schemes that were based on single-channel RyR measurements in lipid bilayers^{56, 57} failed to give stable ECC (but stability could be restored by introducing allosteric RyR interactions³³). The work of Stern et al³³ suggested that there must be a sufficiently strong process that substantially reduces RyR open probability shortly following activation such that stochastic attrition can occur on the timescale of physiological ECC.

Whether or not RyR inactivation or adaptation plays an important role in termination of SR Ca²⁺ release remains controversial (see below). A number of RyR models^{57, 58} were developed to better understand the observation of RyR adaptation⁵⁹, whereby an RyR can reopen in response successive increases in Ca²⁺ concentration, indicating they have not entered a conventional absorbing CDI state. Rice et al⁶⁰ developed a stochastic model of Ca²⁺ release in the dyadic junction which demonstrated that RyR adaptation modulated Ca²⁺ release duration and amplitude but was not required for termination of Ca²⁺ release (i.e. JSR depletion played an important role). This model achieved high gain and graded release without tracking the spatial gradients of [Ca²⁺]_d. In contrast, the RyR model of Shannon et al⁵⁴ is a modification of the phenomenological four-state model of Stern et al³³, which introduced an important modulatory role for SR luminal Ca²⁺ in RyR gating but which still depends upon an inactivation/adaptation mechanism for release termination. Variations of this model have been incorporated into a variety of recent models which have successfully described SR load and frequency dependent properties of ECC and APs in rabbit⁵⁴ and human⁶¹, the role of RyR phosphorylation on Ca²⁺ dynamics and the AP⁵⁵, and the role of spatial coupling between dyadic release sites in Ca²⁺ spark-induced sparks and Ca²⁺ alternans⁴⁸.

In 2002, Sobie et al⁶² developed a Ca²⁺ spark model to further investigate mechanisms underlying termination of SR Ca²⁺ release. In this model each release site is composed of a large number of two-state RyRs which incorporate two additional experimental observations: (1) elevated SR luminal Ca²⁺ increases the Ca²⁺-sensitivity of RyR activation⁶³, and (2) RyR coupling cooperatively influences their gating properties within a cluster⁶⁴. These mechanisms of RyR gating yield a “sticky cluster” model which reproduces fundamental features of Ca²⁺ sparks and robust termination of release that arises as a result of the combined effects of these two mechanisms. In this model, the assumption of coupled RyR gating is essential for reliable SR release termination. However, it remains unclear how RyRs would influence the gating properties of all other RyRs in a cluster (as opposed to only adjacent RyRs³³) as implemented in this model (see ^{65, 66} for alternative approaches to modeling the functional effects of RyR coupling). In addition, the >90% SR depletion required for release termination in the Sobie et al⁶² model may not be realistic as experiments have demonstrated that 40–75% of releasable Ca²⁺ remains in the JSR following whole-cell triggered SR release^{67, 68}. Despite these issues, the majority of recent experiments^68–70 have strengthened the idea that termination of SR release is primarily controlled by luminal SR Ca²⁺ rather than an RyR inactivation mechanism.

While many controversies as to the details of CICR remain to be resolved, the models of dyadic Ca²⁺ dynamics, Ca²⁺ sparks and CICR have helped affirm or disprove a variety of mechanistic hypotheses regarding cardiac ECC. Most of these ECC models, however, have been implemented at the sub-cellular scale, isolated from the physiological environment and influence of other cellular processes. The first mathematical model to incorporate the mechanisms of local control of SR Ca²⁺ release at the level of the cardiac dyad into an integrative model of the cardiac action potential was published in 2002 by Greenstein and Winslow³⁴ (Greenstein-Winslow model). This model is described in detail below in the section “Multi-scale modeling of CICR”.

Multi-scale modeling of CICR

Quantitative understanding of CICR requires that Ca²⁺ signaling be understood across a wide range of spatio-temporal scales. The length-scale over which CICR occurs within the dyad is on the order of nanometers, and relevant time-scales are of the order of microseconds. Integration to the level of the cell requires formulation of models that describe behavior at spatio-temporal scales of several hundred microns and tens to hundreds of seconds. Recently, we have developed several new approaches for multi-scale modeling of CICR spanning these spatio-temporal scales^{34, 71–73}. In this section, we present these models and the mathematical techniques for moving across these spatio-temporal scales.

The Nano-Scale Model of CICR

We have recently developed a computational model of Ca²⁺ signaling in the dyad that simulates motion of Ca²⁺ ions, binding of ions to RyR receptor sites, and Ca²⁺ release from RyR. This model was developed in order to understand factors shaping CICR at the nano-scale level. We addressed the following three questions: 1) what is the number of Ca²⁺ ions that are present in the dyad during CICR?; 2) how does the physical arrangement of large proteins within the dyad influence CICR?; and 3) how does “signaling noise” due to the potentially small number of Ca²⁺ ions within the dyad affect the nature of CICR? We addressed these questions by developing a molecularly- and structurally-detailed computational model of the cardiac dyad describing motions of Ca²⁺ ions, as influenced by thermal energy and electrostatic potentials.

The small size of the dyadic cleft (~ 4 × 10⁵ nm³ with ~ 10–40 RyRs)^{10, 11}, in combination with the relatively large proteins that reside in the cleft, results in a space in which Ca²⁺ diffusion is highly restricted. Figure 1B shows a representation of an LCC, RyR, and a single calmodulin (CaM) molecule in the dyad based directly on structural data^74–76. Models predict that during an AP, peak Ca²⁺ concentration in the dyad ranges from 100 to 1,000 μmol/L^{49, 50}, which corresponds to as few as 20–200 free Ca²⁺ ions⁷³. Therefore, application of laws of mass-action to analysis of signaling events mediated by this relatively small number of ion may not be justified⁷⁷. Rather, the stochastic motion of Ca²⁺ ions in the dyad may impart a degree of signaling noise between LCCs and RyRs, thereby influencing properties of CICR⁷³. In addition, the physical location and dimensions of dyad proteins may have considerable influence on motion of Ca²⁺ ions and hence, CICR.

Development of the nano-scale model is presented in detail elsewhere⁷³. Briefly, a simplified dyad was modeled using a 200 nm × 200 nm × 15 nm lattice containing 20 RyRs arranged in a 4 × 5 matrix. Four LCCs were positioned randomly across this lattice to achieve a 5:1 RyR:LCC ratio. The geometry of each LCC and RyR protein was modeled as shown in Fig. 1B, with each LCC tethering with one CaM. LCC gating was simulated stochastically using the model of Fig. 1A. The gating kinetics of the RyR were described using the four-state Markov model of Stern^33,78. Entry of Ca²⁺ ions into the dyad via open LCCs and RyRs was modeled as a Poisson process with rate governed by channel permeabilities measured experimentally⁷⁹. CDI of an LCC required that the two carboxyl-terminal Ca²⁺ binding sites of the associated CaM were occupied. Opening of an RyR required that Ca²⁺ was bound to all four activation sites. RyRs were assumed to inactivate when Ca²⁺ was bound to at least one out of four distinct inactivation sites. Sarcolemmal anionic sites acted as Ca²⁺ buffers^{49, 50}. The joint positions of Ca²⁺ ions present in the dyad were modeled as a Brownian motion in a potential field, describing both interactions of Ca²⁺ ions with other Ca²⁺ ions as well as electrostatic potentials based on the Fokker-Planck equation (FPE)⁸⁰. We generated sample paths of Ca²⁺ ion movement in the dyad using a finite difference representation of the FPE that can be interpreted as a spatially discrete Markov process as described by Wang et al⁸¹.

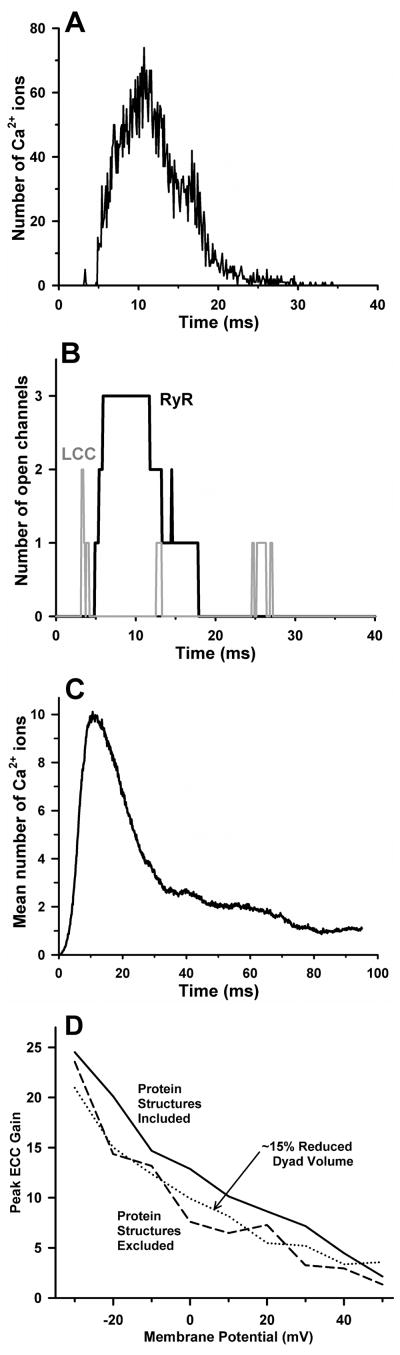
A 10 ms simulation of a model dyad containing only one LCC located at its center at a membrane potential of 0 mV generated an average of ~ 0.5 Ca²⁺ ions within a 50 nm radius of the LCC (see Fig. 8 of⁷³), with a minimum of zero and a maximum of 7 Ca²⁺ ions, corresponding to 98.7 μmol/L [Ca²⁺]_d. A similar protocol using a single RyR in the SR membrane (in which the RyR is initially open) generated an average of ~ 22.8 Ca²⁺ ions. The number of Ca²⁺ ions peaked at 49 during Ca²⁺ release, which corresponds to a concentration of ~ 0.7 mmol/L Ca²⁺, similar to the concentration of Ca²⁺ found in the JSR⁸². With a coefficient of variation of 64%, RyR gating produces a high degree of variability in the number of dyadic Ca²⁺ ions, showing that the LCC-RyR signaling involved in CICR at the dyad level is a noisy process mediated by tens of Ca²⁺ ions.

Panels A and B of Figure 2 demonstrate fundamental features of a representative Ca²⁺ release event in a dyad in response to a voltage clamp to 0 mV at time zero. Panel A shows the number of Ca²⁺ ions in the dyad, and panel B shows the number of LCCs (gray line) and RyRs (black line) that are open as a function of time during the release event. Two LCCs open at ~ 3 ms following the voltage clamp, and Ca²⁺ influx into the dyad triggers the opening of 3 RyRs 1–2 ms later, which inactivate after ~ 7 ms, ~ 9 ms, and ~ 13 ms, respectively. The temporal shape of the Ca²⁺ signal in the dyad (Fig. 2A) is closely correlated to the number of open RyRs (Fig. 2B). Figure 2C shows the average dyadic Ca²⁺ signal, calculated by averaging the number of Ca²⁺ ions at each point in time across 400 independent dyads. The duration of the average local Ca²⁺ transient shown in Panel C is ~ 20 ms (at half-maximal amplitude), similar to that measured for Ca²⁺ spikes in myocytes^{21, 24, 52}.

Figure 2.

A CICR event in a single dyad evoked by a 0 mV voltage clamp step at time zero (from⁷³). (A) The number of free Ca²⁺ ions in the dyad volume as a function of time. (B) The number of open RyRs (black solid line) and the number of open LCCs (gray solid line) in the dyad during the release event depicted in panel A. (C) The average number of free Ca²⁺ ions in the dyad as calculated from 400 independent dyads. (D) ECC gain as a function of membrane potential for the baseline model which includes space-filling geometric models of protein structure in the dyad (solid line), for the model with protein structures excluded (dashed line), and for a modified model with dyad height reduced from 15 nm to 13 nm and protein structures excluded (dotted line).

We demonstrated that ECC gain is a robust and reproducible measurement of CICR because the variability in gain that arises from the stochastic gating of LCCs and RyRs is small for a whole-cell population of dyads at potentials near and above 0 mV (see Fig. 11 of⁷³). The functional influence of protein structures on ECC is shown in Fig. 2D. Peak ECC gain obtained for the baseline model (solid line) is compared to that for the model in which LCC, RyR, and CaM molecule structures were omitted (dashed line). Ca²⁺ binding site locations for the no-structure simulations remain at the same positions in space as when the protein structures are in place. Over a wide range of potentials, the peak ECC gain is decreased upon removal of the protein structures from the dyad. The protein structures occupy ~ 15% of the dyad volume. In order to show that the difference in ECC gain in the presence vs. absence of protein structures is not simply attributable to the difference in Ca²⁺-accessible dyad volume, peak ECC gain was obtained with protein structures absent and dyad volume reduced by ~ 15% (dotted line). ECC gain values for this model were clearly are not increased to the level obtained in the presence of protein structures. These data indicate that the physical shape and configuration of dyad proteins influences Ca²⁺ diffusion during CICR in such a way as to enhance ECC gain. In addition, the probability of triggering a release event was 0.152 with protein structures excluded and 0.105 with protein structures intact, a 44% increase. These data suggest that when LCCs are directly apposed to RyRs, the diffusion obstacle imposed by the structure of RyRs leads to an increase in the probability that trigger Ca²⁺ ions bind to activation sites on the RyRs, and hence increases ECC gain.

These data demonstrate that at the level of single dyads, CICR is a highly noisy process and that models based on laws of mass action may not accurately capture dyadic Ca²⁺ dynamics. Further, in ensembles of dyads, the fundamental properties of local control of CICR arise de novo as a consequence of the underlying physical structure and channel gating properties, including voltage-dependence of ECC gain. Finally, the physical shape and location of RyRs relative to LCCs is likely to have a major influence on properties of CICR.

The Integrated Local-Control Model of the Cardiac Myocyte

The Greenstein-Winslow³⁴ model of the cardiac ventricular myocyte was the first to fully integrate mechanisms of local control of CICR into a model of the cardiac AP. This was accomplished by updating and extending the common-pool model of Winslow et al.³⁸ to include a population of dyadic Ca²⁺ release units (CaRUs). In essence, this integrated local control model is generated from the nano-scale model by simplifying the dyad description to that of well-mixed Ca²⁺ compartment, and incorporating a large population of such dyads into a whole-cell model. Detailed properties of the nano-scale model (e.g. effect of protein structure on ECC gain) are retained in this integrated model by adjusting parameters that influence the effectively equivalent property at this scale (e.g. effective Ca²⁺ sensitivity of RyRs). In this model, local interactions of individual LCCs with nearby RyRs are simulated stochastically, with these local simulations embedded within the numerical integration of the ordinary differential equations (ODEs) describing ionic and membrane pump/exchanger currents, SR Ca²⁺ cycling, and time-varying cytosolic ion concentrations.

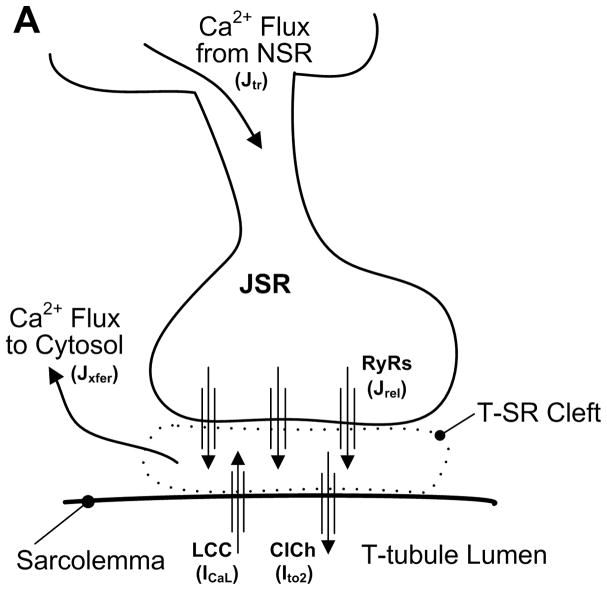
The Greenstein-Winslow model was formulated to capture fundamental properties such as graded release, while at the same time needed to be computationally tractable. A full mathematical description of the stochastic state models, dynamical equations, parameters, and initial conditions defining the myocyte model are given in Appendix I of ³⁴. Figure 3A shows a schematic of the CaRU model which is intended to mimic the properties of Ca²⁺ sparks in the t-tubule/SR (T-SR) junction. Figure 3B shows a cross-section of the model T-SR cleft, which is divided into four individual dyadic subspace compartments arranged on a 2 × 2 grid. Each subspace compartment contains a single LCC and 5 RyRs in its JSR and sarcolemmal membranes, respectively⁸³. The division of the CaRU into four subunits allows for the possibility that an LCC may trigger Ca²⁺ release in adjacent subspaces (i.e., RyR recruitment). Upon activation of RyRs, subspace [Ca²⁺] will become elevated. This Ca²⁺ freely diffuses to either adjacent subspace compartments (J_iss) or into the cytosol (J_xfer). The local JSR compartment is refilled via passive diffusion of Ca²⁺ from the NSR compartment (J_tr). The number of active LCCs was chosen such that the amplitude of the ensemble current summed over all LCCs corresponds to whole-cell measurements in canine myocytes⁸⁴ which corresponded to 50,000 LCCs (12,500 CaRUs) and agrees with experimental estimates of LCC density⁷⁹. LCC and RyR gating were based on previous models^{31, 85}, and the channels (ClCh) that carry the Ca²⁺-dependent transient outward chloride (Cl⁻) current (I_to2) are included within the CaRU.⁸⁶ A detailed description of the local control simulation algorithm is given in Appendix II of ³⁴. Stochastic fluctuations in model outputs are the natural result of the ensemble behavior of ion channel and CaRUs, and introduce a degree of variability to simulation output and can be physiologically important to understanding some physiological phenomena such as EADs⁸⁷.

Figure 3.

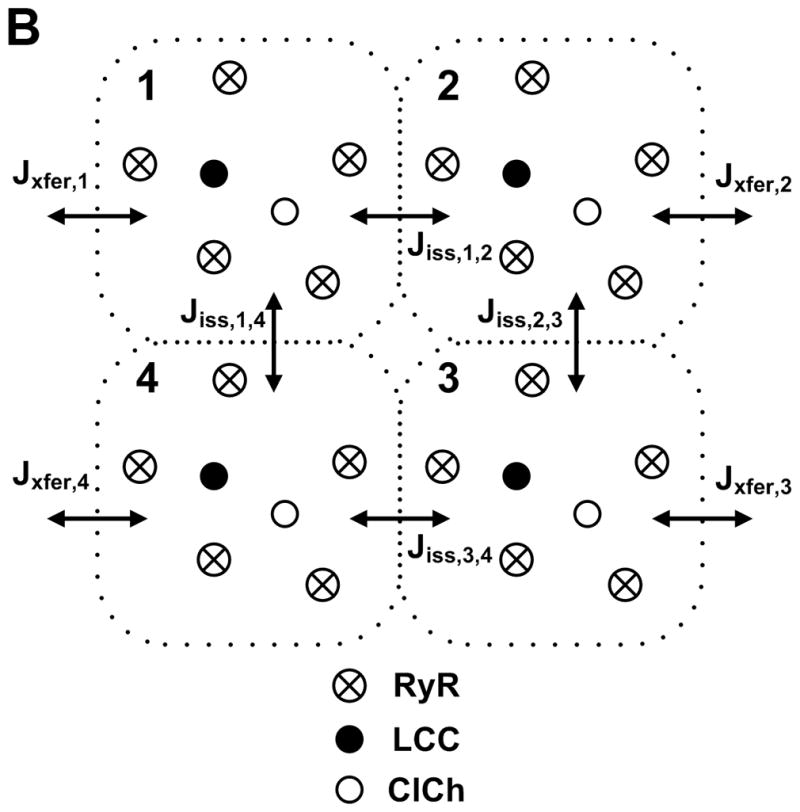
Schematic representation of the CaRU³⁴. (A) Trigger Ca²⁺ influx through the LCCs enters into the T-SR cleft (dyadic space), RyRs and ClChs open, local Ca²⁺ passively diffuses into the cytosol, and JSR Ca²⁺ is refilled via passive diffusion from the NSR. (B) The T-SR cleft (shown in cross-section) is composed of four dyadic subspace volumes, arranged on a 2 × 2 grid, each containing 1 LCC, 1 ClCh, and 5 RyRs. Ca²⁺ in any subspace may diffuse to a neighboring subspace (J_iss) or to the cytosol (J_xfer).

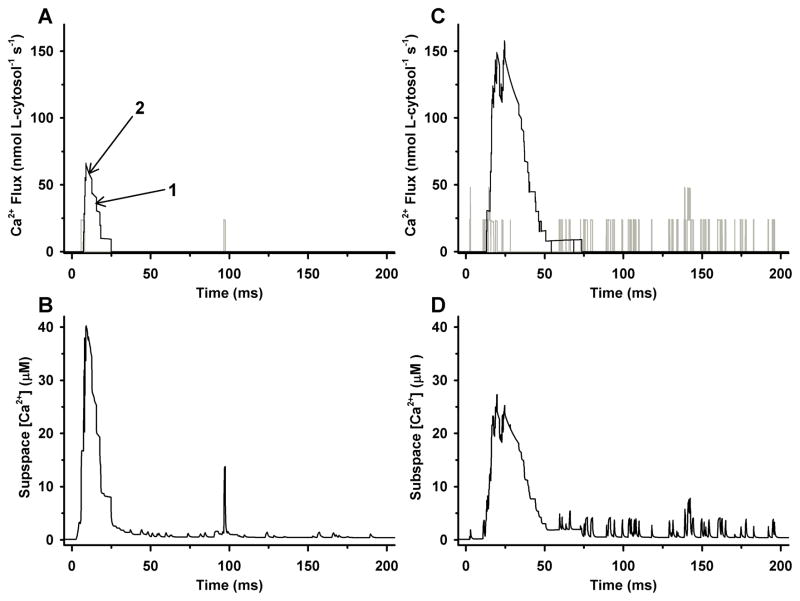
Panels A and B of Fig. 4 demonstrate the most elementary model release event during CICR, as triggered by a single LCC at 0 mV. Ca²⁺ flux through an LCC (gray line) and the net SR Ca²⁺ release flux through the five adjacent RyRs (black line) are shown in Fig. 4A. Local JSR release flux is triggered by the first LCC opening (at ~ 5 ms) and lasts ~20 ms, far longer than the LCC open duration (<1 ms). The amplitude of the release flux varies with the number of open RyRs and the local Ca²⁺ gradient across the JSR membrane. Figure 4B shows the corresponding subspace [Ca²⁺], which reaches a peak value of ~ 40 μmol/L. Total Ca²⁺ influx through the set of four LCCs (gray line) and the net SR Ca²⁺ release flux through the set of 20 RyRs (black line) that make up a single T-SR junction are shown in Fig. 4C. LCC Ca²⁺ influx rises to a level consistent with two open channels within a short time following the initiation of the pulse. The spatial average of Ca²⁺ concentration in the four subspace compartments of the CaRU is intended to represent a Ca²⁺ spark-like event (Fig. 4D), and has duration of 25 ms (at half-maximal amplitude) similar to that measured in myocytes (20–50 ms) ^{21, 24, 52}.

Figure 4.

Sample results for a single CaRU in response to a 200-ms voltage clamp to 0 mV³⁴. (A) Ca²⁺ flux through a single LCC (gray line) and through the set of five RyRs (black line) within a single dyadic subspace compartment. Arrows 1 and 2 highlight RyR number and Ca²⁺ gradient driven changes in SR Ca²⁺ release flux, respectively. (B) Subspace [Ca²⁺] associated with the events of panel A. (C) Ca²⁺ flux through the set of four LCCs (gray line) and the set of 20 RyRs (black line) within a single CaRU. (D). Mean subspace [Ca²⁺] in the four subspace compartments associated with the events in the CaRU described in panel C.

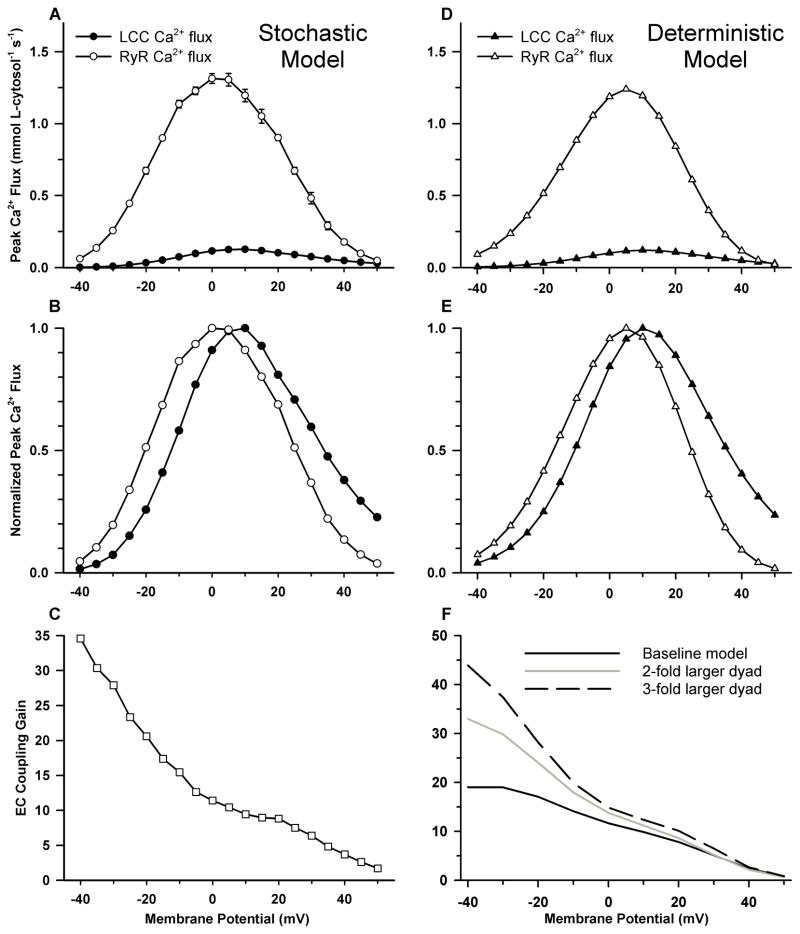
Previous experimental studies^{25, 88} and mathematical models^{27, 33} have shown significant differences between the voltage dependence of I_CaL and RyR Ca²⁺ release flux even though SR Ca²⁺ release is exclusively controlled by LCC Ca²⁺ entry. These differences underlie the phenomenon of “variable” EC coupling gain. Figure 5A shows the voltage dependence of LCC (filled circles) and RyR (open circles) Ca²⁺ flux. In Fig. 5B, the peak fluxes of Fig. 5A have been normalized based on their respective maxima. Maximal LCC Ca²⁺ influx occurs at 10 mV, whereas maximal RyR Ca²⁺ release flux occurs at 0 mV. EC coupling gain is plotted as a function of voltage in Fig. 5C (triangles), and is monotonically decreasing with increasing membrane potential in agreement with experimental measurements^{24, 25, 88}. In the negative voltage range LCC open probability is submaximal, leading to sparse LCC openings (i.e. submaximal recruitment of CaRUs), but large amplitude unitary currents efficiently trigger adjacent RyRs, resulting in high values of ECC gain. More CaRUs are recruited with increasing membrane potential as a result of increasing LCC open probability, however ECC gain decreases with increasing membrane potential because the higher LCC open probability leads to redundancy in LCC openings as a result of which a fraction of LCCs are attempting to trigger refractory RyRs and at even higher potentials the decrease in LCC unitary current amplitude reduces the fidelity of local coupling between LCCs and RyRs.

Figure 5.

Ca²⁺ fluxes and ECC gain for the Greenstein-Winslow model (panels A-C)³⁴ and coupled LCC-RyR model (panels D-F)⁷¹. (A) Mean peak LCC (filled circles) and RyR (open circles) Ca²⁺ flux amplitudes as a function of membrane voltage. (B) Normalized peak Ca²⁺ fluxes (data of panel A). (C) ECC gain under control conditions. (D) Peak LCC (filled triangles) and RyR (open triangles) Ca²⁺ flux amplitudes. (E) Normalized peak Ca²⁺ fluxes (data of panel D). (F) ECC gain for the baseline model (solid line), and models in which dyad size and number of channels per dyad is increased twofold (gray line), and threefold (dashed line).

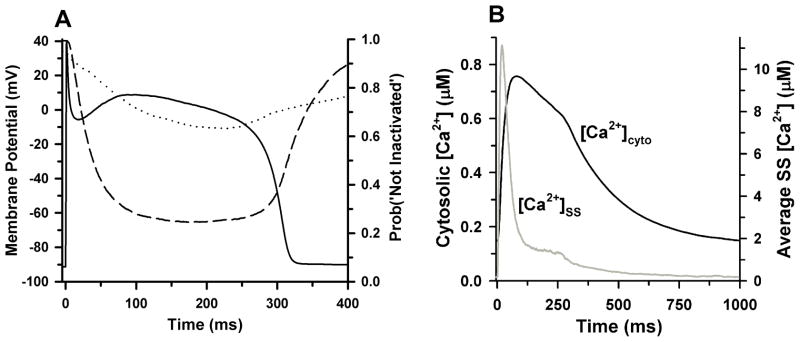
Figure 6 demonstrates the ability of the Greenstein-Winslow model to reconstruct APs and cytosolic Ca²⁺ transients of normal canine midmyocardial ventricular myocytes. In Fig. 6A, a normal 1-Hz steady-state AP is shown (solid black line). AP properties are similar to those measured in experiments³⁹, with APD of ~300 ms. Also shown in Fig. 6A are the kinetics of CDI (dashed line) and VDI (dotted line), demonstrating that this model conforms with experimental findings that indicate LCC CDI is strong while VDI is relatively slow and incomplete^{46, 47}. Figure 6B shows cytosolic (black line) and mean subspace (gray line) Ca²⁺ transients. The cytosolic Ca²⁺ transient peaks at ~ 0.75 μmol/L and lasts longer than the duration of the AP whereas Ca²⁺ in the subspace reaches ~11 μmol/L on average, and equilibrates to near-cytosolic levels rapidly, within ~ 100 – 150 ms. The simulations of Figs. 4–6 demonstrate that this multi-scale model faithfully reproduces a variety of experimental observations that span from single-channel to whole myocyte.

Figure 6.

AP and Ca²⁺ transients at 1-Hz steady state pacing³⁴. (A) Membrane potential (solid line, left axis), and probability that CDI and VDI (dashed and dotted lines, respectively, right axis) has not occurred as a function of time under normal conditions. (B) Cytosolic (black line, left axis) and mean subspace (gray line, right axis) Ca²⁺ concentrations corresponding to the AP simulated in panel A.

The Coupled LCC-RyR Local Control Model

A limitation of the Greenstein-Winslow³⁴ local control model is that it is far more computationally demanding than deterministic models. To address this, we recently developed an analytical “first-principles” approach for deriving simplified mechanistic models of CICR by applying a carefully chosen set of approximations that allow for the ensemble behavior of CaRUs to be represented by a low dimensional system of ODEs, eliminating the need for computationally expensive stochastic simulations. This model, termed the coupled LCC-RyR model⁷², retains the biophysically based description of local control of CICR, and captures its key properties including graded SR Ca²⁺ release and voltage dependent ECC gain and is the basis of a deterministic local control model of the cardiac myocyte⁷¹.

Following the methods described by Hinch et al⁷², LCC and RyR models composed of the minimum number of states necessary to capture fundamental dynamics of channel gating were designed and constrained based on experimental data sets. A simplified CaRU model consisting of only a single LCC and a single RyR was formed. The relatively fast diffusion (i.e. short diffusion distance) of Ca²⁺ from dyad to cytosol (as compared to the time scale of LCC and RyR gating)⁶² allows for the application of a steady state approximation for dyadic Ca²⁺ diffusion. This allows the resulting CaRU to be analytically simplified into a single Markov state model in which each state represents a unique configuration of channel states for the combined set of LCCs and RyRs in the CaRU. In the resulting formulation, the dynamics of a population of CaRUs can be described by a deterministic set of coupled ODEs. Other elegant methods have been derived to improve computational efficiency of ECC simulations as well^{37, 89, 90}, but have not yet been implemented in an integrated myocyte model using biophysically detailed channel models.

Panels D–F of Figure 5 demonstrate that the deterministic coupled LCC-RyR model reproduces the fundamental quantitative properties of CICR in a similar manner to its stochastic predecessor³⁴ in panels A–C. The effect of dyad size on ECC was analyzed using models with 2-fold and 3-fold larger dyads (Fig. 5F, gray and dashed lines, respectively). In each case the number of dyads per cell was reduced such that the total number of LCCs and RyRs per cell was conserved, and the RyR/LCC stoichiometry was unchanged. At potentials more negative than −10 mV, the increase in CaRU size yields a substantial increase in gain such that the ECC gain curve acquires the steep slope similar to those observed experimentally^{24, 25}. This arises as a result of a model-dependent increase in the functional RyR/LCC ratio because it is likely that a single LCC opening will trigger regenerative release from most RyRs in a CaRU. The coupled LCC-RyR local control model reconstructs APs and Ca²⁺ transients of canine midmyocardial ventricular cells (see Fig. 6 of ⁷¹ for details) at a variety of pacing frequencies, and similar to the Greenstein-Winslow model, has an I_CaL which exhibits strong CDI and weak VDI. The ability of this model to reproduce all of the core features of the stochastic local control model in an efficient manner has made it a candidate for use in large scale tissue simulations⁹¹.

Additional domains of localized Ca²⁺ signaling

There have been a number of recent models in which Ca²⁺ signaling in localized compartments other than the dyad have been investigated. Experimental measurements of NCX current¹⁸ have provided evidence that this transport mechanism, and possibly the sarcolemmal Ca²⁺-ATPase, may be driven by subsarcolemmal Ca²⁺, which is elevated relative to Ca²⁺ concentration in the bulk cytosol as a result of Ca²⁺ diffusion limitations. The rabbit ventricular myocyte model of Shannon et al⁵⁴ was the first to introduce a subsarcolemmal Ca²⁺ compartment, and a number of recent models now include a subsarcolemmal Ca²⁺ compartment^{35, 61, 92, 93}. Elevated subsarcolemmal Ca²⁺ may have a particularly important influence on NCX. It has been suggested that elevated subsarcolemmal Ca²⁺ during the early phase of the AP may modulate NCX reversal potential, reducing entry of Ca²⁺.⁹⁴ More needs to be done to quantify the functional consequences of sensing subsarcolemmal Ca²⁺ and NCX function. This is particularly important given the role of NCX in shaping AP properties and its possible role in the generation of delayed after-depolarizations. Very interestingly, the Pasek et al⁹⁵ model of the guinea pig ventricular myocyte includes a diffusive t-tubule system with a heterogeneous distribution of ion channels between tubular and surface membranes, thus introducing a new extracellular compartment. This model predicted that Ca²⁺ depletion and K⁺ accumulation in the t-tubule during APs leads to a reduction in SR Ca²⁺ load, which would impact ECC.

There is now substantial electrophysiological evidence that extra-dyadic processes also influence CICR. Evidence suggests that Ca²⁺ entry via reverse-mode NCX activity may either trigger or modulate CICR^{96, 97} and that CICR modulates NCX function⁹⁸. NCX has also been identified in the t-tubules at a high level. However, the precise location of NCX within⁹⁹ and/or near¹⁰⁰ the dyad remains uncertain. Lines et al¹⁰¹ used a model of the cardiac dyad which accounted for details of both Ca²⁺ and Na⁺ diffusion to demonstrate that if fast Na⁺ channels are in the dyadic cleft then NCX (driven by the local elevation in [Na⁺]) can influence the timing of local CICR. Recent evidence also suggests NCX may form a functional complex with NKA and its accessory protein phospholemman¹⁰². Furthermore, one study suggests that NCX and NKA constitute a physically interacting molecular complex with ankyrin-B and an inositol 1,4,5-phosphate operated Ca²⁺-releasing channel (InsP₃R) in the t-tubules that is distinct from the LCC-RyR complex¹⁰⁰. This hypothetical “ankyrin-B complex” may play an important role in the regulation of local Na⁺ and Ca²⁺ concentrations and possibly modulate CICR by regulating the boundary conditions on dyadic Ca²⁺. Again, it is likely that these regulatory interactions are mediated by small numbers of Ca²⁺ ions. This may be a common theme in cases where proteins interact over nanometer length scales.

Recent work also demonstrates that mitochondria are positioned near dyads^{103, 104}. Electron-dense structures that link the mitochondrial outer membrane with JSR, NSR, and t-tubules have been observed. These structures appear to be preferentially located, with one population forming attachments to NSR, and another set of bridges being near the dyadic cleft. Attachments to t-tubules were observed, but were rare. Ca²⁺ is taken up by mitochondria via the mitochondrial Ca²⁺-uniporter¹⁰⁵. Therefore, spatial co-localization of mitochondria near the dyadic cleft may give rise to an additional Ca²⁺-signaling micro-domain involved in the regulation of mitochondrial ATP production, and which modulates dyadic Ca²⁺ concentrations and Ca²⁺ diffusion between adjacent RyR couplons¹⁰⁶.

Regulation of CICR by cell signaling pathways

Cardiac proteins involved in CICR and ECC are primary targets for regulation via cell signaling pathways and models have played a key role in understanding this regulation (see accompanying article in this series by Yang and Saucerman). The Greenstein-Winslow³⁴ model was extended to study effects of the β-adrenergic signaling pathway by the incorporation of protein kinase A (PKA)-mediated functional changes in target proteins¹⁰⁷ and could explain PKA-mediated changes in AP shape, dissected the specific effects of PKA-mediated phosphorylation of LCCs and RyRs on the voltage-dependent gain of CICR, and predicted a mechanism by which increasing levels of LCC phosphorylation could lead to increased frequency of EADs⁸⁷. Saucerman et al¹⁰⁸ developed a differential-algebraic model of the β-adrenergic signaling pathway and incorporated it into the rabbit myocyte model of Puglisi et al¹⁰⁹ and used this model to quantitatively understand and predict effects of specific molecular perturbations on cAMP dynamics and contractility via changes in function of target proteins resulting from altered phosphorylation dynamics. Recently, the model of Saucerman et al¹⁰⁸ was incorporated into the guinea pig ventricular model of Faber and Rudy¹¹⁰ in a study of the role of β-adrenergic agonists and antagonists in long-QT syndrome¹¹¹.

An important Ca²⁺ cycling regulatory mechanism of recent interest is the signaling pathway involving Ca²⁺/CaM-dependent protein kinase II (CaMKII), whose targets proteins include LCCs, RyRs, PLB, and the SERCA pump, as well as Na⁺ and K⁺ channels¹¹². Evidence suggests that CaMKII is directly associated with its target proteins^{113, 114} (implying that CaMKII signaling occurs locally in the dyadic junction), and that CaMKII activity is elevated in heart failure¹¹⁵. The first model of the cardiac myocyte to integrate the role of CaMKII was presented by Hund and Rudy⁴³, which predicted that CaMKII plays an important role in the rate dependent properties of the cytosolic Ca²⁺ transient, but not APD. Saucerman and Bers⁹³ incorporated models of CaM, CaMKII, and calcineurin (CaN) into the Shannon et al⁵⁴ model in order to better understand the functional consequences of the different affinities of CaM for CaMKII and CaN during APs. The model predicted that in the cardiac dyad, Ca²⁺ levels lead to a high degree of CaM activity which results in frequency-dependent CaMKII activation and constitutive CaN activation, whereas the lower Ca²⁺ levels in the cytosol only minimally activate CaM, which allows for gradual CaN activation, but no significant activation of CaMKII. Grandi et al¹¹⁶ developed a model of CaMKII overexpression in the rabbit ventricular myocyte, including the role of CaMKII phosphorylation of fast Na⁺ channels, LCCs, and the transient outward K⁺ current (I_to1), which revealed a net effect of APD reduction with CaMKII. Recently, Hashambhoy et al³⁶ described dynamic CaMKII phosphorylation of LCCs in an extension of the Greenstein-Winslow³⁴ model. In this model it is assumed that a single CaMKII holoenzyme is tethered to each LCC, each CaMKII monomer can transition among a variety of activity states (see Fig. 2 of Hashambhoy et al³⁶), and CaMKII monomers can catalyze phosphorylation of individual LCCs. This model demonstrated that CaMKII-dependent shifts of LCC gating patterns into high activity gating modes may be the underlying mechanism of a variety of experimentally observed phenomena associated with I_CaL facilitation. Hashambhoy et al⁵⁵ further expanded this model to include CaMKII-dependent regulation of RyRs and demonstrated that under physiological conditions, CaMKII phosphorylation of LCCs ultimately has a greater effect on RyR leak flux and APD as compared with phosphorylation of RyRs (Fig. 7A). APD was shown to correlate well with a CaMKII-mediated shift in modal gating of LCCs (Fig. 7B).

Figure 7.

(A) Simulated Results from a 1-Hz AP pacing protocol under different LCC and/or RyR phosphorylation conditions. (B) APD as a function of average LCC phosphorylation levels. Fully phosphorylated LCCs gate in Mode 2 which exhibit long duration openings.⁵⁵

Future Directions in ECC Modeling

A number of mechanistic questions remain unanswered in cardiac ECC. As noted above, controversy remains as to mechanisms involved in termination of SR Ca²⁺ release. The high degree of technical difficulty involved in experimentally assessing RyR and CaRU properties under physiological conditions has resulted in limited and difficult-to-reproduce measures of certain key features of CICR such as RyR gating properties (e.g. coupled gating of RyRs), the degree of local JSR Ca²⁺ depletion associated with Ca²⁺ sparks (Ca²⁺ blinks), and the rate of local refilling of JSR. Models have been able to reveal and demonstrate multiple possible mechanisms of SR Ca²⁺ release termination, but the lack of consensus on a single experimentally verified mechanism has allowed a variety of mathematical model formulations of SR Ca²⁺ release to coexist. Improved resolution of both structural and functional imaging of ECC domain ultrastructure and localized Ca²⁺ dynamics will help to resolve these questions and to further validate and refine nano- and microscale models of ECC^{10, 11}. Additional areas of recent interest, where mechanistic models have yet to be fully developed, include regulation of ECC by mitochondrial Ca²⁺ dynamics (see above) and functional alteration of key ECC proteins arising from oxidative-stress (e.g. effects of mitochondria-derived reactive oxygen species) associated with heart failure. Recently, Tadross et al¹¹⁷ used a combination of elegant models and experiments to elucidate a mechanism underlying Ca²⁺ channel CDI, by which CaM in complex with an LCC, can sense and decode local and global Ca²⁺ signals. The implications of this mechanism on our understanding of dyadic Ca²⁺ dynamics and cardiac ECC have yet to be studied with models. Finally, the mathematical techniques used in developing models that span multiple biological scales are not adequate for all applications and themselves are an ongoing area of theoretical study (see ref 37 for a recent review of model reduction methods). Mechanistic model reproduction of phenomena such as Ca²⁺ alternans and delayed after depolarizations depend on the ability of a Ca²⁺ spark to trigger neighboring release sites and form intracellular Ca²⁺ waves⁴⁸. While model reduction techniques have captured important features of local control of ECC (as described above), the lack of low-dimensional models that can capture Ca²⁺ wave mechanisms has made it difficult to extend such models to the tissue and whole heart level in order to study how these events trigger large scale arrhythmias. The development of models that can accomplish this task in a tractable formulation will greatly improve our ability to understand the mechanistic links between disease-related changes in ECC and arrhythmia.

Conclusion

Integrative modeling of cardiac ECC and myocyte physiology has played a critical role in revealing mechanistic insights at and across a range of biological scales. At the smallest scale, models have shed light on how Ca²⁺ ions and proteins in the cardiac junction interact during LCC and RyR gating. Expanding our view, simplified models of individual release sites have allowed for detailed simulations that reveal determinants of Ca²⁺ spark activation and termination properties. On an intermediate scale, models of independent dyadic junctions have revealed how characteristic whole-myocyte properties of ECC emerge from the ensemble behavior of individual release sites. Incorporation of such Ca²⁺ release sites into whole-cell models elucidates the bidirectional interaction between ECC and membrane potential that determine properties of the cardiac AP. Incorporation of ECC regulatory signaling pathways into models has further refined our understanding of this integrative system (see accompanying article in this series by Yang and Saucerman). At the highest scale, such models can be used as building blocks for large scale tissue and whole heart models which can reveal how wave propagation in a normal heart tissue can degenerate into an arrhythmia as a result of defective ECC (see accompanying articles in this series by Weiss et al and Trayanova et al). The continuum of biological scales spanned by these models leads to the formation of powerful multi-scale approaches whereby macroscopic phenotypes (e.g. steep ECC gain curve) can be understood as resulting from microscopic mechanisms (e.g. Ca²⁺ funneling by RyR protein geometry). In the same way that Hodgkin and Huxley formed a mathematical framework that now defines the way in which we conceptualize ion channel function, modern multi-scale models of cardiac ECC have provided a framework for understanding complex ECC mechanisms, interpreting experimental data, and making mechanistic predictions that guide experimental design.

Non-standard Abbreviations and Acronyms

AP

action potential

APD

action potential duration

CaM

calmodulin

CaMKII

Ca²⁺/calmodulin-dependent protein kinase II

CaN

calcineurin

CaRU

Ca²⁺ release unit

CDI

Ca²⁺-dependent inactivation

CICR

Ca²⁺-induced Ca²⁺ release

ClCh

Ca²⁺-dependent Cl⁻ channel

EAD

early after depolarization

ECC

excitation-contraction coupling

FPE

Fokker-Plank equation

JSR

junctional sarcoplasmic reticulum

LCC

L-type Ca²⁺ channel

LRII

Luo-Rudy phase II

NCX

Na⁺-Ca²⁺ exchanger

NSR

network sarcoplasmic reticulum

ODE

ordinary differential equation

PKA

protein kinase A

PLB

phospholamban

RyR

ryanodine receptor

SERCA pump

SR Ca²⁺ ATPase

SR

sarcoplasmic reticulum

T-SR

t-tubule/sarcoplasmic reticulum

VDI

voltage-dependent inactivation