Semi-Automated Atlas-based Analysis of Brain Histological Sections

Abstract

Quantifying the location and/or number of features in a histological section of the brain currently requires one to first, manually register a corresponding section from a tissue atlas onto the experimental section and second, count the features. No automated method exists for the first process (registering), and most automated methods for the second process (feature counting) operate reliably only in a high signal-to-noise regime. To reduce experimenter bias and inconsistencies and increase the speed of these analyses, we developed Atlas Fitter, a semi-automated, open-source MatLab-based software package that assists in rapidly registering atlas panels onto histological sections. We also developed CellCounter, a novel fully-automated cell counting algorithm that is designed to operate on images with non-uniform background intensities and low signal-to-noise ratios.

1. Introduction

As part of the scientific process, investigators often mark biological tissue in a variety of ways: e.g., using tissue-specific dyes, colorimetric assays for mRNA or protein expression levels, or through lesions. Typically, two measures are then taken: first, a determination of the location of the marking (e.g., “which areas of the brain have been marked?”) and second, a quantification of the extent of marking (e.g., “how many cells show immunoreactivity?”). Precision in either of these two steps is non-trivial. For the first step (localization) precision is particularly difficult when different regions of the experimental tissue are not obviously distinguishable. This is often the case with areas of the brain which are very different based on known function and connectivity, but which can look very similar to each other in typical stains (e.g. Nissl). The standard procedure in these cases is to register the experimental tissue sample with a standardized tissue atlas: a correspondence between distinguishable features in the experimental sample and similar features in the standardized atlas is established, points between the features are interpolated, and the subdivision into different areas found in the atlas can then be used to subdivide the sample into putatively different areas. This process is usually performed manually, which can be slow and potentially introduce human error. Here we present Atlas Fitter (available at http://brodylab.princeton.edu/wiki/index.php/AtlasFitter), a semi-automated, open-source Matlab software package that greatly aids and speeds up registering of 2-dimensional tissue sections onto standardized atlases.

The second non-trivial step referred to above, quantification of the extent of marking, can also benefit greatly from automation. We focus on the counting of marked cells. Current freely available automated cell-counting algorithms (e.g. ImageJ V1.42 automated nuclei counter plug-in V1.6 and cell counter plug-in, Pixcavator V2.3, and CellAnalyst V2.0) work best on images with uniform background intensity and a high signal-to-noise ratio, such as fluorescence images. But they fail on noisy colorimetric images, such as those acquired from in situ hybridization and immuno-histochemistry. Manual counting is, again, painstakingly slow, and subject to unintentional bias and experimenter inconsistencies. Here we present CellCounter (available at http://brodylab.princeton.edu/wiki/index.php/CellCounter), a fully automated cell counting algorithm designed to work well under noisy conditions.

2. Material and Methods

2.1 Generating wire-frame atlas

The Paxinos and Watson coronal rat brain atlas (Paxinos and Watson, 2005) was manually traced using AtlasTracer (available at http://brodylab.princeton.edu/wiki/index.php/AtlasTracer), a custom written open source MatLab program.

2.2 Ibotenic acid lesion

A solution of 10mg/mL ibotenic acid (Sigma) was injected via a glass pipette (tip 1cm long, 10–30um outer diameter) driven by a nanoject (Drummond Scientific). Between 110 and 140nL were injected per site (4 sites spaced 1mm AP), 28nL per pulse, 5s inter-pulse interval, 1 minute following last pulse before removal of pipette. Animals euthanized for histology 12 days following lesion.

2.3 Nissl stain

Animals were transcardially perfused with 4% paraformaldehyde, brains were postfixed overnight, 50um sections were then cut on a vibratome, and sections were mounted on gelatin-subbed slides. Staining consisted of the following steps: 30min 50% chloroform 50% ethanol; 2min each of 95%, 70%, and 50% ethanol; water rinse; 30s 0.5% cresyl violet; water rinse; 2min each of 50%, 70%, and 95% ethanol; 95% ethanol with 1% glacial acetic acid until contrast develops; 2min each 2× 100% ethanol and 2× xylenes. Sections were then coverslipped with Permount. Images are a tiled mosaic captured at 10× magnification on a brightfield microscope.

2.4 In situ hybridization

Animals were transcardially perfused with 100mL 0.05% heparin in 0.9% saline followed by 250mL of 4% paraformaldehyde in PBS. Brains were then post-fixed and cryoprotected for 3 days at room temperature in 4% PFA 20% sucrose in PBS, followed by freezing and sectioning (50um) on a cryostat at −23°C. AP series contain every 8^th section. Staining consists of the following steps: 10min 4% PFA in PBS; 5min each 2x PBS; 10min 6ug/mL ProteinaseK, 0.1% Tween in PBS; 5min 0.2% glycine in PBS; 10min 0.25% acetic anhydride, 1.33% triethanolamine, 0.18% HCl; 30min 1% Triton X-100 in PBS; 5min each 3x PBS; 2 hours prehyb solution (50% formamide, 5x SSC, 5x Denharts, 250ug/mL yeast RNA (Sigma), 500ug/mL Herring Sperm DNA (Sigma)) coverslipped at 63°C; 5min 2x each 2x SSC remove coverslips; overnight hyb solution (300ng probe per mL prehyb, probe heated 80°C 5min then 10min on ice) at 63°C; 30min 2x each 2x SSC at 63°C remove coverslips; 40min 2x each 0.2x SSC 63°C; 5min 0.2x SSC room temperature; 5min B1 buffer (0.1M Tris pH 7.5, 0.15M NaCl); 1 hour 10% HINGS (heat inactivated goat serum) in B1; overnight 1:5000 anti-DIG 1% HINGS in B1 at 4°C; 5min 3x each B1; 5min B3 buffer (0.1M NaCl, 0.05M MgCl₂, 0.1M Tris pH 9.5, filtered); 6–12 hours 0.324mg/mL NBT, 0.166mg/mL BCIP in B3; 30s 0.1M Tris pH 9.5, 0.01M EDTA; mount with Crystal Mount. Images were captured on a Leica DMRA2 microscope with a 12V 100W halogen lamp illumination (set at 11V with a 2 lens collector and a grooved diffusing screen) using a Leica DFC490 camera (8 bit), a 1.25× 0.04NA PL Fluotar objective, and Leica Application Suite V3.1.0 software (flat field and white balance features enabled).

3. Results

3.1 Atlas Fitter

Atlas Fitter employs a range of automated and manual tools to register an atlas panel onto a 2-dimensional histological section.

3.1.1 Atlas panel choice

The first step is to determine which panel of the atlas best corresponds to the experimental section. If the user has only a single section, Atlas Fitter still requires this selection to be performed manually. Very often, however, histological sections are part of a series, i.e., each section is a flat slice from a vertical stack of slices. In this case, the user manually selects the atlas panels that best correspond to the first and to the last histological sections. Assuming that the spacing between slices was uniform, Atlas Fitter will then use linear interpolation to suggest the atlas panel that best corresponds to each of the remaining sections.

3.1.2 Non-uniform image registration

Having chosen the best-corresponding atlas panel (3.1.1), the next step is to establish a map of locations within the atlas panel to locations in the experimental slice. Atlas Fitter assumes that digitized images of both the atlas panels and the experimental section are available. The question is then what transformation from one image to the other is required to result in the best match between the two images. For small sections usually subject to little torsion, a global rotation, translation, and scaling of the atlas are likely to suffice. More commonly, however, experimental sections are subject to several different forces across their extent: one part of the section may have been twisted or stretched, while another may be relatively intact. To address this problem, we use a landmark-based, non-uniform transformation from one image to the other. Rather than warping the histological section (Gefen et al., 2003; Ju et al., 2006) and potentially altering one’s data, here we warp the atlas to match the section as-is.

Atlas Fitter first automatically finds the outer boundaries of the experimental tissue section. This is done using a simple intensity threshold for edge detection, together with “opening” and “closing” morphological filters (Ronse and Heijmans, 1991; Serra, 1982) to smooth over any small bumps (opening) or tears (closing) that may occur along the edge of the tissue. Here we typically lowpass filter the image with a 10 pixels standard deviation Gaussian function, use a threshold defined in the green color channel, and then apply a 50 pixel diameter disk as the opening and closing filter structuring element. The specific parameters for the edge detection can be tuned to work on any magnification, tissue type, and stain combination.

The user is then asked to identify a minimum of three landmark points on the outer boundary of the atlas panel, together with their corresponding locations in the experimental image (Figure 1A). The locations of the remaining boundary points are then linearly interpolated between the manually defined landmarks along the detected tissue boundary (maintaining the relative direct distance between points not necessarily the distance along the traced boundary). For each boundary point a horizontal and vertical translation are now defined according to Equation 1.

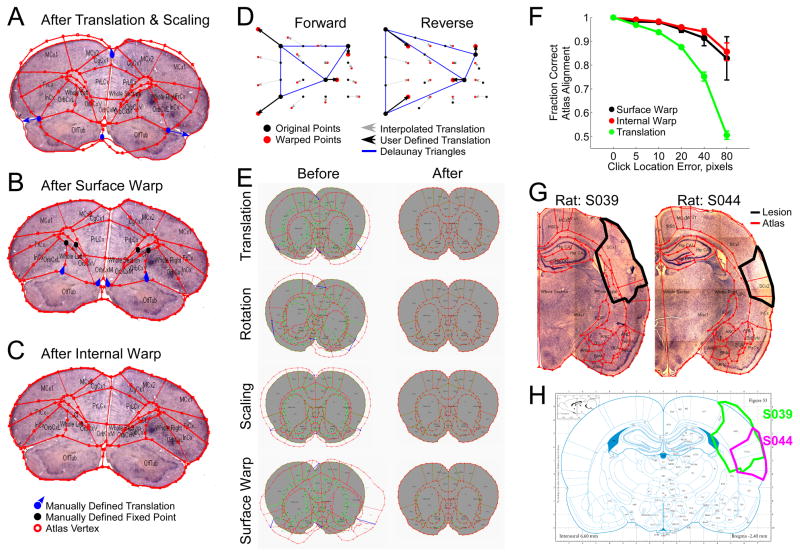
Figure 1.

Registering atlas panels with histological sections. A) Atlas panel subject to global rotation, translation, and scaling shows poor alignment with a coronal rat brain section. B) Surface warp applied to atlas in A. Warp algorithm need not be applied to a translated and scaled atlas as it performs equally well when applied to the raw atlas. C) Interpolated warp algorithm reapplied to internal points of atlas in B. Manually defined translations are shown in blue and manually defined fixed points are shown in black. D) Left: Interpolated warp algorithm applied to a uniform grid of points. Right: Reverse translation applied on the warped points from the left panel restores the uniform grid of points. E) The surface warp algorithm used to reverse three linear transformations (translation, rotation, and scaling) and one non-linear transformation (the surface warp algorithm itself). F) Sensitivity of both the surface and internal warp algorithms, and translations to error in landmark point placement. N = 5, error bars standard deviation. G) Cortical lesions in two rats are manually defined on Nissl stained coronal sections. Atlas region overlap S039: SCx1 63.1%, SCx2 57.4%, InCx 0.3%, CPu 30.0%; S044: SCx1 20.7%, SCx2 99.9%, InCx 17.2%, CPu 0.1% SCx1: Primary Somatosensory Cortex; SCx2: Secondary Somatosensory Cortex; InCx: Insular Cortex; CPu: Caudate and Putamen. H) Lesion boundaries are back-warped onto the corresponding panel from the Paxinos and Watson Rat Brain Atlas (Paxinos and Watson, 2005).

$$\text{translation}(\text{H},\text{V})=\text{atlas}\text{new}(\text{x},\text{y})-\text{atlas}\text{original}(\text{x},\text{y})$$ Equation 1

Atlas Fitter now interpolates the horizontal and vertical translation for each internal point on the atlas using the boundary point translations as a reference (Figure 1B). To interpolate the translations for the internal points, the image is first divided into the Delaunay triangles (using only the boundary points as vertices). Delaunay triangulation is defined such that no vertex exists inside any of the circumcircles for the resulting triangles (Barber et al., 1996; Delaunay, 1934). This form of triangulation maximizes the minimum angle of the resulting triangles, i.e. it minimizes the occurrence of long skinny triangles. To compute the translation for each internal point we first transform each point’s Cartesian coordinates (x,y) into a Barycentric coordinate system (t1,t2,t3) according to Equation 2.

$$\begin{array}{l}\text{t}1=((\text{y}2-\text{y}3)(\text{x}-\text{x}3)+(\text{x}3-\text{x}2)(\text{y}-\text{y}3))/((\text{y}2-\text{y}3)(\text{x}1-\text{x}3)+(\text{x}3-\text{x}2)(\text{y}1-\text{y}3))\\ \text{t}2=((\text{y}3-\text{y}1)(\text{x}-\text{x}3)+(\text{x}1-\text{x}3)(\text{y}-\text{y}3))/((\text{y}2-\text{y}3)(\text{x}1-\text{x}3)+(\text{x}3-\text{x}2)(\text{y}1-\text{y}3))\\ \text{t}3=1-\text{t}1-\text{t}2\end{array}$$ Equation 2

where (x1,y1), (x2,y2), and (x3,y3) are the coordinates of the vertices of the circumscribing Delaunay triangle and (x,y) are the coordinates of the internal point (Barber et al., 1996).

The translation of each internal point is then given by equation 3.

$$(\text{H},\text{V})=\text{t}1(\text{H}1,\text{V}1)+\text{t}2(\text{H}2,\text{V}2)+\text{t}3(\text{H}3,\text{V}3)$$ Equation 3

Where (Hn,Vn) are the horizontal and vertical translations at each of the vertices of the circumscribing Delaunay triangle and (t1,t2,t3) are the Barycentric coordinates for the internal point (Barber et al., 1996).

The resulting horizontal and vertical translations, or “warp”, can then be applied to the atlas to produce an image that can be directly compared to the experimental image. We call this procedure the “interpolated warp algorithm.” Figure 1D demonstrates how the interpolated warp algorithm affects a uniform grid of points. Any points that lie outside all Delaunay triangles use the translation values associated with the nearest point on a Delaunay triangle edge.

Larger histological sections tend to suffer from greater stretching and bending during the mounting process. This can cause internal structures to still be misaligned with the atlas panel following the first application of the interpolated warp algorithm described above. Any remaining internal misalignments can be corrected with a second application of the interpolated warp algorithm. The user is free to select any atlas point and manually define its correct position, thus defining the horizontal and vertical translations for that point. Since the external boundary points have already been “warped” into place, they are kept fixed with horizontal and vertical translations of 0 and continue to serve as vertices for the triangulation. The translations for all remaining internal points can be recalculated, as described above, and applied. By this point the atlas panel and the histological image should be well aligned with one another (Figure 1C). The typical atlas fitting procedure is outlined in Figure 3.

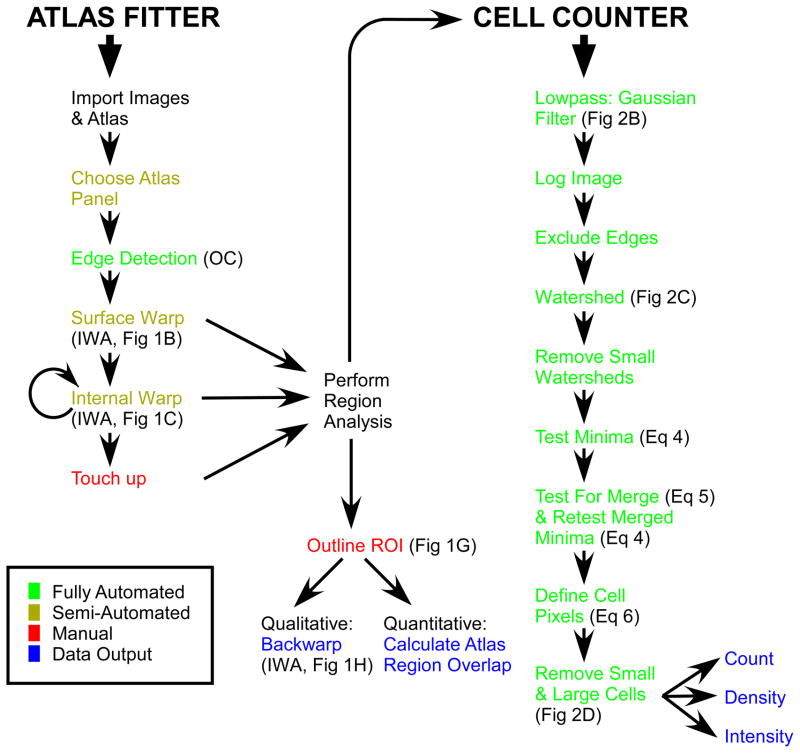
Figure 3.

Flowchart of atlas fitting and cell counting procedures. OC: opening and closing morphological filters. IWA: interpolated warp algorithm. ROI: region of interest. Relevant figure panels and equations are highlighted next to each step.

The number of iterations of the interpolated warp algorithm and the number of landmark points required to bring an atlas panel into proper registration with a histological section will vary depending on the degree of distortion the tissue has suffered. Here we measured the best alignment that could be achieved across 4 coronal rat brain sections using either linear transformations, the surface warp algorithm (with 4 landmark points), or the surface warp algorithm (4 landmark points) and the internal warp algorithm (average 6 landmark points) compared with a fully manually positioned atlas. On average we achieved alignments of 66.3%, 88.8%, and 98.9% respectively.

This warp algorithm is perfectly reversible (Figure 1D) under the condition that the triangulation does not change. To minimize changes in the triangulation following application of the surface warp algorithm and increase the accuracy of the resulting warp we also include the centroid of the atlas as a vertex in the triangulation. The horizontal and vertical translation for the atlas’ centroid is defined as the difference between it and the centroid of the histological section. The surface warp algorithm is also capable of accurately reversing both linear transformations, including translations, rotations, and scaling (98.2%, 98.3%, and 97.6% alignment respectively), as well as non-linear transformations such as the surface warp algorithm itself (97.1% alignment) (Figure 1E).

Since the interpolated warp algorithm requires the user to manually identify landmark points, the accuracy of the resulting alignment is dependent on the accuracy of the placement of those points. Small errors in landmark point placement can result in misalignments even when there is no change in the triangulation (as seen above with the attempt to reverse the linear transformations). We therefore sought to measure the sensitivity of the warp algorithm to errors in landmark placement. Here we applied the surface warp algorithm using 4 landmark points, the internal warp algorithm again with 4 landmark points (and the surface points held fixed), and a simple translation with 1 landmark point. The position of the landmark points was then jittered by some fixed distance, the transformations applied, and the alignment of the atlas compared to the transformation with no jitter computed (Figure 1F). In general we found that both warp algorithms are less sensitive to landmark location errors than a simple translation. This is because independent errors tend to average out across points and in the surface warp algorithm the points are constrained to be on the surface of the histological section.

3.1.3 Uniform image registration

Occasionally a simple uniform transformation, such as sliding the atlas to the right, stretching the atlas vertically, or rotating it clockwise, may be all that’s necessary to align an atlas panel to a histological section. For that reason Atlas Fitter also comes equipped with a range of manual atlas manipulating tools. Users can translate, flip, rotate, stretch, and shrink individual or groups of atlas subregions. For sectioning planes that possess symmetry (such as coronal brain sections with symmetric left and right hemispheres), the program is able to treat the left and right halves independently. Users can also reposition individual points for fine touch ups.

3.1.4 Region of Interest feature analysis

Once an atlas panel is registered to the histological section (3.1.2–3), quantitative feature analysis becomes possible. One such application is to quantify the extent of a lesion. Often, to determine the effect of a lesion on an animal’s behavior, it is important to not only know which brain areas were lesions, but also to what extent, i.e. area Y lesioned X%. For any such application users will first manually trace out regions of interest (ROIs), corresponding to the feature of interest such as the tissue lesion. The program can then calculate the percent overlap between the ROI and each of the subregions in the atlas (Figure 1G). When one wants to compare the extent of lesions across multiple animals, a graphical display showing the boundary of each lesion drawn over the atlas panel is often useful. However, because the shape of each brain is not identical, the atlas panel registered to each section will be warped slightly differently, therefore one cannot simply superimpose the lesion ROIs on top of one another for direct comparison. So to facilitate the graphical comparison of ROIs drawn on different sections Atlas Fitter can apply the warp algorithm that was used to bring the atlas panel into alignment with the tissue section in reverse (fully automated) to the user defined ROI. This results in the ROI being projected back onto the raw unwarped atlas panel (Figure 1H). Now lesions from multiple subjects can be superimposed over a single atlas panel for direct qualitative comparison.

3.2 CellCounter

CellCounter allows for the fully automated detection of cells in histological sections with variable signal-to-noise and background intensities.

3.2.1 Automated Cell Counting Overview

Our interest is in quantifying the extent of gene expression across various regions in the adult rat brain. For that we wish to determine the number of cells in each brain region that express our gene of interest. The first step is to align the appropriate atlas panel to the histological image as discussed above (3.1). After applying an automated cell identification algorithm, the program can then count the number of cells that lie within the region boundaries marked out by the atlas panel. In this way we get a quantitative account of gene expression as cell count per brain region.

Some freely available cell counting algorithms exist (such as ImageJ, Pixcavator, and CellAnalyst) and generally work by applying a size exclusion and an intensity threshold to identify and count cell features in a histological image (since not all software is open source, we are unable to evaluate exactly how all of these algorithms operate). Such algorithms work best on images with uniform background and a high signal-to-noise ratio. However, colorimetric in situ hybridizations and immuno-histochemistries routinely lack both. For example, setting the intensity threshold too low will cause every smudge in regions of high background to be counted as cells, while setting it too high will cause weakly stained cells on regions of low background to be missed. We therefore found the need for an automated cell identification algorithm that is both less sensitive to changes in background intensity and cell density.

To avoid the problem that fixed threshold based detection suffers when background is not uniform as discussed above, our algorithm measures a cell against its local environment. The higher the background staining, the stronger the cell must be stained in order for it to be counted. This still leaves us with the problem of how to define the local background. If background is calculated as a predefined area surrounding a putative cell, then any other cells within that area will affect the background value and therefore affect whether or not that cell gets counted. Variations in cell density must therefore also be taken into account. This sets up a conundrum, as we cannot determine background until we know which features in the image are cells, but we can’t determine which features are cells until we define the background. To get around this problem we make use of the watershed algorithm (Beucher and Lantuejoul, 1979; Meyer, 1994), which automatically subdivides an image into multiple subregions, or watersheds. Here we specifically use the flooding algorithm developed by Fernand Meyer (Meyer, 1994) which follows the following 4 steps: 1) Each local minima is assigned a unique label; 2) All pixels neighboring labeled pixels are placed in a set; 3) Pixels in the set are tested in order of ascending pixel value, if all labeled pixels neighboring that pixel have the same label, that pixel is assigned that label; 4) Repeat steps 2 and 3 until no new pixels are labeled. The labeled pixels belong to their respective watersheds while the unlabeled pixels mark the boundaries between watersheds. Each watershed is defined as a contiguous block of pixels that contain only a single local minimum, and therefore only a single putative cell. From here the task simply becomes one of determining if that local minimum is or is not a cell.

3.2.2 Automated Cell Counting Algorithm

The entire cell identification algorithm involves the following 7 steps. 1) Raw images (Figure 2A,B) are lowpass filtered with a Gaussian function (width of Gaussian kernel (WGK)= 9.6um, standard deviation Gaussian function (SGF) = 1.9um where 1 pixel = 1.9um) to remove random noise in the image, the color channels are added to produce a monochrome image, and the logarithm of the pixel values are taken (Figure 2C). This removes any weak local minima in the image which becomes important in the next step. 2) Sharp edges (e.g. tears in the tissue, blood vessels, air bubbles) are detected (Canny, 1986) and regions immediately adjacent to them are excluded from analysis. 3) The watershed algorithm (Beucher and Lantuejoul, 1979; Meyer, 1994) is applied to partition the image into multiple regions (watersheds), each containing only one local minimum (a potential cell) (Figure 2C). From here on all watersheds are analyzed independently. The goal is to determine if the local minimum within each watershed is or is not a cell. 4) Watersheds with an area smaller than a minimum number of pixels (here minWS = 50) are discarded. Small watersheds contain too few pixels to obtain an accurate significance score in the next step and can also be the result of random pixel noise, and therefore should be discarded. 5) A significance score is applied to the local minima within each watershed (Equation 1), and those with scores below a threshold are discarded.

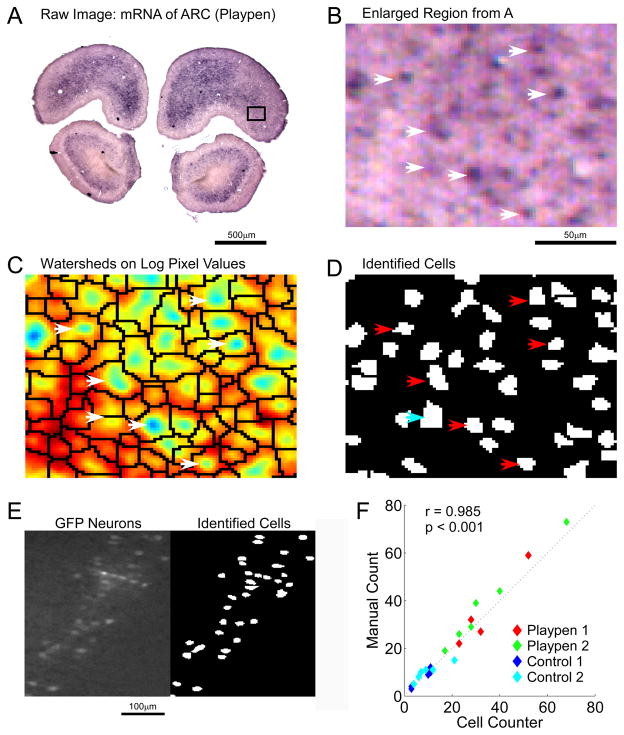
Figure 2.

Automated detection of cell bodies in histological sections. A) In situ hybridization against the immediate early gene Arc in a coronal rat brain section. B) Enlargement of black rectangular region in A captured at 1.25x C) Logarithm of lowpass pixel intensities displayed using a colormap (blue represents dark regions of high stain). Watershed boundaries, shown in black, divide the image into regions each containing one local minimum. D) Pixels identified as belonging to cells. Arrows identify cells between images. Blue arrow identifies two putative cells that were fused to produce a single cell. E) Left: GFP expressing neurons in a coronal section of rat primary somatosensory cortex. Right: CellCounter automated cell identification. F) Automated and manual count of Arc positive cells in the infralimbic cortex of playpen and control rats. Each data point represents the count from one hemisphere of one coronal section in one rat.

$$\begin{array}{l}\text{Signal}(\text{S})=\text{mean}\text{darkest}\text{c}\text{pixels}(\text{here}\text{c}=15)\\ \text{Background}(\text{B})=\text{mean}\text{brightest}\text{b}\text{percent}\text{pixels}(\text{here}\text{b}=30)\\ \text{Noise}(\text{N})=\text{standard}\text{deviation}\text{background}\text{pixels}(\text{same}\text{pixels}\text{as}\text{for}\text{B})\\ \text{Cell}\text{Score}=(\text{abs}(\text{S}-\text{B})/\text{N})\ast (\text{abs}(\text{S}-\text{B}))(\text{threshold}\text{CS}>=0.08)\end{array}$$ Equation 4

The significance score is a measure of the local minima against the local background within the watershed. It is therefore not affected by changes in background staining or cell density. 6) Neighboring watersheds that are both deemed to contain cells (i.e. contain local minima that exceed threshold from the previous step) are tested to determine if they should be fused (i.e. do they subdivide one continuous local minimum) using the following equation:

$$\begin{array}{l}\text{Signal}(\text{S})=\text{mean}\text{darkest}10\%\text{pixels}\text{in}\text{the}\text{weaker}\text{of}\text{the}\text{two}\text{neighboring}\text{cells}\\ \text{Noise}(\text{N})=\text{standard}\text{deviation}\text{of}\text{same}\text{pixels}\text{as}\text{S}\\ \text{Border}(\text{B})=\text{mean}3\text{darkest}\text{pixels}\text{on}\text{border}\text{between}\text{watersheds}\\ \text{Fuse}\text{Score}=(\text{abs}(\text{S}-\text{B})/\text{N})\ast (\text{abs}(\text{S}-\text{B}))(\text{threshold}\text{FS}>=0.0005)\end{array}$$ Equation 5

Any watersheds that are fused are retested for significance with Equation 4 (Figure 2D blue arrow). 7) Cell boundaries are defined within each remaining watershed according to the following equation (Figure 2D):

$$\begin{array}{l}\text{Signal}(\text{S})=\text{mean}\text{darkest}\text{c}\text{pixels}(\text{here}\text{c}=15)\\ \text{Background}(\text{B})=\text{mean}\text{brightest}\text{b}\text{percent}\text{pixels}(\text{here}\text{b}=30)\\ \text{Cell}\text{Threshold}(\text{CT})=((\text{S}-\text{B})/2)+\text{B}(\text{pixels}<=\text{CT}\text{are}\text{part}\text{of}\text{the}\text{cell})\end{array}$$ Equation 6

Any cells that are smaller than a minimum size threshold (minCS = 15 pixels), or larger than a maximum size threshold (maxCS = 300 pixels), are discarded. Cell counting algorithms based on image segmentation have been developed previously (Chen et al., 1999), but lacked a means of discarding false positives and fusing neighboring regions. The CellCounter algorithm is outlined in Figure 3.

3.2.3 Determining Cell Counting Algorithm Parameter Values

The entire cell counting algorithm involves 9 free parameters (see equations and discussion above (3.2.2): WGK= 5, SGF = 1, minWS = 50, c = 15, b = 30, CS = 0.08, FS = 0.0005, minCS = 15, and maxCS = 300). The precise value of each depends on the tissue type, stain, magnification, and expected signal-to-noise ratio for each application. To determine the parameter values we took the following approach. First, four representative images were captured across various brain regions with the same magnification of the images we wished to analyze. The representative images were selected to contain regions of high and low background intensity, and high and low cell density. For independent verification, human observers manually identified all cells within the images. The master cell identification was taken as the consensus of the human observers. The algorithm was then seeded with random values for each of the nine parameters and a gradient ascent was used to find a set of parameters that minimized the difference between the cells identified by the algorithm and the cells identified manually by human observers. The gradient ascent attempted to maximize the following score.

$$\text{Score}=(\#\text{correct}\text{cells}-\#\text{errors})/\#\text{correct}\text{cells})$$ Equation 7

If no improvement was made in 30 iterations it was assumed we had found a local maximum, the search was stopped and a new random parameter seed was started. We kept the parameter values that produced the highest score. Over the 4 images containing a total of 496 manually identified cells the algorithm had a false positive rate of 11.3% and a false negative rate of 5.4%. For comparison we trained a basic intensity and size threshold algorithm on the same images and obtained a false positive rate of 5.4% and a false negative rate of 66.3%. To underscore the ambiguity of cell identification in these low signal to noise images, the total error rate (false positive + false negative) between human observers was 17.6%, indicating the algorithm performs as well as human observers.

We also tested the ability of CellCounter to work on fluorescence images. Here GFP expressing neurons were imaged from coronal rat brain sections (Figure 2E). Again, using manually identified cells in a series of test images spanning low to high cell densities, we fit the free parameters (WGK= 6, SGF = 1, minWS = 16, c = 15, b = 35, CS = 0.16, FS = 0, minCS = 10, and maxCS = 800) achieving a false positive rate of 7.5% and the false negative rate of 8.7% over a total of 241 cells. CellCounter again outperformed a basic intensity and size threshold algorithm which at best achieved 0.8% false positives and 75.5% false negatives.

3.3 Experimental Validation

Prefrontal cortex is generally believed to be the seat of many higher cognitive functions such as decision making. Exploration of novel environments is known to activate the hippocampus (Guzowski et al., 1999; Guzowski et al., 2001), but we were interested to determine the effect of these experiences on prefrontal regions. For this we had two adult male Long Evans rats explore a highly-enriched novel environment for 30 minutes (“playpen”) while their cage mates remained in their home cages (“control”). At the end of 30 minutes, all animals were rapidly perfused and processed for in situ hybridization against the Immediate Early Gene (IEG) Arc. IEGs are a class of genes whose expression is upregulated following prolonged periods of elevated neuronal activity (Simonato et al., 1991; Worley et al., 1993). Therefore, IEG expression can serve as a surrogate for mapping neuronal activity (Burke et al., 2005; Feenders et al., 2008; Guzowski et al., 2005; Horita et al., 2010; Kelly and Deadwyler, 2003). By determining which brain regions show elevated Arc expression in the rat allowed to explore the novel environment compared to the control cage mates, we can identify which brain areas were active during the exploratory behavior. To quantify the expression of Arc between these animals we used the Atlas Fitter program to register a wire frame version of the Paxinos and Watson Coronal Rat Brain Atlas (Paxinos and Watson, 2005), generated using AtlasTracer, onto the histological sections (3.1), and the CellCounter algorithm to identify and count Arc-positive cells (3.2) (Figure 3). Results are shown in Table 1. Here we found that Arc expression is upregulated in all frontal cortical regions with subregions comprising the medial prefrontal cortex (Dorsal Peduncular, Dorsal Tinia Tecta, Infralimbic, and Prelimbic Cortexes), the medial and ventral portions of the Orbital Frontal Cortex, and the Claustrum showing some of the largest enhancements.

Table 1.

Comparison of Arc expression between rats allowed to explore a novel environment (playpen) and their cage mate controls across a range of frontal cortical regions. Values are the base-2 log of the ratio between the playpen rat and the control. Values are then normalized by each cortical region’s area, and represent the average of two experiments. Count is the cell count. Signal is the sum of pixel values for pixels deemed to be cells. Cell intensity is the sum of all pixels belonging to that cell. Positive values indicate an up-regulation of expression in the playpen animals.

Brain Region	Normalized Count	Normalized Signal	Median Cell Intensity
Cingulate Cortex - Primary	0.92	1.23	0.35
Claustrum	1.02	1.50	0.33
Dorsal Peduncular Cortex	1.03	0.53	0.17
Dorsal Tinia Tecta	1.39	1.48	0.25
Frontal Associational Cortex	0.35	0.50	0.25
Frontal Cortex	0.47	0.54	0.11
Infralimbic Cortex	1.89	1.67	0.21
Insular Cortex	0.67	0.82	0.19
Motor Cortex - Primary	0.68	0.75	0.18
Motor Cortex - Secondary	0.70	0.86	0.26
Olfactory Tubercle	0.37	0.40	0.19
Orbital Cortex - Dorsal Lateral	0.37	0.50	0.23
Orbital Cortex - Lateral	0.68	1.16	0.39
Orbital Cortex - Medial	1.10	1.68	0.61
Orbital Cortex - Ventral	1.13	1.60	0.50
Piriform Cortex	0.37	0.33	0.11
Prelimbic Cortex	1.42	1.74	0.47
Somatosensory Cortex	0.86	0.98	0.14

Values = mean(Log₂(Playpen Rat/Control Rat))

Normalized Values = mean(Log₂((Playpen/Region Area)/(Control/Region Area))

To again validate the cell count obtained by CellCounter we manually counted all Arc positive cells in both hemispheres of the Infralimbic Cortex across all 4 rats. Manual counts are plotted against the automated counts in Figure 2F. Here we found a significant correlation between the two counts (r = 0.985 p < 0.001). The normalized count ratio obtained for the infralimbic cortex with the automated and manual counts are also very similar (1.89 from the automated count (Table 1) and 1.95 from the manual count).

4. Discussion

The advantage of Atlas Fitter is that it can be applied to any tissue and sectioning plane for which an atlas has been created. It is not limited to analysis of coronal sections of the adult rat brain, as we used here (3.3). With Atlas Fitter the user is required to manually locate only the most obvious morphological landmarks, with the position of the remaining atlas points being interpolated between them. There are other fully-automated atlas-image registering programs which require the software to automatically detect specific morphological landmarks on the tissue (Bello et al., 2007). However, morphological landmarks are tissue- and plane-specific. Even coronal sections through a brain look entirely different from sagittal sections. Therefore, such software needs to be custom written for the specific tissue type and sectioning plane used, and is not generalizable like Atlas Fitter.

Unbiased, automated, quantitative analysis of histological data is required for answering many questions in a diverse range of biological disciplines. For that reason we developed the Atlas Fitter program along with the automated cell-counting algorithm. Combined, these tools allow one to rapidly quantify gene expression across entire organisms or within complex organs such as the brain. Here we showed two examples of their use, to quantify the extent of tissue lesions, and to identify regions of elevated neuronal activity during behavioral tasks.