Comparison of edge chipping resistance of PFM and veneered zirconia specimens

Abstract

Objectives

To investigate the chipping resistance of veneered zirconia specimens and compare it to the chipping resistance of porcelain fused to metal (PFM) specimens.

Methods

Veneered zirconia and PFM bar specimens were prepared in clinically relevant thicknesses. The specimen edges were chipped with different magnitude forces, producing chips of various sizes. The range of sizes included small chips that did not penetrate all the way through the veneers to the substrates, and also chips that were very large and reached the zirconia or metal substrates. The relationship between force magnitude and chip size (edge distance) was graphed. The resulting curves were compared for the veneered zirconia and PFM specimens. Knoop hardness vs. force graphs for the veneers and substrates were also obtained.

Results

The zirconia and PFM veneer chipping data followed a power law (coefficient of determination, R² > 0.93) as expected from the literature. The curves overlapped within the combined data scatter, indicating similar resistance to chipping. The chips made in both types of specimens detached and did not penetrate into the substrate when they reached the veneer/substrate intersections. The hardness–load curves for the veneers and substrates all exhibited an indentation size effect (ISE) at low loads. The Knoop hardness values with uncertainties of ±one standard deviation at 4 N loads for the metal, zirconia, and the metal and zirconia veneers are: (2.02 ± 0.08, 12.01 ± 0.39, 4.24 ± 0.16 and 4.36 ± 0.02 GPa), respectively, with no statistically significant difference between the veneers (Tukey pairwise comparison at 0.95 family confidence).

Significance

This work indicates that a similar resistance to chipping might be expected for veneered zirconia and PFM restorations, in spite of the large difference in substrate hardness. Differences in susceptibility to chip spalling were not detected, but the chips in both specimen types detached off the sides in a similar manner instead of extending into the substrates.

1. Introduction

Explorations into the use of yttria-stabilized zirconium oxide (zirconia, YSZ) as a biomaterial began in the 1960s [1]. Soon thereafter, the promising in vitro properties, as well as the history of orthopedic use, attracted the attention of dental materials researchers. Over the last decade, zirconia has been used as a substructure material for the fabrication of fixed prosthodontic restorations. Marketed in the dental arena under numerous brand names, zirconia is regarded as offering superior strength, toughness and reliability over other ceramic materials due to the transformation toughening mechanisms of its microstructure [2–4].

Clinical studies are now available that support zirconia’s performance potential, with indications of expanded functionality compared with other ceramics, such as use in long span bridges [5–9]. The primary issues noted in such studies were not related to framework integrity, but rather chipping, wear, and fracture of the veneering ceramics [10,11]. A recent study suggests that such chipping could also be an issue around endodontic access openings for all-ceramic crowns [12].

These observations prompted thinking about differences between porcelain fused to metal (PFM) veneering ceramics, which have been used for over 40 years [13], and the more recently developed veneering ceramics intended for zirconia. The veneering ceramics exhibit some compositional and microstructural differences, but are manufactured to identical international standards in terms of mechanical properties [14]. Based on clinical observations, as well as the in vitro materials data, the question arises whether zirconia veneers are more susceptible to chipping than PFM veneers.

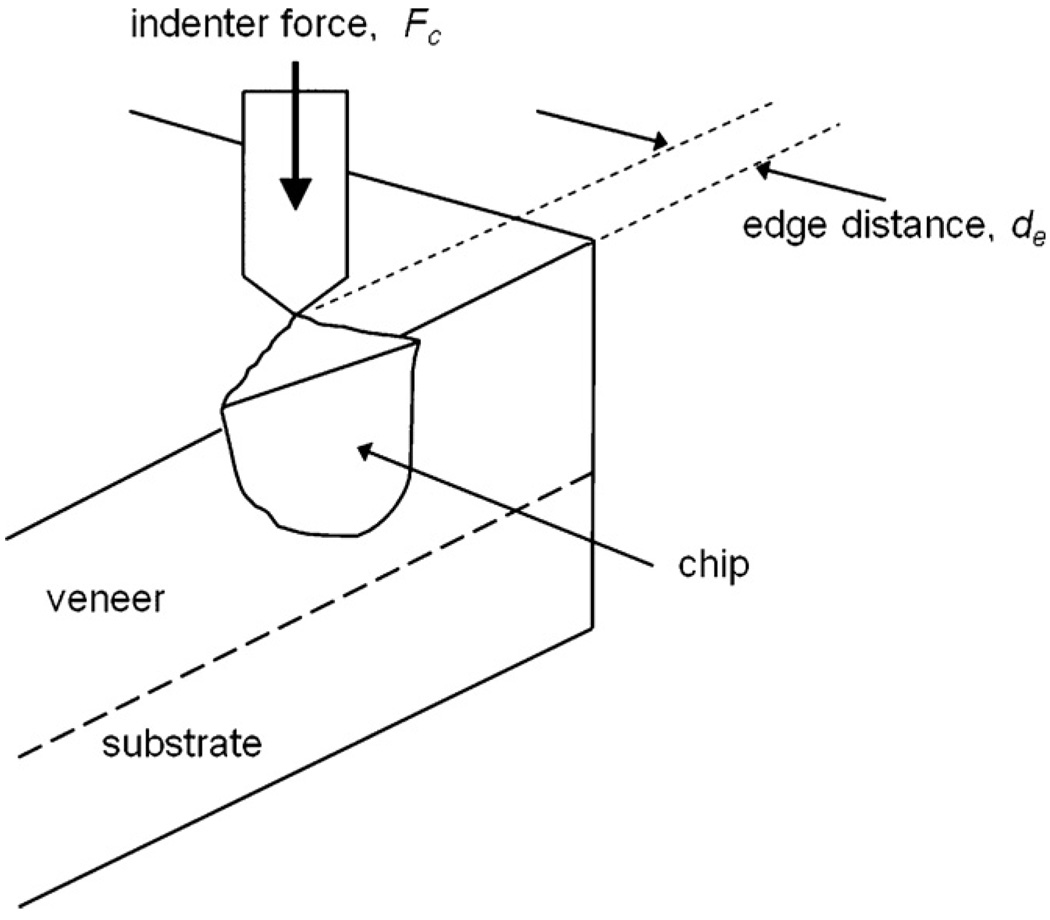
One way to investigate this question is to utilize an edge chipping test. This test involves the purposeful formation of chips in a material utilizing an indenter or stylus, with an attached load cell to measure the chip-forming forces (Fig. 1). The edge chip test is being utilized in diverse applications such as evaluation of cutting tool materials [15–17], ceramics [17], ceramic valves [18], machinability of brittle materials [19], heat treatment effects in archeological flint-knapping [20], and dental materials [19,21–25]. Although many groups have adapted conventional hardness machines or universal strength testing machines for edge chipping experiments, at least one commercial edge testing machine has been developed.¹,² A conference on fractography of glasses and ceramics featured a technical session on edge chipping fractography [26]. Gogotsi and Mudrik [27] recently commented on the diversity of indenter shapes and analyses that have been used for edge chipping experiments. “Edge chipping” resistance, which is alternatively referred to as “edge strength,” “edge fracture,” or “edge flaking resistance,” has been strongly correlated with fracture toughness, K_Ic [15–19,28] or the critical strain energy release rate, G_Ic [15–17].

Fig. 1.

Schematic of the edge chip test. An increasing indenter force is applied at a distance from the edge, d_e, until a chip is formed at a critical force, F_c.

In this study, the edge chipping test is used to compare the resistance of PFM and zirconia veneered specimens to chipping. The null hypothesis is that the edge chip resistances of the two material systems are different. Hardness measurements at different loads were also obtained for the veneers and substrates, given the dependence of measured hardness on load for ceramics (indentation size effect or ISE) which has been related to brittleness and susceptibility to cracking [29–31].

2. Materials and methods

2.1. Materials

Layered specimens for the edge chipping tests were constructed by laminating metal and zirconia substrates with appropriate veneers. The materials were all donated by Dentsply Ceramco (York, PA), with the following product trade names material descriptions, and compositions from the company literature. The PFM substrates were cast using Ultracrown SF alloy of 0.65 mass fraction Au and 0.26 mass fraction Pd, with small amounts of In, Ga, Ru and Sn. This alloy is listed as being compatible with most conventional and low fusing porcelains. In the current study, it was veneered with Ceramco 3, a feldspathic veneering porcelain containing about 0.30 volume fraction leucite. The zirconia substrates were milled out of Cercon, composed of zirconia stabilized with 3 mole% yttria, with small amounts of hafnia, alumina and silica present. They were veneered with Ceramco PFZ, a feldspathic veneering porcelain with no leucite, engineered to be compatible with zirconia frameworks.

2.2. Methods: specimen preparation

A bar shape specimen was selected for ease of testing in the edge chipping machine, but the specimen preparation and layering thicknesses were chosen with regard to clinical relevancy. Ten substrates for each material system were provided in thin (≈0.5 mm) 4 mm × 40 mm rectangular slabs and coated with a thin liner and then veneered in two layers following procedures recommended in the manufacturer’s literature. A vacuum dental furnace (model: Centurion VPC, Ney Dental, Inc., Burlington, NJ) was used to fire the veneers. The Ceramco 3 veneer for the alloy had a heat up rate of 55 °C/min to a peak firing temperature of 960 °C and 0 min hold. The Ceramco PFZ veneer for the zirconia had a heat up rate of 60 °C/min to a peak temperature of 900 °C and a short 15 s hold on the first firing and 890 °C and 0 min hold on the second firing. After veneering, the specimens were rough-polished on the bottom substrate surface (350 grit) to eliminate any bowing or small surface lumps so that the specimens lay flat in the edge chipping machine. The top veneered surfaces were more carefully polished with successively smaller grits down to 1200 grit, in order to provide a smooth, consistent surface for applying the edge chipping force and measuring the chip size. Three specimens of veneered zirconia and three PFM bar specimens were prepared in this manner to obtain edges suitable for chipping. These were sufficient to provide enough total edge length for the edge chipping experiments described below.

The layered specimens were then placed in a holder (Fig. 2) that enabled the side edges to be polished to 1200 grit at right angles to the specimen’s top and bottom surfaces. This step was not essential since small differences in specimen side surface preparation and substrate thicknesses are not expected to affect the amount of force needed to cause chipping in these experiments, as the chip cracks initiate at the specimen top surface veneer beneath the indenter and emerge at the specimen sides without penetrating the substrate. However, the extra side surface polishing step was done to make the chips are easier to see and measure.

Fig. 2.

(a) A PFM specimen in the holder for polishing a 90° edge. (b) A PFM specimen that has been edge chipped, angled so the chips are visible on the upper edge.

2.3. Methods: dimension measurement

The final specimen and specimen veneer thicknesses after polishing were measured in a stereoptical microscope (model MZ-16, Leica, Heerbrugge, Switzerland) with a traveling stage capable of providing measurements to the nearest µm. Eight thickness measurements of the veneering ceramic and eight total thickness measurements were made for each of the six specimens, for a total of 96 measurements. The thickness (with uncertainties of ±one standard deviation) of the specimen veneers on the metal and zirconia substrates were measured to be 0.777 ± 0.060 and 0.769 ± 0.052 mm, respectively, with no significant difference for Tukey pairwise comparison at 0.90 family confidence. The total specimen thickness uncertainties of ±one standard deviation for the PFM and veneered zirconia specimens were measured to be 1.216 ± 0.041 and 1.278 ± 0.040 mm, respectively. This difference is small, but statistically significant for Tukey pairwise comparison at 0.90 family confidence. The reason the zirconia specimens were slightly thicker was that they were slightly less bowed after removal from the furnace and were not polished as much on the bottom substrate surface. The final veneer and total specimen thicknesses are within the range used for restoration crown preparation in normal clinical practice.

2.4. Methods: edge chipping measurements

The prepared specimens were placed in an Engineering Systems Model CK 10 edge chipping machine (Nottingham, UK), with a 1000 N load cell and a conical 120° diamond scribe indenter with a very sharp tip (with a radius less than 10 µm). This indenter is very inexpensive (less than $15 US) and easy to replace as opposed to the Rockwell, Vickers, or Knoop indenters used by other investigators. The load readout resolution was 0.1 N and the load cell was certified to be accurate to better than 0.1 N. Load was gradually applied until the chip fractured off the specimen and the peak load was recorded. The contact locations were spaced well apart from each other, typically two or more times the chip widths as shown in Fig. 2, to avoid any interference between chips. Forces up to 120 N were used to create 56 chips of various sizes in the veneered specimens. The indenter was frequently viewed under an optical microscope to confirm the integrity of the diamond tip between test series. Ten to fifteen chips were made in each specimen. The edge distance as shown in Fig. 1 was measured in mm from the center of the indentation location to the edge using the previously described stereoscopic microscope system.

2.5. Methods: hardness (ISE) measurements

Two additional specimens, one of veneered zirconia and one PFM, were polished along one side using the holder in Fig. 2 and tested for Knoop hardness with a Wilson Tukon hardness machine (Binghamton, NY) according to ASTM C1326 [32]. In order to determine the hardness dependence on load (indentation size effect, ISE), loads ranging from 0.098 to 3.92 N were used, with 10 indentations at each load. The ISE graphs for both the PFM and zirconia veneers and the metal and zirconia substrates were obtained. Indentations were made both near and remote from the interface to get a sense of whether residual stresses may have been present at the interface, but no difference in hardness with location was detected. The indenter was in contact with the test piece at peak load for 15 s in accordance with ASTM C 1326.

3. Results

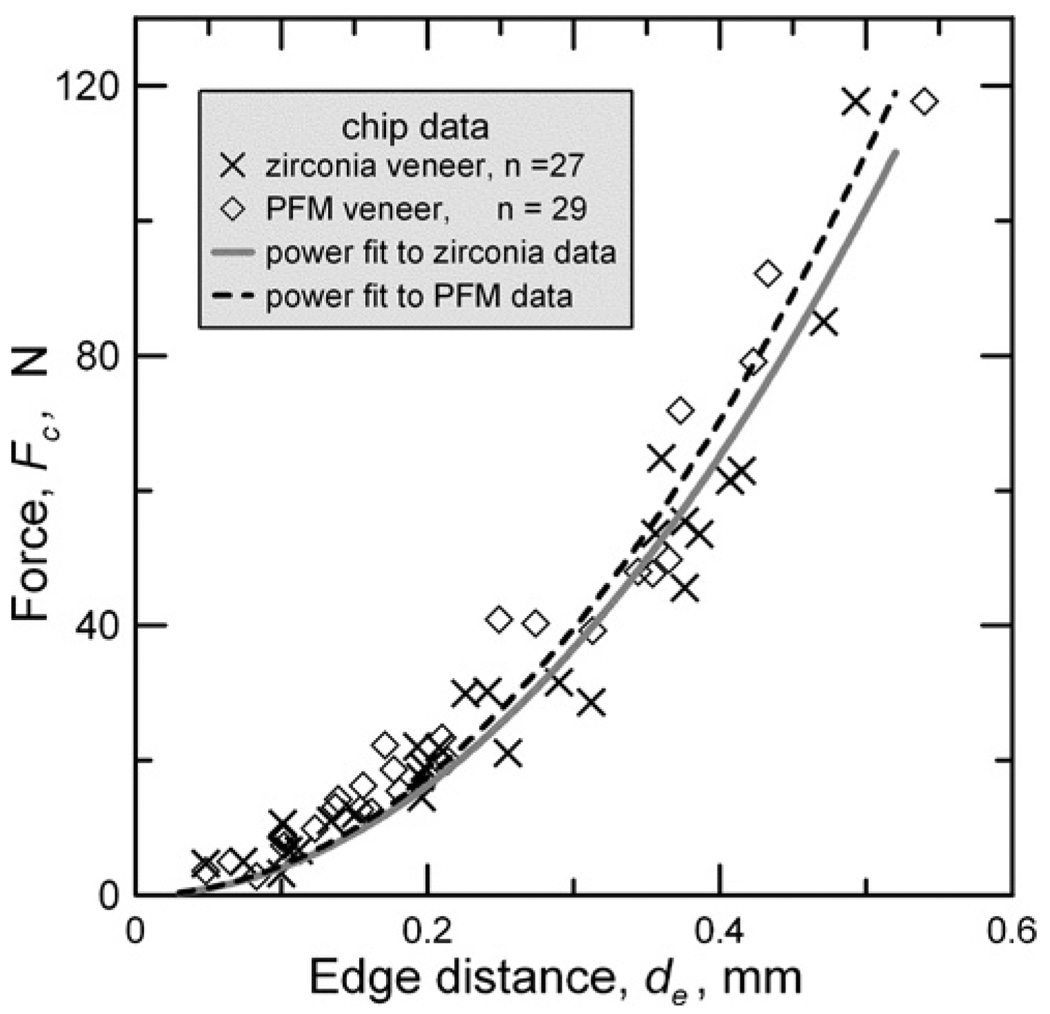
Chips readily formed in both the PFM and veneered zirconia specimens. A graph of the force to form a chip (F_c) vs. the distance from the edge (d_e) is shown in Fig. 3. There was only a small variability in the force necessary to create a chip at a particular distance from the edge. No abrupt changes in the curves are evident where the chips are large enough to go through the veneer and reach the substrate, generally in the vicinity of 30 N. Differences in the fitted curves in this vicinity are within experimental error of the force and chip size measurements. The chips large enough to reach down to the substrates changed direction and spalled off instead of continuing through the substrate interface in both types of specimens, as shown in Fig. 4.

Fig. 3.

Force vs. edge distance graph for chip formation for the zirconia and PFM systems. Edge chips intersected the specimen sides at the substrate interface at approximately 30 N for both types of specimens. The quadratic power law fits were chosen for convenience and goodness of fit and as yet have no theoretical basis.

Fig. 4.

Chips in layered specimens. Arrows delineate the chip boundaries in the side views. (a) The chip formed in this PFM specimen at 18.6 N almost touches the liner in the side view. (b) The 55.4 N chip intersects, but does not penetrate, the zirconia substrate in the side view. (c) The 92.2 N chip in this PFM specimen is quite large, but does not penetrate into the metal substrate. The chips have the same shape in the top views, but the magnifications are different, as can be surmised from the side views of the similar sized specimens.

Regression curves were fit through the edge chipping data using a simple power law with an exponent of 2:

$$F_c={\mathit{\text{Ad}}}_e^2$$ (1)

where A is a proportionality constant. For Fig. 2 curves, A = 407 N/mm² for the zirconia layered specimens and A = 440 N/mm² for the PFM specimens. There is no theoretical basis for choosing the power relationship with an exponent of 2. It was chosen to visually aid comparisons and because of simplicity and a reasonable observed fit, with coefficients of determination (R²) of 0.94 and 0.96 for the zirconia and PFM specimens, respectively. A power law (but with a range of exponents from 1.28 to 1.56) was chosen to fit similar edge chip data in our previous publications [19–21]. An exponent of 1.5 is supported by a simple fracture mechanics model [28]. With an exponent of 2, A has units of stress N/mm² or MPa and thus A could be considered as an edge chip strength. The commonly used linear relationships that have been used in other studies (e.g., 15–18) and our earlier work [19–21] do not match low load data as well as the power law relationship.

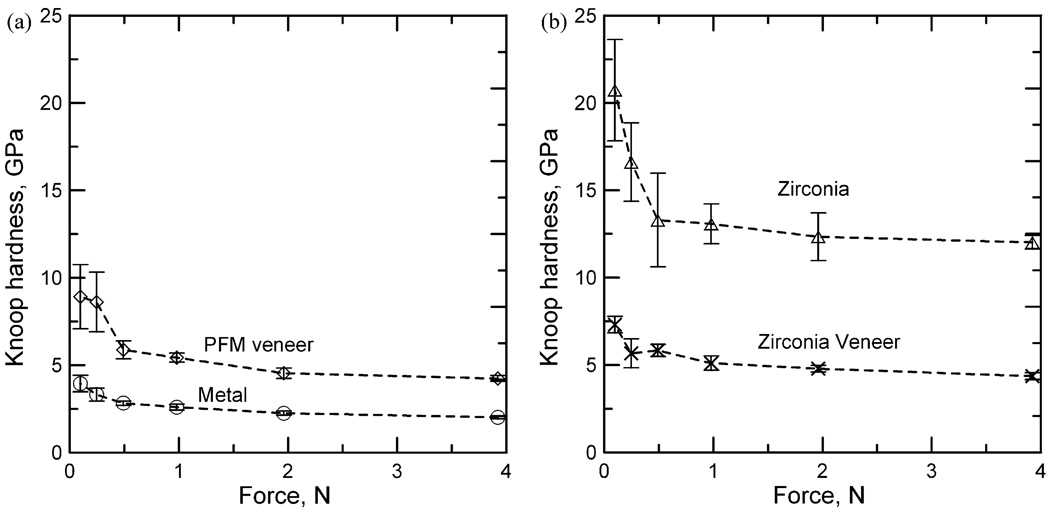
Fig. 5(a) and (b) shows the results of the Knoop hardness tests for the zirconia and PFM specimens, respectively. All of the specimens exhibit a hardness dependence on load, the ISE, at very low loads. As the loads increase, the hardness becomes less load dependent, as expected [30,31]. The Knoop hardness (with an uncertainty of ±one standard deviation) of the veneers at the highest load of 3.92 N for the layered zirconia is 4.36 ± 0.20 and 4.24 ± 0.16 GPa for the PFM specimens. There is no significant difference between these two values for Tukey’s pairwise comparison using a 95% family confidence coefficient. Indeed, the similarities of the two veneers are obvious in looking at the graphs.

Fig. 5.

Hardness load relationships (ISE) for the PFM materials (a) and the PFZ materials (b) of this study. The uncertainty bars are ±one standard deviation. The ISE of the veneers are similar for the zirconia and PFM systems. The metal, however, is softer than the associated porcelain veneer, while the zirconia is much harder. In spite of the difference in hardness, both veneers were similarly susceptible to chipping as shown in Fig. 3.

The hardnesses of the two substrates, however, are quite different. The Knoop hardness of the zirconia substrate at the highest load of 3.92 N is 12.01 ± 0.39 GPa, and for the metal substrate, only 2.02 ± 0.08 GPa. Thus, the zirconia veneer is placed over a much harder substrate, while the PFM veneer is placed over a softer substrate.

4. Discussion

The similarity in chipping behavior of the two types of specimens was unexpected and the null hypothesis that they are different is rejected. Also unexpected was the apparently smooth continuation of the edge chipping curves as the chip sizes became large enough to intersect (but not penetrate past) the interface between the veneer and the substrates. The chipping resistance for the two specimen types appeared to be not greatly affected by differences in the substrate materials, not even when the chips were large enough to extensively intersect the substrates, as in Fig. 4(c). This is different from the results of fatigue tests where cracking from balls repeatedly pressed into layered structures was reported to be highly dependent on substrate layer properties [33,34]. There may be a difference in mechanisms leading to chipping and such fatigue cracking. Provided that the substrate offers adequate support, chip resistance is probably controlled more by the local material properties at the top of the chip in the veneer material than by the properties at the bottom of the chip where the crack finally emerges. Also, the layers in the fatigue studies were of different transparent materials to allow for visibility in order to observe crack progression during cyclic loading. The primary concern for materials chosen for this edge chipping study, however, was clinical relevance in zirconia system and PFM comparisons. A possible future study might involve correlations of edge chipping susceptibility and fatigue cracking in the same layered systems.

The similarity in behavior of the two veneers is interesting, as they differ somewhat in microstructure and chemistry. The absence of the high expansion leucite reinforcement, necessary to create thermal compatibility with metal substructures, did not have a noticeable effect on the hardness nor chip resistance of the zirconia veneers. It would be expected that the leucite would have increased the hardness and toughness of the PFM veneer [35], and thus also the chipping resistance which has been found to be related to fracture toughness [15–19,21,28]. This lack of difference between the two materials suggests that the difference in clinical behavior may not be related to fundamental material differences, but rather to processing and placement artifacts. For example, damage may be induced in unreinforced veneering ceramics if water cooling is not used during occlusal adjustment [36]. Another hypothesis to be considered is that the size distribution of the leucite crystals in the PFM veneering ceramic (5–30 µm in range) offers a less substantial toughening effect than those observable in veneering ceramics with different leucite distributions. Residual stresses in the veneer could play a role in the edge chip and fatigue resistances. It has recently been reported that they are a key factor in the chip resistance of zirconia veneers [37,38]. The dental furnace used in our study, like many in use, did not have a controlled final cool down sequence. Once the firing cycle final hold step was finished, the furnace partially opened and exposed the test pieces to air cooling. So our test specimens went through the glass transition temperature at an unrecorded rate. Nevertheless, our edge chip specimens were thin and flat and sat directly on the furnace floor with its substantial thermal inertia. Hence, thermal gradients in the test pieces were probably minimal and the actual cool down rate may not as severe as what might have been experienced by larger more complex shapes. The orientation of the specimens in our study may have deemphasized interface residual stresses since our indentations and loads were applied to the top veneer surface. One variant of the test might be to turn the bilayer specimen on its side and indent-chip at various distances and observing whether an abrupt change in the force–distance trend occurred once the indenter approached the veneer–substrate interface. Future studies could evaluate these and other hypotheses to identify underlying mechanisms.

The indentation size effect (ISE) hardness curves shown in Fig. 5 are similar for the two veneers, and suggest they have similar brittleness [31]. Pronounced differences in ISE curves can be correlated to marked differences in cracking around an indentation and also with the material’s brittleness [39,40]. This ISE similarity would be expected for materials with similar edge toughness properties. Also unsurprising is the power law relationship between the force and edge distance in Fig. 3. As noted previously, initial experiments involving edge chipping suggested linear relationships [15–21], it was found that for very low loads and for noncrystalline materials, a power law provides a much better fit [19–21]. This is more pronounced as the amount of crystallinity within a porcelain decreases and it has been suggested this is at least partially due to densification beneath the indenter prior to fracture [19].

Finally, it should be noted that the chips in both types of specimens detached once the veneer/substrate intersection was reached, rather than continue into the substrate. This suggests that the substrates in both types of specimens provided an effective barrier to continued crack growth. The question of vulnerability to chip spalling then arises. From a clinical standpoint, a chipped veneer that simply reaches but does not penetrate into the substrate may be easier to repair than a chip fracture that has continued through the substrate. The ideal would be to decrease the veneer susceptibility to chipping as well as susceptibility to spallation. However, initial evaluations of the bond strength of veneering ceramics to zirconia and metal substrates using flexural testing, suggest an equivalent and acceptable result [41,42]. The edge chipping test may also aid in providing a means of evaluation in this regard.

Finally, we note that although an increasing number of investigators are using edge chipping tests, variations in procedures and interpretations are proliferating and are creating confusion. Different indenter types (sharp Knoop, Vickers, or conical or blunt Rockwell) make intercomparsion of data more difficult [27], since initiation and propagation of a crack are crucial steps in the formation of a large chip. Morrell and Gant [17] and Gogotsi and Mudrik [27] have commented on the different responses to different indenters. Many investigators fit a linear regression line through their force–distance data (albeit with widely variable intercepts) and interpret the slope M (or T or F_R) as “edge toughness” [15–21,27]. This has units of force/distance which is dimensionally analogous to force × distance/area or energy/area, which can be correlated to G_Ic, the critical strain energy release rate, or to γ_f, the fracture surface energy. Both are related to K_Ic, the fracture toughness. Early workers in this field [15–18] recognized the relationship between chipping resistance and these traditional fracture properties. Alternatively, one can graph force vs. distance and define “edge strength” as the force necessary to create a chip as a specified distance such as 0.5 mm [24,25]. In other studies including the present work, a power law relationship is a better fit. If the exponent is 2, then the constant A may also be deemed an “edge strength”. The exponent of 2 may be the exception rather than the norm, however, since seven materials from earlier studies on dental materials had exponents ranging from as low as 1.28 to 1.56 [19–21]. A recent indentation fracture mechanics model [28] for edge chip resistance supports a power law relationship, but only for an exponent of 1.5, which clearly does not fit the data in the present case or several data sets from our earlier studies [19–21]. The indentation model shares many of the shortcomings of the common indentation fracture mechanics models [43] and it should not be surprising that actual behavior deviates from the model and that the claimed accuracy is not better than 25% [28]. Adding to the confusion is work [27] that advocates measuring the chip distance from the back of the chip formed by a blunt Rockwell indenter as opposed to the point of force application, the approach that nearly all other studies have used. An interlaboratory comparison project for edge fracture, edge flaking, edge chip, or edge strength resistances would appear to be appropriate.

5. Conclusion

The tested PFM and veneered zirconia specimens had similar resistance to edge chipping, in spite of very different substrate properties. Thus, veneered zirconia is not likely to be associated with increased chipping susceptibility in clinical outcomes from a materials viewpoint unless there are pronounced residual stresses or interface faults. Edge chipping tests might be useful in determining the sensitivity of different materials systems to chip spallation or processing errors such as those involving temperature regulation.