Muscle short-range stiffness can be used to estimate the endpoint stiffness of the human arm

Abstract

The mechanical properties of the human arm are regulated to maintain stability across many tasks. The static mechanics of the arm can be characterized by estimates of endpoint stiffness, considered especially relevant for the maintenance of posture. At a fixed posture, endpoint stiffness can be regulated by changes in muscle activation, but which activation-dependent muscle properties contribute to this global measure of limb mechanics remains unclear. We evaluated the role of muscle properties in the regulation of endpoint stiffness by incorporating scalable models of muscle stiffness into a three-dimensional musculoskeletal model of the human arm. Two classes of muscle models were tested: one characterizing short-range stiffness and two estimating stiffness from the slope of the force-length curve. All models were compared with previously collected experimental data describing how endpoint stiffness varies with changes in voluntary force. Importantly, muscle properties were not fit to the experimental data but scaled only by the geometry of individual muscles in the model. We found that force-dependent variations in endpoint stiffness were accurately described by the short-range stiffness of active arm muscles. Over the wide range of evaluated arm postures and voluntary forces, the musculoskeletal model incorporating short-range stiffness accounted for 98 ± 2, 91 ± 4, and 82 ± 12% of the variance in stiffness orientation, shape, and area, respectively, across all simulated subjects. In contrast, estimates based on muscle force-length curves were less accurate in all measures, especially stiffness area. These results suggest that muscle short-range stiffness is a major contributor to endpoint stiffness of the human arm. Furthermore, the developed model provides an important tool for assessing how the nervous system may regulate endpoint stiffness via changes in muscle activation.

we commonly use our hands to move and manipulate objects in different environments. Many of these tasks tend to destabilize arm posture (Rancourt and Hogan 2001). Nevertheless, they can be completed because the central nervous system regulates the mechanical properties of the arm to compensate for these instabilities, usually ensuring that the coupled system of the arm and its environment remains stable so that posture can be maintained (McIntyre et al. 1996). Understanding how this regulation occurs and the relative contributions of the nervous system and the intrinsic biomechanics of the arm remains an important problem in motor control.

Arm mechanics are typically quantified by applying controlled displacements, measuring the corresponding forces, and characterizing the relationship between the two using estimates of arm impedance. The static component of impedance, known as stiffness, is thought to be especially important during the maintenance of posture. Estimates of endpoint stiffness are often used to summarize the mechanical properties of the whole arm at the endpoint, or point of contact with the environment (Mussa-Ivaldi et al. 1985). Many physiological mechanisms contribute to the forces measured in these experiments and to the corresponding estimates of endpoint stiffness. Actively controlled mechanisms at a specific arm posture include the intrinsic properties of the muscles within the arm, which are dependent on their steady state or feedforward activation, and transient changes in muscle activation that may occur via feedback pathways such as stretch reflexes or voluntary responses to the imposed displacements. Although numerous studies have characterized the behavioral characteristics of endpoint stiffness (Burdet et al. 2001; Darainy et al. 2004; Franklin et al. 2003; Franklin et al. 2007; Gomi and Osu 1998; Perreault et al. 2001; Tsuji et al. 1995) and the feedback responses that may modulate this stiffness (Krutky et al. 2010; Perreault et al. 2008), few have directly assessed which muscle properties contribute most to the stiffness properties of an entire limb. This knowledge is essential for understanding how changes in neural activation alter limb stiffness or how impairments to muscular or neuromotor systems may impact the ability to regulate stiffness in a contextually appropriate manner.

The intrinsic stiffness of individual muscles is undoubtedly a major contributor to the endpoint stiffness of the human arm. However, there has been little consensus regarding how muscle stiffness should be defined with respect to its contributions to the stiffness of an intact limb. A common approach has been to consider the slope of the force-length curve as the only activation-dependent stiffness component of muscle (Brown and Loeb 2000; Iqbal and Roy 2004; Stroeve 1999; Verdaasdonk et al. 2004). The slope of this curve may be scaled uniformly with changes in muscle activation or nonuniformly to represent the increasing length at which peak forces are generated for submaximal contractions (Rack and Westbury 1969). Although the force-length curve describes the isometric force generated when a muscle is activated at different lengths, it does not describe how muscle force changes when length is changed (Joyce et al. 1969). For small rapid perturbations, the initial forces generated by a muscle can be described in terms of its short-range stiffness (Rack and Westbury 1974), which is thought to depend largely on the stiffness of the active cross-bridges acting in series with the passive structures of the muscle (Morgan 1977). It has been suggested that the short-range stiffness properties of muscle are a major factor in determining the stiffness of a joint (Bunderson et al. 2008; Colebatch and McCloskey 1987; Grillner 1972; Hufschmidt and Schwaller 1987; Joyce et al. 1974; Kirsch et al. 1994; Misiaszek 2006), but the importance of short-range stiffness has not been evaluated directly, particularly in the context of multijoint mechanics.

The primary objective of this work was to evaluate the hypothesis that the endpoint stiffness of the human arm can be accurately described by the intrinsic short-range stiffness of its active muscles, coupled to a realistic model of musculoskeletal geometry. This hypothesis was evaluated by adding scalable models of short-range stiffness (Cui et al. 2008) to an existing three-dimensional (3-D) musculoskeletal model of the human upper limb (Holzbaur et al. 2005) and comparing the predictions of the resulting model with previously collected experimental data (Cannon and Zahalak 1982; Perreault et al. 2001). The efficacy of this model was compared with models that considered only the force-length properties of muscle. Our results clearly demonstrate that intrinsic muscle properties can account for previously reported variations in arm stiffness when short-range stiffness is considered but not when using muscle models that consider only force-length properties. These results clarify how intrinsic muscle properties can contribute to the regulation of limb mechanics in the absence of neural feedback. Furthermore, experimental deviations from the model predictions can be used to identify situations in which neural control strategies beyond feedforward muscle activation are required to regulate arm stiffness in a task-appropriate manner. Portions of this work have been presented previously in abstract form (Hu et al. 2009a,b).

METHODS

Modeling.

To evaluate the extent to which the endpoint stiffness produced during small, rapid perturbations is dominated by the short-range stiffness of active muscles, we performed simulations that coupled a musculoskeletal model of the upper limb with a scalable model of muscle stiffness. This muscle model estimates the short-range stiffness of a given muscle based on its geometry and active force (Cui et al. 2008). We compared these results with simulations that combined the same musculoskeletal model with muscle stiffness estimated using 1) the slope of the isometric force-length relationship during full activation (Zajac 1989), and 2) the slope of the isometric force-length relationship, adjusted based on muscle activation level to reflect the shift in optimal fiber length with activation (Lloyd and Besier 2003).

The musculoskeletal model of the upper limb implemented in our study was adapted from the model described by Holzbaur et al. (2005). Our simulations incorporated kinematic representations of the shoulder and elbow joints and included a total of 37 muscle segments. These segments corresponded to 9 shoulder muscles, separated into 15 segments; 14 elbow muscles, represented by 19 segments; and 2 biarticular muscles, represented by 3 segments. This model was used to obtain parameter values for optimal muscle fiber lengths, maximum isometric muscle forces, tendon slack lengths, and muscle moment arms, as needed for our simulations. Both the moment arms and the isometric force-generating capacity of the muscles estimated using this model vary as a function of joint posture. The parameter values in the musculoskeletal model describing the peak isometric forces for individual muscles were scaled from their original values (which were based on anatomic data collected in cadavers) using recent data describing both muscle volumes (Holzbaur et al. 2007b) and joint strength (Holzbaur et al. 2007a) in the upper limb in the same healthy subjects. Similarly, tendon slack length of the brachioradialis was decreased from the nominal value reported by Holzbaur et al. (2005) to reflect recently reported intraoperative measurements (Murray et al. 2006). Finally, the flexion moment arm angle relationship of anterior deltoid was replaced by the measurements reported by Kuechle et al. (1997), made in a posture more relevant to our simulations; this change decreased the moment arm over the range of interest for this paper.

Muscle short-range stiffness was estimated using the model developed by Cui et al. (2008) for muscles in the cat hindlimb. The model assumes that the short-range stiffness of a muscle-tendon unit, K, results from the stiffness of the muscle fibers, K^m, in series with the stiffness of the tendon, K^t (Eq. 1).

$$K=\frac{K^m{K}^t}{\left(K^m+K^t\right)}$$ (1)

K^m is a function of muscle force (Eq. 2), F^m, optimal muscle fiber length at maximum activation, l₀^m, and a dimensionless scaling constant γ = 23.4.

$$K^m=\frac{\gamma {\text{F}}^{\text{m}}}{l_0^m}$$ (2)

K^t was defined by the slope of the generic, dimensionless force-strain curve scaled for each individual tendon (Zajac 1989). This is different from the scaling equation suggested by Cui et al. (2008) since the geometric properties required for their tendon model were not available for all of the muscles in our model. The impact of using a different tendon model was assessed using the sensitivity analyses described below.

Estimation of muscle forces.

Optimization was used to estimate the distribution of muscle forces for a specific set of joint torques. The cost (u) for this analysis was the sum of the squared muscle forces, expressed as a fraction of the maximum force for each muscle (Eq. 3) (Anderson and Pandy 2001; Crowninshield and Brand 1981). The problem was constrained such that 1) the resulting muscle forces summed to the specified joint torques (Eq. 4), and 2) muscle forces were positive and less than or equal to the maximum achievable forces at the current arm posture (Eq. 5). In these equations, F_i^m is the actual force and F_i0^m is the posture-dependent maximum isometric force for ith muscle, respectively, r_ij is the posture-dependent moment arm for the ith muscle relative to the jth joint, and TQ_j is the torque about the jth joint. The summation over 37 elements corresponds to the number of muscle segments crossing the elbow and shoulder in our musculoskeletal model. The same cost function has been shown to work well in isometric force regulation tasks at arm postures similar to those used in the present study (Van Bolhuis and Gielen 1999).

$$u=\min {\displaystyle \sum _{i=1}^{37}{\left(\frac{{\text{F}}_{\text{i}}^{\text{m}}}{{\text{F}}_{\text{i}0}^{\text{m}}}\right)}^2}$$ (3)

$$T{Q}_j={\displaystyle \sum _{i=1}^{37}{r}_{ij}\times {\text{F}}_{\text{i}}^{\text{m}}\hspace{0.17em}i=1,\hspace{0.17em}\dots ,37;\hspace{0.17em}j=1,2}$$ (4)

$$0\le {\text{F}}_{\text{i}}^{\text{m}}\le {\text{F}}_{\text{i}0}^{\text{m}}$$ (5)

Model-based estimation of arm stiffness.

Once muscle forces were estimated, we computed the corresponding joint and endpoint stiffnesses. The estimated force for each muscle (F_i^m) was used to calculate the corresponding short-range stiffness of the muscle-tendon unit, K_i, using Eqs. 1 and 2. Joint stiffness (K^j) was calculated from muscle-tendon stiffness by considering the kinematic relationship between changes in joint angles and changes in muscle-tendon length (Eq. 6) (McIntyre et al. 1996):

$$K^j=J^T\overrightarrow{K}J+\frac{\partial J^T}{\partial \theta }{\overrightarrow{F}}^{\text{m}}$$ (6)

where θ is a vector describing the joint angles, J is the Jacobian matrix relating changes in joint angles to changes in muscle length (it contains the moment arms of the muscles about the shoulder and elbow joints at the specified posture),

$$\overrightarrow{K}$$

is a diagonal matrix in which the nonzero elements represent the stiffness for each muscle in the model, and ${\overrightarrow{F}}^{\text{m}}$ is the vector of muscle forces. The second term in the equation accounts for how angle-dependent changes in muscle moment arms influence joint stiffness.

As described previously (McIntyre et al. 1996), endpoint stiffness (K^e) was computed from joint stiffness by considering the Jacobian (G) relating changes in joint angles to changes in endpoint displacement (Eq. 7):

$$K^e={\left(G^{-1}\right)}^T\left[K^j-\frac{\partial G^T}{\partial \theta }{\text{F}}^{\text{end}}\right]G^{-1}$$ (7)

where F^end is the vector of endpoint forces.

Simulated experiments.

The proposed model was used to simulate the endpoint stiffness measurements made in a previously published study (Perreault et al. 2001). Endpoint stiffness can be visualized as an ellipse (Mussa-Ivaldi et al. 1985). Such representations typically are quantified by area (a measure of magnitude), orientation (the direction of maximal endpoint stiffness), and shape (a measure of stiffness anisotropy). These parameters were computed as described previously (Gomi and Osu 1998) and used to compare the model-based estimates of endpoint stiffness to those measured experimentally.

The experimental measurements involved estimating endpoint stiffness as subjects exerted constant levels of endpoint force against a rigid manipulator. All measurements were made in the horizontal plane with a shoulder abduction angle of 90° and are described in detail in the original publication (Perreault et al. 2001). In summary, the subjects' hands were positioned either directly in front of the sternum (medial posture), in front of the shoulder (central posture), or lateral to the shoulder (lateral posture). For the purpose of our endpoint stiffness simulations, we selected data corresponding to all five subjects tested in the previous study. We simulated the endpoint stiffness of these subjects at four endpoint force magnitudes, corresponding to 7.5, 15, 22.5, and 30% of the subjects' maximum voluntary contractions. These forces were oriented along one of four directions (±X, lateral and medial; and ±Y, anterior and posterior). Using the model, joint torques (TQ) were calculated from the measured endpoint forces (F^end) using the standard relationship shown in Eq. 8.

$$TQ=G^T{\text{F}}^{\text{end}}$$ (8)

Given these joint torques, a model-based estimate of endpoint stiffness could be obtained by solving Eqs. 1–7, as described above. Experimental estimates made under passive conditions were used to define the passive properties of the joints within the model.

We also compared model-based estimates of elbow stiffness with those obtained from the multijoint experimental study described above and with those measured in a previously published single-joint experiment (Cannon and Zahalak 1982). For these estimates, the model was compared with the previously published group results to obtain estimates of the expected experimental variability across subjects. All predictions were restricted to elbow moments between −20 and 20 Nm to remain within the range of previously reported experimental results.

Model comparisons.

As an alternative to characterizing muscle stiffness, K^m, by estimates of short-range stiffness, we also estimated muscle stiffness as the slope of the force-length relationship and then used Eq. 1 to compute the total stiffness of the muscle-tendon unit. Tendon stiffness was kept the same for both methods. The force-length relationship implemented in SIMM (Delp and Loan 2000) was used for muscle stiffness estimation. It uses a force-length relationship defined by a dimensionless curve (Delp and Loan 2000; Zajac 1989). The slope of the curve, scaled by the muscle activation level, was defined as the muscle fiber stiffness. The activation level for a given muscle was specified by the force in the muscle that resulted from the optimization, normalized by the maximum isometric force the muscle could produce at the arm posture of interest, as defined by the musculoskeletal model.

It is well-known that the peak of the force-length curve for a muscle shifts to longer muscle lengths at submaximal levels of activation (Rack and Westbury 1969; Roszek et al. 1994). To take this characteristic into account, the following relationship developed by Lloyd and Besier (2003) was also evaluated in this study:

$$l_0^m\left(t\right)=l_0^m\left\{\lambda \left[1-a\left(t\right)\right]+1\right\}$$ (9)

where λ is the percentage change in optimal fiber length, a(t) the activation at time t, and l₀^m(t) the optimal fiber length at time t and activation a(t). λ was chosen as 0.15, which means the optimal fiber length is 15% longer at zero activation (Lloyd and Besier 2003).

The activation a(t) in Eq. 9 was determined in a different way from that used for activation-independent force-length curve. First, for each muscle, the force resulting from the optimization was used in a force balance equation to calculate the force in the tendon and, therefore, the tendon length. Next, muscle fiber length was determined by subtracting the calculated tendon length from the musculotendon length, which was explicitly defined by the musculoskeletal model as a function of arm geometry. The combination of muscle force and fiber length that resulted from this process uniquely determined activation.

Sensitivity analysis.

Because of the unavoidable variability in physiological parameters, Monte Carlo analyses (Hughes and An 1997; Santos and Valero-Cuevas 2006) were conducted to evaluate the sensitivity of our model-based estimates of endpoint stiffness to four types of model parameters: muscle moment arms, tendon stiffness, joint angles, and the maximum isometric force of each muscle. This analysis was done at the maximum endpoint forces measured in the experimental study (30% maximum voluntary contraction) along each of the four voluntary force directions (±X and ±Y). For each set of simulations, model parameters were selected from a normal distribution centered about the nominal parameter values defined by our model with a standard deviation that was equal to the plausible range over which these parameters could be expected to vary across different individuals, as defined by experimental data reported in the literature. Standard deviations for tendon stiffnesses and muscle moment arms were set to 25 and 20% of the nominal parameter values, respectively (Murray et al. 2002; Zajac 1989). Standard deviations for joint angles were set to 4°, the accuracy with which joint posture can be measured with a goniometer (Fish and Wingate 1985; Grohmann 1983).

The plausible range of peak muscle forces was estimated by typical variations in muscle volume. The maximum force a muscle can produce is determined by its physiological cross-sectional area (PCSA). PCSA is a measure of the total volume of the muscle normalized by fiber length and adjusted by pennation angle so that the maximum isometric force-generating capability of muscles with different lengths and orientations of fibers can be compared directly, based only on anatomic measurements (Spector et al. 1980). When comparing the same muscle (i.e., the triceps brachii of a small female with the triceps brachii of a large male), differences in muscle volume dominate intersubject variability. For example, the relative variance (standard deviation ÷ mean) of triceps volume was 47% in a study of 10 healthy subjects spanning a large size range (Holzbaur et al. 2007b). In contrast, optimal fascicle length in triceps long head varied by only 17% in a cadaver study that included a comparable range of specimen sizes (Murray et al. 2000). Total muscle volume in the upper limb varied 3-fold across young healthy subjects, whereas volume fraction (defined as individual muscle volume ÷ total muscle volume) had a standard deviation of ∼20% on average (Holzbaur et al. 2007b). Variation in volume fraction was used to assess the sensitivity of our stiffness estimates to the uncertainty in our parameters defining relative muscle strength within a given subject. Changes in absolute strength across subjects were assessed separately, as described below.

The influence of variability in moment arms, tendon stiffness, joint angles, and muscle volume fraction on our results was assessed independently. Three hundred simulations were performed per set for a total of 1,200 simulations (4 parameter types × 300 individual simulations). In each individual simulation, the parameter of interest was selected randomly for each muscle (or joint for simulations that explored variability in joint posture).

The results of these simulations were summarized by the standard deviation of the endpoint stiffness characteristics described previously: area, orientation, and shape. The sensitivity of each model output to a given parameter was reported as the standard deviation of the output across the 300 Monte Carlo simulations performed for each parameter. The standard deviations of estimated stiffness area and shape were normalized by their nominal values. The standard deviation of the estimated endpoint stiffness orientation, however, was described in absolute units since the nominal values depend on the defined coordinate system orientation and are not meaningful for these purposes.

The isometric strength of our model is based on average data describing young, healthy male subjects (Holzbaur et al. 2007a). To examine the influence of variations in absolute strength on our results, we scaled the muscle volumes in the nominal model (total muscle volume = 3,600.6 cm³) to reflect three sets of subject-specific data reported in the literature (Holzbaur et al. 2007b) (smallest female subject, total muscle volume = 1,426.9 cm³; smallest male subject, total muscle volume = 2,954.8 cm³; and largest male subject, total muscle volume = 4,426.8 cm³). These results are reported independently from the Monte Carlo analyses.

RESULTS

Model-based estimation of elbow stiffness.

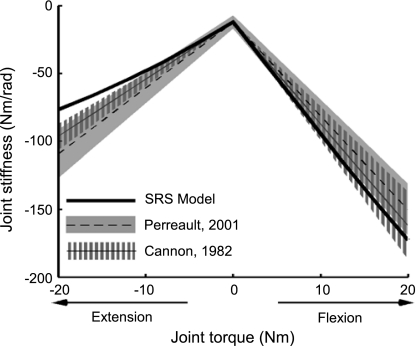
The developed model characterized many important features of how elbow stiffness varied with changes in elbow torque. The simulated elbow stiffness increased with increasing elbow torque and was larger in flexion than in extension, as has been documented experimentally (Fig. 1). For all simulated subjects, the predictions of how elbow stiffness varied with changes in elbow flexion torque fell within the 95% confidence intervals for the average data reported in two experimental studies (Cannon and Zahalak 1982; Perreault et al. 2001). The model-based estimates of elbow stiffness during flexion were at most 13 ± 2 and 21 ± 3% higher than the average experimental results reported by Cannon and Zahalak (1982) and Perreault et al. (2001), respectively. Larger differences were found for the predictions of how elbow stiffness varied with changes in elbow extension torque. For extension, the model-based estimates were lower than the experimental results reported by Cannon and Zahalak (1982) and Perreault et al. (2001) by up to 21 ± 1 and 30 ± 1%, respectively.

Fig. 1.

Single joint elbow stiffness predictions from short-range stiffness (SRS) model compared with 2 experimental measurements (Cannon and Zahalak 1982; Perreault et al. 2001). The kinematic parameters of the model were matched to those of subject 4 in Perreault et al. (2001). Negative torque is extension; positive torque is flexion. The experimental data shown are averages across all the subjects in each study. The elbow stiffness reported in Perreault et al. (2001) was transformed from measured endpoint stiffness of the human arm. Shaded areas show the 95% confidence intervals of the experimental data. The 95% confidence interval of Cannon and Zahalak (1982) was computed based on the data of 10 subjects.

Model-based estimation of endpoint stiffness.

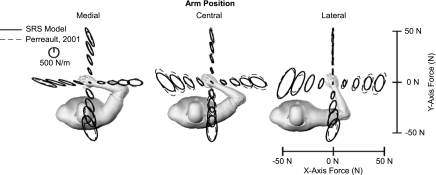
The model-based estimates of endpoint stiffness were similar to the experimental results in orientation, shape, and area over the full range of tested forces and postures across all subjects. Typical model estimates for a single subject (no. 4) are shown in Fig. 2. On average, the model accounted for 98 ± 2% of the variation in stiffness orientation across all tested conditions. Over the same range of conditions, the model accounted for an average of 91 ± 4 and 82 ± 12% of the variability in stiffness shape and area, respectively (Table 1).

Fig. 2.

Endpoint stiffness predictions from SRS model at 3 arm positions (the medial, central, and lateral positions) compared with 1 previous experimental study (Perreault et al. 2001). The kinematic parameters of the model were matched to those of subject 4 in the experimental study. Each ellipse is centered at a location proportional to the endpoint force direction and magnitude the subject was exerting.

Table 1.

Comparison of experimental and model-based estimates of endpoint stiffness

		VAF, %
	Arm Position	Orientation	Shape	Area
Short-range stiffness model	Medial	97 ± 2	88 ± 6	80 ± 19
	Central	99 ± 1	93 ± 1	85 ± 4
	Lateral	98 ± 1	91 ± 3	81 ± 11
F-L relationship	Central	84 ± 7	57 ± 22	13 ± 2
Coupled F-L relationship	Central	82 ± 10	55 ± 20	20 ± 6

Values are means ± SD. F-L, force-length; VAF, variance accounted for.

Stiffness estimation from the force-length relationship.

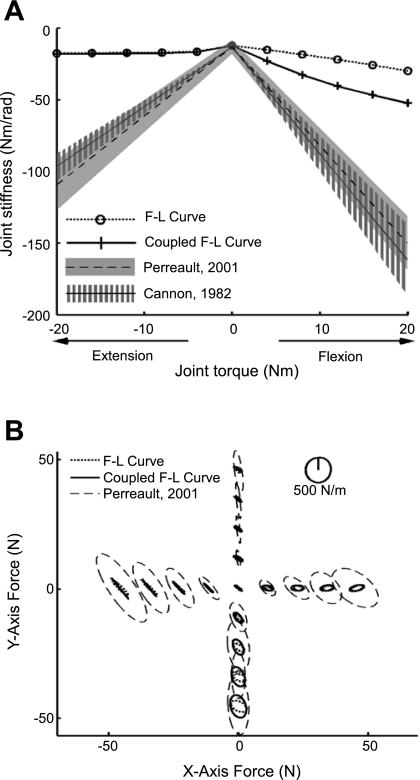
Model-based stiffness estimates based on the slope of the force-length curve dramatically underestimated the magnitude of joint and endpoint stiffness. For elbow joint stiffness, estimations from the force-length relationship were much lower than the 95% confidence intervals reported in both experimental studies (Cannon and Zahalak 1982; Perreault et al. 2001) (Fig. 3A, typical data of subject 4). The simulated elbow stiffness was up to 82 ± 3 and 82 ± 1% lower than the experimental stiffness for both flexion and extension. Small improvements were observed when using the modified force-length relationship (Lloyd and Besier 2003). These improvements were largely for elbow flexion, although these model-based estimates were still lower than the experimental estimates by more than 69 ± 8%. No substantial improvements were observed for elbow extension, in which the model-based estimates remained more than 79 ± 2% lower than the experimental estimates.

Fig. 3.

A and B: elbow joint stiffness and endpoint stiffness model estimates based on the slope of the force-length (F-L) relationship. The experimental data shown in Fig. 1 are repeated here for comparison (Cannon and Zahalak 1982; Perreault et al. 2001). A shows the elbow joint stiffness estimation. B shows the endpoint stiffness estimation at the central arm position.

The model-based estimates of endpoint stiffness obtained using the slope of the force-length curve also were much smaller than the experimental estimates (Fig. 3B, typical data of subject 4). Specifically, the estimation only accounted for 13 ± 2% of variance in the area of stiffness ellipses at the central arm position, although it accounted for 84 ± 7 and 57 ± 22% of variance in the orientation and shape at the same arm position (Table 1). Applying the coupled force-length relationship gave similar results, accounting for only 20 ± 6% of variance in the area. The area of ellipses represents the magnitude of endpoint stiffness, thus the estimation from both types of force-length relationships greatly underestimated the magnitude of the measured endpoint stiffness.

Sensitivity analysis.

The model-based estimates of endpoint stiffness were relatively insensitive to changes of model parameters. The maximum expected errors in the estimated endpoint stiffness orientation, shape, and area were 6.3°, 22%, and 23%, respectively (Table 2). Model-based estimates of endpoint stiffness generally were most sensitive to errors in model moment arms, volume fraction, and joint angles. The model-based estimates were approximately an order of magnitude less sensitive to errors in the estimated tendon properties. Orientation was most sensitive to changes in joint angles, although even this sensitivity was small, resulting in a maximum expected orientation error of <7°. Endpoint stiffness shape and area were most sensitive to uncertainty in moment arm values. Again, these sensitivities were small, resulting in expected errors <25% for parameter errors at the maximum of the plausible range.

Table 2.

Expected variation of model outputs over the range of plausible model parameters

	Orientation, °	Shape, %	Area, %
Moment arm	6.0	22	23
Tendon stiffness	0.6	2	3
Joint angle	6.3	13	11
Volume fraction	3.4	14	14

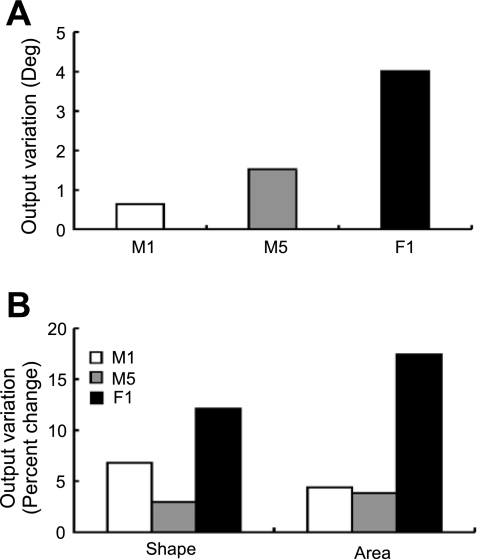
Changes in total muscle volume also did not substantially influence the model predictions. From smallest (M1) to the largest (M5) male subjects (total muscle volume increased by 50%), the variation in the model output relative to the nominal parameter values was <2° for the orientation (Fig. 4A) and 10% for the shape and the area (Fig. 4B). For the smallest female (F1), the variation in the model output was ∼4° for endpoint stiffness orientation (Fig. 4A) and 15% for the shape and the area (Fig. 4B). Although the model worked best with male subjects, which the nominal parameter values represented, it also gave reasonably good estimates for the smallest female subject (∼4° variation in the orientation and ∼15% variation in the shape and the area) whose total muscle volume was only ∼40% of the average male subject represented by our model.

Fig. 4.

A and B: the comparison between the average total muscle volume of male subjects and the subject-specific total muscle volume of female and male subjects F1, M1, and M5. A indicates the variations of stiffness orientation in absolute units (degrees). B indicates the variations of stiffness shape and area normalized by their nominal values.

DISCUSSION

The purpose of this study was to quantify the degree to which the endpoint stiffness of the human arm could be attributed to the short-range stiffness of the active muscles within the arm. This was accomplished by combining scalable models of short-range stiffness with a 3-D musculoskeletal model of the upper limb and evaluating how well this combined model could explain previously collected experimental data. We found that the combined model accurately described the variation in endpoint stiffness across a range of arm postures and voluntary forces. Importantly, these predictions were made without fitting any model parameters to the experimental data. In contrast, muscle stiffness estimates obtained from the slope of the force-length curve were unable to describe the experimentally measured variations in endpoint stiffness. These results suggest that the short-range stiffness of muscles within the arm is a major contributor to endpoint stiffness. Furthermore, the model we have developed provides an important tool for assessing how the nervous system can regulate endpoint stiffness via changes in muscle cocontraction in addition the reciprocal activation needed to generate the forces for a specific task.

Muscle properties contributing to endpoint stiffness.

Our results suggest that short-range stiffness is a major contributor to the endpoint stiffness of the human arm. It is important, however, to consider the experimental conditions used to estimate endpoint stiffness. Isolated muscles exhibit short-range stiffness when stretched less than 2–3% of the muscle fiber length or through movements covering approximately 3–4% of the physiological range (Rack and Westbury 1974). The perturbations used in the experiments we considered (Perreault et al. 2001) did not exceed this range. Those perturbations had peak-to-peak amplitudes of 2 cm, which generated maximum movements of ∼3° at the shoulder and 2° at the elbow. These joint rotations represent only ∼2% of the range of motion for these joints within the horizontal plane, well within the limits of short-range stiffness. It is likely that experiments incorporating larger perturbations would not be so well-characterized by our current model. Indeed, it has been demonstrated that the estimated stiffness of single and multijoint systems decreases with increasing perturbation amplitude (Kearney and Hunter 1982; Shadmehr et al. 1993), as would be expected when muscle exceed their region of short-range stiffness (Rack and Westbury 1974). Beyond this range, more complex models that consider the dynamics of cross-bridge cycling would likely be necessary.

Endpoint stiffness cannot be described by the slope of the force-length curve, even though this has commonly been assumed to approximate the stiffness properties of individual muscles. The force-length curve represents the isometric force that a muscle can generate at a specific length rather than the change in muscle force that occurs with rapid changes in length, as are required to estimate stiffness. These two properties are known to differ (Joyce et al. 1969). The force-length properties are determined largely by the overlap of the actin and myosin filaments at different muscle lengths (Gordon et al. 1966), whereas the short-range stiffness properties are thought to arise from the number of bound cross-bridges (Morgan 1977; Rack and Westbury 1974). In contrast to the slope of the force-length curve, short-range stiffness is length-independent and changes primarily with changes in muscle force (Morgan 1977), which greatly simplifies the problem of estimating muscle contributions to limb mechanics at different postures.

It is important to note that stiffness is only one component of muscle and limb impedance. Inertial, viscous, and higher order properties also contribute substantially to the mechanical properties of a limb. Our model focuses only on limb stiffness, which has been proposed to play an important role in the control of posture and movement (Hogan 1985) and to contribute to limb stability during different tasks that destabilize limb posture (Burdet et al. 2001; Selen et al. 2009). We have demonstrated how muscle short-range stiffness contributes to the stiffness of the entire limb. Identifying a similar relationship for limb viscosity would allow for a more complete description of how intrinsic muscle properties contribute to the mechanical properties of a limb in the absence of changes in muscle activation resulting from neural control.

Influence of muscle activation on estimates of endpoint stiffness.

Short-range stiffness scales with muscle force, and the accuracy of our endpoint stiffness model depends on the accuracy with which individual muscle forces can be estimated. Because of the redundant nature of the musculoskeletal system, we used optimization to estimate the individual muscle forces contributing to the endpoint forces measured during the experimental studies. We selected a common cost function that minimizes the relative activation of all muscles (Anderson and Pandy 2001; Crowninshield and Brand 1981) and which has been shown to work well during isometric the force regulation tasks (Van Bolhuis and Gielen 1999) relevant to our study. Such a cost function, however, does not predict cocontraction of antagonistic muscles (Collins 1995) and is certain to be inadequate in tasks that require cocontraction, thereby altering limb stiffness without corresponding changes in net joint torque (Gomi and Osu 1998; Milner et al. 1995). These limitations may have contributed to the low values of elbow stiffness predicted by our model during extension tasks. Nevertheless, the majority of our predictions were surprisingly accurate given that our model was not fit to the experimental data. This is likely due to the presence of minimal cocontraction in the experiments we attempted to replicate in simulation. For tasks with substantial cocontraction, different methods will be needed for estimating individual muscle forces, such as EMG-assisted optimization (Cholewicki and McGill 1994).

Sensitivity of model predictions to parameter errors.

Our predictions of endpoint stiffness were robust with respect to changes in model parameters that were within the range of plausible variations. Endpoint stiffness predictions were most sensitive to changes in model geometry, such as moment arms and joint angles, emphasizing the need to use realistic musculoskeletal models when assessing the contributions of muscle properties to endpoint stiffness. Our model was not sensitive to changes in total muscle volume and was moderately sensitive to the volume fraction of individual muscles. The latter sensitivity is likely due to the optimization algorithm used to estimate muscle forces. Crowninshield and Brand (1981) noted that the optimization algorithm we employed tended to allocate more force to stronger muscles. This redistribution would alter the relative contributions of synergistic muscles to the net joint torques and stiffness. This redistribution of synergistic forces would affect limb stiffness only for muscles with different geometric properties, such as fiber lengths (Eq. 2) or moment arms (Eq. 6).

Model predictions were least sensitive to changes in tendon stiffness. This is likely due to the fact that short-range stiffness is dominated by muscle stiffness at low activation levels (Cui et al. 2007) and that the maximum endpoint forces assessed in this study never exceeded 30% of the maximum strength. Tendon stiffness may play a more important role at higher force levels and for muscles with relatively long tendons, such as those in the distal parts of the upper and lower limbs. In those cases, our assumption of uniform material properties for all tendons, which is known to be incorrect (Bennett et al. 1986; Cui et al. 2009; Zajac 1989), may lead to larger prediction errors.

Feedback contributions to endpoint stiffness.

Our model predicts how steady-state changes in muscle activation, such as those usually attributable to voluntary feedforward motor commands, contribute to changes in endpoint stiffness. The model does not explicitly represent contributions from feedback pathways. As a result, it may fail to characterize endpoint stiffness estimated using protocols in which transient feedback responses to an applied perturbation contribute substantially to the net endpoint force. The modeled experiments (Perreault et al. 2001) used continuous stochastic perturbations to estimate endpoint stiffness. The fact that our model accurately described the stiffness estimated in those experiments suggests either that feedback contributions were small, as has been reported previously for perturbations with a high average velocity (Kearney et al. 1997), or that the muscle contractions were largely fused. During fused contractions, feedback would largely serve to increase the tonic force level.

Feedback responses to transient perturbations of endpoint position can be large (Krutky et al. 2010; Perreault et al. 2008), and protocols that use transient perturbations to estimate endpoint stiffness (Burdet et al. 2001; Darainy et al. 2004; Franklin et al. 2007) may not be well-represented by our model. Deviations between our model predictions and stiffness estimates made using transient perturbations may be useful for beginning to assess reflex contributions to the regulation of endpoint stiffness.

Comparison with other models of endpoint stiffness.

Because of its importance in understanding how the nervous system regulates the mechanical properties of the arm, there have been numerous attempts to develop models of endpoint stiffness. Although each has contributed to our understanding of stiffness regulation, we are unaware of any that have incorporated 3-D musculoskeletal geometry or that have directly assessed which muscle properties are most relevant to stiffness regulation. Many models have considered stiffness regulation only at the joint level (Flash and Mussa-Ivaldi 1990; Gomi and Osu 1998; Tee et al. 2004). Those models that have directly incorporated muscles (Osu and Gomi 1999; Shin et al. 2009; Tee et al. 2010) have considered only a reduced muscle set and constant moment arms, at times selected for computational simplicity or to fit best the experimental data. Although these assumptions have been sufficient for the intended purposes, they may not readily allow for generalization to novel situations, especially given our finding that stiffness estimates are most sensitive to the geometric properties of the model.

Models also have been developed that incorporate more complex mechanisms, including muscle dynamics in the form of Hill-type models and feedback pathways to represent reflex behaviors (Gribble et al. 1998; Stroeve 1999). Neither model incorporated short-range stiffness. Although both models have been shown to generalize across conditions, their complexity makes it difficult to assess which of the modeled mechanisms are most relevant to the simulated behaviors. Interestingly, Stroeve (1999) suggested that reflexes are a major contributor to the simulated endpoint stiffness but noted that the Hill-type models used in his simulations do “not fully represent the intrinsic, low-frequency components of the impedance.” Wagner and Blickhan (1999) reached similar conclusions by evaluating how muscle properties contribute to postural stability during standing. They concluded that simple Hill-type models were not able to maintain stability. Stable postures could be obtained only with sufficiently large parallel stiffness, as could be provided by the short-range stiffness of active cross-bridges, or with sufficient feedback control. Our model provides a direct means to evaluate the contributions that can be expected from the intrinsic stiffness of muscle in the absence of feedback. Failure to incorporate these intrinsic properties of muscle may lead to an overestimation of the role that feedback plays in the regulation of limb mechanics and stability.

In contrast to previous models of endpoint stiffness, we have developed a mechanistically simple model that is able to replicate measures of endpoint stiffness without explicitly fitting any parameters to the experimental data. This was done by incorporating experimentally validated, scalable models of muscle short-range stiffness into a realistic musculoskeletal model of the human arm. This provides us with a means to assess how the nervous system may regulate endpoint stiffness via changes in the steady-state activation of arm muscles.

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant R01-NS-053813 and the Searle Funds at the Chicago Community Trust.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).