Quantization and Analysis of Hippocampal Morphometric Changes Due to Dementia of Alzheimer Type Using Metric Distances Based on Large Deformation Diffeomorphic Metric Mapping

Abstract

The metric distance obtained from the Large Deformation Diffeomorphic Metric Mapping (LDDMM) algorithm is used to quantize changes in morphometry of brain structures due to neuropsychiatric diseases. For illustrative purposes we consider changes in hippocampal morphometry (shape and size) due to very mild dementia of the Alzheimer type (DAT). LDDMM, which was previously used to calculate dense one-to-one correspondence vector fields between hippocampal shapes, measures the morphometric differences with respect to a template hippocampus by assigning metric distances on the space of anatomical images thereby allowing for direct comparison of morphometric differences. We characterize what information the metric distances provide in terms of size and shape given the hippocampal, brain and intracranial volumes. We demonstrate that metric distance is a measure of morphometry (i.e., shape and size) but mostly a measure of shape, while volume is mostly a measure of size. Moreover, we show how metric distances can be used in cross-sectional, longitudinal analysis, as well as left-right asymmetry comparisons, and provide how the metric distances can serve as a discriminative tool using logistic regression. Thus, we show that metric distances with respect to a template computed via LDDMM can be a powerful tool in detecting differences in shape.

1 Introduction

Methods developed in the field of Computational Anatomy (CA) that enable quantification of brain structure volumes and shapes between and within groups of individuals with and without various neurological diseases have emerged from several groups in recent years [1-6]. Based on the mathematical principles of general pattern theory [4, 7-10], these methods combine image-based diffeomorphic maps between MR scans with representations of brain structures as smooth manifolds. Because of their high repeatability and sensitivity to changes in neuroanatomical shapes, they can be especially sensitive to abnormalities of brain structures associated with a disease. Numerous post-mortem studies have shown that hippocampus is implicated with dementia of the Alzheimer type (DAT) [11-17]. The accumulation of neurofibrillary tangles and amyloid plaques characteristic of AD are associated with neuronal damage and death [18]. Furthermore, macroscopic gray matter losses from the accumulation of microscopic scale neuronal destruction are detectable in living subjects using currently available magnetic resonance (MR) imaging. Specifically, volume losses within the hippocampus [19-24] have recently been reported in subjects with mild-to-moderate AD. Using image-based diffeomorphic maps, we previously demonstrated that the combined assessment of hippocampal volume loss and shape deformity optimally distinguished subjects with very mild DAT from both elder nondemented subjects and younger healthy subjects [20]. These methods also allowed us to demonstrate that hippocampal shape deformities associated with very mild DAT and nondemented aging were distinct [25]. These methods were also extended to quantify changes in neuroanatomical volumes and shapes within the same individuals over time [26]. Other longitudinal neuroimaging analysis of hippocampal structures in individuals with AD have also emerged [27-38].

An important task in CA is the study of neuroanatomical variability. The anatomic model is a quadruple (Ω, G, I, P) consisting of Ω the template coordinate space (in R³), defined as the union of 0, 1, 2, and 3-dimensional manifolds, G : Ω ↔ Ω a set of diffeomorphic transformations on Ω, I the space of anatomies is the orbit of a template anatomy I₀ under G, and P the family of probability measures on G. In this framework, a geodesic ϕ: [0, 1] → G is computed where each point ϕ_t = ϕ(t) ∈ G, t ∈ [0, 1] is a diffeomorphism in the domain Ω. The evolution of the template image I₀ along path is given by ${\varphi }_t{I}_0=I_0\circ {\varphi }_t^{-1}$ such that the end point of the geodesic connects the template I₀ to the target I₁ via $I_1={\varphi }_1{I}_0=I_0\circ {\varphi }_1^{-1}$. Thus, anatomical variability in the target is encoded by these geodesic transformations when a template is fixed. Furthermore, geodesic curves induce metric distances between the template and the target shapes in the orbit as follows. The diffeomorphisms are constructed as a flow of ordinary differential equations ϕ_t = υ_t(ϕ_t), t ∈ [0, 1] with ϕ₀ = id the identity map, and associated vector fields, υ_t, t ∈ [0, 1]. The optimal velocity vector field parameterizing the geodesic path is found by solving

$$\widehat{\upsilon }=\underset{\underset{{\varphi }_0=\mathit{id}}{\upsilon :\varphi ={\mathit{\int }}_0^1{\upsilon }_t({\varphi }_t)\mathit{dt},}}{\arg \inf }{\mathit{\int }}_0^1\parallel {\upsilon }_t{\parallel }_V^2\mathit{dt}\mathrm{such\; that}{I}_0\circ {\varphi }_1^{-1}=I_{1,}$$ (1)

where υ_t ∈ V, the Hilbert space of smooth vector fields with norm ∥·∥_V defined through a differential operator enforcing smoothness [26]. The length of the minimal length path through the space of transformations connecting the given anatomical configurations in I₀ and I₁ defines a metric distance between anatomical shapes in I₀ and I₁ via

$$d(I_0,I_1)={\mathit{\int }}_0^1\parallel {\widehat{\upsilon }}_t{\parallel }_V\mathit{dt},$$ (2)

where υ̂_t is the optimizer calculated from the Large Deformation Diffeomorphic Metric Mapping (LDDMM) algorithm [39]. Here, the metric distance does not have any units. The construction of such a metric space allows one to quantify similarities and differences between anatomical shapes in the orbit. This is the vision laid out by D’Arcy W. Thompson almost one hundred years ago. Figure 1 exemplifies the change in the metric distance during the evolution of the diffeomorphic map from the template shape to the target shape.

Figure 1.

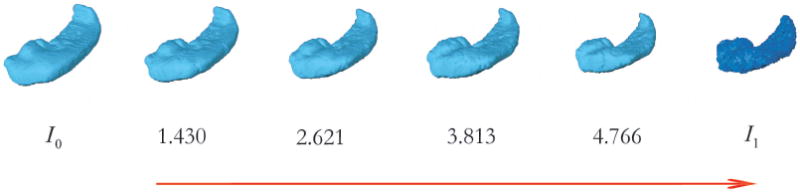
Change in metric distance during diffeomorphic flow from template (I₀) to target ( $I_1={\varphi }_1{I}_0=I_0\circ {\varphi }_1^{-1}$). The numbers are the metric distance estimates at the three intermediate stages and the final stage of the LDDMM algorithm.

The notion of mathematical biomarker in the form of metric distance can be used in different ways. One is to generate metric distances of shapes relative to a template [39, 40]. Another is to generate metric distances between each shape within a collection [41]. The latter approach allows for sophisticated pattern classification analysis; it is however computationally expensive. We present an analysis based on the former approach which could provide a powerful tool in analyzing subtle shape changes over time with considerably less computational load. This approach may allow detecting the subtle morphometric changes observed in the hippocampus in DAT subjects in particular for those previously analyzed [26, 42]. These studies compared rates of change in hippocampal volume and shape in subjects with very mild DAT and matched (for age and gender) nondemented subjects. The change in hippocampal shape over time was defined as a residual vector field resulting from rigid-body motion registration, and changes in patterns along hippocampal surfaces were visualized and analyzed via a statistical measure of individual and group change in hippocampal shape over time and used to distinguish between the subject groups. Hence the motivation to analyze LDDMM generated metric distances between binary hippocampus images at baseline and at follow-up with respect to the same template hippocampus image. That is, the template was compared again, and not propagated between time points. One might wonder why we do not track changes within a subject directly, rather than via a reference template, as it could give a more sensitive measure of shape change since the small difference in shape would make finding correspondence more accurate. Although we have considered doing this, the difficulty is that since the template (or origin) is different for each longitudinal computation, how to correctly perform statistical comparison of group change is not completely settled. This is actively being developed by using the concept of “parallel transport” [43, 44].

In this study, we compute and characterize what metric distance conveys and provide a statistical methodology to analyze metric distances based on the data used in [26]. In fact, [26] used a previous implementation of the present technology called large-deformation high-dimensional brain mapping (or HDBM-LD). The method was also based on use of a single template and large deformation diffeomorphic mappings. The difference between the methodology of [26] and this article is the way in which the resulting deformation fields that represent morphometric differences were analyzed. For the former was analyzed using singular value decomposition (SVD) applied on each incremental deformation field; the present is analyzed according to only its metric shape difference.

The morphometric differences are measured with respect to a template, so the differences in morphometry are relative to this template. However, such differences might also imply the correlation of morphometry with certain types of conditions. For example, a cross-sectional analysis of distances for different conditions or groups might suggest changes in morphometry due to a disease. Longitudinal analysis of distances might provide how the morphometry changes over time and whether the change is different between the groups. Under certain restrictions, even left-right anatomical asymmetry may be measured and analyzed for different groups. Moreover, metric distances (together with some other measures such as volume) might also be used for discriminative purposes; i.e., they can be used as biomarkers to distinguish healthy tissues from diseased ones.

We briefly describe computation of metric distances via LDDMM in Section 2.1, the hippocampal data set in Section 2.2, statistical methods we employ in Section 2.3. Furthermore, we provide the analysis on metric distances and volumes in Section 3, compare volumes and metric distances in Section 3.8, and analyze annual percentage rate of change in volumes and distances in Section 4. In the final section, we discuss the use of metric distances for baseline-followup studies, group comparisons, and discrimination analysis.

2 Methods

2.1 Computing Metric Distance via Large Deformation Diffeomorphic Metric Mapping

Metric distances between the binary images and the template image are obtained by computing diffeomorphisms between the images. Computation and analysis of these diffeomorphic mappings have been previously described [45]. Diffeomorphisms are estimated via the variational problem that, in the space of smooth velocity vector fields V on domain Ω, takes the form [39]:

$$\widehat{\upsilon }=\underset{\upsilon :{\dot{\varphi }}_t={\upsilon }_t({\varphi }_t)}{\arg \min }\left({\mathit{\int }}_0^1\parallel {\upsilon }_t{\parallel }_V^2\mathit{dt}+\frac{1}{{\sigma }^2}\parallel I_0\circ {\varphi }_1^{-1}-I_1{\parallel }_{L^2}^2\right).$$ (3)

The optimizer of this cost generates the optimal change of coordinates $\phi ={\varphi }_1^{\widehat{\upsilon }}$ upon integration $d{\widehat{\varphi }}_t^{\upsilon }/\mathit{dt}={\widehat{\upsilon }}_t\left({\widehat{\varphi }}_t^{\upsilon }\right)$, ϕ₀ = id, where the subscript υ in ϕ^υ is used to explicitly denote the dependence of ϕ on the associated velocity field υ. Enforcing a sufficient amount of smoothness on the elements of the space V of allowable velocity vector fields ensures that the solution to the differential equation ϕ̇_t = υ_t(ϕ_t), t ∈ [0, 1], υ_t ∈ V is in the space of diffeomorphisms [46, 47]. The required smoothness is enforced by defining the norm on the space V of smooth velocity vector fields through a differential operator L of the type L = (−αΔ + γ)^αI_n×n where α > 1.5 in 3-dimensional space such that ∥f∥_V = ∥Lf∥_L2 and ∥·∥_L2 is the standard L₂ norm for square integrable functions defined on Ω. The gradient of this cost is given by

$${\nabla }_{\upsilon }{E}_t=2{\widehat{\upsilon }}_t-K\left(\frac{2}{{\sigma }^2}\mid D{\varphi }_{t,1}^{\widehat{\upsilon }}\mid \nabla J_t^0\left(J_t^0-J_t^1\right)\right)$$ (4)

where $J_t^0=I_0\circ {\varphi }_t$ and $J_t^1=I_1\circ {\varphi }_t^{-1}$, |Dg| is the determinant of the Jacobian matrix for g and K is a compact self-adjoint operator K : L₂ (Ω, R^d) → V uniquely defined by < a, b > _L2=< K a, b >_V such that for any smooth vector field f ∈ V, K (L^†L)f = f holds. The metric distance is then calculated via Equation (2).

2.2 Subjects and Data Acquisition

Detailed description of subjects can be found in [26] where 18 very mild DAT subjects (Clinical Dementia Rating Scale, CDR0.5) and 26 age-matched nondemented controls (CDR0) were each scanned approximately two years apart. Clinical Dementia Rating (CDR) scale assessments which detect the severity of dementia symptoms were performed annually in all subjects by experienced clinicians without reference to neuropsychological tests or in-vivo neuroimaging data. The experienced clinician conducted semi-structured interviews with an informant and the subject to assess the subject’s cognitive and functional performance; a neurological examination was also obtained. The clinician determined the presence or absence of dementia and, when present, its severity with the CDR. Overall CDR scores of 0 indicate no dementia, while CDR scores of 0.5, 1, 2, and 3 indicate very mild, mild, moderate and severe dementia, respectively [48]. CDR assessments have been shown to have an inter-rater reliability of κ = 0.74 (weighted kappa coefficient [49] κ of 0.87) [50], and this high degree of inter-rater reliability has been confirmed in multi-center dementia studies [51]. Elderly subjects with no clinical evidence of dementia (i.e., CDR0 subject) have been confirmed with normal brains at autopsy with 80% accuracy; i.e., approximately 20% of such individuals show evidence of AD [52]. CDR0.5 subjects have subtle cognitive impairment, and 93% of them progress to more severe stages of illness (i.e., CDR > 0.5) and show neuropathological signs of AD at autopsy [52-54]. Although elsewhere the CDR0.5 individuals in our sample may be considered to have MCI [55], they fulfill our diagnostic criteria for very mild DAT and at autopsy overwhelmingly have neuropathologic AD [56]. A summary of subject information is listed in Table 1.

Table 1.

Summary information of subjects (I); means and SDs of brain and intracranial volumes by diagnosis group (III); means and SDs of hippocampal volumes by diagnosis group (IV); and means and SDs of metric distances by diagnosis group (V).

I- Summary Information of Subjects
	Gender (M/F)	Age (years) (mean ± SD)	Scan interval (years) ([Min-Max])	Education (years) (mean ± SD)
CDR0	12/14	75.2±7.0	2.2 [1.4-4.1]	14.8± 2.7
CDR0.5	11/7	75.7±4.4	2.0 [1.0-2.6]	13.7± 2.8
overall	23/21	75.4±6.1	2.1 [1.0-4.1]	14.3± 2.8
pL	NA	0.4224	NA	0.0001
pW	NA	0.8202	NA	0.2101

III- Mean ± SD Values of Brain and Intracranial Volumes
	BV1	BV3	ICV1	ICV3
CDR0	1006892± 104214.0	1003319.4± 101129.0	1407972 ± 156067.1	1464494± 177496.0
CDR0.5	1003850± 92293.4	993380.8 ± 95425.0	1408507± 134912.6	1454966± 138931.2
overall	1005647± 98408.2	999253.6 ± 97828.6	1408191± 146140.3	1460596± 161152.7
pL	0.2302	0.0079	0.0503	0.1070
pW	0.5192	0.3277	0.7929	0.8299

IV- Mean ± SD of Hippocampal Volumes
	LB	LF	RB	RF
CDR0	2081.4 ± 354.8	2081.4 ± 354.8	2081.4 ± 354.8	2081.4 ± 354.8
CDR0.5	1717.6 ± 224.8	1717.6 ± 224.8	1717.6 ± 224.8	1717.6 ± 224.8
overall	1932.6 ± 354.8	1932.6 ± 354.8	1932.6 ± 354.8	1932.6 ± 354.8
pL	0.3528	0.0268	0.2001	0.2359
pW	0.0003	< 0.0001	0.0149	0.0004

V- Mean ± SD of Metric Distances
	LB	LF	RB	RF
CDR0	3.34 ± 0.62	3.41 ± 0.54	3.63 ± 0.57	3.83 ± 0.47
CDR0.5	3.48 ± 0.76	3.82 ± 0.98	3.68 ± 0.81	4.37 ± 0.78
Overall	3.40 ± 0.68	3.57 ± 0.77	3.65 ± 0.67	4.05 ± 0.67
pL	0.0498	0.4718	0.2891	0.1084
pW	0.5994	0.1590	0.9145	0.02058

p_L: p-value based on Lilliefor’s test of normality, p_W: p-value based on Wilcoxon rank sum test. NA: not applicable; BV1 (BV3): brain volume at baseline (followup); ICV1(ICV3): intracranial volume at baseline (followup); LB: left baseline; LF: left followup; RB: right baseline; and RF: right followup.

The scans were obtained using a Magnetom SP-4000 1.5 Tesla imaging system, a standard head coil, and a magnetization prepared rapid gradient echo (MPRAGE) sequence. The MPRAGE sequence (TR/TE - 10/4, ACQ - 1, Matrix - 256 × 256, Scanning time - 11.0 min) produced 3D data with a 1 mm × 1 mm in-plane resolution and 1 mm slice thickness across the entire cranium.

A neuroanatomical template was produced using an MR image from an additional elder control (i.e., CDR0 or non-demented) subject (male, age = 69). The choice and a detailed description of the template is provided in [45]. The subject selected to produce this template was obtained from the same source as the other subjects in the study, but was not otherwise included in the data analysis. Data used are the left and right hippocampal surfaces in the template scan created from expert-produced manual outlines using methods previously described [25, 57], and the left and right hippocampal surfaces of each subject generated at baseline and follow-up. These surfaces were converted to binary hippocampus volumetric images by flood filling the inside of the surface and giving it label 1, and the outside of the surface was labeled as 0, or background. Each individual hippocampal surface was aligned with the template surface via a rigid-body rotation and translation before converting to volumetric binary images. In [57] we showed that mapping accuracy could be enhanced at higher resolution because of smaller voxels – voxels at the periphery of the structure (i.e., surface) account for much more of the structural volume at 1 mm³ voxel resolution versus 0.5 mm³. Since then we have adapted this as part of the standard mapping procedure. These surfaces were then converted into binarized image of dimension 64 × 112 × 64 with voxel resolutions of 0.5 × 0.5 × 0.5 mm³, followed by smoothing by a Gaussian filter of 9 × 9 × 9-voxel window and one voxel standard deviation to smooth out the edges for LDDMM, which was then applied to each template-subject pair to compute metric distances, $d_k^b,d_k^f(k=1,\dots ,44)$, in each hemisphere at baseline (b) and at follow-up (f) as illustrated in Figure 2. Segmentation of hippocampal MRI shapes across subjects, especially in diseased states, is a challenging problem. However the accuracy of the segmentation is not the point of this paper and has been demonstrated before [20, 45, 57].

Figure 2.

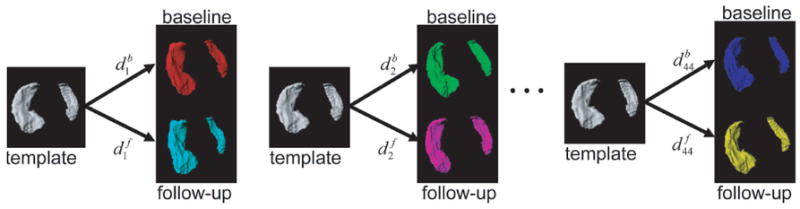
Generation of metric distances $d_k^{\{b,f\}}$ for subjects k = 1, … , 44 at baseline (b) and at follow-up (f).

In addition to the metric distances, our data set also consists of the following variables: gender, age, education in years (these variables are used for controlling the confounding affects of these factors on hippocampus morphometry). Furthermore, we have brain and intracranial volumes at baseline and followup, and hippocampus volumes for left and right hippocampi at baseline and follow-up. For the left data, hippocampi at baseline for CDR0.5 subjects are labeled as LB-CDR0.5, at follow-up they are labeled as LF-CDR0.5. CDR0 hippocampi are labeled as LB-CDR0 and LF-CDR0 accordingly. Similar labeling is done for the right metric distances.

2.3 Statistical Methods

First, we investigate what metric distance measures and how it is related to hippocampal, brain, and intracranial volumes. That is, as a compound measure of morphometry, how much of the metric distance is related to shape and volume. Along this line, we provide the correlation between volume and metric distance measures by the pairs plots at baseline and follow-up of left and right hippocampi. Furthermore, we perform a principal component analysis (PCA) on metric distance and volumes to characterize the major traits these quantities measure [58, 59]. Since the metric distance between two images is just a single number, the PCA involves only the relationships among metric distance, volume, follow-up interval, and functional measurements.

We also provide a statistical methodology for the analysis of metric distances. We apply repeated-measures analysis of variance (ANOVA) on metric distances with diagnosis group as the main effect factor and side×timepoint as the repeated factor, since there is within-subject dependence of metric distances for left and right hemispheres and at baseline and follow-up. With this set-up we can both perform cross-sectional and longitudinal comparisons with metric distances. We apply four possible competing models each assuming a different variance-covariance structure to obtain the model that best fit to our data set. The first model assumes compound symmetry, in which the diagonals (i.e., the variances) are equal, and so are the off diagonals (i.e., the covariances). The other three models assume unstructured, autoregressive (AR), and autoregressive heterogeneous variances, respectively. In the unstructured model, each variance and covariance term is different, in the AR model, the variances are assumed to be equal but the covariances change by time, and in the ARH model, the variances are also different and the covariances change by time [60-62]. We use various model selection criteria (such as Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), Log-likelihood) to compare competing models to see which model best fits our data [63].

For post-hoc comparison of the metric distances for baseline left, baseline right, and follow-up left, follow-up right hippocampi, we use Wilcoxon test and Brown and Forsythe’s (B-F) test (i.e., Levene’s test with absolute deviations from the median) for homogeneity of the variances [64]. The metric distances of the same person’s hippocampus at baseline and follow-up are dependent, hence we use Wilcoxon signed rank test to compare them. Likewise, the distances for the left and right hippocampi of the same person are also dependent. We estimate the empirical cumulative distribution functions (cdf) of the metric distances and compare them by Kolmogorov-Smirnov (K-S) test.

We apply logistic discrimination with metric distances and other variables, since the diagnosis have only two levels, namely CDR0 and CDR0.5. We use logistic regression to estimate or predict the risk or probability of having DAT using metric distances, together with side (i.e., hemisphere) and timepoint (baseline vs follow-up) factors. In other words, we model the probability that the subject is CDR0.5 given the metric distance of the subject for left or right hippocampus at baseline or follow-up. In standard logistic regression the model-parameters are obtained via maximum likelihood estimators. For more on logistic regression and logistic discrimination, see [65] and [58], respectively. First we model with one predictor variable at a time from side, timepoint, and metric distance, etc., if the variable is not significant at .05 level, we omit that variable from further consideration. We consider the full logistic model with the response logit p = log [p/(1 − p)] where p = P(Y = 1) (i.e., the probability that the subject is diagnosed with CDR0.5) with one predictor variable at a time from side, timepoint, and metric distance, etc., if the variable is not significant at .05 level, we omit that variable from further consideration. The remaining variables with all possible interactions among them as the predictor variables constitute the full model. On this full model, we choose a reduced model by AIC in a stepwise algorithm and then use stepwise backward elimination procedure on the resulting model [63]. We stop the elimination procedure when all the remaining variables are significant at α = 0.05 level. Based on the final model with significant predictors, we apply logistic discrimination. In general, if the estimated probability is larger than a prespecified probability π_o, the subject is classified as CDR0.5, otherwise the subject is classified as CDR0 (i.e., healthy). This means our decision function reduces to

$${\widehat{\pi }}_k=P(Y=1\mid \mathrm{metric\; distance})\{\begin{array}{l}>{\pi }_0\Rightarrow \mathrm{classify}\mathrm{CDR}0.5,\\ \le {\pi }_0\Rightarrow \mathrm{classify}\mathrm{CDR}0,\end{array}$$ (5)

where π_o is usually taken to be 0.5. This threshold probability π_o can also be optimized with respect to a cost function which incorporates correct classification rates, sensitivity, and/or specificity [66].

We also investigate the sensitivity and specificity of the classification procedures. Sensitivity is the proportion of subjects that are classified to be CDR0.5 (i.e., positive) of all CDR0.5 subjects. That is, sensitivity is defined as P_sens = (T_CDR0.5/N_CDR0.5) × 100% where T_CDR0.5 is the number of correctly classified CDR0.5 subjects and N_CDR0.5 is the total number of CDR0.5 subjects in the data set (in our data set N_CDR0.5 = 18). Notice that the higher the sensitivity, the fewer real cases of DAT go undetected. Specificity is the proportion of subjects that are classified CDR0 (i.e., negative, control, or healthy) of all CDR0 subjects; that is P_spec = (T_CDR0/N_CDR0) × 100% where T_CDR0 is the number of correctly classified CDR0 subjects and N_CDR0 is the total number of CDR0 subjects in the data set (in our data set N_CDR0 = 26). Notice that the higher the specificity, the fewer healthy individuals are labeled as diseased.

We apply the same analysis procedure on hippocampal volumes to compare the results with metric distances. Furthermore, we find the differential volume loss and metric distance change by using the annual percentage rate of change (APC) in volume and metric distance (see [66] for APC in volume for entorhinal cortex). We also consider the logistic discrimination models that incorporate volume and metric distance together and APC in volumes and metric distances together.

In [26], volume change from baseline to follow-up (not the raw volumes) are analyzed with repeated-measures ANOVA. The shape change vector fields which are obtained using the LDDMM algorithm are analyzed by the SVD on the covariance structure where the eigenfunctions that explain at least 75 % of the total variance are selected. Then multivariate ANOVA (MANOVA) is applied on these eigenfunctions to test for group differences. If significant group differences were found, then logistic regression was performed to model the change due to aging versus change due to dementia. On the other hand, in [67], voxel-wise statistical tests are performed between the Jacobian maps in each group using the spatially normalized Jacobian maps. These maps encode longitudinal brain changes and are compared using both spatial average of Jacobian values within specific regions and voxel-wise tests controlled for multiple testing. The two-sample t-test with unequal variances is employed in the voxel-wise testing. The cdfs of these t-tests are used to compare the effect sizes of group differences and effects of covariates in the diagnostic groups. Correlations of Jacobian values (i.e., brain differences) with clinical measurements (such as CDR scores) and biomarkers are also measured.

3 Analysis of Metric Distances and Volumes of Hippocampi

3.1 Preliminary Analysis of Metric Distances and Other Variables

The summary measures for the variables are provided in Table 1. Observe that the subjects are evenly distributed in terms of gender, years of education, scan intervals, and age between the diagnostic groups so that these variables are accounted for as covariates. The brain and intracranial volumes are much larger in scale than the hippocampal volumes which are larger than the metric distances. Notice that brain and hippocampal volumes all decrease by time and are smaller in CDR0.5 subjects compared to CDR0 subjects compared to CDR0 subjects. On the other hand, the metric distances tend to increase by time and are larger for the CDR0.5 subjects. Also presented in Table 1 are the p-values for Lilliefor’s test of normality (p_L) and Wilcoxon rank sum test for differences between the diagnostic groups (p_W). Notice that most variables can be assumed to follow a Gaussian distribution, but since a few of the variables are non-Gaussian, we apply the Wilcoxon rank sum test instead of Welch’s t-test. The diagnostic groups do not significantly differ in age, education, brain and intracranial volumes. Furthermore, among the metric distances, we see that only right follow-up metric distances are significantly different between the diagnostic groups.

We present the pairs plot (scatter plot of each pair) of continuous variables in Figure 3 and calculate the correlation coefficients between each pair of the variables (not presented). We observe that age and education are not significantly correlated with any of the other variables. Hence we discard them in our prospective analysis (except for logistic discrimination). We observe significant correlation between each pair of hippocampal volumes, and between each pair of brain and intracranial volumes. The metric distances are only moderately correlated with each other. Hippocampal volumes are mildly correlated with brain and intracranial volumes. The same holds for the metric distances but to a lesser extent.

Figure 3.

Pairs plots of the continuous variables for the hippocampi at baseline and follow-up. HLV: volume of left hippocampus; HRV: volume of right hippocampus; HLM: metric distance for left hippocampus; HRM: metric distance for right hippocampus; BV: brain volume; ICV: intracranial volume. The numbers 1 and 3 stand for year 1 (i.e., baseline) and year 3 (i.e., follow-up), respectively.

See Figure 4 for the (jittered) scatter plots of the metric distances by group, where the crosses are centered at the mean distances and the points are jittered (scattered) along the horizontal axis in order to avoid frequent point concurrence and tight clustering of points, thereby making the plot better for visualization. Observe that CDR0 distances are smaller than CDR0.5 distances at baseline and at follow-up for both left and right hippocampi. This suggests that the morphometric differences of CDR0 hippocampi with respect to the template hippocampus are smaller than those of CDR0.5 hippocampi. This is not surprising, considering the template hippocampus being one of the CDR0 hippocampi. Furthermore, the standard deviations of the distances for CDR0 subjects tend to be smaller than those of CDR0.5 subjects. That is, the morphometric variability of CDR0 hippocampi with respect to the template hippocampus is smaller than that of CDR0.5 hippocampi. The statistical significance of these results will be provided in the following sections.

Figure 4.

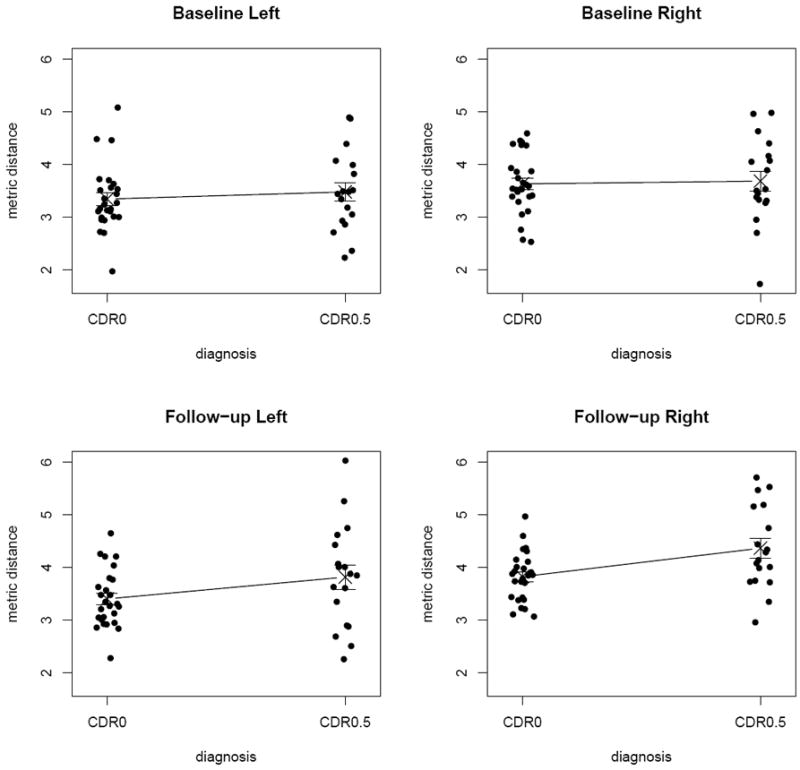
Scatter plots of the metric distances for the left and right distances at baseline and follow-up. The metric distances are jittered for better visualization and the crosses represent the mean distance values.

3.2 Principal Component Analysis of the Volumes and Metric Distances

The volumes and metric distances measure different but related aspects of morphometry, so some of the variables are highly correlated with each other (see Figure 3). We perform principal component analysis (PCA) to obtain a set of uncorrelated variables that hopefully represent some identifiable aspect of the morphometry [58, 59]. In [26], a PCA in the form of singular value decomposition (SVD) was applied to the matrix of change in the vector fields (i.e., matrix of voxel displacements as a function of original coordinates), which is also obtained from the LDDMM algorithm. However, in this article, we perform the PCA procedure on hippocampal volume, metric distance, brain volume, and intracranial volume measures. When PCA (with eigenvalues based on the covariance matrix) on metric distances and volumes of left hippocampi at baseline is performed, we observe that the first principal component (PC1) accounts for almost all the variation (see Table 2). Considering the variable loadings, PC1 seems to be the head size component, PC2 is the contrast between brain and intracranial volumes, PC3 is the hippocampus size, and PC4 is the metric distance component. However, the volumes are in mm³ and metric distances are unitless, hence the data are not to scale. In particular, the brain and intracranial volumes have the largest variation in the data set, hence dominate the PCs. To remove the influence of the scale (or unit), we apply PCA with eigenvalues based on the correlation matrix (i.e., PCA on the standardized variables). The importance scores of principal components and variable loadings from the PCA of metric distances and volumes of left hippocampi at baseline with eigenvalues based on the correlation matrix are presented in Table 3. Notice that with the correlation matrix, the first three PCs account for almost all the variation in the variables. Comparing the variable loadings, PC1 seems to be the head size component, PC2 is the hippocampus shape, PC3 is the hippocampus size and the contrast between hippocampus and head size, and PC4 is the contrast between brain and intracranial volume. The PCA on variables for left hippocampi at followup and right hippocampi at baseline and followup yields similar results (see [68]).

Table 2.

The importance of principal components and variable loadings from the principal component analysis of metric distances and volumes of left hippocampi at baseline with eigenvalues based on the covariance matrix.

Importance of Components
	PC1	PC2	PC3	PC4
Prop. Var	.9877	.0123	~ 0.0	~ 0.0
Cum. Prop	.9877	~ 1.0	~ 1.0	1.0
Variable Loadings
	PC1	PC2	PC3	PC4
HLV1	~ 0.0	~ 0.0	1.00	~ 0.0
HLM1	~ 0.0	~ 0.0	~ 0.0	1.00
BV1	.55	-.83	~ 0.0	~ 0.0
ICV1	.83	.55	~ 0.0	~ 0.0

PCi stands for principal component i for i = 1, 2, 3, 4; Prop.Var: proportion of variance explained by the principal components; Cum.Prop: cumulative proportion of the variance explained by the particular principal component; HLV1: volume of left hippocampus at baseline; HLM1: metric distance of left hippocampus at baseline; BV1: brain volume at baseline; ICV1: intracranial volume at baseline.

Table 3.

The importance of principal components and variable loadings from the principal component analysis of metric distances and volumes of left hippocampi at baseline and followup with eigenvalues based on the correlation matrix.

Baseline					Followup
Importance of Components					Importance of Components
	PC1	PC2	PC3	PC4	PC1	PC2	PC3	PC4
Prop. Var	.57	.27	.15	.01	.54	.32	.12	.02
Cum. Prop.	.57	.84	.99	1.0	.54	.86	.98	1.0
Variable Loadings					Variable Loadings
	PC1	PC2	PC3	PC4	PC1	PC2	PC3	PC4
HLV	.37	.59	.71	~ 0.0	.41	.55	.73	~ 0.0
HLM	.22	-.80	.55	~ 0.0	~ 0.0	-.80	.60	~ 0.0
BV	.64	~ 0.0	-.27	-.72	.65	-.16	-.18	-.72
ICV	.63	~ 0.0	-.33	.70	.64	-.17	-.29	.69

HLV: volume of left hippocampus; HLM: metric distance of left hippocampus; BV: brain volume; ICV: intracranial volume. The other abbreviations are as in Table 2.

The variable loadings for the variables suggest that brain and intracranial volumes are mostly measures of head size, metric distance is mostly a measure of hippocampus shape and partly related to head and hippocampus sizes, and hippocampus volume is mostly a measure of hippocampus size and partly related to hippocampus shape and head size. Hence, one should use volume and metric distance in morphometric analysis of brain tissues as they provide complementary information.

3.3 Repeated-Measures Analysis of Metric Distances and Hippocampal Volumes

Due to within-subject dependence of metric distances for left and right hemispheres and for baseline and follow-up measures, we apply repeated-measures analysis with group or side as main effects and timepoint as the repeated factor (see [68]), and group as main effect and side×timepoint as the repeated factor (see below). We have four measurements for each subject, namely left metric distance at baseline, left metric distance at followup, right metric distance at baseline, and right metric distance at followup, so repeated-measures analysis can be performed on our data set.

We model the Var-Cov structure for the repeated-measures for each subject. We have four correlated measures per subject, namely LDB, LDF, RDB, and RDF. We try compound symmetry, unstructured, autoregressive (AR), and autoregressive heterogeneous (ARH) Var-Cov structures. The variances (in the diagonal) suggest homogeneity, but covariances seem to differ. See [68] for the comparison of models. We choose the model with AR Var-Cov structure based on AIC and BIC. The corresponding model is

$$d_{\mathit{ijkl}}=\mu +{\alpha }_i^S+{\alpha }_j^D+{\alpha }_k^T+{\alpha }_{\mathit{ij}}^{\mathit{SD}}+{\alpha }_{\mathit{ik}}^{\mathit{ST}}+{\alpha }_{\mathit{jk}}^{\mathit{DT}}+{\alpha }_{\mathit{ijk}}^{\mathit{SDT}}+{\epsilon }_{\mathit{ijkl}},$$ (6)

where d_ijkl is the distance for subject l for side i (1 for left; 2 for right) with diagnosis j (j = 1 for CDR0; 2 for CDR0.5) at timepoint k (k = 1 for baseline; 2 for follow-up), μ is the overall mean, ${\alpha }_i^S$ is the effect of side level i, ${\alpha }_j^D$ is the effect of diagnosis level j, ${\alpha }_k^T$ is the effect of timepoint level k, ${\alpha }_{\mathit{ij}}^{\mathit{SD}}$ is the side×diagnosis interaction, ${\alpha }_{\mathit{ik}}^{\mathit{ST}}$ is the side×timepoint interaction, ${\alpha }_{\mathit{jk}}^{\mathit{DT}}$ is the diagnosis×timepoint interaction, ${\alpha }_{\mathit{ijk}}^{\mathit{SDT}}$ is the side×diagnosis×timepoint interaction, and ε_ijkl is the error term. The Var-Cov structure for the error term (for the four measures per subject) is

$$\mathbf{Cov}({\epsilon }_{\mathit{ijkl}},{\epsilon }_{i^{\prime }{\mathit{jk}}^{\prime }l})=\left[\begin{array}{cccc}{\sigma }^2& & & \\ \sigma \rho & {\sigma }^2& & \\ \sigma {\rho }^2& \sigma \rho & {\sigma }^2& \\ \sigma {\rho }^3& \sigma {\rho }^2& \sigma \rho & {\sigma }^2\end{array}\right].$$

The three way interaction of side×group×timepoint is not significant (F = 0.50, df = 1, 168, p = 0.4823), and neither are the two way side×group (F = 0.76, df = 1, 168, p = 0.3860), and side×timepoint interactions (F = 2.25, df = 1, 168, p = 0.1359). On the other hand, the group×timepoint interaction is significant (F = 8.47, df = 1, 168, p = 0.0041). The main effects of side, group, and timepoint are all significant (F = 6.12, df = 1, 168, p = 0.0143; F = 4.05, df = 1, 168, p = 0.0457; and F = 19.52, df = 1, 168, p < 0.0001, respectively), but due to interaction, the groups should be compared at each time point instead of an overall comparison of group means. So the resulting model with significant terms at α = .05 level is

$$d_{\mathit{ijkl}}=\mu +{\alpha }_i^S+{\alpha }_j^D+{\alpha }_k^T+{\alpha }_{\mathit{jk}}^{\mathit{DT}}+{\epsilon }_{\mathit{ijkl}},$$

The interaction plots of diagnosis levels over the time-points for left and right hippocampi are presented in Figure 5, where we observe that the lines are not parallel for the diagnosis which agrees with the significant group×timepoint interaction. But, the main effects of timepoint and side being significant is interpretable between baseline and follow-up.

Figure 5.

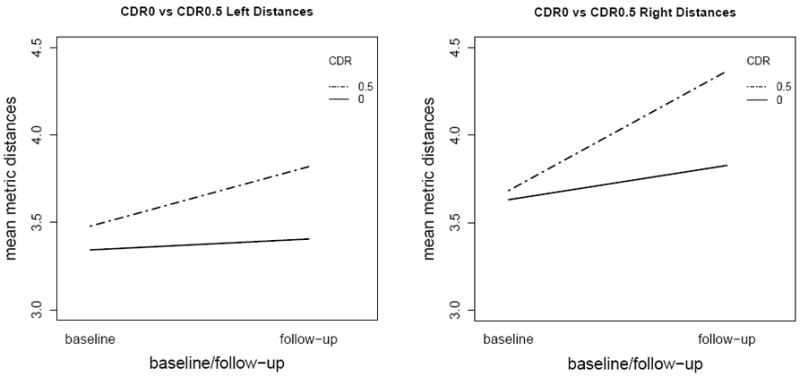
Interaction plots for diagnosis levels over the timepoint levels for left and right metric distances demonstrating that the slopes are different between diagnostic groups (with slope differences in the right being larger).

For modeling hippocampal volumes using the repeated-measures ANOVA with group as main effect and compound symmetry in Var-Cov structure and volume measurements repeated over time for each subject, and for modeling volumes using the repeated measures ANOVA with side as main effect and compound symmetry in Var-Cov structure and volume measurements repeated over time, see [68]. Volume measurements were also presented in detail in [26]. For the model that includes the diagnosis, side, and diagnosis×side interaction, we find that the most promising model based on likelihood ratio test, BIC, and AIC is the one with unstructured Var-Cov matrix. The corresponding model with significant terms at α = .05 level is

$$V_{\mathit{ijklm}}=\mu +{\alpha }_i^S+{\alpha }_j^D+{\alpha }_k^T+{\alpha }_{\mathit{ik}}^{\mathit{ST}}+{\alpha }_{\mathit{jk}}^{\mathit{DT}}+{\alpha }_l^G+{\epsilon }_{\mathit{ijklm}},$$ (7)

where V_ijklm is the volume for subject m for side i with diagnosis j at timepoint k with gender l (1 for female, 2 for male), μ is the overall mean, ${\alpha }_i^S$ is the effect of side level i, ${\alpha }_j^D$ is the effect of diagnosis level j, ${\alpha }_k^T$ is the effect of timepoint level k = 1, 3, ${\alpha }_{\mathit{ik}}^{\mathit{ST}}$ is the side×timepoint interaction, ${\alpha }_{\mathit{jk}}^{\mathit{DT}}$ is the diagnosis×timepoint interaction, ${\alpha }_l^G$ is the effect of gender level l, and ε_ijklm is the error term. The (unstructured) Var-Cov structure for the error term is

$$\mathbf{Cov}({\epsilon }_{\mathit{ijkl}},{\epsilon }_{i^{\prime }{\mathit{jk}}^{\prime }l})=\left[\begin{array}{cccc}{\sigma }^2& & & \\ {\sigma }_{21}& {\sigma }^2& & \\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }^2& \\ {\sigma }_{41}& {\sigma }_{42}& {\sigma }_{43}& {\sigma }^2\end{array}\right].$$

The main effects of side, group, and timepoint are all significant (F = 120.10, df = 1, 170, p < .0001; F = 25.25, df = 1, 170, p < .0001; and F = 89.53, df = 1, 170, p < 0.0001, respectively). But due to interaction, the main effect for diagnosis (i.e., group) is close to clinically meaningless, i.e., the group means should be compared at each time point or hemisphere instead of comparing the overall means of the groups.

In [26], a similar repeated-measures ANOVA was performed for volumes only, and hemisphere (i.e., side), gender, and hemisphere×side interactions were not considered. In this article, we consider repeated-measures ANOVA on metric distances and volumes with more variables, and perform a model selection procedure which captures the most significant variables. Our findings of significant time×diagnosis group interaction for volumes agree with results of [26], but we also discover a significant side×time interaction for volumes. On the other hand, for metric distances we only find a significant group×time interaction. Due to interaction, we compare groups in terms of metric distances and volumes at each time point and hemisphere in the following section. Such a post-hoc comparison is not presented in [26], instead a detailed morphometric change analysis is performed based on the eigenfunctions obtained from SVD of vector field changes.

3.4 Post-Hoc Comparison of Volumes and Metric Distances in CDR0.5 and CDR0 Groups

For the p-values regarding the comparison of independent groups, see Table 4. The distance distribution of each group can be assumed to come from a Gaussian distribution (all p-values greater than 0.10). Moreover, LB-CDR0.5 and LB-CDR0 distances can be assumed to have equal variances (p = 0.2948), and so can RB-CDR0.5 and RB-CDR0 (p = 0.2273). But, the variance of LF-CDR0 distances is significantly smaller than that of LF-CDR0.5 distances (p = 0.0294), and similarly for RF-CDR0 versus RF-CDR0.5 (p = 0.0262). So for consistency in our results we will only present the Wilcoxon rank sum tests [69] in this article. The p-values from the t-tests [70] are presented in [68].

Table 4.

The p-values based on Wilcoxon rank sum test for both left and right metric distances and volumes and p-values based on Wilcoxon signed rank test for metric distances and volumes.

Independent Group Comparisons of Metric Distances
	p-values for t-test			p-values for Wilcoxon test
Groups	2-sided	1st < 2nd	1st > 2nd	2-sided	1st < 2nd	1st > 2nd
LB-CDR0.5,LB-CDR0	.6078	.7044	.3039	.0002*	.0001*	.9999
LF-CDR0.5,LF-CDR0	.1625	.9223	.0813	< .0001*	< .0001*	≈ 1.000
RB-CDR0.5,RB-CDR0	.9239	.5475	.462	.0143*	.0071*	.9933
RF-CDR0.5,RF-CDR0	.0212*	.9900	.0106*	.0002*	.0001*	.9999
Dependent Group Comparisons of Metric Distances
	p-values for paired t-test			p-values for paired Wilcoxon test
Groups	2-sided	1st < 2nd	1st > 2nd	2-sided	1st < 2nd	1st > 2nd
LB-CDR0.5,LF-CDR0.5	.0311*	.0155*	.9861	.0001*	≈ 1.000	< .0001*
RB-CDR0.5,RF-CDR0.5	.0005*	.0002*	.9998	< .0001*	≈ 1.000	< .0001*
LB-CDR0,LF-CDR0	.7127	.3563	.6531	.0001*	.9999	< .0001*
RB-CDR0,RF-CDR0	.1244	.0622	.9409	.0002*	.9999	.0001*
LB-CDR0.5,RB-CDR0.5	.3465	.1733	.8376	< .0001*	< .0001*	≈ 1.000
LF-CDR0.5,RF-CDR0.5	.0385*	.0192*	.9829	.0001*	.0001*	≈ 1.000
LB-CDR0,RB-CDR0	.0585	.0292*	.9724	< .0001*	< .0001*	≈ 1.000
LF-CDR0,RF-CDR0	.0059*	.0029*	.9973	< .0001*	< .0001*	≈ 1.000

^*Significant p-values at .05 level are marked with an asterisk.

RF-CDR0.5 mean distances are significantly larger than RF-CDR0 mean distances at .05 level (p = 0.0106), and LF-CDR0.5 distances are almost significantly larger than LF-CDR0 distances (p = 0.0813). On the other hand, LB-CDR0.5 and LB-CDR0 distances are not significantly different (p = 0.5362), and likewise for RB-CDR0.5 and RB-CDR0 distances (p = 0.8176). This implies that at baseline, the morphometric differences of CDR0.5 and CDR0 hippocampi with respect to the template hippocampus are about same, which might indicate no significant shape differences in the left and right hippocampi due to dementia. However, since the metric distances do not necessarily provide direction in either shape or size, this is not a decisive implication. At follow-up, the morphometric differences of left and right hippocampi of CDR0.5 subjects from the template are significantly larger than those of CDR0 subjects. Moreover, right hippocampi of CDR0.5 subjects tend to undergo more alteration in morphometry compared to right hippocampi of CDR0 subjects over time.

In the post hoc comparison of hippocampal volumes, we find that the variances of volumes are not significantly different for (LB-CDR0.5, LB-CDR0), (RB-CDR0.5, RB-CDR0), and (RF-CDR0.5, RF-CDR0) groups, but volumes of LF-CDR0 hippocampi are significantly larger than volumes of LF-CDR0.5 hippocampi (p = .0268). The CDR0.5 volumes are significantly smaller than CDR0 volumes in left hippocampi at baseline (p = .0001) and follow-up (p < .0001), and for right hippocampi at baseline (p = .0071) and follow-up (p = .0001).

For the cdf comparisons, the samples (groups) should be independent for these tests to be valid, so we only compare CDR0.5 vs CDR0 groups. The results are provided in detail in [68] and for more on cdf comparisons, see [71, 72]. The cdf of RF-CDR0.5 distances is significantly smaller than the cdf of RF-CDR0 distances (p = 0.0259 for K-S test). That is, RF-CDR0.5 metric distances are stochastically larger than RF-CDR0 right metric distances. In other words, RF-CDR0.5 hippocampus shapes are more likely to be different than the template hippocampus compared to RF-CDR0 hippocampus shapes. Furthermore, the cdf of LF-CDR0.5 distances is almost significantly smaller than the cdf of LF-CDR0 distances (p = 0.0604). Observe that these results are in agreement with the ones in Table 4. The CDR0.5 volumes are stochastically smaller than CDR0 volumes for left hippocampi at baseline (p = .0007) and follow-up (p = .0003), and for right hippocampi at baseline (p = .0064) and follow-up (p = .0028).

Remark 3.1

Although volume is a measure of size and metric distance is a measure of overall morphometric difference from a template, the repeated measure analysis and post-hoc analysis of volumes and metric distances provide similar results. The main difference is that volumes tend to decrease, while metric distances tend to increase by time.

3.5 Comparison of Baseline and Follow-up Metric Distances and Hippocampal Volumes

For the comparison of dependent groups by paired difference method, see Table 4. Observe that LB-CDR0.5 metric distances are significantly smaller than LF-CDR0.5 distances at α = .05 (p = 0.0259). The same holds for RB-CDR0.5 vs RF-CDR0.5 distances (p = 0.0002). That is, CDR0.5 hippocampi tend to become more different in morphometry from the template, which implies that for both left and right distances there is significant change in morphometry (perhaps reduction in size) of CDR0.5 hippocampi over time. In fact, significant volume reduction over time is detected [26]. The morphometric changes in CDR0.5 right hippocampi from baseline to follow-up is barely significantly larger than those of CDR0.5 left hippocampi (p = 0.0445). The associated p-value here is obtained by testing the difference sets (LB-CDR0.5)-(LF-CDR0.5) versus (RB-CDR0)-(RF-CDR0.5) using the usual paired t-test. On the other hand, only RB-CDR0 is almost significantly less than RF-CDR0 (p = 0.0621), which implies there is some weak evidence for mild change in right hippocampi as a result of aging. Furthermore, the morphometric changes in CDR0 right hippocampi from baseline to follow-up are not significantly different from those of CDR0 left hippocampi (p = 0.3817).

The morphometric changes in CDR0.5 left hippocampi from baseline to follow-up are not significantly different from those of CDR0 left hippocampi (p = 0.1337), while the morphometric changes in CDR0.5 right hippocampi from baseline to follow-up are significantly larger from those of CDR0 right hippocampi (p = 0.0074). Therefore, over time, DAT influences the morphometry of right hippocampi more compared to left hippocampi.

The volumes decrease significantly by time in CDR0 group for both left and right hippocampi (p < .0001 for both); the same holds for CDR0.5 group also (p = .0001 for both). The volumetric reduction is significantly larger in CDR0.5 right hippocampi compared to CDR0.5 left hippocampi (p = .0407); but the same holds only barely in CDR0 group (p = .0524). On the other hand, the volumetric reduction is significantly larger in CDR0.5 left hippocampi compared to CDR0 left hippocampi (p = .0108); the same holds for right hippocampi also (p = .0418).

Such a baseline versus follow-up comparison is not performed in [26] neither in volumes nor in metric distances. The morphometric change in the subjects over time is analyzed based on the eigenfunctions obtained from the SVD procedure.

3.6 Comparison of Left and Right Hippocampi

We also compare the presence of left-right morphometric asymmetry in hippocampi of healthy and diseased subjects. Such an asymmetry comparison is not performed in [26]. The left versus right comparisons are also presented in Table 4, where we see that LB-CDR0.5 and RB-CDR0.5 distances are not significantly different from each other (p = 0.3046), LF-CDR0.5 distances are significantly smaller than RF-CDR0.5 distances at .05 level (p = 0.0179), the same holds for LB-CDR0 vs RB-CDR0.5 (p = 0.0215) and LF-CDR0 vs RF-CDR0 (p = 0.0021) comparisons. This implies that at baseline morphometric differences of CDR0.5 left hippocampi from the left template are about the same as those of CDR0.5 right hippocampi from the right template. On the other hand at follow-up, morphometric differences of CDR0.5 left hippocampi are smaller than those of CDR0.5 right hippocampi. At baseline and follow-up, morphometric differences of CDR0 left hippocampi from the left template are smaller than those of CDR0 right hippocampi. That is, CDR0 left hippocampi are more similar in morphometry to the left template when compared to CDR0 right hippocampi to the right template. These distance comparisons for left versus right hippocampi would imply left-right morphometric asymmetry, only if the left and right hippocampi of the template subject were same (up to a reflection). Otherwise, these comparisons are only suggestive of morphometric differences from the respective hemisphere (side) of the hippocampi.

The left hippocampus volumes are significantly smaller than the right hippocampus volumes at both baseline and follow-up years (i.e., there is significant volumetric left-right asymmetry in hippocampi); baseline volumes are larger than follow-up volumes for both left and right hippocampi (i.e., there is significant reduction in volume by time) (p < .0001 for each comparison). We observe the same trend in the overall comparison for each group also. However, left-right volumetric asymmetry significantly reduces by time in CDR0.5 group (p = .0407); but the same holds only barely in CDR0 group (p = .0524). The level of left-right volumetric asymmetry is about the same in both CDR0 and CDR0.5 groups at baseline (p = .3495) and follow-up (p = .4853).

Remark 3.2

Correlation between Metric Distances of Dependent Hippocampi: Correlation coefficients between metric distances for baseline and follow-up (overall and by group) and for the left and right hippocampi are provided in [68]. Except for the CDR0 right hippocampi, the baseline and follow-up metric distances are significantly correlated for each group. That is, except for CDR0 right hippocampi, the distances tend to increase at baseline together with distances at follow-up. That is, as the morphometric differences from the template hippocampus increase at baseline, so do the differences from the template at follow-up (except for CDR0 right hippocampi). From the correlation analysis of left and right distances, we observe there is mild correlation between left and right metric distances. That is, as the morphometric differences of left hippocampi from the left template increase, differences of right hippocampi from the right template tend to increase slightly.

3.7 Logistic Discrimination with Metric Distances and Volumes

First we consider the full logistic model (designated as M_I(D)) with side, timepoint, and distance with all possible interactions being the predictor variables. In this model, each hippocampus MRI is treated as a distinct subject, hence we have 44 × 4 = 176 values for each variable. When the stepwise model selection procedure is applied, the resulting model is logit p_k = β₀ + β₁ d_ijk where p_k is the probability of subject k having DAT and d_ijk the distance for subject k with diagnosis i (i = 1 for CDR0 and 2 for CDR0.5) at timepoint j (j = 1 for baseline and 2 for follow-up), β₀ is the intercept and β₁ is the slope of the fitted line. However, the graph of the proportions of CDR0.5 subjects for grouped metric distances in Figure 6 suggests that the relationship is a quadratic one (in fact, we found that the higher order distance terms are not significant). That is, the analysis of deviance table indicates that only the linear and quadratic terms are significant (p = 0.001 and p = 0.010). So the resulting model is

$$M_{\mathit{II}}(D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{d}_{\mathit{ijk}}+{\beta }_2{d}_{\mathit{ijk}}^2$$ (8)

where β₂ is the coefficient of the quadratic term. In the logistic discrimination procedure, we can treat each hippo-campus from left, right, baseline or follow-up hippocampi as a distinct subject. However, from a clinical point of view, each subject has four hippocampus MRIs in this study, and one MRI classified as CDR0.5 would suffice to classify the subject as CDR0.5, while all four MRIs should be classified as CDR0 for the subject to be classified as CDR0.

Figure 6.

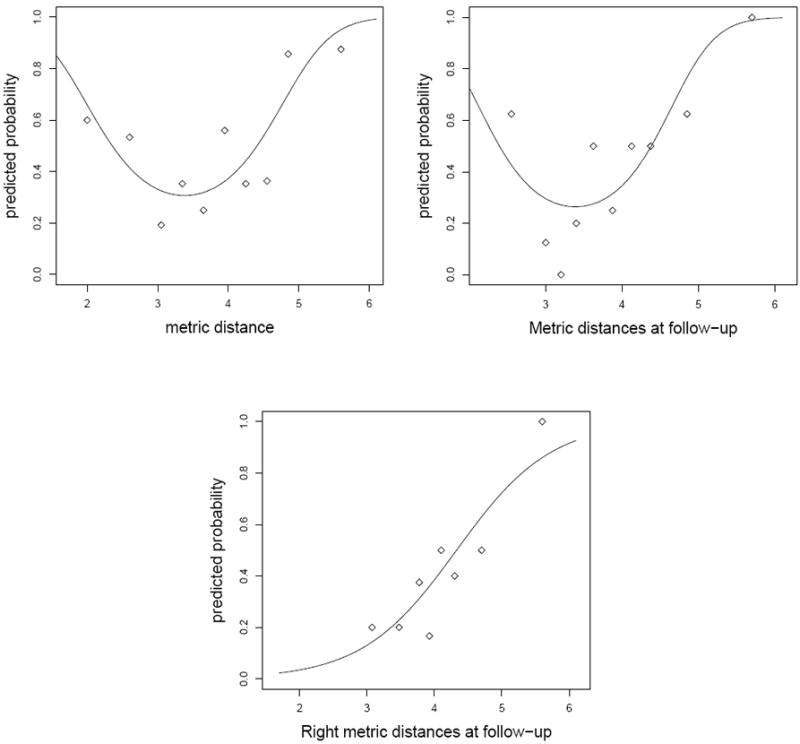
Fitted probability for having mild dementia (CDR0.5) and observed proportion in metric distances with model (9) (top-left); model (10) (top-right); and model (11) (bottom),

Due to significant group×timepoint interaction, we need to consider diagnosis groups at each time point. When we use baseline and followup distances one at a time in a logistic model, we will have 44 × 2 = 88 values for each variable and we see that only the model

$$M_{\mathit{III}}(D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{d}_{\mathit{ik}}^F+{\beta }_2{\left(d_{\mathit{ik}}^F\right)}^2$$ (9)

has significant coefficients for the distance terms. Again, labeling one of left or right hippocampi as CDR0.5 is sufficient to label the subject as CDR0.5 while both left and right MRIs should be classified as CDR0 for the subject to be classified as CDR0. Moreover, when we use baseline left, baseline right, follow-up left, and follow-up right distances (i.e., $d_k^{\mathit{LB}},d_k^{\mathit{LF}},d_k^{\mathit{RB}}$, and $d_k^{\mathit{RF}}$) one at a time in a logistic model, we will only have 44 values for each variable and we see that only the model

$$M_{\mathit{IV}}(D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{d}_k^{\mathit{RF}}$$ (10)

has a significant coefficient for the distance term.

We apply the similar logistic discrimination methods on hippocampal volumes also. First we consider the full logistic model (designated as M_I (V)) with side, timepoint, and volume with all possible interactions being the predictor variables. After a stepwise elimination procedure we get the following reduced model:

$$M_{\mathit{II}}(V):\mathrm{logit}{p}_l={\beta }_0+{\alpha }_k^S+{\beta }_1{V}_{\mathit{ijkl}},$$ (11)

where p_l is the probability of subject l having DAT and V_ijkl the volume for subject l with diagnosis i ( i = 1 for CDR0 and 2 for CDR0.5) at timepoint j (j = 1 for baseline and 2 for follow-up) with side k (k = 1 for left and 2 for right), β₀ is the overall intercept, ${\alpha }_k^S$ is the effect of side level k, and β₁ is the slope of the fitted line. When we use baseline and followup volumes (i.e., $V_{\mathit{ikl}}^B$ and $V_{\mathit{ikl}}^F$) one at a time in a logistic model, we see that the model

$$M_{\mathit{III}}(V):\mathrm{logit}{p}_l={\beta }_0+{\alpha }_k^S+{\beta }_1{V}_{\mathit{ikl}}^F$$ (12)

has the most significant coefficients for the volume terms. Moreover, when we use baseline left, baseline right, follow-up left, and follow-up right volumes (i.e., $V_{\mathit{kl}}^{\mathit{LB}},V_{\mathit{kl}}^{\mathit{LF}},V_{\mathit{kl}}^{\mathit{RB}}$, and $V_{\mathit{kl}}^{\mathit{RF}}$) one at a time in a logistic model, we see that the following model has the best fit.

$$M_{\mathit{IV}}(V):\mathrm{logit}{p}_l={\beta }_0+{\beta }_1{V}_{\mathit{kl}}^{\mathit{LF}}$$ (13)

We could change the threshold probability in Equation (5). The correct classification rates, sensitivity, and specificity percentages with π_o ∈ {1/2, 18/44} are presented in Table 5. Observe that with π_o = 1/2 the best classifier among models M_I (D) − M_IV (D) is based on M_III (D) and with π_o = 18/44 the best classifier is based on M_IV (D). Setting π_o = 18/44 (the proportion of CDR0.5 subjects in the data set) we get higher sensitivity rates than those with π_o = 1/2. Among models M_I (V) − M_IV (V), with π_o = 1/2 the best classifier is based on model M_III(V) and with π_o = 18/44 the best classifier is based on model M_IV (V). However, as π_o decreases, the correct classification rate and specificity tend to decrease.

Table 5.

The correct classification rates (P_CCR), sensitivity (P_sens), and specificity (P_spec) percentages for the classification procedures based on models M_I (D) − M_IV (D) using metric distances and volumes with optimum threshold values π_o = π_opt based on the cost function C₁(π_o, w₁, w₂) with w₁ = w₂ = 1 and w₁ = 1, w₂ = 3 (top); and with optimum threshold values π_o = π_opt based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and η₁ = .3, η₂ = 0.7 (bottom).

	πo = 1/2				πo = 18/44
	MI (D)	MII (D)	MIII (D)*	MIV (D)	MI (D)	MII (D)	MIII (D)	MIV (D)*
PCCR	66%	64%	73%	68%	57%	47%	66%	68%
Psens	56%	56%	56%	44%	83%	67%	67%	61%
Pspec	73%	69%	85%	85%	38%	35%	65%	73%
Using optimum πo based on cost function C1(πo, w1, w2) with
	w1 = w2 = 1				w1 = 1, w2 = 3
	MI (D)	MII (D)	MIII (D)	MIV (D)*	MI (D)	MII (D)	MIII (D)	MIV (D)*
πopt	.51	.50	.45	.38	.51	.47	.36,.37	.38
PCCR	68%	64%	70%	70%	68%	57%	68%	70%
Psens	56%	56%	67%	72%	56%	61%	78%	72%
Pspec	77%	69%	73%	69%	77%	54%	61%	69%
Using optimum πo based on cost function C2(πo) with
	η1 = η2 = 0.5				η1 = .3, η2 = 0.7
	MI (D)	MII (D)	MIII (D)	MIV (D)*	MI (D)	MII (D)	MIII (D)*	MIV (D)
πopt	.81-.82	.76-.78	.50-.52	.38	.37	.37	.33-.34	.22-.29
PCCR	75%	73%	73%	70%	59%	61%	66%	55%
Psens	39%	39%	56%	72%	95%	100%	89%	89%
Pspec	100%	96%	85%	69%	35%	35%	50%	31%

^*The model with the best classification performance is marked with an asterisk.

One can optimize the threshold value of π_o in Equation (5) to maximize the correct classification rates and minimize the misclassification rates using an appropriately chosen cost function. For example one can consider the cost function

$$C_1({\pi }_0,w_1,w_2)=-{(T_{\mathit{CDR}0}-F_{\mathit{CDR}0})}^{w_1}{(T_{\mathit{CDR}0.5}-F_{\mathit{CDR}0.5})}^{w_2},$$ (14)

where w₁ ≤ w₂ are positive odd numbers, F_CDR0 is the number of CDR0.5 subjects classified (falsely) as CDR0 and F_CDR0.5 is the number of CDR0 subjects classified (falsely) as CDR0.5. Minimizing this cost function will maximize the correct classification rates and minimize the misclassification rates. Alternatively we can maximize the sensitivity and specificity rates by minimizing the following cost function

$$C_2({\pi }_o,{\eta }_1,{\eta }_2)=-\left({\eta }_1\frac{(T_{\mathit{CDR}0}-F_{\mathit{CDR}0})}{N_{\mathit{CDR}0}}+{\eta }_2\frac{(T_{\mathit{CDR}0.5}-F_{\mathit{CDR}0.5})}{N_{\mathit{CDR}0.5}}\right),$$ (15)

where η₁, η₂ ≥ 0 and η₁ + η₂ = 1. Notice that as either of sensitivity or specificity increases, the cost function C₂(π_o, η₁, η₂) decreases. If equal weight is put on the sensitivity and specificity, we can choose w₁ = w₂ = 1 in C₁(π_o,w₁, w₂) and η₁ = η₂ = 0.5 in C₂(π_o, η₁, η₂).

Using w₁ = w₂ = 1, optimal threshold values are π_o = 0.5 for model M_II (D) in Equation (9), π_o = 0.45 for model M_III (D) in Equation (10), and optimal π_o = 0.38 for model M_IV (D) in Equation (11). The specificity rates are 69%, 73%, and 69%, respectively. The sensitivity rates are 56%, 67%, and 72%, respectively. Obviously, from a clinical point of view, misclassifying a CDR0.5 subject as CDR0 (i.e., classifying a diseased subject as healthy) might be less desirable, since a subject labeled as CDR0.5 will undergo further screening but a subject labeled as CDR0 will be released. So the parameters w₁ and w₂ could be modified to reflect such practical concerns and then a different set of threshold π_o values could be found. For example, we set w₁ = 1 and w₂ = 3 which favors correct classification of CDR0.5 subjects more than that of CDR0 subjects (i.e., favors higher sensitivity). Observe that with w₁ = w₂ = 1 the best classifier is based on model M_IV (D) and with w₁ = 1 and w₂ = 3 the best classifier is based on model M_III (D). With η₁ = η₂ = 0.5 the best classifier is based on model M_IV (D) and with η₁ = .3, η₂ = 0.7 the best classifier is based on model M_III(D). Observe that from η₁ = η₂ = 0.5 to η₁ = .3, η₂ = 0.7, sensitivity increases, correct classification rate and specificity tend to decrease.

The classification rates based on the logistic discrimination with hippocampal volumes are presented in Table 6. Observe that with π_o = 1/2 the best classifier is based on model M_III(V) and with π_o = 18/44 the best classifier is based on model M_IV (V). Furthermore, as π_o decreases from 1/2, sensitivity increases but the correct classification rate and specificity decreases. We use the cost function C₁(π_o,w₁, w₂) with w₁ = w₂ = 1 and with w₁ = 1 and w₂ = 3 to calculate the optimal π_o values for each of the models M_I(V) − M_IV(V). Observe that with w₁ = w₂ = 1 the best classifier is based on model M_IV (V) and with w₁ = 1 and w₂ = 3 the best classifier is based on model M_III(V). We find the optimal π_o values based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and with η₁ = .3, η₂ = 0.7 for each of models M_I (V) − M_IV (V). With η₁ = η₂ = 0.5 the best classifier is based on model M_IV (V) and with η₁ = .3, η₂ = 0.7 the best classifier is based on model M_I (V). Observe that from η₁ = η₂ = 0.5 to η₁ = .3, η₂ = 0.7, sensitivity increases, correct classification rate and specificity tend to decrease.

Table 6.

The correct classification rates (P_CCR), sensitivity (P_sens), and specificity (P_spec) percentages for the classification procedures based on models M_I (V) − M_IV (V) using metric distances and volumes with optimum threshold values π_o = π_opt based on the cost function C₁(π_o, w₁,w₂) with w₁ = w₂ = 1 and w₁ = 1, w₂ = 3 (top); and with optimum threshold values π_o = π_opt based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and η₁ = .3, η₂ = 0.7 (bottom).

Using optimum πo based on cost function C1 (πo, w1, w2) with
	w1 = w2 = 1				w1 = 1, w2 = 3
	MI (V)	MII (V)	MIII (V)	MIV (V)*	MI (V)	MII (V)	MIII (V)	MIV (V)*
πopt	.64-.66	.62-.63	.55-.58	.35-.42	.61-.62	.58-.60	.55-.58	.35-.36
PCCR	82%	75%	77%	80%	80%	73%	77%	80%
Psens	78%	78%	83%	89%	83%	83%	83%	89%
Pspec	85%	73%	73%	73%	77%	65%	73%	73%
Using optimum πo based on cost function C2(πo, η1, η2) with
	η1 = η2 = 0.5				η1 = .3, η2 = 0.7
	MI (V)	MII (V)	MIII (V)	MIV (V)*	MI (V)	MII (V)	MIII (V)	MIV (V)*
πopt	.64-.66	.70	.69	.35-.36	.31	.31	.25-.32	.26
PCCR	82%	80%	82%	80%	70%	66%	70%	77%
Psens	78%	61%	61%	89%	100%	100%	94%	94%
Pspec	85%	92%	96%	73%	50%	42%	54%	65%

^*The model with the best classification performance is marked with an asterisk.

3.8 Comparison of Logistic Discrimination Procedures with Hippocampal Volumes and Metric Distances

Although volume is a measure of size and metric distance is a measure of overall morphometric difference from a template, the repeated measure analysis and post-hoc analysis of volumes and metric distances provide similar results. The main difference is that volumes tend to decrease, while metric distances tend to increase by time. The logistic discrimination models are similar, except model M_IV (D) for metric distances contains right follow-up distances, while model M_IV (V) for volumes contains left follow-up volumes. The classification performances with π_o = 1/2 and π_o = 18/44 suggest that volume models have better performance than the metric distance models (see Tables 5 and 6). Using the optimal π_o values with the cost functions C₁(π_o,w₁,w₂) and C₂(π_o, η₁, η₂), the classification performances are significantly different for models M_I (V) − M_IV (V) of volumes and M_I (D)−M_IV (D) metric distances. Comparing Tables 5 and 6, we see that logistic discrimination with volumes has better performance.

We apply the logistic discrimination using both volume and metric distance as predictors. The models we consider are the full logistic model (designated as model M_I (V, D)) with side, timepoint, volume, and metric distances with all possible interactions being predictor variables. We apply the same stepwise elimination procedure as in Section 3.7 and get

$$M_{\mathit{II}}(V,D):\mathrm{logit}{p}_l={\beta }_0+{\alpha }_k^S+{\beta }_1{V}_{\mathit{ijkl}}+{\beta }_2{d}_{\mathit{ijkl}}^9+{\beta }_3{V}_{\mathit{ijkl}}{d}_{\mathit{ijkl}}$$

where p_l is the probability of subject l having DAT and V_ijkl the volume and d_ijkl the distance for subject l with diagnosis i (i = 1 for CDR0 and 2 for CDR0.5) at timepoint j (j = 1 for baseline and 2 for follow-up) with side k (k = 1 for left and 2 for right), β₀ is the overall intercept, ${\alpha }_k^S$ is the effect of side level k, β₁ is the coefficient for volume, β₂ is the coefficient for ninth power of the distance, β₃ is the coefficient for the interaction between volume and distance. When we use baseline or follow-up measures one at a time in a logistic model, we see that the model

$$M_{\mathit{III}}(V,D):\mathrm{logit}{p}_l={\beta }_0+{\alpha }_k^S+{\beta }_1{V}_{\mathit{ikl}}^F+{\beta }_2{(d_{\mathit{ikl}}^F)}^5$$

has the most significant coefficients. When we use side×timepoint combinations one at a time in a logistic model, we see that the following model has the best fit:

$$M_{\mathit{IV}}(V,D):\mathrm{logit}{p}_l={\beta }_0+{\beta }_1{\left(d_{\mathit{ikl}}^F\right)}^3+{\beta }_2{V}_{\mathit{kl}}^{\mathit{LF}}.$$

The corresponding classification rates are presented in Table 7. Observe that considering metric distance and volume together in the logistic discrimination procedure with the cost functions C₁(π_o,w₁, w₂) and C₂(π_o, η₁, η₂), we get better classification rates compared to logistic models with only one of metric distance or volume being the predictors.

Table 7.

The correct classification rates (P_CCR), sensitivity (P_sens), and specificity (P_spec) percentages for the classification procedures based on models M_I(V, D) − M_IV (V, D) using hippocampal LDDMM metrics and volumes with optimum threshold values π_o = π_opt based on the cost function C₁(π_o, w₁, w₂) with w₁ = w₂ = 1 and w₁ = 1, w₂ = 3 (top); and with optimum threshold values π_o = π_opt based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and η₁ = .3, η₂ = 0.7 (bottom).

Using optimum πo based on cost function C1 (πo, w1, w2) with
	w1 = w2 = 1				w1 = 1, w2 = 3
	MI(V, D)*	MII(V, D)	MIII(V, D)	MIV(V, D)	MI(V, D)*	MII(V, D)	MIII(V, D)	MIV(V, D)
πopt	.64-.65	.66	.48-.58	.48	.64-.65	.66	.48-.54	.28-.33
PCCR	84%	84%	75%	84%	84%	84%	75%	80%
Psens	89%	83%	83%	83%	89%	83%	83%	89%
Pspec	81%	85%	69%	85%	81%	85%	69%	73%
Using optimum πo based on cost function C2(πo, η1, η2) with
	η1 = η2 = 0.5				η1 = .3, η2 = 0.7
	MI(V, D)*	MII(V, D)	MIII(V, D)	MIV(V, D)	MI(V, D)*	MII(V, D)	MIII(V, D)	MIV(V, D)
πopt	.64-.65	.66	.68-.72	.48	.64-.65	.66	.23	.20-.22
PCCR	84%	84%	80%	84%	84%	84%	70%	75%
Psens	89%	83%	61%	83%	89%	83%	100%	94%
Pspec	81%	85%	92%	85%	81%	85%	50%	61%

^*The model with the best classification performance is marked with an asterisk.

In [26], logistic discrimination procedure is applied with either on the first 12 eigenfunctions obtained from the SVD of vector field changes, or on these eigenfunctions together with the hippocampal volume changes. In this article, we perform logistic discrimination on volumes (hippocampal, brain and intracranial) and metric distances together with a model selection procedure. In the above logistic models, we consider the volumes only not the volume changes.

4 Annual Percentage Rates of Change in Hippocampal Volumes and in Metric Distances

Our volume and metric distance comparisons are cross-sectional or longitudinal by construction. However these measures might need to be adjusted for anatomic variability, since intersubject variability might add substantial amount of noise to volume or distance measurements at baseline or follow-up. There is no simple way to correct for this noise in practice. Differential volume loss or distance change over time might be self-correcting for such variability. For example, entorhinal cortex volume loss over time was shown to be a better indicator for DAT than cross-sectional measurements [66].

The hippocampal volume change over time can be written as the following annual percentage rate of change (APC) [66]:

$$V^{\mathit{APC}}=\frac{V_k^b-V_k^f}{V_k^b\times T}\times 100\%,$$ (16)

where T is the interscan interval in years (T ≈ 2 in our data).

For modeling annual percentage rate of change in volume V ^APC using the repeated-measures ANOVA with group as main effect and compound symmetry in Var-Cov structure and V ^APC measures repeated over side for each subject, the model is

$$V_{\mathit{ijk}}^{\mathit{APC}}=\mu +{\alpha }_i^D+{\alpha }_j^S+{\alpha }_{\mathit{ij}}^{\mathit{DS}}+{\epsilon }_{\mathit{ijk}},$$ (17)

where $V_{\mathit{ijk}}^{\mathit{APC}}$ is the APC in volume for side j of subject k with diagnosis i, μ is the overall mean, ${\alpha }_i^D$ is the effect of diagnosis level i (i = 1 for CDR0; 2 for CDR0.5), ${\alpha }_j^S$ is the effect of side level j (j = 1 for left and 2 for right), ${\alpha }_{\mathit{ij}}^{\mathit{DS}}$ is the diagnosis×side interaction, and ε_ijk is the error term. The diagnosis main effect is significant (F = 18.62, df = 1, 84, p < .0001) but neither side main effect (F = 0.72, df = 1, 84, p = .3754) nor diagnosis×side interaction is significant (F = 0.11, df = 1, 84, p = 0.7384). Consequently, we conclude that the lines that join the mean V ^APC values in the interaction plot are parallel and far apart, the main effect of diagnosis comparison is meaningful, and about the same at each hemisphere. The post hoc comparison of V ^APC values indicate that the APC in CDR0.5 volumes are significantly larger than APC in CDR0 volumes (p = .0001).

The hippocampal metric distance change over time can be written as the following annual percentage rate of change:

$$D^{\mathit{APC}}=\frac{d_k^f-d_k^b}{d_k^b\times T}\times 100\%.$$ (18)

Notice that to make APC in metric distance positive, we take the difference $d_k^f-d_k^b$ as opposed to the order in the APC in volume definition. However, since volume has a unit but metric distance is unitless, the same correction for anatomic variability might not work well for both measures. For metric distances, we recommend the measurement of the distance between follow-up and baseline hippocampi instead. In fact, the repeated-measures analysis of APC in metric distances do not perform better than the distances or APC in volumes [68].

4.1 Logistic Discrimination Based on Annual Percentage Rates

We also apply the logistic discrimination methods of Section 3.7 on APC in hippocampal volumes. First we consider the full logistic model (designated as M_I (V ^APC) with side and APC in volume with all possible interactions being the predictor variables. We apply the same stepwise elimination procedure as in Section 3.7 and get

$$M_{\mathit{II}}(V^{\mathit{APC}}):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{V}_{\mathit{ijk}}^{\mathit{APC}}+{\beta }_2{(V_{\mathit{ijk}}^{\mathit{APC}})}^3$$ (19)

where p_k is the probability of subject k having DAT.

Furthermore, when we use $V_{\mathit{ijk}}^{\mathit{APC},L}$ and $V_{\mathit{ijk}}^{\mathit{APC},R}$ as predictors in a logistic model, we see that the following model has the best fit.

$$M_{\mathit{III}}(V^{\mathit{APC}}):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{V}_{\mathit{ik}}^{\mathit{APC},L}+{\beta }_2{V}_{\mathit{ik}}^{\mathit{APC},R}+{\beta }_3{\left(V_{\mathit{ik}}^{\mathit{APC},L}\right)}^2.$$ (20)

The classification rates with π_o = 1/2 and π_o = 18/44 and optimal π_o values with respect to the cost functions are presented in Table 8. Observe that the classifier using the cost function C₂(π_o, η₁, η₂) with η₁ = .3, η₂ = 0.7 in model M_I (V ^APC) has the best performance. Comparing Tables 6 and 7, we observe that correct classification rates, sensitivity, and specificity percentages with the classifiers based on APC in volume are about the same as those with volume only. Unlike the findings of [66] hippocampal volume loss over time is not a better indicator for DAT than cross-sectional measurements. On the other hand, the classifier based on volume and distance together performs better compared to models based on only one of volume, distance, or APC in volume values.

Table 8.

The correct classification rates (P_CCR), sensitivity (P_sens), and specificity (P_spec) percentages for the classification procedures based on models M_I (V ^APC) − M_III (V ^APC) using APC in hippocampal volumes with optimum threshold values π_o = π_opt based on the cost function C₁(π_o, w₁, w₂) with w₁ = w₂ = 1 and w₁ = 1, w₂ = 3 (top); and with optimum threshold values π_o = π_opt based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and η₁ = .3, η₂ = 0.7 (bottom).

Using optimum πo based on cost function C1 (πo, w1, w2) with
	w1 = w2 = 1			w1 = 1, w2 = 3
	MI (V APC)*	MII (V APC)	MIII (V APC)	MI (V APC)*	MII (V APC)	MIII (V APC)
πopt	.55-.55	.38-.39	.27-.28	.54-.55	.34	.25
PCCR	80%	75%	75%	80%	73%	73%
Psens	72%	72%	78%	72%	83%	83%
Pspec	85%	81%	73%	85%	65%	65%
Using optimum πo based on cost function C2(πo, η1, η2) with
	η1 = η2 = 0.5			η1 = .3, η2 = 0.7
	MI (V APC)*	MII (V APC)	MIII (V APC)	MI (V APC)	MII (V APC)	MIII (V APC)
πopt	.54-.55	.82-.85	.61-.69	.39	.34	.18-.21
PCCR	80%	82%	82%	64%	73%	70%
Psens	72%	56%	56%	89%	83%	100%
Pspec	85%	100%	100%	46%	65%	50%

^*The model with the best classification performance is marked with an asterisk.

We apply the logistic discrimination methods of Section 3.7 on APC in hippocampal metric distances also in [68] where we demonstrate that hippocampal metric distance change over time is a poor indicator for DAT.

We apply the logistic discrimination based on both the distance and APC in volumes. First we consider the full logistic model (designated as M_I (V ^APC, D)) with side and APC in volume, and distances with all possible interactions being the predictor variables. We apply the same stepwise elimination procedure as in Section 3.7 and get

$$M_{\mathit{II}}(V^{\mathit{APC}},D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{V}_{\mathit{ijk}}^{\mathit{APC}}+{\beta }_2{\left(V_{\mathit{ijk}}^{\mathit{APC}}\right)}^3+{\beta }_3{\left(d_{\mathit{ik}}^F\right)}^2.$$ (21)

Furthermore, when we use and left and right measures as predictors in a logistic model, we see that the following model has the best fit.

$$M_{\mathit{III}}(V^{\mathit{APC}},D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{V}_{\mathit{ik}}^{\mathit{APC},L}+{\beta }_2{V}_{\mathit{ik}}^{\mathit{APC},R}+{\beta }_3{d}_{\mathit{ik}}^{\mathit{RF}}.$$ (22)

The classification rates with π_o = 1/2 and π_o = 18/44 and optimal π_o values with respect to the cost functions are presented in Table 10. With the cost function C₁(π_o,w₁ = 1,w₂ = 1), the best classifier is based on M_III (V ^APC,D) for which the optimal threshold value is π_o ≈ .37, the correct classification rate is 80%, sensitivity is 78%, and specificity is 81%. Likewise, with the cost function C₁(π_o,w₁ = 1,w₂ = 3), the best classifier is based on M_I (V ^APC, D) for which the optimal threshold value is π_o = .56, the correct classification rate is 80%, sensitivity is 78%, and specificity is 81%. On the other hand, with cost function C₂(π_o, η₁ = .5, η₂ = .5) the best classifier is based on $M_I^{\mathit{APC}}$ (V,D) for which the optimal threshold value is π_o = .64, the correct classification rate is 84%, sensitivity is 72%, and specificity is 92%. With cost function C₂(π_o, η₁ = .3, η₂ = .7), the best classifier is again based on $M_I^{\mathit{APC}}$ (V,D) for which the optimal threshold value is π_o = .56, the correct classification rate is 80%, sensitivity is 78%, and specificity is 81%. Comparing Tables 7 and 10, we observe that the classifiers based on metric distance and volume usually perform better compared to the classifiers based on metric distance and APC in volume. Comparing Table 8 and 10, we observe that adding the metric distance to the logistic model with APC in volume improves the classification performance. Hence the model with hippocampal volume loss over time and metric distance is a better indicator for DAT compared to either variable used separately in logistic discrimination.

Table 10.

The correct classification rates (P_CCR), sensitivity (P_sens), and specificity (P_spec) percentages for the classification procedures based on models M_I (V^APC, D) − M_III (V^APC, D) and M_I (V, V^APC, D) − M_III (V, V^APC, D) using metric distance, and APC in hippocampal volumes with threshold probabilities with optimum threshold values π_o = π_opt based on the cost function C₁(π_o, w₁, w₂) with w₁ = w₂ = 1 and w₁ = 1, w₂ = 3 (top); and with optimum threshold values π_o = π_opt based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and η₁ = .3, η₂= 0.7 (bottom).

Using optimum πo based on cost function C1 (πo, w1, w2 ) with
	w1 = w2 = 1			w1 = 1, w2 = 3
	MI (V APC, D)	MII (V APC, D)	MIII (V APC, D)*	MI (V APC, D)*	MII (V APC, D)	MIII (V APC, D)
πopt	.61	.53-.73	.35-.40	.56	.35-.36	.31-.32
PCCR	84%	82%	80%	80%	70%	75%
Psens	72%	67%	78%	78%	78%	83%
Pspec	92%	92%	81%	81%	65%	69%
Using optimum πo based on cost function C2(πo, η1, η2) with
	η1 = η2 = 0.5			η1 = .3, η2 = 0.7
	MI (V APC, D)*	MII (V APC, D)	MIII (V APC, D)	MI (V APC, D)*	MII (V APC, D)	MIII (V APC, D)
πopt	.61	.53-.73	.49	.56	.23-.25	.31-.32
PCCR	84%	82%	82%	80%	55%	75%
Psens	72%	67%	67%	78%	100%	83%
Pspec	92%	92%	92%	81%	23%	69%
Using optimum πo based on cost function C1 (πo, w1, w2) with
	w1 = w2 = 1			w1 = 1, w2 = 3
	MI (V, V APC, D)	MII (V, V APC, D)	MIII (V, V APC, D)*	MI (V, V APC,D)	MII (V, V APC,D)	MIII (V, VAPC,D)*
πopt	.56-.57	.48-.51	.39-.42	.56-.57	.48-.51	.39-.42
PCCR	89%	89%	91%	89%	89%	91%
Psens	94%	89%	94%	94%	89%	94%
Pspec	85%	88%	88%	85%	88%	88%
Using optimum πo based on cost function C2(πo, η1, η2) with
	η1 = η2 = 0.5			η1 = .3, η2 = 0.7
	MI (V, V APC,D)	MII (V, V APC,D)	MIII (V, V APC,D)*	MI (V, V APC,D)	MII (V, V APC,D)	MIII (V, V APC,D)*
πopt	.56-.57	.48-.51	.39-.42	.56-.57	.48-.51	.39-.42
PCCR	89%	89%	91%	89%	89%	91%
Psens	94%	89%	94%	94%	89%	94%
Pspec	85%	88%	88%	85%	88%	88%

^*The models with the best classification performance are marked with an asterisk.

We also apply the logistic discrimination based on volume, distance, and APC in volumes. First we consider the full logistic model (designated as M_I (V, V ^APC, D)) with side, volume, and APC in volume, and distances with all possible interactions being the predictor variables. We apply the same stepwise elimination procedure as in Section 3.7 and get

$$M_{\mathit{II}}(V,V^{\mathit{APC}},D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{V}_{\mathit{ijk}}^B+{\beta }_2{V}_{\mathit{ijk}}^{\mathit{APC}}+{\beta }_3{\left(V_{\mathit{ijk}}^{\mathit{APC}}\right)}^3+{\beta }_4{\left(d_{\mathit{ijk}}^F\right)}^3.$$ (23)

Furthermore, when we use and left and right measures as predictors in a logistic model, we see that the following model has the best fit.

$$M_{\mathit{III}}(V,V^{\mathit{APC}},D):\mathrm{logit}{p}_k={\beta }_0+{\beta }_1{V}_{\mathit{ik}}^{\mathit{RF}}+{\beta }_2{d}_{\mathit{ik}}^{\mathit{LF}}+{\beta }_3{V}_{\mathit{ik}}^{\mathit{APC},R}+{\beta }_4{\left(V_{\mathit{ik}}^{\mathit{APC},L}\right)}^3+{\beta }_5{\left(d_{\mathit{ik}}^{\mathit{RF}}\right)}^3.$$ (24)

The classification rates the optimal π_o values with respect to the cost functions are presented in Table 10. With the cost function C₁ (π_o, w₁ = 1, w₂ = 1), the best classifier is based on M_III (V, V ^APC, D). Comparing Table 10 with Tables 5, 6, 8, 9, and 7, we observe that the classifiers based on metric distance, volume, and APC in volumes usually perform better compared to the classifiers based on other models. Hence the model with volume, hippocampal volume loss over time, and metric distance is a better indicator for DAT compared to other models based on subsets of these variables.

Table 9.

The correct classification rates (P_CCR), sensitivity (P_sens), and specificity (P_spec) percentages for the classification procedures based on models M_I (D^APC) − M_III (D^APC) using APC in metric distances with optimum threshold values π_o = π_opt based on the cost function C₁(π_o, w₁, w₂) with w₁ = w₂ = 1 and w₁ = 1, w₂ = 3 (top); and with optimum threshold values π_o = π_opt based on the cost function C₂(π_o, η₁, η₂) with η₁ = η₂ = 0.5 and η₁ = .3, η₂ = 0.7 (bottom).

Using optimum πo based on cost function C1 (πo, w1, w2 ) with
	w1 = w2 = 1			w1 = 1, w2 = 3
	MI (DAPC)*	MII (DAPC)*	MIII (DAPC)	MI (DAPC)	MII (DAPC)	MIII (DAPC)
πopt	.45	.45-.46	.41	.42	.45-.46	.36
PCCR	66%	66%	66%	61%	66%	64%
Psens	61%	61%	56%	67%	61%	78%
Pspec	69%	69%	73%	58%	69%	54%
Using optimum πo based on cost function C2(πo, η1, η2) with
	η1 = η2 = 0.5			η1 = .3, η2 = 0.7
	MI (DAPC)	MII (DAPC)	MIII (DAPC)*	MI (DAPC)	MII (DAPC)	MIII (DAPC)
πopt	.45	.45-.46	.32	.37	.35-.36	.29
PCCR	66%	66%	64%	52%	55%	59%
Psens	61%	61%	89%	100%	100%	100%
Pspec	69%	69%	46%	19%	23%	31%

^*The model with the best classification performance is marked with an asterisk.

The hippocampal volume change (together with the first 12 eigenfunctions) was used in [26] for logistic discrimination, but in this section, we use not the volume change but a function of it (namely annual percentage change) in logistic discrimination. Moreover, we also consider annual percentage change in metric distances in logistic discrimination.

5 Discussion and Conclusions

In this study, we consider the use and analysis of metric distances between brain tissues that are computed from the vector fields generated by Large Deformation Diffeomorphic Metric Mappings (LDDMM) with respect to an anatomical template. In particular, we use hippocampi in groups of subjects with and without Dementia of Alzheimer type (DAT) in its mild form (labeled as CDR0.5 and CDR0 patients, respectively) at baseline and follow-up as examples. The subjects in this paper have been previously analyzed using related but different tools. More specifically, the data was analyzed using the “greedy algorithm implementation of the diffeomorphic mapping and comparing displacement vector fields” [26]. [39] showed that this approach or the small deformation one used in many mapping methods do not generate true metric distances. Furthermore, in [26], as a single scalar measure, volumes were used for diagnosis group comparisons at baseline and follow-up and in [45] displacement momentum vector fields based on LDDMM were used for discrimination. At the same time [45] showed that statistical analysis of (momentum) vector fields generated by LDDMM was consistent with those generated by HDBM in [26]. But the metric distances computed from LDDMM has not hitherto been used in diagnosis group analysis. The metric distance gives a single number reflecting the global morphometry (i.e., the size and shape) while volume measurements mostly provide information on size. So metric distances provide additional morphometric information not conveyed by volume whereas momentum vector fields also provide local information on shape changes. Further, the morphometric information conveyed by the metric distance depends on the choice of the template, while the morphometric information conveyed by momentum vector fields is independent of the template chosen. That is, although the vector fields change when the template changes, the morphometric information they convey is the same. However, the vector field data is highly multidimensional and harder to interpret compared to the metric distances.

There have been other methods for hippocampus morphometry ([67, 73-78] to name a few of the recent studies). Compared to these methods, the advantage of the current approach is that it enjoys all three of the following properties whereas the other methods only satisfy one or two of them. That is, the metric distance (1) provides a single global measure of shape and size, (2) can be used for group and discrimination analysis, and (3) indicates relative distance between subjects. For example, in [67], hippocampus was included as part of the temporal lobe and the tensor-based morphometry analysis was done using Jacobian maps created with a LDDMM type registration algorithm [79] but does not use the induced metric. Although the Jacobian maps calculated with LDDMM can be used for tensor-based morphometry analysis and can be compared with [67], it is beyond the scope of this work.

The metric distances may be used for cross-sectional comparisons of the morphometry of diagnostic groups. For example, in our example data set, metric distances did not detect any significant difference in morphometry at baseline (see Table 4), but follow-up metric distances for the right hippocampus in CDR0.5 (i.e., mildly demented) subjects are found to be significantly larger than those in CDR0 (i.e., non-demented) subjects (see Table 4). Wang et al. also analyzed the velocity vector fields for the baseline hippocampi of the same data set and found that the left hippocampus in the DAT group shows significant shape abnormality and the right hippocampus shows similar pattern of abnormality [45]. The reason for the metric failing to detect such abnormality in the baseline hippocampi is that metric distance is a compound and oversummarizing measure of global morphometry.

The metric distances might also be used in longitudinal analysis in order to see how morphometry (with respect to the template) changes over time. For example, from baseline to follow-up, metric distances for CDR0.5 subjects significantly increase while those in CDR0 subjects do not (see Table 4). That is, the morphometry (shape and size) of hippocampus in CDR0.5 subjects changes significantly over time, but not in CDR0 subjects. Atrophy - over two years - might occur with aging, and this is captured by metric distances (see Table 4). However the increase in the metric distances in CDR0 subjects is not found to be statistically significant. Differences and changes (over time) in morphometry can also be used for diagnostic discrimination of subjects in non-demented or demented groups. Many discrimination techniques such as Fisher’s linear discriminant functions, support vector machines, and logistic discrimination can be applied to the metric distances, together with other qualitative variables. In this study we applied logistic discrimination based on metric distances, as logistic regression not only provides a means for classification, but also yields a probability estimate for having DAT. Furthermore, one can optimize the threshold probability for a particular cost function for the entire training data set, or by a cross-validation technique. The correct classification rate of the hippocampi was about 70% in our logistic regression analysis. In [45] PCA of the initial momentum of the same data set led to correct classification of 12 out of 18 (i.e., 67% of the) demented subjects and 22 out of 26 (i.e., 85% of the) control subjects. Metric distances can be used to distinguish AD from normal aging quantitatively; however, to be able to use it for diagnostic purposes, the method should be improved to a greater extent.

The atrophy in the temporal lobe was also observed by [67], where hippocampus was included as a part of the temporal lobe (as opposed to our study where only hippocampus atrophy is analyzed). In [67], it has been shown that brain atrophy rates are greater in DAT and MCI (mild cognitively impaired) patients, compared to healthy subjects. Moreover, MCI subjects who converted to DAT exhibited faster atrophy rates than the ones who did not convert, and slower rates compared to DAT subjects. This is somewhat in agreement with our findings that the rate of change in morphometry is larger in DAT subjects compared to healthy ones. However, volume (as a measure of tissue size) is not analyzed in this article. Furthermore, compared to the vector field changes, Jacobian changes are used in the analysis of morphometric changes.

We perform a principal component analysis on metric distances and hippocampus, brain, and intracranial volumes. Considering the variable loadings, we conclude that volumes are mostly measures of size and partly related to shape, while the metric distance is mostly a measure of shape and partly related to size.

We also compare the cross-sectional, longitudinal, and discrimination results of metric distances with those of volumes. We observe that cross-sectional and longitudinal analysis give similar results, although metric distances increase and volumes decrease by time. The metric distance, being an extremely condensed summary measure gives very similar results as the hippocampal volume. Furthermore, the differential volume and distance changes are measured by annual percentage rate of change (APC) for the two year period in the study. Similar to the results of [66], we found that APC in volumes may be a good indicator for early stage of DAT. However, APC in metric distances do not provide a good performance in classification of CDR0 versus CCDR0.5 hippocampi. The best classifiers in our logistic discrimination procedure are the ones which use hippocampal volume, metric distance, and annual percentage change in volumes (see Table 10). Notice that the best performer models (marked with *) have correct classification rates of 91%, sensitivity rate of 94%, and specificity rate of 88%. On the other hand, in [26], the logistic discrimination with the first 12 eigenfunctions based on SVD yields a correct classification rate of 84.0%, sensitivity rate of 83.3%, and specificity rate of 84.6%; and the logistic discrimination with the first 12 eigenfunctions together with hippocampal volume changes yields a correct classification rate of 86.0%, sensitivity rate of 72.2%, and specificity rate of 92.6%. Therefore, in classification of healthy versus diseased hippocampi, our model (with volume, metric distance, and annual percentage change in volume) seems to perform better compared to the classification models of [26] in the classification rates. Hence these measures may constitute a reliable biomarker when used together.

The clinical implications of the findings are deferred to [68]. We have presented detailed statistical analysis of metric distances computed with LDDMM and show that this is potentially a powerful tool in detecting morphometric changes between diagnosis groups or changes in morphometry over time. Metric distances depend on the choice of template anatomy used. However, in this article we do not address the issue of template selection for optimal differentiation between hippocampus morphometry. As a compound but brief measure of morphometry, metric distances can thus serve as a first step to identify the morphometric differences, and can be used as a pointer to which direction a clinician or data analyst could go. The metric distance results agree with the volume comparisons of [26], hence volume (i.e., scale) might be highly dominating the morphometric changes in the hippocampi. In other words, the significant volume reduction in left and right hippocampi might dominate the change in shape, when morphometry is measured by metric distances. To remove the size influence so as to measure the shapes only, one can perform scaling on the hippocampi and then apply LDDMM to normalize the size differences.