The human semicircular canal model of galvanic vestibular stimulation

Abstract

A vector summation model of the action of galvanic stimuli on the semicircular canals has been shown to explain empirical balance and perceptual responses to binaural-bipolar stimuli. However, published data suggest binaural-monopolar stimuli evoke responses that are in the reverse direction of the model prediction. Here, we confirm this by measuring balance responses to binaural-monopolar stimulation as movements of the upper trunk. One explanation for the discrepancy is that the galvanic stimulus might evoke an oppositely directed balance response from the otolith organs that sums with and overrides the semicircular canal response. We tested this hypothesis by measuring sway responses across the full range of head pitch. The results showed some modulation of sway with pitch such that the maximal response occurred with the head in the primary position. However, the effect fell a long way short of that required to reverse the canal sway response. This indicates that the model is incomplete. Here, we examine alterations to the model that could explain both the bipolar and monopolar-evoked behavioural responses. An explanation was sought by remodelling the canal response with more recent data on the orientation of the individual canals. This improved matters but did not reverse the model prediction. However, the model response could be reversed by either rotating the entire labyrinth in the skull or by altering the gains of the individual canals. The most parsimonious solution was to use the more recent canal orientation data coupled with a small increase in posterior canal gain.

Introduction

In an effort to understand the nature of the signals produced by galvanic vestibular stimulation (GVS), Fitzpatrick and Day (2004) modelled the total GVS-evoked input from semicircular canal afferents. The model was based on first principles and relied on simple assumptions largely fuelled by observations made by Goldberg and colleagues on the responses of primary vestibular afferents to direct current stimuli in the monkey (Goldberg et al. 1982, 1984). Thus, it was assumed that a stimulus delivered to the mastoid processes would (1) modulate the vestibular afferents’ spontaneous firing with a cathodal current increasing firing frequency and an anodal current equally decreasing firing frequency and (2) evoke afferent activity equally from all semicircular canals. This total activity would then (3) be summed vectorially in the brain with equal central weighting of each canal. With these assumptions together with knowledge of the orientation of the canals in the human skull (Blanks et al. 1975), Fitzpatrick and Day estimated the net GVS-evoked signal from all six canals. With an anode on the right mastoid and a cathode on the left (binaural-bipolar stimulation) they estimated that the net signal would be equivalent to a head rotation about an axis directed backwards in the mid-sagittal plane of the head and angled upwards 18.8° with respect to Reid’s plane (Fig. 2a). A reversal of stimulus polarity would simply reverse the direction of this apparent head rotation.

Fig. 2.

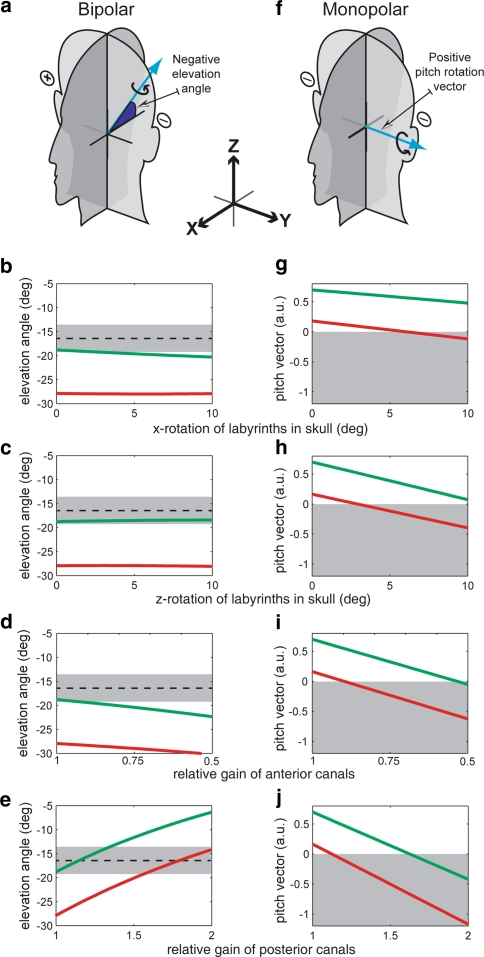
Simulated effects of changing model parameters. Top panels (a, f) show net rotation vectors (blue arrows) of the apparent head rotation evoked by GVS and their sign conventions for two stimulation conditions. Rotation vectors are drawn according to the right-hand rule. a–e shows the elevation angle relative to Reid’s plane of the rotation vector in the sagittal plane predicted by the model to binaural-bipolar stimulation with left cathode and right anode. Dashed line and grey band correspond to mean ± SEM empirically derived elevation angle from Day and Fitzpatrick (2005). f–j shows magnitude in arbitrary units (a.u.) and direction (positive or negative) of the pitch rotation vector predicted by the model to binaural-monopolar stimulation with cathodes. Grey shaded area corresponds to the negative direction of pitch rotation (towards right ear) that will lead to a forward sway response as observed empirically. Simulations consisted of mirror rotating the right and left labyrinths about the x-axis (b, g) or the z-axis (c, h), or by selectively attenuating the anterior canals gain (d, i) or augmenting the posterior canals gain (e, j). Solid lines on graphs show model simulations based on the semicircular canals orientation data either from Blanks et al. (green) or from Della Santina et al. (red)

This estimated virtual rotation vector is in good agreement with the empirically determined vector of 16.4° above Reid’s plane based on GVS-evoked perceptions of whole-body rotation (Day and Fitzpatrick 2005). It also fits well with observations of head pitch effects on GVS-evoked balance responses (Cathers et al. 2005; Mian et al. 2010) and navigation responses during walking (Fitzpatrick et al. 2006). However, a discrepancy occurs when the left and right mastoids receive the same polarity of stimulation (binaural-monopolar stimulation). As shown originally by Magnusson et al. (1990) and later by others (Day et al. 2010; Séverac Cauquil et al. 2000), monopolar GVS with the head in the primary position evokes balance responses predominantly in the anterior–posterior (AP) direction, in contrast to the mediolateral (ML) response with the more conventional bipolar stimulus. Fitzpatrick and Day’s model predicts these different response planes if it is assumed that the balance system ascribes the net head rotation vector to an unplanned body motion for which it compensates by counter-rotating the body in the same plane. The different response directions occur because the estimated net rotation vector lies close to the roll axis with bipolar stimulation, whereas with monopolar stimulation it is directed along the pitch axis (Fig. 2b). The model correctly predicts a compensatory mediolateral balance response towards the anode for the bipolar stimulus. However, the predicted response is in the wrong direction for the monopolar stimulus. The model predicts a forward response to binaural anodes and a backward response to binaural cathodes, whereas the opposite directions are observed empirically (Day et al. 2010; Séverac Cauquil et al. 2000).

One possible explanation for this discrepancy could be that GVS evokes a net otolith signal in addition to a net semicircular canal signal. If the otolith signal mimics a linear acceleration in the sagittal plane with a component in the AP direction, it would likely evoke a compensatory AP balance response. Furthermore, if this otolith response were larger and oppositely directed to the semicircular canal response, the model discrepancy would be explained. In the present experiments, we test this hypothesis by measuring the direction of the GVS-evoked balance response to monaural stimuli with the head pitch angle varied over a 180° range. The rationale is that such a change in head pitch angle will not affect the GVS-evoked semicircular canal signal of rotation about a pitch axis, but will dramatically affect the direction of a GVS-evoked linear acceleration signal in the sagittal plane. Varying the linear acceleration signal over 180° should at some point contribute a zero component to an AP balance response (when it points in a vertical direction), or even reverse the sign of its balance component at some point. Either way, there should be a position of head pitch at which the GVS-evoked AP response direction agrees with the model prediction. However, the current findings do not support this hypothesis. We take this as evidence that the Fitzpatrick and Day model is incomplete and here investigate some possible modifications to the model that would bring it back into line with empirical observation.

Methods

With ethics committee approval and according to the declaration of Helsinki, seven healthy subjects (six male, one female; age range 22–37 years; mean ± SD, 27.9 ± 5.2 years), with no history of a neurological or vestibular disorder, consented to participate.

Stimuli and equipment

Two custom-built constant current stimulators were used for galvanic vestibular stimulation (GVS). Independent stimuli were delivered to each side via a pair of 2.5-cm-diameter circular neurostimulation electrodes (PALs plus, Nidd Valley Medical Ltd, Knaresborough, UK) placed over the mastoid process and 2-cm ipsilateral to the T2 spinous process (Day et al. 2010). The electrodes were secured using adhesive tape and conductive electrode gel was applied at the electrode–skin interface to improve conductance. GVS consisted of a rectangular current profile of 2.0 mA lasting for 2 s. The polarity of stimulation was always the same for the two sides (binaural-monopolar GVS).

Orientation of the head in space and motion of the body were measured from the 3-dimensional positions of infrared markers using a CODA system (mpx30/cx1 hybrid: Charnwood Dynamics, Rothley, UK). Four head markers were used (two on each side) placed near the external auditory meatus and the lower margin of the orbit in such a way as to define Reid’s plane. Motion of the body was measured from a marker fixed to the skin at the level of the C7 spinous process. Marker positions were sampled at 200 Hz.

Procedure

Subjects stood facing forward with feet together, eyes closed and head pitched at the angle instructed by the experimenter. Five head pitch positions were attempted (−90, −45, 0, 45, 90°). A pitch angle of zero indicates Reid’s plane horizontal; positive pitch values indicate nose-up head posture. Most of the pitch angle was achieved by neck flexion/extension, but additional trunk flexion/extension was allowed when necessary, which was always the case for the extreme angles (±90°). With the aid of a protractor the experimenter assessed the approximate pitch angle and asked for adjustments if required. The extreme head pitch angles (±90°) were not always achievable, in which case the maximum pitch possible was used. A given pitch angle was maintained for a block of 20 trials, and the order of pitch angle was randomised between blocks and between subjects. Within a block, the stimulus polarity (anodes or cathodes applied to both mastoids) was pseudo-randomised between trials. A trial was initiated by the experimenter using a button press, with data collection commencing after a random delay of 500–1,500 ms and lasting for 6 s. Breaks were taken as necessary during which subjects could open their eyes and relax their posture. Upon resumption of data collection, the subjects’ heads were realigned to the required pitch angle. For the extreme head pitch postures these breaks were often frequent occurring every 2–5 trials in some subjects. Seated rests were allowed between blocks.

Data analysis

The mean head pitch angle was measured during the initial 2-s pre-stimulus period of each trial. These values were averaged across a block to give a mean angle for each subject for each of the five head pitch conditions.

The components of the C7 marker displacement in the anteroposterior and mediolateral directions were time-locked to the stimulus and averaged across the ten trials of each subject’s head position and polarity condition using Matlab (MathWorks Inc, Natik, MA, USA). The response magnitude and direction was measured from each of these average traces as the position change from 0.2 to 1.0 s after stimulus onset (Day et al. 2010).

The responses were analysed using repeated measures ANOVA (General Linear Model, SPSS) with two within-subject factors of polarity (anode, cathode) and pitch (−90, −45, 0, 45, 90). α was set at 0.05.

Model

The GVS semicircular canal model described previously (Fitzpatrick and Day 2004) was scripted in Matlab (MathWorks Inc, Natik, MA, USA) using two different anatomical data sets (Blanks et al. 1975; Della Santina et al. 2005). The Table 1 shows the orientation of each canal in the Reid stereotaxic coordinate system according to these two sources. The model assumes that the afferent response from a canal is maximal when it is rotated about an axis defined by the canal orientation vector. Cathodal GVS, which increases the firing frequency of a canal’s afferents, is therefore equivalent to a physical rotation of the canal about the same axis. Anodal GVS, which decreases afferent firing, is equivalent to rotation in the opposite direction. With the assumption that GVS stimulates afferents from each canal equally, the net equivalent rotation vector (R) was calculated as the vector sum of all six canal orientation vectors and simulated for monopolar and bipolar stimulation conditions.

Table 1.

Orientation of semicircular canals with respect to Reid’s plane based on two independent data sources

	Data from Blanks et al. (1975)			Data from Della Santina et al. (2005)			Angular difference
	X	Y	Z	X	Y	Z	Degree
LA	−0.652	0.753	0.017	−0.58930	0.78839	0.17655	10.0589
LH	−0.365	0.158	0.905	−0.32269	−0.03837	0.94573	11.8139
LP	−0.757	−0.561	−0.320	−0.69432	−0.66693	−0.27042	7.6221
RA	0.652	0.753	−0.017	0.58930	0.78839	−0.17655	10.0589
RH	0.365	0.158	−0.905	0.32269	−0.03837	−0.94573	11.8139
RP	0.757	−0.561	0.320	0.69432	−0.66693	0.27042	7.6221

Values denote the Cartesian position (X, Y, Z), defined in the Reid stereotaxic system (Fig. 2), of the end of a unit vector orthogonal to the plane of each canal and with the start of the vector at an arbitrary origin in the canal plane. The vector direction is given physiological meaning by obeying the right-hand rule for rotation such that positive directions signify the direction of head rotation that would excite the canal afferents. The angular difference indicates the inclusive angle between each pair of canal orientation vectors from the two data sources

LA left anterior canal, LH left horizontal canal, LP left posterior canal, RA right anterior canal, RH right horizontal canal, RP right posterior canal

Monopolar stimulation with left cathode and right cathode:

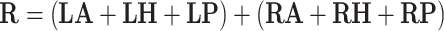Monopolar stimulation with left anode and right anode:

Bipolar stimulation with left cathode and right anode:

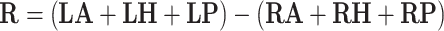Bipolar stimulation with left anode and right cathode:

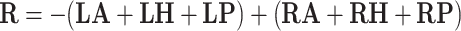where LA, LH, LP, RA, RH, RP denote the orientation vectors of the anterior, horizontal and posterior canals on the left and right side, respectively (Table 1).

The model was used to simulate further the effects of changing anatomical and physiological parameters on the net equivalent rotation vectors evoked by each stimulus polarity. The anatomical parameters were varied by mirror rotating the left and the right canal systems in the skull about each principal axis in turn. The physiological parameters were varied by altering the gain of a left–right canal pair while leaving the remaining two pairs at unity gain (note all canals have unity gain in the equations above).

Results

Effects of head pitch on response direction

For the five postures, the group mean (SD) head pitch angles attained were −78.2° (10.2), −42.9° (7.0), 0.1° (4.7), 38.6° (4.9) and 79.4° (10.8).

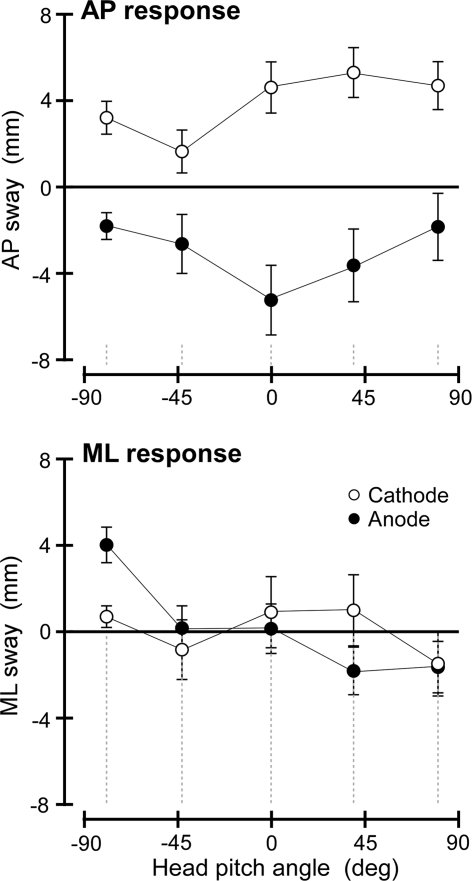
The group mean displacements of the body at the level of C7 for the two polarities of stimulation are shown in Fig. 1 for each head pitch angle. In the mediolateral direction (Fig. 1 lower), there were no significant effects of stimulation (pitch: F(4,24) = 2.444; P = 0.074; polarity: F(1,6) = 0.11; P = 0.920; pitch × polarity: F(4,24) = 1.622; P = 0.201). In the anterior–posterior direction (Fig. 1 upper), for all head pitch angles the mean responses were directed forwards with cathodal stimuli and backwards with anodal stimuli giving rise to a highly significant effect of polarity (F(1,6) = 22.381; P = 0.003). There was not a significant main effect of pitch (F(4,24) = 1.657; P = 0.193), but there was a significant pitch × polarity interaction (F(4,24) = 3.197; P = 0.031). This interaction indicates a weak differential effect of head pitch on responses to the two polarities, but the mean responses were never observed to reverse direction as required by the model.

Fig. 1.

Effect of head pitch on group mean (±SEM) displacement responses to binaural-monopolar GVS in the anterior–posterior direction (top panel) and the mediolateral direction (bottom panel). Positive values indicate forward and rightward direction, respectively. Shown are responses to cathodal (white circles) and anodal (black circles) stimuli

Model simulations

The experimental results show that response directions to binaural-monopolar stimuli are robust over almost 180° of head pitch and not in agreement with model predictions. Here, we investigate some changes that could be made to the model to make it more compatible with empirical observations. The primary empirical observation to be matched is the AP sway direction with monopolar stimulation. The secondary empirical observation is the angle of elevation of the sagittal plane rotation vector with bipolar stimulation (Day and Fitzpatrick 2005). These empirical observations are shown as grey areas in the simulations illustrated in Fig. 2.

Effects of canal orientation data

The output of the model depends critically on the orientation of the canals in the skull. Erroneous orientation values could give rise to the AP sway direction discrepancy. The original model was based on published anatomical data obtained by direct measurement of the dissected bony labyrinth of ten subjects (Blanks et al. 1975). We compared these values with more recently published data obtained from 3-dimensional multiplanar reconstructions of computerised tomography scans of the temporal bones of 22 human subjects (Della Santina et al. 2005). The orientations of the canals from these two sources are contrasted in the Table 1. There are differences between the two data sets leading to substantial angular differences in the orientation of the canals ranging from 7.6 to 11.8°.

We compared the model outputs using the two orientation data sets. With monopolar stimulation the Della Santina orientation data produced a pitch rotation in the same direction as the Blanks orientation data, so it too was incompatible with the observed sway direction. However, the vector magnitude was only 24% of Blanks’ and therefore closer to the empirical finding. With bipolar stimulation, the elevation angle of the net rotation vector in the sagittal plane was closer to the empirically observed angle of −16.4° with the Blanks data (−18.8°) than with the Della Santina data (−27.9°).

Effects of rotating the labyrinth with respect to the skull

We investigated whether it might be possible to resolve the model discrepancy by altering the orientation of the labyrinth in the skull. This simulates a constant error in the anatomical measurements of canal orientation. By rotating the left and right labyrinths symmetrically and in opposite directions about either the x-axis or the z-axis, the model could be made to agree with the empirically determined monopolar response direction (Fig. 2g, h). The critical angle of rotation (when the pitch response direction reverses) was less for z-rotation than x-rotation, and in both cases less for the Della Santina than the Blanks data (critical angle of z-rotation: Della Santina = 2.96°, Blanks = 11.16°; x-rotation: Della Santina = 5.57°, Blanks = 30.17°). Rotating the labyrinths in the skull in these directions had little effect on the elevation angle with bipolar stimulation (Fig. 2b, c).

Effects of changing the relative gains of the canals

An important and unsubstantiated assumption of the model is that each canal contributes to the net vector with equal weighting. We therefore investigated whether departures from this assumption could resolve the model discrepancy. By changing the gain of one canal at a time relative to the other two canals, we indeed found that to be the case. Changes in gain of the horizontal canals had little effect, whereas changes in gain of either the anterior or the posterior canals could reverse the pitch rotation vector appropriately. To achieve this, the anterior canal gain had to be decreased (Fig. 2i) or the posterior canal gain had to be increased from unity (Fig. 2j). The pitch vector was more sensitive to changes in posterior canal gain than in anterior canal gain and in both cases the critical gain change (when the pitch response direction reverses) was less for the Della Santina data than for the Blanks data (critical gain of posterior canal: Della Santina = 1.125, Blanks = 1.624; anterior canal: Della Santina = 0.895, Blanks = 0.535). These changes in the anterior canal gain took the elevation angle with bipolar stimulation further away from the empirically determined value, whereas the changes to the posterior canal gain took it closer (Fig. 2d, e).

Discussion

The measurements of GVS-evoked body motion confirm previous reports that with the head in the primary position the response to a binaural-monopolar stimulus occurs predominantly in the anterior–posterior direction (Day et al. 2010; Magnusson et al. 1990; Séverac Cauquil et al. 2000). They also confirm that with anodes on the mastoids the body sways backwards, while with cathodes it sways forwards (Day et al. 2010; Séverac Cauquil et al. 2000). Changing the head pitch angle over almost 180° did not reverse this relationship. These data are incompatible with the original semicircular canal model of GVS (Fitzpatrick and Day 2004).

Is the discrepancy due to an otolith component?

Our results from varying the head pitch angle suggest that the discrepancy is unlikely to be due to a GVS-evoked otolith component that competes with and overrides the semicircular canal component. If a sagittal plane linear acceleration vector were rotated in pitch over 180°, there should come a point when it points vertically and contributes nothing to anterior–posterior (AP) responses. Arguably, because the head pitch achieved was on average about ±10° short of the full ±90°, we could have missed this ‘vertical’ position. The worst case is if the linear acceleration were to lie exactly in Reid’s plane i.e., horizontal with head pitch of 0°. Then maximum pitch would have left it 10° short of vertical in both pitch directions. If this were the case, it would still contribute some AP component at both extremes of head pitch, but this would amount to only 20% (cosine 78.5°) of its value at 0° pitch. In other words, at worst we have covered 80% of any modulating otolith organ effect. We do not know what its value might be at 0°; all we know is the net value, which according to this theory is the sum of the two opposing effects from the canals and the otolith organs. The worst case is if the canal component is negligible, which would make the AP response at our extreme head pitch positions 20% of that at 0°. Any canal component would reduce this figure. However, after combining the two polarities of the data illustrated in Fig. 1, the actual values obtained experimentally are 66 and 51% at extreme positive and negative pitch angles, respectively. We therefore reject the hypothesis that a response from the otolith organs causes a reversal in the predicted response to monopolar stimulation.

We are not claiming here that there is no otolith component to the GVS-evoked balance response. We merely conclude that if it exists it is not larger and oppositely directed to the canal component when stimulating with binaural-monopolar GVS. It is uncertain from other experiments whether the balance response to GVS does contain an otolith component, although recent work has argued against this possibility (Mian et al. 2010). GVS-evoked eye movements (Kleine et al. 1999; Séverac Cauquil et al.2003; Watson et al. 1998; Zink et al. 1998) and tilt of the subjective visual vertical (Wardman et al. 2003; Watson et al. 1998) both have features that are consistent with an otolith component. However, these features can also be explained on the basis of canal signals alone (Pavlou et al. 2003; Schneider et al. 2002).

Is the discrepancy due to a component of non-vestibular origin?

The results show some modulation of response size with head pitch that could be due to a weak otolith component, but which equally could have a non-vestibular origin. Indeed, Mian et al. (2010) postulated that the short-latency (SL) component of the GVS-evoked balance response could arise from stimulation of non-vestibular afferents. For such a response component to explain our discrepancy it would have to satisfy a number of criteria. First, it would have to be directed in the AP direction, and secondly it would have to be larger in this direction than the semicircular canal component of response. The direction of the SL response with binaural-monopolar stimuli has not been measured, but with stimulation of one ear (monaural) the response direction is very close to the inter-aural direction i.e., negligible AP component (Mian et al. 2010). Binaural-monopolar stimulation by vector summation of the left and right monaural responses would therefore be expected to evoke only a small or negligible AP response. Thirdly, it would have to be only partially modified by head position to explain the modest modulation of response and absence of a reversal with head pitch. However, the SL response direction was shown to be completely modified by head position and well represented in a craniocentric coordinate frame (Mian et al. 2010).

Is the discrepancy due to an error in canal orientation?

If the discrepancy between the empirical data and the model cannot easily be explained by interference from a component of otolith or non-vestibular origin, we must consider that the canal model is either incomplete or in error. First, we consider whether errors in the orientation of the canals in the skull could play a role. Two data sets that fitted a plane to each canal (Blanks et al. 1975; Della Santina et al. 2005) gave subtly different equations for the orientation of the canal planes. This can probably be explained by the radically different measurement methods that the two groups employed, although it is also possible that it reflects differences in their different subject samples. Application of these two data sets to our model did result in substantial quantitative differences in predictions of net rotation vector size and direction, but these differences were insufficient to resolve the discrepancy. A third data set that has recently been published (Bradshaw et al. 2010) fared no better and produced results that were intermediate between the other two data sets (simulation results not shown). With the Bradshaw data the model behaved very similarly to the Della Santina data when simulating monopolar GVS, but behaved similarly to the Blanks data when simulating bipolar GVS.

Nonetheless, these quantitative differences did highlight the fact that modest changes in canal orientation could be a potent factor. Indeed, our simulations of rotation of the whole labyrinth in the skull, particularly about the z-axis, showed that a relatively small rotation of 3° of Della Santina’s canal orientations could reverse the direction of our model response to monopolar stimulation thereby eliminating the discrepancy. It is perhaps unlikely that all canal plane measurements would suffer a constant rotation error about a single axis. However, there are other possible sources of error associated with canal orientation planes. This arises from our assumption in the model that each canal signals a maximal response for head rotations in the measured plane of that canal, which is probably incorrect. It has been shown that maximal response planes of a canal do not necessarily coincide with anatomical canal planes in a number of species including toadfish (Rabbitt 1999), rhesus monkeys (Reisine et al. 1988) and man (Ifediba et al. 2007; Rajguru et al. 2004). The difference in the two planes can be substantial; for instance, the two planes differ by around 16° for the anterior canal of the toadfish (Rabbitt 1999).

Is the discrepancy due to unequal gains of the canals?

A vulnerable assumption of the model is that the afferent input and its central gain are the same for all canals, but we are not aware of any evidence that supports this. The simulations show that relatively small deviations from this equality can result in the discrepancy being resolved. For example, with the Della Santina canal orientations, either a pure reduction of the anterior canal gain from unity to 0.895 or a pure increase in the posterior canal gain to 1.125 was sufficient to reverse the direction of the model response to monopolar GVS. An adjustment of the posterior canal gain parameter is particularly attractive for two reasons. First, model outputs are slightly more sensitive to it. Second, with bipolar GVS, it brings the elevation angle of the rotation vector in the sagittal plane closer to the empirically measured angle.

In this regard, it may be worthy of note that in the cat there appears to be a much greater density of vestibulospinal projections to lower segments of the spinal cord that are activated by posterior canals than by anterior or horizontal canals (Kushiro et al. 2008). This hints at a greater sensitivity of posterior canal signals for controlling human lower limbs and hence balances. This is not the only mechanism by which posterior canals could exert greater influence. For example, it is unlikely that all three human semicircular canals are equally sensitive to mechanical stimuli. Spoor et al. (1994) showed there has been evolutionary pressure to enlarge the anterior and posterior canals relative to the horizontal canal in hominids, which may be related to bipedal behaviour. This is because, in general, longer canals are more sensitive (Muller and Verhagen 1988; Oman et al. 1987; ten Kate et al. 1970) and so this arrangement would increase the sensitivity to vertical plane rotations. Human canals differ in length (Clemente 1985) with the longest and therefore most sensitive being the posterior canal (18–22 mm), followed by the anterior canal (15–20 mm) and then the horizontal canal (12–15 mm). This fits well with the required greater gain of the posterior canal relative to the anterior canal for our model. The problem is GVS bypasses the mechanical transduction apparatus of the canals and so would not be affected by this mechanical sensitivity difference. However, it is possible that evolutionary pressure to alter mechanical sensitivity could similarly have acted to alter neural gains either by (1) increasing the number of afferents, (2) increasing central synaptic weights or (3) increasing the ratio of irregularly to regularly firing afferents. This last option follows from the finding that the galvanic stimulus exerts a much stronger influence on the firing rates of irregularly firing afferents than on the larger number of regularly firing afferents (Ezure et al. 1983; Goldberg 2000; Goldberg et al. 1984). Changes such as these would affect the GVS response and would manifest as an overall gain change in the model.

Conclusions

The predicted response of the Fitzpatrick and Day semicircular canal model to binaural-monopolar GVS is discrepant with the observed direction of the behavioural balance response. The discrepancy cannot be bridged by invoking otolith influences nor is it completely reconciled by using alternative data sets of human semicircular canal orientation. It can be reconciled, however, either by imposing further changes in canal orientation or by changing the model’s anterior or posterior canal gains. A parsimonious solution is obtained by using the alternative canal orientation data of Della Santina et al. (2005) together with a small relative increase in posterior canal gain.