Combined Simulation and Experimental Study of Large Deformation of Red Blood Cells in Microfluidic Systems

Abstract

We investigate the biophysical characteristics of healthy human red blood cells (RBCs) traversing microfluidic channels with cross-sectional areas as small as 2.7 × 3 μm. We combine single RBC optical tweezers and flow experiments with corresponding simulations based on dissipative particle dynamics (DPD), and upon validation of the DPD model, predictive simulations and companion experiments are performed in order to quantify cell deformation and pressure–velocity relationships for different channel sizes and physiologically relevant temperatures. We discuss conditions associated with the shape transitions of RBCs along with the relative effects of membrane and cytosol viscosity, plasma environments, and geometry on flow through microfluidic systems at physiological temperatures. In particular, we identify a cross-sectional area threshold below which the RBC membrane properties begin to dominate its flow behavior at room temperature; at physiological temperatures this effect is less profound.

Introduction

During its typical life span of 120 days upon egress from the bone marrow, the human red blood cell (RBC) circulates through the body delivering oxygen to tissue and carrying carbon dioxide back to the lungs. As it repeatedly traverses capillaries and microvascular passages, the RBC undergoes severe deformation with strains in excess of 100%.^6,18 Such deformation levels are typical, for example, in the spleen, where the RBC squeezes through splenic sinus and inter-endothelial slits with diameters estimated to be approximately 3 μm. Large deformation can also occur in capillaries and arterioles, where RBCs do not travel in isolation and their interactions with one another and the vascular wall cause them to stretch by as much as 150%. As a result, the role of deformability in influencing RBC function has been studied extensively. Furthermore, compromised RBC deformability contributing to human disease pathologies has also been a topic of growing research interest. For example, hereditary blood disorders such as spherocytosis, elliptocytosis, and ovalocytosis, as well as diseases such as diabetes, sickle cell anemia, and malaria all exhibit characteristic losses in RBC deformability with the onset and progression of the pathological state. For the case of Plasmodium falciparum malaria, recent experiments showed that the membrane stiffness of the parasitized RBC can increase more than 50-fold during intraerythrocytic parasite maturation.²⁶ Such changes act in concert with enhanced cytoadherence to other RBCs and the vascular endothelium to facilitate vaso-occlusive events such as stroke or other ischemias.

While single-cell quasistatic assays have helped establish connections between the biophysical characteristics of RBC and disease states, they do not adequately capture the reality of various biorheological events associated with the flow of a population of RBCs through the microvasculature. It has also not been feasible thus far to develop in vivo characterization of blood flow in the regions of largest RBC deformation due to the small length scales and geometric complexity of the microvasculature. In order to overcome this limitation, in vitro assays of RBC flow through glass tubes¹⁴ and microfabricated fluidic structures made of glass, silicon, or polydimethylsiloxane (PDMS) have been developed.^2,13 These experiments have also motivated several (mostly continuum-based) simulations of RBC biorheology.^3,19,23

Despite these advances, there is virtually no quantification to date of flow characteristics (e.g., pressure difference vs. cell velocity) of RBCs through constrictions of the smallest relevant length scales (approx. 3 μm in diameter), whereby the dynamics of RBC deformation characteristic of the conditions in the microvasculature can be simulated and visualized. In a few isolated studies where RBC flow has been studied through small channels,²⁵ the dynamics of flow has not been quantified or analyzed so as to facilitate broad conclusions to be extracted or to help facilitate the development of general computational models. Also, attempts to quantify RBC dynamics to date have not involved realistic in vivo temperature conditions.^1,10 Furthermore, to date no detailed three-dimensional (3D), quantitative simulations, validated by experiments, of RBC flow through microfluidic systems have been reported. Such simulations are essential to (a) develop an understanding of the relevant mechanisms and sensitivities of RBC flow behavior (e.g., the effect of RBC membrane viscosity on resistance) that cannot be systematically probed through experiments alone, (b) quantify the dynamics, rheology, and interactions of RBCs with the plasma, (c) extract biophysical and rheological properties of RBCs, and (d) develop robust models that can be used for in vivo predictions. The insight gained from a systematic combination of simulations and experiments could also be used in the design of novel microfluidic systems and in the interpretation of the role of mechanical and rheological cell properties in disease pathologies.

The current study presents, to the best of our knowledge, the first experimental validation of a new 3D simulation method based on dissipative particle dynamics (DPD)—a coarse-grained molecular dynamics approach. The experiments are specifically designed to test the DPD model under rather extreme conditions with the smallest cross-section of the microfluidic channel being 2.7 × 3 μm. The validated model is then used to quantify the large deformations of RBCs flowing through these very small microchannels at various pressure differences and for room to physiologically relevant temperature values.

Numerical Methods

The RBC membrane comprises a lipid bilayer and an attached cytoskeleton, which consists primarily of spectrin proteins arranged in a network and linked by short actin filaments at junction complexes. There are about 25,000 junction complexes per healthy human RBC. The RBC membrane model based on the properties of the spectrin network was developed in Boey et al.⁴; recent refinements have also been presented in Fedosov et al.⁹ In this model, the RBC membrane is approximated by a collection of points connected by links. Each point directly corresponds to the junction complex in the RBC membrane and each link represents spectrin proteins between junction complexes. The coarse-graining procedure which allows us to reduce the number of points to represent the RBC was developed in Pivkin and Karniadakis.²¹ The resulting coarse-grained RBC model [shown for N = 500 points in Supplemental Material (online)] was successfully validated against experimental data of the mechanical response of an individual cell.²¹ The model takes into account bending and in-plane shear energy, viscous effects of the membrane, and constraints of total area and volume. Specific details of the modeling approach are provided in the Supplemental Material.

The surrounding external fluid and RBC internal fluid (hemoglobin) are modeled using DPD.¹¹ The DPD particles interact with each other through three soft pairwise forces: conservative, dissipative, and random forces. Dissipative and random forces form a DPD thermostat and their magnitudes are related through the fluctuation–dissipation theorem. The functional form of these forces can be varied to alter the viscosity of the DPD fluid. This approach is used to make the internal RBC fluid more viscous compared to the external fluid. Specifically, the internal fluid is 9, 8.5, and 7.6 times more viscous than the external fluid in simulations corresponding to temperature of 25, 37, and 41 °C, respectively.^12,22 The effect of temperature in the experiment on the viscosity of the suspending medium is modeled by changing the viscosity of the DPD fluid surrounding the RBC. Specifically, the viscosity of the external fluid at 37 and 41 °C is decreased by 22 and 28% compared to the viscosity at 25 °C, while the membrane viscosity is decreased by 50 and 63.5%, respectively, to match the experimentally measured RBC relaxation times at these temperatures. Regarding the experimental measurements, we obtained relaxation times at temperatures 25 and 37 °C using an optical trapping technique previously described in Mills et al.¹⁷ The relaxation time at 41 °C was taken as an extrapolation of this data.

In the simulations, each point in the RBC membrane becomes a DPD particle. When the model is immersed into the DPD fluid, each particle experiences membrane elastic and viscous forces in addition to the DPD forces from the internal and external fluid particles. Bounce-back reflection is employed at the membrane surface to ensure no-slip condition and to make the membrane impermeable to internal and external fluids. The channel walls are modeled by freezing DPD particles in combination with bounce-back reflection, similar to Ref. 21. Periodic inlet/outlet boundary conditions are employed. The flow is sustained by applying an external body force.

Experimental Methods

Cell Solution and Buffer Preparation

Whole blood from healthy donors was obtained from an outside supplier (Research Blood Components, Brighton, MA). Blood was collected in plastic tubing with an ACD preservative added during collection. Upon reception, blood was stored at 4 °C. All experiments were performed within 12 h of acquiring blood samples.

The primary buffer used in all cell solution preparations and experiments was RPMI 1640 with 1 wt% of bovine serum albumin (BSA) (pH 7.4). 100 μL of whole blood is suspended in 1 mL of this buffer and centrifuged three times at 1000 rpm. After the final centrifugation, red cells are suspended in 10 mL of BSA/RPMI buffer, resulting in a final hematocrit of approximately 0.4–0.5%. Finally, immediately prior to introduction into the microfluidic channels, 20–30 μL (5 wt%) of 1 μm polystyrene beads (Polysciences Inc., Warrington, PA) were added to the cell solution. If necessary, fresh cell/bead solutions were periodically introduced over the course of a flow experiment. For all cell solutions, not more than 2 h elapsed from the time of its final centrifugation to the time of its flow characterization.

Microfluidic Channel Fabrication and Experimental Procedures

PDMS-based microfluidic channels were fabricated using soft lithography. The master mold is made from SU8 resist using a two mask, two layer process. The first layer defined the region of primary interest in the flow characterization experiments (described below) and the second layer was used to define longer reservoirs for input/output ports and easier interfacing with buffer and cell solutions.

The channel structures and pressure-control system used in this work are illustrated in Fig. 1. At their narrowest point, channels were 30 μm long, 2.7 μm high and had widths ranging from 3 to 6 μm. A sharply converging/diverging structure was used to ensure that it was possible to observe nearly the entire traversal process (channel entrance deformation, channel flow, and channel exit behavior/shape recovery) with the microscope objectives used, typically 20×–50×. In this way, the use of a single channel structure ensured that the hydrodynamics of the experiment was well-controlled and more easily understood. In addition, this approach reduced the physical domain of the experiment so as to allow for a small modeling domain and decrease the computational time required in the evaluation of our modeling approach.

FIGURE 1.

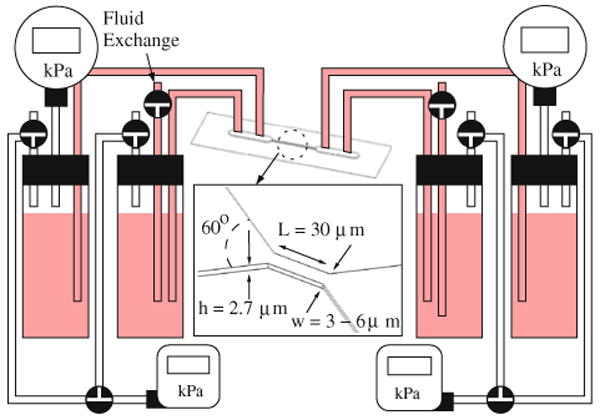
Schematic view of pressure-control flow system and channels used in flow experiments. A combination of pneumatic regulators and relative height adjustments are used to set the desired pressure difference.

In the pressure-control system, a set of dual input and output ports are utilized in order to allow for periodic exchanges of buffer and priming solutions as well as fresh cell solutions. The applied pressure difference was achieved using a combination of pressurized reservoirs and hydrostatic pressure adjustments. The pressure regulators (Proportion Air Inc., McCordsville, IN) utilized a computer-controlled high-resolution solenoid valve and had a range of 0–207 kPa with an applied pressure resolution of approximately 69 Pa (0.01 psi). These regulators exhibited the best response and linearity at pressure levels above 20.7 kPa. Therefore, this was the minimum pressure level applied at the entrance and exit reservoirs. Applied pressure differences were first set by increasing the regulator pressure above this minimum level. Additional hydrostatic pressure adjustments were made by adjusting the relative heights of the pressure columns using a micrometer stage, giving an applied pressure difference resolution of approximately 1 mmH₂O (0.001 psi or 9.8 Pa). A secondary set of pressure gages was used to check the applied pressure difference at the fluid reservoirs in order to ensure there were no significant leaks in the pressure lines leading up to the fluid reservoirs.

Experiments at 37 and 41 °C were carried out using a water bath system in which the channel was bonded into an aluminum dish using a PDMS seal or a parafilm gasket. Pre-heated water was then added to the reservoir to bring the system to the desired temperature. This temperature was maintained by a temperature control system using a flexible heater to radially heat the water bath, a T-type thermocouple temperature probe, and a proportional-integral-derivative (PID) temperature controller (Omega Inc., Stamford, CT). The temperature at the coverslip surface was monitored throughout the experiments using a T-type thermocouple. The use of such a water-bath system ensured that the entire device, including the input and output tubing containing the cells under examination, was maintained at the same temperature. In addition, the high thermal mass of the water-bath system ensured temperature stability for the duration of a typical experiment (1–4 h).

During a typical experiment, the channel system was first primed with a 1 wt% solution of Pluronic F-108 surfactant (Sigma Inc., St. Louis, MO), suspended in PBS (1×). The enhanced wetting properties of the Pluronic solution allows for easy filling of the channel and purging of air bubbles. After the channel is filled, the Pluronic is allowed to incubate for a minimum of 20 min in order to block the PDMS and glass surfaces from further hydrophobic and other non-specific adhesive interactions with the red cell membrane. After this incubation time, the system is flushed with a 1 wt% BSA/RPMI buffer solution. The excess buffer is then removed from the entrance reservoir and the cell solution is added and introduced to the channel reservoir area. After an initial flow of cells across the channel is observed [typically by applying a pressure difference of approximately 0.7 kPa (0.1 psi)], the applied pressure difference is set to zero by first equilibrating the applied pressure from the pressure regulators and then stagnating the flow in the channel by trapping a bead in the center of the channel via relative height (i.e., hydrostatic pressure) adjustments. After this process, pressure differences are typically set using the electronically controlled pressure regulators. However, due to hydrodynamic losses, this applied up-stream and down-stream pressure difference does not correspond to the local pressure difference across the channel. In order to determine this local pressure difference, bead trajectories and velocities are measured using our high speed imaging capabilities and an image processing routine. These measured velocities are used to determine the local pressure difference using a combination of computational fluid dynamics simulations and well-known analytical solutions for flow in rectangular ducts. The details of this procedure are provided in the Supplemental Material.

Flow experiments were performed on a Zeiss Axiovert 200 inverted microscope (Carl Zeiss Inc., Thornwood, NY) using a halogen source and either a 20× or 40× objective. A dry objective (e.g., not an oil or water-immersion objective) was used in order to ensure that the cover slip was sufficiently thermally isolated for experiments at elevated temperatures. Images were recorded on a PCO.1200hs high speed, CMOS camera, operated at typical frame rates of 1000–2000 fps (Cooke Corp., Romulus, MI).

Results

We use high-speed imaging to measure and quantify the temperature-dependent flow characteristics (pressure vs. velocity relationships) and shape transitions of RBCs as they traverse microfluidic channels of varying characteristic size. These results are compared to simulated flow behavior using DPD. An important feature of our modeling approach compared to any other mesoscopic approaches is that the interaction parameters governing the elastic behavior of the RBC membrane are derived from the properties of the individual components of the RBC cytoskeleton. Therefore, the model is capable of capturing the elastic behavior of the RBC without the need for additional fitting parameters. The viscous parameters are defined using additional independent experimental measurements. As a result, the RBC model accurately matches the behavior measured in three different experiments at both room and physiological temperatures:

1. The force–displacement response as measured with optical tweezers²¹;

2. The magnitude of resting membrane thermal fluctuations²⁰; and

3. The characteristic time scale of membrane relaxation following stretching.¹⁷

The membrane and fluid parameters determined from this diverse combination of experiments are applied for all subsequent modeling conditions and are complemented with the results of a single data point from our RBC flow experiments in order to translate non-dimensional DPD simulation results to physical units. More details of the modeling scheme, flow control system, channel geometry, as well as our procedure for determining local pressure gradients across the microfluidic channel are described in the Supplemental Material.

Severe RBC Deformation

Figure 2 shows shape profiles of the RBC as it traverses channels that are 2.7 μm high, 30 μm long and 3–6 μm wide, geometries typical of some of the large deformation conditions in the microvasculature. Figure 2a shows a qualitative comparison of experiment with our DPD model for RBC traversal across a 4 μm wide channel. Three time scales can be identified:

FIGURE 2.

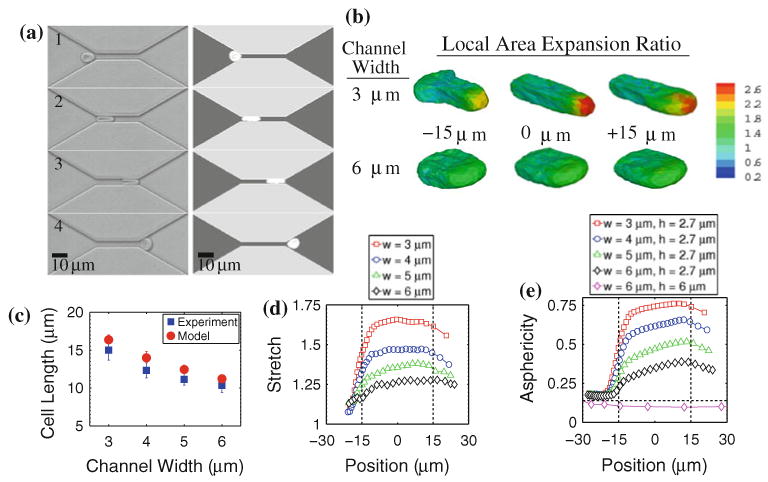
Shape characteristics of RBC traversal across microfluidic channels: (a) experimental (left) and simulated (right) images of erythrocyte traversal across a 4 μm wide, 30 μm long, 2.7 μm high channel at 22 °C and an applied pressure difference of 0.085 kPa; (b) local area expansion contours for an RBC traversing a 3 μm and 6 μm wide (h = 2.7 μm) channel under ΔP = 0.085 kPa; (c) measured and simulated cell lengths at the center of the microfluidic channel for varying channel widths; (d) estimated maximum stretch ratios of RBC spectrin network (simulation results); and (e) asphericity index as the cell passes through different channel widths under ΔP = 0.085 kPa (simulation results). In (d) all channel heights are 2.7 μm. In (e), channel height and width dimensions are indicated. Vertical dashed lines in (d) and (e) indicate locations of channel entrance and exit. Horizontal dashed line in (e) indicates the stress-free, resting asphericity of a normal RBC (α = 0.15).

• (Frames 1–2) the time required for the cell to go from its undeformed state to being completely deformed in the channel;

• (Frames 2–3) the time it takes the cell to traverse the channel length, and

• (Frames 3–4) the time for complete egress from the channel.

Here, the cell undergoes a severe shape transition from its normal biconcave shape to an ellipsoidal shape with a longitudinal axis up to 200% of the average undeformed diameter. Figure 2c illustrates how the longitudinal axis of the cell, measured at the center of the channel, changes with different channel widths. Experimental and simulated longitudinal axes typically differ not more than 10–15%. During such large deformation, the RBC membrane surface area and volume are assumed to be constant in our DPD model. However, the model allows for local area changes during passage through the channel. The contours presented in Fig. 2b show the evolution of such local gradients in area expansion. These results indicate that, for the smallest length scales, the leading edge of the cell deforms significantly as the cell enters the constriction and deforms further as the cell traverses the channel. As expected, little area expansion is seen during flow through the 2.7 μm high × 6 μm wide channel. The local stretch of the underlying spectrin network scales with the square root of local area expansion. Therefore, this information may be used to estimate the maximum stretch of the spectrin network at any point during this traversal process. This result is shown in Fig. 2d for the channel widths used in the experiments. For the smallest width channels, the maximum stretch increases to λ ≥ 1.6.

In Fig. 2e, we compare these shape characteristics to the results of other meso-scale modeling approaches, such as the multiparticle collision dynamics (MPC) models presented by McWhirter et al.¹⁵ Here, the deviation of the RBC shape from that of a sphere is quantified by its average asphericity 〈α〉, where 〈α〉 = 0 for a sphere and 〈α〉 = 0.15 for an undeformed discocyte. In larger vessels, the asphericity approaches 0.05 as the cell assumes its well-known parachute-like shape.¹⁵ Our DPD scheme, when used to model flow in larger vessels, indicates a similar trend as shown in Fig. 2e. However, in the narrowly constricted channels, the average asphericity increases significantly greater than previously known. Thus, our computational model is capable of capturing a range of shape deviations in large and small vessels, which correlate well with experimental measurements for the smallest length scales.

Pressure–Velocity Relationship

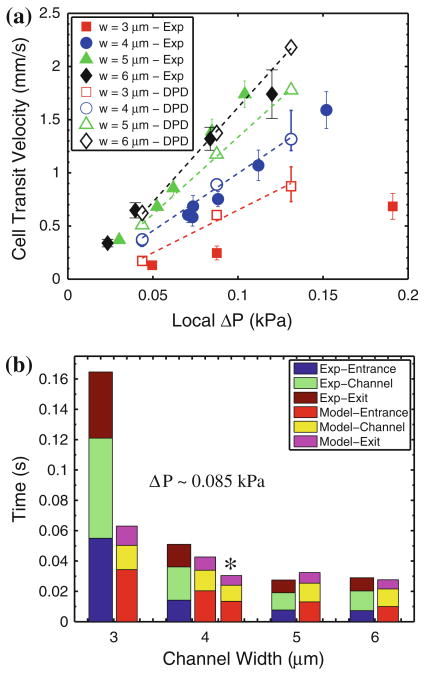
Figure 3a shows pressure–velocity relationships for RBC flow across channels of different cross-sectional dimensions. Local average pressure differences are inferred from the velocity of neutrally buoyant beads, which are mixed with our RBC suspensions. The experimentally measured average bead velocities are translated to pressure differences using known analytical solutions for flow in rectangular ducts as well as the results of a computational fluid dynamics study. (Complete details of these steps are provided in the Supplemental Material.) Average cell velocity measurements are taken between the point just prior to the channel entrance (the first frame in Fig. 2a) and the point at which the cell exits the channel (the final frame in Fig. 2a). As such, the time scale examined in these studies is a combination of entrance times, traversal, and exit times. These individual time scales are plotted in Fig. 3b.

FIGURE 3.

Quantitative flow behaviors of RBC traversal of microfluidic channels. (a) Comparison of DPD simulation results (open markers) with experimentally measured mean velocities (filled markers) of RBC traversal as a function of measured local pressure differences for 3, 4, 5, and 6 μm channel widths (height = 2.7 μm, length = 30 μm). Error bars on experimental data points represent an average ± 1 SD of a minimum of 18 cells. Error bars on modeling data points indicate minimum and maximum variations resulting from a case study exploring the sensitivity of the RBC traversal to channel geometry and cell volume. (b) Experimentally measured and modeled total transit time broken into entrance, channel and exit components for RBC traversal across varying channel widths under ΔP = 0.085 kPa. (*) Modeling results with longer reservoir domain size to examine the role of fluid inertia and periodic boundary conditions.

The DPD model adequately captures the scaling of flow velocity with average pressure difference for 4–6 μm wide channels. The significant overlap in the experimental data for 5–6 μm wide channels can be attributed largely to variations in cell size and small variations in channel geometry introduced during their microfabrication. The relative effects of these variations are the subject of a sensitivity study we present at the end of this section; the variations are illustrated here as error bars on DPD simulation results for select cases. For the smallest channel width of 3 μm, the experimentally measured velocities are as much as half that predicted by the model. This may be attributed to several factors, including non-specific adhesive interactions between the cell membrane and the channel wall due to increased contact. Furthermore, this 3 × 2.7 μm (8.1 μm²) cross-section approaches the theoretical 2.8 μm diameter (6.16 μm²) limit for RBC transit of axisymmetric pores.⁵ Therefore, very small variations in channel height (due, for example, to channel swelling/shrinking due to small variations in temperature and humidity) can have significant effects. Thus, this geometry may be taken as a practical limit of the current modeling scheme for the chosen level of discretization (500 “coarse-grained” nodes, see Pivkin and Karniadakis²¹). In addition, while the total traversal time scales are in close agreement, the data presented in Fig. 3b indicates that the DPD model typically over-predicts the relative amount of time the cell requires to enter the channel constriction. This can be attributed in part to the use of periodic inlet/outlet boundary conditions, which do not allow for an accurate characterization of the incoming fluid momentum. This is clear when examining the sensitivity of the simulated time scales to the size of the modeling domain. Doubling the length of the wide part of the channel (results noted in Fig. 3b) effectively increases the momentum of the fluid and cell as the cell enters the channel, leading to a decrease of the characteristic entrance time but having little effect on the transit and exit times. It is also possible that there is a physical basis for this discrepancy between relative contributions of the cell entrance time. For example, at such high rates of deformation (up to 200% overall stretch in approximately 0.2 s), the RBC might undergo an active reorganization of its spectrin network. Any such molecular reorganization is not accounted for in our model, but could be introduced in future studies.

Temperature Effects

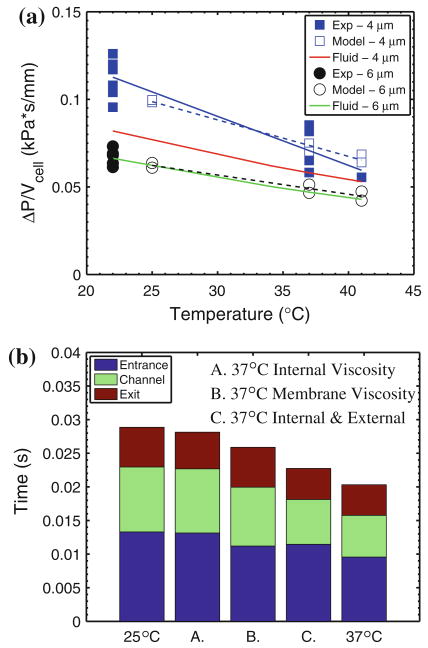
The effect of temperature on the flow dynamics of the RBC is shown in Fig. 4a. Here, we examine the ratio of the local pressure gradient and average cell velocity (ΔP/V) vs. temperature for two different channel geometries. We also present the pressure–velocity ratio for a fluid with the properties of the surrounding media as a function of temperature for each of the respective channel geometries. For a given channel geometry, ΔP/V scales with the effective viscosity of the medium (external fluid, cell membrane, and internal fluid) and the membrane stiffness. Over this temperature range (22–41 °C), quasi-static experiments reveal essentially no effect of temperature on the stiffness of healthy RBCs.^16,28 Here, the observed temperature dependence is ascribed to changes in viscosity. Specifically, a reduced flow resistance (i.e., increased average cell velocities) results from an increase in temperature and a corresponding reduction of the effective viscosity of the medium (the combination of external fluid, internal fluid, and membrane).

FIGURE 4.

Temperature-dependent RBC flow behaviors. (a) Comparison of DPD simulation results with experimentally measured effects of temperature on ratio of local pressure difference and mean velocity of erythrocyte traversal in a 4 and 6 μm wide (h = 2.7 μm, L = 30 μm) microfluidic channel. Solid data points represent an average of a minimum of 18 cells (all p <0.05 in experimental data); hollow data points represent simulation results from center (lower) and off-center (upper) initial positions of the red blood cells in the large channel. (b) Independent effects of external fluid viscosity, membrane viscosity, and internal fluid viscosity on the modeled flow characteristics of RBCs in 4 μm channels subjected to a pressure difference of 0.14 kPa. For cases, A, B, and C the viscosity of the specified components corresponds to 37°, whereas the viscosity of the rest of the components corresponds to 25°.

Our optical trapping measurements have shown that the RBC membrane viscosity at 37 °C is 50% of its value at room temperature. Similarly, the viscosities of the suspending media and internal cytosol decrease by 22 and 27%, respectively.¹² However, the relative influences of the internal fluid, external fluid, and membrane appear to be different for flow across 4 μm and 6 μm channels. In the case of RBC flow across 6 μm wide channels, the effective viscosity is nearly equivalent to the surrounding fluid viscosity. However, RBCs flowing across 4 μm wide channels exhibit a markedly larger apparent viscosity, ranging from approximately twice that of the external fluid at room temperature down to 1.3 times at febrile temperatures. Thus, there appears to be a threshold cross-section below which, the RBC rheology begins to play a significant role in its dynamic flow behavior; however, this effect is not as profound at higher temperatures. The energy dissipation in the membrane is typically higher than in the internal fluid, and hence one might expect its influence on the flow behavior of the RBC across such small cross-sections to be relatively larger than the internal viscosity.⁸ Figure 4b shows the results of a series of simulations designed to determine the relative contributions of the RBC membrane viscosity and its internal and external fluid viscosities for flow across a 4 μm wide channel. It can be seen that, for this 4 μm wide channel, all viscous components affect the RBC transition behavior and that the external fluid and membrane viscosities play an equally significant role.

DPD Sensitivity Study

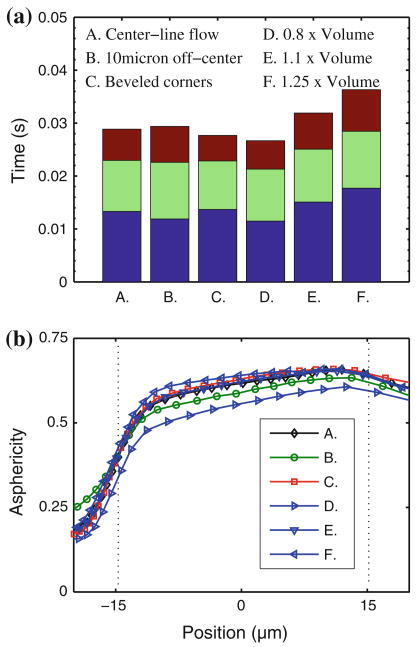
We have performed a series of sensitivity studies taking into account the effects of irregular cross-sectional geometries, RBC initial position, and variations in cell size on flow behavior. The results of these studies are presented in Fig. 5. For a fixed cross-sectional area, the traversal behavior of the RBC does not vary significantly. Similarly, the transit time is relatively insensitive to RBC initial position that is as much as 10 μm away from the centerline of the channel. However, the asphericity index changes, presumably due to the different shape of the RBC at the entrance of the channel, see also Danker et al.⁷ The model predicts a clear dependence of RBC flow on the volume of the cell. Cells with volumes ranging from 80 μm³ (0.8× typical cell volumes) and 125 μm³ (1.25× typical cell volumes) may be approximately 50% different in observed flow behavior, such as transit times or velocities; also, the asphericity index varies with the RBC volume as expected. These bounds on cell volume are given by Canham and Burton⁵ and represent the extents of the error bars presented on modeling data in Fig. 3a.

FIGURE 5.

Case studies using the DPD model to evaluate the sensitivity of RBC flow in a 4 μm wide × 2.7 μm high channel subjected to a pressure difference of 0.14 kPa with respect to variations in initial RBC position (B: off-centerline initial position), channel geometry (C: non-rectangular, beveled corner cross-section with the same cross-sectional area), and cell volume (D, E, F: 0.8, 1.1, and 1.25 times the standard cell volume of 100 μm³, respectively). (a) Comparison of entrance, channel, and exit times. Color legend as in Fig. 4b. (b) Asphericity index as a function of cell position. Vertical dashed lines indicate locations of channel entrance and exit.

Discussion and Summary

In this work, we have presented a combined experimental–computational framework for the quantitative analysis of the flow dynamics of human RBCs in a microfluidic system mimicking smallest dimensions in the microvasculature. In this framework, we employed a 3D computational model using DPD that accurately reproduces the behavior observed in three different independent sets of experiments: force–displacement measurements using optical tweezers, membrane relaxation measurements, and membrane thermal fluctuation measurements. The use of this model to simulate the flow behavior of RBCs in microvasculature is validated using experimental measurements of the flow characteristics of individual RBCs in an in vitro system at room and physiologically relevant temperatures. The validated model provides accurate simulations of the RBC shape transitions. In addition, the model is capable of identifying areas of high non-uniform levels of stretch in the spectrin network during RBC passage through small channels. This information might be used to establish a criterion for hemolysis, which is an important consideration for the design of in vitro diagnostic and blood separation systems as well as heart valves and stents.

Some additional features of the experimental results and modeling predictions should be highlighted. First, the velocities in Fig. 3a compare well to experimental measurements made across 5 μm and 6 μm axisymmetric pores by Frank and Hochmuth¹⁰ as well as aggregate measurements made by Sutton et al.²⁷ in a microfluidic device where control of flow pressure was less robust than in the present case. Also, as in these and other in vitro experiments, the flow resistance in our experiments is significantly smaller than those measured in vivo at smaller characteristic diameters, which would typically result in significantly larger flow resistance.²⁹ This is most likely due to the lack of a glycocalyx layer in these in vitro experiments, which has been hypothesized to increase the flow resistance of the microcirculation in vivo by as much as 10 times that of in vitro experiments of comparable length scales.²⁹

Our simulation and experimental results can also be compared to the predictions²⁴ from an axisymmetric analysis of RBC passage through micropores. Here, pressure differences of 0.1 kPa across 10 μm long pores with diameters ranging from 3.6 μm to 6 μm result in average traversal velocities from approximately 0.2–2 mm/s. These velocities are of the same approximate magnitude as those presented here. However, when the analysis in Secomb and Hsu²⁴ of 5 μm and 6 μm tube traversals are compared to the experimental results of Frank and Hochmuth, it consistently over-predicts the traversal velocities by up to a factor of four. This may be due to increased dissipation of the membrane and fluid due to slight asymmetries of the cell and tube that are not captured using an axisymmetric continuum assumption. However, the use of a fully three-dimensional, discrete approach as in DPD is capable of capturing such asymmetries and giving more robust predictions of RBC flow dynamics at such small length scales.

An interesting finding of the present study is that there exists a cross-sectional area threshold above which the passage of individual RBCs is largely dictated by the properties of the external fluid. However, below this area threshold, the effective viscosity of the RBC and surrounding media is approximately doubled. At physiologically relevant temperatures (37 and 41 °C), this effect is less profound with an effective viscosity increase around 30%. This result suggests a strong temperature-dependence of RBC dynamics that is not captured in traditional quasistatic membrane property measurements of healthy RBCs. This temperature-dependence was further investigated to evaluate the role of individual system components (external fluid, internal fluid, and RBC membrane) in influencing flow dynamics. Results revealed that the RBC membrane viscosity begins to play an equally important role over the effective RBC flow behavior compared to that of the external fluid below a threshold channel cross-sectional area.