Summary
The FNR protein in Escherichia coli is an O2 sensor that modifies global gene expression to adapt the cell to anaerobic growth. Regulation of FNR involves continuous cycling of the protein between its active and inactive states under aerobic conditions without apparent function. This raises the question of what benefit to the overall life cycle might compensate for the cost of cycling and reveals that the role of this process is poorly understood. To address this problem, we introduce the concept of a “system design space”, which provides a rigorous definition of phenotype at the molecular level and a means of visualizing the phenotypic repertoire of the system. Our analysis reveals undesirable and desirable phenotypes with an optimal constellation of parameter values for the system. To facilitate a more concrete understanding of what the design space represents, we analyze mutations that alter the apparent dimerization rate constant of FNR. We show that our estimated wild-type value of this rate constant, which is difficult to measure in situ, is located within this constellation and that the behavior of the system is compromised in mutants if the value of the apparent dimerization rate constant lies beyond the bounds of this optimal constellation.
Keywords: FNR, oxygen sensing, genetic regulation, biochemical systems theory, design principles
Introduction
The balance between aerobic and anaerobic metabolism in Escherichia coli factors significantly into the growth rate and viability of the organism. FNR is one of the global regulators responsible for sensing the environment and maintaining the appropriate growth state. FNR takes its name from mutant strains deficient in fumarate and nitrate reduction (Lambden & Guest, 1976), and its role in E. coli is to sense O2 directly. FNR activity determines whether the cell will maintain an anaerobic or aerobic metabolism. The regulation of this global transcription factor involves a cyclic network of interactions at the post-transcriptional level and autorepression at the transcriptional level [for review see (Green et al., 2009)].
The FNR protein is present under aerobic and anaerobic conditions in similar and sufficient quantities to regulate its downstream targets (Grainger et al., 2007, Sutton et al., 2004a, Unden & Duchene, 1987). FNR dimerizes in the absence of O2, and dimeric FNR is the active DNA-binding form of the regulator (Lazazzera et al., 1996, Moore & Kiley, 2001). Active FNR regulates hundreds of genes leading to the adaptation of E. coli for anaerobic growth and controls one of the best-studied gene regulatory networks in the cell (Kang et al., 2005, Salmon et al., 2003, Grainger et al., 2007). When O2 is abundant, dimeric FNR is destabilized by O2, which converts active FNR into an inactive monomer, and the cell defaults to aerobic growth (Lazazzera et al., 1996, Khoroshilova et al., 1997).
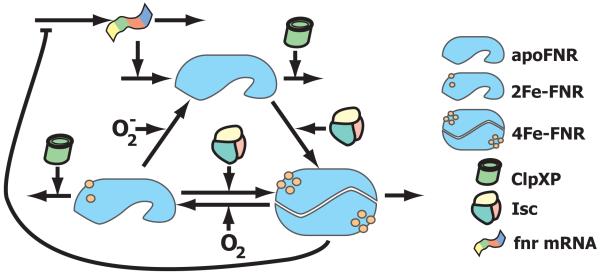
The ability of FNR to dimerize is controlled by an O2 labile Fe-S cluster. The incorporation of Fe-S into the FNR protein is mediated by Isc, and incorporation does not appear to be influenced by O2 (Mettert et al., 2008). The protein exists in three states: dimeric 4Fe-FNR contains one [4Fe-4S]+2 cluster per monomer, monomeric 2Fe-FNR contains a single [2Fe-2S]+2cluster, apoFNR contains no Fe-S cluster (Sutton et al., 2004a, Sutton et al., 2004b, Lazazzera et al., 1996, Moore & Kiley, 2001, Khoroshilova et al., 1997, Crack et al., 2008). The active dimer represses transcription of fnr mRNA, but the strength of this interaction is moderate (Mettert & Kiley, 2007). Decay of monomeric FNR is assisted by the protease ClpXP (Mettert & Kiley, 2005). Dimeric active FNR is protected from ClpXP-mediated degradation and is not subject to any active decay process (Mettert & Kiley, 2005). Therefore, the concentration of dimeric FNR is reduced either by destabilization due to O2 or increased cell volume (i.e. cell growth). Fig. 1 summarizes the essential features of the FNR regulatory network.
Figure 1.
A representation of the FNR (fumarate nitrate reduction) system in E. coli. FNR regulates the transition between aerobic/anaerobic growth. The monomer forms combine to produce the dimeric 4Fe-FNR, an active transcription factor that regulates the adaptation of the cell to O2 limiting conditions. Aerobically, O2 inactivates FNR, but the cell continues to produce and reactivate it. This results in a constant cycling of FNR between its three states apoFNR, 4Fe-FNR, and 2Fe-FNR. Aerobic cycling is tuned so that the inactive apoFNR predominates. Under anaerobic conditions, the absence of O2 results in a rapid buildup of 4Fe-FNR. The 4Fe-FNR form dimerizes to produce an active transcription factor.
Our previous work produced a robust model of the FNR network that integrated existing experimental data into a cohesive system, made predictions of additional mutant behavior that were validated by experimental data, predicted the dynamics of the aerobic-to-anaerobic transition, and provided estimates of active FNR in vivo (Tolla & Savageau, 2010). Although the model and experimental data are consistent, any system as complex as the FNR regulatory circuit has only been examined in the laboratory by sampling a very small number of alternative combinations of alleles and environmental conditions. In nature the system is exposed to an enormous amount of environmental and genetic variation. In the study presented here, we provide an approach to examine a large sampling of these combinations. Our aim is to identify and characterize the qualitatively-distinct phenotypes of our model for the FNR regulatory circuit.
This analysis allows us to address several probing questions about the FNR system. Experimental work generally provides qualitative information; by combing the available information into a model can we extract out any quantitative information? While it is well-known that FNR is inactive under aerobic conditions, what degree of inactivity (e.g. 90%, 60%) is required for proper regulation of its downstream targets? Even with a model in hand, what combinations of parameters represent normal physiological function? Can we describe how extreme a particular mutant is, and quantify its distance from wild-type behavior? Instead of the extremes of aerobic and anaerobic behavior, what can be said about the behavior of the system in the microaerobic environment? What range of concentrations of O2 correspond to this environment, and how might this range change when other aspects of the FNR system are altered? These are questions that can only be addressed by an integrated quantitative approach, which is the focus of this paper. We first review the existing model of the FNR system and introduce a minor modification to better reflect the transition between aerobic and anaerobic growth. Second, we develop its “design space” (Savageau et al., 2009), which provides a means of visualizing the relationships among alternative phenotypes of the system. Regions in this design space correspond to qualitatively-distinct phenotypes for the FNR regulatory circuit. Third, we characterize and rank the performance of the system within each of these regions. Finally, we assess the evolutionary pressures responsible for favoring certain phenotypic regions over others.
Results
Our analysis began with the model pictured in Fig. 2 [see Tolla & Savageau (2010) for details]. In this model, the concentrations of the inactive monomeric forms of FNR have been aggregated into a single variable (x2). This was done to simplify the model without significant loss of information, as both apoFNR and 2Fe-FNR are inactive FNR monomers that share similar degradation kinetics (Mettert & Kiley, 2005). Our original description of the network (Tolla & Savageau, 2010) was a piece-wise representation within the power-law formalism (Savageau, 1971a, Savageau, 2009). It included a sharp break-point, represented by the intersection of the pieces corresponding to aerobic and anaerobic conditions. In the work presented here, we include a minor modification in the model by replacing the sharp break-point with a smooth transition produced by a Hill function (Fig. 3). Then, we recast the modified model into the generalized mass-action representation within the power-law formalism (Savageau, 2001). The recast system is an exact representation of the modified model. The details of these mathematical operations are given in the Modeling Procedures section.
Figure 2.
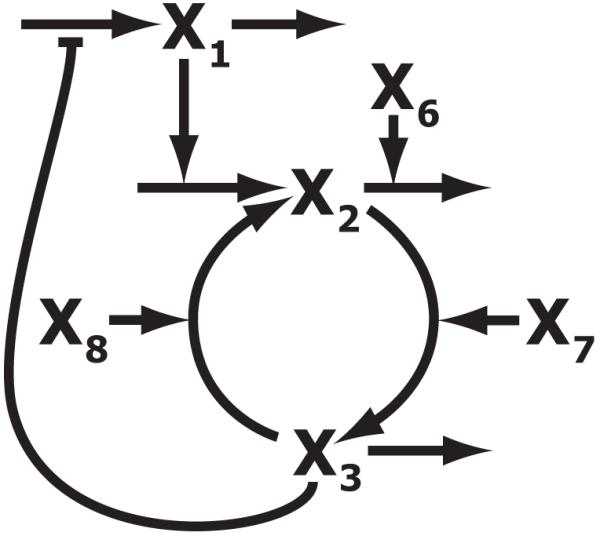
A diagram of the kinetic model for the FNR system. x1 – fnr mRNA, x2 – apoFNR and 2Fe-FNR, x3 – 4Fe-FNR, x6 – ClpXP protease, x7 – iron sulfur cluster assembly proteins (Isc), x8 – molecular O2. The nucleotide and amino acid pools are assumed to be well regulated, and their nearly constant values are implicitly accounted for by the apparent rate constants for transcription and translation (a conventional assumption). The fate of material lost from the system by degradation and/or dilution is not shown. [See Tolla & Savageau (2010) for further details]
Figure 3.
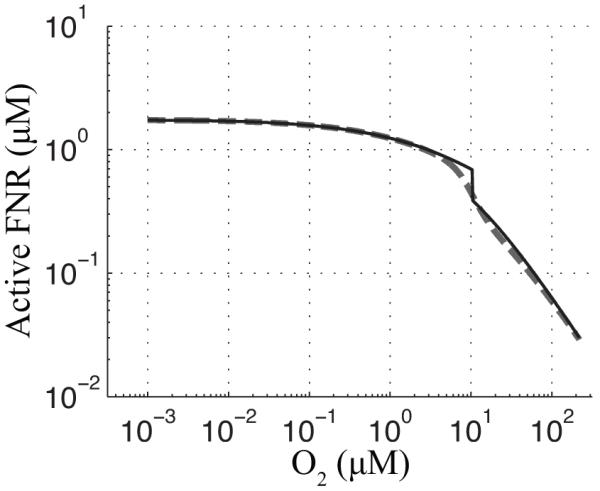
Standard curve for active FNR concentration as a function of O2 saturation. The curve is calculated, both for the original piecewise model (Tolla & Savageau, 2010) (−) [Eqs. (11)-(13)] and the modified Hill model (- -) [Eqs. (1)-(5)], by setting the derivatives to zero and solving for active FNR (x3) over a range of O2 (x8) concentrations.
Construction of Design Space
The design space provides a visual representation for the qualitatively-distinct phenotypes of a system, and has led to insights regarding the phenotypes of other biological systems (Savageau & Fasani, 2009, Coelho et al., 2009). In order to construct the FNR design space, we begin with the equations shown below that correspond to the model pictured in Fig. 2.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Rate constants marked with max or min reflect the fact that this model bridges two distinct environments. There is the aerobic environment, in which O2 is abundant (x8 > K2) and the anaerobic environment in which O2 is limiting or absent (x8 < K2). Maximal rate constants correspond to the aerobic environment in which cells grow faster, and minimal rate constants correspond to the anaerobic environment in which cells grow slower. Equation (1) describes the mRNA pool for which the rate of synthesis proceeds according to a hyperbolic rate law under repression-control mediated by the binding of a single active 4Fe-FNR dimer. The decay kinetics of the fnr mRNA are sensitive to the cellular environment and follow their maximum decay rate under aerobic conditions (x8 > K2) or their minimum decay rate under anaerobic conditions (x8 < K2). Equation (2) describes the combined pool of apoFNR and 2Fe-FNR. The description includes two positive terms -- the rate of apoFNR synthesis and the rate of 4Fe-FNR conversion into 2Fe-FNR -- along with three negative terms -- the rate of apoFNR-2Fe-FNR degradation via ClpXP at the minimal rate, or at its maximal rate, and the apparent dimerization rate of apoFNR-2Fe-FNR into 4Fe-FNR. Equation (3) describes the 4Fe-FNR pool whose rate of change depends on the difference between net influx from the apoFNR-2Fe-FNR pool and net efflux, which is O2-dependent loss back to the apoFNR-2Fe-FNR pool and loss due to dilution resulting from cell growth at either the maximal or minimal rate. Equation (4) results from recasting the hyperbolic rate law in the modified model, and equation (5) results from recasting the Hill function (see Modeling Procedures).
The next step in constructing the design space is based on equations (1)-(5) at steady state. We select one synthetic and one degradative term from each equation, which results in a simplified subsystem of equations. Each term corresponds to a physical process, and at the level of a molecular system, we define a distinct phenotype as a collection of dominant physical processes. To the extent that the model accurately captures the behavior of the real system, the collection of dominant physical processes is a real phenotype. Many factors give rise to the dominance of a particular process, and these factors can be broadly described as either environment changes or changes in the internal structure of the system. If the dominance assumption holds true over a range of parameter values then the subsystem in question represents a valid and distinct phenotypic region, otherwise the conditions for the subsystem are invalid.
For example, suppose we set equations (1)-(5) equal to zero and select the following terms.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
The dominance conditions from Eq. (3) that imply the process of destabilizing dimeric FNR dominates over dilution by growth are given by and . We can solve for the steady state of this subsystem [Eqs. (6)-(10)], which is x1 = α1,max/β1,max , x2 = α1,maxα21/(β1,maxβ21,maxx6), x3 = β22x7/(α22x8)[α1,maxα21/(β1,maxβ21,maxx6)]2 , x4 = K1 , and . By substituting the steady state above into the dominance conditions, we determine which parameter values satisfy the conditions. For the processes selected in equation (8) to dominate the processes described by equation (3), we can conclude that O2 must exceed a specific threshold . Similar conclusions apply for equations (1), (2), (4), and (5). We continue in this fashion of choosing processes and evaluating the conditions under which they dominate until we have exhausted all possible combinations of processes. Further details regarding the construction of the FNR design space are given in the Modeling Procedures section.
The final step in constructing the design space is to choose the variables that we wish to display on its axes. Since the post-transcriptional cycling of FNR is a major aspect of this system in need of further study, we have selected a key variable on each side of the cycle for the axes. The concentration of O2 (x8), which represents a major influence on one arm of the post-transcriptional cycling of FNR, was a logical choice for one of the axes, as this is the environmental variable to which the system responds. The apparent rate constant of dimerization (β22), which represents a major influence on the other side of the cycle (Fig. 2), is a logical choice for the other axis. Using these two variables that affect the two arms of the cycle, we can examine how their variation influences the output of the system as manifested in the activity of 4Fe-FNR.
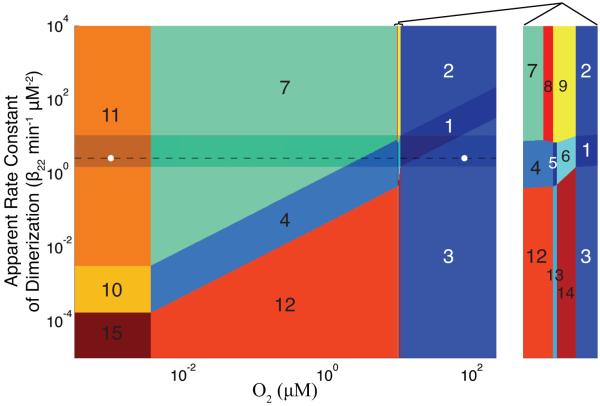
The resulting design space is shown in Fig. 4. We see that of the 144 possible phenotypic regions only 15 of these are valid. In other words, the design space indicated that the FNR cycle is capable of presenting 15 qualitatively-distinct phenotypes. Though some of these phenotypes do correspond to extreme parameter values (e.g. apparent dimerization rate constants three orders of magnitude greater than the wild-type) the design space accounts for the complete list of qualitatively-distinct phenotypes. The dominance conditions for validity of other 129 phenotypic regions cannot be realized when adjusting the FNR cycle.
Figure 4.
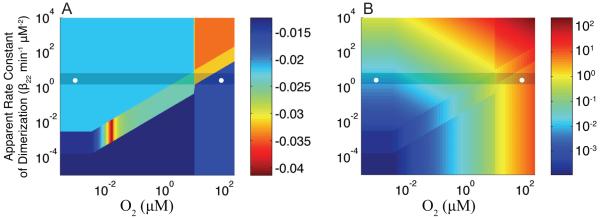
Design space of the FNR regulatory network in E. coli. Regions (1, 2, 3) to the right of the critical O2 threshold (K2 = 10.4 μM) are associated with the aerobic environment, regions (5, 6, 8, 9, 13, 14) lying next to K2 are associated with the microaerobic environment (see the expanded excerpt), and regions (4, 7, 10, 11, 12, 15) in which O2 is very low or absent are associated with the fully anaerobic environment. The range of O2 concentrations (0.001 to 220 μM) does not exceed the maximum dissolved O2 concentration in the wild at 30° C. The nominal aerobic and fully anaerobic locations (○) are shown along with the path (- -) through the spectrum of phenotypes crossed during the transition between the aerobic/anaerobic growth states. The band of optimal performance (shaded area) prevents crossings into areas of poor performance (see text for discussion).
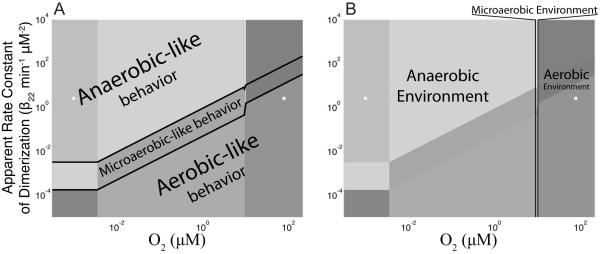
Based on the O2 content of the environment, the design space (Fig. 4) can be separated into three broad environmental categories: aerobic, microaerobic, and anaerobic environments (Fig. 5B). The critical concentration of O2 (K2 = 10.4 μM, see Modeling Procedures) defines a vertical line in the FNR design space separating the aerobic environment (includes regions 1, 2, and 3) from the anaerobic environment (includes regions 4, 7, 10, 11, 12, and 15). The area around the critical threshold of O2 represents the microaerobic environment (includes regions 5, 6, 8, 9, 13, and 14). The separation between these environments is predicted by the boundaries of the design space. Experimental work examining expression of anaerobically induced genes regulated by active FNR agrees with the location of these boundaries (Tseng et al., 1996, Becker et al., 1996) and the active FNR levels as predicted by the model (Tolla & Savageau, 2010).
Figure 5.
Classifying the regions of the FNR design space. (A) Dividing the design space into aerobic-like, microaerobic-like, or anaerobic-like behaviors based on the underlying subsystems (see main text for details), which gives rise to low (aerobic-like regions), medium (microaerobic-like regions), or high (anaerobic-like) levels of the active FNR protein. (B) Dividing the design space into aerobic, microaerobic, or anaerobic environments based on the dissolved O2 content.
Based on the dominant subsystem underlying operation in each region, the design space (Fig. 4) can be separated into three broad behavioral categories: aerobic-like, microaerobic-like, and anaerobic-like behaviors (Fig. 5A). The partitioning of the design space into these behavioral categories depends on the balance between the apparent rate constant of dimerization (β22) and the O2 concentration (x8). Consider for example an extreme case in which the dimerization flux for conversion of inactive FNR into active FNR is many orders of magnitude greater than the O2-dependent flux for dissociation of dimeric FNR. At steady state, the majority of total FNR would be in the active FNR pool and this corresponds to anaerobic-like behavior even if the O2 content of the cell were to reach saturation. The aerobic-like regions (3, 12, 13, 14, and 15) are defined by the following features: the maximal transcription rate (α1,max) dominates the rate of fnr mRNA synthesis, and the active decay process (β21,maxx2x6, β21,minx2x6) dominates the decay of inactive FNR. The anaerobic-like regions (2, 7, 8, 9, and 11) are defined by the following features; repression-mediated control dominates the synthesis of fnr mRNA , and growth-dependent dilution dominates the decay of active FNR . The microaerobic-like regions (1, 4, 5, 6, and 10) have a combination of the aerobic-like and anaerobic-like features. They are defined as those regions that exhibit repression of mRNA synthesis by active FNR (anaerobic-like feature) and active decay as the dominant decay process for inactive FNR (aerobic-like feature).
Transitions between aerobic and anaerobic growth states correspond to movement along the x-axis of the design space. In other words, the range of aerobic-to-anaerobic phenotypes presented by an FNR circuit with a specified apparent rate constant of dimerization (β22) corresponds to a horizontal line in the design space. The dashed line in Fig. 4 indicates the spectrum of phenotypic regions (1, 3, 4, 5, 6, 7, and 11) exhibited by the system with the wild-type set of values for its parameters. If the FNR circuit is to switch its behavior and match the environment such that aerobic-like, anaerobic-like, and microaerobic-like behaviors coincide with the corresponding environments (Fig. 5 A and B) then the apparent rate constant of dimerization must lie above the boundary separating region 10 from region 11 and below the lowermost point of region 2. Operation of the FNR circuit within these boundaries maintains the necessary range of physiological responses to the environment.
Performance Criteria
Before we compare behavior associated with the various regions, we need to articulate a set of performance criteria. These criteria will be used to differentiate a good region from a poor region. These criteria are motivated by the physiological constraints imposed on the FNR system. The following six criteria relate to the local behavior of the system. Local behavior refers to how the system responds to small, sustained changes in the environment or in the internal properties of the circuit.
Criterion 1. The system should be robust to small changes in the rate constants that define the system. Local robustness is quantified by the magnitude of the system’s parameter sensitivities(Savageau, 1971b) [Modeling Procedures].
Several criteria need to be satisfied in order for active FNR to perform effectively as an O2 sensor.
Criterion 2. Under aerobic conditions, active FNR should be responsive to small changes in O2 concentration. The FNR system exhibits a graded response (Tseng et al., 1996, Becker et al., 1996) and cannot switch from complete repression to complete induction without being adapted to the intervening states. The local amplification or attenuation of responses to changes in this input (environmental) variable of the system is quantified by the relevant logarithmic gains (Savageau, 1971a) [Modeling Procedures].
Criterion 3. Under anaerobic conditions the FNR system needs to produce a strong signal promoting anaerobic growth and should not be susceptible to small fluctuations in O2 concentration. This criterion is quantified by the appropriate logarithmic gain.
Criterion 4. In the aerobic state, inactive FNR acts as a reservoir of FNR protein primed for conversion to the active form. Therefore, the aerobic supply of inactive FNR needs to remain well-buffered against small fluctuations in the O2 concentration. This criterion is quantified by the appropriate logarithmic gain.
Criterion 5. The system should have a wide margin of dynamic stability. The margin is quantified by the size of the critical Routh criterion (Savageau, 2009) for local stability [Modeling Procedures].
Criterion 6. The FNR circuit should respond rapidly to local changes in O2 levels. At the molecular level, the environment of a system often undergoes transient fluctuations. In the case of FNR, this could be a small, transient drop in O2 levels. A fast local response time implies that the circuit is better at adjusting for small fluctuations. The local response time is quantified by the magnitude of the eigenvalues for the linearized system in logarithmic space (Savageau, 1998) [Modeling Procedures].
In addition to the criteria for the local behavior of the system, there are three important criteria for the global behavior.
Criterion 7. In order to prevent improper regulation of the downstream targets of active FNR, the concentration of active FNR should be low under aerobic conditions and high under anaerobic conditions.
Criterion 8. The global response time following large changes in O2 concentration should be fast. The global response time of the FNR circuit can be assessed by the determination of two key temporal characteristics: settling time and peak time (Modeling Procedures). Shorter peak and settling times indicate that the system is faster in responding to large changes in O2 tension.
Criterion 9. The system should have large global tolerances; i.e., the system should be tolerant to large changes in the values of parameters that otherwise would convert the wild-type physiological system into a dysfunctional system (Modeling Procedures).
Steady State Analysis
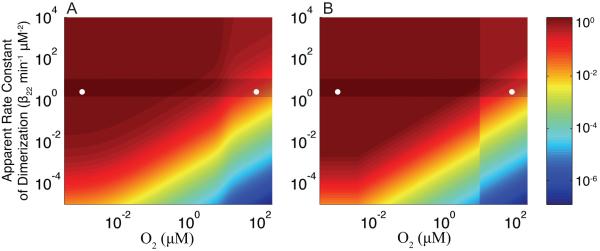
The boundaries of each region are not arbitrary. They arise directly from the system of equations and the dominance conditions responsible for defining the dominant processes. Within each phenotypic region there is a specific subsystem that approximates the behavior of the complete system [Eqs. (1)-(5)]. The goal is not to obtain an exact representation of the complete system. Rather, we wish to enumerate the possible phenotypes with reasonable approximation in order to compare their relative performance. As a check that each regional approximation is reasonable, we can compare the steady-state solutions as computed for the complete system (Fig. 6A) [Eqs. (1)-(5)] with the region-by-region approximate steady-state solutions (Fig. 6B). The results of this comparison make it clear that while not perfect the regional approximations are adequate.
Figure 6.
Comparison of the steady-state solutions (A) computed using the full system [Eqs (1)-(5)] and (B) computed for each phenotypic region. The coloring (z-axis) is the logarithm of the steady-state concentration of active FNR (μM) at each point in the design space, the y-axis is the logarithm of the apparent dimerization rate constant (min−1 μM−2), and the x-axis is the logarithm of the O2 concentration (μM). The shaded area marks the band of optimal performance. The nominal aerobic and anaerobic locations are shown (○).
By comparing the steady-state solution across the three regions in the aerobic environment (1, 2, 3) in Fig. 6B, we uncover an additional prediction of interest. The phenotype associated with region 2 exhibits a high concentration of active FNR regardless of O2 concentration in the environment (violation of Criterion 7). Even at 80 μM dissolved O2, the concentration of active FNR (~1.1 μM) for systems in region 2 is similar to the levels observed for the fully anaerobic system. Avoiding region 2 coincides with avoiding the regions displaying anaerobic-like behavior in an aerobic environment. Therefore, the nominal aerobic values should lie below the line [i.e. for the wild-type set of parameter values] in order to prevent the FNR circuit from operating in region 2.
The steady states alone are not sufficient to discern a difference in performance between the remaining aerobic regions 1 and 3. However, region 3 presents the aerobic-like behavior, whereas region 1 presents microaerobic-like behavior. An additional benefit of operating in region 3 is that it prevents small changes in the apparent dimerization rate constant (β22) from pushing the system into the unregulated phenotype associated with region 2. Thus, it is likely that the wild-type aerobic system is represented in region 3. Characterization of the local and global properties of the phenotypes in each region will (see Local performance, Global performance) identify a robust lower bound on the apparent dimerization rate constant. Our analysis will show that for the FNR system to respond effectively to the spectrum of O2 content in the environment the apparent dimerization rate constant should not drop below the line (= 1.54 min−1 μM−2 for the wild-type set of parameter values).
The physiological constraints on the cell dictate the avoidance of region 2 and maintenance of a sufficient apparent dimerization rate constant that avoids ineffective switching behavior. Thus, there exists a band of optimal operation (Fig. 4 shaded area) as determined by the difference between the maximum and the minimum apparent rate constants of dimerization . These analytical bounds capture the relationship between optimal physiological behavior and the parameters that stand in for the biochemical processes of the FNR system. Based on the boundary conditions, we can predict whether a mutant FNR system will fall outside the band and display pathological behavior. We can additionally formulate a strategy for altering transcription (α1max), translation (α21), or another property of the system to move the boundaries of the band and compensate for a particular mutation. In our previous work (Tolla & Savageau, 2010), which was performed independent of this design space analysis, we fit the parameters of the FNR system using experimental data from the literature. The resulting set of wild-type values for the parameters is consistent with the new results of this study showing that the system is represented within the band of optimal operation (white circles in Fig. 4).
Local Performance
The local performance of the FNR circuit describes the response of the system to small, sustained changes to its structure or environment. Evaluation of the performance criteria characterizes the local response of the system [parameter sensitivities (Criterion 1), logarithmic gains (Criteria 2 – 4), margin of stability (Criterion 5), and local response time (Criterion 6)]. An overview of the parameter sensitivities and logarithmic gains is presented in Table 1. All of the sensitivities are less than one, which indicates that in general small changes in rate constants or other parameters do not produce amplified responses that propagate through the FNR circuit. In each region the sensitivity of active FNR is always greater than that of inactive FNR. This reflects the fact that regulation of active FNR is the function of the FNR circuit. The quantitative values for the sensitivities depend almost entirely on whether a region is categorized as aerobic-like, microaerobic-like, or anaerobic-like. All the aerobic-like regions have mean sensitivities of 0.364 and 0.909 for inactive FNR and active FNR, respectively. All the microaerobic-like regions have mean sensitivities of 0.254 and 0.515 for inactive FNR and active FNR, respectively. All the anaerobic-like regions, with one exception, have mean sensitivities of 0.198 and 0.215 for inactive FNR and active FNR, respectively. These values indicate that both inactive FNR and active FNR are most sensitive to small changes in the parameters when operating in an aerobic-like fashion, less sensitive when operating in a microaerobic-like fashion, and the least sensitive when operating in an anaerobic-like fashion. Thus, the FNR circuit is designed to produce an increasingly robust signal promoting anaerobic growth as the system transitions from an aerobic-like to an anaerobic-like phenotype. The margin of local stability (Criterion 5) is largest in the upper-right corner and smallest in the lower-left corner of the design space (Fig. 7B). Operating points above the optimal band (shaded area Fig. 7B) would have an improved margin of stability, but this would be accompanied by the unregulated phenotype. The logarithmic gains and local response times have a different interpretation in the different environments, as will be discussed below.
Table 1.
Logarithmic gain with respect to O2 and mean parameter sensitivities for all phenotypic regions. Each logarithmic gain represents the percentage change in the steady-state value of the dependent variable, x2 (inactive FNR) or x3 (active FNR), in response to a percentage change in the value of the independent variable x8 (O2). Each parameter sensitivity represents the percentage change in the steady-state value of the dependent variable, x2 (inactive FNR) or x3 (active FNR), in response to a percentage change in the value of one of the parameters that define the system. The mean parameter sensitivity across all the parameters is reported here to show regions in which there is a tendency to amplify/attenuate small changes to the values of the parameters.
| Region | Log Gain of O2 | Mean Sensitivity | ||
|---|---|---|---|---|
| Inactive FNR |
Active FNR |
Inactive FNR |
Active FNR |
|
| 1 | 0.241 | −0.518 | 0.254 | 0.515 |
| 2 | 0.5 | 0 | 0.198 | 0.215 |
| 3 | 0 | −1 | 0.364 | 0.909 |
| 4 | 0.241 | −0.518 | 0.254 | 0.515 |
| 5 | −1.83 | −4.67 | 0.254 | 0.515 |
| 6 | −3.91 | −8.81 | 0.254 | 0.515 |
| 7 | 0.5 | 0 | 0.198 | 0.215 |
| 8 | −0.866 | −2.73 | 0.198 | 0.215 |
| 9 | −2.23 | −5.46 | 0.198 | 0.215 |
| 10 | 0 | 0 | 0.254 | 0.515 |
| 11 | 0 | 0 | 0.182 | 0.215 |
| 12 | 0 | −1 | 0.364 | 0.909 |
| 13 | −4 | −9 | 0.364 | 0.909 |
| 14 | −8 | −17 | 0.364 | 0.909 |
| 15 | 0 | 0 | 0.364 | 0.909 |
Figure 7.
(A) Dominant eigenvalue (z-axis) plotted over the design space. Dark red corresponds to systems whose local dynamics are faster. (B) Margin of stability as determined by the critical Routh criterion (z-axis) plotted over the design space (coloring is log scaled). Eigenvalues (A) and the margin of stability (B) are calculated for each point in the design space using the subsystem in the relevant region.
Phenotypes of regions in the aerobic environment
At a given O2 concentration there are always three possible regions the system can operate in depending on its apparent dimerization rate constant (Fig. 4). The three possible regions always represent, from top to bottom anaerobic-like, microaerobic-like, and aerobic-like behavior (Fig. 5A). For the aerobic environment ([O2]>10.4 μM), we have already observed that of the three potential regions (1, 2, and 3) the wild-type system is represented in the aerobic-like region (region 3). The local response time (Criterion 6) in the aerobic environment becomes faster as the apparent dimerization rate constant (β22) increases (Fig. 7A). Thus, the local response time is the fastest in the anaerobic-like region (region 2), decreases as the system moves down into the microaerobic-like region (region 1) and is the slowest in the aerobic-like region (region 3). However, region 2 is an untenable region of operation under aerobic conditions because in this region active FNR is unregulated.
The logarithmic gains (Table 1) indicate that in region 3 active FNR responds in direct proportion to O2 (Criterion 2), whereas inactive FNR is completely buffered against changes in O2 concentration (Criterion 4), both represent desirable characteristics according to the performance criteria. Conversely, in region 1 (microaerobic-like) active FNR does not respond in direct proportion to O2 (~1/2 less responsive) and inactive FNR is affected by small changes in O2 concentration. Thus, the region 1 phenotype does not respond as effectively as the region 3 phenotype (Criterion 2) and does not provide a well-buffered supply of FNR monomer (Criterion 4). These results indicate that the system should minimize the range of O2 concentrations in which it operates with microaerobic-like behavior. Ideally, the microaerobic-like phenotype would occur just around the boundary that separates the aerobic and anaerobic environments.
Phenotypes of regions in the anaerobic environment
In the extreme case of near zero O2 levels, the FNR circuit can operate in one of three regions (10, 11, or 15). In the extreme anaerobic environment, the local response time (Criterion 6) improves as the apparent dimerization rate constant (β22) increases (Fig. 7A). The logarithmic gains are all zero in regions 10, 11, and 15 (Table 1), which illustrates that in the extremes of the anaerobic environment O2 does not influence the local behavior of the FNR circuit. As noted above, the sensitivity analysis indicates that the anaerobic-like region (region 11) provides the most robust anaerobic growth signal (Criterion 1) and the highest concentration of active FNR (Criterion 7), both represent desirable characteristics according to the performance criteria.
In the anaerobic environments that contain intermediate levels of O2, the FNR circuit can operate in one of three regions (4, 7, or 12). In this span of the anaerobic environment, the local response time (Criterion 6) is fastest in region 4 (Fig. 7A). This corresponds to a microaerobic-like region, and represents the only exception to the rule that local response time improves as the apparent dimerization rate constant (β22) increases. The local response time of the anaerobic-like region (region 7) is better than that of the aerobic-like region (region 12). The aerobic-like region (region 12) also has poor performance with regard to its large parameter sensitivities (Criterion 1), and its directly proportional response to O2 (Criterion 3), neither of these traits are desirable in the anaerobic environment. The microaerobic-like region (region 4) provides an improvement over the aerobic-like region, but its sensitivities, logarithmic gains, and active FNR concentration (Criteria 1,3, and 7) are worse than those of the anaerobic-like region (region 7). These results further reinforce the conclusion that the evolutionary forces responsible for shaping the FNR circuit select for parameters that minimize the range of O2 concentrations in which the system operates with microaerobic-like behavior (Fig. 4).
Phenotypes of regions in the microaerobic environment
The local characteristics of regions in the microaerobic environment follow the same trend observed elsewhere in the design space; the logarithmic gain of active FNR, local response time, and sensitivities increase as the system moves from anaerobic-like, to microaerobic-like, on down to aerobic-like regions, whereas the logarithmic gain of inactive FNR decreases. While it is unclear what constitutes good performance in the microaerobic environment, the local performance (Criteria 1-6) in the aerobic and anaerobic environments will determine where the system should operate. The system is forced to pass through the microaerobic-like regions when transitioning between the aerobic-like regions and the anaerobic-like regions, and we have shown that according to the performance criteria the microaerobic-like regions (1, 4, 5, and 10) do not provide good performance in either the aerobic or anaerobic environment. Thus, if the minimal crossing is optimal then the lower bound on the apparent rate constant of dimerization is given by as mentioned in the initial steady-state analysis (see Steady State Analysis).
Global Performance
Response time
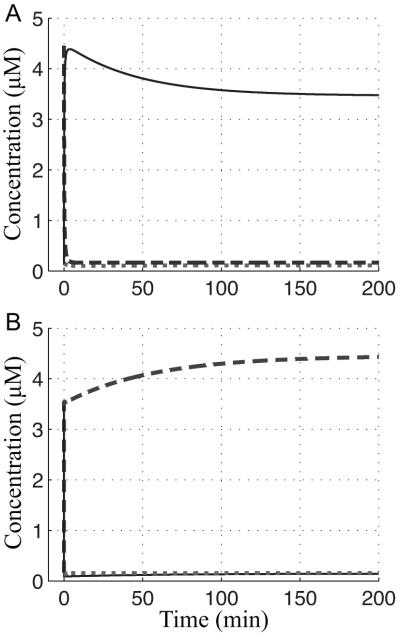
The complement of a system’s local dynamics is its global dynamics, and an environmental sensor is expected to have a rapid dynamic response when the environment undergoes a shift. A typical curve showing the aerobic-to-anaerobic transition and vice versa is shown in Fig. 8. During the aerobic-to-anaerobic transition, active FNR undergoes an initial overshoot (or undershoot in the anaerobic-to-aerobic case) followed by the system settling to a new steady state. Two other studies have made efforts to infer active FNR levels (Sanguinetti et al., 2009, Partridge et al., 2007) and both predicted the existence of an overshoot. The predicted resolution of the overshoot in both these cases was rapid. The mechanistic model predicts a slow resolution of excess 4Fe-FNR consistent with the evidence that cell growth is the primary avenue through which the concentration of active FNR is diluted (Fig. 8A).
Figure 8.
Global response time with the wild-type values of the parameters. In order to compare inactive FNR (- -) to the active FNR dimer (—), the concentration of dimeric active FNR is plotted as twice the concentration of the monomer. The fnr mRNA level (⋯) barely changes during either transition. (A) The aerobic-to-anaerobic transition: The system begins at the initial steady state (x1 = 0.15, x2 = 4.46, x3 = 0.07 μM) with an O2 level of 80 μM and shifts to the final steady state (x1 = 0.11, x2 = 0.17, x3 = 1.73 μM) with a dissolved O2 tension of 0.001 μM. (B) The anaerobic-to-aerobic transition: The system begins at the initial steady state (x1 = 0.11, x2 = 0.17, x3 = 1.73 μM) with an O2 level of 0.001 μM and shifts to the final steady state (x1 = 0.15, x2 = 4.46, x3 = 0.07 μM) with a dissolved O2 tension of 80 μM.
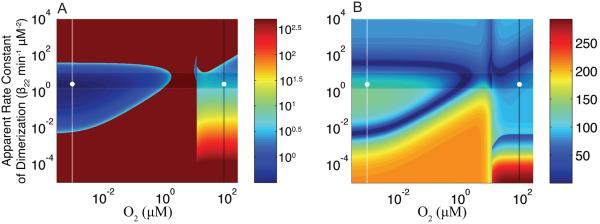
To characterize the global response time of the FNR circuit, we can examine the dynamics of a transition between the aerobic and anaerobic states and assess the peak time as well as the settling time. For this analysis, we select two distinct O2 levels 0.001 μM and 80 μM as representative of anaerobic low-oxygenated and aerobic well-oxygenated environments, but the results of the analysis are not sensitive to this choice of representative values. For any point in the aerobic environment of design space (x8 > K2, Fig. 5B), the O2 level is shifted instantaneously from its initial aerobic value (x8,init) to x8 = 0.001 μM. For any point in the anaerobic or microaerobic environment of design space (x8 < K2, Fig. 5B), the O2 level is shifted instantaneously from its initial anaerobic/microaerobic value (x8,init) to x8 = 80 μM. We associate the peak and settling times with the initial point (x8,init,β22) in the design space and plot their values as the z-coordinate (heat map) in Fig. 9 A and B. Note that not every set of parameters in the design space gives rise to a peak that overshoots (or undershoots) the final steady state (dark red in Fig. 9A).
Figure 9.
Global response times for transitions between aerobic and anaerobic environments. Data points to the right of K2 = 10.4 μM (~1 in log space) represent a system starting at that operating point (various values for O2 concentration and apparent dimerization rate constant) and ending at the nominal anaerobic O2 concentration (white line at which [O2] = 10−3 μM, −3 in log space). These correspond to an aerobic-to-anaerobic transition for a system with a specified apparent rate constant of dimerization and wild-type values for the other parameters of the system. Data points to the left of K2 = 10.4 μM represent a system starting at that operating point (various values for O2 concentration and apparent dimerization rate constant) and ending at the nominal aerobic O2 concentration (black line at which [O2] = 80 μM, ~1.9 in log space). These correspond to an anaerobic-to-aerobic transition for a system with a specified apparent rate constant of dimerization and wild-type values for the other parameters of the system. The global response times are plotted as a color (z-axis) at the operating point of origin in each case. (A) Time at which the concentration of active FNR reaches its peak (aerobic to anaerobic) or trough (anaerobic to aerobic). In the event that no peak/trough occurs for a specific set of values the time assigned is 500 minutes (maximum of the time window). (B) Time at which the concentration of active FNR settles to within ± 5% of its final steady-state value. The shaded area in (A) and (B) marks the band of optimal performance. Note that in (A) coloring corresponds to the logarithm of the peak time, whereas in (B) coloring corresponds directly to the settling time.
The ability of E. coli to transition quickly from aerobic to anaerobic growth depends upon the rapid build up of active FNR. For this reason, the initial response time of the FNR circuit (determined by its peak time or settling time when there is no peak) is critical (Criterion 8). The importance of an initial rapid response, achieved by either a fast peak time or a fast settling time, is illustrated in Fig. 10. There exists the potential for a peak that overshoots the final steady state by a wide margin to dramatically increase the settling time of the system; however, in the FNR circuit the magnitude of the overshoot is modest (Fig 7).
Figure 10.
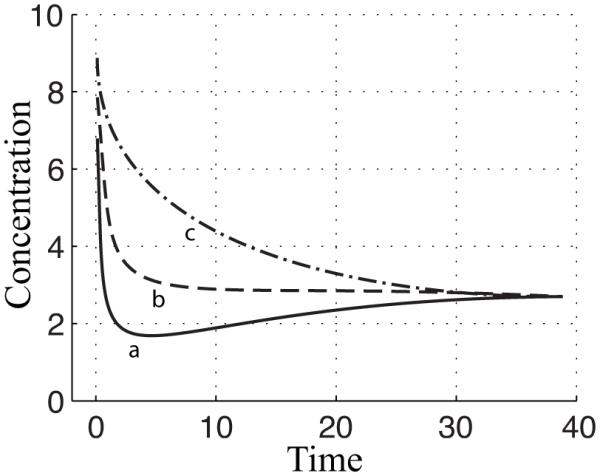
Illustration of the relationship between peak time and settling time. Curve a exhibits a rapid peak time followed by a slow settling time to reach its final steady state. Curve b exhibits a rapid settling time, but does have a peak. Curve c exhibits a slow settling time and has no peak.
If operation of the FNR circuit within the microaerobic-like regions is kept to a minimum range of O2 concentrations, then there is a significant improvement in the response time of the system (Fig. 9 A and B). The mean aerobic-to-anaerobic peak and settling times for systems that do not minimize the range of the microaerobic-like regions are 23.3 ± 2.4 min (peak time) and 84.3 ± 6.8 min (settling time), whereas circuits represented in the optimal band that remain above (for all O2 levels) have a mean peak time of 3.47 ± 0.12 min and a mean settling time of 64.1 ± 8.1 min. Thus, the global response time of active FNR is poorer below the boundary.
The settling time of systems represented within the band of optimal performance can not be improved without moving their operating point above the band, where they would exhibit the unregulated phenotype (Criterion 7). The peak time becomes worse for systems represented above or below the band of optimal performance. The mean peak time for an FNR circuit positioned below the optimal band is significantly slowed because the full width of microaerobic region 4 is included in the spectrum of aerobic-to-anaerobic behavior. Thus, the results for global response time of the system are consistent with the results for the local behavior, and together they identify a strategy of being within an optimal band of design space that avoids region 2 and the majority of regions 1 and 4. This strategy optimizes performance according to Criteria 8 while avoiding the region of dysfunctional regulation (Criteria 7).
Global tolerance
Global tolerance describes the ability of a well-adapted system to tolerate changes in its structure or environment without deviating from the wild-type behavior. The parameters of biological systems are not fixed and are subject to variation due to mutations as well as changes in temperature, pH, and a host of other factors. These parameter variations reflect intrinsic changes in the makeup of the cell or changes in the cellular environment. These changes are well defined in design space and quantified by the global tolerances. Loss of the wild-type phenotype can occur in one of two ways: when the change in a parameter value causes the wild-type operating point to move across a nearby boundary into an adjacent region with less desirable behavior; alternatively, it can occur when the change in a parameter value causes the position of the boundary to move across the wild-type operating point leaving the operating point in the non-physiological region. As an example of the former case, the minimum change in the apparent rate constant for dimerization β22 that moves the operating point out of the optimal band is a 1.69-fold decrease. Increases or decreases in the other parameters, which define the boundaries of the optimal band, can move either the upper boundary or the lower boundary across the operating point. As an example of a parameter change that moves a boundary across an operating point, the minimum change in the parameter for the critical O2 concentration K2 that moves the boundary between regions 1 and 3 across the wild-type operating point in aerobic region 3 is a 4.55-fold increase (the ratio of the value for K2 at the wild-type aerobic operating point of 80 μM to its value at the boundary where K2 = 17.6 μM).
A well-adapted system is expected to have evolved an apparent rate constant for dimerization that is located within the band of optimal operation, which is determined by a constellation of the other system parameters. We can assess the ability of the wild-type parameter set to tolerate large-scale changes by computing the global tolerances with respect to the band of optimal performance. The global tolerances are summarized in Table 2 and indicate that the wild-type system tolerates a minimum 2.6-fold range of parameter variation (considerably more than the percent variation typical of experimental error) without leaving the band of optimal performance (note that these are fold changes rather than percentage changes, which are associated with local parameter sensitivities). The overall trend in the tolerances shows that larger changes in parameter values are required to move the operation of the system above the band of optimal performance as opposed to moving it below. This extra buffering reinforces the assessment that the unregulated behavior in region 2 represents the worst possible behavior in the aerobic environment (Fig. 6B). The performance of the system below may be suboptimal (by Criterion 1-6 and 8) compared to the wild-type phenotype (region 3), but active FNR is still subject to regulation. Therefore, evolution appears to have adapted the parameters of the FNR circuit so that priority is given to avoiding loss of regulatory capacity in region 2 (Criterion 7), whereas avoiding unfavorable parameter sensitivities and slowed response times associated with low apparent dimerization rate constants (Criterion 1-6 and 8) is a secondary priority. The global tolerances are a reflection of these evolutionary pressures.
Table 2.
Global tolerances of the wild-type system to large-scale changes in its parameter values while remaining within the band of optimal performance (Fig. 4). Each Tolerance represents the minimum fold change in the value of the parameter necessary to leave the optimal band.
| Parameter | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α 1,max | α 21 | α 22 | β 1,max | β 1,min | β 21,max | β 21,min | β 22 | β 31,max | β 31,min | K1 | K2 | x6 | x7 | |
|
Tolerance
to Upper Bound |
7.91 | 7.91 | 4.1 | 7.91 | ∞ | 2.03 | ∞ | 4.1 | 2.92 | ∞ | 85.8 | 4.1 | 2.03 | 4.1 |
|
Tolerance
to Lower Bound |
1.3 | 1.3 | 1.69 | 1.3 | ∞ | 1.3 | ∞ | 1.69 | ∞ | ∞ | 1.69 | 1.69 | 1.3 | 1.69 |
Assessment of Dimerization Mutants in Design Space
In the wild-type FNR protein, two negatively charged residues within the predicted dimerization helix (Asp154 and Glu150) are critical in preventing formation of dimeric FNR in the absence of a [4Fe-4S]2+ cluster (Moore et al., 2006). Experimental work on the FNR protein includes site-directed mutagenesis at these two charged amino acids. The activity of these dimerization mutants was characterized in vivo by assaying β-galactosidase activity in strains containing lacZ under control of the FNR-dependent narG promoter (Moore et al., 2006). FNR activity was measured under both aerobic and anaerobic conditions for the mutant strains and expressed as percent of wild-type anaerobic activity (data reprinted in Table 3). In an earlier report, we showed that narG-lacZ expression is highly correlated with the predicted concentration of active FNR in our model (Tolla & Savageau, 2010). By calculating the aerobic steady-state concentration of active FNR as a function of the apparent rate constant for dimerization (β22) in the model, we can predict the relationship between β22 and the activity of the narG-lacZ reporter. We match our calculated lacZ reporter activity to the activity reported by Moore et al. (2006) under aerobic conditions to predict an apparent rate constant for dimerization of each laboratory mutant.
Table 3.
Active FNR concentrations and apparent dimerization rate constants (β22), as predicted by the model, for the FNR mutants constructed by Moore et al. (2006). Mutant strains contain amino acid substitutions in position 154, 152, 150, or 150/154. Experimental characterization of the mutants included an indirect assay for FNR activity using a narG-lacZ reporter construct under both aerobic and anaerobic conditions, and western blot analysis confirmed that FNR protein levels in these mutants are similar to wild-type. Activity was reported as the percentage of β-galactosidase activity in each mutant relative to the wild-type anaerobic β-galactosidase activity of FNR.
| FNR | % Activity (aerobic) |
% Activity (anaerobic) |
Active FNR (μM) |
Dimerization Rate Constant (β22 min−1 μM−2) |
|---|---|---|---|---|
| Wild-type | 4 | 100 | 0.072 ± 0.001 | 2.6 ± 0.63 |
| K152E | 4 ± 1 | 70 ± 7 | 0.0003 ± 0.0001 | 0.01 ± 0.004 |
| E150K-D154K | 6 ± 1 | 143 ± 14 | 0.1 ± 0.006 | 3.8 ± 0.3 |
| E150A | 15 ± 1 | 103 ± 10 | 0.26 ± 0.01 | 16 ± 2 |
| D154V | 15 ± 1 | 111 ± 11 | 0.27 ± 0.01 | 16 ± 2 |
| E150A-D154A | 16 ± 2 | 96 ± 10 | 0.28 ± 0.02 | 18 ± 2 |
| E150Q | 20 ± 2 | 100 ± 10 | 0.35 ± 0.02 | 27 ± 3 |
| E150K | 23 ± 2 | 112 ± 11 | 0.41 ± 0.02 | 39 ± 5 |
| D154G | 28 ± 3 | 116 ± 12 | 0.49 ± 0.03 | 64 ± 10 |
| D154C | 28 ± 3 | 115 ± 11 | 0.45 ± 0.03 | 65 ± 10 |
| D154L | 29 ± 3 | 103 ± 10 | 0.51 ± 0.03 | 72 ± 12 |
| D154N | 30 ± 3 | 140 ± 14 | 0.53 ± 0.03 | 80 ± 14 |
| D154A | 37 ± 4 | 102 ± 10 | 0.66 ± 0.04 | 181 ± 43 |
| E150K-D154A | 38 ± 4 | 115 ± 11 | 0.67 ± 0.04 | 206 ± 51 |
| D154K | 50 ± 5 | 109 ± 11 | 0.9 ± 0.04 | 2266 ± 1051 |
The design space allows us to visualize the operating points of the dimerization mutants in the context of the phenotypic regions (Fig. 11). Based on our analysis of the design space, we expect the mutants operating above the optimal band to tend toward the unregulated phenotype. As Table 3 demonstrates, increasing the apparent rate constant for dimerization leads to unregulated expression of active FNR under aerobic conditions. The anaerobic expression data (Table 3) were not used to calculate the predicted apparent rate constant for dimerization (β22) of the mutants. According to the experimental data, the expression under fully anaerobic conditions is similar to wild-type activity regardless of the predicted apparent rate constant for dimerization (Table 3). This is consistent with the predicted anaerobic position of the mutants in Fig. 11 and the corresponding steady-state levels predicted for active FNR (Fig. 6). Replacing the negatively charged residues at positions 154 and 150 with positively charged residues produces a double mutant (FNR-E150K/D154K) that is expected to behave in a wild-type fashion (Moore et al., 2006). The design space analysis confirms this expectation by showing that the FNR-E150K/D154K mutant is positioned within the band of optimal operation (Fig. 11).
Figure 11.
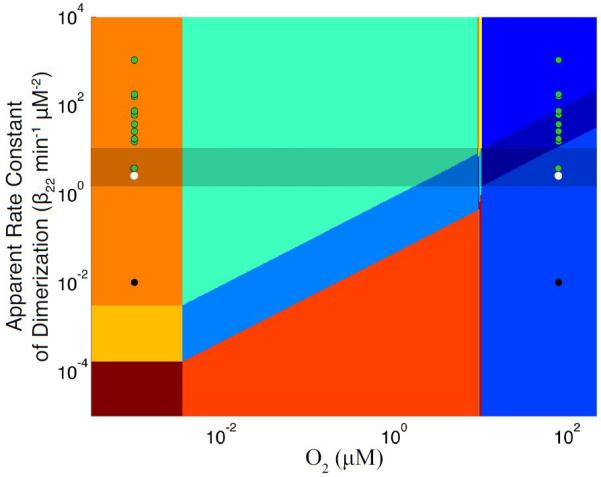
Position in the design space of wild-type (○) and mutant strains from Moore et al. (2006) with increased ( ) or decreased (●) apparent rate constants for dimerization of monomeric FNR into active FNR. The position of each strain is shown under both aerobic (right set of points) and fully anaerobic (left set of points) conditions (see text for discussion).
) or decreased (●) apparent rate constants for dimerization of monomeric FNR into active FNR. The position of each strain is shown under both aerobic (right set of points) and fully anaerobic (left set of points) conditions (see text for discussion).
The FNR-K152E mutant is a separate case from the aforementioned mutants (black circle in Fig. 11). This mutant presents wild-type aerobic activity, but under anaerobic conditions expression from the narG-lacZ reporter construct is reduced (Table 3). We used the lowered anaerobic activity to predict an apparent rate constant for dimerization (β22). The model predicts that at a lowered apparent rate constant for dimerization of 0.01 ± 0.004 there is a reduction in the anaerobic steady-state level of active FNR; however, the predicted activity of the mutant (1.2 ± 0.07 μM active FNR) may not be discernable experimentally from the wild-type (1.73 ± 0.02 μM active FNR), because of background expression from the narG promoter. According to our design space, the FNR-K152E mutant is positioned well below the band of optimal operation (Fig. 11). Our analysis predicts that the peak time of the aerobic-to-anaerobic transition should increase 15 ± 2.6 fold compared to the wild-type and that the settling time should increase 1.2 ± 0.02 fold. Anaerobic-to-aerobic peak time is predicted to increase 5.5 ± 2.4 fold, whereas the anaerobic-to-aerobic settling time decreases by 723 ± 1200 fold. The sharp decrease and large standard deviation in settling time for the K152E mutant results from the predicted β22 value (apparent dimerization rate constant) straddling a region in the FNR design space with extremely rapid settling times (dark blue area crossed by the white line in Fig. 9B). The significant delay predicted in the aerobic-to-anaerobic peak time can be experimentally tested. The K152E mutation should noticeably effect the repression time in the laboratory, whereas the delay in anaerobic-to-aerobic peak time may not be sufficient to produce a detectable deviation from the wild-type.
Discussion
The analysis presented in this study provides a deeper understanding of how aerobic, microaerobic, and anaerobic behaviors are best suited to their respective environments. We examined the phenotypic repertoire of the FNR regulatory circuit in the context of its system design space, which allowed us to enumerate the qualitatively-distinct phenotypes, characterize their local behavior, and analyze transitions between phenotypes. We quantified the performance of each phenotype by evaluating a set of criteria that included robustness of the system to small parameter changes (Criterion 1), responsiveness of active FNR to small O2 changes (Criteria 2 and 3), buffering of the inactive FNR supply in the aerobic state (Criterion 4), a margin that ensures local stability (Criterion 5), rapid local response time of the FNR circuit (Criterion 6), maintenance of appropriate concentrations of active FNR (Criterion 7), global response time of the system (Criterion 8), and a tolerance to large global changes in parameters (Criterion 9). This analysis allowed us to identify desirable and undesirable phenotypes as well as an optimal band of operation across phenotypes, which the model moves through as the O2 content of the environment changes. The optimal band provides a means of determining what combinations of parameters represent normal physiological function, and quantifies how far from wild-type behavior a particular mutation places the FNR system.
FNR Design Space Reveals an Optimal Band of Operation
The behavior associated with regions of design space is categorized as aerobic-like, anaerobic-like, or microaerobic-like depending upon which processes are dominant. The design space provides boundaries on when a system displays a particular category of behavior, including quantifying the boundaries of the microaerobic state. The behavior within each of these categories is not uniform, but they share a few key characteristics with regard to Criteria 1, 2, 3, and 7: The aerobic-like regions maintain low levels of active FNR and respond to small O2 changes; The anaerobic-like regions maintain high levels of active FNR and provide a robust signal promoting anaerobic growth; The microaerobic-like regions maintain intermediate levels of active FNR and an intermediate response to small O2 changes. Due to the relative position of the aerobic-like, anaerobic-like, and microaerobic-like regions there exists a span of the design space that maintains the ability to transition between the extremes of aerobic and anaerobic growth and localizes the microaerobic-like regions at the critical O2 level (Fig 5 A and B). Further assessment of the global dynamics of the FNR circuit (Fig 8 A and B) revealed that region 4 (microaerobic-like) provides comparatively slow induction and repression of active FNR in response to large O2 changes (Criterion 8). This indicated that minimizing the span of O2 in which the system is represented in region 4 best satisfies the goal of maintaining a rapid response time. Thus, the optimal strategy for the FNR circuit involves operating within a specified band that avoids region 2 and the majority of region 4 (Fig. 4). For the FNR circuit with the wild-type values for the parameters, which were independently determined (Tolla & Savageau, 2010), we have shown that it operates within the band of optimal performance.
Position of the FNR System Prevents Loss of Regulation
By computing the global tolerances of the FNR circuit with respect to the boundaries of the band of optimal performance (Table 2), we saw that the system can tolerate substantial changes in the values of its parameters while maintaining optimal O2-sensing performance (Criterion 9). The overall trend in the global tolerances showed that the wild-type parameters locate the system in design space so that larger changes in parameter values are required to shift the operating point above the band of optimal performance than to shift it below the band. This result supports the hypothesis that while operating below the band is unfavorable (Criteria 1-6 and 8), evolutionary pressures have focused on preventing the worst-case scenario in which the system shifts above the band to produce improper regulation of active FNR (Criteria 7).
Suggested Experiments to Test Design Space Conclusions
We were able to predict the expected behavior of dimerization mutants, beyond their characterization in the literature (Moore et al., 2006), and determine which phenotypic traits are amenable to experimental testing. In particular, we predicted that the significant reduction in FNR activity observed for the FNR-K152E mutant should slow the transition from aerobic to anaerobic growth by approximately 15-fold, which we hypothesize will increase the time needed to fully induce active FNR from 3.7 min to ~56 min. This dramatic shift in the aerobic-to-anaerobic dynamics should be detectable experimentally as a decrease in growth rate for mutant strains forced to transition frequently between aerobic and anaerobic growth.
To test the location of the optimal band as predicted by the design space, we propose changing a parameter of the FNR system in the laboratory through mutation. Mutations can adjust the boundaries of the optimal band, and the design space analysis can specify the nature and degree of the mutation necessary to change a pathological phenotype into a physiological phenotype. For example, the D154L mutant exhibits 29 ± 3% active FNR induction under aerobic conditions (Moore et al., 2006). Based on the boundaries of the optimal band, a 3-fold increase in the decay of inactive FNR (β21,max) should suppress the D154L mutation, placing the strain back in the optimal band and restoring its ability to regulate active FNR.
The narrow width of the microaerobic regions and the involvement of potentially conflicting aerobic and anaerobic processes suggest the hypothesis that the FNR system has evolved to minimize the extent of these microaerobic regions. Introducing mutations that alter the positions of the microaerobic regions such that the cell is forced to take a non-minimal crossing would test this prediction. Increasing the rate constant of ClpXP mediated decay (β21,min) or ClpXP levels themselves (x6) will shift the microaerobic regions upward and increase the span of microaerobic behavior involved in shifting between environments. Cells forced to frequently transition between aerobic and anaerobic conditions would be expected to grow slower than wild-type strains or compensate through reversion.
Conclusion
The design space analysis used in this work provides an efficient assessment for whole ranges of parameters. Instead of characterizing the behavior of the system at every point in parameter space, we were able to focus on a small number of regions that capture the full range of behaviors possible for the FNR circuit. By enumerating and characterizing the qualitatively-distinct phenotypes of this O2 sensing circuit, we placed in a visual context the evolutionary pressures that have shaped the circuit. A distinction can be drawn between the phenotypes that evolution has selected for and those specific phenotypes that evolution has selected against. Finally, we calculated the global tolerances to quantify the extent to which evolutionary pressures have buffered a particular system against changes to its phenotype.
Modeling Procedures
The construction of the design space, analysis, and simulation of the model are all carried out in MATLAB R2009b. The mathematical details presented in this manuscript should allow for reproduction of the results using any standard computational software package.
Formulating a Hill Model and Recasting
We arrive at Eqs. (1)-(5) by formulating a “Hill model” based upon our original “piecewise model” (Tolla & Savageau, 2010) [Eqs. (11)-(13)], and then recasting the Hill model into the generalized mass-action formalism. This final step produces a representation that agrees with the Hill model exactly and is amenable to the design space analysis. The original representation is given below.
| (11) |
| (12) |
| (13) |
In this nomenclature X1 is the mRNA pool, X2 is the inactive FNR pool, and X3 is the active FNR pool. Some parameters have state-specific values for the aerobic and anaerobic states. This is due to differences in the growth rate between these two conditions, and these growth-rate differences alter the dilution rate. Thus, not shown in equations [(11) – (13)] are the following state-specific parameters β1,max, β1,min, β21,max, β21,min, β31,max, β31,min. There are also state-specific independent variables that represent the forces modulating the transition between the aerobic and anaerobic states.
In our previous publication (Tolla & Savageau, 2010), we also considered the possibility that the Isc concentration might be a state-dependent variable. We attempted to fit the experimental data with an Isc concentration that varied with the environment or a constant Isc concentration. There was no difference in the quality of the final fit, and the environment specific Isc concentrations would converge to nearly the same value (data not shown). We take this as an indication that while the total Isc pool is likely regulated in an O2 dependent fashion there are fewer targets under anaerobic conditions (Giel et al., 2006, Schwartz et al., 2001). Therefore, we hypothesize that free concentration of Isc is essentially unaltered in the different environments. The independent variables are X4, X5, and X6, where X6,max and X6,min represent the state-specific values for the aerobic and anaerobic environments respectively. The critical concentration of active FNR, X3c, determines when to switch between the aerobic-state and anaerobic-state parameters.
Unlike the sharp transitions in our original model, the real system undergoes a smooth transition between the aerobic and anaerobic states. As a method for representing a smooth transition between these states we replace the step functions in our original model with a Hill-type function for the changes in the rate expressions for decay and a hyperbolic expression for the repression of transcription by active FNR. This modified model agrees with the original model at the extremes of the aerobic-to-anaerobic spectrum (Fig. 3). The equations with the hyperbolic and Hill-type transitions are given below.
| (14) |
| (15) |
| (16) |
The variable and parameter notation in this Hill model of the FNR circuit is the same as that in the original piece-wise model, with two exceptions. There are three additional parameters: K1 is the inhibition concentration for the half-maximal repression of transcription by 4Fe-FNR’s, K2 is the critical O2 threshold, and n is the Hill number. The Hill number is adjustable and increasing its value serves to sharpen the transition between aerobic and anaerobic growth. We have settled on a Hill number of 4, but the exact value does not significantly affect the results of this study. The critical O2 threshold is the O2 level at which the FNR network shifts from aerobic behavior to anaerobic behavior. The specific value of K2 is determined by equating the two piecewise terms describing the transcription of fnr mRNA (i.e. α1,max = α1X3g13) and solving for X3. This is the value of X3 at which the anaerobic and aerobic descriptions of mRNA synthesis meet, and we can set the derivates of Eqs. (11)-(13) to zero and solve for X3 in terms of X6. This yields the following relationship for determining K2.
| (17) |
In order to adapt the system to our general method for formulating a design space, we recast the Hill model into a generalized mass-action representation. The recast system is not an approximation of the Hill model. Rather, it agrees with the Hill model exactly. In the case of Eqs (14)-(16), we need only define two new variables . The resulting generalized mass-action set of equations is in the main text [Eqs. (1)-(5)]. The variables in the final equations have been renamed and renumbered to prevent confusion. The dependent variables are the mRNA (x1), inactive FNR (x2), active FNR (x3), the sum of active FNR and the K1 of repression (x4), and the sum of the current O2 tension and the critical O2 tension (x5).
Constructing the FNR Design Space
For a general discussion regarding the construction of design spaces see Savageau et. al. (Savageau et al., 2009). In formulating the FNR design space, we had to make a further modification to the equations. Our original estimation of the parameters (Tolla & Savageau, 2010) utilized the fact that the rate of transcription is at its half-maximal value (x3= K1) in a completely anaerobic environment. Thus, the rate of transcription will only increase as the environment becomes more aerobic and active FNR (x3) decreases. Our original model captured this behavior and identified a critical value of active FNR by assuming a two-term representation with α1,max above the critical value of active FNR and below the critical value. As shown in equation (17), the critical value of x3 (= 21/g13 K1) corresponds to a critical value of O2 x8 (=K2). Therefore, we have retained this two-term representation for the rate of fnr mRNA synthesis in our construction of the FNR design space. The equations that capture the appropriate subsystems when dominant terms are selected are the following:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
The design space of Fig. 4 is constructed using equations (18)-(22). A subsystem consists of a specified pairing of positive and negative terms, in which one positive and one negative term is selected from each equation, as in the example of equations (6)-(10). All possible combinations of terms are considered, each such subsystem is solved for its steady state, and the state-state solution is substituted into the subsystem’s dominance conditions to evaluate the validity of the solution. If the dominance conditions are satisfied for some range of parameters then the subsystem is valid, and a region in the design space (Fig. 4) represents this valid range.
In some cases the selection of dominant terms implies very rapid cycling between inactive FNR (x2) and active FNR (x3), with no other terms representing fluxes into or out of these pools. This leads to a linear dependency in the solution that dictates a constraint between x2 and x3. In effect, the rapid cycling causes the cycle to behave as an aggregate of the two pools in the context of the complete model, thereby creating a virtual branch point with a single influx (synthesis of inactive FNR) and two effluxes (loss from either the inactive or the active FNR pool). The selection of a dominant loss term from the virtual branch point yields an additional dominance condition. The solution of the steady-state equation for x1, the constraint relation between x2 and x3, together with the steady-state equation that results from the choice of a dominant loss term, yields the steady state for the subsystem. For this subsystem to be valid, its steady-state solution must satisfy all of the dominance conditions (the original ones plus the additional one associated with the virtual branch point).
Quantitative Characterization of System Performance
Logarithmic gains
The change of a dependent concentration variable (e.g., active FNR, x3) in response to a change in value for an independent concentration variable (e.g., O2, x8) is defined by a relative derivative of the explicit steady-state solution (Savageau, 1971a). For example,
| (23) |
Logarithmic gains characterize the extent to which input signals (represented by changes in the independent variables) are amplified or attenuated as they are transmitted throughout the system to generate output signals (represented by changes in the steady states of dependent variables).
Parameter sensitivities
The change of a dependent concentration variable (e.g., inactive FNR, x2) in response to a change in value for one of the parameters that define the structure of the system (e.g., the apparent rate constant for dimerization, β22) is also determined by a relative derivative of the explicit steady-state solution (Savageau, 1971b). For example,
| (24) |
Parameter sensitivities are used to evaluate the circuit’s local robustness to variation in the parameters that define its structure. A robust system should exhibit attenuated responses following changes in its parameters (i.e., it should have sensitivities less than one).
Margin of local stability
The margin of local stability is a measure of how much the parameters of a system can change and have the system remain stable. The last two of the Routh criteria for local stability are critical in the sense that one or the other of these will be violate first when a stable system becomes unstable. Thus, the critical Routh criterion with the smallest magnitude provides a quantitative measure of the margin for local stability (Savageau, 2009).
Local response time
The local response time describes the speed with which a system relaxes back to its steady state following a transient disturbance or adjusts to a new steady state following a small sustained change in the environment. We can assess the local response time about the steady state in each region by computing the eigenvalues for the system. The eigenvalues are determined by a first-order Taylor series approximation in logarithmic space of the differential equation about the steady-state that applies for each valid subsystem (Savageau, 1998). The inverse of the dominant eigenvalue (the one with the largest value for its real part) determines the characteristic time for the final approach to the steady state. Thus, the inverse of the dominant eigenvalue is our measure for the local response time of the system.
Global response time
The global response time is assessed by computer simulation and the determination of two key temporal characteristics. The settling time can be defined as the time at which the solution reaches and remains within ±5% of its final steady-state value; the peak time can be defined as the time at which the concentration of active FNR reaches its minimum or maximum during a transition.
Global tolerance
Global tolerances are measured as the ratio of two distinct values for a specified parameter; the value of the parameter at the boundary of an adjacent region relative to its wild-type value within the region [or the inverse, since the value may decrease or increase at the boundary] (Coelho et al., 2009). Computing the minimum fold change for every parameter gives the full set of global tolerances with respect to the set of parameters values for the wild-type system.
Acknowledgements
This work was supported in part by the U.S. Public Health Service through grant R01-GM30054 and a Stanislaw Ulam Distinguished Scholar Award from the Center for Non-Linear Studies of the Los Alamos National Laboratory (M.A.S.) and by the U.S. Public Health Service through training grant T32-EB003827 and an Earl C. Anthony fellowship (D.A.T.). We thank Rick Fasani and Pedro Coelho for being such excellent sounding boards for discussion on the FNR system. We also offer our sincere appreciation to Patricia Kiley for assisting us in our experimental understanding of the system, and to the editor in helping us to make this work as accessible as possible.
Abbreviations used
- apoFNR
apoprotein FNR
- 2Fe-FNR
[2Fe-2S]2+ FNR
- 4Fe-FNR
[4Fe-4S]2+ FNR
References
- Becker S, Holighaus G, Gabrielczyk T, Unden G. O2 as the regulatory signal for FNR-dependent gene regulation in Escherichia coli. J Bacteriol. 1996;178:4515–4521. doi: 10.1128/jb.178.15.4515-4521.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coelho PM, Salvador A, Savageau MA. Quantifying global tolerance of biochemical systems: design implications for moiety-transfer cycles. PLoS Comput Biol. 2009;5:e1000319. doi: 10.1371/journal.pcbi.1000319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crack JC, Gaskell AA, Green J, Cheesman MR, Le Brun NE, Thomson AJ. Influence of the environment on the [4Fe-4S]2+ to [2Fe-2S]2+ cluster switch in the transcriptional regulator FNR. Journal of the American Chemical Society. 2008;130:1749–1758. doi: 10.1021/ja077455+. [DOI] [PubMed] [Google Scholar]
- Giel JL, Rodionov D, Liu M, Blattner FR, Kiley PJ. IscR-dependent gene expression links iron-sulphur cluster assembly to the control of O2-regulated genes in Escherichia coli. Mol Microbiol. 2006;60:1058–1075. doi: 10.1111/j.1365-2958.2006.05160.x. [DOI] [PubMed] [Google Scholar]
- Grainger DC, Aiba H, Hurd D, Browning DF, Busby SJ. Transcription factor distribution in Escherichia coli: studies with FNR protein. Nucleic acids research. 2007;35:269–278. doi: 10.1093/nar/gkl1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green J, Crack JC, Thomson AJ, LeBrun NE. Bacterial sensors of oxygen. Curr Opin Microbiol. 2009;12:145–151. doi: 10.1016/j.mib.2009.01.008. [DOI] [PubMed] [Google Scholar]
- Kang Y, Weber KD, Qiu Y, Kiley PJ, Blattner FR. Genome-wide expression analysis indicates that FNR of Escherichia coli K-12 regulates a large number of genes of unknown function. J Bacteriol. 2005;187:1135–1160. doi: 10.1128/JB.187.3.1135-1160.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoroshilova N, Popescu C, Munck E, Beinert H, Kiley PJ. Iron-sulfur cluster disassembly in the FNR protein of Escherichia coli by O2: [4Fe-4S] to [2Fe-2S] conversion with loss of biological activity. Proc Natl Acad Sci U S A. 1997;94:6087–6092. doi: 10.1073/pnas.94.12.6087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambden PR, Guest JR. Mutants of Escherichia coli K12 unable to use fumarate as an anaerobic electron acceptor. J Gen Microbiol. 1976;97:145–160. doi: 10.1099/00221287-97-2-145. [DOI] [PubMed] [Google Scholar]
- Lazazzera BA, Beinert H, Khoroshilova N, Kennedy MC, Kiley PJ. DNA binding and dimerization of the Fe-S-containing FNR protein from Escherichia coli are regulated by oxygen. J Biol Chem. 1996;271:2762–2768. doi: 10.1074/jbc.271.5.2762. [DOI] [PubMed] [Google Scholar]
- Mettert EL, Kiley PJ. ClpXP-dependent proteolysis of FNR upon loss of its O2-sensing [4Fe-4S] cluster. J Mol Biol. 2005;354:220–232. doi: 10.1016/j.jmb.2005.09.066. [DOI] [PubMed] [Google Scholar]
- Mettert EL, Kiley PJ. Contributions of [4Fe-4S]-FNR and integration host factor to fnr transcriptional regulation. J Bacteriol. 2007;189:3036–3043. doi: 10.1128/JB.00052-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mettert EL, Outten FW, Wanta B, Kiley PJ. The impact of O2 on the Fe-S cluster biogenesis requirements of Escherichia coli FNR. J Mol Biol. 2008;384:798–811. doi: 10.1016/j.jmb.2008.09.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore LJ, Kiley PJ. Characterization of the dimerization domain in the FNR transcription factor. J Biol Chem. 2001;276:45744–45750. doi: 10.1074/jbc.M106569200. [DOI] [PubMed] [Google Scholar]
- Moore LJ, Mettert EL, Kiley PJ. Regulation of FNR dimerization by subunit charge repulsion. J Biol Chem. 2006;281:33268–33275. doi: 10.1074/jbc.M608331200. [DOI] [PubMed] [Google Scholar]
- Partridge JD, Poole RK, Green J. The Escherichia coli yhjA gene, encoding a predicted cytochrome c peroxidase, is regulated by FNR and OxyR. Microbiology. 2007;153:1499–1507. doi: 10.1099/mic.0.2006/004838-0. [DOI] [PubMed] [Google Scholar]
- Salmon K, Hung SP, Mekjian K, Baldi P, Hatfield GW, Gunsalus RP. Global gene expression profiling in Escherichia coli K12. The effects of oxygen availability and FNR. J Biol Chem. 2003;278:29837–29855. doi: 10.1074/jbc.M213060200. [DOI] [PubMed] [Google Scholar]
- Sanguinetti G, Ruttor A, Opper M, Archambeau C. Switching regulatory models of cellular stress response. Bioinformatics. 2009;25:1280–1286. doi: 10.1093/bioinformatics/btp138. [DOI] [PubMed] [Google Scholar]
- Savageau MA. Concepts relating the behavior of biochemical systems to their underlying molecular properties. Arch Biochem Biophys. 1971;145:612–621. doi: 10.1016/s0003-9861(71)80021-8. [DOI] [PubMed] [Google Scholar]
- Savageau MA. Parameter sensitivity as a criterion for evaluating and comparing the performance of biochemical systems. Nature. 1971;229:542–544. doi: 10.1038/229542a0. [DOI] [PubMed] [Google Scholar]
- Savageau MA. Biochemical Systems Analysis : A Study of Function and Design in Molecular Biology, 40th Anniversary Issue. Addison-Wesley; Reading, Mass.: 2009. A reprinting of the original edition published by Addison-Wesley, Reading, Mass., 1976. [Google Scholar]
- Savageau MA. Development of fractal kinetic theory for enzyme-catalysed reactions and implications for the design of biochemical pathways. Biosystems. 1998;47:9–36. doi: 10.1016/s0303-2647(98)00020-3. [DOI] [PubMed] [Google Scholar]
- Savageau MA. Design principles for elementary gene circuits: Elements, methods, and examples. Chaos. 2001;11:142–159. doi: 10.1063/1.1349892. [DOI] [PubMed] [Google Scholar]
- Savageau MA, Coelho PM, Fasani RA, Tolla DA, Salvador A. Phenotypes and tolerances in the design space of biochemical systems. Proc Natl Acad Sci U S A. 2009;106:6435–6440. doi: 10.1073/pnas.0809869106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savageau MA, Fasani RA. Qualitatively distinct phenotypes in the design space of biochemical systems. FEBS Lett. 2009;583:3914–3922. doi: 10.1016/j.febslet.2009.10.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz CJ, Giel JL, Patschkowski T, Luther C, Ruzicka FJ, Beinert H, Kiley PJ. IscR, an Fe-S cluster-containing transcription factor, represses expression of Escherichia coli genes encoding Fe-S cluster assembly proteins. Proc Natl Acad Sci U S A. 2001;98:14895–14900. doi: 10.1073/pnas.251550898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton VR, Mettert EL, Beinert H, Kiley PJ. Kinetic analysis of the oxidative conversion of the [4Fe-4S]2+ cluster of FNR to a [2Fe-2S]2+ Cluster. J Bacteriol. 2004a;186:8018–8025. doi: 10.1128/JB.186.23.8018-8025.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton VR, Stubna A, Patschkowski T, Munck E, Beinert H, Kiley PJ. Superoxide destroys the [2Fe-2S]2+ cluster of FNR from Escherichia coli. Biochemistry. 2004b;43:791–798. doi: 10.1021/bi0357053. [DOI] [PubMed] [Google Scholar]
- Tolla DA, Savageau MA. Regulation of aerobic-to-anaerobic transitions by the FNR cycle in Escherichia coli. J Mol Biol. 2010;397:893–905. doi: 10.1016/j.jmb.2010.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tseng CP, Albrecht J, Gunsalus RP. Effect of microaerophilic cell growth conditions on expression of the aerobic (cyoABCDE and cydAB) and anaerobic (narGHJI, frdABCD, and dmsABC) respiratory pathway genes in Escherichia coli. J Bacteriol. 1996;178:1094–1098. doi: 10.1128/jb.178.4.1094-1098.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unden G, Duchene A. On the role of cyclic AMP and the Fnr protein in Escherichia coli growing anaerobically. Arch Microbiol. 1987;147:195–200. doi: 10.1007/BF00415284. [DOI] [PubMed] [Google Scholar]