Abstract
Time series analysis of a climate-driven model of malaria transmission shows limited evidence for an increase in suitability during the last century across Africa. Outside areas where climate was always or never suitable, <17% of the continent showed significant trends in malaria transmission. Of these areas, 5.7% showed positive deterministic trends, 6.1% had negative deterministic trends, and 5.1% exhibited stochastic trends. In areas with positive trends, precipitation, rather than temperature, was the primary forcing variable. This analysis highlights the need to examine the relationship between climate and malaria more closely and to fully consider nonclimatic factors as drivers of increased malaria transmission across the continent.
The influence of climate change on the transmission of Plasmodium falciparum malaria continues to be a subject of considerable debate. Temperature influences anopheline mosquito feeding intervals, population density, and longevity (1–4), as well as the reproductive potential of the Plasmodium parasite (1–3, 5). Malaria transmission, however, is a complex interaction of many factors, including not only vector and parasite densities and behavior, but also land-use change (6), public health control measures (7–9), human migration (10–11), and drug resistance (12–15). More suitable climate conditions may facilitate malaria transmission, but evidence for increased incidence has not been clearly linked to climate (14, 16, 17), nor have predictions for the spread of malaria under future climate change scenarios produced the range changes that some have conjectured (18).
Here we examine trends in a climate-driven biological model (19) of malaria transmission for the entire African continent between 1911 and 1995. We specifically address the role of climate change in the African malaria resurgence (12) by using a spatially and temporally extensive gridded climate data-set (ref. 20; Appendix: Methods and Data) to identify locations where the malaria transmission climate suitability index (MTCSI; Appendix: Methods and Data) has changed significantly. In those areas of change, we examine more closely the underlying climate forcing of transmission suitability.
Recent investigations of the influence of climate on malaria transmission in Africa have reached different conclusions. For example, in the East African highlands several current studies (16, 21, 22) found no significant climate trends, whereas others associated the proportion of total admissions caused by malaria at a site with regional temperature anomalies (23) and claim to have shown evidence of regional warming (24). Disagreement remains (24, 25) over the appropriate use of coarse-resolution climate data in drawing inferences at the facility level for which malaria incidence data are available. Further, it has been suggested that even statistically insignificant changes in climate might result in significant changes in malaria transmission potential (24). Concerns have also been raised over the effect of seasonal noise on long-term trend analyses (25). These analyses address these issues. First, scaling concerns are eliminated by performing a comprehensive continental analysis at the original 0.5° latitude and longitude resolution of the climate data. Second, overlooking potentially significant changes in transmission is avoided by examining the MTCSI as opposed to analyzing the climate data directly. Last, there are no issues of seasonal variability confounding the results because the MTCSI is calculated on an annual basis.
Methods and Data
We used monthly surfaces of total rainfall R, mean air temperature T, and mean diurnal temperature range DTR collected from a Climate Research Unit (CRU) time series (TS) data-set (CRU TS 1.0, www.cru.uea.ac.uk) (ref. 20; Appendix: Methods and Data) to drive the MTCSI model (ref. 19; Appendix: Methods and Data). The model transforms temperature and rainfall into an index of transmission potential between zero (unsuitable) and one (suitable) based on biological constraints of climate on malaria parasite and mosquito vector development, with an optimal temperature of 22°C and optimal monthly rainfall of 80 mm.
The MTCSIt for t = 1911–1995 was calculated for each of the 10,246 half-degree grid cells covering Africa. Excluding areas that were never suitable (maximum MTCSIt ≤ 0.1) or perennially suitable (minimum MTCSIt ≥ 0.9) for transmission reduced further analyses to 45% of the continent (4,603 of 10,246 grid cells) for which trends in MTCSI were examined. Autoregressive models were fitted with ordinary least-squares regression to each TS. The presence of trends was assessed with augmented Dickey–Fuller (refs. 26 and 27; Appendix: Methods and Data) tests, and each series was classified according to behavior (stationary or nonstationary) and the statistical significance of the trend (zero or nonzero). Grid cells classified as either “stationary with trend” or “random walk with drift” contained significant deterministic and stochastic trends in climatic suitability, respectively, whereas those classified as “stationary with no trend” and “random walk with no drift” had no significant trend (Appendix: Methods and Data).
Results
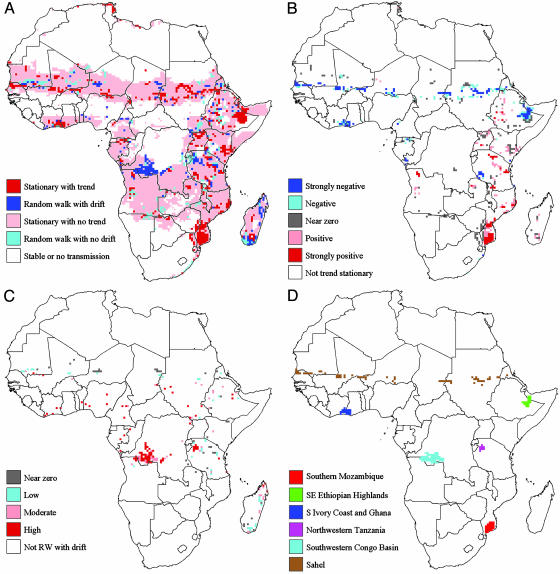
Of the 4,603 grid cells having potentially variable climatic suitability, 83.2% exhibited no significant change in MTCSI, with 78.8% classified as stationary with no trend and 4.4% classified as random walk with no drift. Significant deterministic trends were found in 11.8% of these grid cells; the deterministic trends were nearly equally split between positive (5.7%) and negative (6.1%). The remaining 5.1% exhibited significant stochastic trends. The spatial distribution of the TS classifications (Fig. 1A) showed little pattern in the cells having significant trends with the few exceptions discussed below.
Fig. 1.
Spatial distribution of malaria transmission potential in Africa, 1911–1995. (A) Classification of time series. Cells classified as “stable or no transmission” had either minimum MTCSI of ≥0.9 (stable transmission) or maximum MTCSI of ≤0.1 (no transmission). Cells classified as stationary with trend or random walk with drift contained deterministic and stochastic trends in MTCSI, respectively. Cells classified as stationary with no trend or random walk with no drift contained no statistically significant trends in MTCSI. (B) Magnitude of deterministic trends. Strongly negative regions correspond to a deterministic trend β ≤ –0.002; negative regions correspond to –0.002 < β ≤ –0.001; near zero regions correspond to –0.001 < β < 0.001, positive regions correspond to 0.001 ≤ β < 0.002; and strongly positive regions correspond to β ≥ 0.002. (C) Magnitude of stochastic trends. Near zero regions correspond to a stochastic trend α < 0.19; low regions correspond to 0.19 ≤ α < 0.34; moderate regions correspond to 0.34 ≤ α < 0.50; and high regions correspond to α ≥ 0.5. (D) Six regions with significant deterministic or stochastic trends. These are the regions mapped in Fig. 2.
The value of the deterministic trend (Fig. 1B) ranged from strongly positive to strongly negative, with less than half (261 of 542 cells) revealing an increase in transmission potential. Areas with positive trends were distributed primarily in the east and southeast of Africa, including a large portion of southern Mozambique that was strongly positive. Areas with negative trends were clustered and tended to be strongly negative, with the majority located in the Sahel, the southeastern Ethiopian highlands, and in southern Ivory Coast and Ghana. Stochastic trends, further detailed in Fig. 1C, occurred primarily in the southern Congo basin, northwestern Tanzania, and Madagascar.
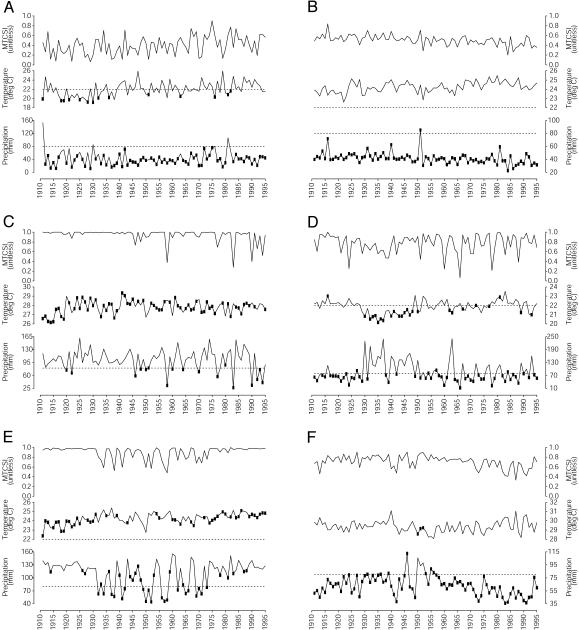
To determine the underlying climate forcings on MTCSI in these specific areas with pronounced trends (Fig. 1D), we further examined the mean annual MTCSI in relation to mean air temperature T and rainfall R during the month most limiting to transmission (Fig. 2). In southern Mozambique (Fig. 2 A), transmission was limited primarily by rainfall. Air temperature, which fluctuated around the 22°C optimum, was the limiting factor in just 14 of the 85 years, mostly before 1940. Precipitation was usually lower than the 80-mm optimum. Rainfall levels were stable from 1945 to 1965 but variable in the earlier and later time periods. The positive MTCSI trend was thus forced by the prevalence of wet, warm years since the mid-1960s.
Fig. 2.
Annual MTCSI and limiting climate for six regions with significant deterministic or stochastic trend in climatic suitability for southern Mozambique (A), southeastern Ethiopian Highlands (B), southern Ivory Coast and Ghana (C), northwestern Tanzania (D), southwestern Congo basin (E), and Sahel (F). MTCSI is the spatial mean over all grid cells in the region. Air temperature and precipitation values are spatial means over all grid cells in the region during the month most limiting to MTCSI. The limiting month m is that for which ym is minimized during the either 3- or 5-month window over which the MTCSI was calculated (Appendix: Methods and Data). Solid squares denote the climatic variable (air temperature or precipitation) contributing to ym in the limiting month, i.e., the limiting climatic factor for MTCSI. Dashed lines indicate the optimal levels for each climatic variable. Absence of dashed lines indicates that the optimal level was not in the range of the observed climatic values for the region.
In the southeastern Ethiopian highlands, MTCSI was always forced by rainfall (Fig. 2B). Mean monthly precipitation was persistently lower than the optimum, with a consistent decline over the time period, resulting in reduced malaria suitability in the region. In contrast, mean MTCSI, temperature, and precipitation for southern Ivory Coast and Ghana (Fig. 2C) suggest transmission in this area was primarily temperature-limited (68 of the 85 years). There was, however, a shift toward precipitation limitation in later years. From 1911 to 1955 there were just 6 rainfall-limited years, but after 1955 there were 11, with 4 of these occurring from 1990 to 1995.
The TS for northwestern Tanzania (Fig. 2D) shows that temperature and rainfall fluctuated around the optimal values, with more temperature-limited, wetter years from 1930 to 1950 and more rainfall-limited, warmer years between 1910 and 1930 and 1950 and 1995. The MTSCI showed a high and increasing interannual variability indicative of a stochastic trend. This region has unstable malaria transmission dominated by variability in the timing and amount of rainfall (28).
The southwestern Congo basin TS (Fig. 2E) showed marked fluctuation in MTCSI in the middle of the time period (1930–1975) but little variation in the earlier (1910–1930) or later (1975–1995) years. This same variability occurred with rainfall, whereas the temperature increased steadily over the time period. The years limited by temperature occurred mostly in the earlier and later periods, when rainfall was high and relatively stable. In contrast, the years with low MTCSI in the middle of the time period were primarily rainfall-limited. This change in variability was likely an artifact of the interpolation method used to generate the climate data (Appendix: Materials and Data), i.e., low variability occurred when rainfall measurements were unavailable within 450 km of the region.
In the Sahel (Fig. 2F), MTCSI was clearly limited by rainfall, with just 3 of the 85 years forced by temperature. The significant negative trend in MTCSI was a result of decreased precipitation over the time period, with a concentration of dry years since the late 1950s.
Discussion
Our analyses suggest malaria transmission suitability has increased because of the climate change in specific locations of limited extent in Africa. The majority of areas with variable transmission potential showed no evidence of trends in climatic suitability. Southern Mozambique was the only region for which climatic suitability consistently increased, and this was caused by increases in precipitation rather than temperature. Climate warming, expressed as a systematic temperature increase over the 85-year period, does not appear to be responsible for an increase in malaria suitability over any region in Africa. Areas where we found evidence that climate was becoming less suitable for transmission had all experienced decreased rainfall. Areas of highly variable, episodic climate suitability (the southwestern Congo basin and northwestern Tanzania) were also driven by fluctuations in rainfall rather than temperature. These results suggest research on the links between climate change and the recent resurgence of malaria across Africa would be best served through refinements in maps and models of precipitation patterns and through closer examination of the role of nonclimatic influences, such as the rise in drug resistance.
Acknowledgments
We acknowledge Stephen Prince, Sarah Randolph, David Rogers, Dennis Shanks, Bob Snow, David Stern, and Andrew Tatem for comments on the manuscript and Robb Wright for help with the graphics. This work was partially supported by National Aeronautics and Space Administration Grant NAG1302010 (to S.J.G.). S.I.H. is currently supported by a Research Career Development Fellowship from the Wellcome Trust (069045).
Appendix: Methods and Data
CRU TS 1.0 Data. The CRU TS 1.0 data-set (20) is unique for its long-term (1901–1995) availability and complete global coverage and has been used to study trends in African climate (29). This gridded data-set was developed by interpolating observations taken at meteorological stations. The CRU climate variables used in this study were mean monthly diurnal air temperature T, mean monthly rainfall total R, and mean monthly diurnal temperature range DTR. We estimated annual winter minimum temperature, Tmin, as min(Tm – 0.5DTRm), where m ranges over all months in the year. Because of the sparseness of observational data before 1911, we chose to exclude the first 10 years of data. Although station observations of diurnal air temperature were well distributed for most nondesert areas after 1911, measurements of monthly rainfall remained sparse in the Congo basin over much of the time period.
Additionally, diurnal temperature range records were sparse before 1941 for the entire continent and before 1961 for all but extreme southern Africa. For time periods where no meteorological station data existed within a specified distance (450 km for rainfall), the grid cell value is set to the long-term mean from the TS. Therefore, the rainfall TS in the Congo basin shows no variability for the time periods where observations within 450 km were not available. The lack of diurnal temperature range data is less problematic as we would expect the Tmin over a half-degree grid cell to have little affect on limiting malaria transmission for most of the African continent.
MTCSI Model. The MTCSI is defined by a series of curves y = cos2{[(x – U)/(S – U)]·(π/2)}, where x is a climate parameter, U is the value of x when conditions are unsuitable, and S is the value of x when conditions are suitable. When S > U, the suitability (1 – y) increases with x; when S < U, the suitability y decreases as x increases. The model defines monthly increasing (S = 22°C, U = 18°C) and decreasing (S = 22°C, U = 32°C) curves for T, a monthly increasing (S = 80 mm, U = 0 mm) curve for R, and a single increasing (S = 6°C, U = 4°C) curve for annual minimum temperature. For each month m = 1, 2,..., 12, we calculated the suitabilities yTm and yRm resulting from temperature and rainfall constraints, respectively. Monthly suitability ym was then computed as ym = min(yTm, yRm). For each year, the suitability yTmin because of annual minimum temperature was estimated by using Tmin = min(Tm – 0.5DTRm). The suitability index for year t is defined as MTCSIt = min(ymax, yTmin), where ymax = max(ym) persisting for 3 months poleward of 8° north latitude and 5 months elsewhere (19).
Augmented Dickey–Fuller Test. Each TS yt was initially fit by ordinary least-squares to a pth-order autoregressive model 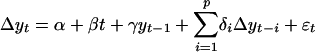 , where Δyn represents the differenced series at a lag of n years; α, β, γ, and the δi are constants; yt–1 is the series lagged 1 year; and the εt are random shocks. Lag order was increased stepwise from p = 0 to p = 4; p for the accepted model was that which maximized the adjusted r2 statistic for the regression. The standard errors SE(α), SE(β), and SE(γ) were estimated for parameters α, β, γ. The residuals εt were tested for autocorrelation by using the Q statistic
, where Δyn represents the differenced series at a lag of n years; α, β, γ, and the δi are constants; yt–1 is the series lagged 1 year; and the εt are random shocks. Lag order was increased stepwise from p = 0 to p = 4; p for the accepted model was that which maximized the adjusted r2 statistic for the regression. The standard errors SE(α), SE(β), and SE(γ) were estimated for parameters α, β, γ. The residuals εt were tested for autocorrelation by using the Q statistic
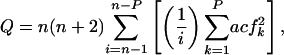 |
where acfk is the error autocorrelation function at lag k and P represents the maximum number of lags to consider (30). We used P = 24 for each fitted model, based on recommendations of P > 20 lags (31). Autocorrelation was sufficiently represented by the inclusion of four or fewer lags; for the 4,603 grid cells analyzed, only 115 had a Q statistic less than the 5% critical value, and these cells did not exhibit any obvious spatial pattern.
Each series was examined to determine its tendency toward being stationary by using the augmented Dickey–Fuller (26, 27) test statistic τt = γ/SE(γ) with null model (γ = 1, β = 0) and alternative (γ ≠ 1). If τt exceeded its order-adjusted 5% critical value (32) then the series was stationary, i.e., the effect of a random shock εi diminished over time and the series tended to revert to its mean value, α + βt. In this case we tested for a deterministic trend by comparing the test statistic τβ = β/SE(β) to the 5% critical value for the student's t distribution. If τβ exceeded the critical value, the series was classified as stationary with trend; otherwise the series was classified as stationary with no trend. For a stationary with trend series, the expected change in MTCSI over t years is βt.
If the null model (γ = 1, β = 0) could not be rejected, then the model was refit by ordinary least-squares but with the linear trend term βt omitted. The test statistic in this case was τα = α/SE(α), with null model (α = 0, β = 0, γ = 1) and alternative (α ≠ 0, β = 0, γ ≠ 1). If τα exceeded the 5% critical value (33), then the series was classified as a random walk with drift; otherwise the series was classified as a random walk with no drift. For a random walk with drift α, the expected value of the time series at time t is αt.
Abbreviations: MTCSI, malaria transmission climate suitability index; CSU, Climate Research Unit; TS, time series.
References
- 1.Lindsay, S. W. & Birley, M. H. (1996) Ann. Trop. Med. Parasitol. 90, 573–588. [DOI] [PubMed] [Google Scholar]
- 2.Detinova, T. S. (1962) Age-Grouping Methods in Diptera of Medical Importance with Special Reference to Some Vectors of Malaria, World Health Organization Monograph Series (World Health Organization, Geneva), No. 49. [PubMed]
- 3.MacDonald, G. (1957) The Epidemiology and Control of Malaria (Oxford Univ. Press, Oxford).
- 4.Davidson, G. (1954) Nature 174, 792–793. [DOI] [PubMed] [Google Scholar]
- 5.MacDonald, G. (1952) Trop. Dis. Bull. 49, 569. [PubMed] [Google Scholar]
- 6.Lindblade, K. A., Walker, E. D., Onapa, A. W., Katungu, J. & Wilson, M. L. (2000) Trop. Med. Int. Health 5, 263–274. [DOI] [PubMed] [Google Scholar]
- 7.Binka, F. N., Kubaje, A., Adjuik, M., Williams, L. A., Lengeler, C., Maude, G. H., Armah, G. E., Kajihara, B., Adiamah, J. H. & Smith, P. G. (1996) Trop. Med. Int. Health 1, 147–154. [DOI] [PubMed] [Google Scholar]
- 8.Snow, R. W., Mung'ala, V. O., Foster, D. & Marsh, K. (1994) Afr. J. Health Sci. 1, 71–75. [PubMed] [Google Scholar]
- 9.Alonso, P. L., Lindsay, S. W., Armstrong, J. R. M., Conteth, M., Hill, A. G., David, P. H., Fegan, G., Defrancisco, A., Hall, A. J., Shenton, F. C., et al (1991) Lancet 337, 1499–1502. [DOI] [PubMed] [Google Scholar]
- 10.Martens, P. & Hall, L. (2000) Emerging Infect. Dis. 6, 103–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Crowe, S. (1997) Lancet 350, 41–41. [DOI] [PubMed] [Google Scholar]
- 12.Snow, R. W., Trape, J. F. & Marsh, K. (2001) Trends Parasitol. 17, 593–597. [DOI] [PubMed] [Google Scholar]
- 13.Trape, J. F. (2001) Am. J. Trop. Med. Hyg. 64, 12–17. [DOI] [PubMed] [Google Scholar]
- 14.Shanks, G. D., Biomndo, K., Hay, S. I. & Snow, R. W. (2000) Trans. R. Soc. Trop. Med. Hyg. 94, 253–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bodker, R., Kisinza, W., Malima, R., Msangeni, H. & Lindsay, S. (2000) Glob. Change Hum. Health 1, 134–153. [Google Scholar]
- 16.Hay, S. I., Rogers, D. J., Randolph, S. E., Stern, D. I., Cox, J., Shanks, G. D. & Snow, R. W. (2002) Trends Parasitol. 18, 530–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mouchet, J., Manguin, S., Sircoulon, J., Laventure, S., Faye, O., Onapa, A. W., Carnevale, P., Julvez, J. & Fontenille, D. (1998) J. Am. Mosq. Control Assoc. 14, 121–130. [PubMed] [Google Scholar]
- 18.Rogers, D. J. & Randolph, S. E. (2000) Science 289, 1763–1766. [DOI] [PubMed] [Google Scholar]
- 19.Craig, M. H., Snow, R. W. & le Sueur, D. (1999) Parasitol. Today 15, 105–111. [DOI] [PubMed] [Google Scholar]
- 20.New, M., Hulme, M. & Jones, P. (2000) J. Clim. 13, 2217–2238. [Google Scholar]
- 21.Hay, S. I., Cox, J., Rogers, D. J., Randolph, S. E., Stern, D. I., Shanks, G. D., Myers, M. F. & Snow, R. W. (2002) Nature 415, 905–909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shanks, G. D., Hay, S. I., Stern, D. I., Biomndo, K. & Snow, R. W. (2002) Emerging Infect. Dis. 8, 1404–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Githeko, A. K. & Ndegwa, W. (2001) Glob. Change Hum. Health 2, 54–63. [Google Scholar]
- 24.Patz, J. A., Hulme, M., Rosenzweig, C., Mitchell, T. D., Goldberg, R. A., Githeko, A. K., Lele, S., McMichael, A. J. & le Sueur, D. (2002) Nature 420, 627–628. [DOI] [PubMed] [Google Scholar]
- 25.Hay, S. I., Cox, J., Rogers, D. J., Randolph, S. E., Stern, D. L., Shanks, G. D., Myers, M. F. & Snow, R. W. (2002) Nature 420, 628–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dickey, D. A. & Fuller, W. A. (1979) J. Am. Stat. Assoc. 74, 427–431. [Google Scholar]
- 27.Dickey, D. A. & Fuller, W. A. (1981) Econometrica 49, 1057–1072. [Google Scholar]
- 28.Omumbo, J. A., Hay, S. I., Goetz, S. J., Snow, R. W. & Rogers, D. J. (2002) Photogramm. Eng. Remote Sens. 68, 161–166. [PMC free article] [PubMed] [Google Scholar]
- 29.Hulme, M., Doherty, R., Ngara, T., New, M. & Lister, D. (2001) Clim. Res. 17, 145–168. [Google Scholar]
- 30.Ljung, G. M. & Box, G. E. P. (1978) Biometrika 65, 297–303. [Google Scholar]
- 31.Granger, W. J. & Newbold, P. (1977) Forecasting Economic Time Series (Academic, New York).
- 32.Cheung, Y. & Lai, K. S. (1995) J. Bus. Econ. Stat. 13, 277–280. [Google Scholar]
- 33.Fuller, W. A. (1976) Introduction to Statistical Time Series (Wiley, New York).