Abstract
Interest in the structure and function of physical biological networks has spurred the development of a number of theoretical models that predict optimal network structures across a broad array of taxonomic groups, from mammals to plants. In many cases, direct tests of predicted network structure are impossible given the lack of suitable empirical methods to quantify physical network geometry with sufficient scope and resolution. There is a long history of empirical methods to quantify the network structure of plants, from roots, to xylem networks in shoots and within leaves. However, with few exceptions, current methods emphasize the analysis of portions of, rather than entire networks. Here, we introduce the Leaf Extraction and Analysis Framework Graphical User Interface (LEAF GUI), a user-assisted software tool that facilitates improved empirical understanding of leaf network structure. LEAF GUI takes images of leaves where veins have been enhanced relative to the background, and following a series of interactive thresholding and cleaning steps, returns a suite of statistics and information on the structure of leaf venation networks and areoles. Metrics include the dimensions, position, and connectivity of all network veins, and the dimensions, shape, and position of the areoles they surround. Available for free download, the LEAF GUI software promises to facilitate improved understanding of the adaptive and ecological significance of leaf vein network structure.
Interest in the geometry and topology of complex networks has grown immensely during the last few decades (Albert and Barabasi, 2002; Newman et al., 2006). Studies of the structure of river networks (Rodriguez-Iturbe and Rinaldo, 1997; Dodds and Rothman, 2000), the internet (Albert and Barabasi, 2002), and social networks (Watts, 1999) have been driven by large amounts of empirical information, often with concomitant theoretical development to explain network structure. More relevant to the study of leaf networks is a resurgence of interest in the structure of physical networks in biology and, in particular, resource delivery networks like cardiovascular networks, xylem networks, or leaf venation networks as a whole (LaBarbera, 1990; Sperry et al., 2003; Sack and Holbrook, 2006; Scarpella et al., 2006; Donner and Scarpella, 2009). However, because of the inherent difficulty in measuring physical biological networks, the growth in theory has arguably outpaced the available data needed to test theoretical predictions or assumptions (West et al., 1997, 1999; Bejan, 2000; Couder et al., 2002; Price et al., 2007; Dodds, 2010).
Given the importance of physical networks in regulating the flow of biological fluid, one might think that libraries of data should exist with detailed measurements on their geometry from which one could evaluate theoretical predictions: this is not the case. While some data exist quantifying the dimensions of mammalian networks in their entirety (e.g. Zamir, 1996), less work has been done on plants (LaBarbera, 1990; McCulloh et al., 2003), and those descriptions that do exist are usually of a part of the network, not the whole. For example, there is a long history of measurements of components of the aboveground structure of xylem networks. Extensive measurements have been made of vein length distributions (Tyree and Zimmerman, 1983), width and scaling of xylem (Anfodillo et al., 2006; Weitz et al., 2006; Coomes et al., 2007; Mencuccini and Holtta, 2007), and even relative hydraulic resistance across distinct components of trees (Tyree and Sperry, 1989; Turcotte et al., 1998; McCulloh et al., 2003). In addition, there is a growing interest in describing detailed root network structure, largely applied to Arabidopsis (Arabidopsis thaliana) as well as to crop plants (French et al., 2009; Iyer-Pascuzzi et al., 2010; Le Bot et al., 2010).
Most attempts to quantify the hydraulic structure of physical networks in leaves have focused on quantification of the geometry of part of the leaf vascular network. By network we mean the hierarchical vessel bundles that pervade leaves and contain xylem, phloem, and structural elements. Those empirical measurements thus far include quantification of: the distribution of branching angles in several leaf species (Bohn et al., 2002), the lengths and diameters of vessel bundles in the side lobe of a leaf (Turcotte et al., 1998), the length per unit area of the higher-order veins (Sack and Frole, 2006; Brodribb et al., 2007; Boyce et al., 2009; Brodribb and Feild, 2010), or the length and width of the primary and sometimes secondary venation (Niinemets et al., 2007a, 2007b). We are aware of only one attempt to quantify the linear dimensions of an entire leaf network that relied on an admirable but painstaking point-and-click approach in relatively small Arabidopsis leaves (Rolland-Lagan et al., 2009), similar to that found in Figure 1, and leaves commonly used in developmental studies. Quantifying the geometry of entire leaf networks has remained elusive in part because of the sheer number of measurements required and because of the difficulties in automated image segmentation.
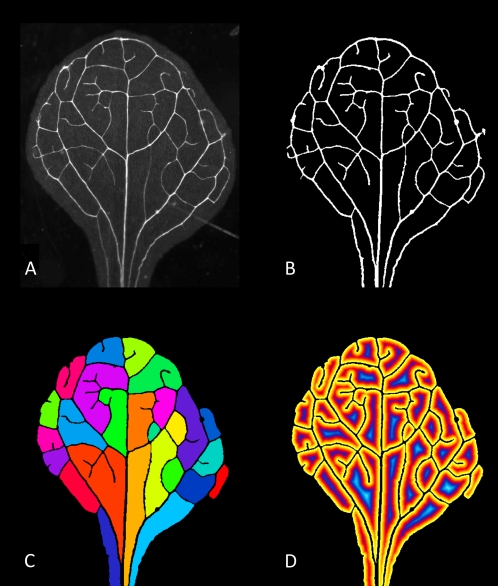
Figure 1.
Series of Arabidopsis images including, original image (A), results of thresholding and cleaning (B), colored labeled areoles (C), and the results of a distance transformation on the areoles (D). These images serve to demonstrate the utility of the software for analyzing images, such as those that might be found in developmental studies. Image in A graciously provided by E. Scarpella and originally published by Donner and Scarpella (2009).
Quantifying the geometry of leaf networks has significant implications for many areas of plant biology. (1) The structure of leaf networks has been implicated in the leaf economics spectrum, with several authors speculating that increased hydrodynamic and structural demands may lead to increased investment in vein networks as leaves become larger (Niinemets et al., 2007a, 2007b; Niklas et al., 2007). (2) Changes in leaf venation structure have the potential to influence mass- or area-based leaf photosynthetic rates via a reduction in specific leaf area, one of the principle dimensions underlying the leaf economics spectrum (Reich et al., 1997; Wright et al., 2004). (3) Recent studies have demonstrated that leaves are the major hydraulic bottleneck in plants (Sack and Holbrook, 2006); thus, detailed measures of vein geometry will inform attempts to model patterns of hydraulic conductance (Cochard et al., 2004). (4) Network structure can limit photosynthesis due to its effects on hydraulic efficiency, with recent studies implicating leaf vein density, defined as total vein length over area, as a strong predictor of photosynthetic rates (Sack and Frole, 2006; Brodribb et al., 2007), which may also have played a role in the diversification of early angiosperms (Brodribb and Feild, 2010; Brodribb et al., 2010). (5) Leaf vein patterning has been shown to be correlated with leaf shape, suggesting shared developmental pathways (Dengler and Kang, 2001). (6) Leaf vein impressions are arguably the most abundant plant macrofossil available to paleobotanists; thus, the ability to more rigorously quantify vein geometry has the potential to aid attempts to identify fossil samples with greater phylogenetic resolution (Behrenmeyer et al., 1992).
To help to address these and other issues we introduce a Leaf Extraction and Analysis Framework Graphical User Interface (LEAF GUI), a stand-alone, platform-independent, executable program available free for academic use. The LEAF GUI was developed in MATLAB and is built upon a series of algorithms designed to threshold, clean, and segment images of leaves in which the vein structure is visible. Vein visibility may be high due to enhancement via several means including, x-ray methods, chemical clearing, biological clearing, or backlit scanning (Bates, 1931; Lersten, 1986; Wing, 1992). Depending on user interests, the results may include information about areole shape and size, vein network connectivity, as well as number, length, width, and location of network edges and nodes. From these data, a large amount of information can be generated to test hypotheses regarding: (1) the structure of leaf hydraulic networks, (2) phylogenetic relationships among species, and (3) the ecological and evolutionary function of leaf vein networks.
OVERVIEW OF THE SOFTWARE SYSTEM
The following can be downloaded freely at http://www.leafgui.org: (1) LEAF GUI for Windows, Mac, and Linux (compiled); (2) detailed installation instructions; (3) user manual, including description of caveats and limitations (Supplemental Document S1); and (4) demonstration videos that illustrate different examples and functionality of the software. Annotated code is also available upon request from the primary author.
LEAF GUI is an interactive software program built in MATLAB. The purpose of the software is to dramatically increase the speed and accuracy of the extraction and processing of vascular and areole structure from digital images of leaves. The program incorporates many image processing and analysis tools into a single graphical user interface. The software is modular in construction, including preprocessing, image cleanup, and leaf network extraction steps. The interactivity of the software allows the user to extract features from monocot or dicot leaves that have been prepared, stained, and imaged using one of many standard protocols (Bates, 1931; Lersten, 1986; Wing, 1992). Although the processing of images is user assisted, the extraction of features is fully automated.
The overall process that a user might take to process a leaf image and measure structure within the leaf network can be broken down into five major steps: (1) setting the scale of the leaf image, (2) initial image cropping, (3) image thresholding, (4) binary image cleaning and processing, and (5) extracting leaf network features. The tools invoked in this series of steps (described in detail below) can be seen in a screenshot of the LEAF GUI with brief descriptions on the various functions it employs (Supplemental Fig. S1). A pipeline describing the workflow, statistics modules, and different image visualization options can be seen in Figure 2. Our software utilizes a number of standard routines included in the MATLAB image processing library and denoted in the code. We will not attempt to describe algorithms created by MATLAB: Extensive descriptions for these calls can be found on the MATLAB Web site (www.mathworks.com) or in the MATLAB documentation. We will describe in detail here only those algorithms that are unique to the LEAF GUI software. To simplify our introduction here, we will assume that the user is attempting to process an red, green, blue (color) image of a cleared leaf that contains some unwanted noise. Videos with examples of all of these steps can be seen on www.leafgui.org.
Figure 2.
Pipeline and processing options available in the LEAF GUI software. A, Screenshot of the LEAF GUI with an image of a leaf of Canarium tomentosum Bl., a member of the Burseraceae. Note images to the right of both the Original and Modified image sections correspond to the region contained within the zoom rectangle as seen in the original image. B, Pipeline illustrating the potential workflow of the software, and a number of the potential results. C, Seven examples of image segmentation and visualization options available as output from the software.
Many leaf networks are reticulate in contrast to hierarchical structures such as tree branches or roots. To describe the reticulate structure of a leaf network, we use conventional terms and their definitions from graph theory. In this manuscript and in the software, we refer to the vessel bundles in a leaf as edges and the point where two or more edges intersect as a node. A single individual edge is defined as the vessel bundle segment occurring between nodes. Thus, for example, the primary or midvein of a leaf would be viewed as a series of connected edges, rather than a single vein. Assuming edges can be approximated as cylinders, the geometry of each individual edge can be described using only its length and diameter. From these two measures, the surface area and volume of a leaf vein network are easily approximated.
STEP 1: SETTING THE SCALE
The conversion of pixels to a unit of length is required for network measurements. There are two options to set the scale, conventionally in pixels/mm. If the scale is known, it can be entered in the text box in the Set Scale panel. Alternatively, if the image contains a scale bar of length L (e.g. in mm), the user directs the software to measure the number of pixels Np in the given scale bar using the Measure Scale tool. The scale in this case will be set to Np/L (pixel/mm). A detailed explanation on how to set the scale is given in the manual and illustrated in Demo Video 2.
STEP 2: CROPPING THE INITIAL IMAGE
Two options are provided to crop the initial image: rectangular or polygonal cropping. Either cropping method is useful when extraneous features such as scale bars, labels, other leaves, or image noise need to be removed from the image. The choice between the two methods depends primarily on the location of the noise in the image. The cropping functions are demonstrated in Demo Video 3.
STEP 3: IMAGE THRESHOLDING AND SEGMENTATION
A necessary precursor to estimate the structure of a leaf vein network is to separate veins from the background. The identification of veins (also called segmentation) is accomplished in two steps: first, thresholding an image so that foreground regions (pixel value 1) are distinguished from background regions (pixel value 0); second, the resulting binary image is cleaned and processed (see next step). In many image analysis programs, the goal is to separate out distinct disconnected entities (like cells) from each other (e.g. Cell Profiler; Carpenter et al., 2006). Here, the objective is to identify edges (a vessel bundle segment) that are connected to each other at nodes.
Two different thresholding methods (local and global) are included in LEAF GUI to be used separately or combined to convert a leaf vein image into a binary image, where leaf veins are represented by ones and nonvein regions by zeros. Global thresholding takes a grayscale copy of the original image, where pixel values range from 0 to 255, and sets pixel values above a certain threshold to 1. Pixels with an intensity value lower than the threshold are set to 0. For example, if a threshold value is 125, then all pixels with a value of 125 or greater will constitute foreground, whereas pixel with lower values will represent background.
Unfortunately, global thresholding may produce poor results for unevenly illuminated images. Adaptive thresholding corrects for uneven illumination by comparing each pixel intensity value, pi, with the mean intensity value, Ii, computed over a local window of size w centered at the pixel. If pi is greater than Ii − X, for some fixed margin X, then the pixel becomes a part of the foreground; otherwise, its value is set to 0. The use of both thresholding methods is described in Demo Video 4.
STEP 4: BINARY IMAGE CLEANING AND PROCESSING
Once the image has been thresholded, a series of steps might be employed to further clean and enhance vein representation in the binary image. The choice and sequence are specific to the user requirements. These include removing unwanted connected regions below a certain size cutoff (e.g. all disconnected foreground regions smaller than 10 pixels), removing the leaf perimeter in single pixel-wide steps, filling single pixel holes, removing extraneous spurs (single pixel-wide extrusions), filling or removing user-specified polygonal regions, clearing regions overlapping the image border, or removing unwanted labeled (color coded) regions. At any point, the user can create a complement of the binary image (inverted image) and perform the same tasks on the part of the image that was previously background. The LEAF GUI also provides an option to create a mask through the use of a very high or low threshold value. In the resulting image, the leaf (everything within the leaf margin) is entirely white and the rest of the image is black. This step is useful in removing unwanted background noise following thresholding (see Demo Video 4).
At any point during this process, the user has the option to use one of several visualization options to inspect how well the image is being segmented. It is important for the user to evaluate image preprocessing and segmentation steps because they will affect computation of different leaf, vein network, and areole statistics. Some of the further computations that the user can make with the processed leaf image include the skeleton of the vein network and a distance transform function on either the areoles or veins (Figs. 1 and 3), labeling leaf veins or areoles (assigning a numerical identifier to each contiguous vein or areole region), both of which can indicate how well the network is connected and consequently how well areoles are delineated (see Demo Video 7).
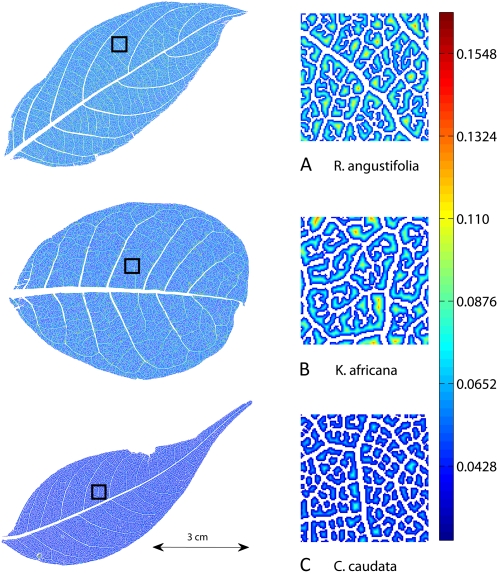
Figure 3.
Three leaves showing the results of vein segmentation and distance transformation options. The zoomed-in regions to the right correspond to the portions of the leaves within the black square on each whole-leaf image at left. Corresponding summary statistics for these three leaves are in Table I. Increasing distance from the nearest vein is indicated by colors at the yellow/red end of the spectrum as in the scale bar at right (mm). Note that the areoles and distance to nearest vein are generally smaller in C. caudata and larger in K. africana as also indicated in Table I.
STEP 5: SUMMARY STATISTICS
There are three primary options the user can select within the Summary Statistics Panel to return descriptive statistics from the leaf image. These are broken down into three buttons corresponding to the different types of statistics: Area Stats, Vein Stats, and Areole Stats. The output is either an Excel spreadsheet (which requires that Excel be installed) or a tab-delimited text file based on user preferences. Examples of all three output options are available as Excel spreadsheets in Supplemental Tables S1–S3 or at www.leafgui.org.
Area Stats
Area Stats returns the area, perimeter, and records the scale of the image. These measures are computed for the entire leaf (Supplemental Table S1).
Areole Stats
Areole Stats returns the area (Fig. 4), convex area (area of the convex hull that just encloses the region), solidity (the ratio of areole area to convex area), eccentricity (the ratio of the major and minor axis of the ellipse that just encloses the region), equivalent diameter (the diameter of a circle with the same area as the region), length of the major and minor axes of the ellipse that just encloses the region, centroid position (x and y coordinates of the region’s center of density), mean distance to the nearest vein, and its variance for each areole in the leaf (Supplemental Table S2).
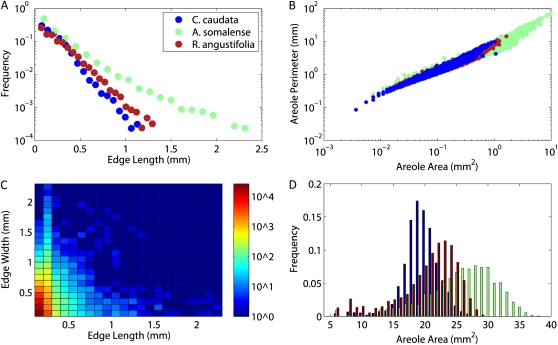
Figure 4.
Examples of some figures that can be generated from the statistics computed by the LEAF GUI software for the three leaves shown in Figure 3. Data shown are for illustration purposes only. A, Frequency distribution of vein lengths. B, Heat map of combined edge length and width frequencies. C, Plot of individual areole perimeter versus area. D, Histogram of areole area frequencies.
Vein Stats
Vein Stats returns two tables, the first (see sheet titled Vein_Stats in the Excel output option; Supplemental Table S3) containing a connectivity matrix, which is a NE × 3 matrix (NE is the number of edges) showing which labeled nodes (columns 2 and 3) are connected by which labeled edges (column 1). The table also contains the length (Fig. 4), width, and spatial position (centroid) of every edge and node of the vein network. In addition the software returns the two-dimensional (2D) area occupied by each edge and estimates for the surface area and volume based on the assumption that each edge is approximately cylindrical. The second table (see sheet titled Summary_Stats in the Excel output option; Supplemental Table S3) includes the total number of nodes and edges, the total length of the network, the total 2D area occupied by the network, and the mean edge length, width, 2D area, three-dimensional surface area, and volume.
NETWORK MEASUREMENT ALGORITHM
All measurement algorithms are performed on binary images where veins are represented in white, and the background is black. The binary image is first skeletonized. The skeleton of the image is obtained by repeatedly thinning the vein network until it is a single pixel wide. During thinning, boundary pixels are removed iteratively from different sides, resulting in the skeleton that consists of the central pixels of the network.
Labeling of individual edges requires a more complicated routine. First, we utilize a standard MATLAB routine to identify the skeleton branchpoints, which we refer to as nodes. However, to label the individual edges, they must be disconnected from each other. To do this, we remove all pixels that have three and more neighbors. As is apparent in Supplemental Fig. S2C, all branching points and some adjacent pixels may have three and more neighbors. By removing these pixels, we disconnect all edges of the network and then label them individually. We then separate the nodes, edges, and tips into three distinct images and then assign a unique numerical label to each individual node, edge, and tip, respectively. Supplemental Figure S2D shows a part of such labeled image of the vein network skeleton; the skeleton consists of edges (labels 112, 103, 120, 125, and 126) and nodes (labels 67 and 71).
We then apply a distance transformation to the original binary image, which indicates the distance from each network pixel (white) to the nearest nonnetwork pixel (black; Supplemental Fig. S2A). The pixel-by-pixel product of this distance transformation image and the skeleton image results in an image that represents the skeleton of the entire network with the distance to the nearest areole (nonvein region) recorded in each pixel (Supplemental Fig. S2B).
To calculate the dimensions of each individual edge, we treat each edge as a series of connected cylinders. Each cylinder is a single pixel in length, the diameter of which is approximated by doubling the value of the distance transform from the previous step, i.e. twice the distance from the medial axis to the nearest nonvein pixel. The total length of the edge is then calculated by walking along its medial axis counting one unit for pixels that share a border, and square root of 2 for pixels that touch on their corners. The diameter of each edge is the mean of the diameters in each skeleton pixel it contains (Supplemental Fig. S2, A and D). The total edge surface area and edge volume are then estimated as 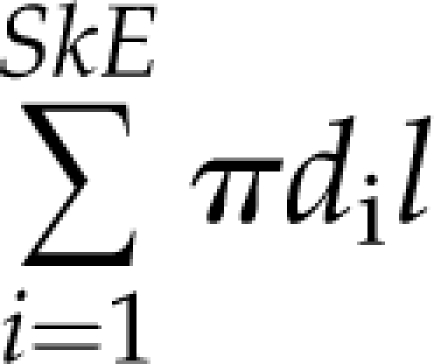 and
and 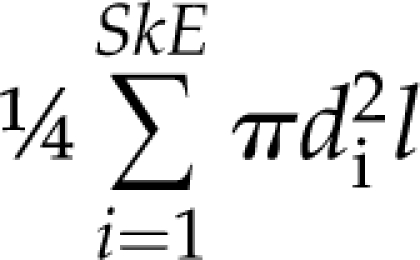 correspondingly, where SkE is the number of pixels in the edge, di is the diameter of the i-th pixel of the edge, and l is the length of a single pixel.
correspondingly, where SkE is the number of pixels in the edge, di is the diameter of the i-th pixel of the edge, and l is the length of a single pixel.
NETWORK CONNECTIVITY ALGORITHM
To generate a connectivity matrix, the 3 × 3 neighborhood around each node is searched to see what edges it is connected to (Supplemental Fig. S2D). The connectivity matrix is then represented as an N × N matrix where N is the number of nodes, rows and column indices represent the list of nodes, and matrix entries are the labels of the edges that connect nodes. This matrix is very sparse (i.e. E << N2, where E is the number of edges); thus, we store it in the condensed form as an E × 3 matrix showing which labeled edges (column 1) are connected by which labeled nodes (columns 2 and 3).
FURTHER COMPUTATIONS
In addition to leaf area and leaf perimeter, the output from the Vein Stats algorithms allows the calculation of cumulative statistics for the entire leaf such as the total number of nodes, total number of edges, total network length, and total network 2D area. Using the distribution of edge dimensions contained in the Vein Stats table, one can also calculate the mean, median, mode, maximum, and minimum for any and all edge measures. Moreover, one can look at the distributions of edge dimensions and compare them with those predicted by theory. Using the Vein Stats table, one can easily plot the data to evaluate theoretical predictions. Similarly, the output from the Areole Stats algorithms can be used to calculate statistics such as total areole area or the frequency distribution of areole sizes or shapes. An example of such cumulative statistics computed for three different leaves is shown in Figure 4. In addition, the combined output data can allow the user to calculate additional summary measures of leaf morphology such as the vein density (network length/leaf area), network volume/leaf area, network surface area/leaf area, or total areole area/leaf area.
THREE-LEAF ANALYSES: NETWORK AND AREOLE DIMENSIONS
To demonstrate the functional capabilities of the LEAF GUI, we present data from the analysis of three-leaf images obtained from the National Cleared Leaf Collection, housed at the American Museum of Natural History (Scott Wing curator). The three species are: Kigelia africana (Apocynaceae), Castanopsis caudata (Fagaceae), and Rockinghamia angustifolia (Euphorbiaceae). The three leaves were chosen somewhat at random, the only criteria for selection being clarity of their venation structure (Fig. 3). All three leaf images were obtained via chemical clearing methods. The data we present are for heuristic purposes only; thus, we are not testing any hypothesis per se. Rather, we are demonstrating some types of measurements and analyses that can be performed using LEAF GUI. All three leaves were thresholded with a global threshold level of 160, and a local threshold of 0.01 with a local window size of 10. Contiguous regions in the image smaller than 5 pixels were removed, isolated single black pixels surrounded by white pixels were filled, and the Remove Spurs option was utilized once.
Table I shows the mean and cumulative measures for the whole-leaf, vein network, and areole statistics that were generated by the LEAF GUI software. The three leaves differ in number of edges and areoles, mean edge length, mean areole area, and a number of other associated measures. These differences may be due to the hydrodynamic demands of the habitats in which these species are found, phylogenetic conservation of vein morphology, or some other factor; it is beyond the scope of this article to analyze the basis for such differences. Not surprisingly, many vein and areole measures are correlated with one another. For example, K. africana has fewer areoles per unit area than the other two species, and its mean areole size and perimeter are larger. In addition, K. africana has fewer edges per unit area, but each individual edge is larger than the other two species and the total vein density is less.
Table I. Processing times and summary statistics for the three leaves depicted in Figure 3.
Whole-leaf statistics are denoted in rows 4 to 15. Areole summary statistics are given in rows 15 to 23, and edge summary statistics are given in rows 26 to 30. Calculation times are reported for a server with a 1.86-GHz processor with 16 GB of RAM and for a laptop with a 998-MHz processor with 2 GB of RAM, respectively. These represent the time it took to return statistics after the leaf image had been thresholded and cleaned. Note that as would be expected, many statistics are correlated with each other; for example, mean areole area and mean edge length are largest in K. africana and smallest in C. caudata, with R. angustifolia intermediate.
| Statistics for the Three Leaves Depicted in Figure 3 | |||
| Family: | Fagaceae | Euphorbiaceae | Apocynaceae |
| Species: | C. caudata | R. angustifolia | K. africana |
| Whole-leaf statistics | |||
| Time to calculate (s) | 66/196 | 58/190 | 84/264 |
| Leaf area (mm2) | 1,723.02 | 2,065.69 | 3,219.07 |
| Leaf perimeter (mm) | 228.99 | 220.35 | 230.54 |
| No. of nodes | 17,465 | 16,334 | 18,099 |
| No. of edges | 25,424 | 24,703 | 29,261 |
| Edges/node | 1.46 | 1.51 | 1.62 |
| No. of areoles | 7,243 | 5,582 | 1,989 |
| Total network length (mm) | 7,410.31 | 7,966.50 | 9,992.85 |
| Vein density (mm/mm2) | 4.30 | 3.86 | 3.10 |
| Total network 2D area (mm2) | 747.71 | 808.89 | 1,230.68 |
| Areoles/area | 4.20 | 2.70 | 0.62 |
| Edges/area | 14.76 | 11.96 | 9.09 |
| Network area/area | 0.43 | 0.39 | 0.38 |
| Areole statistics | |||
| Time to calculate (s) | 38/57 | 32/44 | 19/26 |
| Mean area (mm2) | 0.1294 | 0.2168 | 0.9639 |
| Mean convex area (mm2) | 0.1578 | 0.2712 | 1.4787 |
| Mean eccentricity | 0.7580 | 0.7765 | 0.7509 |
| Mean solidity | 0.8826 | 0.8627 | 0.7621 |
| Mean perimeter (mm) | 1.5155 | 2.1768 | 7.2206 |
| Mean equiv diameter (mm) | 0.3839 | 0.4760 | 0.9354 |
| Mean major axis (mm) | 0.5622 | 0.7153 | 1.5589 |
| Mean minor axis (mm) | 0.3184 | 0.3994 | 0.8773 |
| Mean distance (mm) | 0.0656 | 0.0691 | 0.0764 |
| Edge statistics | |||
| Mean length (mm) | 0.2028 | 0.2315 | 0.2442 |
| Mean width (mm) | 0.1244 | 0.1294 | 0.1365 |
| Mean area (mm2) | 0.0287 | 0.0339 | 0.0415 |
| Mean surface area (mm2) | 0.0902 | 0.1064 | 0.1305 |
| Mean volume (mm3) | 0.0042 | 0.0067 | 0.0122 |
DISCUSSION
The LEAF GUI software is designed for plant biologists and ecologists who wish to analyze the macroscopic structure of veins in leaves. The software allows users to extract descriptive statistics on the dimensions and positions of leaf veins and the areoles they surround by following a series of thresholding, cleaning, and segmentation algorithms given images of leaves where veins have been enhanced relative to the background. The data returned by the LEAF GUI software have the potential to address many long-standing questions in leaf biology and functional ecology. Moreover, several theories have been proffered regarding the structure of leaf vein networks. For example, Price and Enquist (2007) hypothesized that leaf networks might be approximated by fractal structures with underlying power law distributed vein radii and lengths. Alternatively, Banavar and colleagues (1999) suggested power law relationships between network volume and length determined by leaf dimension. These are two examples from a growing number of recent theoretical attempts in need of empirical validation (Banavar et al., 1999; Couder et al., 2002; Runions et al., 2005; Dimitrov and Zucker, 2006; Price and Enquist, 2007; Dodds, 2010; Katifori et al., 2010). However, as mentioned above, to date there has been very limited data with which to test these theories.
The data provided in Table I and Figure 4 serve to illustrate potential tests of the aforementioned theories, and a few of the many types of analyses one could perform using the software. Many of these questions will involve quantifying the investment in vein mass or vein surface area per unit leaf mass or leaf surface area, and placing various investment strategies in ecological or phylogenetic contexts. For example recent work has shown that leaf vein density is correlated with photosynthetic rate and may have played a role in early angiosperm diversification (Brodribb et al., 2007; Brodribb and Feild, 2010).
In addition, a methodology to quantify the structure of leaf vein networks has the potential to add rigor to the classification and description of leaves. For example, current classification of leaves is based on the idea that individual veins fall into discrete rank classes based on vein diameter (Leaf Architecture Working Group, 1999). However, leaf vein sizes vary continuously and many veins appear to change size as they progress through the leaf lamina. While we readily admit that the traditional approach has been very useful in distilling the dizzying array of venation morphologies into useful categories, the concept of vein rank is itself somewhat subjective. Our methods can begin to address this question by providing much more detail regarding the size, position, and connectivity of leaf vein networks, enabling network descriptions and classification based on their inherent continuous nature.
Image segmentation in computer vision is not a trivial issue, and an entire field has developed to address the problem (Haralick and Shapiro, 1985; Sezgin and Sankur, 2004). Thus the extent to which the measurements produced by the LEAF GUI represent actual leaf traits depends both on initial image quality, and the effectiveness of our image processing and feature-extracting algorithms. Further, because LEAF GUI is user assisted, it has the advantage of being able to extract useful information from images of leaf venation networks with variable clearing and imaging methods. Similar approaches have also been taken in the study of root networks (e.g. Le Bot et al., 2010). However because LEAF GUI is user assisted, it is currently not possible to apply the same set of cleaning and extraction steps to a set of images automatically. We hope to address questions of automation in future versions of the software.
In summary, the network structures generated in the use of LEAF GUI are imperfect representations of leaf networks, and future developments, both in the imaging of leaf networks, and in image segmentation, will certainly improve our ability to accurately measure the dimensions of leaf networks. These caveats notwithstanding, the collection of algorithms detailed herein provides a means with which to accurately and rapidly extract network and areole information from leaves imaged under a wide range of conditions. Moreover, because the software and the underlying code are freely available, other investigators have the option to modify methods as needed to answer specific questions, or improve upon current approaches.
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Figure S1. LEAF GUI screenshot with explanatory side text.
Supplemental Figure S2. Series of panels demonstrating aspects of the network measurement algorithm.
Supplemental Table S1. Leaf area statistics.
Supplemental Table S2. Leaf areole statistics.
Supplemental Table S3. Leaf vein statistics.
Supplemental Document S1. LEAF GUI user manual.
Supplementary Material
Acknowledgments
We would like to thank Jane Price and three anonymous reviewers for comments on an earlier draft of this manuscript.
References
- Albert R, Barabasi AL. (2002) Statistical mechanics of complex networks. Rev Mod Phys 74: 47–97 [Google Scholar]
- Anfodillo T, Carraro V, Carrer M, Fior C, Rossi S. (2006) Convergent tapering of xylem conduits in different woody species. New Phytol 169: 279–290 [DOI] [PubMed] [Google Scholar]
- Banavar JR, Maritan A, Rinaldo A. (1999) Size and form in efficient transportation networks. Nature 399: 130–132 [DOI] [PubMed] [Google Scholar]
- Bates JC. (1931) A method for clearing leaves. Am Nat 65: 288 [Google Scholar]
- Behrenmeyer AK, Damuth JD, DiMichele WA, Potts R, Sues HD, Wing SL. (1992) Terrestrial Ecosystems Through Time: Evolutionary Paleoecology of Terrestrial Plants and Animals. University of Chicago Press, Chicago [Google Scholar]
- Bejan A. (2000) Shape and Structure, from Engineering to Nature. Cambridge University Press, Cambridge, UK [Google Scholar]
- Bohn S, Andreotti B, Douady S, Munzinger J, Couder Y. (2002) Constitutive property of the local organization of leaf venation networks. Phys Rev E Stat Nonlin Soft Matter Phys 65: 061914. [DOI] [PubMed] [Google Scholar]
- Boyce CK, Brodribb TJ, Feild TS, Zwieniecki MA. (2009) Angiosperm leaf vein evolution was physiologically and environmentally transformative. Proc Biol Sci 276: 1771–1776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodribb TJ, Feild TS. (2010) Leaf hydraulic evolution led a surge in leaf photosynthetic capacity during early angiosperm diversification. Ecol Lett 13: 175–183 [DOI] [PubMed] [Google Scholar]
- Brodribb TJ, Feild TS, Jordan GJ. (2007) Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiol 144: 1890–1898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodribb TJ, Feild TS, Sack L. (2010) Viewing leaf structure and evolution from a hydraulic perspective. Funct Plant Biol 37: 488–498 [Google Scholar]
- Carpenter AE, Jones TR, Lamprecht MR, Clarke C, Kang IH, Friman O, Guertin DA, Chang JH, Lindquist RA, Moffat J, et al. (2006) CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol 7: R100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cochard H, Nardini A, Coll L. (2004) Hydraulic architecture of leaf blades: where is the main resistance? Plant Cell Environ 27: 1257–1267 [Google Scholar]
- Coomes DA, Jenkins KL, Cole LES. (2007) Scaling of tree vascular transport systems along gradients of nutrient supply and altitude. Biol Lett 3: 86–89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couder Y, Pauchard L, Allain C, Adda-Bedia M, Douady S. (2002) The leaf venation as formed in a tensorial field. Eur Phys J B 28: 135–138 [Google Scholar]
- Dengler N, Kang J. (2001) Vascular patterning and leaf shape. Curr Opin Plant Biol 4: 50–56 [DOI] [PubMed] [Google Scholar]
- Dimitrov P, Zucker SW. (2006) A constant production hypothesis guides leaf venation patterning. Proc Natl Acad Sci USA 103: 9363–9368 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodds PS. (2010) Optimal form of branching supply and collection networks. Phys Rev Lett 104: 048702. [DOI] [PubMed] [Google Scholar]
- Dodds PS, Rothman DH. (2000) Scaling, universality and geomorphology. Annu Rev Earth Planet Sci 28: 571–610 [Google Scholar]
- Donner TJ, Scarpella E. (2009) Auxin-transport-dependent leaf vein formation. Botany 87: 678–684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- French A, Ubeda-Tomás S, Holman TJ, Bennett MJ, Pridmore T. (2009) High-throughput quantification of root growth using a novel image-analysis tool. Plant Physiol 150: 1784–1795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haralick RM, Shapiro LG. (1985) Image segmentation techniques. Comput Vis Graph Image Process 29: 100–132 [Google Scholar]
- Iyer-Pascuzzi AS, Symonova O, Mileyko Y, Hao YL, Belcher H, Harer J, Weitz JS, Benfey PN. (2010) Imaging and analysis platform for automatic phenotyping and trait ranking of plant root systems. Plant Physiol 152: 1148–1157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katifori E, Szöllosi GJ, Magnasco MO. (2010) Damage and fluctuations induce loops in optimal transport networks. Phys Rev Lett 104: 048704. [DOI] [PubMed] [Google Scholar]
- LaBarbera M. (1990) Principles of design of fluid transport systems in zoology. Science 249: 992–1000 [DOI] [PubMed] [Google Scholar]
- Le Bot J, Serra V, Fabre J, Draye X, Adamowicz S, Pages L. (2010) DART: a software to analyse root system architecture and development from captured images. Plant Soil 326: 261–273 [Google Scholar]
- Leaf Architecture Working Group (1999) Manual of Leaf Architecture. Smithsonian Institution [Google Scholar]
- Lersten NR. (1986) Modified clearing method to show sieve tubes in minor veins of leaves. Stain Technol 61: 231–234 [DOI] [PubMed] [Google Scholar]
- McCulloh KA, Sperry JS, Adler FR. (2003) Water transport in plants obeys Murray’s law. Nature 421: 939–942 [DOI] [PubMed] [Google Scholar]
- Mencuccini M, Holtta T. (2007) Sanio’s laws revisited. Size-dependent changes in the xylem architecture of trees. Ecol Lett 10: 1084–1093 [DOI] [PubMed] [Google Scholar]
- Newman MEJ, Barabasi AL, Watts DJ. (2006) The Structure and Dynamics of Complex Networks. Princeton University Press, Princeton [Google Scholar]
- Niinemets U, Portsmuth A, Tena D, Tobias M, Matesanz S, Valladares F. (2007a) Do we underestimate the importance of leaf size in plant economics? Disproportional scaling of support costs within the spectrum of leaf physiognomy. Ann Bot (Lond) 100: 283–303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niinemets U, Portsmuth A, Tobias M. (2007b) Leaf shape and venation pattern alter the support investments within leaf lamina in temperate species: a neglected source of leaf physiological differentiation? Funct Ecol 21: 28–40 [Google Scholar]
- Niklas KJ, Cobb ED, Niinemets Ü, Reich PB, Sellin A, Shipley B, Wright IJ. (2007) “Diminishing returns” in the scaling of functional leaf traits across and within species groups. Proc Natl Acad Sci USA 104: 8891–8896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price CA, Enquist BJ. (2007) Scaling mass and morphology in leaves: an extension of the WBE model. Ecology 88: 1132–1141 [DOI] [PubMed] [Google Scholar]
- Price CA, Enquist BJ, Savage VM. (2007) A general model for allometric covariation in botanical form and function. Proc Natl Acad Sci USA 104: 13204–13209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich PB, Walters MB, Ellsworth DS. (1997) From tropics to tundra: global convergence in plant functioning. Proc Natl Acad Sci USA 94: 13730–13734 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Iturbe I, Rinaldo A. (1997) Fractal River Basins: Chance and Self-Organization. Cambridge University Press, New York [Google Scholar]
- Rolland-Lagan AG, Amin M, Pakulska M. (2009) Quantifying leaf venation patterns: two-dimensional maps. Plant J 57: 195–205 [DOI] [PubMed] [Google Scholar]
- Runions A, Fuhrer M, Lane B, Federl P, Rolland-Lagan AG, Prusinkiewicz P. (2005) Modeling and visualization of leaf venation patterns. ACM Trans Graph 24: 702–711 [Google Scholar]
- Sack L, Frole K. (2006) Leaf structural diversity is related to hydraulic capacity in tropical rain forest trees. Ecology 87: 483–491 [DOI] [PubMed] [Google Scholar]
- Sack L, Holbrook NM. (2006) Leaf hydraulics. Annu Rev Plant Biol 57: 361–381 [DOI] [PubMed] [Google Scholar]
- Scarpella E, Marcos D, Friml J, Berleth T. (2006) Control of leaf vascular patterning by polar auxin transport. Genes Dev 20: 1015–1027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sezgin M, Sankur B. (2004) Survey over image thresholding techniques and quantitative performance evaluation. J Electron Imaging 13: 146–168 [Google Scholar]
- Sperry J, Stiller V, Hacke U. (2003) Xylem hydraulics and the soil-plant-atmosphere continuum: opportunities and unresolved issues. Agron J 95: 1362–1370 [Google Scholar]
- Turcotte DL, Pelletier JD, Newman WI. (1998) Networks with side branching in biology. J Theor Biol 193: 577–592 [DOI] [PubMed] [Google Scholar]
- Tyree MT, Sperry JS. (1989) Vulnerability of xylem to cavitation and embolism. Annu Rev Plant Physiol Plant Mol Biol 40: 19–38 [Google Scholar]
- Tyree MT, Zimmerman MH. (1983) Xylem Structure and the Ascent of Sap. Springer-Verlag, Berlin [Google Scholar]
- Watts DJ. (1999) Networks, dynamics, and the small-world phenomenon. Am J Sociol 105: 493–527 [Google Scholar]
- Weitz JS, Ogle K, Horn HS. (2006) Ontogenetically stable hydraulic design in woody plants. Funct Ecol 20: 191–199 [Google Scholar]
- West GB, Brown JH, Enquist BJ. (1997) A general model for the origin of allometric scaling laws in biology. Science 276: 122–126 [DOI] [PubMed] [Google Scholar]
- West GB, Brown JH, Enquist BJ. (1999) A general model for the structure and allometry of plant vascular systems. Nature 400: 664–667 [Google Scholar]
- Wing SL. (1992) High-resolution leaf x-radiology in systematics and paleobotany. Am J Bot 79: 1320–1324 [Google Scholar]
- Wright IJ, Reich PB, Westoby M, Ackerly DD, Baruch Z, Bongers F, Cavender-Bares J, Chapin T, Cornelissen JHC, Diemer M, et al. (2004) The worldwide leaf economics spectrum. Nature 428: 821–827 [DOI] [PubMed] [Google Scholar]
- Zamir M. (1996) Tree structure and branching characteristics of the right coronary artery in a right-dominant human heart. Can J Cardiol 12: 593–599 [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.