Mechanical Properties of Plant Cell Walls Probed by Relaxation Spectra^,,

Abstract

Transformants and mutants with altered cell wall composition are expected to display a biomechanical phenotype due to the structural role of the cell wall. It is often quite difficult, however, to distinguish the mechanical behavior of a mutant's or transformant's cell walls from that of the wild type. This may be due to the plant’s ability to compensate for the wall modification or because the biophysical method that is often employed, determination of simple elastic modulus and breakstrength, lacks the resolving power necessary for detecting subtle mechanical phenotypes. Here, we apply a method, determination of relaxation spectra, which probes, and can separate, the viscoelastic properties of different cell wall components (i.e. those properties that depend on the elastic behavior of load-bearing wall polymers combined with viscous interactions between them). A computer program, BayesRelax, that deduces relaxation spectra from appropriate rheological measurements is presented and made accessible through a Web interface. BayesRelax models the cell wall as a continuum of relaxing elements, and the ability of the method to resolve small differences in cell wall mechanical properties is demonstrated using tuber tissue from wild-type and transgenic potatoes (Solanum tuberosum) that differ in rhamnogalacturonan I side chain structure.

The cell wall of higher plants is a composite material consisting of threadlike, partially crystalline cellulose microfibrils embedded in a hydrated matrix of pectins, hemicelluloses, and glycoproteins. In vascular plants, more than 200 genes encoding glycosyl transferases, and an unknown number of genes from other families, are probably devoted to the synthesis and assembly of cell wall polysaccharides. The structural complexity of plant cell walls may seem surprising, if conveying mechanical strength to the plant body were their only role, but this is not their only role, as displayed in the review by Jarvis and McCann (2000).

It has long been recognized that permitting the cell wall to expand during growth, and coordinating this expansion with concurrent deposition of new wall material, requires rather sophisticated control over wall rheological properties. “Properties” here refer to diverse phenomena, not only purely physical responses to stresses but also mechanical behavior that arises from enzymatic processes involved in growth and that may be lost in isolated or “dead” wall preparations. Cosgrove (1993) reviewed methods that have been used to gauge these respective aspects of cell wall mechanics, and Schopfer (2006) discussed pitfalls in data interpretation that can result from not appreciating this distinction. Yet, ever since Kamiya et al. (1963), it has been clear that plant cell walls exhibit viscoelastic properties like retarded elasticity, and most workers since Probine and Preston (1962) have assumed that these properties should be important to cell growth and/or other aspects of plant cell function that depend on cell wall behavior (Thompson, 2008).

The discoveries of xyloglucan endotransglycosylases (Nishitani and Tominaga, 1992; Fry et al., 1992) and expansins (McQueen-Mason et al., 1992) stimulated research into the biochemical aspects of cell enlargement and a search for gene products that stimulate it, while characterization of cell wall material properties concurrently tended to receive less attention. Cosgrove (1993) foresaw, however, that the ability to alter single wall components in controlled ways (e.g. using mutants or transformants) would allow us to relate wall structure and polymer composition to both rheological theory and physiological function. Mechanically significant structural changes in mutants may not necessarily be easily detectable by determining monosaccharide profiles (Bosca et al., 2006) or from other types of relatively simple compositional analysis. Architectural modifications may occur that impact wall mechanical properties and are detectable by appropriate biophysical methods but for which all but the most detailed chemical analyses fall short. Biophysical analysis has yet to be employed as a screen to identify cell wall mutants, but a number of characterized mutants have been found to have altered cell wall mechanical properties (Reiter et al., 1993; Ryden et al., 2003; Peña et al., 2004; Zhong et al., 2005).

Although mechanical measurements on cell walls, stimulated by the issue of how walls extend during growth, go back at least to the Dutch botanist A.N.J. Heyn (1933), in most of this work, load or stress was recorded at a fixed rate of extension (Cleland, 1967), which does not afford a clear measure of time-dependent rheological properties. Measurement of “creep” under a constant load (Probine and Preston, 1962) can reveal these, but probably the most incisive type of biomechanical analysis, and the one most capable of detecting subtle changes in cell wall rheology, is to determine stress relaxation spectra.

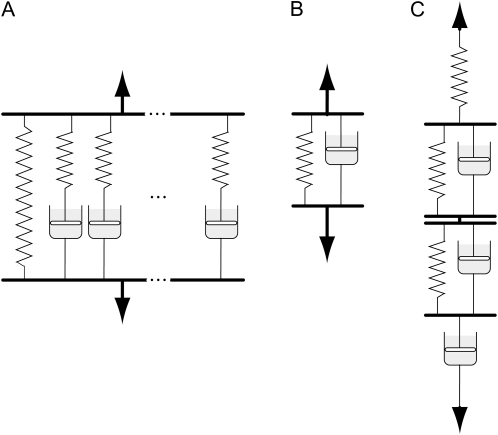
Stress relaxation is a time-dependent decline in stress (or load) when a material is held at a constant, initially load-induced, mechanical deformation or strain. Stress relaxation, and retarded elasticity, reflect viscosity-retarded changes in conformation or position of load-bearing polymer chains. Different changes of this type can occur over widely different time scales, depending on how local or long range these chain displacements are and how large a viscosity consequently restricts them. Mathematical analysis of overall behavior is achieved by considering the behavior of analogous mechanical models containing multiple elements, as in Figure 1, A (for stress relaxation) and C (for retarded elasticity). Any given type of viscosity-restricted conformational change (a single element in Fig. 1, A or C) possesses a characteristic relaxation or retardation time (τ), or time to proceed exponentially all but [1/e]th, or 63.2%, of the way to completion. A relaxation spectrum displays the distribution of different τ values (and hence of rheologically differing mechanical elements) in the material and their relative importance. The “mechanical elements” are often modeled by arrangements of springs and “dashpots,” as in Figure 1. Figure 1A represents the model behind BayesRelax, that is, where the wall polymers are represented by a continuous spectrum of relaxing components (approximated by 100 elements in the algorithm). To deduce a relaxation spectrum from stress relaxation measurements in the most general way, one starts with the possibility that the material could possess many different relaxation mechanisms with τs extending over a wide range; the peaks, at particular τ values, in the spectrum reflect which of these mechanisms are mechanically more important. A specific wall polymer modification that affects just one particular relaxation mechanism might thus be expected to alter some particular part of the relaxation spectrum, even if it does not greatly change the mechanical behavior of the wall overall. This is what makes stress relaxation spectral measurements potentially more sensitive, for detecting subtle changes in cell wall mechanical properties, than simple rheological measurements are.

Figure 1.

Physical models used for analyzing measurements obtained in relaxation, frequency sweep, and creep experiments. A, Generalized Maxwell model, the vertical components of which (except for the simple spring at left) are called Maxwell elements. B, A single Kelvin/Voigt element. C, A Burgers model, containing three elements (two Kelvin/Voigt and one Maxwell) if the spring and dashpot, respectively, at the top and bottom are regarded as a single Maxwell element.

The earliest measurements of stress relaxation in plant cell walls of which we are aware were made by Haughton et al. (1968) and Haughton and Sellen (1969) on four species of algae. Shortly thereafter, Cleland and Haughton (1971) reported stress relaxation curves for oat (Avena sativa) coleoptile cell wall skeletons (intact wall structure of killed tissue). Throughout that decade, Yamamoto, Masuda, and coworkers pursued stress relaxation measurements with coleoptiles and other higher plant cell walls (Yamamoto et al., 1970; Yamamoto and Masuda, 1971; Fujihara et al., 1978; Sakurai et al., 1982), deducing relaxation spectra from simple time courses of stress relaxation. In hindsight, this was a relatively insensitive basis for obtaining relaxation spectra, and these workers lacked more recently developed mathematical tools for analyzing stress relaxation.

A more incisive method for deducing relaxation spectra, applicable to a wider range of relaxation times than can be covered by simple relaxation time courses, is “dynamic” measurement of the variation of stress under an oscillating (usually sinusoidally varying) strain. Dynamic measurements at a single frequency, which have widely been used on food materials and wood and in a few instances on thin-walled plant tissues (Ramana and Taylor, 1994; Takeda et al., 2002), are interesting but do not enable a relaxation spectrum to be deduced. This is possible only if dynamic measurements are made over a range of oscillation frequencies (Findley et al., 1976), which is often called a “frequency sweep.” The main advantages of this method are that (1) rapid relaxation processes (having subsecond relaxation times) can be detected and quantified, and (2) relaxations with longer relaxation times can be characterized more accurately than when they are deduced from small deviations of a time course from a simple exponential decline of stress. The method has been used for analyzing the mechanical properties of wood (Ouis, 2002, and refs. therein) and is introduced for thin, primary plant cell walls in this work. (Frequency sweep measurements were made previously by Whitney et al. [1999] on homogenized tomato [Solanum lycopersicum] fruit cell walls and bacterial cellulose/xyloglucan composites, but they did not deduce relaxation spectra from their data.)

Determining relaxation spectra from frequency sweep biophysical data is not trivial; it is what is termed an “ill-posed problem,” meaning that experimental error due to imprecision of measurement may permit many, including some quite different, solutions. Methods to handle ill-posed problems have been developed (Tikhonov and Arsenin, 1977) and are frequently used in the physical sciences, but apart from limited use in food science, they have thus far received rather little attention in biology.

In most applications, an ill-posed relaxation spectrum problem is “solved” by imposing upon the connection between the data and the spectrum an additional constraint called “regularization.” For example, the “smoothness” regularization constraint gives preference to smoother solutions, suppressing the emergence of spurious spectral peaks. We take this approach here, applying the most recent advances in handling ill-posed problems (Hansen, 2008) to the analysis of cell wall rheology in intact plant tissue. The only spectral peaks allowed by smoothness regularization are those that are required to obtain a satisfactory fit to the experimental data. This conservative approach means that data sets with small relative variance will usually give more feature-rich relaxation spectra than more noisy data sets will. The computer program developed for this study, BayesRelax, as well as a user’s guide, are made available to the scientific community through the Web site at www.BayesRelax.org.

We employ potato (Solanum tuberosum) tuber tissue, both wild type and transgenic tissue with altered rhamnogalacturonan I (RG-I) side chains, as a case study of the use of BayesRelax. Compared with the wild type, the transformants are reduced either in RG-I β-1,4-galactans (line T13.1; Sørensen et al., 2000) or in RG-I α-1,5-arabinans (line T7.2; Skjøt et al., 2002). Previous investigation (Ulvskov et al., 2005) by more conventional methods suggested that T13.1 cell walls differ mechanically from those of the wild type. Potato tubers afford ample amounts of relatively homogenous tissue suitable for frequency sweep measurements in standard rheometers used in the food industry. Our experience with this material suggested that its cell walls’ natural state of hydration and of normally imposed tension (due to turgor pressure, hereafter denoted P) are probably important factors in its mechanical behavior. Therefore, we consider that it is biologically relevant to make these measurements on living, normally hydrated and turgid, tissue. However, the use of such tissue involves potential complications, resulting both from the possibility of progressive metabolic modification of the cell wall during the measurements and from the dependence of a turgid tissue’s elastic properties upon P, which could change for any of several reasons during the measurement. Problems raised by changes in P are considered in both “Results” and “Discussion” and are dealt with in detail in Supplemental Data S1. We demonstrate the successful determination of relaxation spectra that distinguish the transformants from the wild type, despite data that are rather noisy, apparently due primarily to the P problem.

RESULTS

Dynamic Stress Relaxation Measurements

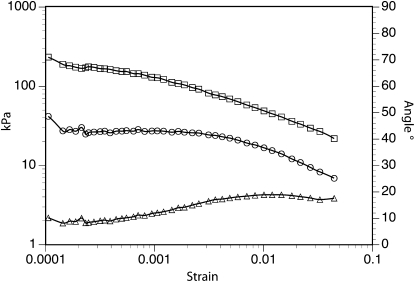
Operation of the rheometer yields, for each strain-oscillation frequency (ω), a value for what is called the complex modulus and its two components, storage modulus and loss modulus. Storage modulus (G′) reflects that part of the deformation work that can be recovered and hence represents the elastic component of the mechanical properties, while loss modulus (G′′) reflects the fraction of the deformation work that cannot be recovered but is dissipated as heat, due to viscous flow in the material. A relaxation spectrum can be validly derived from these data only if G′ and G′′ do not vary as a function of small changes in deformation (strain). Therefore, a strain sweep (varying the magnitude of the oscillatorily imposed strain) was performed to determine if potato tissue possesses a linear elastic range. G′ and G′′ were nearly constant up to a strain of 0.1%, the limit of linear viscoelasticity (Fig. 2). The rheometer was subsequently operated in constant maximum stress mode with maximum shear stress preset to 26 Pa. This setting led to maximum shear strains in the range of 1 to 5 × 10⁻⁴.

Figure 2.

Identification of the linear elastic range for a potato tuber disc subjected to strain sweep at 0.1 s^–1. Storage (squares) and loss (circles) moduli are shown on the left axis, and phase angle (triangles) is shown on the right axis.

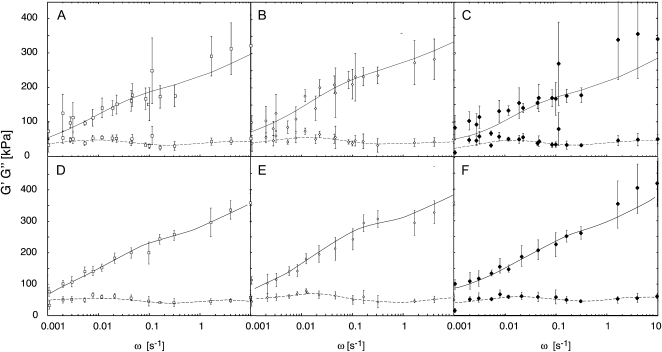
Frequency sweep measurements were then performed using these settings. Figure 3 (A–C) shows the mean G′ and G′′ values obtained from all the employed frequencies, plotted against ω on a log scale, for the wild type and the two transformed lines with modified cell walls. The curve that is drawn for each data set was fitted to the data as described in the next section. As shown by the error bars, variance among replicate measurements at particular frequencies was often quite large. Great variability was similarly noted by Alvarez and Canet (2000) in creep time courses on potato tissue under shear stress, obtained using a comparable rheometer.

Figure 3.

Frequency sweep measurements in the range 0.001 to 10 Hz for potato tuber discs of dimensions 15 × 3 mm. Error bars indicate sd. Solid lines represent fitting of storage modulus (G′) and dashed lines represent fitting of loss modulus (G′′) by Fredholm equations with parameters deduced as explained in the text. A to C show raw data, and D to F show the data after normalizing to an NF of 30 g, as described in “Materials and Methods.” A and D, The wild type. B and E, T7.2. C and F, T13.1.

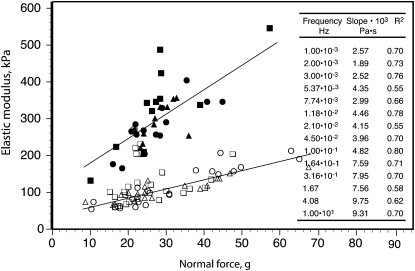
An important source of variance in our data is related to the variable normal force (NF) to which the tissue specimen is subjected in order to hold it firmly between the oscillating plates of the rheometer during the measurement. Although the rheometer was set to deliver a target NF of 30 g, the NF that the instrument initially reported, which was often higher (and sometimes much higher) than 30 g, subsequently relaxed, rapidly during the 1-min premeasurement equilibration period and usually for approximately the first 100 s of measurement, then more gradually. Since the force that a turgid plant cell exerts against a compressive strain imposed externally against its cell wall varies with P (Davies et al., 1998; Lintilhac et al., 2000; Wei et al., 2001), the decline in NF very likely reflects a decline in P. Variations in P are the only reasonable, identifiable source for the large variations in modulus values that the instrument reported, since plant tissue rigidity or elastic modulus varies with P over a very wide range (Falk et al., 1958; Niklas, 1988; Davies et al., 1998; Wei et al., 2001). This is apparently why the modulus values at any strain-oscillation frequency correlate strongly with NF. Figure 4 gives two examples of this correlation, and its inset shows the slopes and correlation coefficients (r² values) for similar plots of G′ versus NF for all the applied ω values (here, and in the following, data from originally applied ω values that differed by less than 10% have been combined for further analysis; see “Materials and Methods”).

Figure 4.

Examples of the correlation between G′ and NF values at two particular frequencies within the range of the measurements. White symbols represent 3 × 10⁻³ Hz, and black symbols represent 10 Hz. Different symbols show data from the different genotypes: the wild type (triangles), T7.2 (circles), and T13.1 (squares). Similar correlations were obtained at other frequencies, for G′′ as well as G′. The inset table lists the slopes of the regressions and the correlation coefficients (r² values) for G′ for all the employed frequencies.

The variance in G′ and G′′ values, therefore, was reduced by normalizing the data to a standard NF value of 30 g. Normalization was performed by linear regression separately for each of the nominal frequencies for the pooled data from all genotypes. Ignoring possible differences between genotypes avoids introducing, in the normalization, any bias between different genotypes that might either lead to, or increase, an apparently significant difference among their relaxation spectra. The data thus normalized, plotted in Figure 3 (D–F), show considerably reduced variance, as expected.

Relaxation Spectra

Relaxation spectra are typically derived from dynamic measurements using a generalized Maxwell model comprising a large (ideally an infinite) number of Maxwell elements in parallel (Ferry, 1980), as in Figure 1A. For solids, which presumably include nongrowing cell walls, one of the parallel elements is simply a spring, which precludes any steady, irreversible flow. A relaxation time, τ, is associated with each of the remaining elements i, with τ_i = η_i/E_i, where η_i is the viscous resistance of dashpot i and E_i is the tensile modulus of spring i. Each of these components contributes to relaxation over about two decades of log(time); the τ for any one of them is the time needed for that one to proceed (1 – 1/e)th, or 63.2%, of the way toward complete relaxation. The presently used rheometer imposes shear strain on the material rather than extension, so we deal with shear moduli (G) rather than the tensile moduli (E) that would nominally apply to the model in Figure 1A, but the mathematics of the relationship between the relaxation spectrum and the modulus values are just the same.

A relaxation spectrum H(τ) depicts the relative contributions of Maxwell elements (Fig. 1A), with different τ values, to the overall relaxation capability of the tissue. H(τ) does this, for any given τ value τ_i, by representing this contribution as the increase in overall modulus (dG)_i per infinitesimal bit of increase in log τ in the neighborhood of τ_i, that is, (δG/δ log τ)_i. Since G has units of Pa and log τ is dimensionless, H(τ) has units of Pa.

As described in “Materials and Methods,” the relationship between a relaxation spectrum and the G′(ω) and G′′(ω) values obtainable from frequency sweep data is given by a pair of equations called the Fredholm equations. For each of our data sets, the BayesRelax program derived a relaxation spectrum by obtaining, by a method of successive approximations, the H(τ) function that, when tested in the Fredholm equations by numerical integration, gave the best fit to the given set of G′(ω) and G′′(ω) values, subject to the regularization constraint that was imposed. The G′(ω) and G′′(ω) profiles that could be calculated from the Fredholm equations, using the thus-deduced H(τ) functions, are the curves drawn through the data points in Figure 3. In deriving each relaxation spectrum, the continuum of relaxing elements in the generalized Maxwell model was approximated with 100 discrete relaxation times.

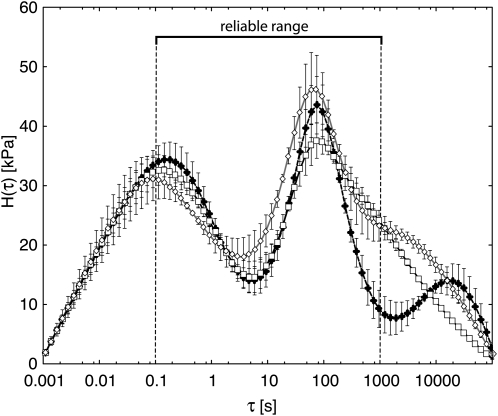
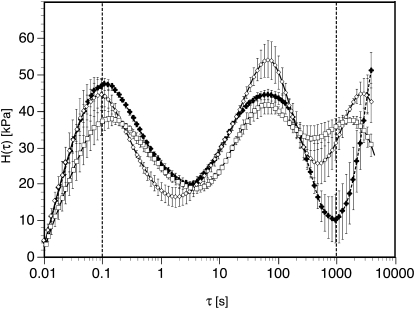
Figure 5 shows the entirety of each spectrum as fitted to the raw data (Fig. 3, A–C) using the smoothness regularization constraint mentioned previously. Figure 6 gives comparable spectra obtained from the data after these were normalized to the standard NF of 30 g (Fig. 3, D–F) as explained above. This normalization obviously did not change the basic form of the spectra, although it reduced the error bars associated with some portions of the curves and thereby increased somewhat the extent to which the three spectra appear to differ from one another significantly. Each error bar represents the range of H(τ) values within which the true value of H(τ) for that point falls with a probability of 67% (see “Materials and Methods”).

Figure 5.

Relaxation spectra corresponding to data in Figure 3 (A–C) fitted using BayesRelax with the smoothing constraint. Squares indicate the wild type, white diamonds indicate T7.2, and black diamonds indicate T13.1. Bars show the 67% probability range for each calculated point (see “Materials and Methods”).

Figure 6.

Relaxation spectra corresponding to data in Figure 3 (D–F) fitted using BayesRelax with the smoothing constraint. Squares indicate the wild type, white diamonds indicate T7.2, and black diamonds indicate T13.1. Bars are as in Figure 5.

In Figures 5 and 6, only the range between τ = 0.1 and 1,000 s, corresponding roughly to the range of frequencies used in our frequency sweep, can be regarded as reliably fitted. In the range between 0.1 and 1,000 s, the relaxation spectrum is mainly determined by the constraints from the measured data, while the form of the estimated plot outside this interval is heavily influenced by the smoothness constraint and by a requirement that H(τ) fall to 0 at the lower and upper limits that must be set for the spectrum (beyond the range of the actual data; see “Materials and Methods”) in order to perform the Fredholm equation integrations. Hence, the interval between 0.1 and 1,000 s is marked “reliable range” in Figure 5, and its limits are indicated with vertical dashed lines in Figure 6. Due to the correlations between neighboring points in the relaxation spectrum that is introduced by the smoothness constraint, the reliable range may actually extend slightly beyond the indicated interval. However, as the extent of valid extrapolation is somewhat unclear and depends on the noise level in the data, we indicate only the “traditional” reliable range in Figures 5 and 6.

The spectra resolve two peaks of relaxing components: a quickly relaxing one with τ values shorter than about 2 s (apparently peaking at approximately 0.1 s), and a slowly relaxing peak with τ values from 10 s up to approximately 200 s. The quickly relaxing peak behaved relatively similarly in all three potato lines. On the other hand, compared with the wild type, line T13.1 shows a significantly reduced relaxation intensity at τ values between 200 and 1,000 s in both Figures 5 and 6, plus an apparently significant increase (Fig. 6) between τ = 0.1 and 0.6 s. The latter might represent a downshift (to lower τ values) of at least part of the relaxation capability that has disappeared from the 200- to 1,000-s region. Small but significant (judging from the error bars) differences between the wild type and T7.2 occur in two parts of the reliable range in Figures 5 and 6 and might be interpreted as a minor part of T7.2 relaxation capability having been shifted from the 10-s region down into the 0.75-s τ region.

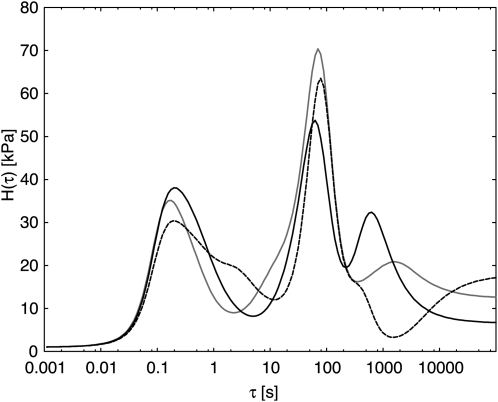
The consequences of applying the smoothness constraint that was used for the spectra in Figures 5 and 6 can be illustrated by comparing the results given there with those of a different constraint that is often used, the maximum entropy method (Elster and Honerkamp, 1991). Figure 7 is equivalent to Figure 6, except for the fitting constraint that was employed. The maximum entropy constraint favors low peak height and, as a side effect, tends to favor solutions with extra peaks and shoulders. These features may reflect something real, but they may instead, if there is appreciable experimental error, be artifacts of fitting that lead data interpretation astray. The plots in Figure 7 agree in general with those in Figure 6, depicting line T13.1 as having a substantial drop in H(τ) below that of the wild type in the τ range above about 200 s. However, Figure 7 displays a shoulder of increase in T13.1 H(τ) above the wild type value around τ = 3 s, which is found in neither Figure 5 nor Figure 6. The spectra of Figure 7 are shown without error bars for clarity and serve mainly to confirm, using a different method of analysis, the general features of the relaxation spectra of the three potato lines.

Figure 7.

Relaxation spectra corresponding to Figure 5 but fitted using the maximum entropy constraint. Black solid line indicates the wild type, gray solid line indicates T7.2, and dashed line indicates T13.1.

DISCUSSION

Our measurements of stress relaxation in potato tuber tissue by the “dynamic” (sinusoidally oscillating strain) method yield a prominently two-peaked relaxation spectrum (Figs. 5 and 6). Contrary to possible naive impression, the peaks do not represent times at which there is a maximum rate of relaxation. The rate of relaxation of all Maxwellian elements is actually maximum at the start of the process; the τ of any element is the time at which it will have gone 63.2% of the way to completion. H(τ) plotted on the ordinate is the rate of decrease in modulus (or in stress) relative to log(time); thus defined, for any given relaxing element, H reaches a maximum at a time (after strain and stress are imposed) equal to this element’s τ. A peak in H(τ) can be caused by simply a shoulder, or an inflection, in the change in modulus with time, or in the increase in moduli with ω. A peak in H in the log(τ) plot means just that more total relaxation occurs in that decade of log time than in the decades to either side. The H(τ) minimum at τ values between 1 and 10 s, which separates the two peaks in our spectra, is brought on by the minimum in G′′ and the slight inflections in the curve for G′ in the ω range around 0.2 to 2 s⁻¹ in our frequency sweep data (Fig. 3).

A two-peaked relaxation spectrum is characteristic of amorphous, synthetic polymers with chains long enough to create “entanglement coupling.” This is where occasional kinking of long, randomly coiled chains around each other creates a transient network structure (or alternatively, where movement [“reptation”] of very long chains within the “sheath” of adjacent chains that confines them is retarded by an extra-large resistance compared with that for shorter range molecular motions; Ferry, 1980). The peak at a low τ value reflects local movements of chain segments, while the large τ peak reflects a much slower slippage of entire chains past coupling points (or these chains’ reptation) under an imposed stress. In entanglement coupling, the respective spectral peaks, however, often seem to be separated by about five decades of log τ (Ferry, 1980), in contrast to our peaks, which are only about three decades apart.

Unlike an amorphous polymer, as noted in the introduction, cell walls involve structure, namely, cellulose microfibrils and intervening matrix polymers, which might instead be responsible for multiple relaxation spectral peaks. When a wall is strained elastically, its virtually inextensible microfibrils must become displaced relative to one another, either by separation or (more generally) by slip (lengthwise movement of a microfibril relative to an adjacent, more or less parallel, one). The former would require modest extension straining of the matrix, while the latter must locally shear strain, much more strongly than the macroscopic strain in the wall, the matrix intervening between adjacent, more or less parallel, fibrils.

Whitney et al. (1999) suggested that “entanglement of cellulosic rods” is the most important factor in stress relaxation of tomato fruit cell walls and polysaccharide composites containing bacterial cellulose. Wilson et al. (2000) interpreted dynamic two-dimensional Fourier transform infrared measurements as indicating that both pectins and cellulose in onion (Allium cepa) epidermal cell walls reorient under a cyclically (20-Hz) imposed strain within the frequency range of Whitney et al.’s (1999) measurements. This suggests that our rapid relaxation peak may involve local polymer conformation changes associated with only modestly retarded (relatively close to instantaneously elastic) strains that occur in the matrix as the microfibrils are initially displaced, as well as any retardation that might be associated with straightening of curved microfibrils or with slippage between microfibrils at any points of direct contact. Our higher τ (approximately 100-s) peak might reflect longer distance, matrix polymer chain displacements that are driven by the initial, local shear strain and that would be retarded by much greater viscous resistance as noted above.

Comparison with Previous Rheological Measurements on Primary Walls

Our two-peaked spectrum contrasts considerably with some of the relaxation spectra that have been reported for thin-walled, higher plant tissues using other approaches. Yamamoto, Masuda, and coworkers reported time courses of extension-induced stress relaxation that were nearly linear, with log(time), for methanol-killed coleoptiles (Yamamoto et al., 1970; Yamamoto and Masuda, 1971; Masuda et al., 1972) and pea (Pisum sativum) stem epidermis (Yamamoto et al., 1974; Fujihara et al., 1978). From these, they deduced relaxation spectra that had a “box” shape, nearly flat over as many as six decades of log τ (in one case, more than nine decades; Kawamura et al., 1995), and terminating sharply at specific minimum and maximum τ values as far apart as 0.02 and greater than 10⁶ s. The displayed width seems unsatisfactory, because the time courses that they published did not extend much over 1,000 s and often lasted only 60 to 100 s.

Later attempts (Fujihara et al., 1978; Kawamura et al., 1995) to correct these spectra for the technique’s inability to accurately measure relaxations with small τ values yielded what might be two-peaked spectra if the area under their very wide, higher τ shoulder (the box part of the earlier published spectra) were collapsed down into the limited time range actually embraced by the measurements.

Taylor and Cosgrove (1989) reported stress relaxation spectra for cell wall specimens from killed cucumber (Cucumis sativus) hypocotyls, which showed a broad, but not box-like, maximum centered between 0.2 and 0.6 s (in different spectra) and a minimum at near 100 s, the increase above which did not reach a maximum by the spectrum’s upper limit of 200 s but presumably would have given a second peak beyond this point. These spectra thus appear to be two peaked, like ours, but right shifted to higher τ values (relatively slower rates of relaxation) than those of our peaks. This shift is to be expected from measurements on killed, turgorless tissue as against our turgid potato cells, because, as previously noted, P increases a tissue’s elastic moduli and τ is inversely related to modulus.

More recent authors have used time courses of creep under a steadily applied load to deduce rheological properties of thin-walled plant tissues. Although the same mechanisms participate in creep as in stress relaxation, a feasible analysis of retardation uses not the generalized Maxwell model (Fig. 1A) but instead a “Burgers” model (Fig. 1C), which comprises a number of “Kelvin” or “Voigt” elements (Fig. 1B) in series along with one Maxwell element. The latter allows for instantaneous (unretarded) elasticity and for the possibility of steady flow (its dashpot’s viscosity being infinite if steady flow cannot occur), while the former represent multiple retarded-elastic straining mechanisms with different retardation times (times for 63.2% extension under a fixed load). The retardation time of any given structural element is typically longer than its relaxation time, because during relaxation, extension of any Kelvin/Voigt element’s spring is opposed by compression of other springs in series with it in a Burgers model, whereas during retarded extension, it is not so opposed, which allows it to approach equilibrium extension more gradually. Because of this and the fact that retarded elasticity is measured as compliance, which is the reciprocal of the moduli involved in relaxation, the relaxation and retardation spectra of a given material usually do not resemble each other closely but tend to have peaks and valleys at τ values that are not remotely distant from one another (Ferry, 1980).

Alvarez and Canet (1998, 2000) and Thompson (2001, 2005, 2008) analyzed creep data using a Burgers model comprising two Kelvin elements in series with a steady-flow viscosity. The materials that Thompson tested are not structurally comparable with potato tissue, but Alvarez and Canet used living, turgid potato tissue equivalent to that studied here. From creep curves that extended over just 2 min, they inferred τ values, in different measurements, ranging from about 100 to 700 s for one Kelvin element and 14 to 62 s for the second one (which was not consistently detected; Alvarez and Canet, 2000). Their higher τ component falls within the general τ range of the slower (longer τ) peak in our relaxation spectra (Figs. 5 and 6), but their lower τ component falls in the range in which our spectra display a minimum. As is evident from the mentioned numbers and from their statements (Alvarez et al., 1998; Alvarez and Canet, 2000), the results of their curve fitting for any given material were extremely variable and thus presumably inaccurate. Also, the one actual creep time course that they published appears to lack the initial part of the postloading response, which would be needed to detect any retarded-elastic straining having τs in the range less than 1 s, comparable to the lower τ peak in our spectra.

We consider that simple creep as well as simple stress relaxation time courses for cell walls, even if low in noise, are not data rich enough to distinguish specific rheological models, like those of the foregoing authors, from a generalized Burgers or Maxwell model involving a spectrum of retardation or relaxation times, as has generally been found necessary for polymeric materials (Ferry, 1980). To obtain data that are rich enough in detail to adequately define such spectra, or to justify models with only a limited number of components, it seems necessary to employ dynamic (frequency sweep) stress relaxation measurements and to analyze them assuming a near continuum of possible relaxation times.

Problems in Stress Relaxation Measurements

Without a regularization procedure, fitting experimental data to a model containing more parameters than the amount of information in the data will lead to instability in the fitting routine, giving parameter values that cannot be trusted. An apparently good fit can then be due merely to the extra parameters employed. For a reliable analysis, the number of fitting parameters should not exceed the effective number of degrees of freedom in the data. This has often been overlooked in stress relaxation work.

The emulsified or homogenized preparations from which relaxation spectra of synthetic polymers are commonly obtained (Tan et al., 2000) have been imitated for plant tissue by homogenizing, ethanol washing, drying, and rehydrating its cell walls (Kunzek et al., 1997; Whitney et al., 1999). However, such preparations are probably not very relevant to the biological properties of the cell walls of living tissue. For one thing, completely dried cell walls most likely cannot be fully reconstituted, by rehydration, back into their native rheological condition. The analogous problem is termed “retrogradation” in the chemistry of solubilized polysaccharides and “hornification” in wood pulp fiber technology (Fernandez Diniz et al., 2004).

We have instead shouldered the complications of using living tissue in order to study cell walls in their native states of hydration and physical condition. These complications comprise, first, biochemical activities of the tissue, including the possibility of irreversible cell wall extension (growth) as well as of wound reactions to cutting of tissue discs, and second, problems with turgor pressure and osmotic relaxation.

The postharvest metabolism of RG-I side chains in potato tubers (Bush et al., 2001) implies that the walls might not remain in their initial biochemical state during a protracted incubation of isolated potato discs during stress relaxation measurement. We guarded against this by keeping pretreatment and measurement periods as short as practicable (1 min and 20 min or less, respectively). The range of ω values used here were limited, on the slow end, by this short time requirement. On the fast end, usable ω values were limited by an apparent tendency of the tissue discs to begin slipping between the rheometer plates (as indicated by G values falling with ω) at ω values greater than 10 s⁻¹, despite the rheometer’s arrangements to hold specimens firmly, whose consequences are noted below.

Walls of turgid cells may differ mechanically from those of nonturgid cells in that their walls are compressed in the normal (perpendicular to the cell surface) direction by P, potentially affording more and/or closer interpolymer contacts within the wall structure than would occur in fully relaxed walls. This would probably increase the effective viscosities governing stress relaxation and could also affect their degree of hydration, which is probably also important to these viscosities. Thus, it is biologically relevant to try to probe walls of turgid cells, as was done here. However, most of the problems encountered in interpreting dynamic rheological measurements on a living plant tissue are related to its P. This is because a plant tissue’s rigidity or elastic modulus varies strongly with its P, as noted above, and P can change during the measurements. Because most of these problems are relevant not only to this work but would need to be faced in any future frequency sweep measurements on living plant tissues, it is desirable to consider them. However, due to their number and physiological complexity, to analyze them adequately requires considerably more space than can be devoted to it here. Therefore, we undertake this in Supplemental Data S1. Table I here provides a key to the topics considered there and gives, in the right column, our conclusions, from that analysis, as to which aspect(s) of this work each listed problem actually affects.

Table I. Physiological/technical problems for dynamic rheological measurements on turgid tissues.

These problems are analyzed in Supplemental Data S1.

No.	Problem	Pertinencea
		Potential	Actual
1	“In vivo stress relaxation” related to a cell’s capacity for irreversible wall expansion (cell growth)b	A, B	(B)c
2	Osmotic relaxation of P after a change in P imposed by rheometer action	A, B	0d
3	Change in P due to one or more of the viscoelastic mechanisms of wall stress relaxatione	B	0d
4	Compression, and resulting collapse, of cells impacted by the rheometer sample grip or antislip arrangementsf	B	B
5	Leakage, from cells that collapse due to No. 4, of solutes into a tissue’s cell wall space, causing water loss from other cells	B	B
6	Evaporative water loss from a tissue sample’s edges having unprotected contact with ambient air	B	B
7	Variations in thickness of tissue discsg and in pressure applied to them by sample gripping arrangementsh	C	C

^aPertinence of listed problem to any of the following: A, direct contribution to relaxation spectrum; B, P relaxation during measurement run, leading to decline in NF and resulting scatter of G′ and G′′ values at a given ω; C, effect on NF that should not correlate consistently with G′ and G′′, contributing to scatter of NF-normalized G values.

^bCosgrove (1985, 1987).

^cOnly a marginal influence, at most.

^dPotential problem that we conclude (in Supplemental Data S1) does not influence our measurements on potato discs but could affect other work.

^ePotential problem for potato relaxation spectrum because NF rapidly declines over the same time scale as the spectrum’s longer τ peak.

^fIn this work, local compression of cells by antislip knurls on the rheometer’s pressure plates.

^gVariations in disc thickness cause variations in initial NF if pressure plates cease advancing at exactly the target separation.

^hPressure plate behavior in the rheometer used here is not under the operator’s manual control and seems variable, contributing to variations in initial NF.

Rheological Changes in Tissues with Modified Wall Polymers

The regularization method employed to obtain Figures 5 and 6 (which we recommend) is very conservative with regard to disclosing differences. However, it is able to differentiate all three potato genetic lines.

Potato line T13.1 is reduced by 70% in RG-I galactans, which translates into a 6% overall change in cell wall composition compared with the wild-type line Posmo (Sørensen et al., 2000). We previously inferred that in T13.1, a slowly relaxing component had been lost (Ulvskov et al., 2005). Our relaxation spectra here confirm this, indicating that in T13.1, a component with a τ value of around 1,000 s is greatly reduced. However, according to Figure 6, components with τ values in the 6- to 30-s and the 0.2- to 0.5-s ranges have increased in total by about the same amount as the decrease in the τ approximately 1,000-s region.

¹³C-NMR measurements have been interpreted as indicating that galactans are among the most freely mobile polymers in hydrated, pectin-rich primary walls of onion bulbs and a few other plant materials (Foster et al., 1996; Ha et al., 1997), including potato (Tang et al., 1999). Thus, pectic galactans might be expected to have short relaxation times, rather than τ values near the upper limit of our spectrum. The τ approximately 1,000-s component that is reduced in T13.1 thus probably reflects an indirect effect of the missing galactan on other wall components.

Galactan side chains, although themselves mobile, might restrict the RG-I polymer backbone mobility, as branches or side chains on synthetic polymers typically do (Ferry, 1980). In that case, shortening or eliminating many of these side chains might reduce the viscous resistance that retards RG-I backbone motion. Since the larger the value of τ, the higher the associated viscous resistance, this change would downshift the part of the spectrum that reflects RG-I backbone mobility, corresponding to the apparent downshift noted in “Results.”

On the other hand, RG-I side chains might act as hydrated spacers within the wall, limiting direct contacts between RG-I and homogalacturonan backbones and possibly also between cellulose micofibrils. Eliminating side chains would then increase these associations and stiffen the wall, as indicated for arabinan side chains by Jones et al. (2003) for stomatal guard cell walls, and as our previous experiments suggested (Ulvskov et al., 2005). Wild-type component(s) with τ values approximately 1,000 s would, in T13.1, have become immobile enough that their relaxation lies beyond the upper τ limit of our spectrum’s reliable range. This is suggested by the sharp rise in H with τ in the 5,000- to 10,000-s range of the T13.1 spectrum (Figs. 5 and 6), although since this is above the reliable range, this feature is not compelling. In this case, the apparently increased H, in Figure 6, in T13.1 H values in the τ ranges below 200 s could represent a comparable upshift in the contribution of components whose relaxation, in the wild type, lies below the lower limit of the spectrum’s reliable range, rather than representing a downshift from τ approximately 1,000 s, as suggested in the preceding paragraph.

The spectral difference between line T7.2 and the wild type is smaller than that between T13.1 and the wild type. However, this is not really surprising, because although T7.2 is reduced in RG-I arabinans by approximately 70%, potato RG-I contains only a quarter as much arabinan as galactan, so this reduction amounts to a less than 2% change in wall composition (Skjøt et al., 2002).

Judging from the error bars in Figures 5 and 6, in T7.2, the rheological contribution of elements with τ values between 10 and 200 s is significantly greater than in the wild type, while Figure 6 suggests that in T7.2, the contribution of elements with τ values between 0.3 and 2 s is significantly reduced. This suggests that the removal of arabinan side chains from RG-I backbones in T7.2 may have increased, by some 10- to 100-fold, the viscous resistance that retards the movement of some wall component(s). If this component were RG-I itself, this would diverge from the above-mentioned expectation that side groups tend to restrict backbone mobility, but it would agree with the conclusion of Jones et al. (2003, 2005) that removing arabinans stiffens stomatal guard cell walls.

We suggested earlier (Ulvskov et al., 2005) that a difference in wall water status between the wild type and the transformant might contribute to the observed wall mechanical effects. Evered et al. (2007) demonstrated that hydration state influences primary wall mechanical properties. Tang et al. (1999) found that hydration greatly increased the mobility of pectic components of potato and water chestnut (Trapa spp.) cell walls. Moore et al. (2008) suggested that arabinans can be especially important to the mobility or “plasticizing” of pectins during water stress. Thus, the spectral shift toward a higher τ range in T7.2 might reflect a decrease in wall hydration, and thus in pectin mobility, when its arabinan content is reduced.

CONCLUSION

The BayesRelax algorithm for deducing relaxation spectra from rheological measurements has here been tested in what may be considered a very challenging or even worst-case scenario on biochemically active, turgid tissues, yet it was able to discriminate between wild-type and transgenic tissues with rather small wall changes. The computer program is of course equally useful for determining the relaxation spectra of materials that have been subjected to pretreatments that render them more amenable to frequency sweep measurements or even for solutions of isolated biopolymers that can be analyzed similarly.

MATERIALS AND METHODS

Plant Material

Wild-type potatoes (Solanum tuberosum ‘Posmo’; Kartoffelforædlingsstationen i Vandel) and the transformed lines T13.1 with reduced RG-I linear β-1,4-galactan (Sørensen et al., 2000) and T7.2 with reduced α-1,5-arabinan (Skjøt et al., 2002) were grown in open air in containers in two-thirds peat moss and one-third Perlite. Tubers approximately 6 to 8 cm long were used for rheological measurements within 5 h of harvest. Samples were collected, and measurements made, over two growing seasons. Cylinders, 15 mm in diameter, were excised with a cork borer, and discs 3 mm thick were sliced from them using a custom-built potato guillotine (Mikrolaboratoriet). No more than two discs were cut from any one cylinder.

Rheological Measurements

Instrumentation

Small-amplitude oscillatory rheological measurements were performed using a Bohlin C-VOR rheometer (Malvern Instruments). The rheometer was equipped with a Peltier element to control the temperature (20°C ± 1°C) during the measurements. The measurement system consisted of two parallel, serrated plates (diameter, 15 mm). The discs of potato tissue, described above, were mounted between the plates before the measurement was started. During a 1-min equilibration period, the instrument was set to aim for a target gap of 2.80 mm between the plates and a NF of 30 g between the plates and the tissue disc. During the sequence of measurements that were then made on a particular disc, plate separation remained constant while NF declined. At the end of each measurement, the rheometer reported G′, G′′, and NF values, this last being the value that prevailed at the moment the measurement ended.

Strain Sweep

A strain sweep was performed in order to determine the linear elastic range of the material. The small-amplitude oscillatory rheological properties were measured over the strain interval 10⁻⁶ to 10⁻¹.

Frequency Sweep

For these measurements, maximum shear stress set at 26 Pa was used, since this gave strains within the linear range. Oscillation frequencies, 18 in all, over the range 0.001 to 10 s⁻¹, were applied successively to individual potato tissue discs in sets that kept the duration of the entire measurement run for any one disc to 20 min or less (15 min or less in runs that did not include the lowest frequency, 0.001 s⁻¹). At least 10 replicate measurements at each frequency, made on different individual discs, were ultimately recorded for each potato genetic line, except for the lowest frequencies, 0.001 and 0.002 s⁻¹, which require the longest measurement times and for which five and eight measurements, respectively, were recorded. Ten oscillations were averaged for the fastest frequency, five at 4 s^–1, two at 1.67 s^–1, and one oscillation for slower frequencies. The duration of individual measurements varied between about 60 s for the highest frequencies to about 1,000 s for the lowest (0.001 and 0.002 s⁻¹). For any one disc, frequencies were ordered in a randomized sequence to ensure that no single frequency was always recorded last, at a time when the material had undergone considerable NF relaxation, or first, when the NF was at its maximum. Data from tissue discs whose NF dropped nearly to 0 during measurement, indicating that the disc was no longer firmly clamped, were discarded.

Fitting Relaxation Spectra

Writing ω for the frequency of oscillating strain, the relation between the relaxation spectrum H(τ) and the measured storage and loss moduli G′(ω) and G′′(ω), respectively, is given by the two Fredholm integral equations (Tschoegl, 1989):

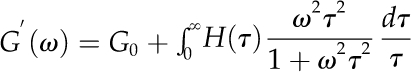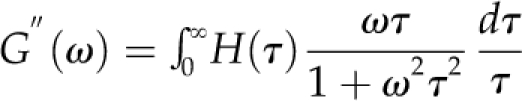For a viscoelastic liquid, the residual modulus G₀ = 0, and for a viscoelastic solid, G₀ ≠ 0.

The quality of a fit to the data is measured through the χ², which is defined in the conventional manner (i.e. for measurements at M frequencies):

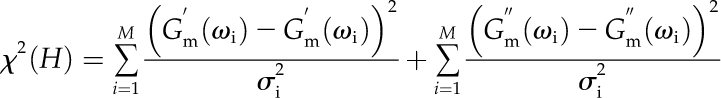where, leaving out primes, G_m(ω_i) is the measured modulus, G(ω_i) is the calculated modulus (from the integral equations), and σ_i is the sd of the noise at data point i.

The estimation of H(τ) using the χ² may lead to a number of statistically acceptable but quite different solutions, as mentioned in the introduction. This problem is solved by regularization, which replaces χ² by the functional (Tikhonov and Arsenin, 1977) where α is a Lagrange multiplier and

gives preference to smoother solutions. The functional form for S(H) may differ (Honerkamp and Weese, 1989), but the objective of the smoothness regularization functional S(H) used here is to impose an additional smoothness constraint upon the fitting procedure. As an alternative, S(H) may be chosen to give bias toward the baseline 0, but this choice can lead to additional (possibly artifactual) peaks in the estimated spectrum (Hansen, 2008), as illustrated by the results obtained using the maximum entropy (“Maxent”) method of regularization (Fig. 7).

For a given choice of Lagrange multiplier, minimizing αS(H) + χ² will select the smoothest solution for the relaxation spectrum H(τ) corresponding to the noise level in the data (scatter of individual measurements around their means), which determines α.

As S(H) takes its least value for a uniform H(τ), this means that in the absence of constraints from the data, the estimate for H(τ) will be a uniform (flat) function. The estimation of the value for the Lagrange multiplier has been given considerable attention in the literature (Honerkamp and Weese, 1990). A probabilistic (Bayesian) approach to the problem has been used in this article (details are given in Hansen, 2008).

Measuring the storage and loss moduli over the ω interval 0.001 to 10 s⁻¹ allows the estimated relaxation spectrum to be interpreted safely over the corresponding range of τ values 0.5 to 200 s (Davies and Anderssen, 1997). Due to the correlation between neighboring points, induced by the smoothness constraint, this interval may be extended to a τ range of 0.1 to 1,000 s, which corresponds to the conventional reliable interval used for interpretation. For numerical reasons, at least one extra decade of τ values should be included, in the analytical procedure, at each end of this interval. The end points for the spectra were here chosen as τ_min = 0.001 s and τ_max = 100,000 s [below τ_min and above τ_max, we assumed that H(τ) = 0]. The continuous distribution of τ values in the Fredholm equations was approximated using 100 discrete τ values distributed log linearly over that interval. These τ values are plotted on the abscissa of Figures 5 and 6.

The 67% probability error bars were obtained by a calculation, specified in the BayesRelax program, that assumes (1) a Gaussian distribution of data error and (2) that the Fredholm equations correctly model the relaxation process. It deduces a probability distribution for each point in a spectrum using the sum of the χ² and the α*S terms mentioned above (for an analysis of the probability problem that is involved, see Hansen and Wilkins, 1994).

BayesRelax can be accessed through its Web interface at www.BayesRelax.org. All spectra were calculated using the default settings, except that 100 points were calculated (specified under “optional parameters”). Normalization to NF of 30 g was carried out by two operations. The rheometer software had chosen to apply a series of ω values, some members of which did not always correspond perfectly in different runs but, when not identical, did not differ greatly (closely adjacent ω points in Fig. 3, A–C). Therefore, for normalization, data from ω values that differed by less than 10% were pooled, and to this pool the mean of these ω values was nominally assigned. Linear regression against NF was then performed, for every nominal ω (whether from pooled, closely similar ω values or not), on the pooled data from several potato lines (not just the three lines presented here) in order to avoid bias in the normalization. Each regression yielded a slope, β, for the dependence of either G′ or G′′ on NF at each ω. Normalization consisted of adding the term (30 − NF)·β to each G′ or G′′ measurement at a particular NF, using the β for the particular modulus and the measurement’s nominal ω.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Data S1. An in-depth discussion of the technical issues listed in Table I.