Abstract
Tension wood is widespread in the organs of woody plants. During its formation, it generates a large tensile mechanical stress called maturation stress. Maturation stress performs essential biomechanical functions such as optimizing the mechanical resistance of the stem, performing adaptive movements, and ensuring the long-term stability of growing plants. Although various hypotheses have recently been proposed, the mechanism generating maturation stress is not yet fully understood. In order to discriminate between these hypotheses, we investigated structural changes in cellulose microfibrils along sequences of xylem cell differentiation in tension and normal wood of poplar (Populus deltoides × Populus trichocarpa ‘I45-51’). Synchrotron radiation microdiffraction was used to measure the evolution of the angle and lattice spacing of crystalline cellulose associated with the deposition of successive cell wall layers. Profiles of normal and tension wood were very similar in early development stages corresponding to the formation of the S1 layer and the outer part of the S2 layer. Subsequent layers were found with a lower microfibril angle (MFA), corresponding to the inner part of the S2 layer of normal wood (MFA approximately 10°) and the G layer of tension wood (MFA approximately 0°). In tension wood only, this steep decrease in MFA occurred together with an increase in cellulose lattice spacing. The relative increase in lattice spacing was found close to the usual value of maturation strains. Analysis showed that this increase in lattice spacing is at least partly due to mechanical stress induced in cellulose microfibrils soon after their deposition, suggesting that the G layer directly generates and supports the tensile maturation stress in poplar tension wood.
Wood cells are produced in the cambium at the periphery of the stem. The formation of the secondary wall occurs at the end of cell elongation by the deposition of successive layers made of cellulose microfibrils bounded by an amorphous polymeric matrix. Each layer has a specific chemical composition and is characterized by a particular orientation of the microfibrils relative to the cell axis (Mellerowicz and Sundberg, 2008). Microfibrils are made of crystalline cellulose and are by far the stiffest constituent of the cell wall. The microfibril angle (MFA) in each layer is determinant for cell wall architecture and wood mechanical properties.
During the formation of wood cells, a mechanical stress of a large magnitude, known as “maturation stress” or “growth stress” (Archer, 1986; Fournier et al., 1991) occurs in the cell walls. This stress fulfills essential biomechanical functions for the tree. It compensates for the comparatively low compressive strength of wood and thus improves the stem resistance against bending loads. It also provides the tree with a motor system (Moulia et al., 2006), necessary to maintain the stem at a constant angle during growth (Alméras and Fournier, 2009) or to achieve adaptive reorientations. In angiosperms, a large tensile maturation stress is generated by a specialized tissue called “tension wood.” In poplar (Populus deltoides × Populus trichocarpa), as in most temperate tree species, tension wood fibers are characterized by the presence of a specific layer, called the G layer (Jourez et al., 2001; Fang et al., 2008; Gorshkova et al., 2010), where the matrix is almost devoid of lignin (Pilate et al., 2004) and the microfibrils are oriented parallel to the fiber axis (Fujita et al., 1974). This type of reaction cell is common in plant organs whose function involves the bending or contraction of axes, such as tendrils, twinning vines (Bowling and Vaughn, 2009), or roots (Fisher, 2008).
The mechanism at the origin of tensile maturation stress has been the subject of a lot of controversy and is still not fully understood. However, several recent publications have greatly improved our knowledge about the ultrastructure, chemical composition, molecular activity, mechanical state, and behavior of tension wood. Different models have been proposed and discussed to explain the origin of maturation stress (Boyd, 1972; Bamber, 1987, 2001; Okuyama et al., 1994, 1995; Yamamoto, 1998, 2004; Alméras et al., 2005, 2006; Bowling and Vaughn, 2008; Goswami et al., 2008; Mellerowicz et al., 2008). The specific organization of the G layer suggests a tensile force induced in the microfibrils during the maturation process. Different hypotheses have been proposed to explain this mechanism, such as the contraction of amorphous zones within the cellulose microfibrils (Yamamoto, 2004), the action of xyloglucans during the formation of microfibril aggregates (Nishikubo et al., 2007; Mellerowicz et al., 2008), or the effect of changes in moisture content stimulated by pectin-like substances (Bowling and Vaughn, 2008). A recent work (Goswami et al., 2008) argued an alternative model, initially proposed by Münch (1938), which proposed that the maturation stress originates in the swelling of the G layer during cell maturation and is transmitted to the adjacent secondary layers, where the larger MFAs allow an efficient conversion of lateral stress into axial tensile stress. Although the proposed model is not consistent with the known hygroscopic behavior of tension wood, which shrinks when it dries and not when it takes up water (Clair and Thibaut, 2001; Fang et al., 2007; Clair et al., 2008), this hypothesis focused attention on mechanisms that do not involve the shrinkage of crystalline cellulose microfibrils.
In order to further discriminate between these hypotheses, direct observations of the mechanical state of the different cell wall layers and their evolution during the formation of the tension wood fibers are needed. X-ray diffraction can be used to investigate the orientation of microfibrils (Cave, 1966, 1997a, 1997b; Peura et al., 2007, 2008a, 2008b) and the lattice spacing of crystalline cellulose. The 004 axial lattice spacing (d004) is the distance between successive monomers along a cellulose microfibril and is related to its state of mechanical stress (Clair et al., 2006; Peura et al., 2007). If cellulose microfibrils support a tensile stress, they should be found in an extended state of deformation. Under this assumption, the progressive development of maturation stress during cell wall formation should be accompanied by an increase in cellulose lattice spacing. Synchrotron radiation allows a reduction in the size of the x-ray beam to some micrometers while retaining a strong signal, whereby diffraction analysis can be performed at a very local scale (Riekel, 2000). This technique has been used to study sequences of wood cell development (Hori et al., 2000; Müller et al., 2002). In this study, we report an experiment where a microbeam was used to analyze the structural changes of cellulose in the cell wall layers of tension wood and normal wood fibers along the sequence of xylem cell differentiation extending from the cambium to mature wood (Fig. 1). The experiment was designed to make this measurement in planta in order to minimize sources of mechanical disturbance and to be as close as possible to the native mechanical state (Clair et al., 2006). The 200 and 004 diffraction patterns of cellulose were analyzed to investigate the process of maturation stress generation in tension wood.
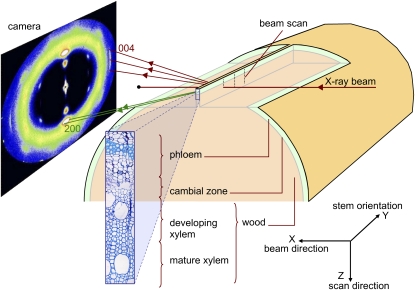
Figure 1.
Schematic of the experimental setup, showing the x-ray beam passing perpendicular to the longitudinal-radial plane of wood and the contribution of the 004 and 200 crystal planes to the diffraction pattern recorded by the camera. [See online article for color version of this figure.]
RESULTS
Typical diffraction patterns obtained from one tension wood and one normal wood sample are shown in Figures 2 and 3 (results for other samples are shown in Supplemental Data S2).
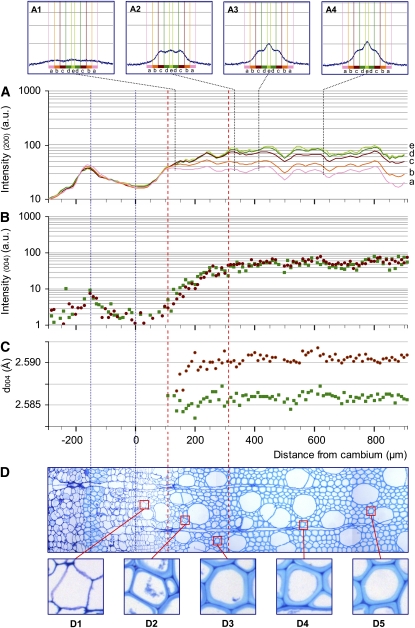
Figure 2.
Profiles of the 200 and 004 reflection intensities and d004 lattice spacing along a sequence of normal wood development with the corresponding sample anatomy. A, Intensity in log scale of the 200 diffraction for five ranges of azimuth angle: a, 40° to 52°; b, 28° to 40°; c, 16° to 28°; d, 4° to 16°; e, 0° to 4°. A1 to A4 illustrate full 200 diffraction patterns at different distances from the cambium (140, 330, 410, and 630 μm, respectively). B, Intensity in log scale of the 004 diffraction. C, Lattice spacing (d004). B and C are given with distinctions between the contributions of microfibrils oriented at large angles (greater than 16°; red circles) and small angles (less than 16°; green squares). D, Cross-section of a portion of the tissue traversed by the beam from periphloem fibers to mature wood. D1 to D5 show details of fibers along the development sequence. [See online article for color version of this figure.]
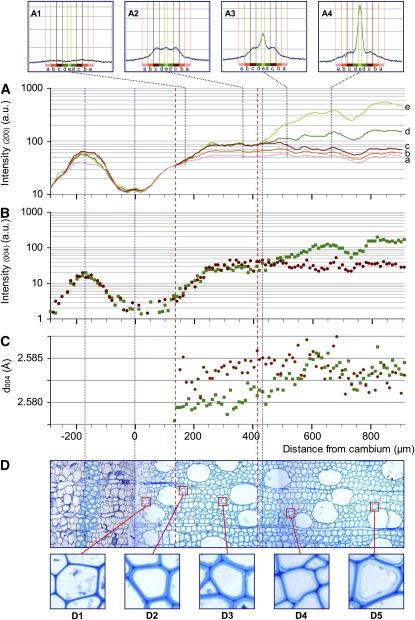
Figure 3.
Profiles of the 200 and 004 reflection intensities and d004 lattice spacing along a sequence of tension wood development with the corresponding sample anatomy. A, Intensity in log scale of the 200 diffraction for five ranges of azimuth angle: a, 40° to 52°; b, 28° to 40°; c, 16° to 28°; d, 4° to 16°; e, 0° to 4°. A1 to A4 show examples of full 200 diffraction patterns at different distances from the cambium (170, 360, 510, and 660 μm, respectively). B, Intensity in log scale of the 004 diffraction. C, Lattice spacing (d004). B and C are given with distinctions between the contributions of microfibrils oriented at large angles (greater than 16°; red circles) and small angles (less than 16°; green squares). D, Cross-section of a portion of the tissue traversed by the beam from periphloem fibers to mature wood with differentiated G layer. D1 to D5 show details of fibers along the development sequence. [See online article for color version of this figure.]
Anatomy of the Studied Samples
Figures 2D and 3D show transverse sections of the studied sample strips that are focused on a 1,200-μm-long radial strip extending from the phloem to the mature wood. A 40- to 80-μm-thick tangential strip of periphloem fibers is visible in the bark, centered around 150 μm from the cambial area. These thick-walled cells are easily detected on the x-ray intensity patterns of both 004 and 200 cellulose crystal planes and were used to match the diffraction patterns and the microscopic observations.
In the first 300 μm after the cambium, the progressive thickening of the fiber secondary wall (formation of the S1 and S2 layers) is clearly visible both in normal wood and tension wood (D1–D3 in Figs. 2 and 3). No difference in cell wall appearance between tension wood and normal wood could be noticed in this area. After 300 μm, the thickening of the cell walls is complete for the normal wood sample (D4 and D5 in Fig. 2). In the tension wood sample, G layers (D4 and D5 in Fig. 3) start to become visible in fibers 430 μm after the cambium (thin dotted line in Fig. 3). No G layer was observed in the normal wood sample.
Changes in the Amount of Cellulose along a Development Sequence
The intensity of the 004 reflection depends on the amount of diffracting microfibrils crossed by the beam. Therefore, local variations in density (e.g. related to the presence of vessels) create slight fluctuations of the intensity profiles (but this does not affect the position of the peak, i.e. the lattice spacing of cellulose). The contributions of small MFA (less than 16°) and large MFA (greater than 16°) to the intensity profiles are shown separately in Figures 2C and 3C. Intensity is represented on a log scale in order that variations at low intensity can be seen despite the high intensity reached in mature wood. Comparison between these profiles indicates the relative abundance of cellulose oriented with a large angle and a small angle at each position.
After the first peak in the periphloem fibers, the cambial zone is characterized by a very low signal due to the absence of secondary walls. The intensity increases along 250 to 300 μm after the cambium, parallel to the thickening of the cell wall. During this phase, similar intensity profiles are observed for small MFA and large MFA in both normal wood and tension wood samples. After this phase, the signal of normal wood and tension wood begins to clearly differ. In normal wood, large and small angles have similar constant-intensity patterns, consistent with the fact that the cell walls have reached their final thickness. In tension wood, the signal emerging from small MFA deviates from the large MFA, where the former becomes 3 to 5 times higher than the latter. This steep increase in intensity for small MFA starts approximately 410 μm after the cambium, when the G layers become visible.
Changes in MFA along a Development Sequence
The changes in intensity of the 200 reflection are shown in Figures 2A and 3A (on a log scale) for different azimuthal sectors. The diffraction patterns are similar to those obtained for the 004 reflection for equivalent angle classes, consistent with the fact that both reflect the variations in cellulose quantity. The 200 reflections, however, were less scattered and therefore more suitable for the analysis of a wider range of MFAs.
Insets in Figures 2A and 3A show the full 200 reflection patterns at some specific locations. In the first 100 to 150 μm after the cambium, the signal is very low (data not shown). Cell walls at that stage are composed only of the primary walls, and the very low quality of the signal does not allow the analysis of microfibril orientation (Müller et al., 2002). At the end of this stage (represented by the vertical red dotted line farthest to the left located at +110 μm and +140 μm for normal and tension wood, respectively), a signal at large angles can be detected (A1 in Figs. 2 and 3), showing the dominant contribution of the large MFA (estimated to be approximately 45°) of the S1 layer. In the next 200 μm, the signal intensity continues to increase together with the thickening of the cell wall. Clearly, this increase occurs at different rates for different classes of MFA. The contribution of MFA < 28° increases much more quickly than that of larger MFAs. This indicates that the developing layer has a lower MFA than the previous one and probably corresponds to the development of the S2 layer. The peak angle at that stage is approximately 22° (A2 in Fig. 2), indicating that the mean MFA is about 25° (Supplemental Data S1). Normal wood and tension wood have very similar patterns until a point where the signal from MFA < 16° diverges from larger MFAs (second red dotted line from the left, located at +310 μm in normal wood and +410 μm in tension wood). This divergence indicates that the cell wall layers deposited from that point have a MFA < 16° both in normal wood and tension wood. In normal wood, the contribution of this class of angles stops increasing near +350 μm (A3 and A4 in Fig. 2) and remains modest. In tension wood, the increase is much larger (A3 and A4 in Fig. 3) and continues until +650 μm, parallel to the increase in small-MFA 004 reflection intensity noted previously. Analysis of the 200 reflection intensity for tension wood reveals a very large specific contribution at small angles, with intensity 5 times higher than for large angles, parallel to the development of the G layer.
Changes in Axial Lattice Spacing of Cellulose along a Development Sequence
The evolution of the d004 is shown separately for the small MFA (less than 16°) and large MFA (greater than 16°) classes (Figs. 2C and 3C). The graph displays only the points with a signal clear enough to accurately determine the lattice spacing.
In normal wood, d004 remains constant along the profile for both small- and large-angle microfibrils. In tension wood, the d004 profile for large angles is also roughly constant, although more scattered because of the comparatively lower intensity of the signal for this category of angles. For small MFA in tension wood, one can clearly see a progressive increase in lattice spacing in the first 600 μm after the cambium. This increase is particularly steep in the area where the innermost part of the cell wall, dominated by small MFA, diverges on the intensity signal (Fig. 3A). This area clearly corresponds to the development of the G layer. Similar patterns were observed in almost all studied profiles of normal wood and tension wood, except one tension wood profile out of six, for which the d004 signal was very scattered (Supplemental Data S2).
The axial strain of cellulose was computed as the relative change in d004 observed in this area. For small-angle microfibrils in tension wood, it ranged between +0.1% to +0.3% with a mean of +0.18% for the five tension wood profiles. In most of the tension wood profiles, no or very little delay was observable between the deposition of cellulose (detected by intensity) and the increase in mean lattice spacing.
DISCUSSION
X-ray microdiffraction allowed the exploration of changes in cellulose ultrastructure along sequences of cell wall development in normal and tension wood. Variations in intensity were consistent with the deposition of crystalline cellulose during the progressive thickening of the cell walls. Variations of the 200 and 004 reflection intensities were observed along the sequences and interpreted in terms of MFA of the developing layer and change in cellulose lattice spacing. The different patterns observed in normal and tension wood revealed new information about the particular ultrastructure of tension wood secondary walls and their mechanical behavior during fiber development.
MFA of Cell Wall Layers
Interpretation of the 200 reflection profiles, in terms of MFA distribution, is not straightforward because walls that are not perpendicular to the beam create some artificial increase of the signal at small azimuth angles (Cave, 1997b). Therefore, the signal intensity at small azimuth does not always reflect the amount of cellulose with small MFA and must be interpreted with caution. We used a numerical model to assess our results (Supplemental Data S1). Based on this analysis, we found that the development of the secondary wall started with the deposition of a layer having a large mean MFA and assumed that this corresponds to the S1 layer. This stage was followed by an abrupt decrease in MFA of the deposited layers assumed to correspond to the early development of the S2 layer. The MFA of this layer was evaluated to be approximately 25° in both normal and tension wood, which is in the upper range of mean MFA usually reported for poplar. After this stage, we observed that further increase in wall thickness occurred along with a steep decrease in MFA of the deposited wall layers in both normal and tension wood. Accurate determination of this MFA was not possible, but simulations clearly show that the mean MFA is less than 10° in normal wood and close to 0° in tension wood. Microscopic observations showed that this occurs during the development of the inner part of the S2 layer for normal wood and during the development of the G layer for tension wood.
These observations indicate that the MFA is not uniform in the S2 layer of the studied normal wood samples. Donaldson and Xu (2005), observing individual cell walls with polarized light, reported that the S2 layer of Pinus radiata had relatively uniform microfibril angles but noticed a trend of increasing MFA toward the S1 layer. Using x-ray microdiffraction across single walls of Norway spruce (Picea abies), Peura et al. (2005) showed that the dominant MFA had a broad distribution ranging over approximately 20° to 30°. Our observations suggest that there is a decrease in MFA of the S2 layer toward the lumen in poplar normal wood.
Our results also show that the MFA of the S2 layer is close to 25° in tension wood (i.e. similar to that of the equivalent layer of normal wood). This result was compared with previous reports about the MFA of the S2 layer in poplar tension wood. Müller et al. (2006) analyzed the 200 diffraction patterns of mature tension wood. These patterns were dominated by a very strong central peak, but the authors detected “shoulders” beside this peak, very similar to what we observed (A3 and A4 in Fig. 3) and ascribed them to the reflection of the S2 layer. They concluded that the MFA of the S2 layer was between 20° and 25°. This is consistent with the MFA we determined for the tension wood S2 layer. Goswami et al. (2008) used selective enzymes to remove the G layer from a tension wood block and measured the MFA using x-ray diffraction. They found a value of approximately 36°, larger than the usual values of MFA of poplar normal wood, and assumed that this was representative of the S2 layer of tension wood. However, careful observation of their micrographs (Fig. 1 in Goswami et al., 2008) reveals that the enzyme treatment probably removed not only the G layer but also part of the S2 layer. In that case, the large observed MFA would be representative of the S1 layer and the outer part of the S2 layer, consistent with what we found here.
Analysis of Observed Variations in Cellulose Lattice Spacing
Our procedure was designed to measure the evolution of cellulose d004 along a sequence of cell wall development. Several studies demonstrated that the occurrence of mechanical strains in the cellulose crystal produces such a change in d004 (Ishikawa et al., 1997; Nakai et al., 2005; Clair et al., 2006; Peura et al., 2007; Zabler et al., 2010), strongly suggesting that our observations provide evidence for the direct implication of the G layer in the generation of maturation stress.
However, to support this conclusion, at least three alternative interpretations must be examined. The first is a possible artifact in data processing: a change of the 004 peak position on the screen may result either from a change in d004 or from a change in the distance between the sample and the detector. This possibility of artifact has been minimized due to the special care taken with the control of sample vertical alignment during the measurement. The flatness of all profiles obtained for normal wood confirms the quality of this vertical alignment.
The second possible artifact is related to the mechanical perturbation of wood during sample preparation, such as the suppression of the tree self-weight when cutting the segment or the release of maturation stress when preparing the sample. We designed our procedure in order to minimize these effects, and we subsequently checked numerically that these effects were negligible. The overall reliability of our procedure is again attested by the flatness of the profiles obtained for normal wood.
The third alternative interpretation is that the change in d004 may be due to a change in equilibrium lattice spacing rather than to a change in the mechanical state of the cellulose crystal. Such variations in equilibrium lattice spacing between different sources of cellulose have actually been reported and interpreted as the consequence of variations in the width of the cellulose crystal (Davidson et al., 2004). This hypothesis deserves further examination, since differences in apparent crystal width have repeatedly been reported between the G layer and other cell wall layers (Müller et al., 2002, 2006), or between normal and tension wood (Washusen and Evans, 2001; Ruelle et al., 2007), or between the tension wood of different species (Ruelle et al., 2007).
The above-mentioned apparent crystal sizes were all obtained from the measurement of the broadening of the 200 diffraction peak and the application of the Sherrer equation. The Sherrer equation expresses the relation between the size L (nm) of the crystal and the broadening parameter H (rad), defined as the full width of the diffraction peak at half maximum: L = 0.9 × λ/(H cosθ), where λ is the x-ray wavelength and θ is the Bragg angle.
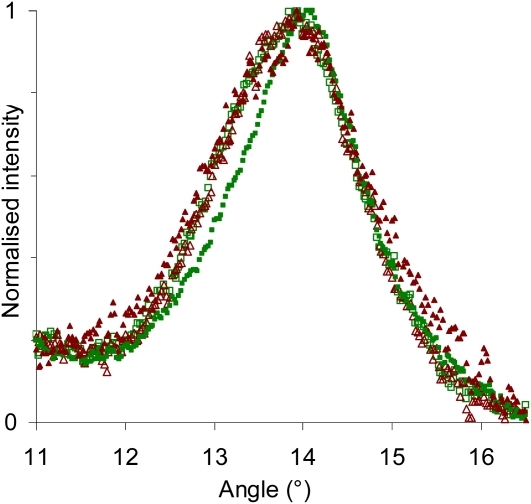
Figure 4 shows the peak broadening obtained from our data for different categories of microfibrils in tension wood, oriented either at the small or large angle and located either in the S2 layer or the G layer. It clearly shows that the microfibrils oriented at the small angle in the G layer have a narrower peak.
Figure 4.
Broadening of the 200 diffraction peak for different categories of microfibrils in tension wood. Closed symbols, G layer; open symbols, S2 layer; dark red triangles, large MFA; light green squares, low MFA. [See online article for color version of this figure.]
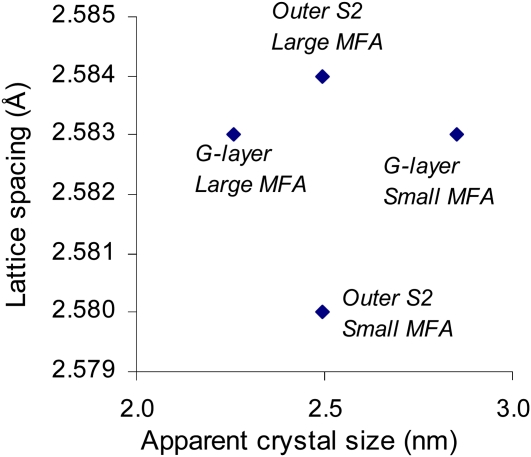
The apparent crystal sizes have been estimated for each category using the Sherrer equation and are plotted in Figure 5, together with their measured lattice spacing. This clearly shows that the two parameters are not linearly related in our data set, demonstrating that variations in lattice spacing do not result only from variations in equilibrium lattice spacing due to the crystal size effect proposed by Davidson et al. (2004) but also from mechanical strains as we postulate in this paper.
Figure 5.
Absence of relation between apparent crystal width and lattice spacing of different categories of microfibrils in tension wood. [See online article for color version of this figure.]
Interpretation in Relation to Maturation Stress Generation
We have provided evidence that the cellulose lattice spacing increases during the deposition of the G layer in tension wood but not during the deposition of the inner part of the S2 layer of normal wood. Assuming that most of this change in lattice distance is related to mechanical strains in the cellulose crystal rather than to a change in equilibrium lattice spacing, these observations suggest that microfibrils of the G layer are put under tension just after their incorporation to the cell wall. Furthermore, the magnitude of the strain deduced from our experiments (between 0.1% and 0.3%) is very close to the macroscopic released strain of maturation stress usually reported for poplar tension wood (Fang et al., 2008).
Several previous observations have supported the assumption that the tensile maturation stress in poplar tension wood develops inside the G layer. First, a positive correlation between the released strain of maturation stress and the amount of G layer in the tissue has been reported on several different wood materials (Clair et al., 2003; Yamamoto et al., 2005; Fang et al., 2008). This shows that, in species where the G layer occurs, it takes an active part in the generation of maturation stress. Moreover, the longitudinal contraction of the G layer observed on longitudinal sections of poplar and beech (Fagus silvatica) tension wood with light microscopy (Clair et al., 2005) and on transverse sections using atomic force microscopy (Clair and Thibaut, 2001) very probably results from this preexisting tensile stress. This state of tension of the G layer would also be consistent with the observation that a tension wood block extends longitudinally when G layers are removed using selective enzyme (Goswami et al., 2008). Our study provides a direct confirmation of this assumption and further shows that the elastic energy associated with this tensile stress is stored within microfibrils rather than, for example, within the hemicellulosic matrix.
CONCLUSION
We showed that the microfibrils are put under tension during the maturation of the G layer in tension wood, while this does not occur in the S2 layer of tension wood. To further understand the generation of maturation stress in tension wood, we still need to identify the mechanism by which tension is set inside G layer microfibrils. At least two hypotheses can be formulated: either the stress is set directly within the microfibrils during maturation, for example, due to the contraction of amorphous cellulose regions (Yamamoto, 2004), or this stress is generated by physicochemical changes occurring in the matrix (e.g. changes in moisture content or in ion concentration) and is transmitted to the microfibrils by a mechanism yet to be identified. This last hypothesis seems consistent with recent observations of the presence of pectin-like substances (Bowling and Vaughn, 2008) that are likely to induce moisture changes to the matrix and with the nanoporous structure of the G layer recently evidenced by nitrogen sorption isotherms (Clair et al., 2008; Chang et al., 2009).
MATERIALS AND METHODS
Plant Material
Experiments were performed on young poplar trees (Populus deltoides × Populus trichocarpa ‘I45-51’). In early spring 2007, trees were grown from cuttings in the INRA center at Orleans, France. They were tilted 35° from vertical to induce the formation of tension wood with high-tensile maturation stress on the upper side of the stems. On June 24, trees were moved to the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. They were kept tilted, outdoors, and were regularly watered until the start of the experiments. After preliminary experiments, four trees, approximately 2 m high, were selected and studied successively between June 27 and June 28. Sample preparation and measurements of each tree were carried out within 8 h.
Sample Preparation
Sample preparation was designed to prevent the release of mechanical stress within the segment, in order to keep the sample as close as possible to its in planta mechanical state (Clair et al., 2006). On each tree, a 40-cm-long stem segment (approximately 3 cm in diameter) was taken from the curved basal part of the stem. This length was chosen so that the central part of the segment was far enough from its ends to minimize mechanical disturbance of the studied area. The segment was then prepared so as to leave a thin strip of peripheral wood on the mid part of one side (Fig. 1) using a homemade device made of two parallel razor blades inserted radially into the segment. Special care was taken to remain parallel to the fibers and thus to avoid chopping them. Bark and wood were removed on both sides of the strip in order to leave a window for the x-ray beam. The strip, approximately 400 μm thick in the tangential direction, included the bark, the cambial area, and the first 2 mm of wood. The samples were kept wet during the whole preparation process.
Three stem segments were sampled on the upper side of the tilted stems, and one was sampled on the opposite side. However, later anatomical observations revealed that one of the segments sampled on the upper side had not produced G-fibers and had a MFA typical of normal wood, so that our sample material finally included two strips representative of tension wood and two strips representative of normal wood.
X-Ray Setup and Experimental Method
The experiment was carried out at the ID13 beamline of the ESRF using a 5-μm beam (Riekel, 2000). The wavelength of the monochromatic x-ray beam was λ = 0.961176 Å. A MAR165 CCD detector (16-bit readout with 2,048 × 2,048 pixels) was placed at approximately 177 mm from the sample so that it recorded both the 200 and 004 reflections. The distance between the sample and the detector was determined by using a silver-behenate calibration powder (Blanton et al., 1995), which was directly applied on the wood strip after the measurements.
The sample holder was designed to maintain the stem segment perpendicular to the beam while allowing precisely monitored vertical and lateral displacements. On each wood strip, three radial profiles (1 mm apart from each other along the fiber direction) were recorded in the transition zone between bark and mature wood (Fig. 1). Each profile contains 150 measurement points at successive radial positions separated by 10 μm, extending from outer bark to mature wood. Samples were kept wet during the measurements using a microdrop system fixed to the wood segment.
Data Processing
A total of 1,800 diffraction patterns were recorded for this study. They were processed using the Fit2D software (http://www.esrf.eu/computing/scientific/FIT2D/) and homemade software procedures programmed with Microsoft Excel/Visual Basic. Despite the very small amount of wood material crossed by the x-ray beam (low thickness and small beam size), the data yielded a high-quality signal with very low noise, allowing a detailed analysis of the 004 and 200 reflections.
The 200 reflection in each pattern (centered at θ200 = 7.31°) was radially integrated across its profile in order to obtain a plot of the azimuthal intensity distribution of 200 planes. The azimuthal plot was used to obtain information about the orientation of microfibrils. The diffraction patterns were interpreted in terms of MFA distribution. For cell walls oriented perpendicular to the beam, the variation of intensity as a function of azimuthal position is a direct image of the MFA distribution (Cave, 1997b). The contribution of cell walls that are not perpendicular to the beam creates some distortion of the signal, but this distortion can be taken into account in the interpretation (Supplemental Data S1).
The 004 reflection was used to obtain information about cellulose lattice spacing. The diffraction patterns were integrated on a defined azimuthal sector (see below), and the intensity was plotted as a function of the radial position on the image. The radial position of maximal intensity (rmax) was determined using local polynomial fitting. Any radial position r on the pattern corresponds to a value of the Bragg angle: θ004 = ½atan(r/L), where L is the distance between the sample and the camera. The Bragg angle of the cellulose 004 reflection is approximately equal to 10.73° at the experimental wavelength of λ = 0.961176 Å, but variations in cellulose lattice spacing d004 induce slight changes according to the equation of diffraction: d004 = λ/(2sinθ004). Therefore, the mean lattice spacing was computed as d004 = λ/(2sin[(atan(rmax/L))/2]).
A given microfibril contributes to the 004 reflection at an azimuthal position that depends on the microfibril orientation. Therefore, the lattice spacing of cellulose can be computed separately for different classes of MFA by analyzing the signal in specific azimuthal sectors. The above-mentioned calculations were carried out for two distinct azimuthal integration sectors (±0°–12° and ±12°–24°), yielding two distinct sets of lattice spacings. The first is representative of the fraction of cellulose with MFA < 16°, and the second is representative of the fraction with MFA > 16° (Supplemental Data S1).
Microscopic Observations
The studied wood strips were taken from the segment just after the x-ray diffraction experiment and kept in water at 4°C until further processing. First, samples were dehydrated in ethanol, then in propylene oxide, and finally embedded in Epon after polymerization at 60°C. Transverse sections of 1 μm thickness were stained with methylene blue/AzurII mix and observed with a light microscope (Leica DMR; Leica Microsystems).
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Data S1. Interpretation of diffraction patterns.
Supplemental Data S2. Changes in lattice spacing in all studied profiles.
Supplementary Material
Acknowledgments
We gratefully acknowledge Richard Davies (ID13-ESRF) for technical support, Françoise Laurans and Alain Moreau (UR588 Amélioration, Génétique, et Physiologie Forestières, INRA Orleans) for excellent assistance in preparing the histological sections, and J. Paul MacLean (Laboratoire de Mécanique et Génie Civil, CNRS, Université Montpellier 2) for checking the English and making improvements to the manuscript.
References
- Alméras T, Fournier M. (2009) Biomechanical design and long-term stability of trees: morphological and wood traits involved in the balance between weight increase and the gravitropic reaction. J Theor Biol 256: 370–381 [DOI] [PubMed] [Google Scholar]
- Alméras T, Gril J, Yamamoto H. (2005) Modelling anisotropic maturation strains in wood in relation to fibre boundary conditions, microstructure and maturation kinetics. Holzforschung 59: 347–353 [Google Scholar]
- Alméras T, Yoshida M, Okuyama T. (2006) The generation of longitudinal maturation stress in wood is not dependent on diurnal changes in diameter of trunk. J Wood Sci 52: 452–455 [Google Scholar]
- Archer RR. (1986) Growth Stresses and Strains in Trees. Springer Verlag, Berlin [Google Scholar]
- Bamber RK. (1987) The origin of growth stresses: a rebuttal. IAWA Bull 8: 80–84 [Google Scholar]
- Bamber RK. (2001) A general theory for the origin of growth stresses in reaction wood: how trees stay upright. IAWA J 22: 205–212 [Google Scholar]
- Blanton T, Huang T, Toraya H, Hubbard C, Robie S, Louer D, Goebel H, Will G, Gilles R, Raftery T. (1995) JCPDS-International Centre for Diffraction Data round robin study of silver behenate: a possible low-angle x-ray diffraction calibration standard. Powder Diffraction 10: 91–95 [Google Scholar]
- Bowling AJ, Vaughn KC. (2008) Immunocytochemical characterization of tension wood: gelatinous fibers contain more than just cellulose. Am J Bot 95: 655–663 [DOI] [PubMed] [Google Scholar]
- Bowling AJ, Vaughn KC. (2009) Gelatinous fibers are widespread in coiling tendrils and twining vines. Am J Bot 96: 719–727 [DOI] [PubMed] [Google Scholar]
- Boyd JD. (1972) Tree growth stresses. Part V. Evidence of an origin in differentiation and lignification. Wood Sci Technol 6: 251–262 [Google Scholar]
- Cave ID. (1966) Theory of x-ray measurement of microfibril angle in wood. For Prod J 16: 37–42 [Google Scholar]
- Cave ID. (1997a) Theory of x-ray measurement of microfibril angle in wood. Part 1. The condition for reflection x-ray diffraction by materials with fibre type symmetry. Wood Sci Technol 31: 143–152 [Google Scholar]
- Cave ID. (1997b) Theory of x-ray measurement of microfibril angle in wood. Part 2. The diffraction diagram x-ray diffraction by materials with fibre type symmetry. Wood Sci Technol 31: 225–234 [Google Scholar]
- Chang SS, Clair B, Ruelle J, Beauchêne J, Di Renzo F, Quignard F, Zhao GJ, Yamamoto H, Gril J. (2009) Mesoporosity as a new parameter for understanding tension stress generation in trees. J Exp Bot 60: 3023–3030 [DOI] [PubMed] [Google Scholar]
- Clair B, Alméras T, Yamamoto H, Okuyama T, Sugiyama J. (2006) Mechanical behavior of cellulose microfibrils in tension wood, in relation with maturation stress generation. Biophys J 91: 1128–1135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clair B, Gril J, Baba K, Thibaut B, Sugiyama J. (2005) Precautions for the structural analysis of the gelatinous layer in tension wood. IAWA J 26: 189–195 [Google Scholar]
- Clair B, Gril J, Di Renzo F, Yamamoto H, Quignard F. (2008) Characterization of a gel in the cell wall to elucidate the paradoxical shrinkage of tension wood. Biomacromolecules 9: 494–498 [DOI] [PubMed] [Google Scholar]
- Clair B, Ruelle J, Thibaut B. (2003) Relationship between growth stress, mechano-physical properties and proportion of fibre with gelatinous layer in chestnut (Castanea sativa Mill.). Holzforschung 57: 189–195 [Google Scholar]
- Clair B, Thibaut B. (2001) Shrinkage of the gelatinous layer of poplar and beech tension wood. IAWA J 22: 121–131 [Google Scholar]
- Davidson TC, Newman RH, Ryan MJ. (2004) Variations in the fibre repeat between samples of cellulose I from different sources. Carbohydr Res 339: 2889–2893 [DOI] [PubMed] [Google Scholar]
- Donaldson L, Xu P. (2005) Microfibril orientation across the secondary cell wall of radiata pine tracheids. Trees Struct Funct 19: 644–653 [Google Scholar]
- Fang CH, Clair B, Gril J, Alméras T. (2007) Transverse shrinkage in G-fibers as a function of cell wall layering and growth strain. Wood Sci Technol 41: 659–671 [Google Scholar]
- Fang CH, Clair B, Gril J, Liu SQ. (2008) Growth stresses are highly controlled by the amount of G-layer in poplar tension wood. IAWA J 29: 237–246 [Google Scholar]
- Fisher JB. (2008) Anatomy of axis contraction in seedlings from a fire prone habitat. Am J Bot 95: 1337–1348 [DOI] [PubMed] [Google Scholar]
- Fournier M, Chanson B, Thibaut B, Guitard D. (1991) Mechanics of standing trees: modelling a growing structure submitted to continuous and fluctuating loads. 2. Tridimensional analysis of maturation stresses: case of standard hardwood. Ann Sci For 48: 527–546 (in French) [Google Scholar]
- Fujita M, Saiki H, Harada H. (1974) Electron microscopy of microtubules and cellulose microfibrils in secondary wall formation of poplar tension wood fibers. Mokuzai Gakkaishi 20: 147–156 [Google Scholar]
- Gorshkova TA, Gurjanov OP, Mikshina PV, Ibragimova NN, Mokshina NE, Salnikov VV, Ageeva MV, Amenitskii SI, Chernova TE, Chemikosova SB. (2010) Specific type of secondary cell wall formed by plant fibers. Russ J Plant Physiol 57: 328–341 [Google Scholar]
- Goswami L, Dunlop JWC, Jungnikl K, Eder M, Gierlinger N, Coutand C, Jeronimidis G, Fratzl P, Burgert I. (2008) Stress generation in the tension wood of poplar is based on the lateral swelling power of the G-layer. Plant J 56: 531–538 [DOI] [PubMed] [Google Scholar]
- Hori R, Sugiyama J, Itoh T, Müller M. (2000) Synchrotron x-ray diffraction analysis of cellulose in developing xylem cell walls from Cryptomeria japonica. Wood Res 87: 19–20 [Google Scholar]
- Ishikawa A, Okano T, Sugiyama J. (1997) Fine structure and tensile properties of ramie fibres in the crystalline form of cellulose I, II, III and IV. Polymer (Guildf) 38: 463–468 [Google Scholar]
- Jourez B, Riboux A, Leclercq A. (2001) Anatomical characteristics of tension wood and opposite wood in young inclined stems of poplar (Populus euramericana cv “Ghoy”). IAWA J 22: 133–157 [Google Scholar]
- Mellerowicz EJ, Immerzeel P, Hayashi T. (2008) Xyloglucan: the molecular muscle of trees. Ann Bot (Lond) 102: 659–665 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellerowicz EJ, Sundberg B. (2008) Wood cell walls: biosynthesis, developmental dynamics and their implications for wood properties. Curr Opin Plant Biol 11: 293–300 [DOI] [PubMed] [Google Scholar]
- Moulia B, Coutand C, Lenne C. (2006) Posture control and skeletal mechanical acclimation in terrestrial plants: implications for mechanical modeling of plant architecture. Am J Bot 93: 1477–1489 [DOI] [PubMed] [Google Scholar]
- Müller M, Burghammer M, Sugiyama J. (2006) Direct investigation of the structural properties of tension wood cellulose microfibrils using microbeam x-ray fibre diffraction. Holzforschung 60: 474–479 [Google Scholar]
- Müller M, Hori R, Itoh T, Sugiyama J. (2002) X-ray microbeam and electron diffraction experiments on developing xylem cell walls. Biomacromolecules 3: 182–186 [DOI] [PubMed] [Google Scholar]
- Münch E. (1938) Statik und Dynamik des Schraubigen Baus der Zwellwand, besonders der Druck- and Zugholzes. Flora 32: 357–424 [Google Scholar]
- Nakai T, Yamamoto H, Nakao T. (2005) The relationship between macroscopic strain and crystal lattice strain in wood under uniaxial stress in the fiber direction. J Wood Sci 51: 193–194 [Google Scholar]
- Nishikubo N, Awano T, Banasiak A, Bourquin V, Ibatullin F, Funada R, Brumer H, Teeri TT, Hayashi T, Sundberg B, et al. (2007) Xyloglucan endo-transglycosylase (XET) functions in gelatinous layers of tension wood fibers in poplar: a glimpse into the mechanism of the balancing act of trees. Plant Cell Physiol 48: 843–855 [DOI] [PubMed] [Google Scholar]
- Okuyama T, Yamamoto H, Yoshida M, Hattori Y, Archer RR. (1994) Growth stresses in tension wood: role of microfibrils and lignification. Ann Sci For 51: 291–300 [Google Scholar]
- Okuyama T, Yoshida M, Yamamoto H. (1995) An estimation of the turgor pressure change as one of the factors of growth stress generation in cell walls: diurnal change of tangential strain of inner bark. Mokuzai Gakkaishi 41: 1070–1078 [Google Scholar]
- Peura M, Kölln K, Grotkopp I, Saranpää P, Müller M, Serimaa R. (2007) The effect of axial strain on crystalline cellulose in Norway spruce. Wood Sci Technol 41: 565–583 [Google Scholar]
- Peura M, Müller M, Serimaa R, Vainio U, Saren MP, Saranpää P, Burghammer M. (2005) Structural studies of single wood cell walls by synchrotron x-ray microdiffraction and polarised light microscopy. Nucl Instrum Methods Phys Res B 238: 16–20 [Google Scholar]
- Peura M, Müller M, Vainio U, Saren MP, Saranpää P, Serimaa R. (2008a) X-ray microdiffraction reveals the orientation of cellulose microfibrils and the size of cellulose crystallites in single Norway spruce tracheids. Trees Struct Funct 22: 49–61 [Google Scholar]
- Peura M, Saren MP, Laukkanen J, Nygard K, Andersson S, Saranpää P, Paakkari T, Hamalainen K, Serimaa R. (2008b) The elemental composition, the microfibril angle distribution and the shape of the cell cross-section in Norway spruce xylem. Trees Struct Funct 22: 499–510 [Google Scholar]
- Pilate G, Chabbert B, Cathala B, Yoshinaga A, Leplé JC, Laurans F, Lapierre C, Ruel K. (2004) Lignification and tension wood. C R Biol 327: 889–901 [DOI] [PubMed] [Google Scholar]
- Riekel C. (2000) New avenues in x-ray microbeam experiments. Rep Prog Phys 63: 233–262 [Google Scholar]
- Ruelle J, Yamamoto H, Thibaut B. (2007) Growth stresses and cellulose structural parameters in tension and normal wood from three tropical rainforest angiosperm species. BioResources 2: 235–251 [Google Scholar]
- Washusen R, Evans R. (2001) The association between cellulose crystallite width and tension wood occurrence in Eucalyptus globulus. IAWA J 22: 235–243 [Google Scholar]
- Yamamoto H. (1998) Generation mechanism of growth stresses in wood cell walls: roles of lignin deposition and cellulose microfibril during cell wall maturation. Wood Sci Technol 32: 171–182 [Google Scholar]
- Yamamoto H. (2004) Role of the gelatinous layer on the origin of the physical properties of the tension wood. J Wood Sci 50: 197–208 [Google Scholar]
- Yamamoto H, Abe K, Arakawa Y, Okuyama T, Gril J. (2005) Role of the gelatinous layer (G-layer) on the origin of the physical properties of the tension wood of Acer sieboldianum. J Wood Sci 51: 222–233 [Google Scholar]
- Zabler S, Paris O, Burgert I, Fratzl P. (2010) Moisture changes in the plant cell wall force cellulose crystallites to deform. J Struct Biol 171: 133–141 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.