Rapid protein fold determination using unassigned NMR data

Abstract

Experimental structure determination by x-ray crystallography and NMR spectroscopy is slow and time-consuming compared with the rate at which new protein sequences are being identified. NMR spectroscopy has the advantage of rapidly providing the structurally relevant information in the form of unassigned chemical shifts (CSs), intensities of NOESY crosspeaks [nuclear Overhauser effects (NOEs)], and residual dipolar couplings (RDCs), but use of these data are limited by the time and effort needed to assign individual resonances to specific atoms. Here, we develop a method for generating low-resolution protein structures by using unassigned NMR data that relies on the de novo protein structure prediction algorithm, rosetta [Simons, K. T., Kooperberg, C., Huang, E. & Baker, D. (1997) J. Mol. Biol. 268, 209–225] and a Monte Carlo procedure that searches for the assignment of resonances to atoms that produces the best fit of the experimental NMR data to a candidate 3D structure. A large ensemble of models is generated from sequence information alone by using rosetta, an optimal assignment is identified for each model, and the models are then ranked based on their fit with the NMR data assuming the identified assignments. The method was tested on nine protein sequences between 56 and 140 amino acids and published CS, NOE, and RDC data. The procedure yielded models with rms deviations between 3 and 6 Å, and, in four of the nine cases, the partial assignments obtained by the method could be used to refine the structures to high resolution (0.6–1.8 Å) by repeated cycles of structure generation guided by the partial assignments, followed by reassignment using the newly generated models.

Knowledge of the 3D structures of proteins is critical for many biological questions, but the time-consuming process of structure elucidation through x-ray crystallography or NMR spectroscopy cannot keep up with the rapidly growing number of sequenced genes and genomes. In contrast to x-ray crystallography, where the growing of suitable crystals is often the time-consuming step, the collection of data can be done rapidly by NMR spectroscopy, once the protein is expressed. Techniques such as the use of residual dipolar couplings (RDCs) (1, 2), gradient techniques (3), and crosscorrelated relaxation (4), offer possibilities for the rapid collection of structural information, and, hence, the application of NMR spectroscopy in the field of structural genomics (5). However, rapid NMR structure determination is limited by the time-consuming and error-prone step of assigning observed resonances to individual atoms.

Traditional methods for assigning resonances to atoms rely on experiments that couple atoms on adjacent residues. These experiments are complicated by the large total number of signals that result in numerous spectral overlaps and poorly resolved peaks. Alternatively, if a 3D structure is already known, one can in principle evaluate different possible assignments, based on the match between the experimental data and simulated data generated from the structure assuming a particular assignment. In the absence of a known structure or a structure of a homologous protein, models generated by de novo structure prediction methods that are based on amino acid sequence information alone can, in principle, be used for evaluating possible assignments.

Even the best current method for de novo structure prediction, rosetta (6), generates structures with the correct overall topology only a relatively small fraction of the time. For roughly half of proteins <150 amino acids, one of the five largest clusters of structures found is structurally similar to the true structure after large numbers of independent folding simulations (7). This success rate can be pushed >50% if more than five clusters are considered. However, to distinguish among these possible structures, experimental data are necessary, and, given a method for finding an optimal assignment, unassigned NMR data can potentially help to identify and refine the most accurate model.

Here, we develop a method for global fold generation that utilizes unassigned chemical shifts (CSs), intensities of NOESY crosspeaks [nuclear Overhauser effects (NOEs)], and RDCs in conjunction with the rosetta structure prediction approach to build a low- to medium-resolution structural model in a short period, refine this model to higher resolution, and gain a partial CS–atom assignment.

Materials and Methods

We present a computational approach that enables the generation of an experimentally validated protein structure within a time frame of 12–48 h, based on unassigned NMR data including CSs, NOEs, and RDCs. We assume a worst case scenario where no homologues of known structure are present in the Protein Data Bank (and, therefore, only low-resolution de novo models are available) and no NMR data points are assigned to individual atoms (and, therefore, the complete assignment needs to be evaluated); only the amino acid sequence and peak lists of unassigned data are available. A simplified flow chart of the algorithm is shown in Fig. 1.

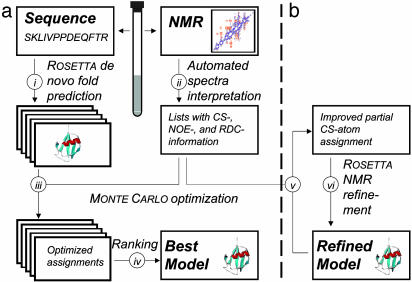
Fig. 1.

Simplified flow chart of the two steps of the algorithm. In the first step (a), an experimentally validated model of the protein is generated by computational methods. Parallel with the collection of the NMR data (i), rosetta is used to generate possible 3D models for the sequence (ii). For each model, an optimized assignment is identified by a Monte Carlo search (iii). Models are ranked according to their consistency with the NMR data (iv). In the second step (b), the best-ranked models are refined by detecting partial CS–atom assignments (v) and by using the derived constraints as input for rosettanmr (vi).

Generating Possible Structural Models de Novo F (Fig. 1ai). rosetta has proven to be one of the most successful approaches for de novo fold prediction as demonstrated in the Critical Assessment of Techniques for Protein Structure Prediction experiments CASP3, CASP4, and CASP5 (8, 9). The sequence of the unknown structure is cut into overlapping fragments of three and nine amino acids. The Protein Data Bank is subsequently screened for fragments that have a high primary sequence homology and a secondary structure that matches the predicted secondary structure (10–12) of the query sequence. These fragments, which sample possible conformations for the protein backbone, are combined using a Monte Carlo algorithm. Thousands of models are generated, and five representative models are selected by using a clustering procedure. This procedure is explained in detail in recent publications (7–9) and is, therefore, only discussed briefly in this work.

Input of Unassigned NMR Data (Fig. 1aii). NMR spectra can be analyzed manually or in an automated fashion (e.g., refs. 13–16) to obtain lists of experimental data that are the starting point for our approach. For the current protocol, a CS list, an NOE list, and an RDC list are used. The first list consists of all of the observed resonance frequencies (as CSs in ppm) for hydrogens, nitrogens, and carbon atoms in the protein. This information is useful because CSs are sensitive to the local conformation of the protein backbone, e.g., secondary structure elements (17, 18). Crosspeaks in NOESY spectra can be represented as a list of two hydrogen CSs (taken from the CS list) and one NOE intensity, which reflects an effective distance between the two groups of hydrogen atoms assigned to the two CS values. The network of unassigned NOE data can be seen as a description of the 3D density distribution of hydrogens in the unknown protein (19, 20). In a similar fashion, RDCs form a list of two CS values, plus one RDC value, and indirectly code the relative orientation of atom–atom vectors, because the relative orientation of a bond vector (e.g., N–H^N) to the molecular alignment frame is described (21–24).

From the list of RDCs, an additional list of connectivity constraints is derived, requiring that the atoms assigned to those CS values are separated by one or two bonds in the bonding network, respectively. Such connectivity constraints limit the possible space of assignments, and, are therefore valuable information. They are implemented in a very general fashion, requiring that at least one pair of atoms assigned to a pair of CSs is separated by a certain number of bonds in the bonding network. Hence, they can also be used if additional connectivity information from triple resonance spectra is available. Even simpler, although not used here, is the addition of partial assignments by fixing the mapping of a certain atom of the protein to a certain CS value.

All three sources of information (CSs, NOEs, and RDCs) have inherent ambiguities. Hydrogen atom CS signals heavily overlap and several hydrogen atoms can appear to have one and the same CS value. In turn, NOE and RDC data cannot be unambiguously assigned to a single atom without additional information. However, if a structural model exists, and one particular assignment is assumed, theoretical CS, NOE, and RDC data can be computed and compared with the experiment.

The experimental data used for the eight example proteins (see below) were obtained from the Protein Data Bank (www.pdb.org) and the BioMagResBank (www.bmrb.wisc.edu). To ensure as realistic as possible a set of data, the following processing was applied to the published CS, NOE, and RDC information: all atom references in the NOE and RDC lists were replaced with references to the respective entry in the CS list; the information about the particular atom assigned to a CS value was removed from the CS list and only the atom type information (hydrogen, carbon, or nitrogen) was kept; the distances given in the NOE list were replaced with intensities by computing 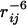; and signals that might overlap in the spectra were combined to one entry in the CS list. If two hydrogen atoms having a given distance to a common partner were merged, the respective NOE entry was combined by adding the two intensities. Two signals were assumed to be potentially unresolved if they were marked in the BioMagResBank entry as overlapping, ambiguous NOEs to a common partner were reported, or the CS values were similar (ΔCS_H < 0.02 ppm, ΔCS_C < 0.2 ppm, and ΔCS_N < 0.2 ppm). The average CS value was assigned to these entries in the CS list (4). For calculation of the score S (see below), an SD and a maximum tolerance were assigned to every experimental data point. Due to the lack of experimental error estimates, the following rather large values were used: CS_H: ± 0.25 and ± 1.00 ppm, CS_C: ± 1.00 and ± 4.00 ppm, and CS_N: ± 2.50 and ± 10.00 ppm, NOE: the intensity equivalent for ± 0.25 and ± 1.00 Å, and RDC: ± 2.5% and ± 10.0% of the axial tensor component as determined from the histogram (25). As discussed below, all predicted values that have a deviation to the experiment smaller than the SD are treated as completely satisfied. Hence, all published experimental data points (that were potentially refined on the published solution structure) are converted into broad ranges that are consistent with the experiment. The knowledge of the exact number is thus removed and only blurred information is left that is first, more realistic in terms of automatically picked data, and, second, more likely to fit low-resolution models.

Scoring of a Particular CS–Atom Assignment by Using a 3D Model (Fig. 1aiii). Individual assignments were scored in the context of a particular structure model, based on the consistency of the CS, NOE, and HRDC data with the model, given the assignments.

For scoring the consistency of the experimental CS values with a given assignment and structure model, theoretical CS values were computed from the model by using a neural-network approach (www.jens-meiler.de/proshift.html; ref. 26). The neural-network input consists of sequence information, backbone conformation, as well as local atom environments and predicts ¹H, ¹³C, and ¹⁵N CSs for all backbone and side-chain atoms. The SD of the predictions are 0.3, 1.3, and 2.6 ppm respectively.

Theoretical crosspeak intensities 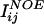between two CS values i and j in a NOESY spectrum were obtained from the 3D model, together with the assignment by computing the sum 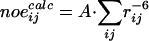over all pairs of hydrogen atoms assigned to the respective CS values, where A is a global scaling factor that was fitted to give the best overall agreement of experimental and back-computed NOE values.

RDC values are given by 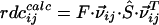where F is a constatnt known factor, 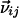is the vector that connects the interacting nuclei in the molecular frame, and Ŝ is the Saupe order matrix that describes size and orientation of the alignment frame relative to the molecular frame. By singular value decomposition, the 3 × 3 symmetric and traceless Saupe order matrix, Ŝ is determined in such a way that 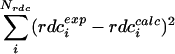is minimized (27).

The individual score of a single data point, S_i ∈ [0, 1] (i = CS, NOE, or RDC) is computed applying a fuzzy-logic filter. The score is set to be 1 if the value is reproduced from the structural model within the SD and 0 if it lies outside the maximum tolerance. Between standard and maximum deviation a linear decay is applied. The advantage of this function over a more standard quadratic penalty function is that it is more tolerant of errors in the model (e.g., an incorrect loop) and mispicked NMR signals. Both scenarios are likely to occur when using de novo fold prediction and automated peak-picking methods and result in a fraction of unfeasible restraints. Large penalties from these data could overshadow significant similarities in other parts of the structure and assignment. The overall S^cs, S^noe, and S^rdc are defined as the arithmetic averages of the respective individual scores.

The weight associated with a single CS, NOE, or RDC data point is determined by optimizing the discrimination of good from bad models assuming the correct assignment in a set of eight proteins with a total of 80 models (see below). The optimal ratio between the weights on the three terms was found to be 2:5:70. Because this ratio was determined across a set of eight different proteins with different composition of experimental data, it is assumed to be universal and was kept constant; 25% changes in the relative weight do not alter the result significantly. The ratio of 2:5:70 refers to a single CS, NOE, or RDC data point rather than to the complete set of data. This finding ensures that the relative influence of CSs, NOEs, or RDCs increases if their number increases and decreases (or even vanishes) if fewer (or no) experimental data are available (compare Eq. 1). Because the number of CSs and NOEs is usually higher than the number of RDCs, the actual relative influence (S^cs:S^noe:S^rdc) is ≈1:3:6, but varies from protein to protein depending on the ratio of collected CS, NOE, and RDC data points. If for example the number of RDC data points increases, the relative weight of the score, S^rdc, will increase too. The overall consistency of the NMR data with a structural model, S, can be written as:

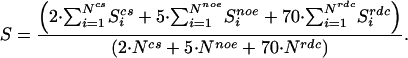[1]

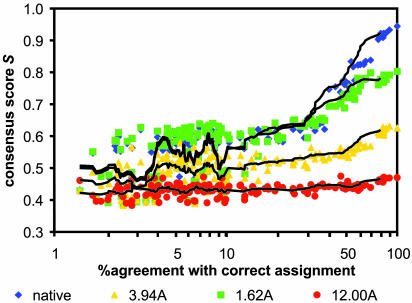
Monte Carlo Search for an Optimal Assignment Given a Model (Fig. 1aiii). As shown in Fig. 2, given an accurate model not only the correct assignment but also a large number of similar assignments show considerable agreement with the experimental data. The number of assignments that produce good agreement with the experimental data decreases as the model becomes worse. Thus, in contrast to high-resolution structure elucidation, for distinguishing the correct fold from incorrect conformations, it is not necessary to find a completely correct assignment. If the space of all possible assignments is sampled sufficiently densely, good models can be identified by their statistically improved agreement with the experimental data after alignment optimization.

Fig. 2.

Scoring of alternative assignments. The consistency score S (y axes) is plotted versus assignment accuracy (x axes) for the native protein, 1ghh, a refined model (1.6 Å), the cluster center closest to the native (3.9 Å), and the cluster center farthest away from the native (12.0 Å).

To sample the (huge) space of possible CS–atom assignments, a Monte Carlo algorithm was implemented. A random CS–atom assignment is generated by assigning every atom to one CS signal. The only biases are the connectivity constraints obtained from the RDCs, and that, after completion, a maximum number of CS signals have at least one atom assigned. Starting from this random assignment, two moves are possible: (i) A single atom is reassigned to a different CS value, and (ii) two atoms exchange their assigned CS signals. The agreement between the structure and the experimental data for the current assignment is assessed by the consistency score, S [0, 1] that reflects CS, NOE, and RDC information (Eq. 1 above). No moves are considered that would result in a violation of the bond constraints derived from the RDCs.

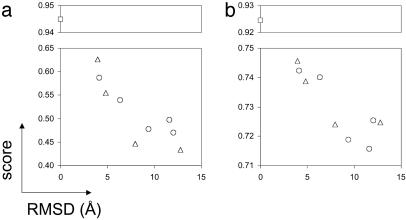
Model Selection by Using the Consistency Score, S (Fig. 1aiv). It is expected that not only the correct assignments but also the optimized assignments found for the native structure and near native structures will produce higher scores than assignments based on incorrect structures. As shown in Fig. 3 a and b, this is indeed the case: the lower the rms deviation (rmsd) of the model to the correct structure, the higher its consistency score, S ∈ [1].

Fig. 3.

The consistency score, S (y axis), for 10 different conformations of the DNA-damage-inducible protein I (1ghh) with the correct assignment (a) and with the assignment achieved by the optimization procedure (b) is plotted versus the rmsd to the correct structure (x axis). □, native structure; ○, cluster centers; ▵, four additional hand-picked models.

To rank a set of possible structure models, for each structure 100 random assignments are generated and 100,000 Monte Carlo optimization steps are performed in a first round. The best 20 scoring assignments per model are selected and a second round of 900,000 additional optimization steps is applied. The average score of the five highest scoring assignments per model are used to build the ranking.

Extraction of Reliable Partial Assignments by Consensus (Fig. 1bv). Once a model is selected, it is desirable to be able to identify the subset of atoms that are most confidently assigned to NMR signals. Atoms have a higher chance to be correctly assigned if they are commonly assigned to one and the same signal in different optimization runs. To increase the reliability in the detection of such atoms, 1,000 random assignments for the model selected in Fig. 1aiv were optimized for 100000 steps and the 100 best-scoring assignments were further optimized for a total of 1,000,000 steps. If one atom was assigned to one and the same signal in at least 12 (60%) of the 20 best-scoring assignments, this assignment was assumed to be correct.

Refinement of the Assignment and the Structure (Fig. 1bvi). The NOEs and RDCs associated with the subset of atoms detected in Fig. 1bv have a high probability to be correctly assigned to the structure. This probability was further increased by excluding NOEs and RDCs inconsistent with the current structure. By using the remaining experimental data points as restraints, structural models were built refining the previous model. The rosetta algorithm was applied as modified for the utilization of NMR data (28, 29). Of 100 generated models, the one with the best agreement with the experimental data was selected and used as a starting point for generating assignments as described in Fig. 1bv.

Results and Discussion

The method was applied to eight proteins with published CS, NOE, and RDC data: the Ca²⁺ binding rat apo-S100(ββ) (1b4c; ref. 30), the human G^α-interacting protein (1cmz; ref. 31), the immunoglobin-binding domain of protein G (1gb1; refs. 32–34), the DNA-damage-inducible protein I (1ghh; ref. 35), the C-terminal KH domain of heterogeneous nuclear ribonucleoprotein K (1khm; ref. 36), ubiquitin (1ubi; ref. 37), cyanovirin-N (2ezm; ref. 38), and the human barrier-to-autointegration factor (2ezxA; ref. 39). These proteins range from 56 to 128 amino acids in length and include all α-, β-, and α/β-folds (Table 1).

Table 1. Results of rosetta fold prediction and filtering with unassigned NMR data.

Protein			NMR data			Ranking of rosetta models using NMR data
PDB ID code	Fold type	No. of residues	CS	NOE	RDC	Correlation coefficient*	Best-scoring cluster rmsd, ņ	Correctly assigned backbone atoms, %‡
1b4c	α	92	472	830	218	-0.73	4.58	3.1
1cmz	α	128	1,042	1,221	104	-0.72	6.67	1.4
1gbl	αβ	56	471	612	283	-0.90	4.46	6.6
1ghh	αβ	81	771	760	530	-0.86	4.81	10.9
1khm	αβ	88	735	1,128	206	-0.87	4.45	4.1
1ubi	αβ	76	803	1,240	628	-0.91	3.43	13.5
2ezm	β	101	767	1,005	327	-0.81	6.23	3.2
2ezxA	α	89	808	729	245	-0.85	6.29	2.7

^*Correlation coefficient between the rmsd of the nine protein models to the native structure and the average score of the top five assignments for each of the models

^†rmsd of the best-scoring cluster to the native structure.

^‡Average percentage of correctly assigned backbone atoms for the best-scoring cluster center.

Two tests were carried out: First, unassigned NMR spectra were used to distinguish models that adopt the native fold from incorrect conformations (model selection, Fig. 1a). Second, the structure of the selected models was refined to fulfill the NMR data even better (model refinement, Fig. 1b). The procedure and the algorithms are described in detail in Materials and Methods. In the following, only the fundamental results and conclusions are discussed.

Model Selection. Ten models, the five largest rosetta-generated cluster centers, four additional rosetta-generated models chosen to span a wide rmsd range, and the native, were used as input along with the unassigned NMR data to the Monte Carlo assignment search procedure (Fig. 1a). A correlation between the score of the optimized CS–atom assignments and the rmsd of the model was obtained in all cases (Table 1 and Figs. 2 and 3b). The correlation between rmsd and score is significant, particularly in the important range from 2 to 8 Å, and the cluster center closest to the native rmsd-wise could consistently be identified by its consistency score, S, that reflects the consistency of a particular model with the experimental data when a certain CS–atom assignment is assumed.

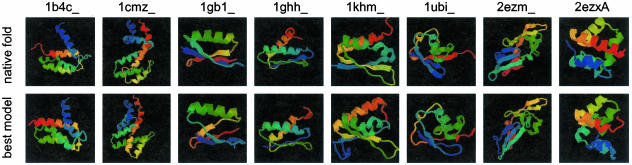
The cluster center with the best agreement with the unassigned data is selected as the best candidate model before the refinement step. Fig. 4 compares the structures of these selected models to the true structures for the eight proteins. The topology as well as the relative orientation of secondary structure elements is correctly determined in all models. Larger discrepancies between native fold and model are obtained in the length of some secondary structure elements and many of the loop and coil regions.

Fig. 4.

The best-scoring rosetta models obtained before refinement in comparison with the native structure.

If the correct native structure is used for optimizing the CS–atom assignment, between 50% and 90% of all nuclei can be correctly assigned to their CS value. The high agreement suffers, of course, if imperfect models are used; in particular, the fraction of correctly assigned side-chain atoms drops, because no dipolar couplings are available in these regions. Using rosetta models with a 3–6 Å rmsd from the native structure, the percentage of correctly assigned atoms ranges from 5% to 40%, with a higher fraction for smaller proteins with fewer possible assignments. As the model is refined to high resolution (see below), this fraction increases up to 70% (Table 2). The majority of the correctly assigned atoms are in the protein backbone due to the additional RDC information.

Table 2. Improvement of the top 20 assignments during refinement of 1ubi, 1gb1, 1ghh, 1khm.

			Average no. correctly assigned atoms (%)		Consensus assigned atoms		Experimental data used for refinement
	rmsd, Å	Average score	Overall	Backbone	Overall	Correct	NOEs	RDCs
Iubi Cluster center	3.43	0.643	32 (5)	27 (8)	16	16	—	36
First cycle	2.07	0.656	67 (11)	59 (17)	33	28	5	56
Second cycle	1.55	0.668	127 (20)	113 (33)	114	102	34	195
Third cycle	1.16	0.701	168 (26)	153 (45)	173	164	70	323
Fourth cycle	0.76	0.782	253 (40)	225 (66)	221	205	130	403
Fifth cycle	0.60	0.801	272 (43)	235 (69)	333	282	249	395
1gbl Ciuster center	4.46	0.593	25 (4)	18 (6)	20	20	0	40
Eighth cycle	1.36	0.763	116 (18)	110 (39)	77	65	10	117
1ghh Cluster center	4.81	0.557	47 (5)	40 (10)	25	25	10	38
Ninth cycle	1.54	0.708	393 (42)	283 (70)	303	268	145	337
1khm Cluster center	4.45	0.431	30 (3)	22 (5)	20	15	3	21
Seventh cycle	1.97	0.632	101 (10)	92 (21)	113	76	9	31

To detect these correctly assigned signals, similarities between multiple optimized assignments are analyzed. The selection of consensus assigned CS–atom pairs among these assignments clearly enriches for correctly assigned CS–atom pairs (Table 2). In individual assignments, 5–10% of the atoms were correctly assigned to their CS signal for the cluster center closest to the native. In the consensus subset of signals, this fraction increased to lay between 75% and 100%. The overall percentage of CS–atom pairs that are detected by this procedure drops to ≈50% relative to the average percentage of correctly assigned CS–atom pairs in the individual assignments. However, these rather small subsets were sufficient to obtain restraints for refining the models using rosettanmr (28, 29).

Model Refinement. The iterative refinement process is illustrated for 1ubi in Fig. 5 and summarized for 1ubi, 1gb1, 1ghh, and 1khm in Table 2. In these cases, a small number of RDCs and NOEs used initially was sufficient to restrict the structural space significantly and allow rosettanmr to build improved models. These models can be detected by their excellent agreement with the experimental data, and, in turn, can be used to obtain even better assignments. An iterative application of these steps (Fig. 1b) decreases the rmsd of the model and increases the consistency score, the average percentage of correctly assigned signals, and the number of detected signals. The rmsd to the native structure decreases below 2 Å for all four examples.

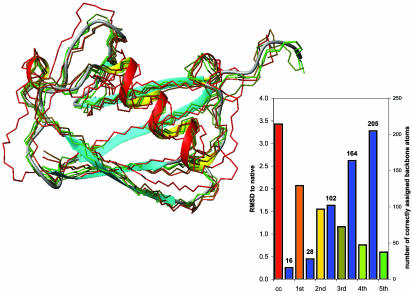
Fig. 5.

Refinement of the best-scoring ubiquitin model to high resolution. Five cycles of the optimization process were necessary to achieve convergence. Starting from the best-scoring cluster center (cc) with an rmsd of 3.43 Å, the number of correctly assigned atoms that were detectable (blue bars) steadily increases and the rmsd of the refined model decreases (bars shown in the color of the corresponding backbone model shown on the left). Both the backbone (green model, rmsd = 0.60 Å) and side-chain (rmsd = 0.76 Å) conformation in the final structure are quite close to the correct structure (ribbon). The number of correctly assigned backbone atoms increases from 16 to 205.

The success of the structure refinement protocol depends critically on the percentage of correctly assigned CS–atom pairs in the initial models. As described, the better agreement with the experimental data obtained for structures that are closer to the native results in a higher probability of good scoring assignments that are sufficient to detect those models. Successful refinement requires that at least 15–25 CS–atom pairs are consistently assigned to one another in the best-scoring assignments and can therefore be detected by the consensus analysis. This scoring cannot be achieved if the average fraction of correctly assigned backbone atoms drops under a critical threshold, which is ≈4% (see Table 1). In these cases, the increased score for some of the optimized assignments was sufficient enough to detect the best cluster center. However, the fraction of correctly assigned signals was lower, which, in turn, reduces the consensus part of optimized assignments. If this part becomes too small, not enough CS–atom pairs are reliably detectable. This result explains why refinement for 1b4c, 1cmz, 2ezm, and 2ezxA was impossible.

This limit can be pushed either by having better models (which results in better assignments), using more experimental data (which restricts the space of possible CS–atom assignments and therefore increases the chance that a high scoring assignment is also one with a significant fraction of correctly assigned atoms), or increasing the number of analyzed assignments. It should be remembered that this experiment was designed to be a worst case scenario: de novo structural models were used with completely unassigned NMR data. Often better structural models will be available through comparative modeling approaches. Moreover, the optimization algorithm is written in a way that easily allows the addition of experimental information about obligate bond connections, as obtainable through HN(CO)Cα experiments and dihedral angles derived from J-couplings or crosscorrelated relaxation. Triple resonance NMR data can also constrain NOEs by connecting one of the two hydrogen atoms to the directly bonded carbon or nitrogen atom. Such information is considered by introducing additional constraints that require the respective CS values to be assigned to bond hydrogen and carbon/nitrogen atoms as already derived and used for the RDC information.

The quality achievable by the refinement is somewhat limited by the capabilities of rosettanmr, which is not designed to generate highest-resolution models. rosettanmr currently does not handle high-resolution side-chain NOEs, and, therefore, does not take advantage of the number of unambiguously assigned side-chain NOE increases. Also, rosettanmr, in its current implementation, is unable to handle ambiguities caused by overlapping signals, because only unambiguous distance constraints can be input. Thus, further improvement of the models might become possible by using programs designed for high-resolution structure elucidation [e.g., x-plor (40), cns (41), and aria (42)]. However, the strength of the rosettanmr algorithm, namely the ability to built excellent models from only a few data points, is certainly critical for the success of the described approach. The models are similar in quality to those generated by rosettanmr using sparse assigned datasets (28, 29).

An alternative approach for using unassigned NMR data has recently been described by Grishaev and Llinas (19, 20) and Hus et al. (43). The “clouds” algorithm of Grishaev and Llinas (19, 20) searches for a proton distribution consistent with the distance information contained within NOESY spectra and fits the protein structure into this distribution by using molecular dynamics. Hus et al. (43) described the automated protein backbone assignment from RDC by means of a combinatorial optimization algorithm, if the x-ray structure of the protein is known.

The major advantage of our approach in comparison with the latter methods is the simultaneous incorporation of NOE, RDC, and CS information, together with the utilization of protein structure prediction algorithms. The derivation of a low-resolution model, together with a partial assignment, makes the algorithm well suited as a step in structure elucidation. Its capability of incorporating partial assignments as input and running the protocol iteratively also suggests its value for accompanying the structure elucidation process. The algorithm is nondeterministic, which makes it robust with respect to overlap in the obtained spectra, missing signals or additional artifacts, which should allow using the output of automated peak-picking protocols as input. It is also forgiving regarding the quality of the initial protein model.

The algorithm was recently applied to unassigned NMR data for the 140 amino acids fumarate sensor, DcuS (44). The protein is a prototype for a sensory histidine kinase with transmembrane signal transfer. A total of 1,100 CS signals, 3,000 NOESY crosspeak intensities, and 209 RDCs were extracted from the original spectra and directly used as input to the algorithm. De novo structure prediction as well as comparative modeling using a remote homologue (GAF domain 1f5mA: ref. 45) was performed. Two comparative models and six cluster centers from de novo prediction were selected for analysis. While the high-resolution structure elucidation has not been completed, we can compare theses eight models with a near-final model (44). The cluster center most similar to the DcuS model (rmsd = 6.0 Å) as well as the two comparative models (rmsd = 8.3 and 9.4 Å) have the correct topology and are scored significantly better than the remaining cluster centers (Fig. 6).

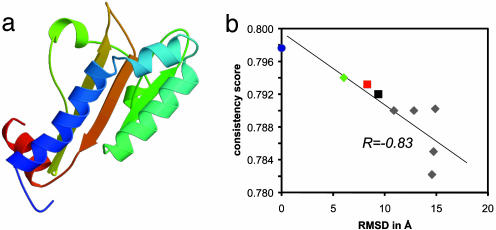
Fig. 6.

The structure of the fumarate sensor DcuS (a) as determined using rosetta de novo fold prediction and unassigned CSs, NOEs, and RDCs. The suggested model adopts the correct topology and has an rmsd of 6.0 Å to a near-final NMR model (44). (b) The correlation between the rmsd to this near-final structure (blue circle) and the consistency score, S. The de novo cluster center (green diamond) and the two comparative models (red and black squares) score better than the incorrect folded cluster centers (gray diamonds).

Conclusions

We have developed a rapid method for protein fold determination from unassigned NMR for proteins with up to 130 amino acids. Depending on NMR and computational resources, the procedure could be completed soon after the protein is expressed. In combination with the automation of the protocol, this approach has the potential to be scaled up for protein fold prediction in structural genomics. The low-resolution models produced can be used to identify the structural family of the protein, assist the search for related proteins, help to identify the function, and accelerate high-resolution NMR structure determination greatly. The analysis of the consensus of several different assignments optimized for one and the same structural model allows the detection of CS–atom assignments with a high probability of being correct, and these partial assignments can allow a refinement of the initial model to higher resolution, automatically and without manually assigning signals. However, the applicability of this refinement protocol depends on the quality of the obtained assignments, and, therefore, critically on the amount of experimental data as well as the quality of the structural models produced by rosetta.