A macroscopic scale model of bacterial flagellar bundling

Abstract

Escherichia coli and other bacteria use rotating helical filaments to swim. Each cell typically has about four filaments, which bundle or disperse depending on the sense of motor rotation. To study the bundling process, we built a macroscopic scale model consisting of stepper motor-driven polymer helices in a tank filled with a high-viscosity silicone oil. The Reynolds number, the ratio of viscous to elastic stresses, and the helix geometry of our experimental model approximately match the corresponding quantities of the full-scale E. coli cells. We analyze digital video images of the rotating helices to show that the initial rate of bundling is proportional to the motor frequency and is independent of the characteristic relaxation time of the filament. We also determine which combinations of helix handedness and sense of motor rotation lead to bundling.

The cells of Escherichia coli and Salmonella typhimurium have several helical propellers, or flagella, which they use to swim. Each flagellum consists of a rotary motor embedded in the cell wall, a short (50 nm) flexible hook that acts as a universal joint, and a helical filament ≈20 nm in diameter and ≈10 μm long (1). The trajectory of an individual swimming cell consists of runs interrupted by tumbles. For most of a run, the motors turn counterclockwise when viewed from outside the cell, the filaments wrap into a tight bundle, and the cell swims along a roughly straight path. Near the end of a run, one or more of the motors reverses direction, the corresponding filaments come out of the bundle, and the cell moves erratically, or tumbles. The tumbling process is complex and involves polymorphic transitions of the filament first from the left-handed “normal” state to the right-handed “semicoiled” state, and then to the “curly-1” state (2). The first transition reorients the cell body. When the motors resume their counterclockwise rotation, the curly-1 filaments transform directly to the normal state and rejoin the bundle, and the cell resumes its initial speed (2).

The chemotaxis strategy of E. coli is to decrease the likelihood of tumbling during runs that happen to carry the cell toward higher concentrations of chemoattractants. Thus, the formation and dispersal of the helical bundle is central to bacterial chemotaxis. Since the radius of the flagellar filament is well below optical wavelengths, and the motor rotation is relatively rapid (100 Hz), it is difficult to study the mechanics of the bundling process directly. Therefore, we built a macroscopic scale-model system consisting of flexible rotating helices in a very viscous fluid. By including the viscous fluid and properly accounting for the relative strengths of viscous and elastic stresses, our scale model builds on and extends the work of Macnab, who studied the geometry of rotating flexible helices in a bundle (3).

Our article begins with a discussion of the material parameters of bacterial flagella and how we chose the parameters for the experimental model. The next section describes the geometry of bundled helices and the symmetry requirements for bundling, including helix handedness, motor-rotation sense and relative speed, and phase relations. Finally, we describe measurements of the characteristic time scale governing the initial stages of the bundling process.

Scale Model

E. coli usually has several filaments per cell, but for the purpose of studying bundling it is simplest to consider the case with two filaments. Unless the two helices are identical and placed on diametrically opposite sides of the body (an unlikely occurrence), the hydrodynamic torque on the rotating helices causes the cell body to counterrotate to make the total torque on the cell vanish. This counterrotation plays some role in bundle formation (4, 5), since it tends to wrap the filaments around each other. However, this mechanism for bundling does not lead to tight bundles (5). Furthermore, bundles readily form from filaments of stationary cells bonded to a surface (H. C. Berg and L. Turner, personal communication). Therefore, we disregard the effects of body rotation and translation and consider two helices rotated by stationary motors. We also neglect the effect of the cell body itself on the flow.

At the characteristic length and time scales of bacteria, viscous effects dominate inertial effects (6). To see why, recall that the Reynolds number Re = ρνℓ/η determines the relative importance of inertia to viscous stresses, where ρ is the density of the fluid, η is the viscosity, ν is a characteristic flow velocity, and ℓ is a characteristic length over which the flow varies. Using 30 μm/s as a typical swimming speed, 1 μm as a typical cell body size, and the density and viscosity of water (ρ ≈ 1,000 kg/m³, η ≈ 10^–3 N·s/m²) yields a Reynolds number of Re ≈ 3 × 10^–5. (Using the typical helix radius ℓ ≈ 0.2 μm and the linear azimuthal helix velocity ν ≈ 2π×100 Hz × ℓ yields approximately the same Reynolds number.) At low Reynolds number, the flow field induced by a point force falls off inversely with distance (7), leading to a long-range hydrodynamic interaction between two rotating helices. (Since the net force on a swimming bacterium vanishes, the far field flow induced by a swimming bacterium falls off faster than 1/r, roughly like a dipole, 1/r².) Another characteristic of low Reynolds number flow is that the drag per unit length on a long slender body depends weakly on the filament diameter and the shape of the cross section (8).

Elastic stresses balance the viscous stresses on rotating bacterial flagella, causing the filaments to bend and twist as they wrap into a bundle. Filaments can also undergo polymorphic transformations when the motors turn clockwise; for simplicity, we do not attempt to include polymorphic transformations in our macroscopic model. The bending modulus A = EI determines the resistance of an elastic rod to bending, where E is the Young's modulus and I is the moment of inertia of the cross section (9). There are few measurements of the bending resistance, with reported values ranging from 10^–24 N·m² (10) to 10^–22 N·m² (11). Likewise, the value of twist modulus C of the filament is not precisely characterized, although the twist compliance of ≈0.2 μm-long filaments attached to the hook and a locked motor has been measured (12). Since it is difficult to separate the twist modulus of the hook from the modulus of the filament in this measurement, we will simply assume that C ≈ A for the filament. For a filament with axial length L, the product of the characteristic filament relaxation time and the motor angular velocity, M = ηωL⁴/A, determines the importance of viscous drag relative to flexibility (see refs. 13 and 14). Since A = EI ∝ Ea⁴, where a is the filament radius, M depends sensitively on the aspect ratio L/a. To estimate M for the bacteria, we will use L = 7 μm, the typical length of the filaments of ref. 2. Using ω = 100 × 2π rad/s, η = 10^–3 N·s/m², and A = 10^–23 N·m² yields M ≈ 150 for the bacterial filaments. Note that the persistence length (15) ξ_P = A/(k_BT) ≈ 2.5 mm is large, allowing us to disregard thermal fluctuations.

There are three dimensionless numbers that determine the helix shape: P/L, R/L, and a/L, where P is the helical pitch, and R is the helical radius. Note that the ratio R/P determines the pitch angle α via tanα = 2πR/P, and that P and L determine the number of turns (which need not be an integer). If we consider two helices with initially parallel axes, then the final geometrical parameter of interest is the spacing h between the two motors.

Methods

Fig. 1 shows the macroscopic model. Two stationary stepper motors under independent control rotate flexible polymer helices in a tank of silicone oil. The viscosity of the silicone oil is 100 N·s/m², or ≈10⁵ times the viscosity of water. The motors typically rotate at ≈0.1 Hz, and the helix radius is ≈13 mm. For these parameters, the Reynolds number Re ≈10^–3, not quite as low as 10^–5 but low enough to justify our neglect of inertial effects. To minimize the effects of the walls of the tank on the flow near the helices, all experiments are carried out with the helices near the center of the tank. The base of the tank is 420 mm by 420 mm, and the depth of the silicone oil is 330 mm. The helices are made by wrapping a Tygon tube around a cylindrical mandrel and filling the tube with epoxy. Food coloring is added to provide contrast in the video images. Once the epoxy hardens, the tube maintains its helical shape but is also flexible. We vary the flexibility by varying the radius of the Tygon tube. To get appropriate values of M in our model, we use helices with a filament radius of a few millimeters. The bending stiffness of each helix is approximately determined by measuring the deflection under a known force of a straight tube filled with hardened epoxy; for 2a = 4.0, 4.7, and 5.6 mm, we found A = (3.46 ± 0.14) × 10^–3 N·m², (10.53 ± 0.14) × 10^–3 N·m², and (22.50 ± 0.14) × 10^–3 N·m², respectively. As in the case of the bacterial filaments, we assume C ≈ A. Since the aspect ratio L/a for our model is much smaller than that of the full-scale bacterial flagella, our model is not a true scale model. However, since the drag of a slender body depends only weakly on the filament radius (8), it is not necessary to attain exact geometric similarity. We used two representative helical geometries for our filaments (see Table 1 for a comparison of the dimensions of our model helices and bacterial flagella). We systematically varied the stiffness of the “semicoiled” model. Note that the (inner) radii of our model helices are all the same, since both types of helices were formed from the same mandrel, whereas the helical radius of the bacterial filament varies from polymorph to polymorph. All experiments reported here were carried out with a motor shaft-to-shaft separation of h = 61 mm, which would roughly correspond to the typical spacing of 1 μm in the full-scale bacteria. To allay concerns about effects of fatigue and plastic deformation of the helices during the experiments, we compared the deflection of the helices under a known weight before and after some representative trials and found that these effects were insignificant.

Fig. 1.

Bundling sequence. (Upper) Our left-handed model semicoiled helices (see Table 1) at t = 0, 96, 168, and 264 s. (Lower) The helices shown at the same times, viewed from the side. The scale bars are 100 mm long; the helices are 310 mm long (from chuck to tip), 4.0 mm in diameter, and turning at 0.1 Hz.

Table 1. Helix parameters.

Form	Pitch, μm	Diameter, μm	Handedness
Normal	2.3	0.4	Left
Semicoiled	1.1	0.5	Right
Curly-1	1.0	0.3	Right
Model normal	11 × 104	2.54 × 104	Left
Model semicoiled	6.4 × 104	2.54 × 104	Right and left

Approximate pitch, approximate diameter, and handedness for some polymorphic forms of flagellar filaments from ref. 2 and H. C. Berg and L. Turner, personal communication. We also include the dimensions of our model helices. For the models, the diameter is the diameter of the mandrel.

Bundling in the Scale Model

Fig. 1 shows a sequence of snapshots of two rotating left-handed helices (with four turns each) at M ≈ 170 (see Movie 1, which is published as supporting information on the PNAS web site). The induced flows cause large deflections, and a bundle forms when the motors turn counterclockwise. Note that the helices wrap around each other in a right-handed sense; the flow field generated by each helix tilts the other helix, causing the helices to roll around each other and form a right-handed wrapping. In contrast with the case of two helices, the deflection of a single rotating helix with M ≈ 170 is small, with the axial compression or extension <10% of the axial length. But an understanding of the flow induced by a single helix sheds light on the flows that cause bundling. Consider a left-handed helix. As the helix rotates counterclockwise as viewed from the helix side of the motor, apparent helical waves travel along the filament away from the motor and push fluid elements in the same direction. These fluid elements also rotate about the vertical axis of the helix in the same sense as the helix, counterclockwise, leading to a right-handed trajectory for each fluid element.

Early scale-model experiments by Macnab (3) using steel helices in air showed that left-handed helices twisted around each other in a right-handed manner can rotate indefinitely without jamming, but that left-handed wrapping leads to jamming for clockwise rotation and unwinding for counterclockwise rotation. Macnab also pointed out that the state of lowest elastic stress of two left-handed helices with right-handed intertwisting is one in which the helices are coaxial, in phase, and in contact. Since this interwound state is unstable in the absence of external torque, Macnab used a guide at the end of the bundle to keep the helices from unraveling. In our experiment, viscous drag provides the stabilizing torques that keep the helices interwound. Note that the helices rotate against each other, leading to a region of high shear between the filaments. When the motors turn counterclockwise, we find that the bundle persists indefinitely as long as the motor speeds are sufficiently low. If the motor speed is >0.1 Hz, then the Y-shaped junction in the upper right panel of Fig. 1 migrates up to the motors, causing a jam. Jams can also form when the motors turning the helices in a steady-state bundle reverse; if a jam fails to form, the filaments simply unwind.

In the example shown in Fig. 1, the two helices have no initial phase difference. Since the motors run at a common constant velocity and do not slip, the phase difference between the motor shafts is constant. If there is an initial phase difference, then the helices must bend and twist to attain the in-phase interwound state. Typically one helix bends more than the other, leading to a bundle that is tilted relative to the axis of rotation of each motor. The motor characteristic in the scale model, constant speed, differs from that of the bacterial motor, which for typical loads and temperatures is roughly constant torque (16, 17). Thus, the phase locking observed in the bacterial flagella may arise from a different mechanism than that observed here.

In the scale model, it is crucial for the rotation speeds of the two motors to be close for bundling to occur. If the motors' speeds differ by as little as 8%, left-handed helices rotated counterclockwise do not bundle. The helices cross each other, with the faster helix bending more than the slower helix. The axis of the faster helix waves back and forth, but never wraps around the slower helix.

Since left-handed helices turning counterclockwise bundle, symmetry implies that right-handed helices turning clockwise will also bundle. Indeed, bundles of semicoiled or curly flagella have been observed in fluorescently labeled filaments (2). On the other hand, left-handed helices turning clockwise do not bundle. When the motors driving a bundle reverse, the bundle unwinds. Once the bundle has unwound, or if the (left-handed) helices are initially stationary, then the flow induced by the clockwise rotation causes the helices to roll around each other and wrap in a left-handed sense. However, the wrapping is not nearly as tight as the counterclockwise sense. The helices cross, and the crossing point migrates up to the motors (see Fig. 2). When the crossing point reaches the motors, instead of jamming, the helices distort at the proximal ends to allow the rotation to continue. None of the other combinations of handedness and sense of rotation led to bundling in our scale-model experiment. Helices of the same handedness but turning in opposite directions tilt away from each other and also tilt away from the plane containing the initial helix axes. Helices of opposite handedness turning in the same sense cross and do not bundle; helices of opposite handedness turning in opposite senses tilt away from each other.

Fig. 2.

Sequence of left-handed helices turning clockwise at 0.075 Hz, at times t = 102 s, t = 119 s, and t = 146 s. The helices cross, and the crossing point migrates up to the motor, where the helices periodically distort to escape a jam.

Characteristic Time Scale

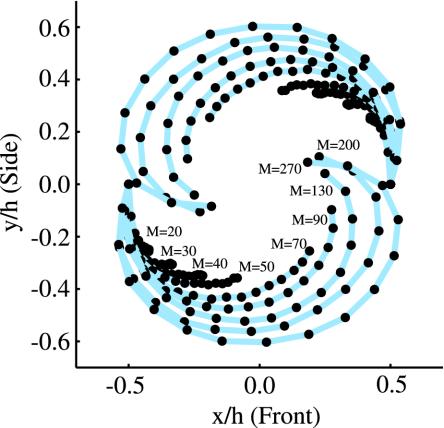
There are two natural time scales governing the dynamics of our system: the motor period 2π/ω, and the elastic relaxation time scale ηL⁴/A. To determine which combination of these controls the initial rate of bundling, we measured the deflection of each helix as a function of time. More precisely, we measured the position of the projection of the tip of each helix onto the local axis of rotation for the corresponding helix. Fig. 3 shows the trajectories of these points projected to the xy-plane. In contrast to the case of Fig. 1, we used helices with three turns (L = 240 mm) since with short helices it is easier to attain small values of M. For M <70, the viscous stresses induced by the rotating helices are too weak to deflect the helices much. The helices cross when M ≈70 and begin to wrap around each other when M ≈130. Since we focus on the early stages of bundling, we do not show the complete trajectories for moderate to large M (M >50). Defining Δ as the distance between ends of the helices in the side view (yz-plane, where z is parallel to the initial helix axes, and x is parallel to the line connecting the two motors; Fig. 1), dimensional analysis implies

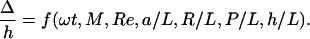[1]

Since we approximate C = A, we omit A/C from the list of dimensionless groups. In this article we do not report how f depends on the geometrical parameters R/L, P/L, and h/L; we present results for semicoiled helices (P/R ≈5) with three turns, h = 61 mm, and L = 240 mm. We varied rotation speed ω and filament radius a. The function f depends on ω implicitly through M and Re, and explicitly through ωt. Since Re ≪ 1, we can approximate Re ≈ 0 and consider f to depend on ω only through M and ωt. Likewise, f depends on a implicitly through M and explicitly through a/L. The explicit a/L dependence of f arises from viscous drag because the Young's modulus E = πa⁴/4 enters through M. Since the drag on a slender body depends weakly on a/L, and since M depends sensitively on a/L, we consider f to depend on a only through M. Thus, for the fixed geometrical parameters described above, we measure f as a function of ωt and M.

Fig. 3.

Trajectories of (projected) helix tips in the xy-plane. The spacing of the dots on each curve corresponds to one revolution.

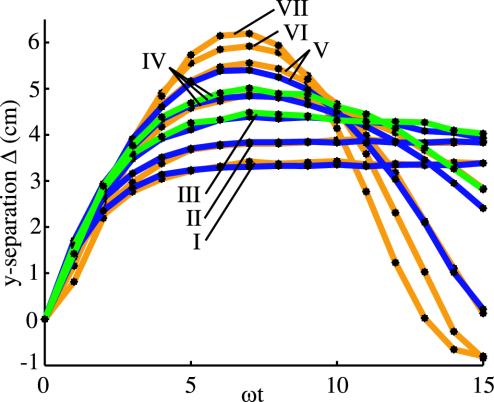
Fig. 4 shows Δ as a function of ωt for various rotation speeds and bending moduli, and Table 2 shows the speed corresponding to each Δ vs. ωt curve. The ratio of the speeds for the overlapping gold and blue curves is roughly constant (see Table 2). Note that the gold and blue curves labeled V do not overlap as closely as those labeled I, II, and III; correspondingly, ω₁/ω₂ for the pair V noticeably differs from the ratios for I, II, and III. Likewise, the blue and green curves labeled IV do not overlap as closely as those labeled III, leading to the discrepancy between the ω₂/ω₃ values for pairs III and IV. Although M systematically increases as the curve label varies from I to VII, there is a significant spread in the values of M for overlapping curves. This spread implies that our identification of the bending modulus of a straight tube with that of a helix with the same diameter tube leads to an uncertainty greater than that of our measurements of A. Such an uncertainty is not unexpected since we neglect the effects of the helix twist modulus C for simplicity. Despite the uncertainty in the helix bending modulus, the data of Fig. 4 and Table 2 are strong evidence for the scaling behavior of the bundling helices: two helices of different stiffness but the same shape will yield the same Δ vs. ωt curves for the proper ratio of rotation speeds. In fact, if we assume that the closely overlapping curves of Fig. 4 have the same M, then we can get a better estimate of elasticity ratios by using A₁/A₂ = ω₁/ω₂, since we can measure the rotation speeds to high accuracy.

Fig. 4.

Side view of (projected) tip separation as a function of time for rotation speeds and bending moduli; see Table 2 for values. On each curve, there is a black dot for every revolution. The gold curves are for the 4.0-mm tube, the blue are for the 4.7-mm tube, and the green are for the 5.6-mm tube.

Table 2.

Rotation speeds and ratios for the curves (labeled I-VII) shown in Fig. 4

Curve label	ω1, rad/s	ω2, rad/s	ω3, rad/s	ω1/ω2	ω2/ω3
I	0.314	0.707		0.44
II	0.393	0.943		0.42
III		1.17	2.12		0.56
IV	0.707	1.65	2.83	0.43	0.41
V	1.18	2.36		0.50
VI	1.65
VII	3.06

The columns labeled ω₁, ω₂, and ω₃ correspond to the 4.0-, 4.7-, and 5.6-mm tubes, respectively. The empty spaces arise because most of the overlapping sets of curves (except for case IV) consist of just two curves.

A characteristic time of the early stages of the bundling process is the time at which the separation Δ reaches a maximum. Fig. 4 reveals that the position of this maximum is proportional to the motor period and depends only weakly on the elastic relaxation time scale. Thus, in the early stages of bundling, the helices follow the induced flow and the motor period determines the characteristic time scale. The helices begin to bundle after about six revolutions, in rough agreement with the corresponding time for bacterial flagella (2).

Conclusion

Our macroscopic scale model demonstrates that the bundling of bacterial flagella is a purely mechanical phenomenon, arising from the interplay of hydrodynamic interactions, bending and twisting elasticity, and geometry. Our model allows us to study how the bundling phenomenon is affected by parameters that are difficult to control in the full-scale bacteria, such as the rate and direction of motor rotation. For fixed values of the geometrical parameters, we quantitatively characterized the early stages of the bundling process and found that the initial rate of bundling is determined mainly by the motor period. Future work should address the role of twisting vs. bending stiffness, the effect on bundling of the translational and rotational flow fields induced by a swimming bacterium, and bundle formation when there are more than two filaments.