Abstract
The flux of solvent water coupled to the transit of ions through protein pores is considerable. The effect of this electroosmotic solvent flow on the binding of a neutral molecule [β-cyclodextrin (βCD)] to sites within the staphylococcal α-hemolysin pore was investigated. Mutant α-hemolysin pores were used to which βCD can bind from either entrance and through which the direction of water flow can be controlled by choosing the charge selectivity of the pore and the polarity of the applied potential. The Kd values for βCD for individual mutant pores varied by >100-fold with the applied potential over a range of –120 to +120 mV. In all cases, the signs of the changes in binding free energy and the influence of potential on the association and dissociation rate constants for βCD were consistent with an electroosmotic effect.
We have been interested in the interaction of the staphylococcal α-hemolysin (αHL) pore with β-cyclodextrin (βCD) and other small, rigid host molecules, because they can act as molecular adapters after becoming lodged in the lumen of the pore. There, they alter conductance (1, 2) and ion selectivity (3) and act as sites where blockers can bind (1). The latter allows αHL·βCD complexes to act as components of stochastic sensors for organic analytes (1, 4). In a recent study, we suggested that the interaction of the neutral βCD molecule with the αHL pore could be strengthened or weakened by electrokinetically driven water flow (5). Here, we test this idea thoroughly by using mutant αHL pores to which βCD can bind from either entrance.
The WT αHL pore is a heptamer of known structure (6) with a unitary conductance of 650 pS at –40 mV in 1 M NaCl at pH 7.5 (7). If the pore were completely charge-selective (it is not; see Results), the current at –40 mV would translate into a unidirectional movement of 1.6 × 108 ions s–1. Assuming that ≈10 water molecules are carried through the pore with each ion (see chapter 10 of ref. 8 and refs. 9 and 10), the water flux would be >109 molecules s–1. Therefore, even where charge selectivity is modest (for the WT αHL pore PNa+/PCl– = 0.78, pH 7.5), the water flux is well above 108 molecules s–1. Here, we show that this flux, i.e., electroosmotic flow, can provide a driving force that significantly alters the binding strength of the neutral βCD molecule within the lumen of the αHL pore.
Electroosmotic flow has been examined previously for channels with a wide range of dimensions. For example, electroosmosis has been used to produce solvent flow through channels in microfluidic systems, which range from a few to several hundred micrometers in diameter (11–13). In these systems, the electrical double layer (EDL) is small compared to the diameter of the channel, generating convective plug flow (14, 15) that includes dissolved neutral molecules. Despite its apparent simplicity, the theoretical basis of electroosmotic flow in relatively wide channels remains under active discussion and experimental evaluation (16–19). Individual polymer-filled cation-selective pores of ≈100-μm diameter have been studied by White and colleagues (20, 21). They used a scanning electrochemical microscope tip to measure the rate of transport of neutral molecules, such as hydroquinone.
Electroosmotic flow in nonbiological pores of much smaller dimensions has also been investigated. For example, Martin and colleagues (22) investigated carbon nanotubes of ≈200-nm diameter and made a direct measurement of the transport of a neutral molecule, phenol. Under the conditions of their experiments, the EDL was still considerably smaller than the diameter of the pore, and conventional electrohydrodynamic theory could again be applied.
Water transport has also been examined in narrow biological channels and pores. In two early studies, the movement of water molecules coupled to cation transport in gramicidin channels was measured (23, 24). The authors determined the electrical (streaming) potential (Vs) produced by osmotic pressure generated by a nonelectrolyte and used a thermodynamic relationship to determine Nw, the number of water molecules coupled to each ion transported:
 |
[1] |
where V̄w is the partial molar volume of water, ϕP is the molal osmotic coefficient of the nonelectrolyte, and Δmi is the difference in molality of the nonelectrolyte across the membrane. This approach, which is appropriate for highly ion-selective channels and pores, has been followed by others (25–29), and values of Nw ≤ 10 have been found.
Electroosmosis also plays a role in iontophoretic transdermal drug delivery (30) and the transport of molecules into electroporated cells (31). But, despite this abundance of information, so far as we know, the effects of electroosmotic flow on the binding of neutral molecules to sites within membrane channels and pores have not been investigated previously. Here we examine such a case: the binding of βCD within the αHL pore. It should be noted from the outset that the αHL pore is of intermediate dimensions: the width of the EDL is comparable with the diameter, and hydrated ions move through the pore, which is nonetheless weakly charge-selective. In addition, the internal diameter of the pore is comparable with the dimensions of βCD, which suggests that the movement of βCD must be impeded by the walls.
Materials and Methods
Mutagenesis. αHL-E111N/M113D/K147N, αHL-E111N/M113E/K147N, αHL-E111N/M113K/K147N, and αHL-E111N/M113R/K147N are the subunits that constitute the homoheptameric pores PNN-D, PNN-E, PNN-K, and PNN-R, respectively. To construct genes encoding αHL-E111N/M113D/K147N, αHL-E111N/M113E/K147N, αHL-E111N/M113K/K147N, and αHL-E111N/M113R/K147N, pT7-αHL-K147N (5) was digested with SacII and HpaI and the resulting small fragment was replaced, respectively, with DNA cassette I, 5′-GGAATTCGATTGATACAAAAAATTAT-GATAGTACGTT (sense) and 5′-AACGTACTATCATA-ATTTTTTGTATCAATCGAATTCCGC (antisense); cassette II, 5′-GGAATTCGATTGATACAAAAAATTATGAAAGTACGTT (sense) and 5′-AACGTACTTTCATAATTTTTTGTATCAATCGAATTCCGC (antisense); cassette III, 5′-GGAATTCGATTGATACAAAAAATTATAAAAGTACGTT (sense) and 5′-AACGTACTTTTATAATTTTTTGTATCAATCGAATTCCGC (antisense); or cassette IV, 5′-GGAATTCGATTGATACAAAAAATTATAGAAGTACGTT (sense) and 5′-AACGTACTTCTATAATTTTTTGTATCAATCGAATTCCGC (antisense). New codons in each of the four cassettes are in bold italic. Replacements were verified by DNA sequencing. The other mutants of αHL used in this paper had been prepared earlier (5).
Synthesis, Assembly, and Purification of Mutant αHL Pores. Mutant αHL polypeptides were synthesized and assembled in vitro by coupled transcription and translation in the presence of washed rabbit red blood cell membranes and then purified by SDS/PAGE as described (32).
Measurement of Charge Selectivity of the αHL Pores. Planar bilayer recordings were carried out as described (5, 7). αHL heptamers were added to the cis chamber. The applied potential is given with respect to the cis chamber, which is taken as ground. Filtering was at 5 kHz, and acquisition was at 20 kHz. Single-channel conductance values were obtained by fitting peaks in amplitude histograms to Gaussian functions. The charge selectivities of the αHL pores were measured in 10 mM Tris·HCl, pH 7.5, containing NaCl (Table 1, which is published as supporting information on the PNAS web site). The permeability ratios (PNa+/PCl–) were calculated from reversal potentials by using the Goldman–Hodgkin–Katz equation (8) (Table 1).
For PNN-D, PNN-E, PNN-K, and PNN-R, the charge selectivities were examined in 1,000 mM (cis)/200 mM (trans) and 200 mM (cis)/1,000 mM (trans) NaCl buffer. The permeability ratios varied with the direction of the salt concentration gradient. We chose the smaller of the two values, because high salt concentrations decrease the permeability ratio; therefore, the permeability ratio in symmetrical 1 M salt was expected to be smaller than in either asymmetrical configuration. For all other pores, including the WT pore at different pH values, charge selectivities were examined in 1,000 mM (cis)/200 mM (trans) NaCl buffer. Each determination was repeated three times.
Measurement of βCD Binding to the αHL Pores. To examine binding to the various αHL pores, βCD was added to the trans or the cis chamber at 40 μM, unless otherwise specified. Three or more separate experiments were performed for each condition reported, in which data acquired for at least 2 min were analyzed. For each mutant, τon, the interevent interval, and τoff, the residence time of βCD, were obtained over a range of applied potentials by using dwell-time histograms fitted to single exponentials by the Levenberg–Marquardt procedure. In most cases, the coefficient of determination of the fits was R ≥ 0.90. Separate segments of the data yielded similar τ values, suggesting that stationary kinetics prevailed. Kinetic constants were calculated by using koff = 1/τoff, kon = 1/(τon[βCD]), and Kd = koff/kon, where [βCD] is the concentration of βCD (Table 1).
This analysis is valid for a simple binary interaction:
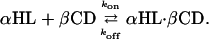 |
[Scheme 1] |
The validity of this assumption was tested previously for βCD binding to αHL pores from the trans side of the bilayer. As expected from Scheme 1, plots of 1/τon versus [βCD] were straight lines and 1/τoff was independent of [βCD]. In the present work, we are required to show that Scheme 1 holds for binding from the cis side of the membrane. This was tested with PNN-E and PNN-R and found to be the case (Fig. 6, which is published as supporting information on the PNAS web site).
Results
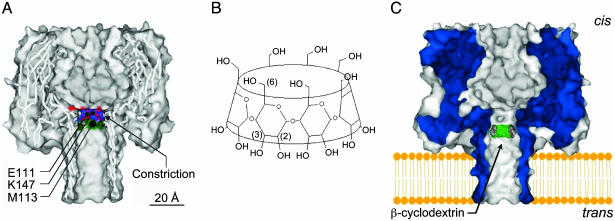
αHL Mutants Used in This Work. We discovered earlier that βCD can become lodged in the lumen of the αHL pore for tens of milliseconds in the case of WT αHL (1) and for considerably longer for various mutant αHL pores (1, 2, 5, 7). We suggested that the effects of an applied transmembrane potential on the Kd of the αHL·βCD complex might arise from electroosmotic solvent flow (5). In previous work, we studied the binding of βCD applied to the trans side of the membrane (Fig. 1). In none of the cases examined did βCD bind when applied from the cis side, with the exception of preliminary experiments with homoheptameric pores formed from E111N/K147N (PNN-M in the present nomenclature). In this case, the charge selectivity was small but sufficient to produce a voltage-dependent effect on binding that supported the idea of an electroosmotic effect. To confirm this hypothesis, we needed to measure βCD binding from both sides of the bilayer with more highly charge-selective pores. To accomplish this, mutants in which the two charged residues near the internal constriction were substituted with Asn, αHL-E111N/K147N, were again used, as described here. Additional substitutions at position 113 were used to alter charge selectivity (Fig. 1).
Fig. 1.
Molecular models of αHL and βCD. (A) Sagittal section through a model of WT αHL built by using the coordinates from the crystal structure of the pore (6). The mutated side chains, Met (M)-113, Glu (E)-111, and Lys (K)-147, which lie in the channel lumen, are shown. (B) Structure of βCD. (C) Model of the WT αHL pore showing a model of βCD docked in the lumen of the channel. The location shown is for βCD presented from the trans side of the bilayer and is based on mutagenesis data (1, 2, 5). In our apparatus, in a positive applied potential, the trans side of the membrane is positive relative to the cis side, which is taken as ground.
Determination of Charge Selectivity of Mutant αHL Pores. The direction of the net ion flux through a pore and, hence, the direction of the electroosmotically driven water flow are determined by the charge selectivity. We determined the charge selectivity of the pores used in this work by measuring reversal potentials in the presence of transmembrane ionic gradients (Table 1). Because the diameter of the αHL pore is 14Å at the narrowest point (Fig. 1), both hydrated cations and anions move through it and charge selectivity is relatively weak (PK+/PCl– = 0.79, WT αHL, pH = 7.5; for other conditions see Materials and Methods and Table 1). Nevertheless, the diameter is small enough that the charge selectivity can be altered by mutagenesis of individual residues, and here we have focused on position 113 (5) (e.g., αHL-M113R, PK+/PCl– = 0.39; αHL-M113E, PK+/PCl– = 2.5). It should be recognized that homoheptamers are used in this work, so each mutated position results in seven replacements in the fully assembled pore.
We suppose that individual ionic currents are independent, an assumption that underlies the Goldman–Hodgkin–Katz equation (8); therefore, the net movement of ions is given by
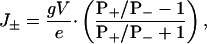 |
[2] |
where J± is the net flux of cations plus the net flux of anions, from trans to cis, per pore in ions s–1; g is the unitary conductance of the pore in S; V is applied potential; and e is the charge of an electron in C.
For example, when PK+/PCl– = 2.5, eJ±/gV = +0.43 and when PK+/PCl– = 0.39, eJ±/gV = –0.44. As we shall see, the water associated with net movements of ions of this magnitude has a significant effect on the binding of βCD to sites within the β barrel of the αHL pore.
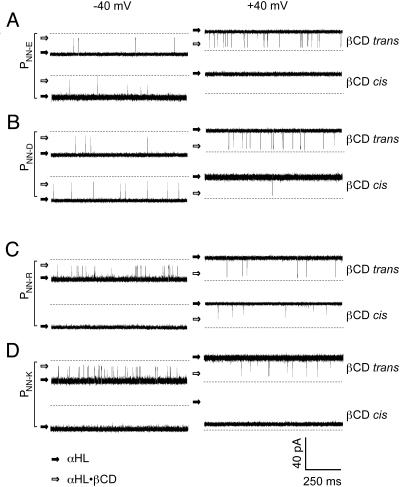
Examination of βCD Binding to Mutant αHL Pores. When βCD becomes lodged in the lumen of the αHL pore, it reduces the unitary conductance by ≈70%. The frequency and duration of the partial blockades can be used to determine the kinetic constants for the interaction, as described in Materials and Methods. In the present work, we exploit mutant αHL pores that bind βCD from both the trans and the cis chamber. In previous work, with WT αHL and various mutants, the binding of βCD was generally restricted to the trans side, presumably because the cyclodextrin (1,135 Da) binds at or near the 14Å constriction formed from the side chains of Glu-111 and Lys-147 (Fig. 1). When we examined the new mutants, we found that PNN-D, PNN-E, and PNN-R bind βCD from both sides (depending on the conditions), whereas PNN-K remains accessible only from the trans side (Fig. 2).
Fig. 2.
Representative current traces from single homoheptameric mutant αHL pores showing blockades by βCD. All traces were recorded under symmetrical buffer conditions with 1 M NaCl and 10 mM Tris·HCl, pH 7.5. The βCD (40 μM) was added to the trans or the cis chamber as indicated. (Left) Traces recorded at –40 mV. (Right) Traces recorded at +40 mV. (A)PNN-E with βCD in the trans or the cis chamber. (B) PNN-D. (C) PNN-R. (D) PNN-K.
The voltage-dependence of binding of βCD to the four PNN-X mutants was examined in detail (Fig. 3). PNN-D (PNa+/PCl– = 2.3) and PNN-E (PNa+/PCl– = 3.5) are cation selective (Table 1). When βCD was applied from the trans chamber, the association rate constant (kon) increased with the applied potential (Fig. 3A). By contrast, kon decreased with the applied potential when βCD bound from the cis side (Fig. 3B). The changes in kon were more than 100-fold over the range of applied potentials that were examined. In the cases of PNN-D and PNN-E, the dissociation rate constants (koff) showed little variation with applied potential, except in the case of PNN-E when βCD was applied from the cis side and koff increased about 5-fold as the potential was increased from –80 to –20 mV (Fig. 3B). In these cases then, the rate of association dominated the variation of Kd with applied potential: βCD bound more tightly from the trans side as the voltage became more positive and more tightly from the cis side as the voltage became more negative (Fig. 3 A and B).
Fig. 3.
Dependence of the kinetic constants for the interaction of βCD with mutant αHL pores on the applied potential and the side from which the cyclodextrin is presented. (Top) Association rate constants, kon.(Middle) Dissociation rate constants, koff.(Bottom) Equilibrium dissociation constants, Kd. Kd values were calculated as koff/kon.(A) Cation-selective mutants PNN-E and PNN-D with βCD presented from the trans chamber. (B)PNN-E and PNN-D with βCD presented from the cis chamber. (C) Anion-selective mutants PNN-R and PNN-K with trans-βCD. (D)PNN-R with cis-βCD. Data were obtained under symmetrical buffer conditions with 1 M NaCl and 10 mM Tris·HCl, pH 7.5. βCD (40 μM) was added to the trans or the cis chamber as indicated (see Materials and Methods for details). When under the conditions of the experiment binding events became infrequent, rate constants were not determined (see B at high positive potentials and D at high negative potentials).
PNN-R (PNa+/PCl– = 0.33) and PNN-K (PNa+/PCl– = 0.59) are anion-selective (Table 1). When βCD was applied from the trans chamber, kon decreased with the applied potential (Fig. 3C). kon increased with the applied potential when βCD bound from the cis side (Fig. 3D). The changes in kon are smaller than those observed with the cation-selective PNN-D and PNN-E. Again, in contrast with PNN-D and PNN-E, the koff values for PNN-R and PNN-K did show voltage dependence. When βCD was applied from the trans side, koff increased with the voltage, whereas a decrease in koff with voltage was seen when βCD was applied in the cis chamber. Both kon and koff contributed to a substantial variation of Kd with applied potential: βCD bound more tightly from the cis side as the voltage became more positive and more tightly from the trans side as the voltage became more negative (Fig. 3 C and D).
Discussion
Electroosmotic Flow in Nanopores. In this article, we suggest that the electroosmotic flow of solvent (water) affects the binding of a neutral molecule (βCD) within the αHL pore. Electroosmotic flow in a tube that is wide relative to the EDL is described by the Helmholtz–Smoluchowksi equation (14):
 |
[3] |
where ε is the dielectric constant, Eappl is applied potential, η is viscosity, and ζ is zeta potential (i.e., the potential near the wall of the tube). In this situation, plug flow occurs, so a single-value νeo provides a sufficient description of the system. When the diameter of the pore is small compared to the EDL, the situation is theoretically more complex. In this case, νeo varies across the diameter of the tube, never reaching the value obtained in a wide tube, and as a consequence the overall flow rate is greatly reduced (15).
Difficulties in estimating ζ have led to approaches that relate the measured current rather than the applied potential to solvent flow. For example, nonequilibrium thermodynamics (33) shows that for a highly charged pore:
 |
[4] |
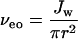 |
[5] |
where Jw is the volume flux of solvent per second, D is the diffusion coefficient of the mobile ion, r is the radius of the pore, η is viscosity, and i is current.
This approach is applicable to narrow tubes, but it is not clear whether values for the bulk phase can be used for D and η, as they have been by some authors, or how reliable alternative values can be obtained. A more empirical approach is to estimate the number of water molecules associated with each ion that moves through the pore and then calculate the water flux from the current. For highly ion-selective pores, the number of water molecules per ion can be determined experimentally from measurements of streaming potentials (24, 34), by using Eq. 1. Most work in this area has been with channels for which strong cation selectivity and single-file transport can be assumed (26, 28, 29, 34, 35). More than two and up to seven water molecules have been found to move with each cation. In the case of a wider, less selective pore, such as the αHL pore, it seems reasonable to assume that the water transported per ion will be equal to that in the primary hydration sphere. Here, both cations and anions are transported in an applied potential, and the net water flux (Jw) will therefore be related to the net ion flux (J±) (Eq. 2).
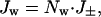 |
[6] |
where Nw is the number of water molecules transported per ion, which we take to be 10 for both anions and cations (8).
Therefore,
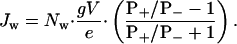 |
[7] |
Below, we also use E, the enhancement factor, which is the flux in an applied potential divided by the passive flux. E can be related to the Peclet number (Pe). When electroosmotic flow is the only form of convective flow, Pe is given by:
 |
[8] |
where x is the distance traveled, D is the diffusion coefficient; and Fick's first law gives νdiff = D/x.
For a neutral molecule (i.e., one with zero electrophoretic mobility) (36):
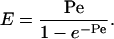 |
[9] |
When Pe is large, E ≈ Pe and
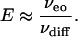 |
[10] |
Relating Kd for βCD with Estimates of Water Flow. The results obtained here indicate that the dissociation constant for βCD is highly correlated with the expected direction of water flow, which in turn depends on the net ion flux, J±. Alternative explanations for the voltage dependence of binding of the neutral βCD molecule were considered earlier and included a small charge or dipole on the βCD molecule, a two-state voltage-dependent conformational change of the αHL pore, or variation of the dissociation constant arising from a continuous structural change of the pore with the membrane potential (5, 7). The first two possibilities were quickly eliminated (7), and the electroosmotic effect suggested a more satisfactory explanation (5) for the phenomenon than a continuous structural change (7).
Here, we have obtained compelling evidence for the role of electroosmosis by using mutant αHL pores, PNN-X mutants that bind βCD from both the trans and the cis chamber. In addition, replacements at residue 113 were exploited to alter the charge selectivity of the pore. In this way, all four possibilities of binding from the cis or trans side, in the presence of cis-to-trans or trans-to-cis water flow, were examined. Binding was always tighter (lower Kd) when association was in the same direction as the water flow and dissociation was against the flow. This is clearly seen for both the cation-selective pores formed from PNN-D and PNN-E and the anion-selective pores formed from PNN-K and PNN-R (Fig. 3). Our observations also suggest that the binding sites for βCD differ depending on whether βCD is presented from the cis or the trans side. If the sites were identical, the values for koff for cis- and trans-βCD would be the same under the same conditions. The koff values differ, and, where there is a voltage dependence, the slopes of the plots (Fig. 3) suggest that βCD dissociates toward the same side as that from which it is presented. This does not alter the conclusion that electroosmosis is responsible for the voltage dependence of the Kd values.
A possible flaw in our argument arises because the mutations carried out to alter ion selectivity are likely to lie close to the βCD binding sites (1, 5). It was possible that the effects on Kd were seen because the applied potential alters the conformation of the pore at the binding sites. For example, with a positively charged group at position 113, a negative potential might make the cis site assume low affinity and the trans site assume high affinity, whereas a positive potential might have a reciprocal effect. A negatively charged group at position 113 would do the opposite. This and other possible effects of substitution at position 113 were ruled out by experiments on PNN-M (with the neutral Met at 113 and the neutral Asn at the nearby positions 111 and 147) in which the pH in the chambers of the apparatus was manipulated (Table 1). At pH 5.0, PNN-M was anion-selective, and, with respect to βCD binding, it acted like mutants that were anion-selective by virtue of substitution at position 113 (PNN-R and PNN-K). At pH 11.0, PNN-M was cation selective and acted like the cation-selective mutants (PNN-E and PNN-D).
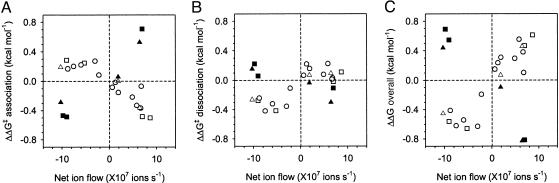
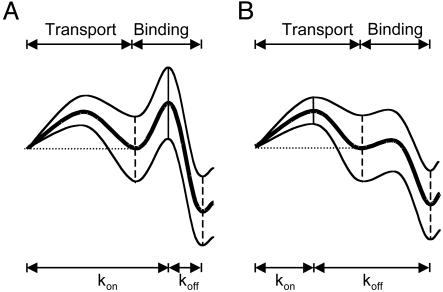
We made a semiquantitative analysis of the electroosmotic effect. ΔΔG for the dissociation constant was plotted versus the net ion flow calculated from Eq. 3. A strong correlation was observed (Fig. 4C, ΔΔG≠ for association and ΔΔG≠ for dissociation are shown in A and B). For the binding of βCD to PNN-D and PNN-E from the trans chamber, koff is hardly affected by the applied potential (Fig. 3). The simplest interpretation is that there is a substantial local barrier to attachment and reattachment at the binding site, which would not be affected by electroosmotic water flow (Fig. 5A). By contrast, kon is affected by potential (Fig. 3). In the cases of PNN-K and PNN-R, electroosmotic flow affects both kon and koff. The effect on koff is likely to result from the dominance of local rebinding after dissociation, which would be enhanced by solvent flow toward the binding site and weakened by flow away from it (Fig. 5B).
Fig. 4.
Relationships between free energies for the interaction of αHL with βCD and the estimated net movement of ions (J±) through the pore. All values (Table 1) are for +40 mV, except PNN-E with βCD in the cis chamber for which koff was too fast to determine and data at –40 mV were used. J± was estimated from the conductance and charge selectivity of each pore as stated in the text. □, PNN-E, PNN-D, PNN-R, and PNN-K with trans-βCD; ▪, PNN-E, PNN-D, PNN-R, and PNN-K with cis-βCD; ▵, PNN-M with trans-βCD at pH 5.0, pH 7.5, and pH 11.0; ▴, PNN-M with cis-βCD at pH 5.0, pH 7.5, and pH 11.0; ○, all other pores including WT αHL, at pH 5.0, pH 7.5, and pH 11.0, M113R, M113K, M113T, M113V, M113P, M113D, M113E, E111N, and K147N. (A) ΔΔG≠ for association: the difference in association activation energy between +40 mV and 0 mV (see Table 1 for derivation from data); (B) ΔΔG≠ for dissociation; (C) overall ΔΔG. An expanded version of Fig. 4, in which each point is identified, is included as Fig. 8, which is published as supporting information on the PNAS web site.
Fig. 5.
Rate constant representations (40) for βCD binding. The representations are not quantitative and are intended to illustrate the two classes of kinetics observed when βCD binds to the αHL pore from the trans side of the bilayer. (A) Rate constant representations for pores exemplified by PNN-E and PNN-D. The thick line is at 0 mV. At positive potentials (bottom line), binding is enhanced for these cation-selective pores. The primary effect is on kon. Binding is diminished at negative potentials (top line). (B) Rate constant representations for pores exemplified by PNN-R and PNN-K. The thick line is at 0 mV. At positive potentials (top line), binding is diminished for these anion-selective pores. Both kon and koff are affected. Binding is enhanced at negative potentials (bottom line).
In the cases of PNN-K and PNN-R, association is dominated by transport through the pore.
Therefore
 |
[11] |
Therefore
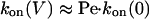 |
[12] |
and
 |
[13] |
For example, for PNN-K at –120 mV with βCD in the trans chamber:
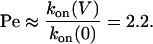 |
Furthermore, for water, νe = 5.0 cm s–1 at –120 mV, as determined from Eqs. 2, 5, and 6. If the flow is convective, βCD will move at the same speed as water in the pore.
Therefore
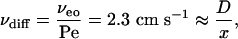 |
where x (distance to the binding site) = 5 × 10–7 cm.
Therefore, DβCD-pore = 1.1 × 10–6 cm2 s–1.
This value is about three times lower than the accepted value of D in bulk water (37). However, it is likely that DβCD-pore is lowered further by collisions with the wall, in keeping with the relatively low observed kon values, in which case both νeo and νdiff would be lowered proportionally and the value of Pe would remain roughly the same.
We also measured the dependence of kon, koff, and Kd on ionic strength. The values were plotted versus current (rather than applied potential) so that the effect of ionic strength on the net movement of ions (J±) would be visualized (see Fig. 7, which is published as supporting information on the PNAS web site). J± depends on the charge selectivity, which in turn depends on the extent to which charged residues lining the pore are screened. Although we have not attempted to fit the data to a quantitative model, it is clear that the values follow the expected trends; i.e., the effects on kon, koff, and Kd are greatest at low ionic strength where surface charge is least effectively screened.
Finally, we asked whether water flow brought about by an osmolyte could cause changes in the affinity of αHL of the same sign and order of magnitude as those caused by electroosmosis. We used M113V, which is only weakly ion-selective (Table 1), and a low applied potential, –40 mV, to minimize electroosmosis. We found that 24% (wt/vol) polyethylene glycol (PEG) 6,000 in the cis chamber increased the affinity of βCD (trans) by 5.3-fold compared with no PEG in either chamber (data not shown). By contrast, 24% (wt/vol) PEG in the trans chamber decreased the affinity of βCD (trans) by 0.22-fold, compared with PEG in both chambers. Taking a mean value of 4.9-fold for the change in affinity: ΔΔG = 0.94 kcal mol–1 (1 kcal = 4.18 kJ). We calculated the water flux through the pore by using Poiseille's formula and the osmotic pressure calculated from a van't Hoff equation modified to account for the variation of the osmotic coefficient of PEG 6,000 with concentration (38). We found Jw = 2.5 × 109 molecules s–1, assuming that the diameter of the pore is 2 nm. Therefore, ΔΔG/Jw = 3.8 × 10–10 kcal mol–1/water molecules s–1. This value can be compared with an overall value for ΔΔG/Jw obtained from the data in Fig. 4C. The slope of a linear fit to the trans data gives ΔΔG/J± = 6.7 × 10–9 kcal mol–1/ions s–1. Using a value of 10 for the number of water molecules carried per cation or anion, ΔΔG/Jw = 6.7 × 10–10 kcal mol–1/water molecules s–1. The rough agreement between the two calculations is gratifying but may be in part fortuitous. For example, the water flux calculated according to Poiseille is highly dependent on the value taken for the diameter of the pore, which is in any case not a cylinder, and the calculated J± values used in Fig. 4C depend strongly on the values of P+/P–.
Conclusions
The work presented here demonstrates that the dissociation constant for the interaction of a neutral molecule with a binding site within the lumen of the αHL pore is voltage-dependent and varies by more than two orders of magnitude over the range of applied potentials from –120 mV to +120 mV. The sign of the effect is in all circumstances in keeping with our basic understanding of electroosmosis, but more theoretical work must be done to provide a quantitative basis for the observations. For example, the analysis outlined above does not take into account the perturbation of flow by the relatively large βCD molecule while it is in the pore. Given the complexities of a quantitative analysis, the phenomenon could be a fruitful area for the application of molecular dynamics simulations. The findings are likely to have implications in several situations where ligands bind within channels and pores. For example, after voltage activation, potassium channels are inactivated when an unstructured N-terminal extension of the polypeptide chain enters the lumen from the cytoplasmic face (39). It is possible that electroosmotic flow contributes to the binding of the largely uncharged polypeptide sequence.
Supplementary Material
Acknowledgments
We thank Charles R. Martin, Terry Conlisk, and the reviewers for their helpful thoughts. This work was funded by the U.S. Department of Energy, the Multidisciplinary University Research Initiative (Office of Naval Research 1999), the National Institutes of Health, and the Defense Advanced Research Planning Agency (Engineered Biomolecular Nanodevices/Systems program). H.B. is the holder of a Royal Society–Wolfson Research Merit Award.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: αHL, staphylococcal α-hemolysin; βCD, β-cyclodextrin; EDL, electrical double layer; PEG, polyethylene glycol.
References
- 1.Gu, L.-Q., Braha, O., Conlan, S., Cheley, S. & Bayley, H. (1999) Nature 398, 686–690. [DOI] [PubMed] [Google Scholar]
- 2.Gu, L.-Q., Cheley, S. & Bayley, H. (2001) Science 291, 636–640. [DOI] [PubMed] [Google Scholar]
- 3.Gu, L.-Q., Dalla Serra, M., Vincent, J. B., Vigh, G., Cheley, S., Braha, O. & Bayley, H. (2000) Proc. Natl. Acad. Sci. USA 97, 3959–3964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bayley, H. & Cremer, P. S. (2001) Nature 413, 226–230. [DOI] [PubMed] [Google Scholar]
- 5.Gu, L.-Q., Cheley, S. & Bayley, H. (2001) J. Gen. Physiol. 118, 481–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Song, L., Hobaugh, M. R., Shustak, C., Cheley, S., Bayley, H. & Gouaux, J. E. (1996) Science 274, 1859–1865. [DOI] [PubMed] [Google Scholar]
- 7.Gu, L.-Q. & Bayley, H. (2000) Biophys. J. 79, 1967–1975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hille, B. (2001) Ion Channels of Excitable Membranes (Sinauer, Sunderland, MA), 3rd. Ed.
- 9.Zhou, Y., Morais-Cabral, J. H., Kaufman, A. & MacKinnon, R. (2001) Nature 414, 43–48. [DOI] [PubMed] [Google Scholar]
- 10.Honeycutt, A. J. & Saykally, R. J. (2003) Science 299, 1329–1330. [DOI] [PubMed] [Google Scholar]
- 11.Bruin, G. J. (2000) Electrophoresis 21, 3931–3951. [DOI] [PubMed] [Google Scholar]
- 12.Bousse, L., Cohen, C., Nikiforov, T., Chow, A., Kopf-Still, A. R., Dubrow, R. & Parce, J. W. (2000) Ann. Rev. Biophys. Biomol. Struct. 29, 155–181. [DOI] [PubMed] [Google Scholar]
- 13.Beebe, D. J., Mensing, G. A. & Walker, G. M. (2002) Ann. Rev. Biomed. Eng. 4, 261–286. [DOI] [PubMed] [Google Scholar]
- 14.Bard, A. J. & Faulkner, L. R. (2001) Electrochemical Methods: Fundamentals and Applications (Wiley, New York).
- 15.Conlisk, A. T., McFerran, J., Zheng, Z. & Hansford, D. (2002) Anal. Chem. 74, 2139–2150. [DOI] [PubMed] [Google Scholar]
- 16.Dutta, P. & Beskok, A. (2001) Anal. Chem. 73, 1979–1986. [DOI] [PubMed] [Google Scholar]
- 17.Santiago, J. G. (2001) Anal. Chem. 73, 2353–2365. [DOI] [PubMed] [Google Scholar]
- 18.Chien, R.-L. & Bousse, L. (2002) Electrophoresis 23, 1862–1869. [DOI] [PubMed] [Google Scholar]
- 19.Devasenathipathy, S., Santiago, J. G. & Takehara, K. (2002) Anal. Chem. 74, 3704–3713. [DOI] [PubMed] [Google Scholar]
- 20.Bath, B. R., Lee, R. D., White, H. S. & Scott, E. R. (1998) Anal. Chem. 70, 1047–1058. [Google Scholar]
- 21.Bath, B. R., White, H. S. & Scott, E. R. (2000) Anal. Chem. 72, 433–442. [DOI] [PubMed] [Google Scholar]
- 22.Miller, S. A., Young, V. Y. & Martin, C. R. (2001) J. Am. Chem. Soc. 123, 12335–12342. [DOI] [PubMed] [Google Scholar]
- 23.Rosenberg, P. A. & Finkelstein, A. (1978) J. Gen. Physiol. 72, 341–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Levitt, D. G., Elias, S. R. & Hautman, J. M. (1978) Biochim. Biophys. Acta 512, 436–451. [DOI] [PubMed] [Google Scholar]
- 25.Miller, C. (1982) Biophys. J. 38, 227–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Alcayaga, C., Cecchi, X., Alvarez, O. & Latorre, R. (1989) Biophys. J. 55, 367–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dani, J. A. (1989) J. Neurosci. 9, 884–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tu, Q., Vélez, P., Brodwick, M. & Fill, M. (1994) Biophys. J. 67, 2280–2285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tripathi, S. & Hladky, S. B. (1998) Biophys. J. 74, 2912–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pikal, M. J. (2001) Adv. Drug Delivery Rev. 46, 281–305. [DOI] [PubMed] [Google Scholar]
- 31.Prausnitz, M. R., Corbett, J. D., Gimm, J. A., Golan, D. E., Langer, R. & Weaver, J. C. (1995) Biophys. J. 68, 1864–1870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cheley, S., Braha, O., Lu, X., Conlan, S. & Bayley, H. (1999) Protein Sci. 8, 1257–1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Katchalsky, A. & Curran, P. F. (1965) Nonequilibrium Thermodynamics in Biophysics (Harvard Univ. Press, Cambridge, MA).
- 34.Rosenberg, P. A. & Finkelstein, A. (1978) J. Gen. Physiol. 72, 327–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Saparov, S. M., Antonenko, Y. N., Koeppe, R. E. & Pohl, P. (2000) Biophys. J. 79, 2526–2534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Srinivasan, V. & Higuchi, W. I. (1990) Int. J. Pharm. 60, 133–138. [Google Scholar]
- 37.Cameron, K. S. & Fleming, L. (2001) J. Org. Chem. 66, 6891–6895. [DOI] [PubMed] [Google Scholar]
- 38.Alexandrowicz, Z. (1959) J. Polymer Sci. 40, 107–112. [Google Scholar]
- 39.Zhou, M., Morais-Cabral, J. H., Mann, S. & MacKinnon, R. (2001) Nature 411, 643–644. [DOI] [PubMed] [Google Scholar]
- 40.Andersen, O. S. (1999) J. Gen. Physiol. 114, 589–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.