Channel gating forces govern accuracy of mechano-electrical transduction in hair cells

Abstract

Sensory hair cells are known for the exquisite displacement sensitivity with which they detect the sound-evoked vibrations in the inner ear. In this article, we determine a stochastically imposed fundamental lower bound on a hair cell's sensitivity to detect mechanically coded information arriving at its hair bundle. Based on measurements of transducer current and its noise in outer hair cells and the application of estimation theory, we show that a hair cell's transducer current carries information that allows the detection of vibrational amplitudes with an accuracy on the order of nanometers. We identify the transducer channel's molecular gating force as the physical factor controlling this accuracy in proportion to the inverse of its magnitude. Further, we show that the match of stochastic channel noise to gating-spring noise implies that the gating apparatus operates at the threshold of negative stiffness.

The main peripheral structure that constitutes the mammalian sense of hearing is the cochlea, a snail-shell-shaped cavity in the temporal bone filled with fluid (1). Sound, via the middle ear, excites these cochlear fluids, which transmit their motion via the organ of Corti to the hair bundles of the sensory hair cells. The hair cells perform the actual mechano-electrical transduction in the ear. They encode the mechanical motion of their hair bundle into a change of the open probability of mechanically gated transducer channels, resulting in a variation of inward transducer current (2, 3). This signal, the first electrically coded stage in the signal-processing cascade of the ear, is further transformed by the hair cells, most likely also via electro-mechanical feedback (4, 5), and sent to the brain.

From the brain's point of view, the transducer channels thus serve as a window onto the mechanical events in the cochlea, which carry the sound-evoked information. Here, unlike most other approaches in hair-cell research, we also follow this information-upstream direction and determine the accuracy with which the position X of a hair bundle can be detected given a certain transducer current, I. Because ion channels have intrinsic stochastic properties that derive from their thermal activation, a specific deflection, X, may result in a range of possible transducer currents. Conversely, in the information-upstream direction, this means that a specific transducer current, I, can result from a range of different deflections of the hair bundle, each having a specific probability of evoking that current. The variance of these deflections will be used here as a measure of accuracy of mechano-electrical transduction.

In addition to this intrinsic-channel accuracy, the elastic elements that have to be tensioned to engage the transducer channels' gates also will convey Brownian noise to the channels and, consequently, will additionally impair the accuracy with which a transducer current can be decoded into the evoking hair-bundle deflection X.

The two-state gating-spring model (6) of mechano-electrical transduction is used to describe this overall accuracy in terms of its gating parameters and thus allows for the identification of the physical limitations of mechano-electrical transduction in hair cells.

Materials and Methods

Electro- and Mechanophysiology. Experiments were performed on apical-coil outer hair cells obtained from acutely isolated organs of Corti taken from CD-1 mice. Animal procedures were regulated under United Kingdom Home Office guidelines.

Transducer currents in response to fluid-jet stimulation were measured under whole-cell voltage clamp with an EPC8 patch clamp amplifier (HEKA Electronics, Lambrecht/Pfalz, Germany) at a –84 mV holding potential (including a –4 mV liquid junction potential correction). Outer hair cells investigated by using the dynamic stimulus protocol (see Data Analysis) were obtained between postnatal days 5 and 7 (P5–7). Pipettes were pulled from soda glass and thickly coated with wax. Extracellular solution contained 135 mM NaCl, 5.8 mM KCl, 1.3 mM CaCl₂, 0.9 mM MgCl₂, 0.7 mM NaH₂ PO₄, 2 mM Na-pyruvate, 5.6 mM d-glucose, and 10 mM Hepes, and vitamins and amino acids were added from concentrates (pH 7.5; 306 mOsm/kg). Intracellular solution contained 137 mM CsCl, 2.5 mM MgCl₂, 2.5 mM Na₂ ATP, 10 mM Na₂-phosphocreatine, 5 mM Hepes, and 1 mM EGTA-NaOH (pH 7.3; 292 mOsm/kg). The contribution of basolateral channels to the measured currents was eliminated by the holding potential used and by the replacement of potassium by caesium in the intracellular solution. The average series resistance was 2.7 ± 0.7 MΩ (n = 11) after compensation, and the average membrane capacitance was 6.2 ± 0.3 pF (n = 11), resulting in a typical noise value of ≈1.7 pA² integrated over the recording bandwidth, which was corrected for in the noise measurements. The average membrane input resistance was 435 ± 195 MΩ (n = 11). Current signals were low-pass filtered with cut-off frequencies of 2.5 or 5 kHz (f_–3dB, eight-pole Bessel), which were always below the cut-off frequency imposed on the measurements by the series resistance of the patch.

Hair-bundle displacement was measured by using a differential photodiode system, which was low-pass filtered (f_–3dB = 5 kHz, eight-pole Bessel) and recorded simultaneously with the transducer current (7). The rms noise caused by the displacement measurement technique was ≈0.3 nm. Fluid-jet stimuli were generated, and elicited responses were recorded with a Power 1401 data acquisition board in combination with the signal software package (CED, Cambridge, United Kingdom). Generated stimuli were low-pass filtered (f_–3dB = 2 kHz, eight-pole Bessel). Current and displacement recordings were oversampled at 50 kHz to allow a proper analysis of the response envelope of the high-frequency component (f₂, see Data Analysis). Hair-bundle stiffness was measured in response to force steps as described (7) in cells held at –84 mV at P7 and P19 (see Discussion). All experiments were performed at room temperature (≈25°C).

Cramér–Rao Bound on Transducer Accuracy. A discrete version of the Cramér–Rao inequality (8, 9) is used to determine a lower bound of the variance of any possible unbiased estimator, X̂, of hair-bundle displacement, X, from a conditional probability density function p(I|X) = p(n_o|X). This function expresses the probability of a total transducer current, I, entering the cell through n_o open channels, given a position, X, of the hair bundle's tip. Here, I = i·n_o, where i is the current flowing through one open channel. The variance, 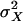, of the estimator, X̂, of the input parameter, X, is then equal to or greater than the Cramér–Rao bound, 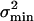, which stems from intrinsic-channel stochastics described by p(n_o|X) according to:

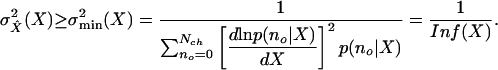[1]

The inverse of 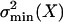is usually referred to as the information, Inf(X), about X contained in I (see ref. 8) and in this case has dimensions equal to m^–2. Assuming a total of N_ch equal and independent operational channels, we may use the binomial distribution for p(n_o|X) (see ref. 10). Then, evaluating the right-hand side denominator of Eq. 1 yields for the information:

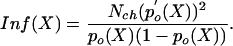[2]

Here, p_o(X) is the (average) open probability and p′_o (X) is the derivative of p_o(X) with respect to X. The information as given by Eq. 2 appears to be closely related to an empirically defined integrated-band signal-to-noise ratio of hair-cell transduction (11). In that study it was proposed that a transducer current power signal, S_I, in response to a small bundle-displacement power, ΔX², around an operational position, X, is related to the change of the channel's open probability according to S_I(X) = [i · N_ch · p′_o(X) · ΔX]², whereas the transducer current noise power is given by (see ref. 12): N_I(X) = i²·N_ch·p_o(X)·(1 – p_o(X)). Combined with the new identity in Eq. 2, this finding means that the signal-to-noise ratio of hair-cell transduction equals the information times the displacement power of its bundle: S_I/N_I = Inf·ΔX². Conversely, our present result also shows that the Cramér–Rao bound on the accuracy, 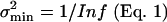, equals the value of hair-bundle displacement power, ΔX², that results in a signal-to-noise ratio of the transducer current, I, of one (S_I/N_I = 1).

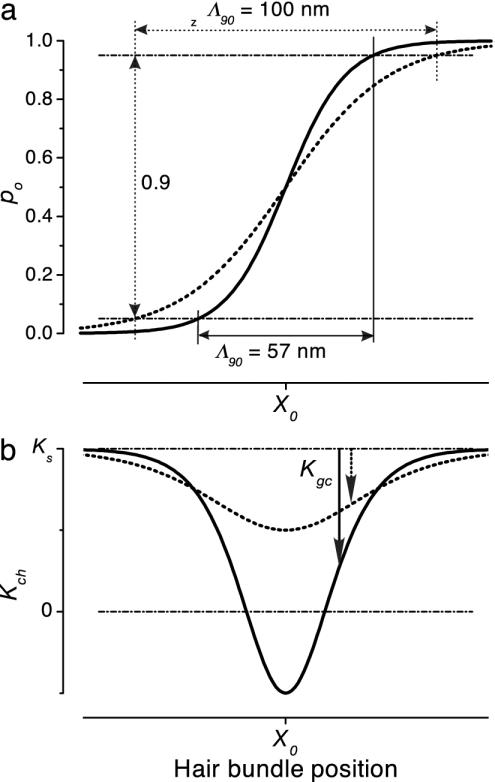
Two-State Gating-Spring Model. For each channel, the basic two-state gating-spring model assumes the action of a gating spring, which at one end is driven by the hair bundle and at the other end engages the channel's gate (6, 13). Thermodynamics then shows that the open probability of the channel, p_o(X), is a sigmoidal function of hair-bundle position X (Fig. 1a) and can be expressed in terms of the gating-spring constant, K_s, and the conformational swing of the channel, D, both as measured at the hair bundle's tip: p_o(X) = [1 + exp(–K_sD·(X – X_o)/kT)]^–1. Here, k is Boltzmann's constant, T is the absolute temperature, and X_o defines the displacement at which p_o(X) = 0.5. The product, K_s·D, has been termed gating force, Z, (6) and defines an effective operational range of hair-bundle displacements, Λ₉₀ = 6 kT/Z, centered at X₀ (Fig. 1a) within which the open probability is ≈90% modulated, apart from the effect of adaptation (14). The model also defines an ensemble averaged stiffness, K_ch(X) = K_s – K_gc(X), of each spring-channel complex (Fig. 1b). This stiffness thus consists of the gating-spring constant, K_s, and in addition includes a displacement-dependent reduction, K_gc(X) = Z²·p_o(X)·(1 – p_o(X))/kT, which is related to the extent of gating and therefore termed gating compliance (6).

Fig. 1.

Effects of differing noise contributions on a single gating-spring-channel complex. Open probability, p_o(X)(a), and related ensemble averaged stiffness curves, K_ch(X) (b), calculated with the two-state model (6). The gating-spring constant, K_s, was fixed (7.5 μN/m), whereas two different values of parameter D (33 and 57 nm) result in 100 nm (dashed line) and 57 nm (solid line) for Λ₉₀ as indicated via the modulation range of open probability of 0.9. This example corresponds to a gating force, Z, of 248 fN (dashed line) and 429 fN (solid line), respectively. The associated noise-matching parameters, M²_c, are 0.5 (dashed line) and 1.5 (solid line). In the latter case, the intrinsic-channel noise, 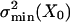, is smaller than the Brownian noise in the gating spring, σ²_B, and leads to negative values for the stiffness of the gating-spring-channel complex in a region around X₀ (see Results). The downward arrows indicate the gating compliances, K_gc, at arbitrary X.

The two-state model, extended also to describe differential engagement (15) of the two states, was used to generate fits to the measured data and results (e.g., Fig. 2 b–d, solid lines). Differential engagement has been introduced to the description of gating of mechano-electrical transducer channels to account for the finite minimum open probability observed at hair-bundle positions more negative than approximately –50 nm. At these bundle positions, gating-spring tension is possibly decoupled from the channel's gate.

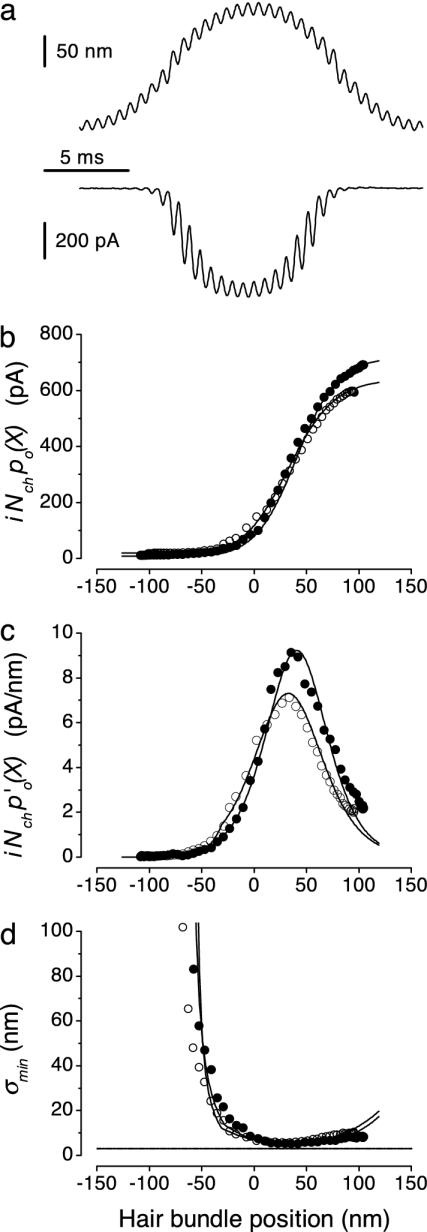
Fig. 2.

Determination of hair-cell accuracy, σ_min(X). (a) Measured hair-bundle displacement (upper trace) and evoked transducer current (lower trace) versus time in response to the double-sine protocol consisting of a large-amplitude, low-frequency component (49 Hz) and a small-amplitude, high-frequency component (1,563 Hz). Traces shown represent averages of 18 responses (bundle height, 3.5 μm). (b) Transducer current as a function of (quasi-static) hair-bundle position, X, in two cells obtained from responses as in a (open symbols represent the same cell as in a). (c) Changes of transducer currents in response to small changes in hair-bundle position normalized to 1 nm as a function of (quasi-static) hair-bundle position obtained from the same cells as shown in b. (d) Cramér–Rao lower bound on accuracy of hair-bundle position, σ_min(X), determined from the data shown in b and c by using Eqs. 1 and 2. Solid lines in b–d give results of fits of the two-state gating-spring model. Parameters (filled and open symbols, respectively): K_s, 6.2 and 7.2 μN/m; D, 34 and 26 nm; N_ch, 74 and 66; σ_min(X₀), 4.5 and 5.4 nm; X₀, 41 and 33 nm. The horizontal line shows the almost identical (3.0 and 2.9 nm) Brownian gating-spring noise levels, σ_B, of the two cells.

Data Analysis. A dynamic stimulus protocol (double-sine), consisting of a sum of two sine waves (f1 ≈ 49 Hz and f2 ≈ 1,563 Hz), displaced the bundle through a large part of its operational range (Fig. 2a). By using the double-sine protocol, p_o(X) relationships (Fig. 2b) were constructed by low-pass filtering of the current response to obtain the low-frequency (f₁) component and its harmonics and displaying them as a function of the associated low-pass-filtered hair-bundle displacement. The envelope of the remaining f₂ current component was calculated and plotted as a function of the associated displacement component at f₁ to obtain p′_o(X) curves (Fig. 2c). The two-state model was used to fit the p_o(X) and p′_o(X) data simultaneously. To match the associated p_o(X) relationships, p′_o(X) data were linearly scaled with a factor (average 0.83 ± 0.09; n = 11) most likely reflecting differences in adaptation (14) at the two frequencies (f₁ and f₂).

Current noise was determined over ≈100-ms time windows during steps of different bundle position, X. Noise power density spectra were determined by using Bartlett's periodogram-averaging method (5× averaging) with a Taylor–Kaiser window (β = 1.8) (16).

Unless indicated otherwise, data are presented as the mean ± SD with the number of observations in parentheses.

Results

Intrinsic-Channel Stochastics. In Materials and Methods it is derived how the intrinsic stochastic properties of N_ch independent and equal transducer channels with an open probability, p_o(X), limit the accuracy with which a hair cell's bundle position, X, can be optimally detected. This accuracy, or Cramér–Rao lower bound, σ_min, is the inverse of the property referred to as information, Inf(X), about X contained in I and depends on N_ch, p_o(X), and its derivative, p′_o(X), according to Eqs. 1 and 2. The interpretation of σ_min as the accuracy of mechano-electrical transduction is illustrated further by the demonstration that 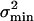equals the bundle displacement power that leads to a transducer current with a signal-to-noise ratio of one (see Materials and Methods and ref. 11).

Cramér–Rao bounds on transducer accuracy, σ_min(X), were determined in 11 apical-coil outer hair cells from simultaneous measurements of transducer current and the position of the hair bundle, which was stimulated with a fluid jet. Fig. 2a shows an example of hair-bundle displacement (upper trace) and evoked current (lower trace) measured in response to the double-sine stimulus protocol used. This stimulus contained a large-amplitude, low-frequency component (49 Hz, 1 period shown) and a small-amplitude, high-frequency component (1,563 Hz, 32 periods shown). Filtering of the responses enabled the construction of p_o(X) curves from the low-frequency components (Fig. 2b, data points). The amplitude of the envelope of the high-frequency component in the current response effectively probes the derivative with respect to displacement, X. This method allows the independent determination of p′_o(X) curves when plotted against the low-frequency component of the displacement (Fig. 2c, data points). The number of operational channels per cell, N_ch, was determined from the saturation current in each cell in combination with the known unitary current (i = 9.7 pA at –84 mV; ref. 7). The average value found for N_ch was 80 ± 26 (n = 11). Fig. 2d shows the resulting lower bound, σ_min(X), as obtained by substituting N_ch and the measured p_o(X) and p′_o(X) data from the same two cells as shown in Fig. 2 b and c into Eqs. 1 and 2. The average optimal accuracy, σ_min, amounts to 5.9 ± 1.9 nm (n = 11; range, 2.9–9.9 nm) and is reached at a hair-bundle position, X, of 44 ± 18 nm (n = 11). This result thus shows that the intrinsic stochastics of the transducer channels prevents a single outer hair cell from reliably detecting mechanical motion of its bundle smaller than on the order of nanometers.

Physical Limits of Transduction. To identify the underlying physics that governs accuracy and related signal-to-noise ratio of hair-cell transduction, we evaluated Inf (Eq. 2) in terms of the gating parameters that define the two-state gating-spring model (refs. 6 and 13 and Materials and Methods). This model was fitted to the measured p_o(X) and p′_o(X) data to obtain the gating parameters for each cell (e.g., Fig. 2 b and c, solid curves). Averages of the results are given in Table 1. The gating-spring model can be considered the most concise quantitative description to date of observations on the transducer channel's gating machinery and allows a straightforward interpretation in terms of its physical parameters. The most important parameter is the elementary gating force, Z, defined as the product of the gating-spring constant, K_s, and the conformational swing of the channel, D.

Table 1. Main parameters used.

Symbol	Value, unit	Description
I	pA	Transducer current
X	nm	Bundle displacement at the tip
po(X)		Transducer channel open probability
Inf(X)	m-2	Information about X contained in I
Sl	pA2	Transducer current power signal
Nl	pA2	Transducer current power noise
Mc	0.50 ± 0.16	Noise-matching parameter
Nch	80 ± 26	Number of transducer channels per cell
X0	44 ± 18 nm	Bundle displacement at which po = 0.5
σmin	5.9 ± 1.9 nm	Intrinsic-channel noise (Cramér—Rao bound)
σB	2.8 ± 0.6 nm	Gating-spring noise
Λ90	156 ± 50 nm	Operational range of transduction
D	23 ± 7 nm	Conformational swing of the channel
Z	174 ± 60 fN	Gating force
Ks	7.4 ± 1.0 μN/m	Gating-spring constant
Kch(X)	μN/m	Stiffness of a single gating-spring-channel complex
Kgc(X)	μN/m	Gating compliance
Kngc(X)		Gating compliance normalized to Ks

Values in the second column, when given, were obtained from fitting the two-state gating-spring model to the measured data (n = 11).

Combining the properties of the two-state gating-spring model with Eq. 2 reveals that each transducer channel of a hair cell contributes an amount of information, ΔInf, to the total information, Inf = N_ch·ΔInf, equal to:

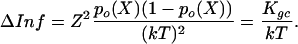[3]

The right-hand side of Eq. 3 offers a useful but also profound insight into the process of mechano-electrical transduction: the amount of information, ΔInf, on hair-bundle position conveyed by each transducer channel via its gated current is equivalent to the gating compliance, K_gc, divided by the thermal noise energy, kT. Nonlinear distortion in hair-bundle mechanics, caused by gating and characterized by the gating compliance, K_gc (see Materials and Methods), therefore seems to be inevitable for information transfer. The amount of information is fundamentally constrained by the level of thermal noise energy. It is obvious from Eq. 3 that the information is maximal at X = X₀ (p_o(X₀) = 0.5), where it amounts to [Z/(2kT)]² so that the optimal accuracy in estimating the hair bundle's position per channel, σ_min(X₀), is 2kT/Z. This theoretical result, with our average experimental value for Z (174 ± 60 fN; n = 11), leads to ≈47 nm per channel and, for 80 ± 26 operational channels, to 5.3 ± 2.6 nm per cell. This finding is in line with the result for the optimal σ_min (5.9 nm) directly obtained from substituting the experimental results obtained for N_ch, p_o(X), and p′_o(X) in Eqs. 1 and 2 (Fig. 2d).

When increased, the gating force, Z, seems to limitlessly improve accuracy (σ_min = 2kT/Z) and related signal-to-noise ratio of a hair cell. At the same time, though, this increase would reduce the effective operational range, Λ₉₀ = 6kT/Z, within which hair-bundle vibrations are predominantly transduced (p_o is modulated ≈90% within Λ₉₀; see Materials and Methods and Fig. 1a). The requirement for a hair cell to transduce the physiological range of hair-bundle vibrations, therefore, undoubtedly puts an upper limit on the value of the gating force. The ratio of operational range, Λ₉₀, and optimal accuracy, σ_min(X₀), defines an upper bound on the dynamic range of transduction per channel, which can now easily be inferred to amount to a factor of 3 (≈9.5 dB) and is surprisingly independent of any parameter of the model. The operational range, Λ₉₀, of an ensemble of identical but independent channels is the same as that of one channel. However, increasing the number of channels to N_ch improves their collective optimal accuracy to 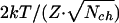, thereby increasing a hair cell's effective dynamic range to 9.5 + 10·log(N_ch) dB. Together with the average number of operational channels found (N_ch = 80), this finding leads to a theoretical dynamic range of ≈28.5 dB. This dynamic range is consistent with the ratio (28.4 dB) of the average operational range Λ₉₀ (156 ± 50 nm; n = 11) and σ_min(X₀) (5.9 nm), both directly obtained from our experimental data.

Gating-Spring Noise. So far we have only considered signal-to-noise ratio and accuracy arising from intrinsic-channel stochastics, which, therefore, are solely related to transduction. However, noise attacks the mechano-transducer system on multiple fronts. At its input, formed by the gating springs, the system also is susceptible to Brownian noise fluctuations. When completely transduced, the Brownian noise of a gating spring evokes a current per channel equivalent to the current evoked by a hair-bundle stimulus variance of σ²_B = kT/K_s (see ref. 17). Because we find from our data a value for K_s of 7.4 ± 1.0 μN/m (n = 11), σ_B equals on average an equivalent stimulus of ≈24 nm for a single channel. Like σ_min, this gating-spring noise also scales down in proportion to the inverse of the square root of the total number of channels, yielding σ_B = 2.8 ± 0.6 nm (n = 11) per cell. In the stimulus domain, the variance induced by the gating-spring noise, 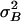, can be expected to add independently to the lower bound on the variance, 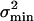, as obtained from the Cramér–Rao inequality.

How do these two noise components compare? Using Eqs. 1–3, together with σ²_B = kT/K_s, yields:

[4]

The ratio of the two noise components thus equals the gating compliance, K_gc, normalized to the gating-spring constant, K_s, and is denoted here as K_ngc(X). Given a gating-spring constant with associated , a smaller summed variance could be obtained by adjusting the gating force so as to reduce . Reducing it considerably more than the inescapable level of σ²_B would, however, not pay off because σ²_B would continue to dominate the summed variance, whereas the operational range would, unfavorably, decrease. On the basis of these considerations, we hypothesize that a hair cell at X = X₀ may operate at closely matched noise levels () from which it follows that the normalized gating compliance, K_ngc(X₀), should be on the order of one (Eq. 4). Interestingly, this condition is equivalent to each gating-spring-channel complex operating close to the threshold of negative stiffness (K_ch(X₀) ≈ 0) as is obvious from the definitions of K_ch and K_ngc (Materials and Methods and Eq. 4). A characteristic matching parameter, M_c, therefore can be defined according to: 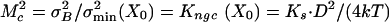. If M_c exceeds 1, a region of negative stiffness of the spring-channel complex exists (Fig. 1b), and gating-spring noise predominates. If, on the other hand, M_c is smaller than 1, stiffness is positive, and intrinsic-channel noise dominates, whereas if M_c is 1, the two noise components in the stimulus domain exactly match at X₀, and K_ch(X₀) = 0.

To test the noise-matching hypothesis (M_c ≈ 1), we determined M_c in outer hair cells by using K_s and D resulting from fits to our data (Table 1). The average value obtained for M_c is 0.50 ± 0.16 (n = 11) and shows that the two components of noise at X₀ are indeed comparable, as also is apparent from the examples in Fig. 2d by comparing the data on σ_min(X₀) (4.5 and 5.4 nm) to the horizontal lines representing σ_B (3.0 and 2.9 nm, respectively).

Discussion

Two noise contributions, intrinsic-channel stochastics and gating-spring noise, both affecting the primary process of mechano-electrical transduction in hair cells, were quantified. These contributions amount to on the order of nanometers, when interpreted in terms of equivalent hair-bundle noise (σ_min and σ_B). The optimum accuracy arising from intrinsic-channel stochastics is reached at a deflection, X₀, ≈45 nm positive of the equilibrium position of the hair bundle, as measured under our experimental conditions (Fig. 2d). Extracellular calcium concentrations, such as found in the cochlear endolymph (≈30 μM; ref. 18) have been shown to bring X₀ close to the equilibrium position (19) via a calcium-mediated process called adaptation (14). This process is therefore a likely candidate to maintain optimal detection accuracy under equilibrium conditions.

On the basis of the hypothesis of matched noise variances in the stimulus domain (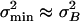), we have demonstrated that the ensemble averaged stiffness of a gating-spring-channel complex of a hair cell becomes negative, a property that has been reported previously in saccular hair cells (20). An unequivocal direct experimental observation in the stimulus domain of the degree of matching of the contributions of mechanical gating-spring noise and intrinsic-channel noise is beyond present experimental possibilities. However, the transducer current noise should reflect both components of the variance in the stimulus domain. We therefore analyzed current noise measurements to investigate whether they were consistent with the inferences made from our analysis on intrinsic-channel noise and the noise-matching hypothesis.

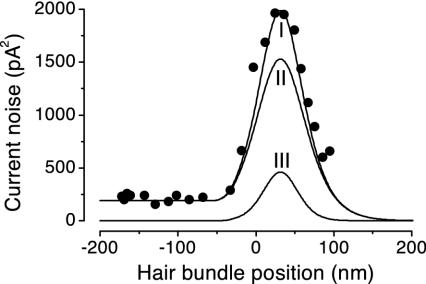
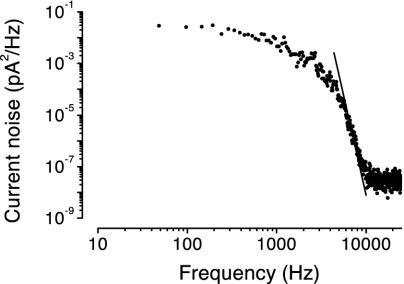
Fig. 3 shows the variance of the current noise measured at different positions of the operational point, X, of the hair bundle. It is compared with noise variances (Fig. 3, solid lines) predicted on the basis of fits of the gating-spring model to the cell's measured p_o(X) and p′_o(X) data (e.g., Fig. 2 b and c). The prediction of the total noise variance (Fig. 3, solid line I), consisting of the sum of the channel stochastics [Fig. 3, solid line II, N_chi²p_o(1 –p_o)] and gating-spring noise [Fig. 3, solid line III, N_chi²(p′_o) σ²_B], adequately follows the shape of the measured noise as a function of hair-bundle position, X. However, the predictions were systematically higher than the actually measured noise with a fixed factor per cell (8.8 ± 3.8; n = 4). The most likely explanation for the lower noise variance measured is that the low-pass filter used cuts off the high-frequency part of the spectrum, producing the predicted shape as a function of X but at a fixed fraction. The steepest roll-off part of the spectrum of the measured noise power (Fig. 4) indeed follows the high-frequency roll-off of the low-pass filter used (Fig. 4, solid line), indicating that the intrinsic cut-off frequency of the transducer channels is beyond the cut-off frequency of the low-pass filter. This result is in line with measured current responses to steps having rise-time constants that were found to be limited by the time constant of the stimulus device used (≈50 μs; data not shown) corresponding to rate-constants of the channel exceeding 3 kHz. Fig. 3 shows that at negative hair-bundle positions (less than approximately –50 nm) the scaled data are in agreement with the differential engaging of the two states, implying a small but constant (≈1%) open probability in that range. The related constant noise in this range excludes the possibility that the noise caused by the gating springs (Fig. 3, solid line III) greatly dominates the stochastic channel noise of the cell (Fig. 3, solid line II). The scaled measurements are consistent with the predicted ratio of the two noise components of M_c (= σ_B/σ_min = 0.55) for this cell. Three other cells were analyzed and gave similar results. Mechanical noise of the whole nonstimulated hair bundle was measured directly and found to be <4 nm². This finding is consistent with the Brownian noise expected from a hair bundle with stiffness on the order of millinewtons per meter (7, 16). In the stimulus domain, whole hair-bundle noise of outer hair cells is therefore approximately an order of magnitude smaller than the average summed noise of the gating springs, 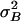(7.6 nm²), and intrinsic-channel noise, 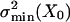(34.2 nm²). Neglecting the whole hair-bundle noise, this combination results in an overall optimal accuracy in the detection of hair-bundle position amounting to 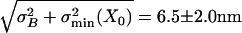(n = 11).

Fig. 3.

Current noise variance as a function of operational position of the hair bundle. Measured data points of this cell were multiplied (fixed factor of 12.3) to fit the summed noise (solid line I) predicted from intrinsic-channel stochastics [solid line II, N_chi²p_o(1 – p_o)] and gating springs [solid line III, 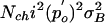] by using the fitted parameters describing the measured open probability and its derivative (e.g., Fig. 2 b and c).

Fig. 4.

Current noise power spectrum. Current noise spectrum obtained at X = 25 nm showing that the high-frequency roll-off equals that of the eight-pole Bessel filter used (solid line, 48 dB/octave), indicating that the intrinsic cut-off frequency of the channels is beyond the cut-off of the filter.

An alternative explanation for the apparent lack in measured noise variance that cannot be completely ruled out on the basis of the present experiments is that the ensemble of N_ch operational channels of a cell may, depending on the stimulus, effectively split up in subensembles with different open probabilities, leading to a lower noise variance than expected from N_ch independently fluctuating channels. Such a noise-reducing mechanism may be effected by a feedback mechanism per channel, for instance, Ca²⁺-binding to the channel (3, 4), and could thereby improve the cell's signal-to-noise ratio. If the observed noise reduction factor (8.8) would completely arise from such a mechanism, σ_min(X₀) would decrease with a factor 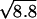, and the best overall accuracy in detecting hair-bundle motion (6.5 nm) would be improved by just a factor of 2 leading to 3.4 nm. Channel interaction, like the cooperative scheme proposed in a recent study (21), is not likely to decrease the channel noise but instead can be expected to increase it. This result can be appreciated from considering the channel noise of N_ch/2 independent pairs, each consisting of two fully cooperating channels, thus effectively having twice the conductance of a single channel.

Other types of hair cells than the outer hair cells considered here might have different bundle mechanics and gating parameters resulting in alternative relative contributions of the individual noise sources. It has been reported that in frog saccular hair cells, bundle noise may dominate (22), and it has been suggested that this property may serve the phenomenon of stochastic resonance (23). Also, the ratio of gating-spring noise and intrinsic-channel noise (σ_B/σ_min = M_c) may vary, possibly related to the specific detection function of a hair cell. Mammalian vestibular hair cells, for instance, may possess spring-channel complexes with an M_c exceeding 1 (15). Results reported on turtle hair-bundle nonlinearity (24) show that M_c in these cells exceeds 0.75, whereas data on fish lateral line hair cells (25) indicate a value of at least 1. A recent report on transduction in frog saccular hair cells (20) translates into an M_c of ≈1.5. The associated collective negative stiffness of the gating springs in those hair cells may even dominate the positive passive stiffness of the hair bundle that results from its pivots in the apical plate and stereociliary side-to-side links, rendering the isolated hair bundle as a whole unstable within a substantial region (≈20 nm). Evidence from outer hair cells so far indicates that their hair bundle's stiffness is dominated by positive passive contributions (15).

What limit is imposed on the threshold of hearing by the noise of the gating apparatus of the transducer channel we considered? First we have to consider whether our results from neonatal hair cells are representative for those in the mature hearing organ. It has recently been demonstrated that transducer channel properties of outer hair cells in rats do not obviously change with the onset of hearing (26). We found the steady-state bundle stiffness of transducing mature hair cells at P19 (3.9 ± 1.2 mN/m; n = 7) to be ≈25% less than the stiffness at P7 (5.1 ± 2.0 mN/m; n = 7). Both values are comparable to previous results from neonatal cochlear cultures (7, 15). The absolute reduction in hair-bundle stiffness exceeds the overall gating-spring contribution (15) and is therefore most likely related to a reduction in the bundle's passive stiffness resulting from structural changes of the bundle or the disappearance of the kinocilium during this stage of development. The latter possibility is in line with a previous report on a relative kinociliary contribution to the whole bundle stiffness of 10–25% (see ref. 27). Both possibilities would not directly affect the mechano-electrical transduction process but could lead to displacement noises scaled up with the same percentage. Also, no signs of spontaneous hair-bundle oscillations were found during the neonatal (P7) or the hearing (P19) stage. We may thus assume that similar transduction-related noise variances as reported in this article apply to the hair cells in the mature hearing organ, including the inner hair cells, which most likely possess very similar transduction characteristics (28).

From our results, we arrive at a displacement variance of (6.5)² nm² contained within a bandwidth of at least 5 kHz. This value corresponds to an upper bound of ≈9 × 10^–2 nm/Hz^½ as a bandwidth-independent inaccuracy per outer hair cell and could even be a factor of ≈3 lower if the hair cells transduce one order of magnitude faster (50 kHz). Whatever the further signal processing mechanisms, the inaccuracy set by the elastic engagement of hair-cell transducer channels cannot be circumvented. Obviously, the threshold in terms of a minimal detectable displacement by a single hair cell may be improved at the expense of the effective bandwidth. Lowering it for instance down to the range of tens to a hundred Hertz would enable a single outer hair cell, if no further noise is added in the filtering process, to match the lowest reported threshold of hearing, which in different organs ranges from fractions of a nanometer to several nanometers (29, 30). This same threshold, however, also may be obtained within a larger bandwidth if more than one hair cell contributes to the signal processing. Therefore, a combination of ensemble averaging across several hair cells and a limited effective bandwidth caused by passive electrical and mechanical filtering, as well as active electro-mechanical feedback, whether mediated by the hair bundle or by prestin (4, 5), would seem to be required to reach the exquisite displacement threshold that some hearing organs possess.