Single-molecule fluorescence resonance energy transfer reveals a dynamic equilibrium between closed and open conformations of syntaxin 1

Abstract

Protein conformational transitions form the molecular basis of many cellular processes, such as signal transduction and membrane traffic. However, in many cases, little is known about their structural dynamics. Here we have used dynamic single-molecule fluorescence to study at high time resolution, conformational transitions of syntaxin 1, a soluble N-ethylmaleimide-sensitive factor attachment protein receptors protein essential for exocytotic membrane fusion. Sets of syntaxin double mutants were randomly labeled with a mix of donor and acceptor dye and their fluorescence resonance energy transfer was measured. For each set, all fluorescence information was recorded simultaneously with high time resolution, providing detailed information on distances and dynamics that were used to create structural models. We found that free syntaxin switches between an inactive closed and an active open configuration with a relaxation time of 0.8 ms, explaining why regulatory proteins are needed to arrest the protein in one conformational state.

Soluble N-ethylmaleimide-sensitive factor attachment protein receptors (SNARE) proteins have emerged as the leading candidates for mediating membrane fusion. They comprise a superfamily of small membrane proteins distinguished by the SNARE motif, a conserved coiled-coil stretch of 60–70 amino acids. SNARE motifs spontaneously assemble into elongated four-helix bundles in which each helix is contributed by a SNARE motif belonging to a separate subclass. Complex formation is assumed to tie membranes together and to initiate membrane fusion along a reaction path involving so-far-unknown conformational transitions (1–3).

In most SNAREs, the SNARE motif is located adjacent to a C-terminal transmembrane domain. Furthermore, many SNAREs contain an independently folded domain at the N terminus that is connected to the SNARE motif by a linker region. In the syntaxin subfamily (also referred to as QaSNAREs), the N-terminal domains consist of antiparallel bundles of three α-helices that are structurally conserved despite high divergence in the primary structure. The N-terminal domains of several syntaxins interact reversibly with the SNARE motif, resulting in two distinct conformations; a closed conformation in which the SNARE motif is blocked (i.e., unable to form SNARE complexes), and an open conformation in which there is presumably no contact between these domains (2). Binding of munc-18, a regulatory protein essential for exocytosis, arrests syntaxin 1 in the closed conformation in which the N-terminal portion of the SNARE motif binds to a groove on the surface of the Habc domain (ref. 4 and Fig. 1). Mutations destabilizing the closed state of syntaxin have profound effects on exocytosis, suggesting that the conformational transition is a key element in the biological function of syntaxin 1 (4, 5).

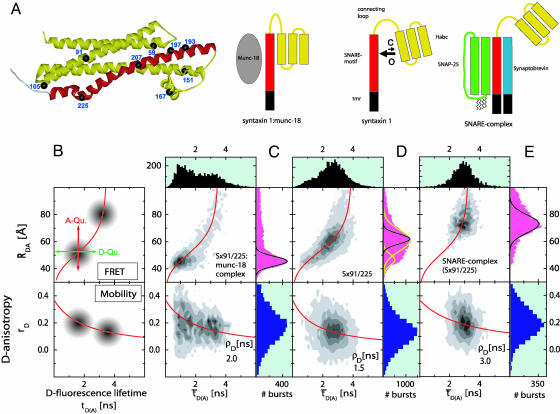
Fig. 1.

(A) Crystal structure of the cytosolic part of syntaxin in complex with munc-18. Munc-18 and the transmembrane region are not shown. Yellow, Habc domain and linker region; red, SNARE motif (H3 domain). Black spheres indicate residues (numbers) substituted by cysteines for dye labeling. (B–E) SmMFD analysis of burst-averaged observables (number of bursts increases from white to black) for different FRET experiments (Upper) with SNARE proteins (sketched below). (B) The sketched new combination of different observables and their specific advantages in precision and accuracy allow to measure absolute interdye distances, R_DA. In particular, the two main sources of errors in distance calculations, individual local quenching effects (Upper) and restricted mobility of the reporter dyes (Lower), can be excluded by SmMFD. First, in 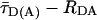plots, local quenching of D and A, respectively (green and red arrows), is distinguished from distance-dependent FRET effects (red sigmoidal curve: Eq. 1 with 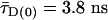, k_FD = 1.6 × 10⁸s^–1, R_0r = 59.1 Å). Second, by connecting two-dimensional plots of 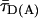vs. the donor anisotropy (r_D) allows one to analyze the dye mobilities (overlaid red curve) not only for the ensemble but also for all substates by computing the average rotation correlation times of the donor (ρ_D) by using the Perrin equation, 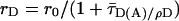, assuming an anisotropy value at time 0 for rhodamine dyes of r₀ = 0.375). (C–E) Following ref. 17, the net fluorescence signal is obtained by correcting the measured green and red signal for the background, B_G = 7.0 kHz, and B_R = 3.5 kHz, spectral crosstalk, α = 0.035, and ratio of green and red detection efficiencies, g_R/g_G = 1.25. B_R also includes direct acceptor excitation, DE = 1.0 kHz. Histograms obtained for Sx 91/225 in complex with munc-18 (C), alone (D), and as part of the ternary SNARE complex (E). Also shown are projections yielding one-dimensional distributions of 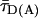(black, Upper), R_DA (magenta, Right Upper), and r_D (dark blue, Right Lower). The measured distance distributions (C–E) are broadened by shot noise and also for certain label positions by structural dynamics. This result is shown in the projected R_DA distributions giving the calculated shot noise described by a Gaussian distribution with SD σ(R_DA) (black lines, equation 5 of ref. 17) and the fit to two Gaussian distributions (yellow lines, D). Molecules containing only the donor dye exhibit apparent distances larger than 85 Å and were excluded from further analysis. For all different syntaxin mutants, environments, and conformations, significant dye interactions can be excluded: (i) no detectable specific local quenching (Upper); and (ii) the average rotation correlation times of the donors, ρ_D, are small for all substates (Lower), which proves the value of the FRET orientation factor, κ², of 2/3.

Conformational transitions such as those discussed above are difficult to observe directly due to limited temporal or spatial resolution. To overcome these limitations, we have recently developed a single-molecule multiparameter fluorescence detection (SmMFD) (6, 7) approach involving the simultaneous collection of all fluorescence parameters (intensity, lifetime, anisotropy in two spectral ranges). SmMFD thus overcomes the pitfalls of fluorescence resonance energy transfer (FRET)-related measurements (8–10) such as incomplete labeling, uncertain assumptions concerning dye anisotropy and quantum yield, and the lack of synchronization in kinetic ensemble studies (11). This single-molecule approach allows for resolving substrates in heterogeneous systems and for studying the trajectories of biomolecular conformational transitions, as well as the structures of associated states in a quantitative manner (12–15). By using this approach, we were able to observe the switch of individual syntaxin molecules between the open and closed state at submillisecond time resolution, and furthermore, to obtain detailed information about the conformational space occupied by the open conformation for which, so far, no structural information is available.

Materials and Methods

Molecules. All proteins were purified as described (ref. 16; for details see Supporting Methods, which is published as supporting information on the PNAS web site). The single cysteine of syntaxin 1a (1–262) in position 145 was replaced by serine, and cysteine double mutants S59C/S91C, S59C/G105C, S59C/D167C, S59C/N207C, S59C/S225C, S91C/D167C, S91C/S193C, S91C/T197C, S91C/N207C, S91C/S225C, G105C/T197C, G105C/N207C, G105C/S225C, T197C/D167C, and S225C/R151C (Fig. 1 A) were generated. For double labeling of syntaxin 1, a mixture of Alexa 488- and Alexa 594-maleimide dyes (Molecular Probes) was used. To obtain an ≈1:1 labeling ratio, an Alexa 488:Alexa 594 ratio of 10:30 was needed. After 3–5 h on ice, the reactions were stopped by 10 mM DTT. The proteins were concentrated and unreacted dye was removed by gel filtration on a PD-10 column, followed by extensive dialysis against PBS (10.4 mM Na₂HPO₄/3.2 mM KH₂PO₄/123 mM NaCl) containing 1 mM DTT and SM-2 Biobeads (Bio-Rad).

In all measurements, PBS buffer was used that was stored on charcoal. For ternary complex formation, a 50-fold molar excess of synaptobrevin and SNAP-25 was applied, and for the munc-18:syntaxin complexes, munc-18 was used in 10-fold molar excess. For multiparameter fluorescence detection (MFD) measurements, the samples were diluted to a final concentration of 10–100 pM. To prevent dissociation of munc-18, the dilution buffer contained 2 μM munc-18 (dialyzed against PBS/charcoal).

MFD. The MFD setup for single-molecule FRET detection described (17) was slightly modified: The active mode-locked argon-ion laser was operated at 477 nm (28 kW/cm²) to minimize direct excitation of Alexa 594. To separate the excitation light from the fluorescence, we applied the dual-band dichroic mirror 488/594PC (AHF Analysentechnik, Tübingen, Germany), and to define the spectral windows for the donor (D) and the acceptor (A), the bandpass filters, IF: HQ535/50 and IF: HQ650/75 (AHF Analysentechnik), were used.

Data Treatment. Individual free diffusing molecules were detected from their fluorescence bursts [translational diffusion time t_TD(syntaxin) = 1.52 ms] as they passed through an open confocal detection volume. For every single burst time, averages for intensity (F), lifetime (t), and anisotropy (r) were determined in two spectral windows below and >595 nm, respectively (18). To reduce the statistical noise in data analysis, only those bursts were considered which (i) contained at least 160 photon counts, and (ii) obeyed the threshold for the mean interphoton time <42.1 μs averaged >30 subsequently registered photon counts (19). Two distinct analyses were performed: First, time average of all photon events in the burst (burstwise analysis) to minimize shot noise; or second, time-resolved study for intraburst kinetics by analyzing smaller time intervals of defined length (time-window analysis) to generate parameter time trajectories. The frequencies of burst- or time-window-averaged parameter values for thousands of bursts or time windows were accumulated in a series of multidimensional histograms with corresponding projections along the different axes for one-dimensional histograms (7, 20).

FRET Analysis. To distinguish FRET from local quenching of each of the two dyes, which implies two degrees of freedom, two independent fluorescence parameters must also be measured (17): the mean fluorescence lifetime (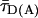) of D in the presence of A and the ratio of fluorescence intensities (F_D/F_A) of D and A converted into the interdye distance (R_DA) through R_DA = R_0r [Φ_FA F_D/F_A]^1/6. Here R_0r is the reduced Förster radius (17), R_0r = 9780·[J(λ)·κ²·n^–4]^(1/6) = 59.1 Å, and Φ_FA = 0.7 is the acceptor fluorescence quantum yield. R_0r is computed by using the D-A spectral overlap integral, J(λ) = 2.29 × 10^–13·M^–1cm³, the refractive index of the medium, n = 1.33, and the geometric factor for the D-A dipole orientation, κ² = 2/3 (assumption verified, see Fig. 1 legend).

Detailed analysis of the fluorescence decay of the subensemble of FRET-active molecules indicated a weak reversible fluorescence quenching of the donor dye, resulting in a double exponential fluorescence decay of an exciplex mechanism (see ref. 21 and Supporting Methods). A linear correction factor of 0.89 was used to rescale all experimentally determined τ_D(A) values to their photo physically meaningful ones represented by species weighted average fluorescence lifetimes .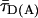

Relating R_DA to 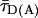in Eq. 1, possible local quenching effects may be recognized as a deviation from the red sigmoidal curve (Fig. 1B).

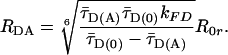[1]

Here, k_FD is the rate constant of fluorescence emission and 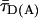is the mean fluorescence lifetime of D in absence of A. Adding a 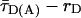histogram, assumptions on the dye mobility can be verified through the donor anisotropy (r_D).

Correlation Analysis. Selecting single-molecule bursts, the autocorrelation (AC_xx) curves of the donor (AC_DD) and the acceptor (AC_AA) are calculated (22) by using the signal in the green (donor) (S_G) or red (acceptor) (S_R) detection channels of DA-labeled molecules exclusively. In a reversible two-state system, the crosscorrelation (CC) curve can be computed as the arithmetic mean of the correlations of the signal in the two spectral detection ranges. For FRET dynamics, the time-dependent portion of the normalized auto- and crosscorrelation functions, normalized by the mean intensity squared 〈S(t)〉², is written as (see Supporting Methods):

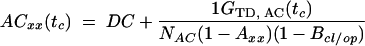[2]

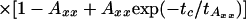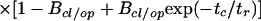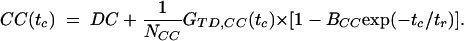In our analysis, the diffusion part, G_TD(t_c), is described by the usual three-dimensional Gaussian term (19), whereby the characteristic observation time (t_TD) is actually determined by cutting the bursts. The amplitude is ideally given by the inverse average number of molecules in the detection volume, (1/N), when correcting for background signal. In the AC functions, bunching terms with the exponential factors A_xx account for fluorophore-specific photochemical processes (e.g., triplet formation). These terms vanish in the crosscorrelation function. The folding-unfolding equilibrium results in variations in the FRET coupling between D and A generating an anticorrelation of the donor and acceptor fluorescence intensities. This results in a unique rise term in the CC curves (anticorrelation) and additional bunching term in AC curves with a common relaxation time, t_r. Ideally, the amplitude of B_CC should equal unity, and B_cl and B_op correspond to the fraction of molecules in the closed and open state, respectively. However, due to reduced fluorescence brightness contrast between the closed and open state, a lower amplitude of B_CC is to be expected and B_cl and B_op are typically considerably smaller than the true fractions.

Structural Analysis. An exhaustive set of protein conformations that are compatible with measured distance distributions was generated by comparing calculated R_DA distributions with the measured ones. To this end, trial conformations were created by a combined Metropolis Monte Carlo/steepest descent approach; from each trial conformation, R_DA distributions were calculated as described in Supporting Methods. Each trial conformation was described by the C^α atom positions of the seven labeled cysteine residues. For improved spatial resolution, the flexible dye linkers were also taken into account. Fluctuations were described through a suitably chosen potential function, V, including soft distance restraints for all 15 residue pairs and a wobbling in a cone model for the dye linkers (Fig. 3 Inset, see Supporting Methods). The resulting average distances between C^α atoms were used to generate atomic models.

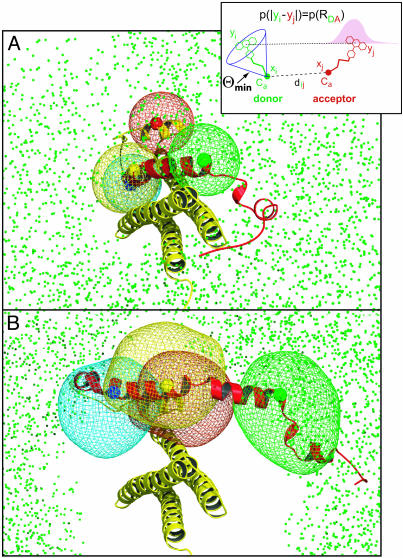
Fig. 3.

(Inset) Protein fluctuations and dye mobilities were described in a generalized wobbling in a cone model. (A and B) X-ray structure of the closed conformation (A) obtained from the munc-18 complex, and a structure model (sketch) of a minimal open conformation (B) that shows the smallest difference to the closed one. For all bimodal R_DA distributions, only the peak assigned to the open conformation was used. The colored spheres show the x-ray C^α positions of residues 167 (red), 197 (blue), 207 (yellow), and 225 (green), respectively. Superimposed is the complete set of FRET-compatible C^α-225 positions (green cloud of dots). The cloud of FRET-compatible C^α positions is not fully localized because (i) the R_DA distributions contain only information on the relative positions of the dyes, but not on the orientation of the C^α/dye linkers, and (ii) the triangulation base in the direction perpendicular to the Habc helix bundle axis is rather short. The contour meshes show the uncertainty of the C^α positions with respect to the Habc domain and enclose 80% of the ensemble.

Results

SmMFD Measurements with Burst-Averaged Analysis. For all experiments, we used neuronal syntaxin 1 as prototype. Syntaxin 1, together with its SNARE partners, synaptobrevin/VAMP and SNAP-25, mediates the exocytotic release of neurotransmitter from neurons. To study the conformational dynamics of syntaxin 1 at the atomic level, 15 double-cysteine substitution mutants of syntaxin 1 (Fig. 1 A) were generated, resulting in a collection of mutant proteins in which the two cysteines were differentially spaced from each other. For FRET measurements, each mutant protein was randomly labeled at the two cysteine residues with a donor (D, Alexa 488) and an acceptor dye (A, Alexa 594), yielding heterogeneous mixtures of all four possible dye combinations. With the SmMFD approach outlined below, FRET-active molecules of the sample were easily identified in the measurement enabling us to exclude DD- and AA-labeled molecules from further analysis.

First, we investigated the conformation of syntaxin by using sets of double-labeled syntaxin variants in complex with munc-18 that arrests syntaxin in the closed conformation. Analyzing photon bursts of free diffusing molecules the histograms were recorded for each mutant (4). As in the representative histogram of Fig. 1C, the R_DA values of all mutants clustered in a sharp peak. Due to limited photon numbers per burst, the R_DA distribution usually has a statistical broadening, referred to as shot noise, σ(R_DA). The widths of the observed R_DA distributions did not exceed σ(R_DA) (Fig. 1C Upper, black lines), which verifies that the molecular ensembles were practically homogenous with the remaining minor subpopulation at longer distances probably contributed by uncomplexed syntaxin (see below). Measured R_DA values agreed with the crystal structure (ref. 4; e.g., series 105/225, 105/207, and 105/197; see Table 1, which is published as supporting information on the PNAS web site), confirming that the ensemble of syntaxin molecules is dominated by the closed conformation when complexed with munc-18.

By using the same set of mutants, the SmMFD analysis was then extended to free syntaxin. In sharp contrast to the results obtained in the presence of munc-18, mutants labeled on both the SNARE motif and the Habc domain exhibited a much broader R_DA distribution than the shot-noise limit (Fig. 1D). Assuming Gaussian distributions, fits through the R_DA distributions suggested the presence of at least two overlapping peaks (yellow curves in Fig. 1D) that reflect different conformations. The peak at the shorter distance (45 Å) consistently overlapped with the corresponding peak of the syntaxin:munc-18 complex (Fig. 1C). We conclude that only a subpopulation of free syntaxin (≈15–30%) is in the closed conformation. The second, larger peak at longer distances suggests that most molecules adopt a conformation in which the Habc domain is separated by larger distances from the SNARE motif, as expected from an open conformation.

Finally, we analyzed the same syntaxin mutants in the ternary SNARE complex with synaptobrevin and SNAP-25. In this complex, syntaxin 1 is unable to form a closed conformation (23, 24). Again, only one peak was observed in the histograms, regardless of which pair of cysteines was labeled. However, mutants labeled on both the SNARE motif and the Habc domain displayed a broad distribution that consistently shifted toward longer distances, partly overlapping with the species carrying only donor dyes (> 80 Å). This result suggests an open conformation with multiple substates in solution. Conversely, mutants with both labeling sites in the Habc domain (Sx59/105 and Sx91/59) exhibited narrow burst distributions that were only slightly broader than the shot noise, regardless of whether syntaxin was free, complexed with munc-18, or in a ternary SNARE complex (see Table 1). This finding proves that the structure of the Habc domain remains stable, with the signal width being influenced only by dye mobility.

Kinetics (Intraburst Analysis and Fluorescence Correlation Spectroscopy). Our data show that free syntaxin exists in a mixture of at least two different conformations, one of which is similar to that observed in the complex with munc-18. This finding could reflect just a static conformational heterogeneity, for which each syntaxin molecule is trapped during the observation time within its specific conformation, or, alternatively, structural dynamics, where the individual molecules interconvert in a dynamic equilibrium. To distinguish between these possibilities, we analyzed the intensity fluctuations within fluorescence bursts from individual molecules.

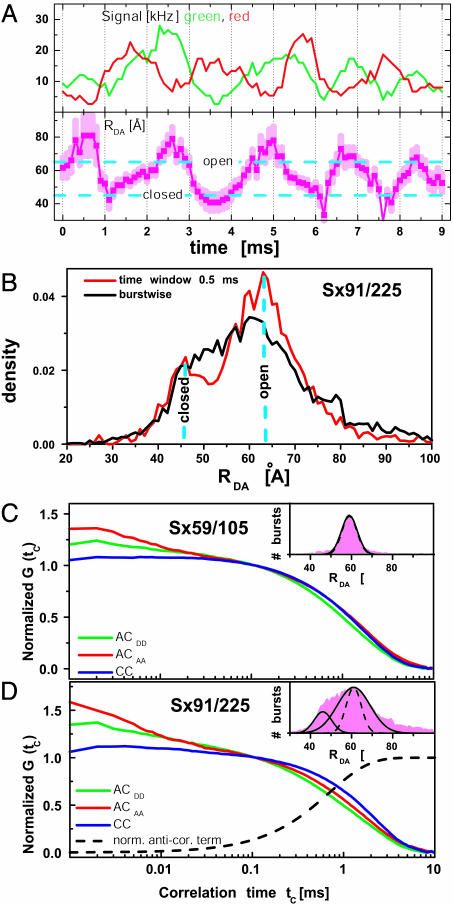
The real-time traces of extra long trajectories (Fig. 2A) directly show an anticorrelated behavior of the green and red intensity signal, indicating submillisecond fluctuations of the calculated R_DA. To obtain precise statistical information on the kinetics of these distance fluctuations, we calculated distances from intensities averaged over increasingly shorter time windows within each burst. Fig. 2B shows the effect of this approach on the R_DA histograms of Sx91/225. When averaging over time windows of 0.5 ms, two short-lived subdistributions, 18 Å apart from each other (cyan, dashed lines), were identified. The width of the short distance distribution (7.2 Å) is similar to that expected from shot noise (7.8 Å), indicating a structurally well defined closed state. In contrast, the width of the long distance distribution is significantly broader (15.4 Å) than the shot-noise limit (8.0 Å), suggesting a structurally more heterogeneous open state. The mean values of the two distance distributions agree well with the observed fluctuations in the trace shown in Fig. 2 A (cyan, dashed lines).

Fig. 2.

(A) Single burst of a Sx91/225 molecule with a passage time of 9 ms. The smoothed (sliding window 0.5 ms) trajectories of the green (donor) and red (acceptor) signal fluctuate in an anticorrelated manner (Upper). The calculated distance trajectory (error bars in light magenta) shows the switching of syntaxin between the closed and open state. The cyan lines are taken from the time-window analysis in B. (B) By analyzing many R_DA trajectories, two distance populations of Sx91/225 can be seen by time-window analysis at 0.5 ms. For comparison, the result of the burstwise analysis is also given. Two visible populations merge into one with decreasing time resolution that reflects the averaging of R_DA. (C and D) AC and CC curves for two mutants Sx59/105 (C) and Sx91/225 (D) with a shot-noise-limited and broad R_DA peak, respectively. In the millisecond time range, the major differences between the AC (green and red) and CC curves (blue) for Sx91/225 are indicative of FRET dynamics. Data analysis was performed in two steps by Eq. 2. First, the specific diffusion parameters G_TD(t_c) of AC_DD, AC_AA, and CC were determined from the mutant Sx59/105 (C). Second, the AA and CC curves of the mutant Sx91/225 with a broad R_DA peak (D) were fitted simultaneously, with t_r as a global parameter, and the other variables as local partially fixed parameters: relaxation time, t_r = 0.8 ± 0.3 ms for the CC rise term (normalized AC term, black dashed line), amplitude B_CC = 0.3 ± 50%, and a characteristic observation time of t_TD = 1.8 ± 0.3 ms. The minor differences in this time range seen for the curves in C are due to chromatic aberration effects.

To further improve the time resolution, intensity correlation analyses (22) of the fluorescence intensity fluctuations of the donor and acceptor dyes were performed. The autocorrelation curves, AC_DD and AC_AA, of each fluorophore (Fig. 2 C and D) show the typical bunching terms due to translational diffusion and photochemical processes. Crosscorrelation curves (CC) are calculated to detect signal fluctuations, which are common to D and A. Considering mutants with DA positions not influenced by conformational dynamics, as evidenced by a sharp R_DA peak (e.g., for the mutant Sx59/105, Fig. 2C), the AC and CC curves were virtually identical in the millisecond time range. In contrast, conformational dynamics, as evidenced by a broad R_DA peak (e.g., for the mutant Sx91/225, Fig. 2D), causes variations in the FRET coupling, resulting in an anticorrelated D and A signal (Fig. 2 A). This finding results in a unique anticorrelation term, lengthening the CC and shortening the AC curves. Indeed, the AC and CC curves differed significantly for all mutants with broad R_DA peaks and not for the others. Analysis by Eq. 2 yielded a relaxation time, t_r = 0.8 ± 0.3 ms for the CC-rise term (black line) and the AC-bunching terms, which is specific for the intramolecular motion (Fig. 2D). The apparent absence of anticorrelation terms at shorter times suggests the absence of any additional major distance changes in the respective syntaxin mutants.

Structural Model. For the structural interpretation of the 15 measured distance distributions, we generated a large set of protein conformations that are compatible with these data. Each conformation was described by the C^α atom positions of the seven labeled cysteine residues. For improved spatial resolution, the flexible dye linkers were also taken into account by using a generalized wobbling in a cone model (ref. 25 and Fig. 3 Inset, see Materials and Methods). From the obtained conformations, R_DA distributions were computed and compared with the measured R_DA distributions.

The FRET data for the closed syntaxin conformation fully agree with the x-ray structure of the syntaxin:munc18 complex (Fig. 3A). For example, the full FRET-compatible set of possible C^α-225 positions in the closed conformation (green dots) form a large “cloud” around the Habc domain, which includes the x-ray position of C^α-225 (green sphere). This finding is also true for the other labeled residues (data not shown). An unequivocal solution for the syntaxin structure could not be derived from the current R_DA set, due to the large flexibility of the linker dyes and the elongated shape of the molecule. However, the data for the R_DA peak of free syntaxin (Fig. 3B), putatively denoted as open, clearly exclude the closed x-ray structure, which is evident from the absence of green dots within the central region. To determine the smallest required conformational transition, we selected from all FRET-compatible conformations the one that is most similar to the closed structure and modeled the open structure sketch shown in Fig. 3B.

The R_DA distributions also contain direct information on the conformational flexibility of the C^α positions. The contour meshes in Fig. 3 show the scatter of the C^α positions in the SNARE motif with respect to the Habc domain. This scatter is due to both (unknown) fluctuations of the dye with respect to the C^α positions and structural fluctuations of the protein. Because similar rotational correlation times (ρ) are found for the donor dyes (Fig. 1 C–E Lower), indicating unchanged dye mobility for both conformations, the increased meshes in Fig. 3B suggest a considerably increased flexibility of the H3 domain and the linker region in the open conformation. Additionally, residue 167 seems to be more flexible in isolated syntaxin than in syntaxin complexed to munc-18. These results corroborate the above finding that the width of the R_DA distributions for the open conformation is, in contrast to the closed conformation, significantly broader than the shot-noise limit.

Discussion

In agreement with previous studies (26), our SmMFD approach shows that the closed conformation of free syntaxin is indistinguishable from that adopted in complex with munc-18. The open conformation, which is more abundant than the closed conformation, contains a flexible H3 domain. Uncomplexed syntaxin 1, thus, does not require additional activation for ternary complex formation, as the H3 domain is already spontaneously released from the Habc domain. The presence of this open state is further supported by the finding that the isolated H3 domain (lacking the Habc part) forms SNARE complexes only 7-fold faster (see Supporting Methods and Fig. 4, which are published as supporting information on the PNAS web site).

At first sight, our data disagree with previous NMR studies (27) suggesting that free syntaxin adopts primarily a closed conformation. However, subsequent analysis of the closed conformation by NMR spectroscopy has revealed substantial broadening of numerous resonances, which is consistent with an equilibrium between open and closed conformations in the submillisecond time scale as observed in our experiments (J. Rizo, personal communication). Furthermore, we cannot exclude, at present, that the equilibrium is shifted toward more closed conformation at high protein concentration.

The SNARE proteins studied in our work are essential components of the membrane fusion machinery in all eukaryotes from yeast to humans. In this context, previous studies (5, 26) indicated that the switch between the open and closed form of syntaxin comprises an important, if not essential, regulatory element in exocytotic membrane fusion. However, it is still difficult to arrive at a molecular model that reconciles the biochemical with the genetic and physiological data. In the test tube, closed syntaxin is not able to enter SNARE complexes, and is thus considered to be inactive. Accordingly, munc-18 is supposed to act as a negative regulator. However, munc-18 and its relatives are as essential as the SNAREs for exocytosis to proceed, suggesting an activating rather than inhibitory role (26). A second difficulty arises from the fact that the ability to adopt a closed conformation is not conserved among syntaxin family members. The closed conformation appears to be most stable in Sso1p, a syntaxin functioning in yeast exocytosis (28). Syntaxin 7, a SNARE involved in the fusion of late endosomes/lysosomes, exhibits properties similar to those of syntaxin 1 (29), whereas in Vam3p, the syntaxin mediating yeast vacuole fusion, no closed conformation can be detected (30). Furthermore, binding of the munc-18 orthologs, Vps45 and Sly1p, to the syntaxins, Tlg2p and Sed5p, respectively, does not require a closed conformation and occurs by a completely different mechanism (31–33).

The presence of dynamic conformational equilibria such as that studied here opens up a fascinating array of questions that can now be experimentally addressed. Whereas it is obvious that interaction with partner proteins are required to arrest syntaxin in one conformational state, it is also possible that the conformational equilibrium is regulated by other mechanisms such as phosphorylation (as recently described for syntaxin 1; ref. 34). However, it is less obvious how the reactivity of the substates is affected by the short half-life of the individual conformations. If reactivity (e.g., functionally relevant interaction with another protein) is not only dependent on the average bulk concentration but also on the lifetime of a conformational substate, even minor changes of the conformational equilibrium may have dramatic consequences for the reactivity of the ensemble and thus on the resulting biological effect. In conclusion, SmMFD provides a tool for quantitative FRET studies of dynamic conformational transitions that promises to be applicable for a wide range of proteins.