SUMMARY
Measuring the rate of consumption of oxygen (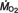 ) during swimming reveals the energetics of fish locomotion. We show that rainbow trout have substantially different oxygen requirements for station holding depending on which hydrodynamic microhabitats they choose to occupy around a cylinder. We used intermittent flow respirometry to show that an energetics hierarchy, whereby certain behaviors are more energetically costly than others, exists both across behaviors at a fixed flow velocity and across speeds for a single behavior. At 3.5 L s–1 (L is total body length) entraining has the lowest
) during swimming reveals the energetics of fish locomotion. We show that rainbow trout have substantially different oxygen requirements for station holding depending on which hydrodynamic microhabitats they choose to occupy around a cylinder. We used intermittent flow respirometry to show that an energetics hierarchy, whereby certain behaviors are more energetically costly than others, exists both across behaviors at a fixed flow velocity and across speeds for a single behavior. At 3.5 L s–1 (L is total body length) entraining has the lowest 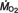 , followed by Kármán gaiting, bow waking and then free stream swimming. As flow speed increases the costs associated with a particular behavior around the cylinder changes in unexpected ways compared with free stream swimming. At times,
, followed by Kármán gaiting, bow waking and then free stream swimming. As flow speed increases the costs associated with a particular behavior around the cylinder changes in unexpected ways compared with free stream swimming. At times, 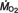 actually decreases as flow velocity increases. Entraining demands the least oxygen at 1.8 L s–1 and 3.5 L s–1, whereas bow waking requires the least oxygen at 5.0 L s–1. Consequently, a behavior at one speed may have a similar cost to another behavior at another speed. We directly confirm that fish Kármán gaiting in a vortex street gain an energetic advantage from vortices beyond the benefit of swimming in a velocity deficit. We propose that the ability to exploit velocity gradients as well as stabilization costs shape the complex patterns of oxygen consumption for behaviors around cylinders. Measuring
actually decreases as flow velocity increases. Entraining demands the least oxygen at 1.8 L s–1 and 3.5 L s–1, whereas bow waking requires the least oxygen at 5.0 L s–1. Consequently, a behavior at one speed may have a similar cost to another behavior at another speed. We directly confirm that fish Kármán gaiting in a vortex street gain an energetic advantage from vortices beyond the benefit of swimming in a velocity deficit. We propose that the ability to exploit velocity gradients as well as stabilization costs shape the complex patterns of oxygen consumption for behaviors around cylinders. Measuring 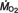 for station holding in turbulent flows advances our attempts to develop ecologically relevant approaches to evaluating fish swimming performance.
for station holding in turbulent flows advances our attempts to develop ecologically relevant approaches to evaluating fish swimming performance.
KEY WORDS: fish swimming, turbulence, energetics, oxygen consumption, respirometry, Kármán gaiting, entraining, bow waking
INTRODUCTION
Measuring the consumption of oxygen during locomotion is a direct and non-invasive way to determine the physiological cost of performing work on the external environment. To swim, fish must generate thrust force sufficient to overcome form and skin friction drag forces (Vogel, 1994). In order to meet increasing physical demands with speed, propulsive force must also increase with swimming speed. Consequently, oxygen consumption increases because of the recruitment of more muscle fibers that are faster and metabolically more costly (Kendall et al., 2007; Roberts et al., 1998; Webb, 1971). Changes in oxygen consumption with swimming speed have been well documented for over 40 years (Beamish, 1978; Brett, 1964; Claireaux et al., 2006; Korsmeyer et al., 2002; Lee et al., 2003a), but these investigations have been limited to uniform (i.e. free stream) flow. We still have very little understanding of how turbulence influences swimming costs with increasing flow, despite an increasing number of studies that demonstrate the ubiquity of turbulence and the important effects it can have on swimming performance (Fausch and Northcote, 1992; Heggenes, 1988; Pavlov et al., 2000; Shirvell and Dungey, 1983).
Fishes swimming in turbulence have been shown to both increase and decrease their energetic demands, depending on the specific conditions of the hydrodynamic environment (Cook and Coughlin, 2010; Enders, 2003; Liao, 2007; Tritico and Cotel, 2010). Studies from both laboratory and field demonstrate that altered flows created by bluff bodies in moving water can be exploited by fishes to enhance swimming performance (Beal et al., 2006; Breder, 1965; Hinch and Rand, 2000; Liao et al., 2003b; Streitlien and Triantafyllou, 1996). In particular, flow past a cylinder creates hydrodynamic microhabitats that are attractive to fish and that do not exist in free stream flow (Liao, 2007; Sutterlin and Waddy, 1975; Webb, 1998). On the upstream side of a cylinder a high-pressure bow wake develops whereby the flow velocity is reduced relative to the free stream (Blevins, 1990; Liao et al., 2003a). Immediately downstream and to both sides of the cylinder, a steep velocity gradient is established by the formation of a suction zone and the adjacent free stream flow (Zdravkovich, 1997). Several cylinder diameters downstream of the cylinder a drag wake develops in the form of a vortex street. Fish alter their swimming kinematics when positioned in these regions (Liao et al., 2003a; Przybilla et al., 2010; Webb, 1998), and if the turbulence is of the appropriate intensity, orientation and scale (J. R. W. Lacey, V. S. Neary, J.C.L., E. C. Enders and H. M. Tritico, unpublished observations), fish show a relative decrease in red axial muscle activity (Liao, 2004; Liao et al., 2003a). Given the availability of similar habitats in the field, several factors might influence the decision to choose one region over another, such as competition, food availability and predator evasion (Fausch, 1984; Fausch and White, 1981; Orth, 1987). But before these factors can be evaluated for their impact on individual fitness, one important question remains to be addressed. What are the energetic costs associated with each of these cylinder-exploiting behaviors?
Swimming performance is commonly measured using critical swimming speed (Ucrit), which is determined using increasing velocity trials to induce fatigue (Brett, 1964). Ucrit is determined under free stream flow conditions, where fish consume oxygen to power sequential contractions of their axial muscles to swim through the water (Liao, 2004; Webb, 1971). Station holding in turbulence represents a departure from the hydrodynamics of swimming in free stream flow, one that is based on exploiting environmental velocity gradients rather than generating thrust from an actively undulating body. Since our work evaluates performance under turbulent conditions to better approximate natural environments, we chose to measure oxygen consumption rate to reveal the cost of swimming in specific regions of turbulence. Fishes that are able to exploit turbulence may show drastically different swimming performance values than the traditional limits set by Ucrit for free stream swimming (Hinch and Rand, 2000; Lee et al., 2003b; Liao et al., 2003b).
In this study we used intermittent flow respirometry to compare oxygen consumption in rainbow trout swimming in different hydrodynamic regions around a stationary cylinder at three flow speeds. We test the hypothesis that oxygen consumption by rainbow trout holding station around a cylinder increases with flow velocity. In addition, we test the hypothesis that rainbow trout in a vortex street consume less oxygen than when swimming at a free stream velocity that approximates the velocity deficit behind the cylinder (Liao et al., 2003a).
MATERIALS AND METHODS
Animals
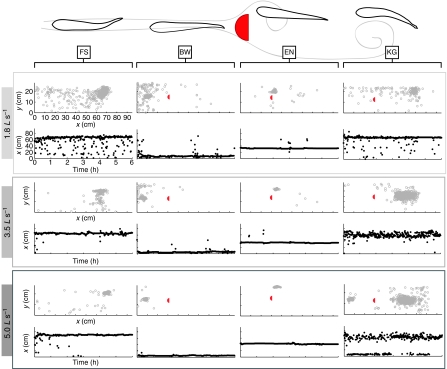
Rainbow trout, Oncorhynchus mykiss Walbaum, were obtained from the Chattahoochee Forest National Fish Hatchery in Suches, Georgia, USA. Fish were held in a 473 liter circular freshwater tank held at 15±1°C (DS-4-TXV Delta Star Chiller, Aqua Logic Inc, San Diego CA, USA) on a 12 h:12 h light:dark cycle and fed commercial trout pellets daily. Total body length (L) was 19.6±0.7 cm and average mass was 107±3.7 g (mean ± s.e.m.). Five rainbow trout were used in the experiments comparing four behaviors (Fig. 2): (1) free stream swimming (FS), (2) bow waking (BW), (3) entraining (EN) and (4) Kármán gaiting (KG) at one speed (3.5 L s–1). Three trout performed FS, BW and EN behaviors at all three speeds (1.8, 3.5 and 5.0 L s–1) providing the opportunity to conduct speed comparisons across multiple behaviors.
Fig. 2.
Illustration of four behaviors: free stream swimming (FS), bow waking (BW), entraining (EN) and Kármán gaiting (KG). Each column contains paired graphs showing the x–y position of the head in the respirometer (top, gray circles) and the downstream position of the head over time (bottom, black dots). For all behaviors except Kármán gaiting, the spatial range of fish distribution contracts as flow velocity increases. Fish swimming in the free stream at 1.8 L s–1 periodically explored the respirometer throughout the experiment but preferred the back corner that is furthest away from the observers. As flow velocity increased, fish spent less time exploring and restricted their positions to smaller areas. This trend was even more striking during bow waking and entraining in the presence of a cylinder. Fish only Kármán gaited continuously at 3.5 L s–1, did not Kármán gait at 1.8 L s–1 and did so part of the time at 5.0 L s–1. Note that at 5.0 L s–1 Kármán gaiting fish are often impinged on the downstream baffle (i.e. downstream of the 80 cm mark) or burst upstream to bow wake. Data shown are from one representative individual. The red semicircle indicates the position of the D-section cylinder.
Experimental procedures
Rainbow trout were removed from their holding tanks and anesthetized in a holding container with 0.0654 g l–1 tricaine methanesulfonate (MS-222; Argent Chemical Laboratories, Redmond, Washington, USA) and pH buffered with potassium hydroxide (Sigma, St Louis, Missouri, USA). After fish became unresponsive to tactile stimuli they were removed to be weighed and measured. Fish were then transferred into a container of fresh water until they righted themselves and began swimming. They were then placed into the unsealed flume respirometer (Fig. 1) maintained at 15±1°C and allowed to recover overnight at low flow (∼1 L s–1). The respirometer was sealed the next morning before the start of the experiment. All trout were starved for 24 h before each experiment.
Fig. 1.

(A) Schematic of experimental setup. Fish were sealed in a flume respirometer in which a cylinder could be mounted. (B) A video camera pointed at a 45 deg front-surface mirror provided a ventral view of the position of the fish during each experiment. (C) Image of the flume respirometer illustrating the position of the oxygen probe (black arrowhead) and the drilled ports for cylinder placement (white arrowheads). The flume was submerged in an ambient temperature water bath (white dot) that is maintained at 100% oxygen saturation, which served as the source to flush the flume between experimental trials (see text). (D) Lateral view of the working section of the flume. Scale bar, 20 cm.
A 175 liter recirculating flow tank respirometer (Loligo Systems, Tjele, Denmark) was custom designed to be able to hold a 5 cm diameter, D-section cylinder in a sealed working section (25×26×87 cm; height × width × length). A digital camcorder (DCR-TRV38, Sony Corp., San Diego, California, USA), which was aimed at a 45 deg front-surface mirror placed below the flow tank, recorded the position of the trout relative to the cylinder.
The rate of oxygen consumption ( ; sampled every second) and video data (head position, sampled every minute) were recorded for rainbow trout swimming at three flow speeds during all four behaviors. To test whether Kármán gaiting trout at 3.5 L s–1 obtained an energetic benefit from cylinder vortices above what is predicted by the velocity deficit (Liao et al., 2003a), we swam trout at the equivalent free stream flow of 1.8 L s–1. Flow speeds in the flume respirometer were calibrated with a Höntzsch HFA flow probe (Waiblingen, Germany). Oxygen measurements were made with a D901 miniature galvanic dissolved oxygen probe (Qubit Systems, Kingston, ON, Canada).
; sampled every second) and video data (head position, sampled every minute) were recorded for rainbow trout swimming at three flow speeds during all four behaviors. To test whether Kármán gaiting trout at 3.5 L s–1 obtained an energetic benefit from cylinder vortices above what is predicted by the velocity deficit (Liao et al., 2003a), we swam trout at the equivalent free stream flow of 1.8 L s–1. Flow speeds in the flume respirometer were calibrated with a Höntzsch HFA flow probe (Waiblingen, Germany). Oxygen measurements were made with a D901 miniature galvanic dissolved oxygen probe (Qubit Systems, Kingston, ON, Canada).
Intermittent flow respirometry
Respirometry studies favor relatively large fish in a small volume of water to quickly measure changes in oxygen consumption. Biomechanical studies favor small fish in a large flume to avoid solid-blocking and wall effects (Bell and Terhune, 1970). This study represents a compromise between the two criteria. We empirically determined the minimum experimental time period required to be able to detect changes in oxygen consumption for relatively small rainbow trout. We adopted the method of intermittent flow respirometry, which combines the benefits of closed and flow-through respirometry to provide a constant oxygen level and no accumulation of metabolites associated with longer trials (Steffensen, 1989). Briefly, the automated measuring procedure consists of three phases: a measuring, a flushing and a waiting period. In the measuring period, the fish respiration rate is calculated from the decline in oxygen. During the flushing period, oxygenated water is pumped into the respirometer from the ambient water bath to bring it back up to 100% oxygen saturation (Fig. 1C). A waiting period is then initiated to account for the lag in system response in a non-linear oxygen curve. This method allowed us to make many continuous measurements without handling and stressing the fish between trials. Solid blocking effects were minimal, given that the maximum cross-sectional area of any individual was less than 2% of the cross-sectional area of the respirometer.
Once sealed in the respirometer, fish adopted one of several regions to hold station around the cylinder. We found that if a fish established position in one region for several minutes, it then displayed a high fidelity to that location and typically stayed in place for hours unless disturbed. To obtain data for all behaviors, we found it useful to apply visual cues (e.g. black strips of paper on the outside of the flume) to encourage fish to change positions around the cylinder between experiments. Once fish adopted a new position around the cylinder, they were allowed at least 15 min to rest before a new experiment began. Although we could make fish change positions, we could not control which position they would choose. Each experiment lasted 6 h and consisted of three consecutive 2-h recording loops in which oxygen level was sampled every second. These three trials were then averaged to obtain the final  for each speed-by-behavior experiment.
for each speed-by-behavior experiment.
At the end each 6-h experiment, the fish was removed and bacterial oxygen consumption was recorded to determine the contribution of background respiration. This value was subsequently subtracted from fish  . In all cases bacterial oxygen consumption levels were negligible (<1% that of the fish). Head position was calculated to evaluate how well the
. In all cases bacterial oxygen consumption levels were negligible (<1% that of the fish). Head position was calculated to evaluate how well the  represented a single station holding behavior. Only experiments where fish adopted a single behavior for more than 80% of the time were included in our analyses. Experiments in which individuals adopted a number of cylinder positions for substantial time periods were not analyzed for this study, as the resulting
represented a single station holding behavior. Only experiments where fish adopted a single behavior for more than 80% of the time were included in our analyses. Experiments in which individuals adopted a number of cylinder positions for substantial time periods were not analyzed for this study, as the resulting  values would be difficult to interpret.
values would be difficult to interpret.
Statistical tests
To analyze behaviors in the presence of the cylinder across flow speeds a three-way, mixed model analysis of variance (ANOVA) was performed with  as the random effect and speed, behavior and individual as the fixed effects (Table 1). Note that fish would only Kármán gait long enough to measure
as the random effect and speed, behavior and individual as the fixed effects (Table 1). Note that fish would only Kármán gait long enough to measure  at one speed (3.5 L s–1), therefore this behavior was excluded from the analysis. A Bonferroni–Dunn post hoc test was conducted to determine whether there were significant differences among swimming speeds and behaviors (α=0.05). The F-value for the fixed effect of behavior and speed was calculated as the mean square of the behavioral (fixed) effect divided by the two-way interaction term of the random (individual) effect and the fixed effect.
at one speed (3.5 L s–1), therefore this behavior was excluded from the analysis. A Bonferroni–Dunn post hoc test was conducted to determine whether there were significant differences among swimming speeds and behaviors (α=0.05). The F-value for the fixed effect of behavior and speed was calculated as the mean square of the behavioral (fixed) effect divided by the two-way interaction term of the random (individual) effect and the fixed effect.
Table 1.
Summary of F-tests for significance of effects in a three-way mixed model ANOVA with 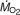 as the dependent variable
as the dependent variable
A two-way, mixed model ANOVA was subsequently performed for  values for the Kármán gait plus all other behaviors at one speed (3.5 L s–1). A Bonferroni–Dunn post hoc test was conducted to determine whether there were significant differences among behaviors and individuals (α=0.05). All values are reported as means ± s.e.m. Statistical tests were performed in Systat 13 (Systat Software Inc., Chicago, IL, USA) and MATLAB vR2009b for the PC (MathWorks, Natick, MA, USA).
values for the Kármán gait plus all other behaviors at one speed (3.5 L s–1). A Bonferroni–Dunn post hoc test was conducted to determine whether there were significant differences among behaviors and individuals (α=0.05). All values are reported as means ± s.e.m. Statistical tests were performed in Systat 13 (Systat Software Inc., Chicago, IL, USA) and MATLAB vR2009b for the PC (MathWorks, Natick, MA, USA).
RESULTS
Behavior
Fish in our analyses were most attracted to the cylinder at intermediate (3.5 L s–1) and high (5.0 L s–1) flows (Fig. 2). Fish explored the flume throughout an experiment, especially at 1.8 L s–1. As flow velocity increased, fish held station in specific locations around the cylinder.
Fish Kármán gaited for long, uninterrupted periods of time at 3.5 L s–1. In contrast, fish did not Kármán gait continuously at 1.8 L s–1 or 5.0 L s–1. At high flow, fish impinged on the downstream baffle or surged upstream to swim in the bow wake in front of the cylinder.
Effects of speed on 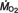 during bow waking and entraining
during bow waking and entraining
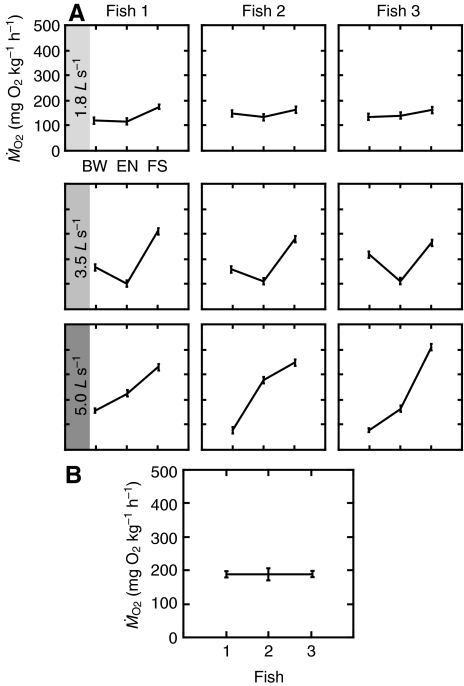
At 1.8 L s–1and 3.5 L s–1,  for all speed-by-behavior treatments was remarkably consistent across individuals, whereas at the highest speed there was larger individual variation in
for all speed-by-behavior treatments was remarkably consistent across individuals, whereas at the highest speed there was larger individual variation in  during bow waking and entraining (Fig. 3A). Overall, the effect of individual on
during bow waking and entraining (Fig. 3A). Overall, the effect of individual on  was not significant (Fig. 3B).
was not significant (Fig. 3B).
Fig. 3.
(A) Patterns of oxygen consumption differ across speed, but remain consistent across individuals. Individual variation in the rate of oxygen consumption (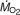 ) was less at 1.8 L s–1 and 3.5 L s–1, but higher at 5.0 L s–1. This observation may be partially attributed to lower fidelity to a cylinder region at lower flow, which results in a homogenization of
) was less at 1.8 L s–1 and 3.5 L s–1, but higher at 5.0 L s–1. This observation may be partially attributed to lower fidelity to a cylinder region at lower flow, which results in a homogenization of 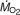 values. (B)
values. (B) 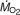 patterns were not dominated by any one individual as there is no significant individual effect on
patterns were not dominated by any one individual as there is no significant individual effect on 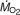 value. BW, bow waking; EN, entraining; FS, free stream swimming. Values are means ± s.e.m.
value. BW, bow waking; EN, entraining; FS, free stream swimming. Values are means ± s.e.m.
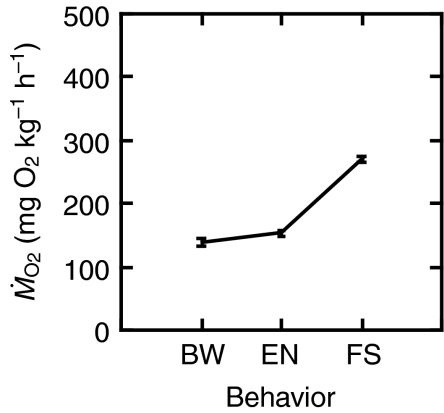
When  values for all speeds within a behavior were averaged, bow waking required the least amount of oxygen (Fig. 4). When
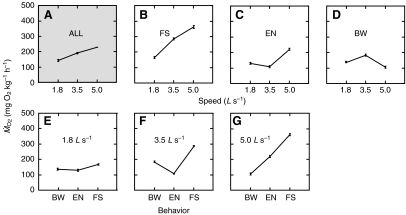
values for all speeds within a behavior were averaged, bow waking required the least amount of oxygen (Fig. 4). When  values for behaviors were pooled within a speed, there was an expected increase in oxygen consumption as speed increased (Fig. 5A).
values for behaviors were pooled within a speed, there was an expected increase in oxygen consumption as speed increased (Fig. 5A).  for each speed within a behavior was analyzed to reveal that rainbow trout holding station in the presence of a cylinder did not show a simple relationship of increased oxygen consumption with flow speed, as in free stream swimming (Fig. 5B). At times, oxygen consumption decreased as velocity increased for entraining and bow waking. Entraining exhibited a minimum
for each speed within a behavior was analyzed to reveal that rainbow trout holding station in the presence of a cylinder did not show a simple relationship of increased oxygen consumption with flow speed, as in free stream swimming (Fig. 5B). At times, oxygen consumption decreased as velocity increased for entraining and bow waking. Entraining exhibited a minimum  value at 3.5 L s–1 (Fig. 5C), with the highest
value at 3.5 L s–1 (Fig. 5C), with the highest  value at the 5.0 L s–1. For bow waking, the opposite was true; the minimum
value at the 5.0 L s–1. For bow waking, the opposite was true; the minimum  occurred at the 5.0 L s–1, whereas the maximum
occurred at the 5.0 L s–1, whereas the maximum  occurred at 3.5 L s–1 (Fig. 5D).
occurred at 3.5 L s–1 (Fig. 5D).
Fig. 4.
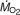 for bow waking (BW), entraining (EN) and free stream swimming (FS), with all speeds averaged. If fish could only perform one behavior at all speeds, bow waking is the most energetically favorable around a cylinder. Values are means ± s.e.m.
for bow waking (BW), entraining (EN) and free stream swimming (FS), with all speeds averaged. If fish could only perform one behavior at all speeds, bow waking is the most energetically favorable around a cylinder. Values are means ± s.e.m.
Fig. 5.
(A) Oxygen consumption increases with flow speed when all behaviors are pooled. When the contribution of each behavior to this trend is individually examined, diverse patterns emerge. (B) Fish swimming in the free stream (FS) consume more oxygen as flow speed increases. (C,D) 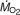 during entraining (EN) and bow waking (BW) varies non-linearly as flow speed increases. Entraining requires the least amount of oxygen at 3.5 L s–1, whereas bow waking requires the least amount of oxygen at 5.0 L s–1. (E–G) The same data re-plotted reveal the least energetically costly behavior at each speed. (E) At 1.8 L s–1, entraining (EN) requires the least oxygen consumption of all behaviors, followed closely by bow waking (BW) and then free stream swimming (FS). (F) At 3.5 L s–1, bow waking uses 64% of the oxygen required to swim in the free stream. Entraining is the most energetically favorable behavior, using less than a half (38%) of the oxygen requirement of free stream swimming. At the highest flow of 5.0 L s–1 (G), bow waking fish consume less than a third (29%) of the oxygen required by fish swimming in the free stream. All behaviors are significantly different from each other at P<0.05, with the exception of bow waking and entraining at 1.8 L s–1 and entraining and bow waking at 3.5 L s–1 and 5.0 L s–1, respectively. Data are averaged from three trials for each speed × behavior treatment (N=3 individuals). Values are means ± s.e.m.
during entraining (EN) and bow waking (BW) varies non-linearly as flow speed increases. Entraining requires the least amount of oxygen at 3.5 L s–1, whereas bow waking requires the least amount of oxygen at 5.0 L s–1. (E–G) The same data re-plotted reveal the least energetically costly behavior at each speed. (E) At 1.8 L s–1, entraining (EN) requires the least oxygen consumption of all behaviors, followed closely by bow waking (BW) and then free stream swimming (FS). (F) At 3.5 L s–1, bow waking uses 64% of the oxygen required to swim in the free stream. Entraining is the most energetically favorable behavior, using less than a half (38%) of the oxygen requirement of free stream swimming. At the highest flow of 5.0 L s–1 (G), bow waking fish consume less than a third (29%) of the oxygen required by fish swimming in the free stream. All behaviors are significantly different from each other at P<0.05, with the exception of bow waking and entraining at 1.8 L s–1 and entraining and bow waking at 3.5 L s–1 and 5.0 L s–1, respectively. Data are averaged from three trials for each speed × behavior treatment (N=3 individuals). Values are means ± s.e.m.
Oxygen consumption across behaviors at a given speed
Fig. 5E shows that at 1.8 L s–1 entraining was the most energetically favorable behavior in the presence of the cylinder (129.9±2.8 mg O2 kg–1 h–1), followed very closely by bow waking (135.2±2.8 mg O2 kg–1 h–1). Entraining required 79% of the oxygen consumed during free stream swimming (165.4±2.8 mg O2 kg–1 h–1; N=3 fish) at the same speed, compared with 82% for bow waking.
At 3.5 L s–1, entraining (Fig. 5F) was again the most energetically favorable behavior (108.6±2.8 mg O2 kg–1 h–1). Bow waking was the next most energetically favorable behavior (181.2± 2.8 mg O2 kg–1 h–1). Unlike at 1.8 L s–1, entraining and bow waking showed substantial energy savings compared with the cost of swimming in free stream flow (283.0±2.8 mg O2 kg–1 h–1). Specifically, entraining involved 38% of the cost of swimming in the free stream, and bow waking involved 64%.
At 5.0 L s–1, bow waking (Fig. 5G) was the most energetically favorable behavior (103.8±2.8 mg O2 kg–1 h–1), followed by entraining (220.3±2.8 mg O2 kg–1 h–1). Bow waking involved only 29% of the free stream swimming costs (362.8±2.8 mg O2 kg–1 h–1) compared with 61% in entraining fish.
We could only measure  reliably for Kármán gaiting fish at 3.5 L s–1, so we performed a separate analysis with a larger sample size for all behaviors at this speed. Analysis of five individuals for which we had complete data sets revealed that the oxygen requirement for Kármán gaiting (136.8±4.0 mg O2 kg–1 h–1) was higher than for entraining but lower than for bow waking (Fig. 6). Kármán gaiting involved 47% the cost of swimming in the free stream at 3.5 L s–1 (289.8±4.3 mg O2 kg–1 h–1). Kármán gaiting fish also used 79% as much oxygen as fish swimming in the free stream at 1.8 L s–1 (172.2±4.5 mg O2 kg–1 h–1), which is the equivalent reduced velocity behind the cylinder (Liao et al., 2003a). Therefore, by exploiting vortices Kármán gaiting fish used significantly less oxygen (P<0.05) than predicted if they were only benefiting from swimming in the reduced velocity of the cylinder wake.
reliably for Kármán gaiting fish at 3.5 L s–1, so we performed a separate analysis with a larger sample size for all behaviors at this speed. Analysis of five individuals for which we had complete data sets revealed that the oxygen requirement for Kármán gaiting (136.8±4.0 mg O2 kg–1 h–1) was higher than for entraining but lower than for bow waking (Fig. 6). Kármán gaiting involved 47% the cost of swimming in the free stream at 3.5 L s–1 (289.8±4.3 mg O2 kg–1 h–1). Kármán gaiting fish also used 79% as much oxygen as fish swimming in the free stream at 1.8 L s–1 (172.2±4.5 mg O2 kg–1 h–1), which is the equivalent reduced velocity behind the cylinder (Liao et al., 2003a). Therefore, by exploiting vortices Kármán gaiting fish used significantly less oxygen (P<0.05) than predicted if they were only benefiting from swimming in the reduced velocity of the cylinder wake.
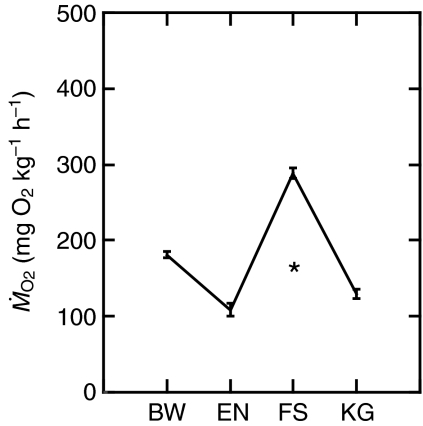
Fig. 6.
Statistical comparison of 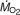 between Kármán gaiting (KG) and other behaviors at 3.5 L s–1. Kármán gaiting requires significantly less oxygen than swimming in the free stream (FS; 47%) and bow waking (BW; 73%), but requires more oxygen than entraining (EN; 116%). Kármán gaiting fish use less oxygen (79%) compared with fish swimming in the free stream at 1.8 L s–1 (asterisk). This supports the original hypothesis that Kármán gaiting fish save energy by exploiting vortices in addition to receiving the benefit of the velocity deficit behind a cylinder (Liao et al., 2003a). Note that the average
between Kármán gaiting (KG) and other behaviors at 3.5 L s–1. Kármán gaiting requires significantly less oxygen than swimming in the free stream (FS; 47%) and bow waking (BW; 73%), but requires more oxygen than entraining (EN; 116%). Kármán gaiting fish use less oxygen (79%) compared with fish swimming in the free stream at 1.8 L s–1 (asterisk). This supports the original hypothesis that Kármán gaiting fish save energy by exploiting vortices in addition to receiving the benefit of the velocity deficit behind a cylinder (Liao et al., 2003a). Note that the average 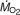 for FS at 1.8 L s–1 was not included in the original ANOVA analysis (see text). Values are means ± s.e.m.
for FS at 1.8 L s–1 was not included in the original ANOVA analysis (see text). Values are means ± s.e.m.
All  values across speed-by-behavior treatments were significantly different from each other at α=0.05, with a few exceptions.
values across speed-by-behavior treatments were significantly different from each other at α=0.05, with a few exceptions.  values for bow waking and entraining at 1.8 L s–1 were not significantly different. Entraining at 3.5 L s–1 was not significantly different from bow waking at 5.0 L s–1.
values for bow waking and entraining at 1.8 L s–1 were not significantly different. Entraining at 3.5 L s–1 was not significantly different from bow waking at 5.0 L s–1.
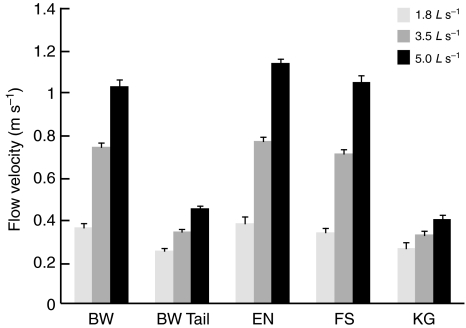
For each of the four behaviors, absolute flow velocity for each of the three prescribed flow treatments was measured in the region where the head was positioned (Fig. 7). In addition, the flow velocity was measured in the region of the tail where bow waking fish were positioned. For bow waking fish, the average flow velocity experienced by the tail was substantially lower than experienced by the head, and this difference increased with prescribed flow speed (44–70%). Bow wake, entraining and free stream fish experience similar flow velocities at the head at each speed (1.8 L s–1: 0.36±0.02 m s–1, 0.38±0.03 m s–1, 0.34±0.02 m s–1; 3.5 L s–1: 0.74±0.02 m s–1, 0.77±0.02 m s–1, 0.71±0.01 m s–1; and 5.0 L s–1: 1.03±0.03 m s–1, 1.14±0.02 m s–1, 1.05±0.03 m s–1, respectively). Kármán gaiting fish experience much lower average flow velocities (1.8 L s–1: 0.26±0.03 m s–1; 3.5 L s–1: 0.34±0.05 m s–1; 5.0 L s–1: 0.40±0.02 m s–1). Bow wake tail velocity (1.8 L s–1: 0.25±0.01 m s–1; 3.5 L s–1: 0.34±0.01 m s–1; 5.0 L s–1: 0.45±0.01 m s–1) is similar to Kármán gait head velocity in magnitude, but differs in nature in that bow wake flows are more stable than the oscillatory flow of a Kármán vortex street.
Fig. 7.
Bar graph showing the average flow velocity at the head of the fish for each of the four behaviors at each of the three prescribed speeds. The average velocity at the tail was also measured for bow waking fish (BWTail). Note that the only reliable 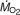 measurement for Kármán gaiting occurred at 3.5 L s–1 (see text), but results from all three prescribed speeds are included.
measurement for Kármán gaiting occurred at 3.5 L s–1 (see text), but results from all three prescribed speeds are included.
DISCUSSION
General behavior
Rainbow trout restrict station holding to smaller areas as flow speed increases (Fig. 2), perhaps to avoid more costly exploratory or turning behaviors (Enders and Herrmann, 2003) or to simplify sensory processing in an unfamiliar environment (Liao, 2006). Kármán gaiting fish are the exception and show a decrease in site fidelity, most probably because of the difficulty in holding station in increased turbulence at the highest flow speed.
We conducted experiments in a relatively large respirometer to avoid wall effects, but as a result could not control the percentage of time that a fish would occupy a cylinder region. This introduces the possibility that  is inflated at low flow because fish show less fidelity to a given region. For example, at 1.8 L s–1 fish spend 83% of the time bow waking (and therefore the rest of the time performing other behaviors), whereas at 5.0 L s–1 fish spend 99% of the time bow waking (Fig. 2). However,
is inflated at low flow because fish show less fidelity to a given region. For example, at 1.8 L s–1 fish spend 83% of the time bow waking (and therefore the rest of the time performing other behaviors), whereas at 5.0 L s–1 fish spend 99% of the time bow waking (Fig. 2). However,  measurements of behaviors other than the intended behavior compose a small percentage of the total activity budget and would not be responsible for the similarity of
measurements of behaviors other than the intended behavior compose a small percentage of the total activity budget and would not be responsible for the similarity of  at 1.8 L s–1 (Fig. 3A). It is more probable that
at 1.8 L s–1 (Fig. 3A). It is more probable that  similarity at low flow is due to stability costs given that trimming forces (i.e. the passive production of lift and drag due to flow interactions with the body and fins) play a smaller role at low flow velocity (Webb, 2002).
similarity at low flow is due to stability costs given that trimming forces (i.e. the passive production of lift and drag due to flow interactions with the body and fins) play a smaller role at low flow velocity (Webb, 2002).
Energetics hierarchy around a cylinder
To summarize our findings, we introduce the concept of an ‘energetics hierarchy’. We define an energetics hierarchy as an arrangement of oxygen consumption values in which either certain behaviors are more energetically costly than others at the same prescribed flow speed, or in which certain flow speeds are more energetically costly than others for a particular behavior.
The behavioral repertoire of a rainbow trout allows it to adapt to its hydrodynamic environment as flow velocity increases. Otherwise, trout would always swim in the bow wake to the exclusion of other behaviors, because it requires, on average, the least amount of oxygen across speeds (Fig. 4). When  is examined for each speed and behavior, values do not simply increase with flow velocity. This is an unexpected result given studies that document the general increase in oxygen consumption with swimming speed (Fig. 5A) (Beamish, 1978; Brett, 1964; Claireaux et al., 2006; Enders, 2003). For behaviors around cylinders, more complex
is examined for each speed and behavior, values do not simply increase with flow velocity. This is an unexpected result given studies that document the general increase in oxygen consumption with swimming speed (Fig. 5A) (Beamish, 1978; Brett, 1964; Claireaux et al., 2006; Enders, 2003). For behaviors around cylinders, more complex  patterns emerge with speed, with minimum
patterns emerge with speed, with minimum  for entraining and swimming in the bow wake occurring at two separate flow velocities (Fig. 5C,D). Therefore, our data allow us to reject our first hypothesis and conclude that station-holding behaviors can become less energetically demanding as flow speed increases. Our results expand the growing pool of knowledge on the interactions between fish and turbulence, by demonstrating that
for entraining and swimming in the bow wake occurring at two separate flow velocities (Fig. 5C,D). Therefore, our data allow us to reject our first hypothesis and conclude that station-holding behaviors can become less energetically demanding as flow speed increases. Our results expand the growing pool of knowledge on the interactions between fish and turbulence, by demonstrating that  can decrease in the presence of periodic or otherwise predictable flows. Indeed, our results are consistent with a similar study in which entraining and Kármán gaiting rainbow trout showed decreased oxygen consumption relative to free stream swimming (Cook and Coughlin, 2010). However, our measurements of
can decrease in the presence of periodic or otherwise predictable flows. Indeed, our results are consistent with a similar study in which entraining and Kármán gaiting rainbow trout showed decreased oxygen consumption relative to free stream swimming (Cook and Coughlin, 2010). However, our measurements of  were substantially lower than those of Cook and Coughlin (Cook and Coughlin, 2010). One possible explanation for this discrepancy may lie in the variation in interpreting each behavior. Although kinematics have been quantified in detail (Liao et al., 2003a), behaviors are commonly identified on the basis of the position of a fish relative to the cylinder, because different regions around a cylinder have unique hydrodynamic conditions that produce characteristic swimming kinematics. However, kinematics (and therefore oxygen consumption) can change substantially given differences in cylinder shape (i.e. round cylinder vs D-cylinder) or even slight differences in station holding position relative to the cylinder. For example, in fig. 2 of Cook and Coughlin, kinematics for entraining trout show substantially larger lateral displacements (attributed to vortex interactions) compared with the trout in fig. 5A of Liao (Cook and Coughlin, 2010; Liao, 2006). Periodic body oscillations have not been previously observed for entraining fishes (Liao, 2006; Przybilla et al., 2010; Webb, 1998) and would probably increase the oxygen demand. In addition, Cook and Coughlin show Kármán gaiting trout holding position within the suction region, which is approximately two cylinder diameters immediately downstream of the cylinder (Zdravkovich, 1997; Cook and Coughlin, 2010). In our experience, fish located in the suction region actively recruit their pectoral fins to stabilize themselves and avoid contacting the cylinder. The differences in kinematics and fish position probably account for the higher
were substantially lower than those of Cook and Coughlin (Cook and Coughlin, 2010). One possible explanation for this discrepancy may lie in the variation in interpreting each behavior. Although kinematics have been quantified in detail (Liao et al., 2003a), behaviors are commonly identified on the basis of the position of a fish relative to the cylinder, because different regions around a cylinder have unique hydrodynamic conditions that produce characteristic swimming kinematics. However, kinematics (and therefore oxygen consumption) can change substantially given differences in cylinder shape (i.e. round cylinder vs D-cylinder) or even slight differences in station holding position relative to the cylinder. For example, in fig. 2 of Cook and Coughlin, kinematics for entraining trout show substantially larger lateral displacements (attributed to vortex interactions) compared with the trout in fig. 5A of Liao (Cook and Coughlin, 2010; Liao, 2006). Periodic body oscillations have not been previously observed for entraining fishes (Liao, 2006; Przybilla et al., 2010; Webb, 1998) and would probably increase the oxygen demand. In addition, Cook and Coughlin show Kármán gaiting trout holding position within the suction region, which is approximately two cylinder diameters immediately downstream of the cylinder (Zdravkovich, 1997; Cook and Coughlin, 2010). In our experience, fish located in the suction region actively recruit their pectoral fins to stabilize themselves and avoid contacting the cylinder. The differences in kinematics and fish position probably account for the higher  values in Cook and Coughlin's study (Cook and Coughlin, 2010). Nevertheless, taken together these studies clearly discourage using Ucrit to evaluate swimming performance in situations where fish commonly encounter turbulent flows.
values in Cook and Coughlin's study (Cook and Coughlin, 2010). Nevertheless, taken together these studies clearly discourage using Ucrit to evaluate swimming performance in situations where fish commonly encounter turbulent flows.
The interplay between lift-based propulsion and stability costs is probably what determines the complex patterns of oxygen consumption for station-holding behaviors across speeds. Once speed-dependent vortical flows become sufficiently developed, fish can exploit them with great energetic savings. For example, entraining and bow waking fish only exhibit intermediate  values at the lowest flow, suggesting that stability costs may be higher at low flow. As velocity increases, fluid interactions with body and fin posture can generate trimming forces to increase thrust passively and lower stability costs (Webb, 2002; Webb, 2004). In addition, lower
values at the lowest flow, suggesting that stability costs may be higher at low flow. As velocity increases, fluid interactions with body and fin posture can generate trimming forces to increase thrust passively and lower stability costs (Webb, 2002; Webb, 2004). In addition, lower  values for entraining and bow waking arise from the transition from branchial pumping to ram ventilation, which has been shown to decrease oxygen consumption by 10% in rainbow trout (Steffensen, 1985).
values for entraining and bow waking arise from the transition from branchial pumping to ram ventilation, which has been shown to decrease oxygen consumption by 10% in rainbow trout (Steffensen, 1985).
Instances when  increases with speed suggest that turbulence contributes to the cost of station holding at low and high flows. This interpretation is supported by the fact that
increases with speed suggest that turbulence contributes to the cost of station holding at low and high flows. This interpretation is supported by the fact that  during entraining is most costly at low and high flow, and experiences a minimum at 3.5 L s–1 (Fig. 5C). At 1.8 L s–1 the flow is insufficient to fully develop the suction region downstream of the cylinder (Liao, 2004; Zdravkovich, 1997). We suspect that the costs associated with stabilizing movements make it suboptimal for trout to entrain under these circumstances. Fins serve as important control surfaces (Drucker and Lauder, 2003; Liao, 2006; Arnold et al., 1991), and trout use them frequently to maintain stability at low flow (Webb, 1998). We hypothesize that 3.5 L s–1 is the optimum speed to release entraining fish from stabilization costs associated with low flow, while not requiring larger, more costly corrective movements of the fins and body to negotiate turbulence at 5.0 L s–1. We speculate that optimum flow with regards to stability is also seen for bow waking fish, which consume more oxygen as flow speed increases up to a point after which the
during entraining is most costly at low and high flow, and experiences a minimum at 3.5 L s–1 (Fig. 5C). At 1.8 L s–1 the flow is insufficient to fully develop the suction region downstream of the cylinder (Liao, 2004; Zdravkovich, 1997). We suspect that the costs associated with stabilizing movements make it suboptimal for trout to entrain under these circumstances. Fins serve as important control surfaces (Drucker and Lauder, 2003; Liao, 2006; Arnold et al., 1991), and trout use them frequently to maintain stability at low flow (Webb, 1998). We hypothesize that 3.5 L s–1 is the optimum speed to release entraining fish from stabilization costs associated with low flow, while not requiring larger, more costly corrective movements of the fins and body to negotiate turbulence at 5.0 L s–1. We speculate that optimum flow with regards to stability is also seen for bow waking fish, which consume more oxygen as flow speed increases up to a point after which the  drops (Fig. 5D). We feel certain that future studies subjecting rainbow trout to a wider flow velocity range would identify increased
drops (Fig. 5D). We feel certain that future studies subjecting rainbow trout to a wider flow velocity range would identify increased  during bow waking as turbulence increases with speed. Thus, along with body length playing a key role in exploiting vortices (Liao et al., 2003a), the selective abilities of fin posture and activity to stabilize the body probably dictate the patterns of
during bow waking as turbulence increases with speed. Thus, along with body length playing a key role in exploiting vortices (Liao et al., 2003a), the selective abilities of fin posture and activity to stabilize the body probably dictate the patterns of  across speed.
across speed.
Average flow velocity experienced by the head of the fish is not a predictor of oxygen consumption. The  pattern across the three prescribed flow speeds (Fig. 5B–D) did not mirror the increasing pattern of absolute flow velocity for each region (Fig. 7). For example, of all behaviors associated with non-oscillatory flow, the absolute flow velocity was lowest for fish swimming in the free stream at 3.5 L s–1, but showed the highest
pattern across the three prescribed flow speeds (Fig. 5B–D) did not mirror the increasing pattern of absolute flow velocity for each region (Fig. 7). For example, of all behaviors associated with non-oscillatory flow, the absolute flow velocity was lowest for fish swimming in the free stream at 3.5 L s–1, but showed the highest  of all behaviors. Kármán gaiting fish experienced by far the lowest flow velocities of all behaviors at 3.5 L s–1, and yet still consumed more oxygen than entraining fish (Fig. 6). Therefore, our results suggest that for behaviors associated with stable flows (i.e. entraining and bow waking) around cylinders, velocity gradients dominate the mechanism for holding station and establish a lower
of all behaviors. Kármán gaiting fish experienced by far the lowest flow velocities of all behaviors at 3.5 L s–1, and yet still consumed more oxygen than entraining fish (Fig. 6). Therefore, our results suggest that for behaviors associated with stable flows (i.e. entraining and bow waking) around cylinders, velocity gradients dominate the mechanism for holding station and establish a lower  than would be expected based on average flow velocity. Low average velocity may contribute to low
than would be expected based on average flow velocity. Low average velocity may contribute to low  for Kármán gaiting, but exploiting periodic shedding of vortices provides a distinct additional benefit. It is interesting that even with this benefit Kármán gaiting fish still consume more oxygen than entraining fish. This is possibly the reason for the observation that fish will opt to entrain behind a cylinder over Kármán gait under certain situations (Liao, 2006; Przybilla et al., 2010; Webb, 1998).
for Kármán gaiting, but exploiting periodic shedding of vortices provides a distinct additional benefit. It is interesting that even with this benefit Kármán gaiting fish still consume more oxygen than entraining fish. This is possibly the reason for the observation that fish will opt to entrain behind a cylinder over Kármán gait under certain situations (Liao, 2006; Przybilla et al., 2010; Webb, 1998).
Do trout always prioritize saving energy?
Why do fish not choose the most energetically favorable behavior at each flow speed? Fish motivated by saving energy should entrain at low and middle speeds, but then switch to bow waking at the highest flow speed. Yet we did not always observe this behavioral pattern. One explanation is that the greater risk of instability (and thus more energy expended from forfeiting and recovering position) during a behavior may be just as important in selecting a position near a cylinder as is the actual cost of the behavior. For example, fish may bow wake at 3.5 L s–1 even though it requires more oxygen than entraining because the risk of forfeiting position from flow instabilities is less than the control costs associated with recovering position after being displaced from entraining (Liao, 2006). This lower-risk, lower-payoff strategy is consistent with our observations of rainbow trout choosing bow waking and Kármán gaiting over entraining at an intermediate flow speed. Another possibility is that the cost of station holding is outweighed by the benefits of maintaining an optimal state of sensory awareness. Bow waking offers the least-obstructed visual field of all behaviors near cylinders as well as the simplest hydrodynamic environment for the lateral line, and thus would seem to enable the most rapid response to avoiding predators or capturing prey. Still, fish that Kármán gait at 5.0 L s–1 will explore the bow wake (which is less energetically demanding) but return to Kármán gaiting (Fig. 2), indicating that other important factors have not been described that influence the decision to hold station in specific cylinder regions. By documenting an energetics hierarchy across behavior and flow speed, we provide a baseline to be able to evaluate the importance of these factors in the future.
Kinematics correlates to oxygen consumption
Trout swimming in different hydrodynamic regions around a cylinder can show kinematic similarities to one another. Bow waking kinematics at low to middle speeds resemble free stream swimming (Liao et al., 2003a). This reflects the observation that average flow velocity experienced by the head is the same as that for fish swimming in the free stream flow. Periodic tail beating is present, but tail beat amplitudes are greatly reduced given that the tail is located in the stagnation point just upstream of the cylinder and experiences little to no flow (i.e. the flow can be less than 50% of that at the head; Fig. 7). At 5.0 L s–1 the stagnation region develops to enable bow waking fish to stop regular tail beat motions and adopt a straight body posture with few corrective movements from the pectoral fins. A rainbow trout positioned in the bow wake experiences a high-pressure region by the tail that allows it to balance in front of the cylinder. Another interpretation is that a suction force is drawing the head upstream, in so much as the steep upstream–downstream velocity gradient within the distance of one body length establishes differential pressure across the body. We think this mechanism allows trout to drastically reduce their energetic requirements for holding station in fast flows, as seen in cetaceans riding in the bow wake of ships (Bose and Lien, 1990; Fejer, 1960; Scholander, 1959). A previous paper suggested, based on kinematics, that rainbow trout swimming in the bow wake may use less energy than swimming in the free stream or Kármán gaiting (Liao et al., 2003a). This idea is now directly supported by our experimental measurements; metabolic costs of bow waking are lowest at 5.0 L s–1 when the velocity difference between the head and the tail are the greatest. Therefore, even though the flow velocity experienced by the head may be similar between fish swimming in the bow wake and free stream, bow waking is much less costly to perform. In this regard, traditional point source measurements of flow velocity in the field (Fausch and White, 1981; Heggenes, 1988) can fail to reveal hydrodynamic habitats that have important energetic consequences to station-holding trout.
Entraining fish exploit a steep velocity gradient established by the formation of a suction region immediately downstream of the cylinder (Zdravkovich, 1997). By tilting the body relative to the axis of free stream flow (Liao, 2006), trout use their body as an airfoil to hold station. This mechanism was recently elucidated by modeling the hydrodynamic forces that are exerted on a rainbow trout during entraining (Przybilla et al., 2010). These investigations revealed that for trout to hold station, an outward (i.e. away from the cylinder) lift force is counteracted by an inward suction force, drawing the body towards the cylinder. When these forces become imbalanced, corrective motions of the pectoral and caudal fins are initiated. We found that the cost of these corrective movements increased dramatically at the highest flow speed, and, like Przybilla et al., attribute this cost to an increase in turbulence (Przybilla et al., 2010). During the course of our experiments we found that bow waking behavior at 5.0 L s–1 is very similar to entraining at 3.5 L s–1 in that they both involve a remarkable absence of body undulation. Not surprisingly, the  for these two treatments is almost identical (Fig. 5F,G). This observation suggests that it is possible that relative swimming costs may be more accurately predicted from kinematics than from average flow velocity under certain circumstances (Fig.7). The importance of developing a non-invasive method for measuring the energetics of swimming in natural populations (Farrell et al., 2003) makes this a potentially useful tool for estimating swimming costs in the field.
for these two treatments is almost identical (Fig. 5F,G). This observation suggests that it is possible that relative swimming costs may be more accurately predicted from kinematics than from average flow velocity under certain circumstances (Fig.7). The importance of developing a non-invasive method for measuring the energetics of swimming in natural populations (Farrell et al., 2003) makes this a potentially useful tool for estimating swimming costs in the field.
Behavior reveals an energetics minimum
The observation that rainbow trout will Kármán gait continuously for several hours at 3.5 L s–1 (but not at 1.8 L s–1 or 5.0 L s–1) in itself may indicate that the minimum cost for this behavior occurs at intermediate flow speeds. Rainbow trout do not Kármán gait at 1.8 L s–1 because the vortex street has not developed sufficiently (Liao, 2004) (Fig. 2). At higher Reynolds numbers, flow instabilities are magnified, where merging and pairing between initial shear layer vortices give rise to secondary structures that contribute to irregular vortex shedding frequencies and amplitudes (Blevins, 1990; Williamson, 1996). We hypothesize that rainbow trout cannot sustain Kármán gaiting at 5.0 L s–1 because the turbulent vortex street exceeds the stabilization abilities of the fish, as evidenced by their ability to Kármán gait at 3.5 L s–1 but their frequent impingement on the downstream baffle at 5.0 L s–1. We fully expect that if fish were forced to Kármán gait continuously for several hours at 1.8 L s–1 and 5.0 L s–1 then  values would be higher than those observed at 3.5 L s–1.
values would be higher than those observed at 3.5 L s–1.
Do rainbow trout benefit from vortices in addition to a velocity deficit behind a cylinder?
Of all the cylinder station-holding behaviors we know the most about the Kármán gait, from previous work (Liao et al., 2003a; Liao et al., 2003b). Kármán gaiting consists of sensing and moving with the lateral component of the sinusoidal flow established by vortices shed downstream from a cylinder (Liao, 2006). Although Kármán gaiting has a large passive component (Beal et al., 2006), rainbow trout do activate anterior red axial muscle (Liao, 2004). Detailed kinematic measurements suggest that fish use their body to establish thrust by interacting with oncoming vortices in addition to experiencing the benefits of being positioned in a reduced velocity zone (Liao et al., 2003a; Streitlien and Triantafyllou, 1996). Although electromyograms reveal fewer regions of red muscle activity compared with free stream swimming at a comparable reduced velocity, we cannot directly evaluate the magnitude of muscle activity between the two behaviors because of differences in resistance across electrodes (Loeb and Gans, 1986). A more consistent measurement of activity is needed to better understand the cost of Kármán gaiting. Although the oscillating body of a Kármán gaiting trout might be expected to require more corrective body and fin motions than when holding station in stable flows (i.e. bow waking and entraining), our  results suggest that this cost is offset by the benefits of vortex exploitation (Fig. 6). The cost of Kármán gaiting at 3.5 L s–1 should be similar to free stream swimming at a flow equal to the cylinder's velocity defect (i.e. 1.8 L s–1), but it is in fact lower. Our
results suggest that this cost is offset by the benefits of vortex exploitation (Fig. 6). The cost of Kármán gaiting at 3.5 L s–1 should be similar to free stream swimming at a flow equal to the cylinder's velocity defect (i.e. 1.8 L s–1), but it is in fact lower. Our  data provide the first direct evidence that Kármán gaiting rainbow trout save energy beyond that of simply swimming in the velocity deficit behind a cylinder, confirming that trout are able to recapture energy from cylinder vortices. Based on previous work, this indicates that it is more costly to activate red muscle in the posterior half of the body during free stream swimming than it is to activate anterior red muscle activity during Kármán gaiting (Liao, 2004). This is significant because although exploiting self-generated vortices has been championed as a mechanism to increase efficiency of locomotion in a diversity of animals (Dickinson et al., 1999; Drucker and Lauder, 2005; Triantafyllou et al., 2000) these data illustrate how exploiting environmentally generated vortices can lead to potentially larger savings in the cost of locomotion.
data provide the first direct evidence that Kármán gaiting rainbow trout save energy beyond that of simply swimming in the velocity deficit behind a cylinder, confirming that trout are able to recapture energy from cylinder vortices. Based on previous work, this indicates that it is more costly to activate red muscle in the posterior half of the body during free stream swimming than it is to activate anterior red muscle activity during Kármán gaiting (Liao, 2004). This is significant because although exploiting self-generated vortices has been championed as a mechanism to increase efficiency of locomotion in a diversity of animals (Dickinson et al., 1999; Drucker and Lauder, 2005; Triantafyllou et al., 2000) these data illustrate how exploiting environmentally generated vortices can lead to potentially larger savings in the cost of locomotion.
Ecological implications
The mechanisms of how fish relate to structures in flow have important ecological implications. For example, body length is the most important factor in determining the optimal cylinder diameter that enables Kármán gaiting (Liao et al., 2003a), implying that fish in nature best exploit habitats that scale to their body size. Matching vortex orientation to the axis of undulation is crucial to enable station holding (Tritico and Cotel, 2010; Webb, 1998), suggesting that fish can only use flows created from structures of certain shapes and orientations in the water column. This study expands our understanding by looking at the energetics of station holding in multiple regions around a cylinder. A key finding is that even within a single size class and flow velocity, rainbow trout have substantially different oxygen demands depending on which locations they choose to hold station around a cylinder. Similarly, different behaviors can have similar costs when surveyed across different flow velocities. For example, entraining at 3.5 L s–1 requires the same amount of oxygen as bow waking at 5.0 L s–1. Bow waking  at 3.5 L s–1 is very similar to free stream
at 3.5 L s–1 is very similar to free stream  at 1.8 L s–1. What this means in a river with temporal and spatial velocity gradients is that fish can maintain constant energy expenditure by choosing different hydrodynamic microhabitats. Likewise, a Kármán gaiting fish located in turbulent flows off a main stream channel may actually be using less energy than a fish swimming in slower free stream flow near the bank. Therefore, without more detailed measurements of fish position, kinematics and local hydraulics, we cannot assume fish holding station in faster flow are exerting more energy than fish in slower flow. The interactions between flow speed and behavior exposes a complexity previously undocumented when considering the effects of turbulence on fish distributions and swimming costs in the natural environment.
at 1.8 L s–1. What this means in a river with temporal and spatial velocity gradients is that fish can maintain constant energy expenditure by choosing different hydrodynamic microhabitats. Likewise, a Kármán gaiting fish located in turbulent flows off a main stream channel may actually be using less energy than a fish swimming in slower free stream flow near the bank. Therefore, without more detailed measurements of fish position, kinematics and local hydraulics, we cannot assume fish holding station in faster flow are exerting more energy than fish in slower flow. The interactions between flow speed and behavior exposes a complexity previously undocumented when considering the effects of turbulence on fish distributions and swimming costs in the natural environment.
ACKNOWLEDGEMENTS
We would like to thank Katherine Decesare for fish care and two anonymous referees for valuable comments on the manuscript.
FOOTNOTES
Support was provided by the Whitney Lab for Marine Bioscience and NIH 1RO1DC010809-01 to J.C.L. Deposited in PMC for release after 12 months.
REFERENCES
- Arnold G. P., Webb P. W., Holford B. H. (1991). The role of the pectoral fins in station-holding of Atlantic salmon parr (Salmo Salar L.). J. Exp. Biol. 156, 625-629 [Google Scholar]
- Beal D. N., Hover F. S., Triantafyllou M. S., Liao J. C., Lauder G. V. (2006). Passive propulsion in vortex wakes. J. Fluid Mech. 549, 385-402 [Google Scholar]
- Beamish F. W. H. (1978). Swimming capacity. In Fish Physiology, Vol. 7 (ed. Hoar W. S., Randall D. J.), pp. 101-189 New York: Academic Press; [Google Scholar]
- Bell W. H., Terhune L. D. B. (1970). Water tunnel design for fisheries research. Fish. Res. Board Can. Tech. Rep. 195, 1-69 [Google Scholar]
- Blevins R. D. (1990). Flow Induced Vibration. Malabar, FL: Krieger Publishing Company; [Google Scholar]
- Bose N., Lien J. (1990). Energy absorption from ocean waves: a free ride for cetaceans. Proc. R. Soc. Lond. B Biol. Sci. 240, 591-605 [DOI] [PubMed] [Google Scholar]
- Breder C. M. (1965). Vortices and fish schools. Zoologica 50, 97-114 [Google Scholar]
- Brett J. R. (1964). The respiratory metabolism and swimming performance of young sockeye salmon. J. Fish. Res. Board Can. 21, 1183-1226 [Google Scholar]
- Claireaux G., Couturier C., Groison A. L. (2006). Effect of temperature on maximum swimming speed and cost of transport in juvenile European sea bass (Dicentrarchus labrax). J. Exp. Biol. 209, 3420-3428 [DOI] [PubMed] [Google Scholar]
- Cook C. L., Coughlin D. J. (2010). Rainbow trout Oncorhynchus mykiss consume less energy when swimming near obstructions. J. Fish Biol. 77, 1716-1723 [DOI] [PubMed] [Google Scholar]
- Dickinson M. H., Lehmann F., Sane S. P. (1999). Wing rotation and the aerodynamic basis of insect flight. Science 284, 1954-1960 [DOI] [PubMed] [Google Scholar]
- Drucker E. G., Lauder G. V. (2003). Function of the pectoral fins in rainbow trout: behavioral repertoire and hydrodynamic forces. J. Exp. Biol. 206, 813-826 [DOI] [PubMed] [Google Scholar]
- Drucker E. G., Lauder G. V. (2005). Locomotor function of the dorsal fin in rainbow trout: kinematic patterns and hydrodynamic forces. J. Exp. Biol. 208, 4479-4494 [DOI] [PubMed] [Google Scholar]
- Enders E. C. (2003). The effect of turbulence on the cost of swimming for juvenile Atlantic salmon. Can. J. Fish. Aquat. Sci. 60, 1149-1160 [Google Scholar]
- Enders E. C., Herrmann J. (2003). Energy costs of spontaneous activity in horse mackerel quantified by a computerised imaging analysis. Arch. Fish. Mar. Res. 50, 205-219 [Google Scholar]
- Farrell A. P., Lee C. G., Tierney K., Hodaly A., Clutterham S., Healey M., Hinch S., Lotto A. (2003). Field-based measurements of oxygen uptake and swimming performance with adult Pacific salmon using a mobile respirometer swim tunnel. J. Fish Biol. 62, 64-84 [Google Scholar]
- Fausch K. D. (1984). Profitable stream positions for salmonids: relating specific growth rate to net energy gain. Can. J. Fish. Aquat. Sci. 62, 441-451 [Google Scholar]
- Fausch K. D., Northcote T. G. (1992). Large woody debris and salmonid habitat in a small coastal British-Columbia stream. Can. J. Fish. Aquat. Sci. 49, 682-693 [Google Scholar]
- Fausch K. D., White R. J. (1981). Competition between brook trout (Salvelinus fontinalis) and brown trout (Salmo trutta) for positions in a Michigan stream. Can. J. Fish. Aquat. Sci. 38, 1220-1227 [Google Scholar]
- Fejer A. A. (1960). Porpoises and the bow-riding of ships under way. Nature 188, 700-703 [Google Scholar]
- Heggenes J. (1988). Effects of short-term flow fluctuations on displacement of, and habitat use by, brown trout in a small stream. Trans. Am. Fish. Soc. 117, 336-344 [Google Scholar]
- Hinch S. G., Rand P. S. (2000). Optimal swimming speeds and forward-assisted propulsion: energy-conserving behaviours if upriver-migrating adult salmon. Can. J. Fish. Aquat. Sci. 57, 2470-2478 [Google Scholar]
- Kendall J. L., Lucey K. S., Jones E. A., Wang J. W., Ellerby D. J. (2007). Mechanical and energetic factors underlying gait transitions in bluegill sunfish (Lepomis macrochirus). J. Exp. Biol. 210, 4265-4271 [DOI] [PubMed] [Google Scholar]
- Korsmeyer K. E., Steffensen J. F., Herskin J. (2002). Energetics of median and paired fin swimming, body and caudal fin swimming, and gait transition in parrotfish Scarus schlegeli and triggerfish Rhinecanthus aculeatus. J. Exp. Biol. 205, 1253-1263 [DOI] [PubMed] [Google Scholar]
- Lee C. G., Farrell A. P., Lotto A., Hinch S. G., Healey M. C. (2003a). Excess post-exercise oxygen consumption in adult sockeye (Oncorhynchus nerka) and coho (O. kisutch) salmon following critical speed swimming. J. Exp. Biol. 206, 3253-3260 [DOI] [PubMed] [Google Scholar]
- Lee C. G., Farrell A. P., Lotto A., MacNutt M. J., Hinch S. G., Healey M. C. (2003b). The effect of temperature on swimming performance and oxygen consumption in adult sockeye (Oncorhynchus nerka) and coho (O. kisutch) salmon stocks. J. Exp. Biol. 206, 3239-3251 [DOI] [PubMed] [Google Scholar]
- Liao J. C. (2004). Neuromuscular control of trout swimming in a vortex street: implications for energy economy during the Kármán gait. J. Exp. Biol. 207, 3495-3506 [DOI] [PubMed] [Google Scholar]
- Liao J. C. (2006). The role of the lateral line and vision on body kinematics and hydrodynamic preference of rainbow trout in turbulent flow. J. Exp. Biol. 209, 4077-4090 [DOI] [PubMed] [Google Scholar]
- Liao J. C. (2007). A review of fish swimming mechanics and behaviour in altered flows. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 1973-1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao J. C., Beal D. N., Lauder G. V., Triantafyllou M. S. (2003a). The Kármán gait; novel kinematics of rainbow trout swimming in a vortex street. J. Exp. Biol. 206, 1059-1073 [DOI] [PubMed] [Google Scholar]
- Liao J. C., Beal D. N., Lauder G. V., Triantafyllou M. S. (2003b). Fish exploiting vortices decrease muscle activity. Science 302, 1566-1569 [DOI] [PubMed] [Google Scholar]
- Loeb G. E., Gans C. (1986). Electromyography for Experimentalists. Chicago: University of Chicago Press; [Google Scholar]
- Orth D. J. (1987). Ecological considerations in the development and application of instream flow-habitat models. Regul. Rivers Res. Manage. 1, 171-181 [Google Scholar]
- Pavlov D. S., Lupandin A. I., Skorobogatov M. A. (2000). The effects of flow turbulence on the behavior and distribution of fish. J. Ichthyol. 40, S232-S261 [Google Scholar]
- Przybilla A., Kunze S., Rudert A., Bleckmann H., Brucker C. (2010). Entraining in trout: a behavioural and hydrodynamic analysis. J. Exp. Biol. 213, 2976-2986 [DOI] [PubMed] [Google Scholar]
- Roberts T. J., Kram R., Weyand P. G., Taylor C. R. (1998). Energetics of bipedal running. I. Metabolic cost of generating force. J. Exp. Biol. 201, 2745-2751 [DOI] [PubMed] [Google Scholar]
- Scholander P. F. (1959). Wave-riding dolphins, how do they do it? Science 129, 1085-1087 [DOI] [PubMed] [Google Scholar]
- Shirvell C. S., Dungey R. G. (1983). Microhabitats chosen by brown trout for feeding and spawning in rivers. Trans. Am. Fish. Soc. 112, 355-367 [Google Scholar]
- Steffensen J. F. (1985). The transition between branchial pumping and ram ventilation in fishes: energtic consequences and dependence on water oxygen tension. J. Exp. Biol. 114, 141-150 [Google Scholar]
- Steffensen J. F. (1989). Some errors in respirometry of aquatic breathers: how to avoid and correct them. Fish Physiol. Biochem. 6, 49-55 [DOI] [PubMed] [Google Scholar]
- Streitlien K., Triantafyllou G. S. (1996). Efficient foil propulsion through vortex control. AIAA J. 34, 2315-2319 [Google Scholar]
- Sutterlin A. M., Waddy S. (1975). Possible role of the posterior lateral line in obstacle entrainment by brook trout (Salvelinus fontinalis). J. Fish. Res. Board Can. 32, 2441-2446 [Google Scholar]
- Triantafyllou M. S., Triantafyllou G. S., Yue D. K. P. (2000). Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32, 33-53 [Google Scholar]
- Tritico H. M., Cotel A. J. (2010). The effects of turbulent eddies on the stability and critical swimming speed of creek chub (Semotilus atromaculatus). J. Exp. Biol. 213, 2284-2293 [DOI] [PubMed] [Google Scholar]
- Vogel S. (1994). Life in Moving Fluids: The Physical Biology of Flow. Princeton, NJ: Princeton University Press; [Google Scholar]
- Webb P. W. (1971). The swimming energetics of trout. II. Oxygen consumption and swimming efficiency. J. Exp. Biol. 55, 521-540 [DOI] [PubMed] [Google Scholar]
- Webb P. W. (1998). Entrainment by river chub Nocomis micropogon and smallmouth bass Micropterus dolomieu on cylinders. J. Exp. Biol. 201, 2403-2412 [DOI] [PubMed] [Google Scholar]
- Webb P. W. (2002). Control of posture, depth, and swimming trajectories of fishes. Integr. Comp. Biol. 42, 94-101 [DOI] [PubMed] [Google Scholar]
- Webb P. W. (2004). Response latencies to postural disturbances in three species of teleostean fishes. J. Exp. Biol. 207, 955-961 [DOI] [PubMed] [Google Scholar]
- Webb P. W., Kostecki P. T., Stevens E. D. (1984). The effect of size and swimming speed on the locomotor kinematics of rainbow trout. J. Exp. Biol. 109, 77-95 [Google Scholar]
- Williamson C. H. K. (1996). Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477-539 [Google Scholar]
- Zdravkovich M. M. (1997). Flow Around Circular Cylinders: A Comprehensive Guide Through Flow Phenomena, Experiments, Applications, Mathematical Models, and Computer Simulations. Oxford: Oxford University Press; [Google Scholar]